| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
Для количественного описания явлений сложения (вычитания) частот нужно использовать уравнения Максвелла, которые дают замкнутое описание, если известна связь их правых частей (поляризации, плотности квадрупольных моментов и т. д.) с падающим электромагнитным полем. Эта связь задается материальными уравнениями среды. В простейшем случае немагнитной среды без пространственной дисперсии материальные уравнения имеют вид  :
:

где  тензор линейной восприимчивости.
тензор линейной восприимчивости.
Обычно оптическая нелинейность среды связывается с ангармонизмом колебаний элементарных излучателей (атомов и молекул). Однако поскольку зависимость электрического поля от расстояния до зарядов нелинейна, даже при гармоническом движении зарядов электрическое поле в данной точке наблюдения меняется со временем не гармонически, что означает излучение
на частотах, отличных от частот колебаний зарядов. Речь идет о мультипольном излучении. Ясно, что оно также будет приводить к эффектам нелинейной оптики, часть из которых (например, генерация оптических гармоник) в макроскопическом проявлении не отличается от вызываемых дипольным излучением ангармонически колеблющейся системы зарядов.
Оценим величину таких нелинейностей следующим образом. По аналогии с выражением для поля мультипольного излучения удаленной системы зарядов [9] можно предположить, что в правой части макроскопического волнового уравнения для среды с распределенным мультипольным моментом  должно быть слагаемое
должно быть слагаемое 

где с — скорость света,  — длина волны излучения. Сравнивая эту оценку с волновым уравнением для среды с распределенным дипольным моментом, приходим к выводу, что влияние мультипольного излучения можно свести к эквивалентной пелинейной восприимчивости, определяемой формулами
— длина волны излучения. Сравнивая эту оценку с волновым уравнением для среды с распределенным дипольным моментом, приходим к выводу, что влияние мультипольного излучения можно свести к эквивалентной пелинейной восприимчивости, определяемой формулами

Как видпо,  меньше
меньше  раз. Однако в средах, где из-за запретов по симметрии
раз. Однако в средах, где из-за запретов по симметрии  становится определяющей величиной. Анализ [10] показывает, что в анизотропной среде квадрупольная нелинейность дает по сравнению с дипольным механизмом нелинейности
становится определяющей величиной. Анализ [10] показывает, что в анизотропной среде квадрупольная нелинейность дает по сравнению с дипольным механизмом нелинейности  постоянная решетки) помимо приведенного выше, вклад порядка Таким образом, в анизотропном случае вклад квадрупольного механизма может быть существенен [10, 11]. В волновом уравнении эта часть квадрупольной нелинейности имеет в точности такой же вид, как дипольный механизм типа (1.6). Поскольку нас интересуют среды с большой нелинейностью, то в дальнейшем используется фенологическое описание на основе выражения типа (1.6).
постоянная решетки) помимо приведенного выше, вклад порядка Таким образом, в анизотропном случае вклад квадрупольного механизма может быть существенен [10, 11]. В волновом уравнении эта часть квадрупольной нелинейности имеет в точности такой же вид, как дипольный механизм типа (1.6). Поскольку нас интересуют среды с большой нелинейностью, то в дальнейшем используется фенологическое описание на основе выражения типа (1.6).
Интегрирование в (1.6) по  ограничено сверху величиной
ограничено сверху величиной  или, что то же самое, интегрирование по
или, что то же самое, интегрирование по  ограничено снизу нулем вследствие принципа причинности. Тот факт, что х зависит только от разности
ограничено снизу нулем вследствие принципа причинности. Тот факт, что х зависит только от разности  отражает стационарность среды. Для удобства вычислений интегрирование в (1.6) можно формально распространить на интервал от
отражает стационарность среды. Для удобства вычислений интегрирование в (1.6) можно формально распространить на интервал от  считая
считая  при
при 
Естественным обобщением формулы (1.6) на случай произвольной зависимости  является выражение
является выражение

Здесь тензор  ранга
ранга  нелинейная восприимчивость
нелинейная восприимчивость  порядка, описывающая отклик системы в момент времени
порядка, описывающая отклик системы в момент времени  на совокупность импульсных возбуждений в моменты времени
на совокупность импульсных возбуждений в моменты времени  Поскольку физическая сущность не зависит от того, какому именно импульсу приписывается время
Поскольку физическая сущность не зависит от того, какому именно импульсу приписывается время  то последнее определяется лишь выбором обозначений. Поэтому можно считать, что
то последнее определяется лишь выбором обозначений. Поэтому можно считать, что

где  значения
значения  произвольно пронумерованные, при этом тензорные индексы
произвольно пронумерованные, при этом тензорные индексы  переставлены соответствующим образом. В случае квадратичной нелинейности вся информация
переставлены соответствующим образом. В случае квадратичной нелинейности вся информация  содержится уже в одной половине первого квадрата плоскости
содержится уже в одной половине первого квадрата плоскости  Поэтому удобно перейти от координат
Поэтому удобно перейти от координат  где
где  Тогда для
Тогда для  имеем
имеем 

Аналогично поляризации второго порядка  можно представить в виде
можно представить в виде 

Очевидно, что  ограниченная величина для всех моментов времени. Поскольку напряженность поля принимает конечные значения, сходимость интеграла будет обеспечена, если
ограниченная величина для всех моментов времени. Поскольку напряженность поля принимает конечные значения, сходимость интеграла будет обеспечена, если  достаточно быстро стремится к нулю при больших
достаточно быстро стремится к нулю при больших  т. е. достаточно давно действующие на среду импульсы поля вносят малый вклад в значение поляризации в данный мот мент времени. Конечная память среды обусловлена процессами диссипации.
т. е. достаточно давно действующие на среду импульсы поля вносят малый вклад в значение поляризации в данный мот мент времени. Конечная память среды обусловлена процессами диссипации.
Выражения (1.6) не учитывают пространственной дисперсии, т. е. взаимодействия между поляризациями, наведенными в разных точках среды. Поэтому в случаях, когда такое взаимодействие существенно, например при анализе вынужденного рассеяния Мандельштама — Бриллюэна, необходимо вернуться к вопросу о выборе материального уравнения.
Помимо взаимосвязи между  во временном представлении не менее важный физический смысл и практическое применение имеет соответствующая связь в частотном представлении. Она задается фурье-преобразованием обеих частей формулы (1.9). Нетрудно получить выражения для линейной и квадратичной поляризации:
во временном представлении не менее важный физический смысл и практическое применение имеет соответствующая связь в частотном представлении. Она задается фурье-преобразованием обеих частей формулы (1.9). Нетрудно получить выражения для линейной и квадратичной поляризации:

Здесь прямое и обратное фурье-преобразования величины определяются формулами

Выражение (1.14) получено следующим образом. Фурье-преобразование применено к обеим частям равенства (1.11), затем  выражены через их фурье-образы и использовано равенство
выражены через их фурье-образы и использовано равенство

где  дельта-функция Дирака.
дельта-функция Дирака.
Для нелинейной поляризации  порядка в частотном представлении можно получить аналогичное (1.14) равенство (см. [5]):
порядка в частотном представлении можно получить аналогичное (1.14) равенство (см. [5]):

Соотношение  порядка в частотном представлении выражается
порядка в частотном представлении выражается  -кратным интегралом, в отличие от временного представления, где кратность соответствующего интеграла равна
-кратным интегралом, в отличие от временного представления, где кратность соответствующего интеграла равна  (см. (1.9)). Это обстоятельство дает определенные преимущества при описании нелинейных процессов в частотном представлении, особенно при рассмотрении дискретного спектра частот.
(см. (1.9)). Это обстоятельство дает определенные преимущества при описании нелинейных процессов в частотном представлении, особенно при рассмотрении дискретного спектра частот.
Поскольку  вещественные функции, их фурье-образы удовлетворяют следующим соотношениям:
вещественные функции, их фурье-образы удовлетворяют следующим соотношениям:

Из соотношения (1.10) следуют свойства симметрии в частотном представлении:

где  значения
значения  , произвольно пронумерованные; тензорные индексы в и также переставлены соответствующим образом.
, произвольно пронумерованные; тензорные индексы в и также переставлены соответствующим образом.
Принцип причинности, ограничивающий область интегрирования в выражениях (1.6) и (1.9), приводит к определенным свойствам аналитичности функций  В результате возникают дисперсионные соотношения, которые в линейном случае являются хорошо известными соотношениями Крамерса — Кронига:
В результате возникают дисперсионные соотношения, которые в линейном случае являются хорошо известными соотношениями Крамерса — Кронига:

Для случая квадратичной нелинейности соответствующие соотношения имеют более сложный вид [5, 6, 12]:

В (1.20) и (1.21) интегралы берутся в смысле главного значения.
Вещественная и мнимая части линейной восприимчивости могут быть выражены через показатель преломления и коэффициент поглощения. Поэтому выражение (1.20) определяет частотную зависимость одной из этих констант через частотную
зависимость другой. Такие соотношения полезны для проверки как экспериментальных данных, так и теоретических моделей. Сказанное относится и к нелинейным восприпмчивостям высших порядков.
Поскольку физические процессы в отсутствие диссипации обратимы, отклик среды доляген инвертироваться во времени под воздействием поля с обращенной зависимостью от времени. Отсюда из формул (1.9), (1.18) следует, что в среде без диссипации нелинейная восприимчивость любого порядка чисто действительна

Для дальнейшего полезно выппсать в явном виде значения нелинейной поляризации, возникающие в квадратично-нелинейной среде при распространении в ней двух квазимонохроматических волн с частотами 

Подставляя (1.23) в (1.14), находим комплексные амплитуды возникающей в среде нелинейной поляризации:

Если одна из частот (например,  равна нулю, то равенства (1.24в, г) переходят в одно и описывают зависимость показателя преломления от постоянного электрического поля, т. е. линейный электрооптический эффект
равна нулю, то равенства (1.24в, г) переходят в одно и описывают зависимость показателя преломления от постоянного электрического поля, т. е. линейный электрооптический эффект

Если со  слагаемые электрического поля одного электромагнитного колебания, то формула для эффекта сложения частот (1.24в) не переходит непосредственно в- формулу для генерации второй гармоники (1.246). Для того чтобы получить правильный переход, необходимо сложить вклады
слагаемые электрического поля одного электромагнитного колебания, то формула для эффекта сложения частот (1.24в) не переходит непосредственно в- формулу для генерации второй гармоники (1.246). Для того чтобы получить правильный переход, необходимо сложить вклады
идентичных в этом случае процессов, описываемых формулами (1.246, в):

Сказанное относится и к переходу (при  формул для эффекта вычитания частот в формулы для оптического выпрямления (ДС-эффект):
формул для эффекта вычитания частот в формулы для оптического выпрямления (ДС-эффект):

Выражения (1.24) можно записать в едином виде, вводя нелинейную восприимчивость  определенную равенством
определенную равенством

Обобщая эту формулу на случай произвольной нелинейной поляризации, получим

Установленные выше свойства симметрии  очевидно, переносятся на
очевидно, переносятся на  В частности:
В частности:

т. е. вещественная и мнимая части каждой компоненты являются соответственно четными и нечетными функциями частоты. Кроме того, из (1.19) следует, что в выражении для  можно произвольно менять местами частоты после точки с запятой при одновременной перестановке соответствующих тензорных индексов, например:
можно произвольно менять местами частоты после точки с запятой при одновременной перестановке соответствующих тензорных индексов, например:

Наконец, из (1.22) вытекает, что в средах без диссипации  вещественно
вещественно

Поскольку х связывает между собой компоненты вектора поляризации и  векторов электрического поля, то при пространственных трансформациях (вращениях
векторов электрического поля, то при пространственных трансформациях (вращениях  и инверсии) величина
и инверсии) величина 
преобразуется как тензор  ранга. Поэтому все пространственные свойства симметрии, присущие конкретной среде, непосредственно отражаются на свойствах симметрии
ранга. Поэтому все пространственные свойства симметрии, присущие конкретной среде, непосредственно отражаются на свойствах симметрии  В частности, в средах с центром инверсии нелинейные эффекты четных порядков отсутствуют.
В частности, в средах с центром инверсии нелинейные эффекты четных порядков отсутствуют.
Рассмотрим, следуя [5], еще одно общее свойство симметрии по отношению к пространственно-частотным преобразованиям, которое справедливо в прозрачных средах. Диссипируемая в единице объема мощность определяется формулой

где  означает усреднение по времени большему, чем световой период, но много меньшему, чем характерное время изменения амплитуд спектральных компонент излучения. Тогда в среде без диссипации выражение (1.32) принимает вид
означает усреднение по времени большему, чем световой период, но много меньшему, чем характерное время изменения амплитуд спектральных компонент излучения. Тогда в среде без диссипации выражение (1.32) принимает вид

Рассмотрим процесс, происходящий в среде с квадратичной нелинейностью, в котором участвуют поля только трех частот  связанных соотношением (так называемое трехволновое взаимодействие)
связанных соотношением (так называемое трехволновое взаимодействие)

Тогда для компонент  имеем
имеем

Если учесть, что  вещественно, и должным образом изменить обозначения встречающихся индексов суммирования, то нетрудно получить соотношение
вещественно, и должным образом изменить обозначения встречающихся индексов суммирования, то нетрудно получить соотношение

Поскольку это равенство должно быть справедливым для произвольных значений амплитуд поля, то из него следует

Подстановка (136) в (137) и требование, чтобы соотношение (137) имело место при произвольных значениях  и ем, приводят к соотношениям симметрии
и ем, приводят к соотношениям симметрии

Эти преобразования симметрии обычно называют пространственно-частотными. Если в трехволновом взаимодействии две волны совпадают, то аналогичные рассуждения приводят к соотношению

Если пренебречь дисперсией нелинейной восприимчивости  в области частот
в области частот  то из (1.28) и (138) следуют так называемые соотношения симметрии Клеймана, согласно которым можно переставлять любые тензорные индексы при сохранении порядка частот без изменения значения восприимчивости:
то из (1.28) и (138) следуют так называемые соотношения симметрии Клеймана, согласно которым можно переставлять любые тензорные индексы при сохранении порядка частот без изменения значения восприимчивости:

Для ряда нелинейных кристаллов в области прозрачности соотношения Клеймана выполняются с точностью до нескольких процентов и могут быть полезны для оценки восприимчивостеи по порядку величины
Симметрия (130) тензора  относительно перестановки последних двух индексов позволяет ввести так называемые фойхтовские обозначения, часто используемые в нелинейной оптике:
относительно перестановки последних двух индексов позволяет ввести так называемые фойхтовские обозначения, часто используемые в нелинейной оптике:

Здесь индекс  меняется от 1 до 3 при
меняется от 1 до 3 при  принимающем значения х, у, z; значениям
принимающем значения х, у, z; значениям  соответствуют
соответствуют  . В такой сокращенной записи симметрия (1.30) учтена автоматически.
. В такой сокращенной записи симметрия (1.30) учтена автоматически.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
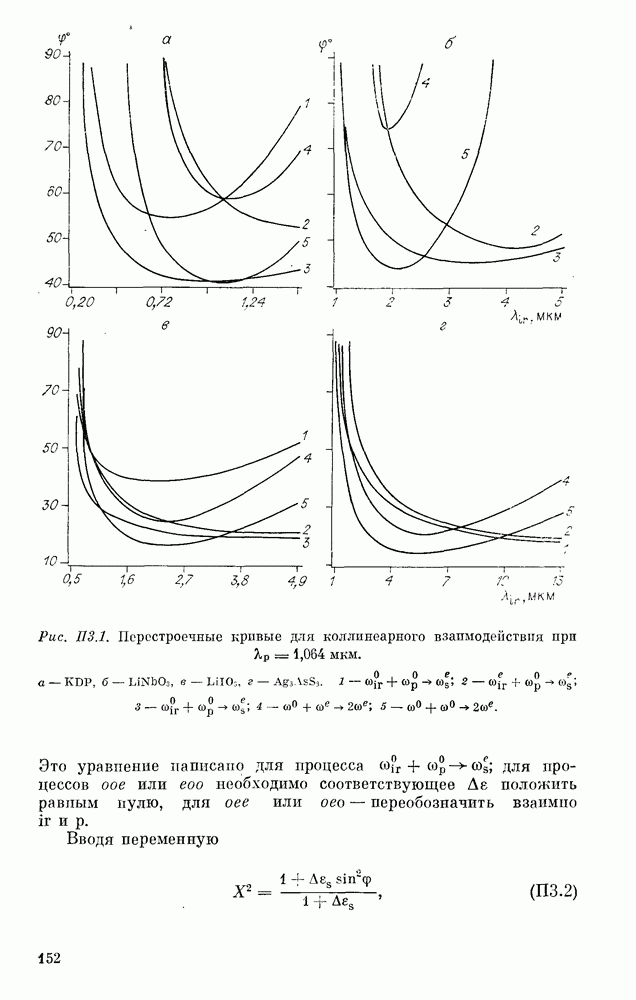
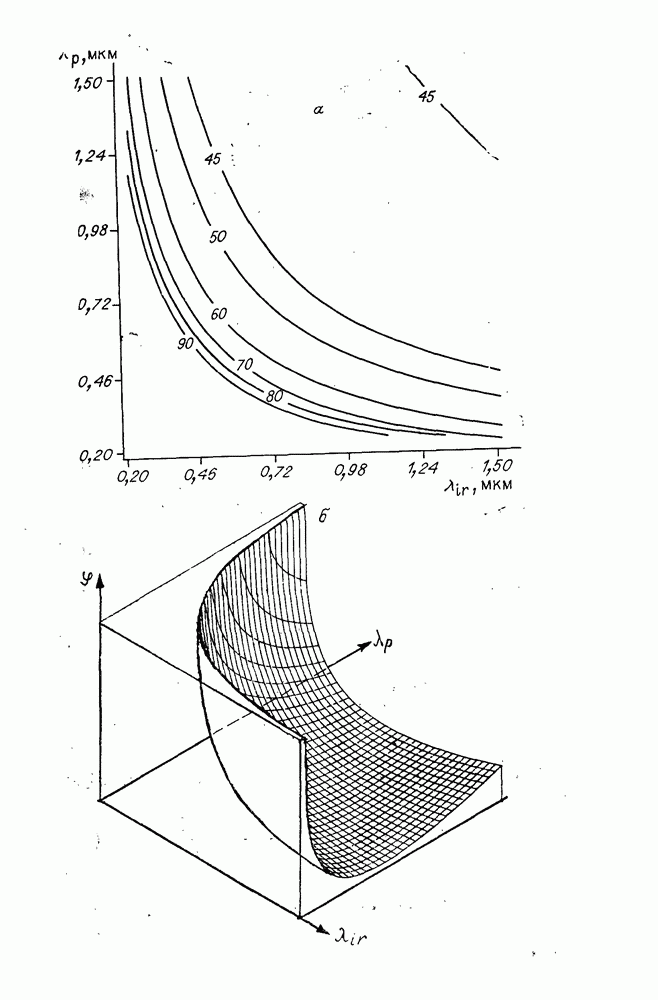
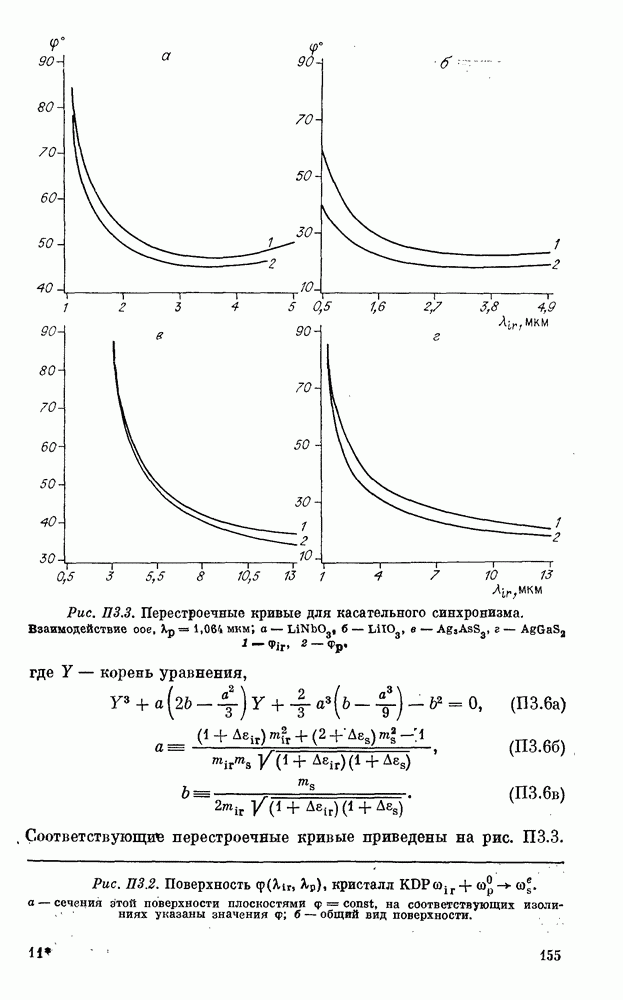
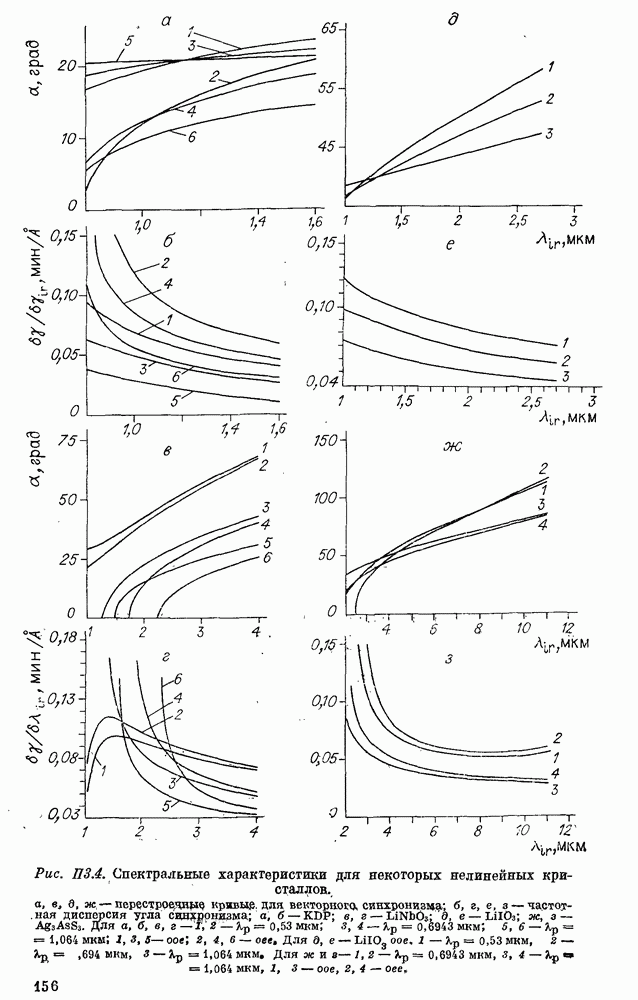
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)