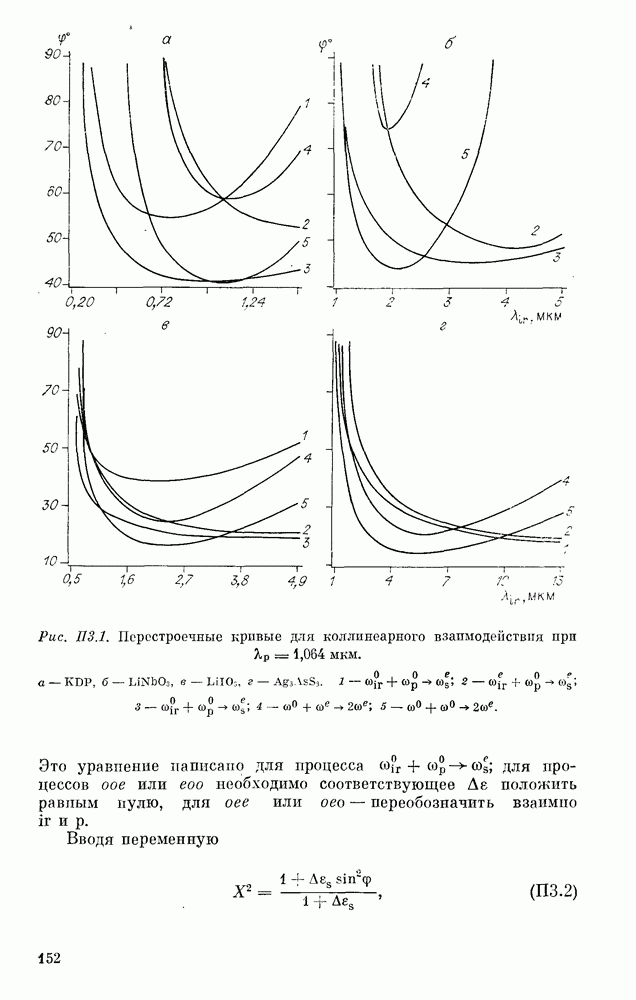
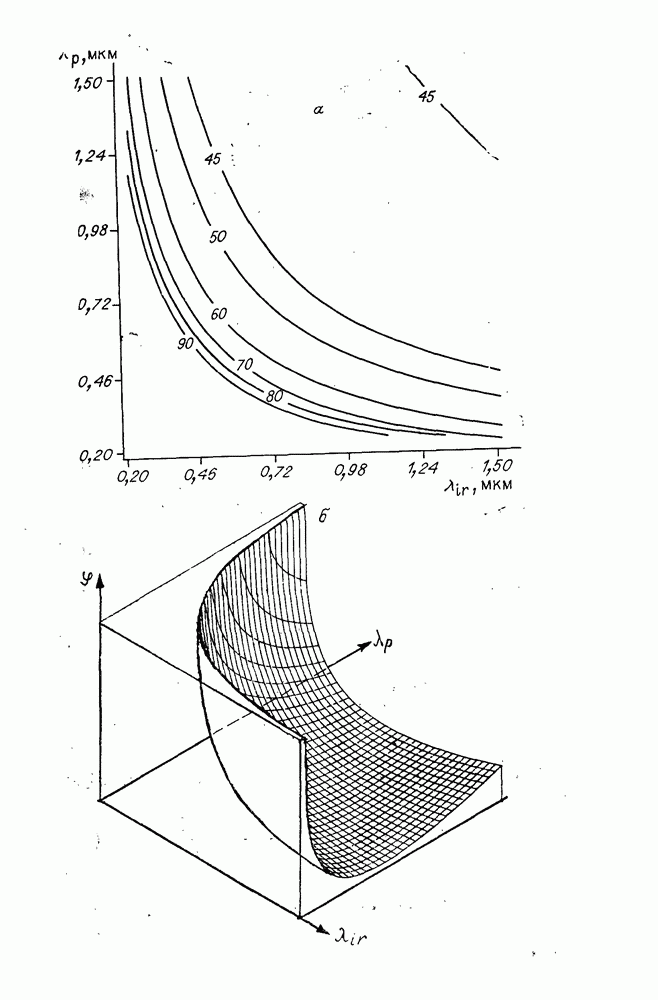
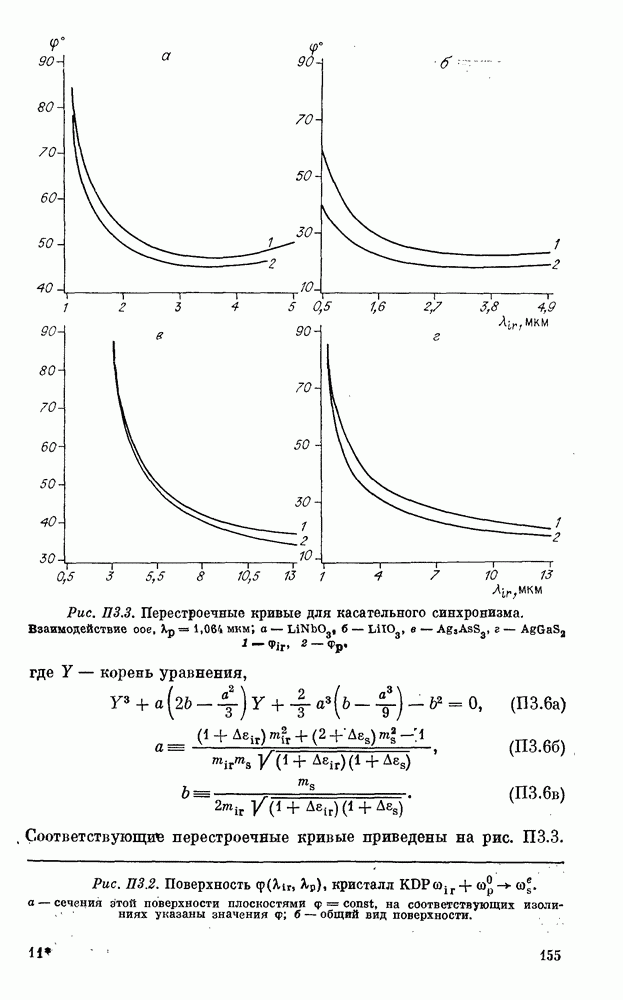
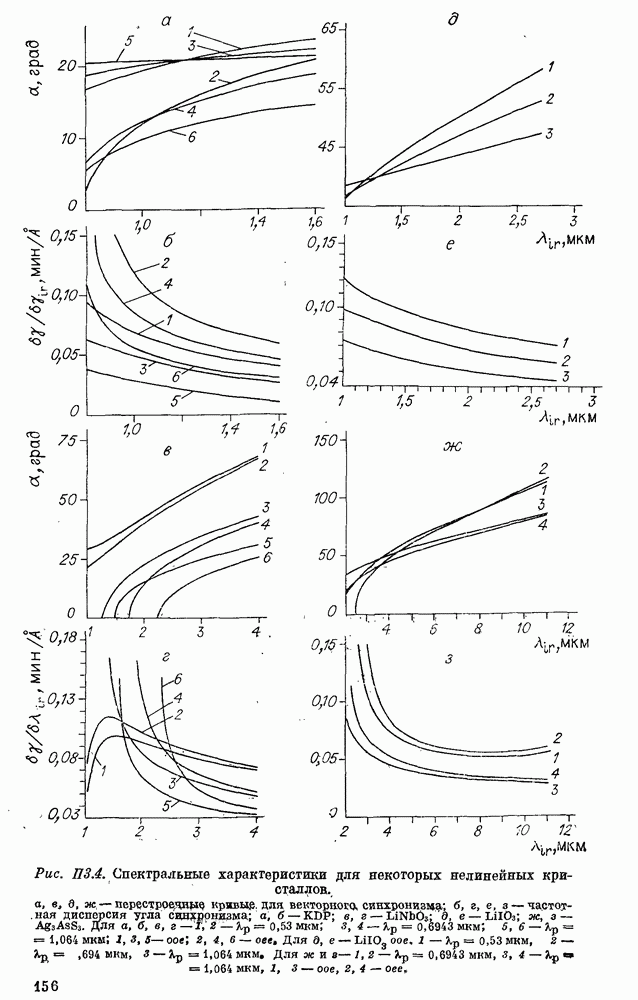
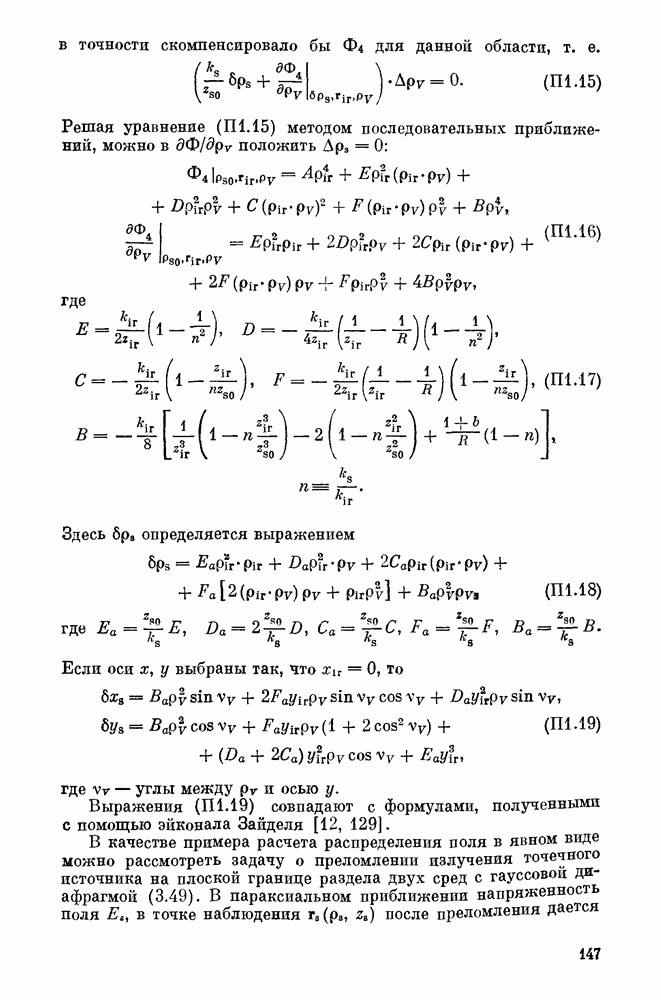| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
§ 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
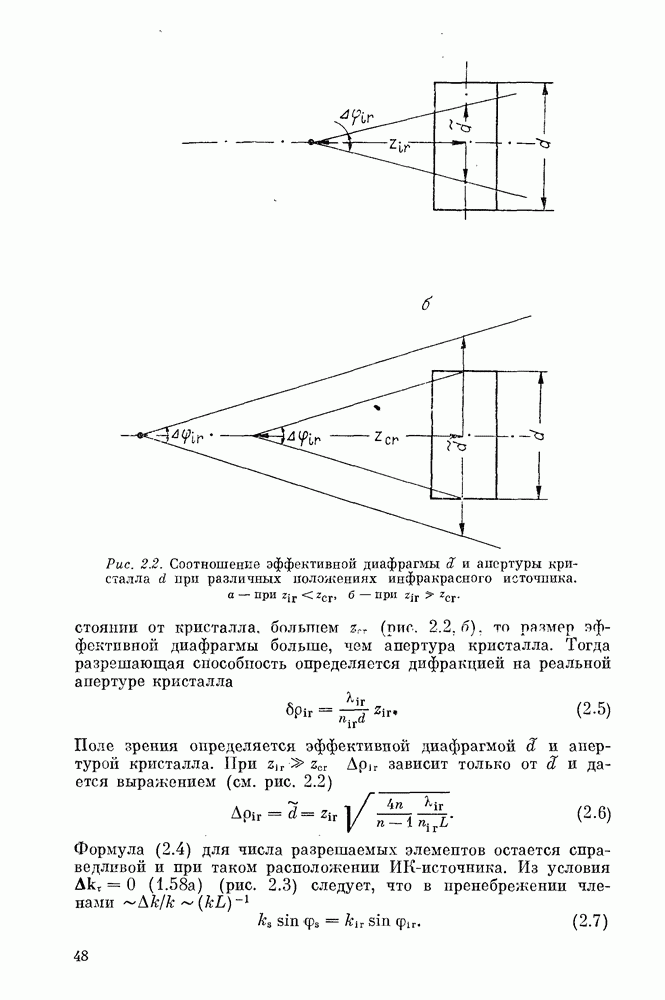
Схемой преобразования изображения, позволяющей выйти за рамки формул (3.29), (3.67), (3.70), (3.71), является схема критичного векторного синхронизма [204—228], где благодаря цилиндрической фокусировке накачки для каждого ИК-луча имеется луч накачки, с которым взаимодействие происходит точно в синхронизме. При этом, благодаря векторному характеру взаимодействия, каждый луч накачки переводит одномерное многообразие инфракрасных лучей, концы которых лежат на некоторой дуге (рис. 4.1). Поэтому для перевода двумерного изображения ИК-лучей достаточно фокусировки, дающей одномерное многообразие лучей накачки. На рис. 4.1 видно, что если

Рис. 4.1. Диаграмма волновых векторов для взаимодействия цилиндрической волны накачки с инфракрасным излучением.
накачка представляет собой цилиндрическую волну, концы переводимых инфракрасных лучей заштрихуют некоторую область на волновой поверхности  приведенной на рисунке. В этой области, размеры которой определяют угловое поле зрения, каждый ИК-луч однозначным образом переводится в луч на суммарной частоте. Таким образом, цилиндрическая фокусировка накачки дает нужный результат. Кроме того, при такой фокусировке и определенном расположении источников (например, ИК-объект на бесконечности) исчезают геометрические аберрации. Так же как и в линейной оптике [7, 8], для получения характеристик преобразователя достаточно исследовать его отклик на точечный источник (см. гл. 2, § 1). Итак, задача сводится к анализу взаимодействия в нелинейной среде цилиндрической волны накачки и сферической волны ИК-источника [223].
приведенной на рисунке. В этой области, размеры которой определяют угловое поле зрения, каждый ИК-луч однозначным образом переводится в луч на суммарной частоте. Таким образом, цилиндрическая фокусировка накачки дает нужный результат. Кроме того, при такой фокусировке и определенном расположении источников (например, ИК-объект на бесконечности) исчезают геометрические аберрации. Так же как и в линейной оптике [7, 8], для получения характеристик преобразователя достаточно исследовать его отклик на точечный источник (см. гл. 2, § 1). Итак, задача сводится к анализу взаимодействия в нелинейной среде цилиндрической волны накачки и сферической волны ИК-источника [223].
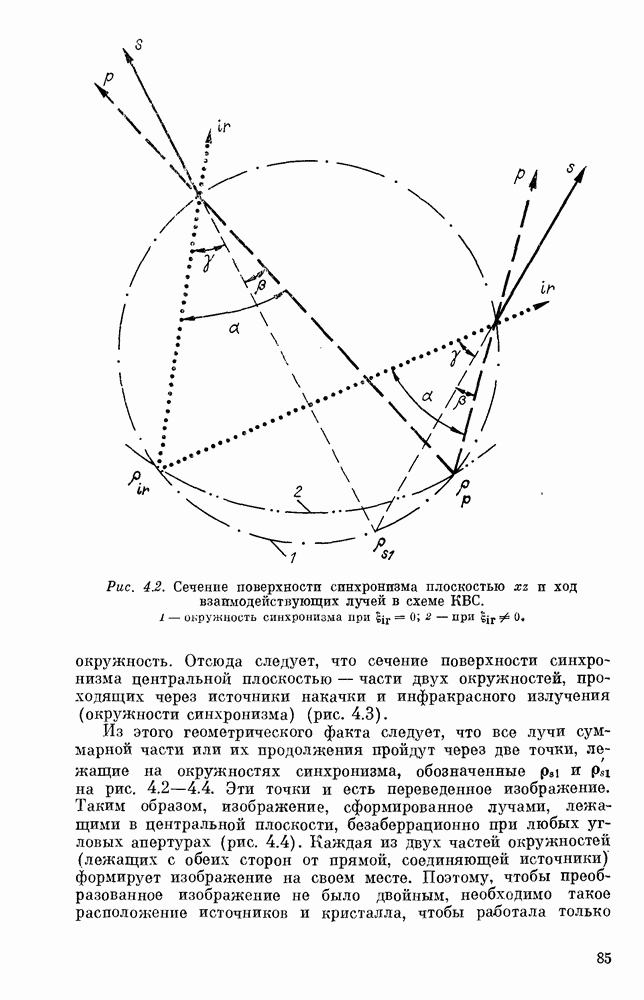
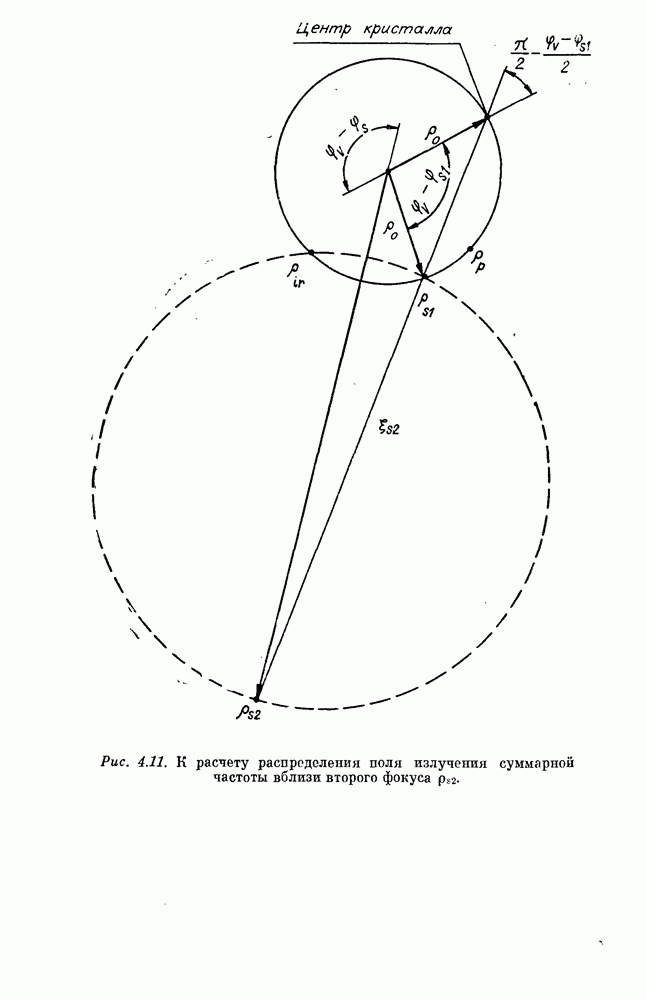
Математически задача о нахождении поверхности синхронизма формулируется следующим образом. Есть две конгруэнции: одна образована лучами, выходящими из точки (ИК-источник), другая — лучами, выходящими из прямой линии (источник накачки) и лежащими в плоскостях, перпендикулярных ей (плоскости фокусировки накачки). Требуется найти поверхность, на которой лучи обеих конгруэнций пересекаются друг с другом под заданным углом а. Зная формулу поверхности синхронизма, нетрудно написать уравнения лучей суммарной частоты — каждый такой луч проходит через какую-нибудь точку поверхности синхронизма и лежит в плоскости, образованной ИК-лучами и лучом накачки, проходящими через эту же точку. Положение луча суммарной частоты в плоскости определено углами  между этим лучом, инфракрасным лучом и лучом накачки (рис. 4.2).
между этим лучом, инфракрасным лучом и лучом накачки (рис. 4.2).
Рассмотрим сначала лучи, лежащие в плоскости фокусировки, проходящей через ИК-источник (центральная плоскость). Геометрическим местом точек, из которых два фиксированных пункта  и
и  видны под определенным углом а, является
видны под определенным углом а, является
Рис. 4.2. (см. скан) Сечение поверхности синхронизма плоскостью  и ход взаимодействующих лучей в схеме КВС. 1 - окружность синхронизма при
и ход взаимодействующих лучей в схеме КВС. 1 - окружность синхронизма при  при
при 
окружность. Отсюда следует, что сечение поверхности синхронизма центральной плоскостью — части двух окружностей, проходящих через источники накачки и инфракрасного излучения (окружности синхронизма) (рис. 4.3).
Из этого геометрического факта следует, что все лучи суммарной части или их продолжения пройдут через две точки, лежащие на окружностях синхронизма, обозначенные  на рис. 4.2-4.4. Эти точки и есть переведенное изображение. Таким образом, изображение, сформированное лучами, лежащими в центральной плоскости, безаберрационно при любых угловых апертурах (рис. 4.4). Каждая из двух частей окружностей (лежащих с обеих сторон от прямой, соединяющей источники) формирует изображение на своем месте. Поэтому, чтобы преобразованное изображение не было двойным, необходимо такое расположение источников и кристалла, чтобы работала только
на рис. 4.2-4.4. Эти точки и есть переведенное изображение. Таким образом, изображение, сформированное лучами, лежащими в центральной плоскости, безаберрационно при любых угловых апертурах (рис. 4.4). Каждая из двух частей окружностей (лежащих с обеих сторон от прямой, соединяющей источники) формирует изображение на своем месте. Поэтому, чтобы преобразованное изображение не было двойным, необходимо такое расположение источников и кристалла, чтобы работала только

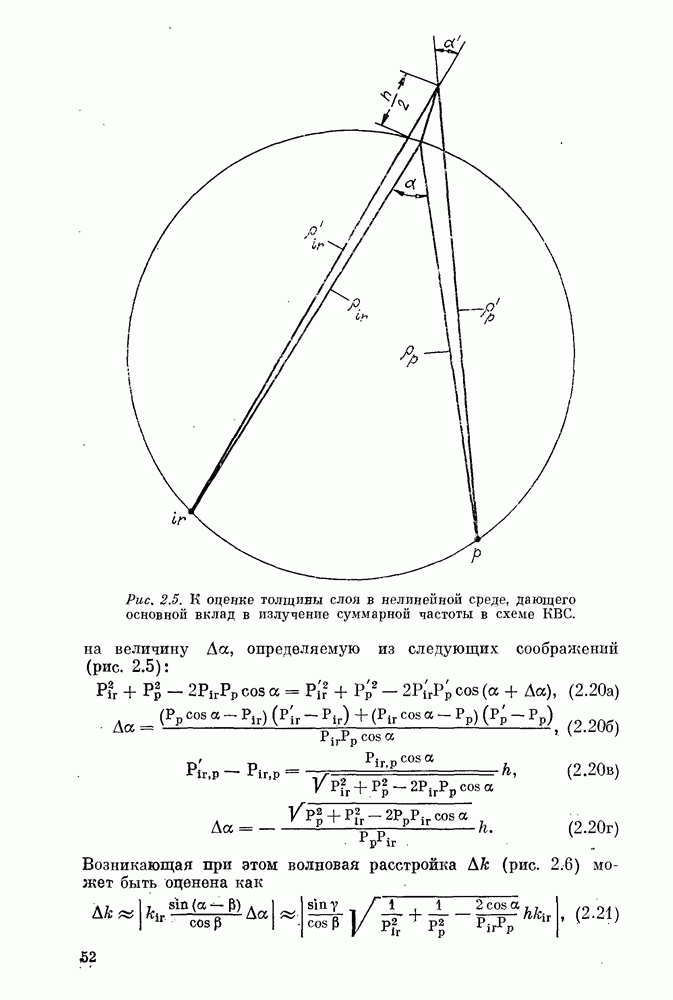
Рис. 4.3. Окружности синхронизма и ход лучей в случае, когда оба источника  излучают расходящиеся (сходящиеся) волны.
излучают расходящиеся (сходящиеся) волны.
одна окружность. Для этого все лучи накачки (или весь нелинейный кристалл) должны лежать по одну сторону от прямой, соединяющей источники; или с одной стороны прямой должны лежать лучи, расходящиеся из источника накачки, а с другой — сходящиеся к нему (рис. 4.5). Дальше всюду будем считать, что такие условия выполнены. Для определенности рассмотрим случай, когда обе волны расходящиеся (или сходящиеся) (см. рис. 4.3). Источники взаимодействующих волн и точка  образуют треугольник, подобный треугольнику волновых векторов (рис. 4.6) при взаимодействии плоских волн. Этот факт позволяет установить подобие треугольников
образуют треугольник, подобный треугольнику волновых векторов (рис. 4.6) при взаимодействии плоских волн. Этот факт позволяет установить подобие треугольников  и
и  (см. рис. 4.6) и заключить, что для лучей, лежащих в центральной плоскости, преобразователь в схеме КВС является идеальной оптической системой. Переход от пространства объектов к пространству изображений состоит в повороте вокруг источника накачки на угол у и сжатия в
(см. рис. 4.6) и заключить, что для лучей, лежащих в центральной плоскости, преобразователь в схеме КВС является идеальной оптической системой. Переход от пространства объектов к пространству изображений состоит в повороте вокруг источника накачки на угол у и сжатия в  раз
раз
Перейдем к рассмотрению формирования изображения при учете ИК-лучей, не лежащих в центральной плоскости. Совместим начало декартовой системы координат с ИК-источником, а ось у направим параллельно линейному источнику накачки, который пересекается с осью z в точке  направлена из ИК-источника на источник накачки). Для определенности предположим, что кристалл расположен в верхней полуплоскости
направлена из ИК-источника на источник накачки). Для определенности предположим, что кристалл расположен в верхней полуплоскости  Будем использовать параметрическую запись уравнений лучей:
Будем использовать параметрическую запись уравнений лучей:

Здесь  радиус-вектор точки на луче;
радиус-вектор точки на луче;  радиус-вектор источника;
радиус-вектор источника;  единичный вектор, направленный вдоль луча;
единичный вектор, направленный вдоль луча;  угол между
угол между  и плоскостью
и плоскостью  угол между проекцией
угол между проекцией  на плоскость
на плоскость  и осью
и осью  В этих обозначениях система
В этих обозначениях система
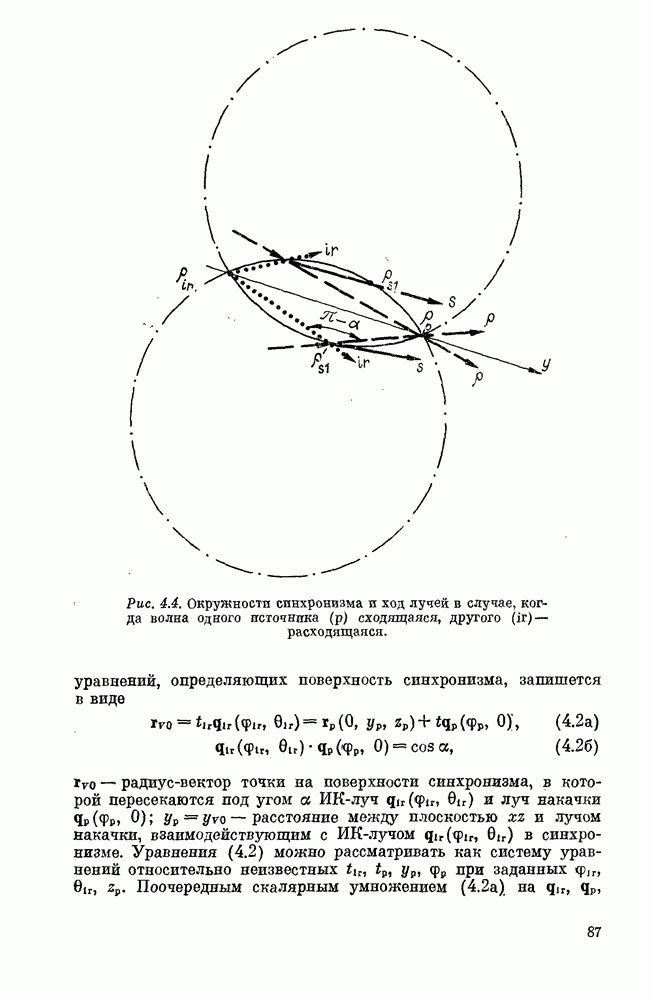
Рис. 4.4. (см. скан) Окружности синхронизма и ход лучей в случае, когда волна одного источника  сходящаяся, другого
сходящаяся, другого  расходящаяся.
расходящаяся.
уравнений, определяющих поверхность синхронизма, запишется в виде

 радиус-вектор точки на поверхности синхронизма, в которой пересекаются под угом а ИК-луч
радиус-вектор точки на поверхности синхронизма, в которой пересекаются под угом а ИК-луч  и луч накачки
и луч накачки  расстояние между плоскостью
расстояние между плоскостью  и лучом накачки, взаимодействующим с ИК-лучом
и лучом накачки, взаимодействующим с ИК-лучом  в синхронизме. Уравнения (4.2) можно рассматривать как систему уравнений относительно неизвестных
в синхронизме. Уравнения (4.2) можно рассматривать как систему уравнений относительно неизвестных  при заданных
при заданных  Поочередным скалярным умножением (4.2а) на
Поочередным скалярным умножением (4.2а) на 

Рис. 4.6. Треугольники  при двух положениях ИК-источника.
при двух положениях ИК-источника. 

Рис. 4.5. Окружности синхронизма и ход лучей в случае, когда волна одного источника  сходяще-расходящаяся, другого
сходяще-расходящаяся, другого  -расходящаяся.
-расходящаяся.
 система (4.2) приводится к виду
система (4.2) приводится к виду

где 
Решение системы (4.3) удобно записать, введя угол 

Уравнение поверхности синхронизма в параметрическом виде (параметры  запишется так:
запишется так:


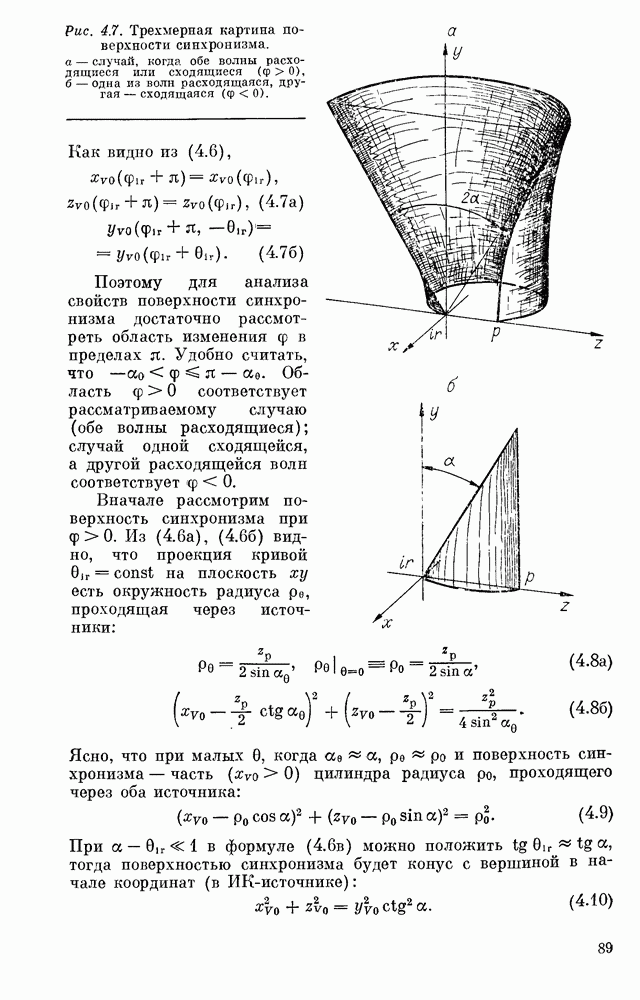
Рис. 4.7. Трехмерная картина поверхности синхронизма. а — случай, когда обе волны расходящиеся или сходящиеся  , б - одна из волн расходящаяся, другая — сходящаяся
, б - одна из волн расходящаяся, другая — сходящаяся 
Как видно из (4.6),

Поэтому для анализа свойств поверхности синхронизма достаточно рассмотреть область изменения  в пределах
в пределах  . Удобно считать, что
. Удобно считать, что  Область
Область  соответствует рассматриваемому случаю (обе волны расходящиеся); случай одной сходящейся, а другой расходящейся волн соответствует
соответствует рассматриваемому случаю (обе волны расходящиеся); случай одной сходящейся, а другой расходящейся волн соответствует 
Вначале рассмотрим поверхность синхронизма при  Из (4.6а), (4.66) видно, что проекция кривой
Из (4.6а), (4.66) видно, что проекция кривой  на плоскость
на плоскость  есть окружность радиуса
есть окружность радиуса  проходящая через источники:
проходящая через источники:

Ясно, что при малых 0, когда  и поверхность синхронизма — часть
и поверхность синхронизма — часть  цилиндра радиуса
цилиндра радиуса  проходящего через оба источника:
проходящего через оба источника:

При  в формуле (4.6в) можно положить
в формуле (4.6в) можно положить  тогда поверхностью синхронизма будет конус с вершиной в начале координат (в ИК-источнике):
тогда поверхностью синхронизма будет конус с вершиной в начале координат (в ИК-источнике):

Поверхнобть синхронизма изображена на рис. 4.7, а. При  поверхность синхронизма — часть
поверхность синхронизма — часть  цилиндра (4.9). При
цилиндра (4.9). При 

Тот факт, что при  (рис. 4.7, б) поверхность синхронизма занимает конечную часть пространства вблизи ИК-источника, имеет простой физический смысл. В самом деле, в этом случае в точке пересечения лучи идут навстречу друг другу (угол пересечения я —а), а такая ситуация может реализоваться только где-то между источниками.
(рис. 4.7, б) поверхность синхронизма занимает конечную часть пространства вблизи ИК-источника, имеет простой физический смысл. В самом деле, в этом случае в точке пересечения лучи идут навстречу друг другу (угол пересечения я —а), а такая ситуация может реализоваться только где-то между источниками.
Перейдем к анализу формирования геометрического изображения. Уравнения преобразованных лучей имеют вид 

Рассмотрим проекции лучей на плоскость  Из (4.12а), (4.126) видно, что преобразование совокупности лучей с
Из (4.12а), (4.126) видно, что преобразование совокупности лучей с  идет так же, как и лучей, лежащих в центральной плоскости
идет так же, как и лучей, лежащих в центральной плоскости  с точностью до замены а на
с точностью до замены а на  на
на  В этом смысле преобразователь в схеме КВС напоминает преломляющую призму.
В этом смысле преобразователь в схеме КВС напоминает преломляющую призму.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
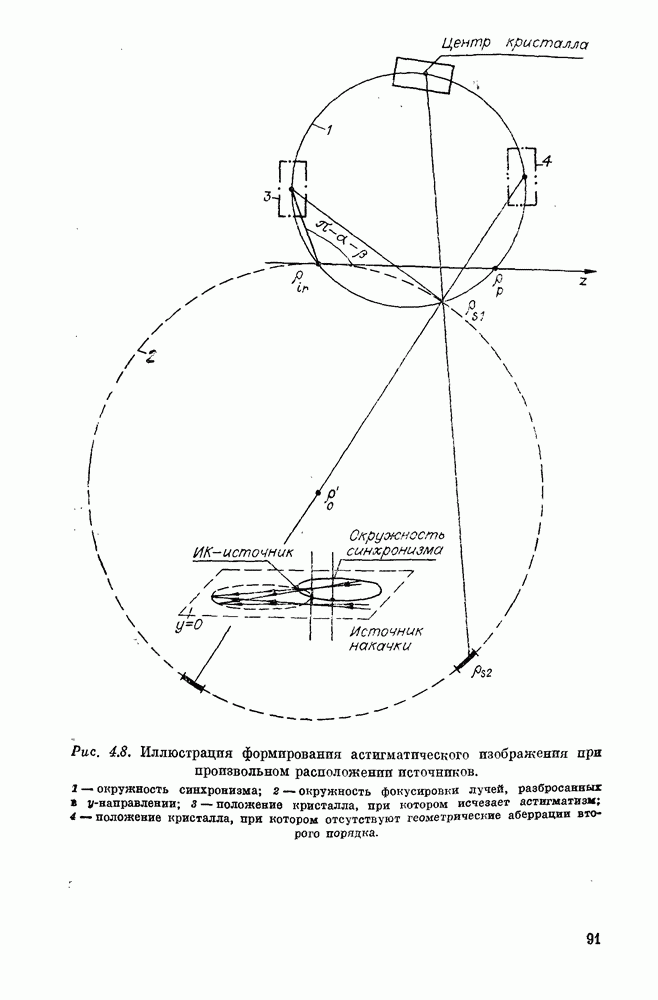
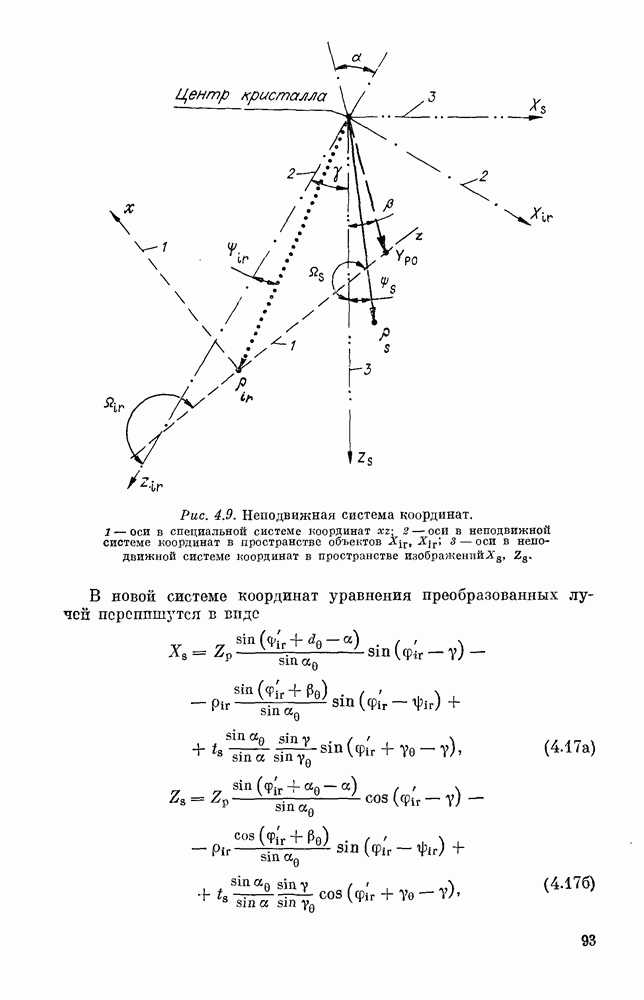
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
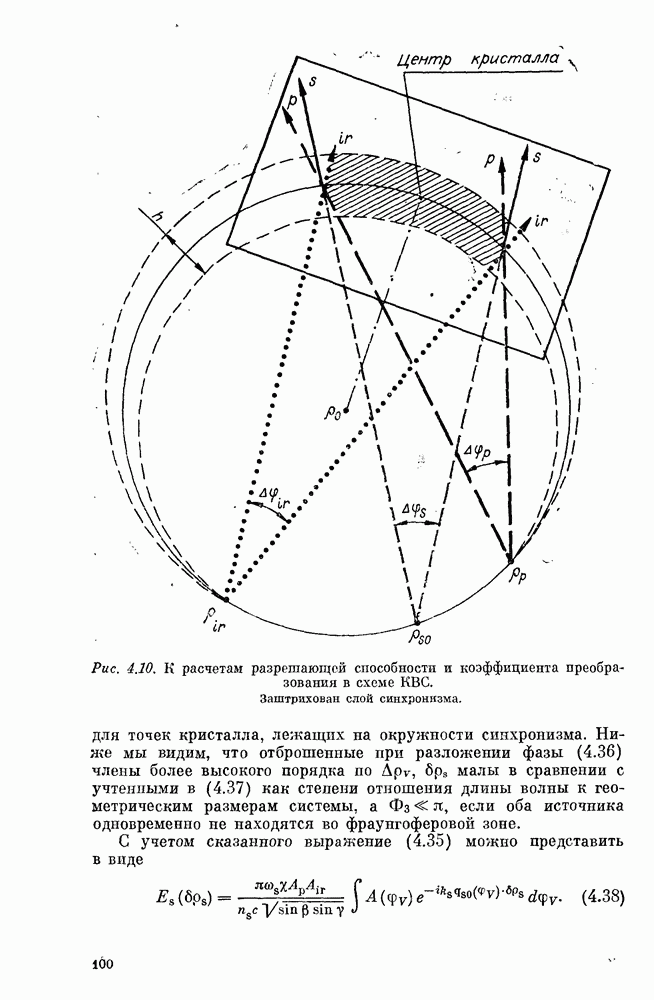
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
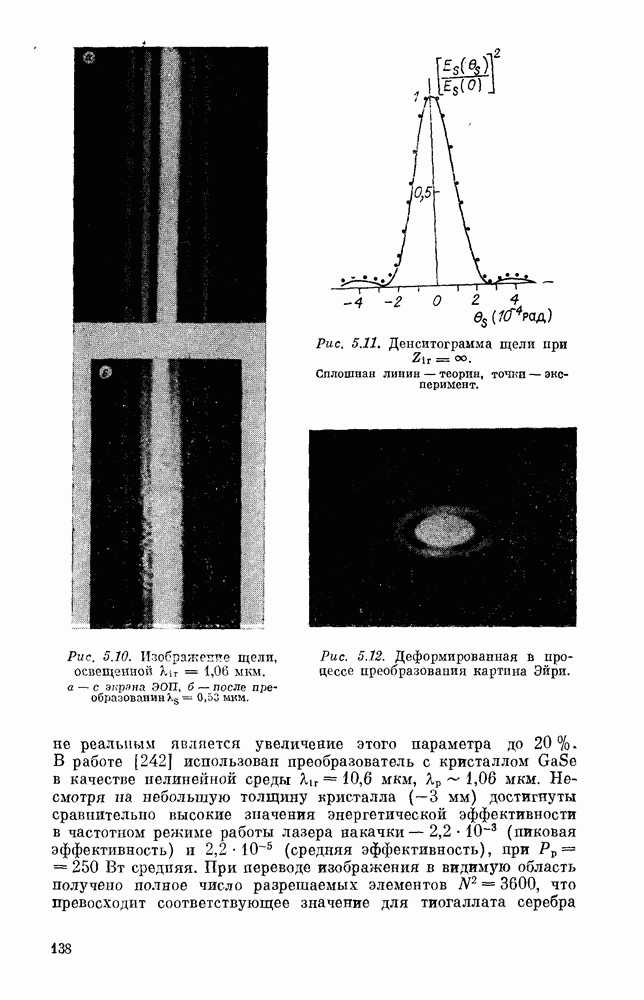
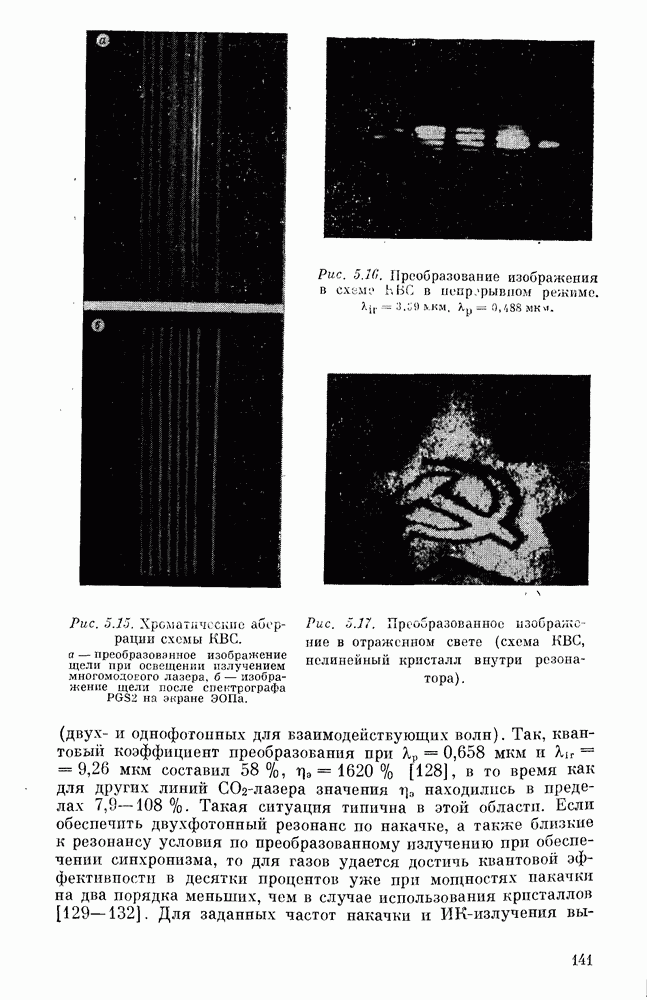
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)