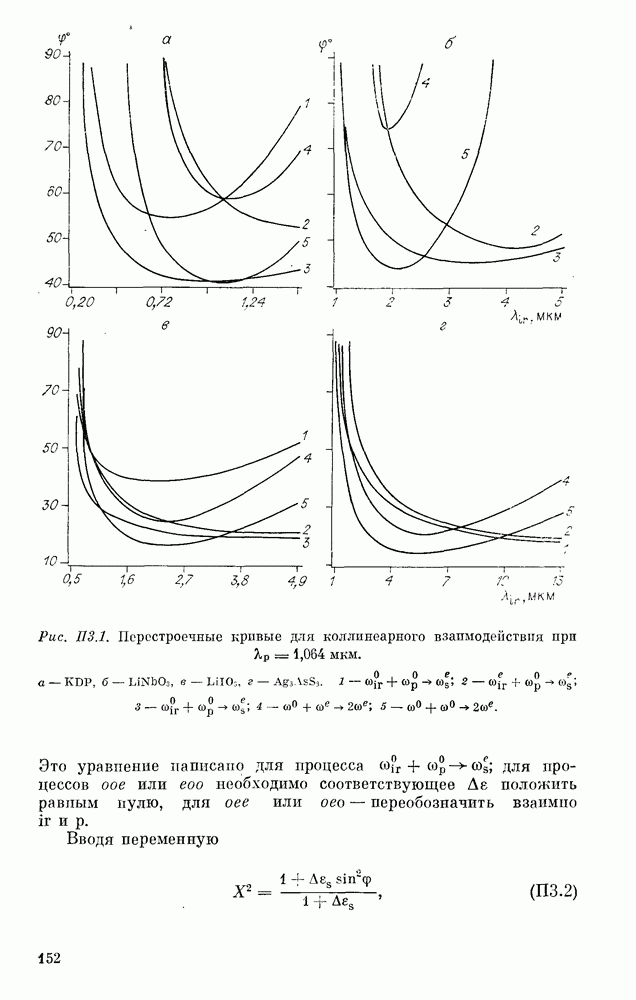
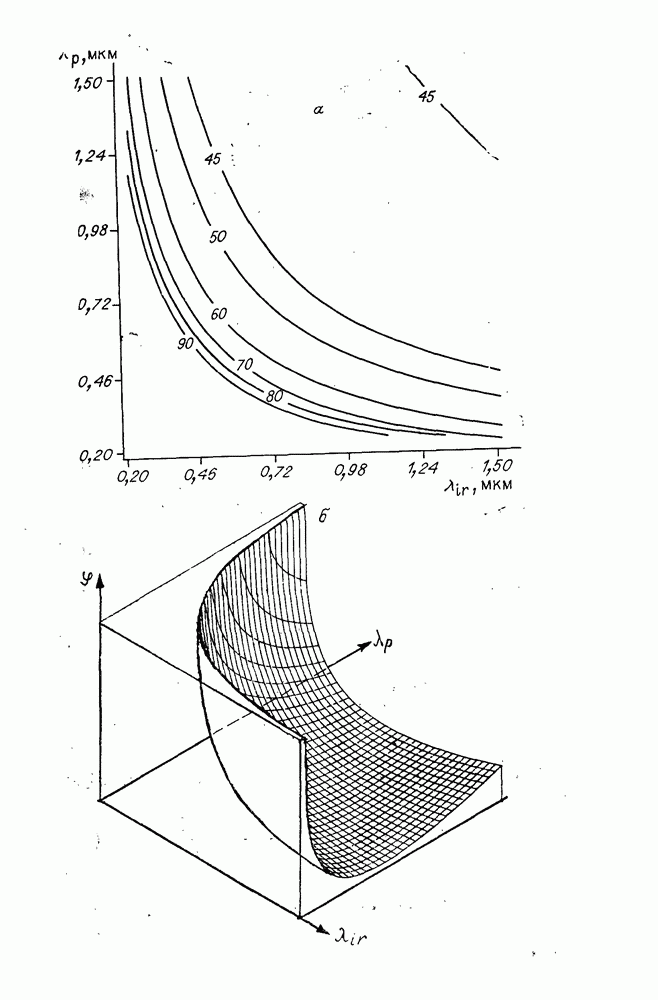
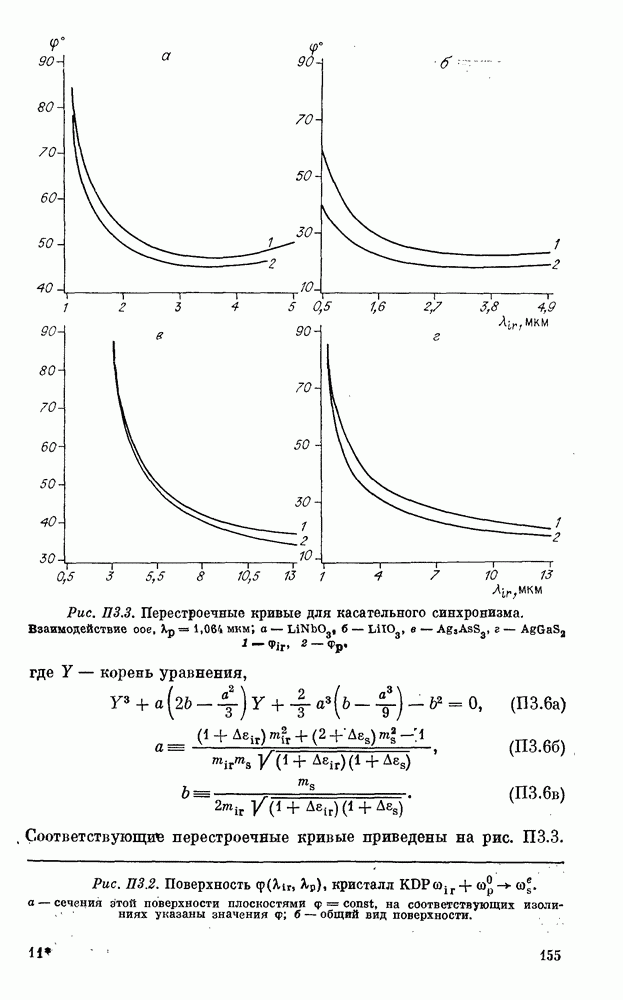
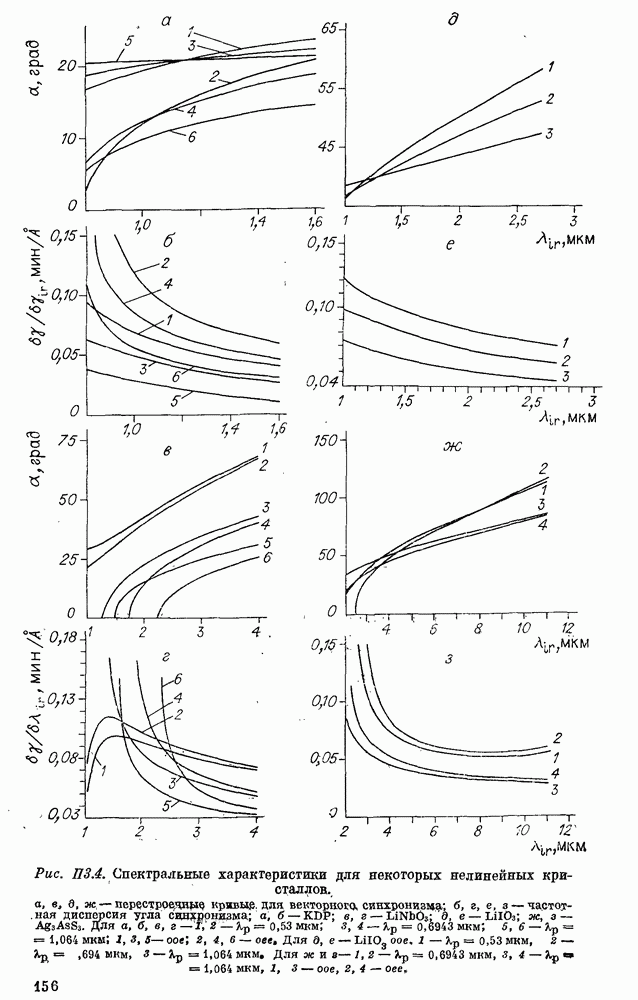
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
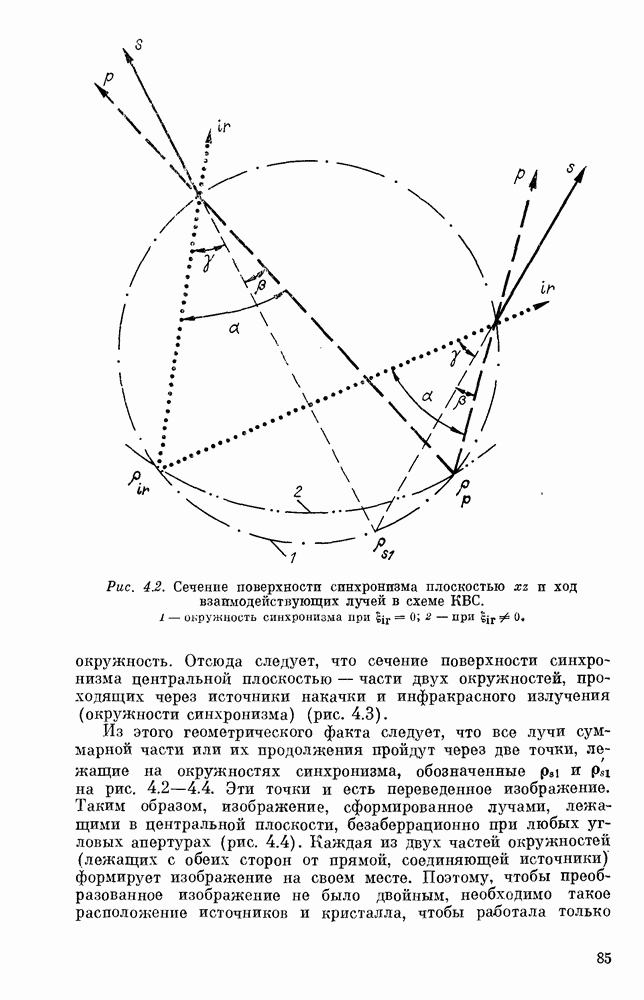
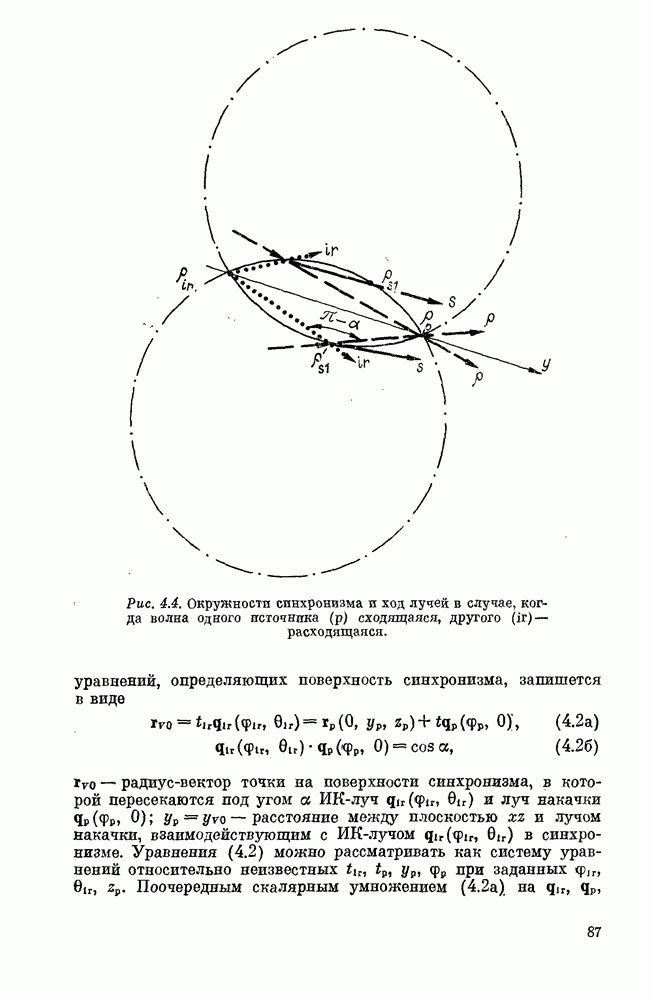
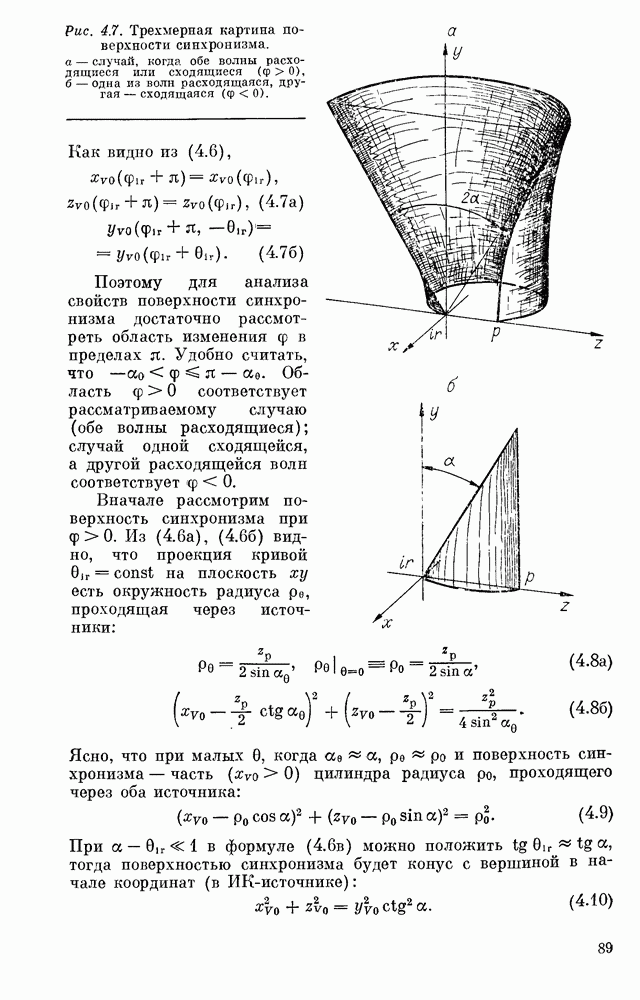
Явления пространственной синфазности (синхронизма)
Электромагнитное поле во второй (нелинейной) среде представляет собой результат интерференции свободной и вынужденной волн. В отличие от падающей и отраженной волн в линейной оптике свободная и вынужденная волны при малых  распространяются в близких направлениях, точно совпадающих при
распространяются в близких направлениях, точно совпадающих при  (см. (1.58) ирис. 1.2). Поэтому имеет смысл проследить эту интерференцию в ятном виде.
(см. (1.58) ирис. 1.2). Поэтому имеет смысл проследить эту интерференцию в ятном виде.
Из формул (1.52), (1.61), (1.63) можно получить выражение для поля  во второй среде [6]. В случае
во второй среде [6]. В случае  -поляризации имеем
-поляризации имеем

Для  -поляризации можно написать:
-поляризации можно написать:

где 
В случае поперечной произвольно поляризованной волны объединяются формулы (1.68), (1.69):


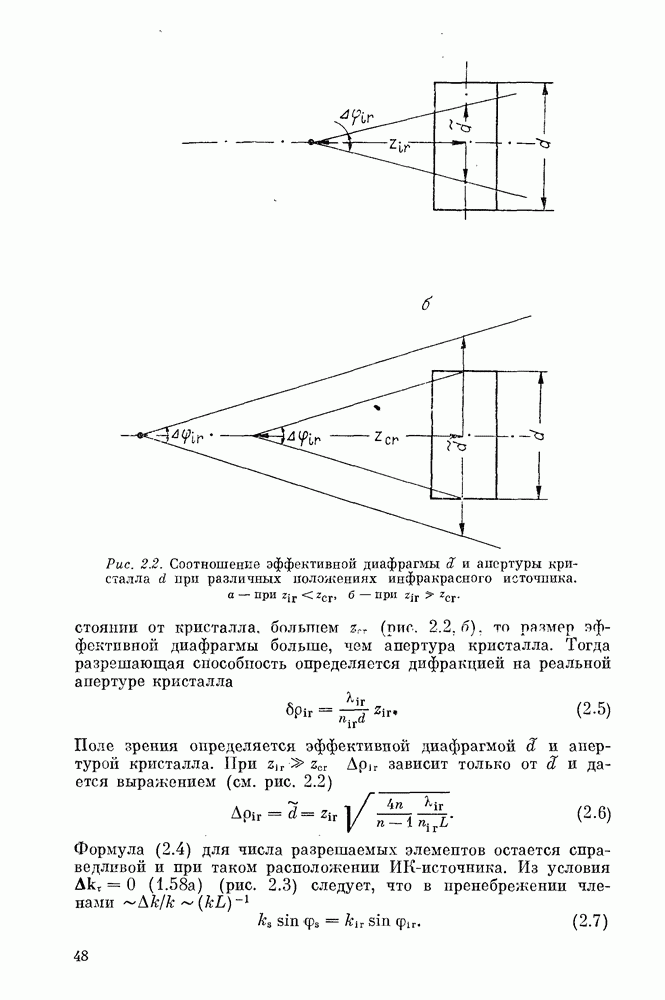
Рис. 1.3. Зависимость амплитуды А электромагнитной волны от z при разных значениях  расстояние от границы нелинейной среды до точки наблюдения, 1—4 — соответственно
расстояние от границы нелинейной среды до точки наблюдения, 1—4 — соответственно 
Мы видим, что поле в нелинейной среде можно представить в виде суммы двух волн. Амплитуда первой, имеющей волновой вектор  так же, как и амплитуда «отраженной» волны
так же, как и амплитуда «отраженной» волны  мала — порядка или меньше амплитуды нелинейной поляризации. Значительно интересней вторая волна, волновой вектор которой равен
мала — порядка или меньше амплитуды нелинейной поляризации. Значительно интересней вторая волна, волновой вектор которой равен  Ее амплитуда промодулирована множителем
Ее амплитуда промодулирована множителем  следовательно, нарастает в глубь среды вплоть до
следовательно, нарастает в глубь среды вплоть до  где длина когерентности
где длина когерентности  определяется выражением (рис. 1.3)
определяется выражением (рис. 1.3)

Поэтому амплитуда второй волны может превосходить амплитуду волны нелинейной поляризации в  или в
или в  раз, если
раз, если  где
где  толщина нелинейной
толщина нелинейной 
Таким образом, нелинейный эффект накапливается по мере распространения волны в глубь нелинейной среды. Накопление имеет простую физическую причину — излучение отдельных слоев нелинейной поляризации складывается в фазе, пока задаваемый величиной  набег фазы при распространении излучения от одного слоя к другому скомпенсирован (с точностью разностью фаз излучателей, находящихся в разных слоях; эта разность определяется величиной
набег фазы при распространении излучения от одного слоя к другому скомпенсирован (с точностью разностью фаз излучателей, находящихся в разных слоях; эта разность определяется величиной  Затем (при
Затем (при  излучение последующих слоев начинает гасить волны, идущие из начала среды. При
излучение последующих слоев начинает гасить волны, идущие из начала среды. При  снова начинается накопление и т. д. Если выполнено условие
снова начинается накопление и т. д. Если выполнено условие

то имеет место линейный рост доля в глубь среды:

Здесь сохранено только второе слагаемое формулы (1.70), так как оно дает главный вклад в  . Нарастание поля или его модуляция по закону
. Нарастание поля или его модуляция по закону  происходит вдоль координаты z независимо от направления распространения
происходит вдоль координаты z независимо от направления распространения  (т. е. направлений
(т. е. направлений  Благодаря множителю
Благодаря множителю  скорость изменения поля
скорость изменения поля
плавно увеличивается при переходе к более пологим по отношению к границе раздела направлениям 
Условие (1.72) есть условие равенства фазовых скоростей волны нелинейной поляризации и рожденных ею электромагнитных волн (условие пространственной синфазности). Более распространенное, хотя и менее точное, название — условие синхронизма. Накопление нелинейного эффекта при согласовании фазовых скоростей  называется явлением синхронизма.
называется явлением синхронизма.
Явление синхронизма относится к числу фундаментальных в нелинейной оптике, поскольку оно может существенно усилить локально-малый нелинейный эффект. Для типичных размеров современных нелинейных кристаллов  , выигрыш в интенсивности
, выигрыш в интенсивности  и достигает восьми — девяти порядков.
и достигает восьми — девяти порядков.
В современных оптических волноводах, где  можно ожидать выигрыша 1018 1020, если проблема фазового согласования будет решена с достаточной точностью.
можно ожидать выигрыша 1018 1020, если проблема фазового согласования будет решена с достаточной точностью.
Для продольной компоненты  из (1.65а) имеем [6]:
из (1.65а) имеем [6]:

Здесь  так же как
так же как  по порядку величины никогда не превосходит
по порядку величины никогда не превосходит  т. е. аффект накопления отсутствует, поскольку продольные электромагнитные волны, как следует из (1.43), существуют только в тех областях пространства, что и породившая их нелинейная поляризация.
т. е. аффект накопления отсутствует, поскольку продольные электромагнитные волны, как следует из (1.43), существуют только в тех областях пространства, что и породившая их нелинейная поляризация.
Накопление, очевидно, отсутствует и для эффекта оптического выпрямления (ДС-эффекта), который состоит в наведении оптическими полями в нелинейном кристалле статической поляризации (см. (1.24а)). Наведенное в кристалле поле, как следует из законов электростатики, определяется равенством

Рассмотрим кратко способы реализации синхронизма на примере эффекта сложения частот (см. (1.24г)), когда две волны возбуждающего излучения с частотами  генерируют волну суммарной частоты
генерируют волну суммарной частоты 

Поскольку в данном случае

то условия синхронизма могут быть выполнены подбором угла между  и в том случае, если
и в том случае, если

Неравенство (1.78) с учетом (1.76) можно переписать в виде

где  показатели преломления на частотах
показатели преломления на частотах 
Из (1.79) следует, что при  синхронизм возможен только в случае, если
синхронизм возможен только в случае, если  Поэтому в условиях нормальной дисперсии
Поэтому в условиях нормальной дисперсии  , так как
, так как  в оптически изотропных и однородных средах реализовать условия синхронизма невозможно.
в оптически изотропных и однородных средах реализовать условия синхронизма невозможно.
Один из вариантов удовлетворения неравенства (1.79) состоит в использовании аномальной дисперсии. Для этого необходимо, чтобы частоты  были разделены одной или двумя достаточно интенсивными полосами поглощения. Такой метод может быть эффективен для нелинейных процессов третьего порядка (например, генерации третьей гармоники в жидкостях). Результат достигается добавлением соответствующего красителя в нужной концентрации. В кристаллах же использование этого метода связано с трудностями, поскольку, как правило,
были разделены одной или двумя достаточно интенсивными полосами поглощения. Такой метод может быть эффективен для нелинейных процессов третьего порядка (например, генерации третьей гармоники в жидкостях). Результат достигается добавлением соответствующего красителя в нужной концентрации. В кристаллах же использование этого метода связано с трудностями, поскольку, как правило,  них отсутствуют полосы поглощения нужной интенсивности и в нужном спектральном диапазоне [6, 13].
них отсутствуют полосы поглощения нужной интенсивности и в нужном спектральном диапазоне [6, 13].
Весьма эффективный метод согласования фаз в кристаллах — использование двулучепреломления. Коэффициенты преломления в двулучепреломляющих кристаллах на данной частоте различны для световых волн различной поляризации [1—8, 10]. Выберем поляризацию на меньших частотах  соответствующую большему показателю преломления — необыкновенную в случае одноосного кристалла с положительным двулучепреломлением и обыкновенную в случае отрицательного двулучепреломления. Пусть тензор нелинейной восприимчивости обеспечивает при этом возникновение
соответствующую большему показателю преломления — необыкновенную в случае одноосного кристалла с положительным двулучепреломлением и обыкновенную в случае отрицательного двулучепреломления. Пусть тензор нелинейной восприимчивости обеспечивает при этом возникновение  поляризованного в направлении, соответствующем меньшему значению
поляризованного в направлении, соответствующем меньшему значению  т. е. п° для положительного и
т. е. п° для положительного и  для отрицательного двулучепреломления (индексы
для отрицательного двулучепреломления (индексы  соответствуют обыкновенной и необыкновенной волнам). Тогда двулучепреломление может скомпенсировать дисперсию и обеспечить фазовое согласование (условие (1.79)). В зависимости от соотношения величин дисперсии и двулучепреломления возникает необходимость иметь обе волны на частотатх
соответствуют обыкновенной и необыкновенной волнам). Тогда двулучепреломление может скомпенсировать дисперсию и обеспечить фазовое согласование (условие (1.79)). В зависимости от соотношения величин дисперсии и двулучепреломления возникает необходимость иметь обе волны на частотатх  обыкновенными:
обыкновенными:

или достаточно, чтобы обыкновенной была одна из них:

Формулы (1.80) относятся к кристаллам с отрицательным двулучепреломлением. Соответствующие формулы для кристаллов с положительным, двулучепреломлением получаются из

Рис. 1.4. Диаграммы зависимости  от направления распространения волн в кристалле.
от направления распространения волн в кристалле.
(1.80) заменой индекса о на  Вариант достижения синхронизма (1.80а) показан на рис. 1.4, а.
Вариант достижения синхронизма (1.80а) показан на рис. 1.4, а.
Здесь же приведены диаграммы, показывающие зависимость  от его направления в кристалле. Точки пересечения а и а диаграмм
от его направления в кристалле. Точки пересечения а и а диаграмм  дают направление реализации фазового согласования.
дают направление реализации фазового согласования.
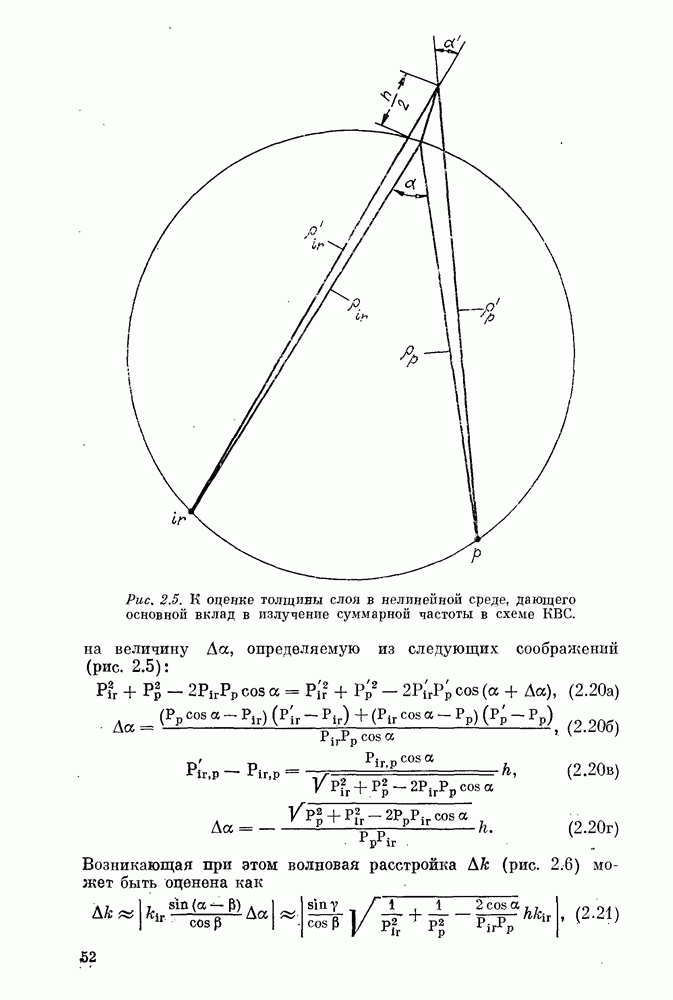
Оценим точность, с которой нужно выдержать направление  в кристалле. Из рис. 1,4, б видно, что фазовая расстройка при уходе от направления синхронизма на угол
в кристалле. Из рис. 1,4, б видно, что фазовая расстройка при уходе от направления синхронизма на угол  дается формулой
дается формулой

где  пересечения волновых поверхностей. Нетрудпо оцепить угловую ширину синхронизма, т. е. диапазон углов расстройки, в котором
пересечения волновых поверхностей. Нетрудпо оцепить угловую ширину синхронизма, т. е. диапазон углов расстройки, в котором

Из (1.81) и (1.82) имеем

В случае генерации второй гармоники излучения неодимового лазера  в кристалле КДР длиной 1 см по типу синхронизма
в кристалле КДР длиной 1 см по типу синхронизма  имеем
имеем  Мы видим, что критичность к настройке по углам
Мы видим, что критичность к настройке по углам  обычно весьма велика. В перпендикулярном направлении критичность к настройке невелика, поскольку показатели преломления не зависят от соответствующего угла 9, и определяется плавной зависимостью компонент нелинейного тензора от углов.
обычно весьма велика. В перпендикулярном направлении критичность к настройке невелика, поскольку показатели преломления не зависят от соответствующего угла 9, и определяется плавной зависимостью компонент нелинейного тензора от углов.
Угловая ширина синхронизма может резко возрастать и в направлении  если в точке синхронизма
если в точке синхронизма  реализуется не пересечение, а касание волновых поверхностей (рис. 1.4, е) [14, 15].
реализуется не пересечение, а касание волновых поверхностей (рис. 1.4, е) [14, 15].
В этом случае вместо (1.81) и (1.82) имеем

и угловая ширина синхронизма может достигать нескольких градусов (см. [14—16]).
Сказанное относится и к частотной ширине синхронизма. Например, волновая расстройка  связанная с изменением частот
связанная с изменением частот  и
и  при
при  в случае линейного синхронизма
в случае линейного синхронизма

определяется следующими выражениями:

Из (1.86) для частотной ширины синхронизма  имеем
имеем

Типичные значения  приведенные, например, в работе [17], составляют пссколько обратных сантиметров. При наличии так называемого дисперсионного согласования
приведенные, например, в работе [17], составляют пссколько обратных сантиметров. При наличии так называемого дисперсионного согласования

частотная ширина синхронизма резко возрастает:

и может достигать нескольких сотен обратных сантиметров [17] 
Таким образом, явление синхронизма важпо в нелинейной оптике не только потому, что оно может существенно усиливать эффекты, но и потому, что резко селектирует нелинейные процессы по типу, спектральным, угловым и поляризационным характеристикам. Последнее облегчает экспериментальное исследование конкретных эффектов и упрощает теоретическое описание.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
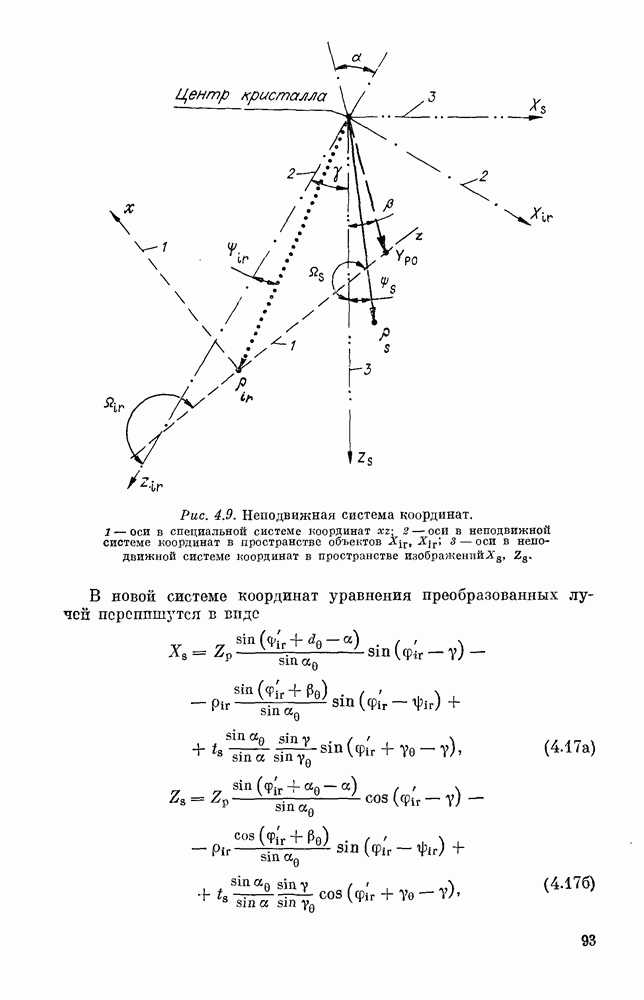
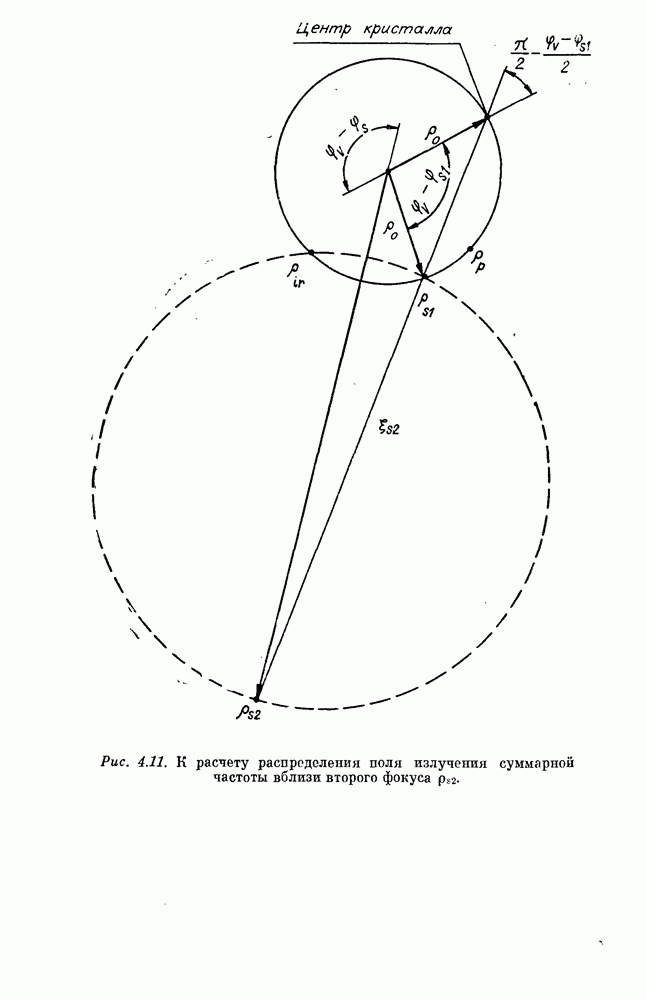
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
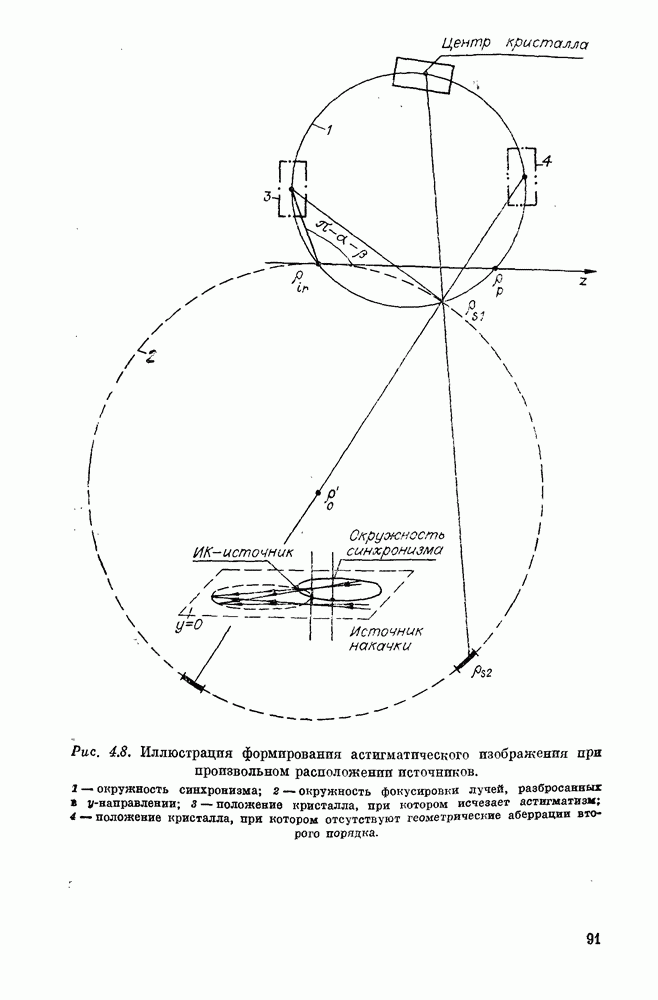
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
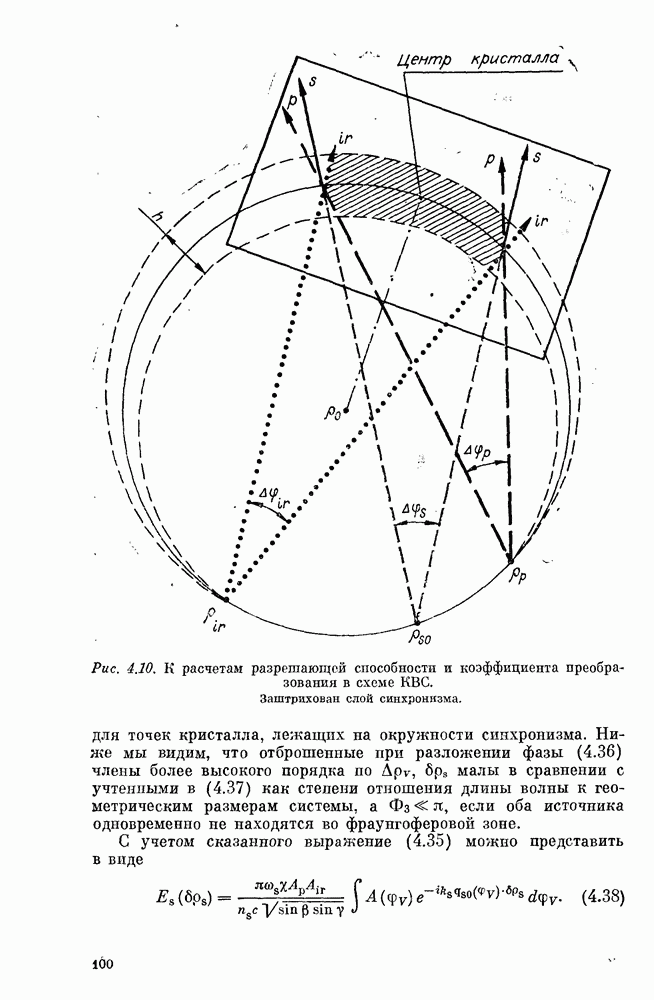
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
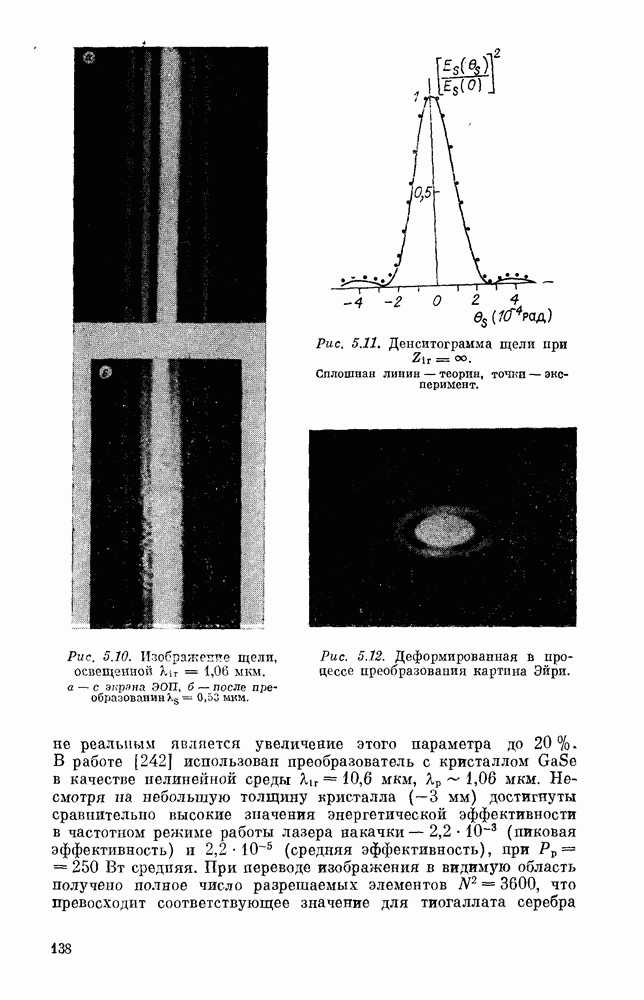
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
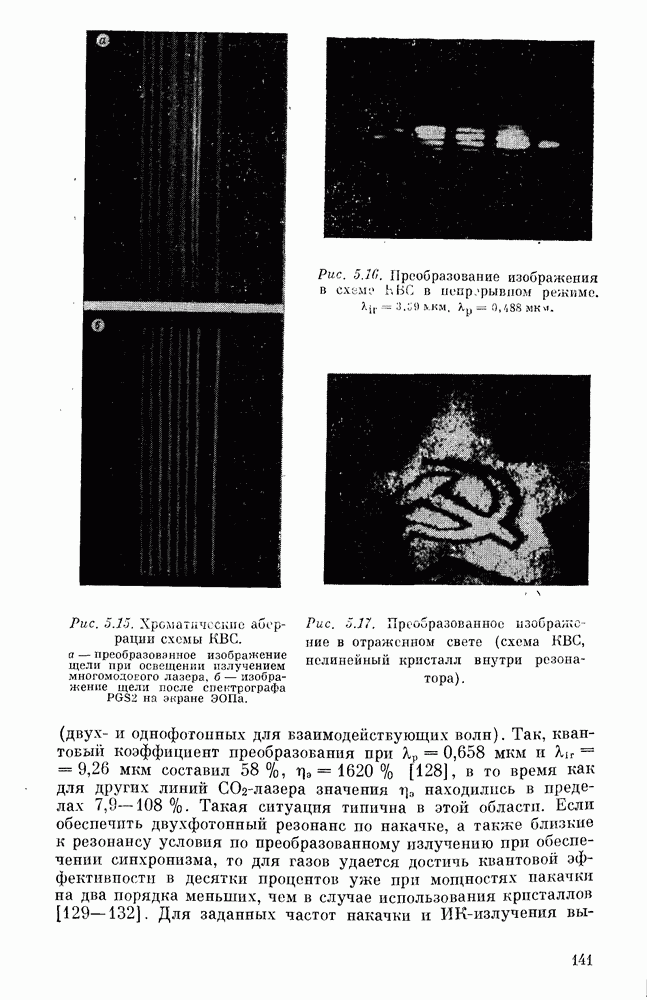
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)