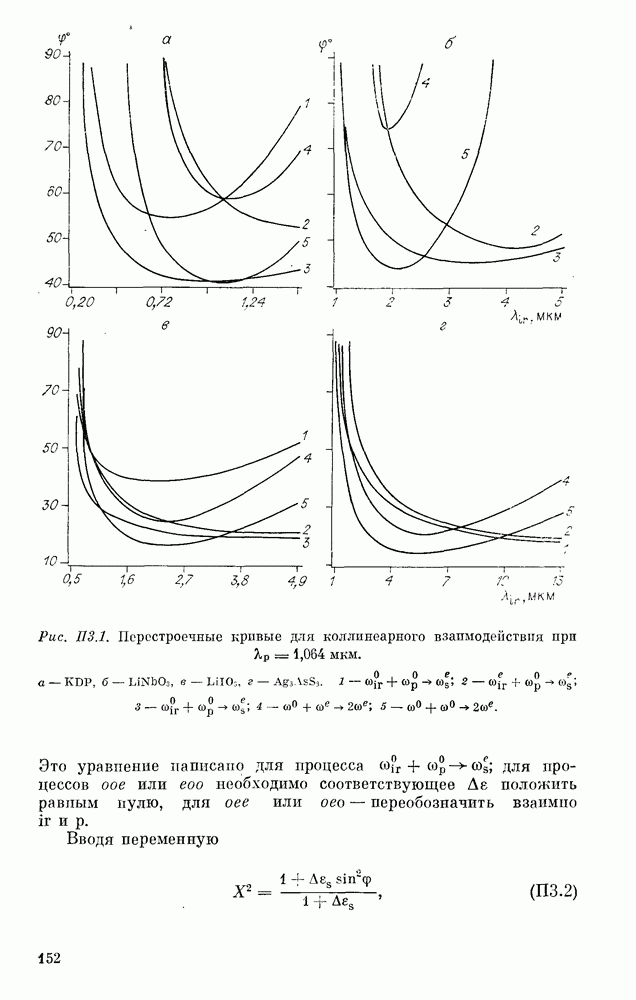
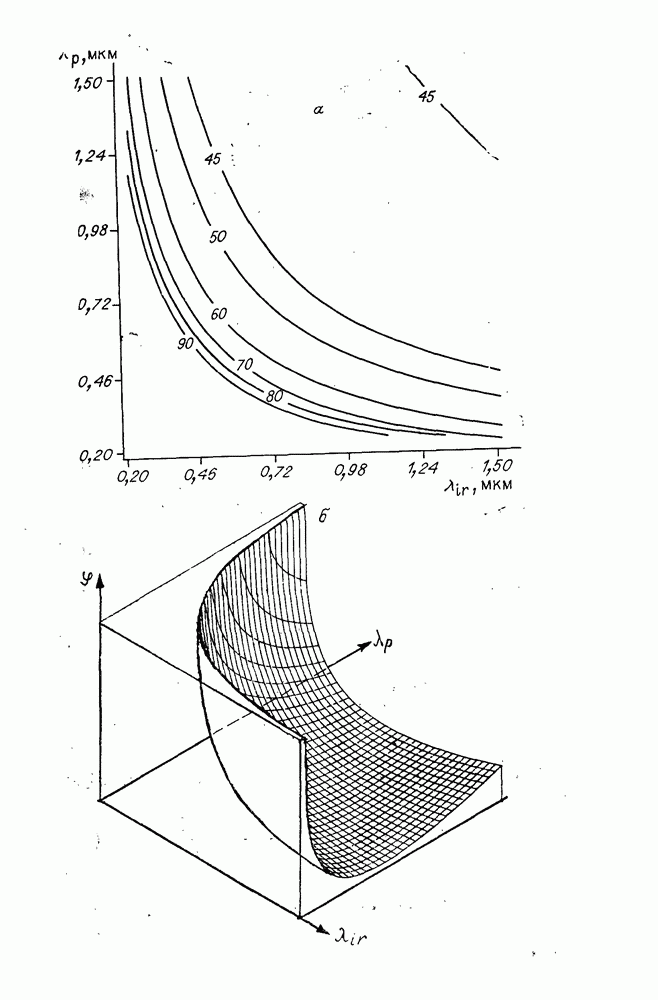
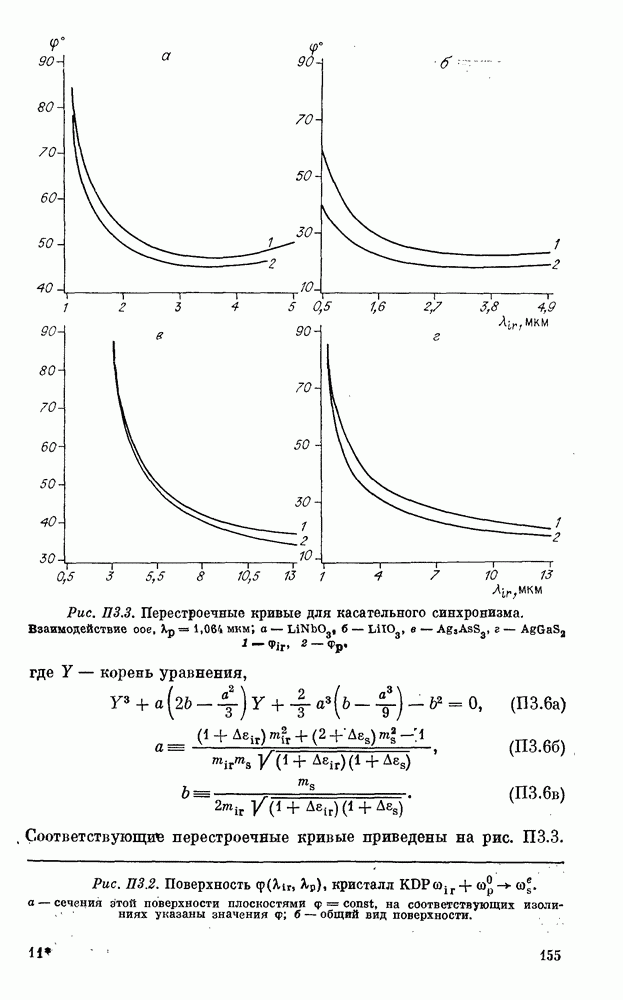
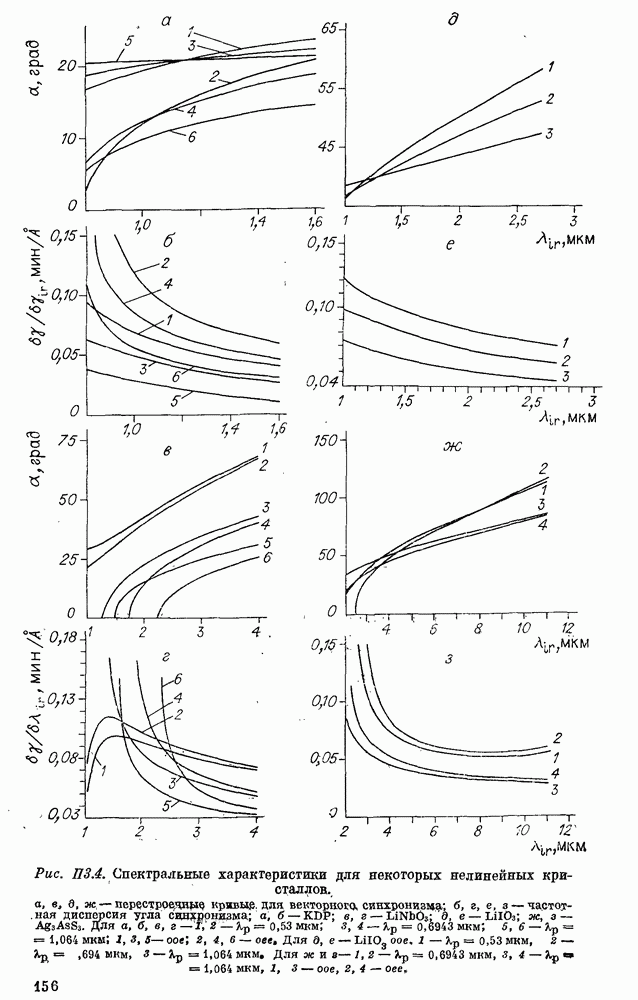
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
Распределение поля, преломленного (отраженного) на границе 2 раздела двух прозрачных сред, волновые числа которых  соответственно описываются интегралом Френеля — Кирхгофа:
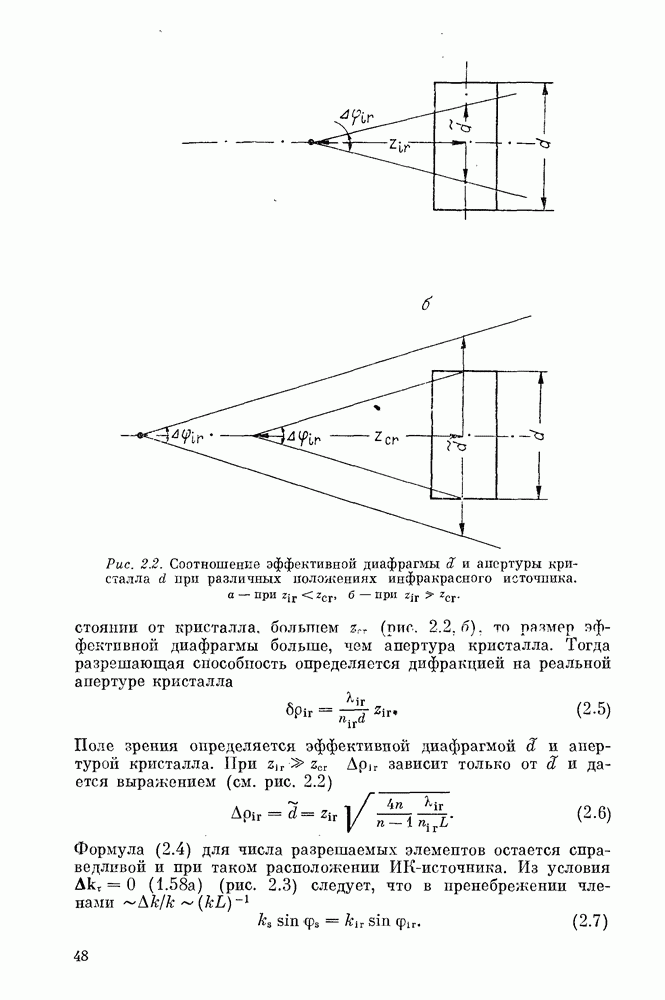
соответственно описываются интегралом Френеля — Кирхгофа:

где  единичный вектор, нормальный к элементу поверхности
единичный вектор, нормальный к элементу поверхности  амплитуда точечного источника, волна от которого преломляется на поверхности 2 или отражается от нее. Знак в показателе экспоненты определяется тем, находится ли точка наблюдения в пространстве действительных
амплитуда точечного источника, волна от которого преломляется на поверхности 2 или отражается от нее. Знак в показателе экспоненты определяется тем, находится ли точка наблюдения в пространстве действительных  или мнимых
или мнимых  изображений. Для преломления пространство мнимых изображений расположено по ту же сторону от поверхности 2, что и источник падающего излучения, а пространство действительных изображений — по другую. Для отражения все соотношения обратные.
изображений. Для преломления пространство мнимых изображений расположено по ту же сторону от поверхности 2, что и источник падающего излучения, а пространство действительных изображений — по другую. Для отражения все соотношения обратные.
Ясно, что интенсивность преломленного или отраженного излучения будет максимальна в тех точках наблюдения  для которых фаза
для которых фаза

постоянна как функция координат точки на преломляющей поверхности 2 или меняется незначительно.
Выберем теперь систему координат так, чтобы начало находилось в центре поверхности 2, а ось  была перпендикулярна ей. Если углы зрения из источника и точки наблюдения на поверхность 2 и углы между осью z и направлениями на источник и точку наблюдения малы
была перпендикулярна ей. Если углы зрения из источника и точки наблюдения на поверхность 2 и углы между осью z и направлениями на источник и точку наблюдения малы

то фазу  можно разложить по отношениям поперечных координат
можно разложить по отношениям поперечных координат  к продольным
к продольным  воспользовавшись соответствующим разложением В:
воспользовавшись соответствующим разложением В:

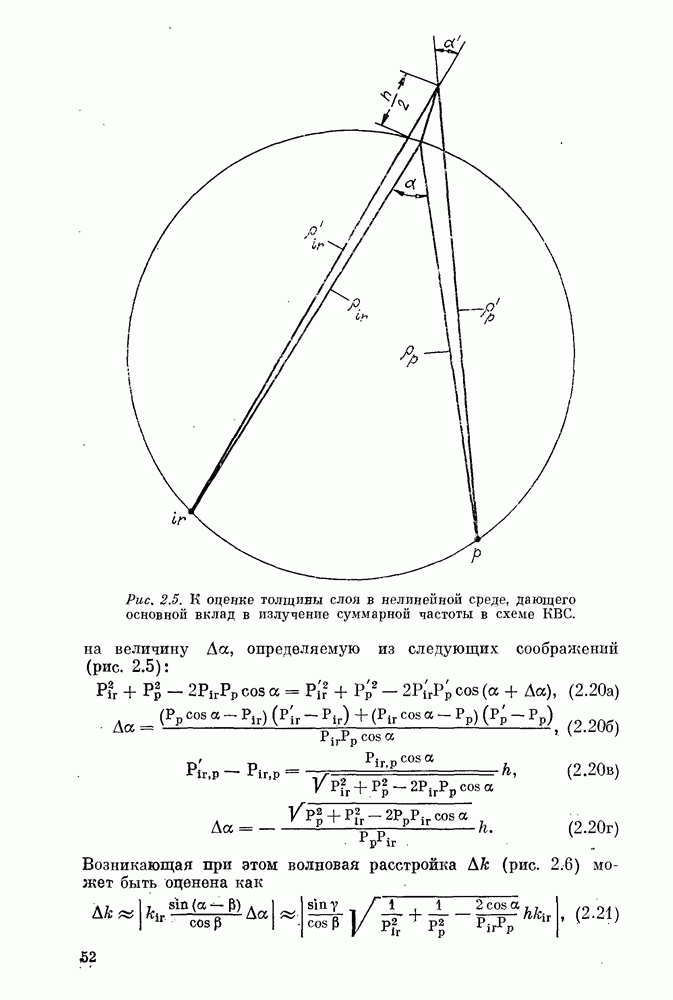
Знак перед скобкой зависит от знака  поскольку в разложение
поскольку в разложение  входит модуль
входит модуль 

где  члены порядка
члены порядка  по малым параметрам
по малым параметрам 

Совокупность точек наблюдения, для которых  определится уравнением
определится уравнением

Оно описывает преломление или отражение луча, проходящего через начало координат и имеет решения даже если последние два условия  не выполнены. Если же эти условия удовлетворены,
не выполнены. Если же эти условия удовлетворены,  запишется в виде
запишется в виде

С учетом описанных выше расположений пространств действительных и мнимых изображений формулы  можно записать в виде одного выражения:
можно записать в виде одного выражения:

считая, что для преломления  а для отражения
а для отражения  С точностью
С точностью  уравнение поверхности
уравнение поверхности  имеет вид
имеет вид

где  соответствующие радиусы кривизны поверхности 2.
соответствующие радиусы кривизны поверхности 2.
В отличие от  уравнение
уравнение  имеет решения только при
имеет решения только при  если два последних условия
если два последних условия  не выполнены, что соответствует отсутствию преломляющей поверхности (в случае, когда
не выполнены, что соответствует отсутствию преломляющей поверхности (в случае, когда  а поверхность 2 является плоской, это соответствует отражению в плоском зеркале). При выполнении всех условий
а поверхность 2 является плоской, это соответствует отражению в плоском зеркале). При выполнении всех условий  выражение
выражение  запишется в виде
запишется в виде

При получении выражения  использованы рассуждения, аналогичные тем, которые позволили перейти от
использованы рассуждения, аналогичные тем, которые позволили перейти от  Знак
Знак  определен так же, к
определен так же, к 
Из выражения  видно, что при
видно, что при 

 не зависит от
не зависит от 
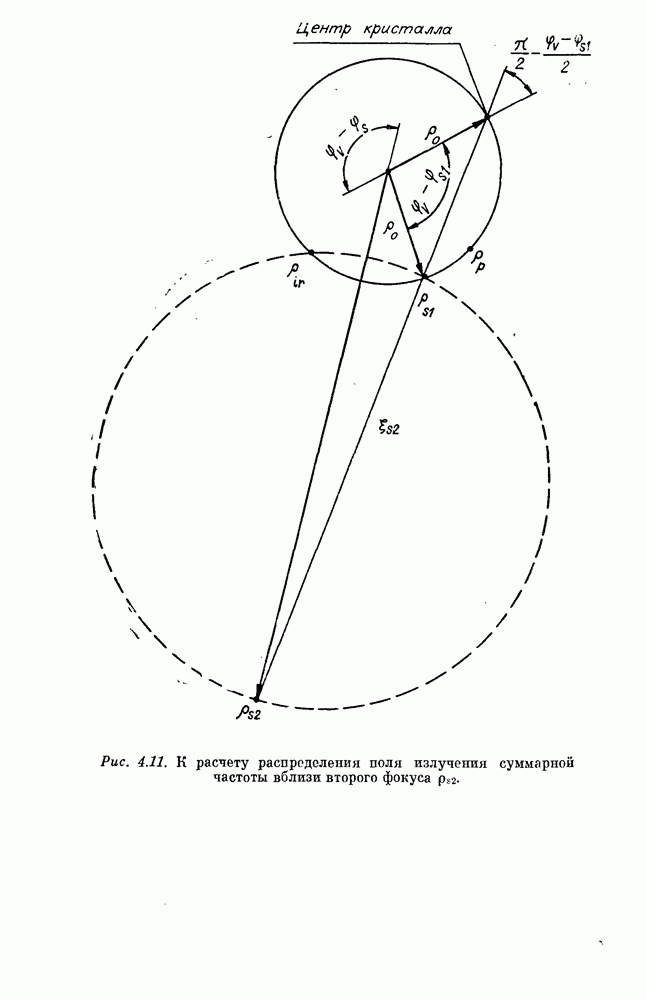
Таким образом, в точке наблюдения  удовлетворяющей уравнениям
удовлетворяющей уравнениям  излучение фокусируется в направлении
излучение фокусируется в направлении  Распределение поля вблизи этого фокуса описывается выражением
Распределение поля вблизи этого фокуса описывается выражением

где  продольная координата точки наблюдения
продольная координата точки наблюдения  в которой происходит фокусировка в направлении
в которой происходит фокусировка в направлении  В силу симметрии
В силу симметрии  относительно замены х на у, а у на х распределение поля вблизи второго фокуса
относительно замены х на у, а у на х распределение поля вблизи второго фокуса  определяемого формулой, аналогичной
определяемого формулой, аналогичной  с заменой х на у описывается формулой
с заменой х на у описывается формулой  тоже с заменой
тоже с заменой  Если поверхность
Если поверхность  является поверхностью вращения
является поверхностью вращения  то положение обоих фокусов совпадает и интеграл по 2 в формуле
то положение обоих фокусов совпадает и интеграл по 2 в формуле  превращается в интеграл Дебая [12]. Для вычисления аберраций необходимо в разложении фазы
превращается в интеграл Дебая [12]. Для вычисления аберраций необходимо в разложении фазы  учесть члены более высокого, чем второй, порядка. Если ограничиться случаев, когда
учесть члены более высокого, чем второй, порядка. Если ограничиться случаев, когда  является поверхностью вращения
является поверхностью вращения

то легко убедиться, что  При этом, вообще говоря, не существует такой точки наблюдения, для которой фаза
При этом, вообще говоря, не существует такой точки наблюдения, для которой фаза  была бы постоянна на всей поверхности 2. Если, однако, разделить поверхность
была бы постоянна на всей поверхности 2. Если, однако, разделить поверхность  на столь малые области, чтобы фазу
на столь малые области, чтобы фазу  в каждой из них можно было считать линейной функцией координат
в каждой из них можно было считать линейной функцией координат  внутри области, то для каждой области можно найти точку наблюдения, относительно которой фаза внутри области постоянна. Совокупность таких точек в плоскости
внутри области, то для каждой области можно найти точку наблюдения, относительно которой фаза внутри области постоянна. Совокупность таких точек в плоскости  где формируется параксиальное изображение, дает
где формируется параксиальное изображение, дает  аберрационное изображение источника. Отклонение
аберрационное изображение источника. Отклонение  от положения параксиального изображения нарушает уравнение
от положения параксиального изображения нарушает уравнение  В результате возникает дополнительное условие:
В результате возникает дополнительное условие:  должно быть выбрано таким образом, чтобы отличие
должно быть выбрано таким образом, чтобы отличие  от нуля
от нуля
в точности скомпенсировало бы  для данной области, т. е.
для данной области, т. е.

Решая уравнение  методом последовательных приближений, можно в
методом последовательных приближений, можно в  положить
положить 

где

Здесь  определяется выражением
определяется выражением

Если оси  выбраны так, что
выбраны так, что  то
то

где  углы между
углы между  и осью у.
и осью у.
Выражения  совпадают с формулами, полученными с помощью эйконала Зайделя [12, 129].
совпадают с формулами, полученными с помощью эйконала Зайделя [12, 129].
В качестве примера расчета распределения поля в явном виде можно рассмотреть задачу о преломлении излучения точечного источника на плоской границе раздела двух сред с гауссовой диафрагмой (3.49). В параксиальном приближении напряженность поля  в точке наблюдения
в точке наблюдения  после преломления дается
после преломления дается
формулой, следующей из 

После выполнения интегрирования по преломляющей поверхности имеем:

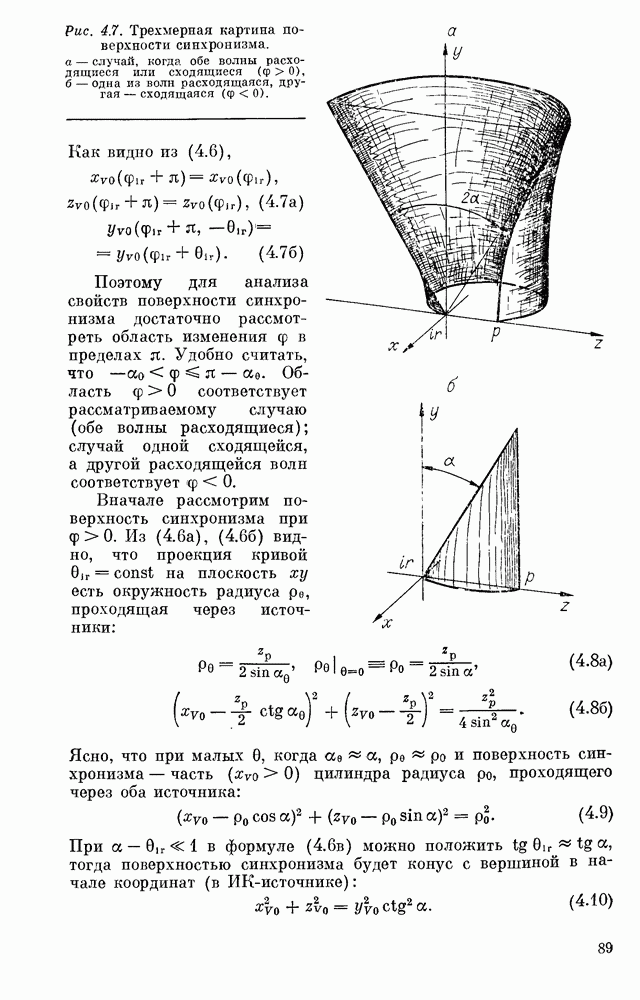
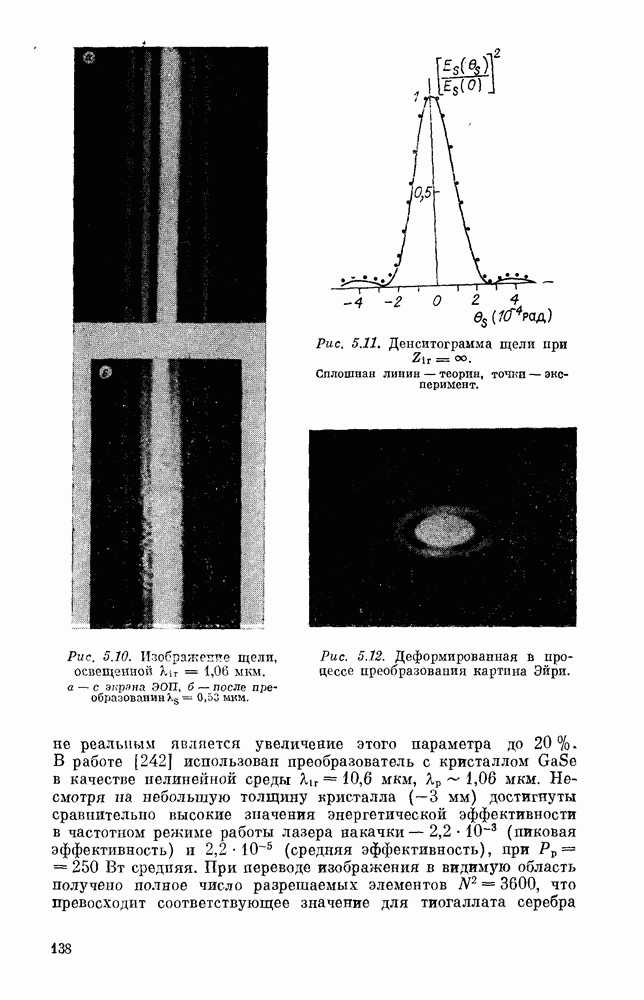
Анализ  приводит к следующим выводам:
приводит к следующим выводам:
— В данной плоскости наблюдения  яркость максимальна в точке
яркость максимальна в точке 

— Характерный размер  яркого пятна
яркого пятна

минимален в плоскости наблюдения

Здесь

При  имеем
имеем

Во фраунгоферовской зоне 

Формулы  имеют простой смысл. Если на плоскую преломляющую поверхность с гауссовой диафрагмой падает плоская волна, то после преломления, очевидно, формируется гауссов пучок с фокусом на диафрагме.
имеют простой смысл. Если на плоскую преломляющую поверхность с гауссовой диафрагмой падает плоская волна, то после преломления, очевидно, формируется гауссов пучок с фокусом на диафрагме.
С точки зрения формирования изображения представляет интерес не плоскость наблюдения, где  минимально, а плоскость наблюдения, по отношению к которой минимально
минимально, а плоскость наблюдения, по отношению к которой минимально 

Отсюда немедленно следуют хорошо известные формулы для параметров изображения, формируемого плоской преломляющей поверхностью с диафрагмой 

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
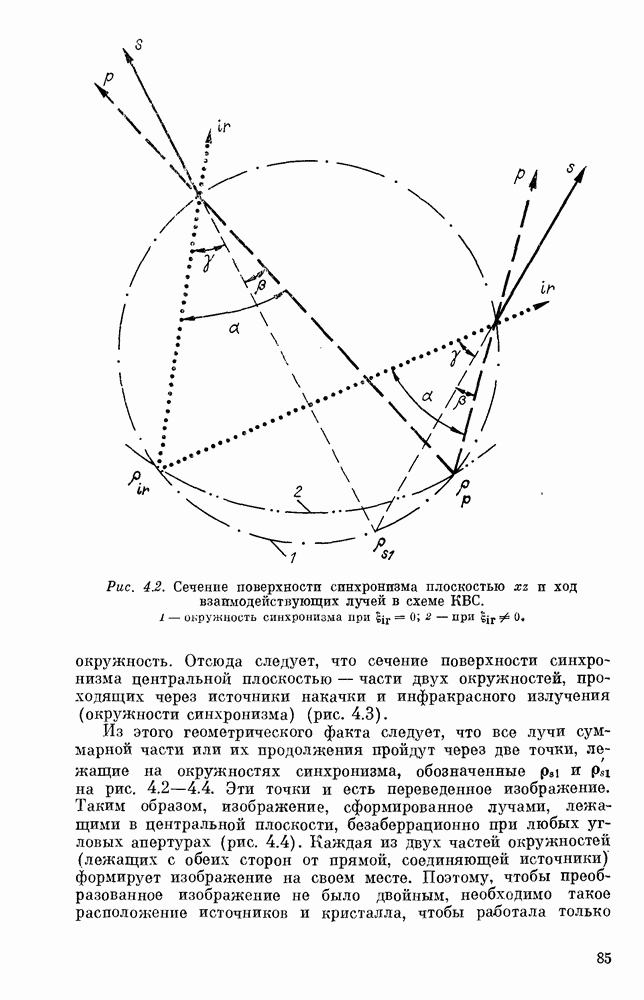
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
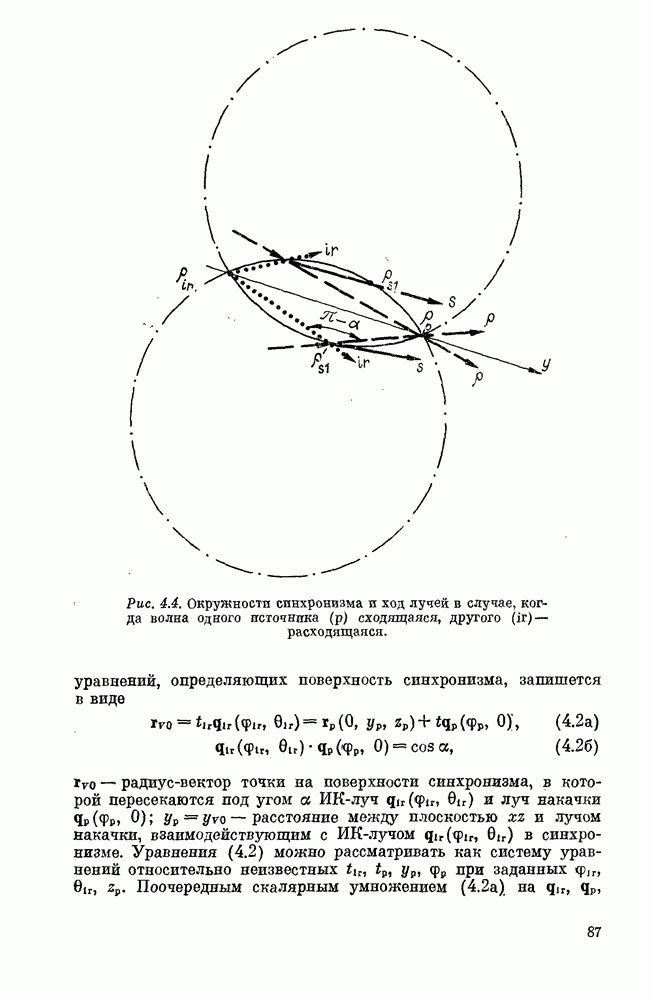
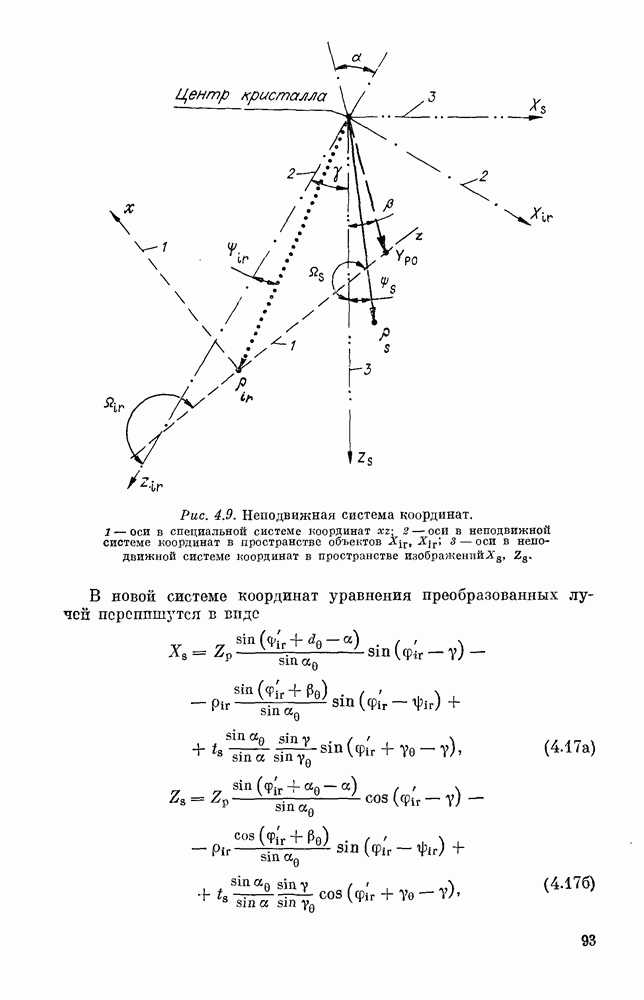
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
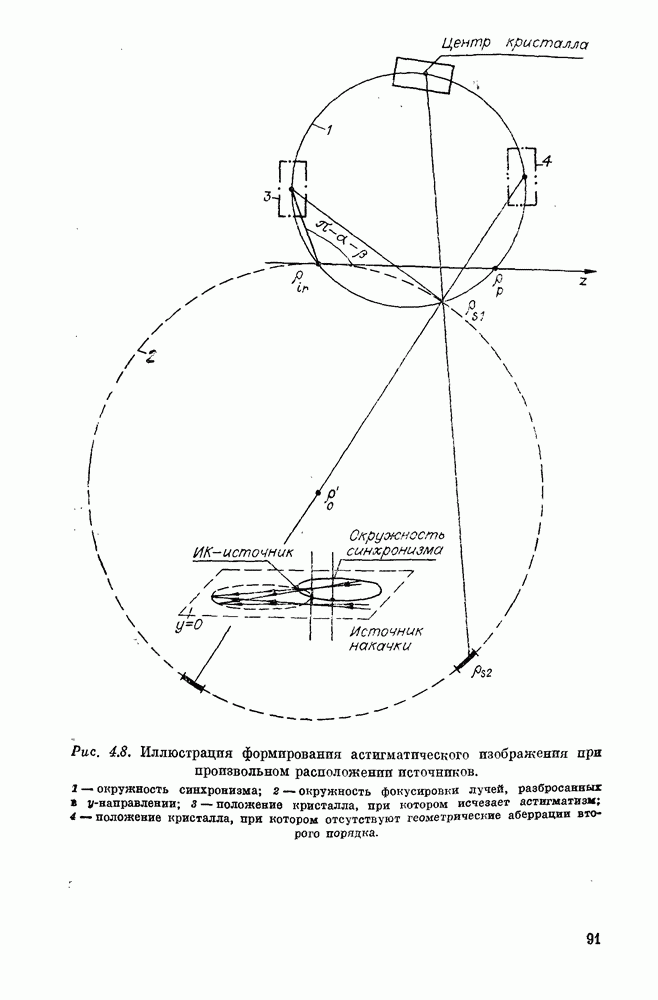
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
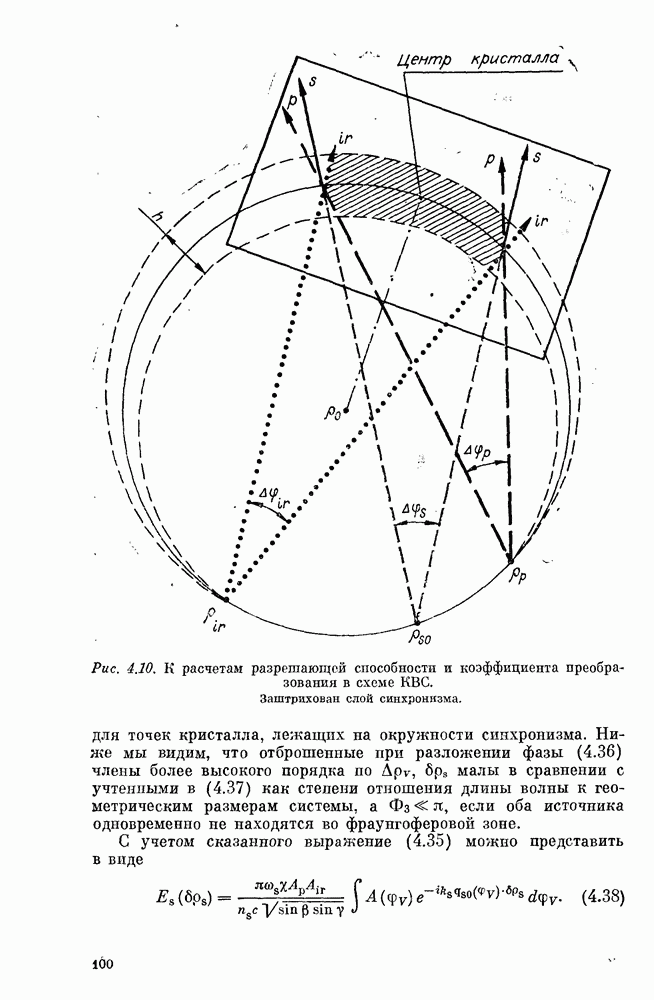
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)