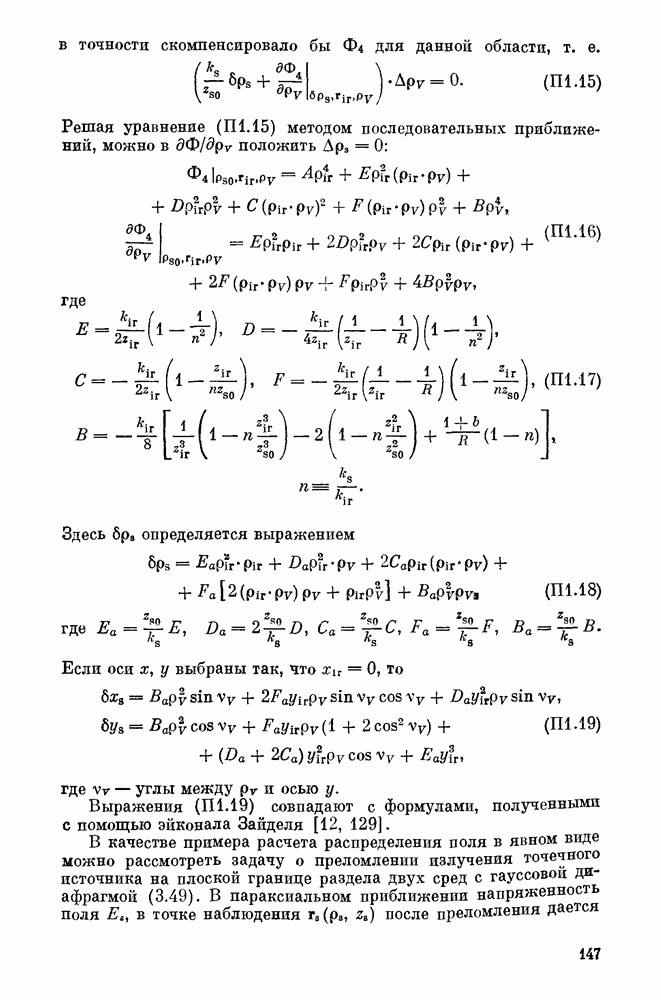| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
Установленная выше аналогия между линейно-оптическим преобразователем и линейной оптической системой (3.6) (преломляющая поверхность  и диафрагмой
и диафрагмой  позволяет весьма просто и в общем виде решить вопрос об эффективности преобразователя
позволяет весьма просто и в общем виде решить вопрос об эффективности преобразователя  определяемой как отношение интенсивностей сигнального излучения суммарной частоты и ИК-излучении:
определяемой как отношение интенсивностей сигнального излучения суммарной частоты и ИК-излучении:

При этом нет необходимости находить форму распределения в явном виде. В самом деле, для получения ответа достаточно
подобрать источник излучения с такой амплитудой, чтобы после прохождения сквозь диафрагму (3.7) возникло иоле, совпадающее с генерируемым параметрическим преобразователем:

Из (3.65) имеем

где  амплитуды соответствующих электромагнитных волн в центре нелинейной среды. Мы видим, что коэффициент преобразования (энергетическая эффективность), определяемый как отношение иптенсивностей сигнального и инфракрасного излучения в апертуре диафрагмы (3.7), в самом общем случае произвольного расположения источников накачки и ИК-излучения совпадает с
амплитуды соответствующих электромагнитных волн в центре нелинейной среды. Мы видим, что коэффициент преобразования (энергетическая эффективность), определяемый как отношение иптенсивностей сигнального и инфракрасного излучения в апертуре диафрагмы (3.7), в самом общем случае произвольного расположения источников накачки и ИК-излучения совпадает с  имеющим место при взаимодействии плоских волн (источники на бесконечности) (см. (1.73), (1.134)).
имеющим место при взаимодействии плоских волн (источники на бесконечности) (см. (1.73), (1.134)).
Для понимания принципиальных возможностей схемы касательного синхронизма удобно связать коэффициент преобразования с числом разрешаемых элементов и полной мощностью накачки, комбинируя тем или иным способом формулы (3.66), (3.9):

Мы видим, что величина

есть инвариант, определяющийся только частотой преобразованного излучения и свойствами нелинейной среды — показателями преломления взаимодействующих волн и нелинейной восприимчивостью.
В случае преобразования широкополосного спектра помимо коэффициента преобразования и числа разрешаемых элементов важной характеристикой является ширина преобразуемого спектра (1.87), (1.89). Комбинируя эти формулы с (3.676),
можно, исключив  получить более общие, чем (3.68), инварианты. При
получить более общие, чем (3.68), инварианты. При

коэффициент преобразования и упомянутый инвариант определяются выражениями:

В случае дисперсионного согласования, когда справедливо неравенство, обратное (3.69), вместо (3.70) имеем

Формулы (3.9), (3.20)-(3.29), (3.58), (1.87), (1.89), (3.66), (3.67) позволяют рассчитать характеристики конкретного преобразователя, если известны нелинейная восприимчивость и показатели преломления нелинейной среды, ее размеры, а также параметры накачки. Инварианты (3.68), (3.70), (3.71) позволяют оценить принципиальные возможности схемы касательного синхронизма и понять, насколько можно, варьируя, например, размеры нелинейной среды, улучшить одни характеристики преобразователя за счет других.
В заключение главы упомянем некоторые дополнительные свойства схемы касательного синхронизма. Слабое  затухание волн в кристалле очевидным образом влияет на коэффициент преобразования и несколько уменьшает ширину функции разброса, что обусловлено уменьшением (благодаря затуханию) эффективной длины кристалла [180].
затухание волн в кристалле очевидным образом влияет на коэффициент преобразования и несколько уменьшает ширину функции разброса, что обусловлено уменьшением (благодаря затуханию) эффективной длины кристалла [180].
Наличие оптических неоднородностей в кристалле приводит к ухудшению поперечного разрешения в  раз, где
раз, где  корреляционный радиус функции
корреляционный радиус функции  набег фаз за счет неоднородностей [179].
набег фаз за счет неоднородностей [179].
Пространственная или временная некогерентность накачки не ухудшает разрешающей способности до тех пор, пока ширины спектров (частотного и/или углового) не превосходят соответствующих ширин синхронизма. При дальнейшем ухудшении когерентности накачки ширина функции разброса уменьшается, но появляется фон, ухудшающий контрастность изображения. Коэффициент преобразования меняется существенно: начиная с некоторых интенсивностей накачки он перестает от нее зависеть и максимальное значение эффективности по числу квантов
составляет 50%, а не 100% (как для идеальной накачки). Эти результаты получены теоретически и проверены экспериментально в работе [123]. Ранее вид функции разброса в таких условиях подробно проанализирован в [181]. Общий вывод состоит в том, что влияние немонохроматичности и расходимости накачки резко падает при помещении инфракрасного объекта в середину нелинейного кристалла (с учетом преломления  а не
а не 
Двухкаскадное преобразование инфракрасного излучения реализовано экспериментально в [59, 60]. Такая методика позволяет использовать кристаллы с большой нелинейностью в сочетании с удобными для эксперимента лазерами накачки (например,  для перевода достаточно длинноволнового
для перевода достаточно длинноволнового  излучения в видимую область. В [58] рассчитана функция разброса двухкаскадного преобразователя изображения. Разрешающая способность преобразователя определяется кристаллом с меньшей угловой шириной синхронизма. В оптимальном случае равных ширин разрешение двухкаскадной схемы, рассчитанное по полуширине функции разброса, оказалось выше для двухкаскадной схемы по сравнению с однокаскадной, существенно уменьшается и отношение амплитуд побочного и главного максимума. Сказанное объясняется тем, что фактор
излучения в видимую область. В [58] рассчитана функция разброса двухкаскадного преобразователя изображения. Разрешающая способность преобразователя определяется кристаллом с меньшей угловой шириной синхронизма. В оптимальном случае равных ширин разрешение двухкаскадной схемы, рассчитанное по полуширине функции разброса, оказалось выше для двухкаскадной схемы по сравнению с однокаскадной, существенно уменьшается и отношение амплитуд побочного и главного максимума. Сказанное объясняется тем, что фактор  (двухкаскадный вариант) не имеет отрицательных областей и не меняет фазы подынтегрального выражения в (3.50) в отличие от однокаскадного фактора
(двухкаскадный вариант) не имеет отрицательных областей и не меняет фазы подынтегрального выражения в (3.50) в отличие от однокаскадного фактора 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
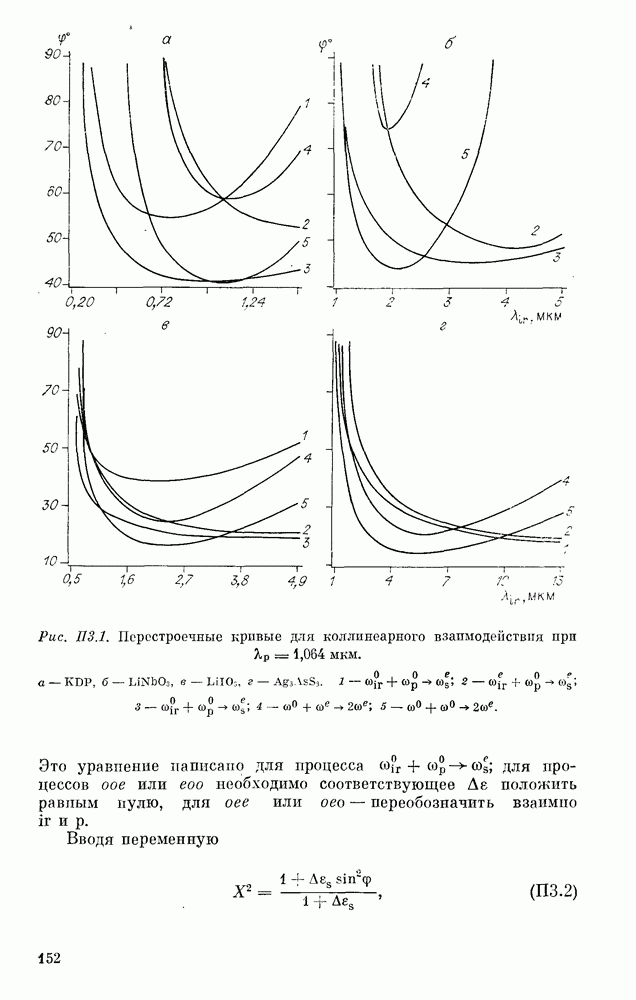
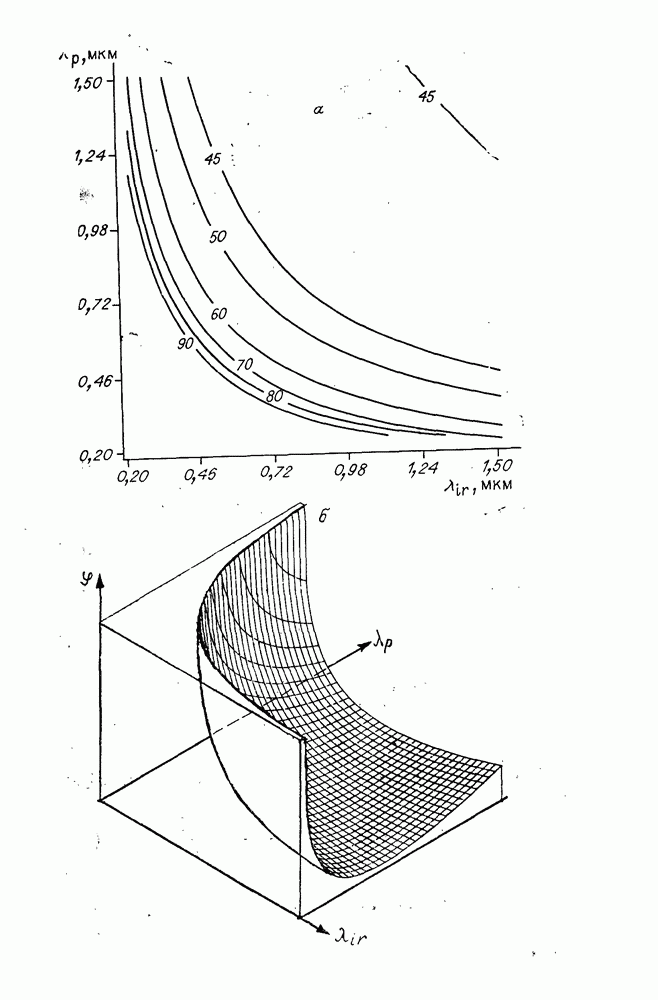
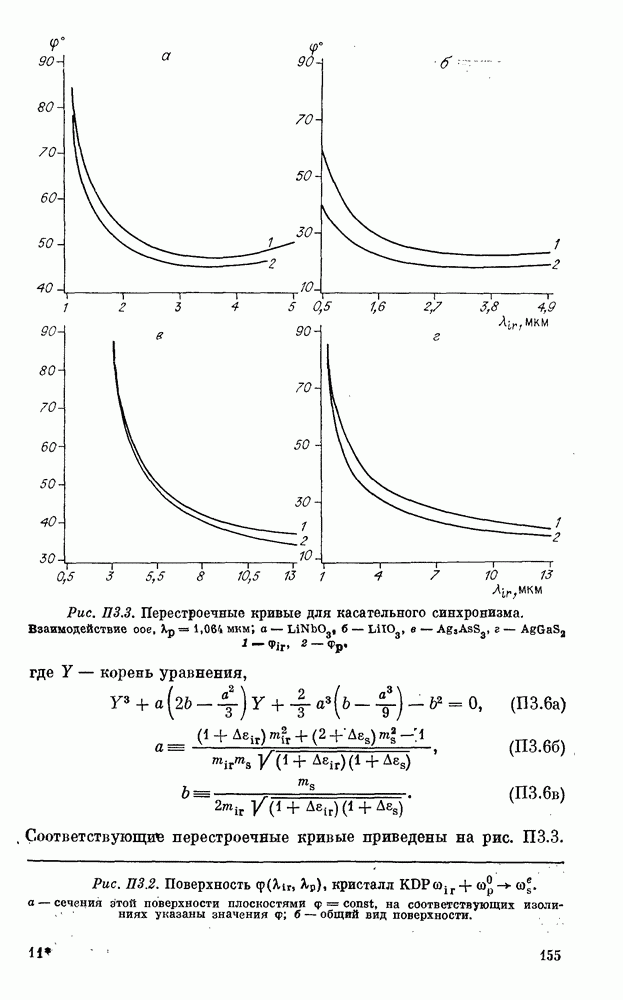
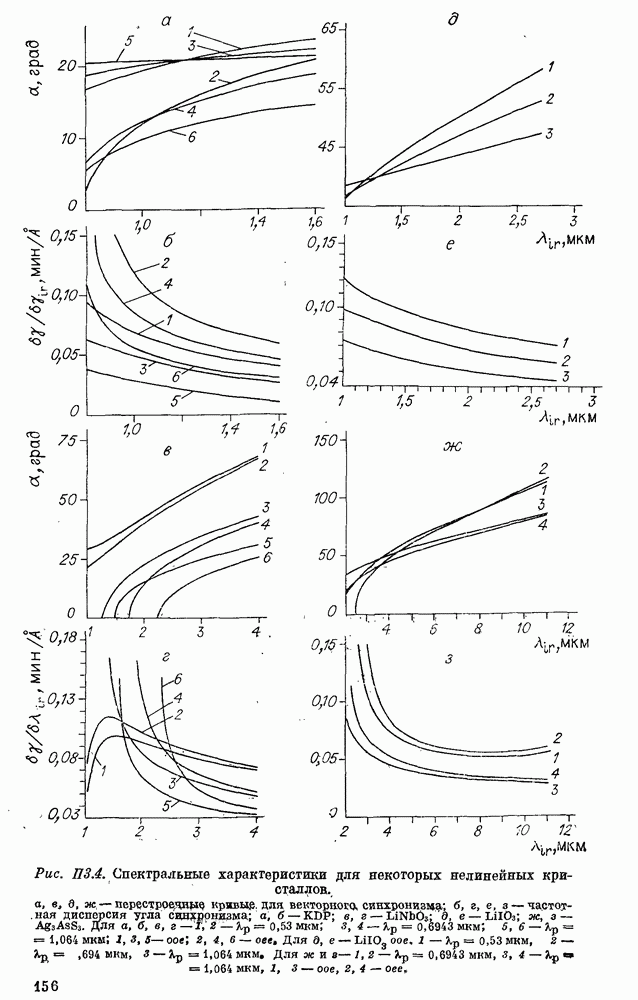
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)