| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
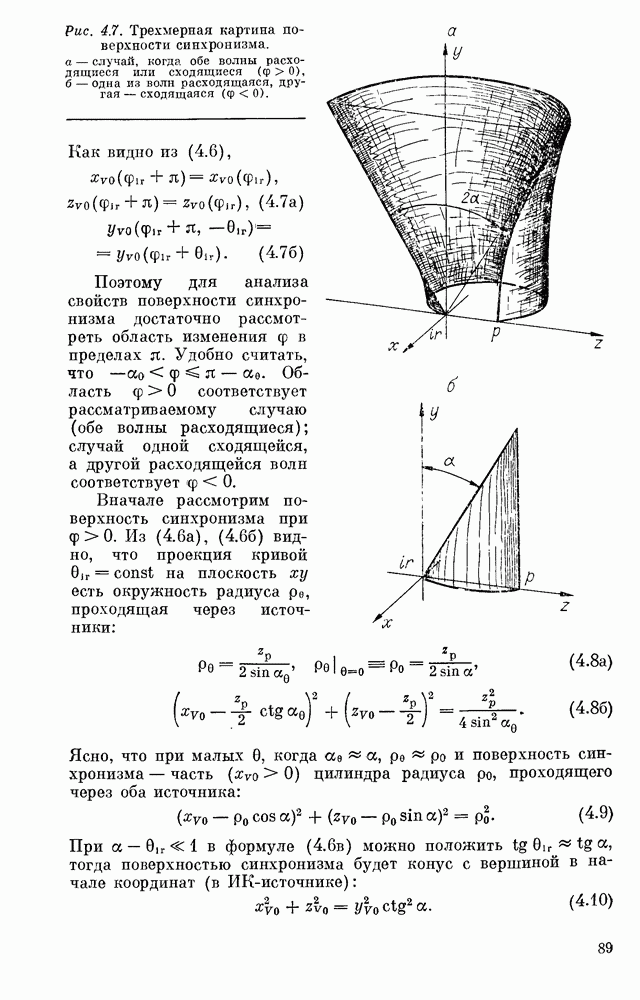
§ 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
Рассмотрим случай, когда накачка представляет собой сферическую волну с центром в точке  Формула (2.27), описывающая распределение поля суммарной частоты, принимает вид
Формула (2.27), описывающая распределение поля суммарной частоты, принимает вид

где  амплитуды сферических волн накачки и ИК-излучения соответственно.
амплитуды сферических волн накачки и ИК-излучения соответственно.
Фаза подынтегрального выражения (3.1)

При смещении вдоль оси  не меняется, если выполнено условие касательного синхронизма:
не меняется, если выполнено условие касательного синхронизма:

При смещении вдоль любой прямой, параллельной оси  и проходящей через точку
и проходящей через точку  фаза (3.2) (с учетом (3.3а)) меняется с изменением
фаза (3.2) (с учетом (3.3а)) меняется с изменением  тем быстрее, чем больше
тем быстрее, чем больше  (проекция радиуса-вектора
(проекция радиуса-вектора  на плоскость
на плоскость  Набег фазы по длине кристалла
Набег фазы по длине кристалла  больше
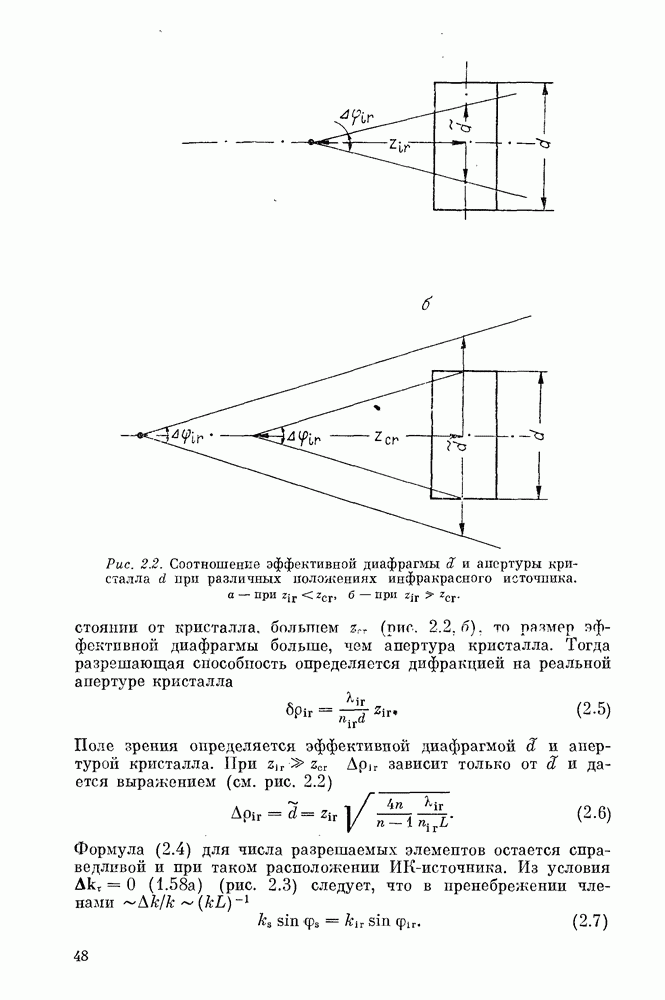
больше  приводит к незначительному вкладу в преобразованное излучение соответствующих частей нелинейной среды из-за эффекта интерференции. Таким образом, когерентность объемно расположенных источников приводит к возникновению эффективной диафрагмы.
приводит к незначительному вкладу в преобразованное излучение соответствующих частей нелинейной среды из-за эффекта интерференции. Таким образом, когерентность объемно расположенных источников приводит к возникновению эффективной диафрагмы.
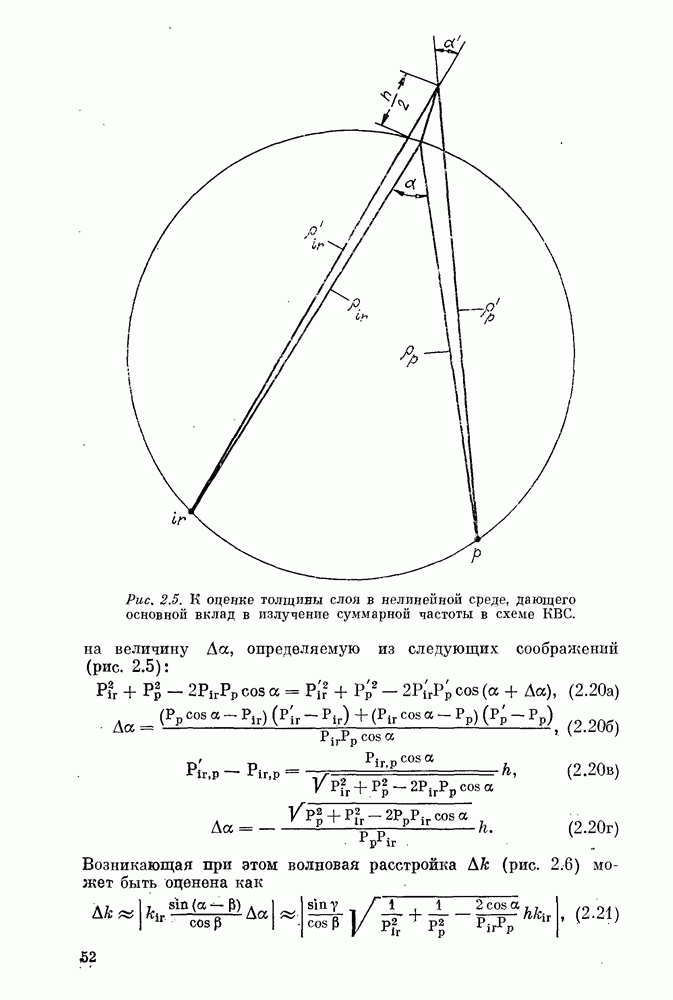
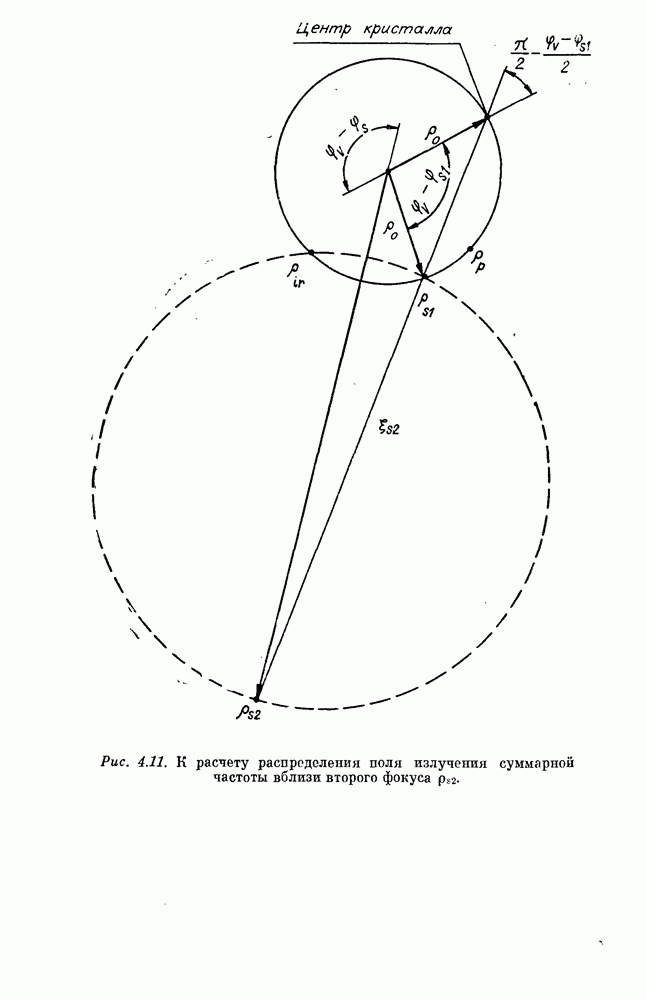
Рассмотрим случай, когда оба источника находятся настолько далеко от кристалла, что фазу (3.2) можно считать линейной функцией продольной координаты 

 углы между осью z и прямыми, соединяющими точку
углы между осью z и прямыми, соединяющими точку  с источником накачки
с источником накачки  ИК-излучения
ИК-излучения  и точкой, в которой формируется изображение фазовой поверхностью накачки, проходящей через центр кристалла (рис. 3.1)
и точкой, в которой формируется изображение фазовой поверхностью накачки, проходящей через центр кристалла (рис. 3.1)  радиусы-векторы точек в кристалле, лежащие на
радиусы-векторы точек в кристалле, лежащие на

Рис. 3.1. К расчету линейной по  части фазы (3.2), (3.4).
части фазы (3.2), (3.4).
указанной фазовой поверхности. Условия применимости выражений (3.4), подробно рассмотренные в следующем параграфе, можно приближенно записать следующим образом:

С учетом сказанного выражение (3.2) принимает вид

 - амплитудная прозрачность упомянутой диафрагмы
- амплитудная прозрачность упомянутой диафрагмы

Интегрирование в (3.6) идет по поверхности  совпадающей с фазовым фронтом накачки, проходящим через центр кристалла.
совпадающей с фазовым фронтом накачки, проходящим через центр кристалла.
Интеграл по  в (3.6) по форме совпадает с интегралом Френеля — Кирхгофа для преломляющей поверхности
в (3.6) по форме совпадает с интегралом Френеля — Кирхгофа для преломляющей поверхности  Поэтому формулы (3.6), (3.7) подтверждают, что параметрический преобразователь в схеме касательного синхронизма эквивалентен сферической преломляющей поверхности с радиусом
Поэтому формулы (3.6), (3.7) подтверждают, что параметрический преобразователь в схеме касательного синхронизма эквивалентен сферической преломляющей поверхности с радиусом  и показателем преломления
и показателем преломления  расположенной в центре кристалла, с апертурной диафрагмой (3.7), зависящей от положения ИК-источника.
расположенной в центре кристалла, с апертурной диафрагмой (3.7), зависящей от положения ИК-источника.
В параксиальном приближении  от (3.46) можно перейти к следующему выражению для
от (3.46) можно перейти к следующему выражению для 

Формулы тонкой линзы определяют положение идеального изображения:

Для упрощения выражений рассмотрим случай  тогда
тогда  В пренебрежении членами
В пренебрежении членами 
 выражение (3.8) принимает вид
выражение (3.8) принимает вид

Распределение поля вблизи точки формирования идеального изображения  описывается интегралом Дебая, в который переходит выражение (3.6) после разложения фазы в показателе экспоненты в ряд по степеням
описывается интегралом Дебая, в который переходит выражение (3.6) после разложения фазы в показателе экспоненты в ряд по степеням  и пренебрежения всеми членами, кроме первого [7, 223]. Здесь
и пренебрежения всеми членами, кроме первого [7, 223]. Здесь  отклонение точки наблюдения от положения идеального изображения
отклонение точки наблюдения от положения идеального изображения  Итак, вместо (3.6) с учетом (3.7) имеем
Итак, вместо (3.6) с учетом (3.7) имеем

В плоскости идеального изображения  распределение поля при наличии осевой симметрии системы описывается формулой
распределение поля при наличии осевой симметрии системы описывается формулой

где  функция Бесселя нулевого порядка,
функция Бесселя нулевого порядка,  апертура нелинейной среды. Видим, что характерный диаметр
апертура нелинейной среды. Видим, что характерный диаметр  эффективной диафрагмы (3.7) при
эффективной диафрагмы (3.7) при  дается выражением
дается выражением

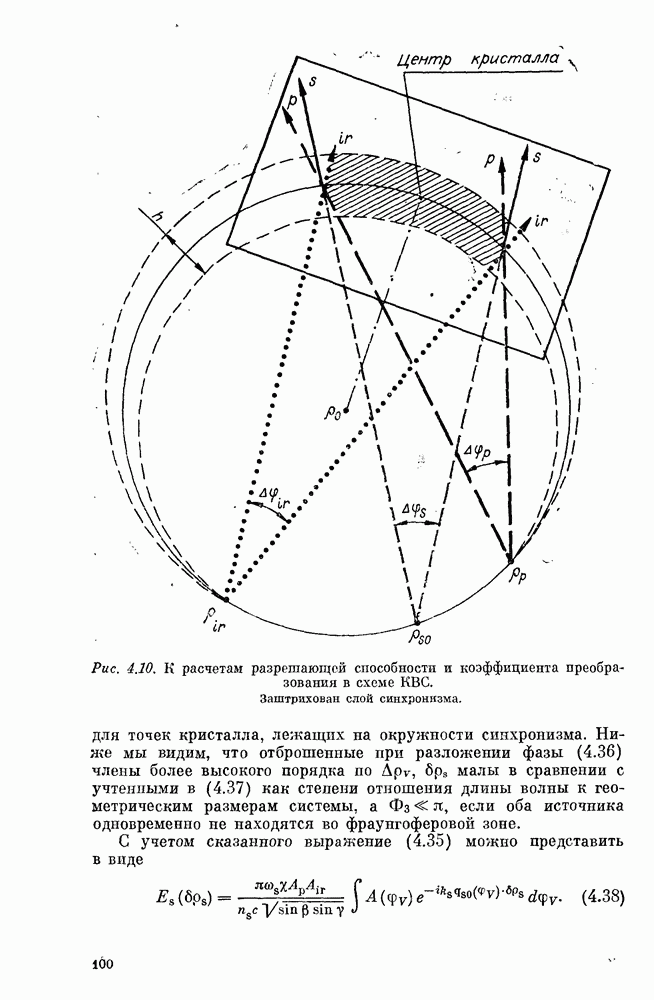
Размытие изображения определяется дифракцией или геометрическими аберрациями в зависимости от соотношения диаметра с? диафрагмы  кривизны фазового фронта накачки и положения ИК-источника относительно кристалла. Ясно, что в ситуациях, когда диаметр
кривизны фазового фронта накачки и положения ИК-источника относительно кристалла. Ясно, что в ситуациях, когда диаметр  диафрагмы (3.7) больше апертуры кристалла
диафрагмы (3.7) больше апертуры кристалла  размытие изображения определяется именно апертурой кристалла.
размытие изображения определяется именно апертурой кристалла.
Заметим, что введение положительной расстройки  увеличивает размер эффективной диафрагмы. Очевидно, что это обстоятельство связано с некоторым увеличением угловой ширины синхронизма по сравнению со случаем
увеличивает размер эффективной диафрагмы. Очевидно, что это обстоятельство связано с некоторым увеличением угловой ширины синхронизма по сравнению со случаем  Оптимальное
Оптимальное 
чепие  ограничено сверху условием, чтобы прозрачность диафрагмы (3.7) в центре
ограничено сверху условием, чтобы прозрачность диафрагмы (3.7) в центре  оставалась не слишком малой. При
оставалась не слишком малой. При  как видно из
как видно из  возрастает вдвое, что означает увеличение разрешающей способности приблизительно в полтора раза. Точные цифры можно получить численными методами с помощью выражения (3.116). Проведенный в работе [180] (см. § 3) и основанный на более громоздких вычислениях, связанных с разложением по плоским волнам, анализ для плоской волны накачки
возрастает вдвое, что означает увеличение разрешающей способности приблизительно в полтора раза. Точные цифры можно получить численными методами с помощью выражения (3.116). Проведенный в работе [180] (см. § 3) и основанный на более громоздких вычислениях, связанных с разложением по плоским волнам, анализ для плоской волны накачки  гауссовой апертурной диафрагмой дал оптимальное значение
гауссовой апертурной диафрагмой дал оптимальное значение  и увеличение разрешающей способности вдвое по сравнению, со случаем
и увеличение разрешающей способности вдвое по сравнению, со случаем 
Как видно из формулы (3.11), фокусировка накачки позволяет увеличить разрещающую способность преобразователя в схеме касательного синхронизма вплоть до дифракционной (при  Чтобы найти число разрешаемых элементов, кроме (3.6), (3.7), необходимо иметь такие выражения, относящиеся к произвольным положениям ИК-источника. Соответствующие результаты приведены в следующем параграфе.
Чтобы найти число разрешаемых элементов, кроме (3.6), (3.7), необходимо иметь такие выражения, относящиеся к произвольным положениям ИК-источника. Соответствующие результаты приведены в следующем параграфе.
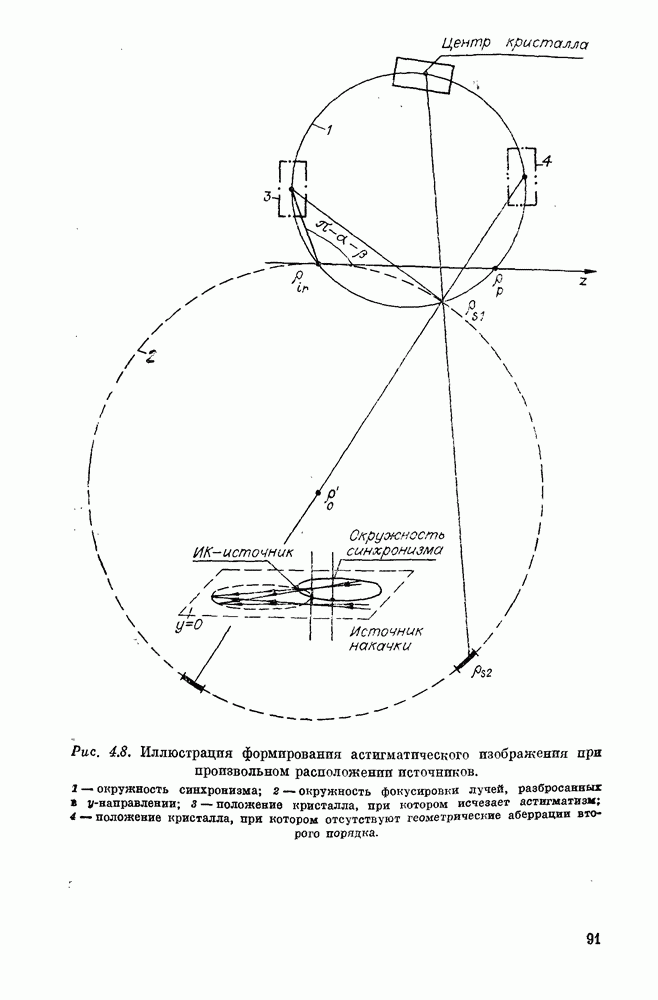
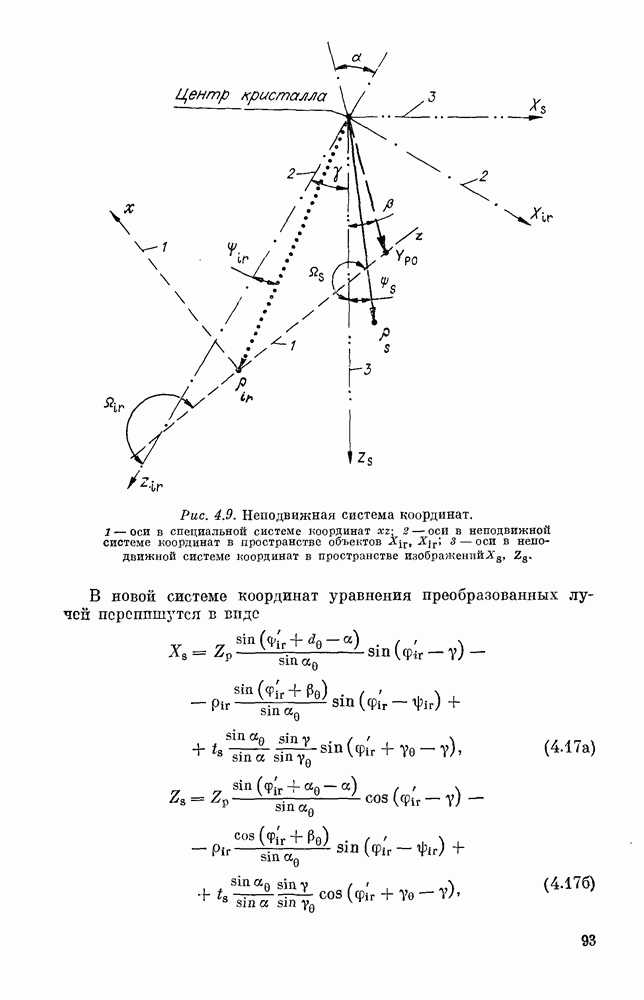
Слияние анизотропии кристалла на формирование изображения можно учесть в рамках изложенного метода в параксиальном приближении, используя выражение (2.27) с функцией Грина, определяемой формулами  или
или  вместо (2.26), и соответствующие выражения для идущих от точечных источников волп ИК-излучения и накачки вместо (2.33). Такой подход позволяет получить все основные эффекты, связанные с анизотропией и проанализированные в § 3 настоящей главы разложением по плоским волнам. Можно, в частности, убедиться, что при малой анизотропии ее роль сводится к «сносу» изображения.
вместо (2.26), и соответствующие выражения для идущих от точечных источников волп ИК-излучения и накачки вместо (2.33). Такой подход позволяет получить все основные эффекты, связанные с анизотропией и проанализированные в § 3 настоящей главы разложением по плоским волнам. Можно, в частности, убедиться, что при малой анизотропии ее роль сводится к «сносу» изображения.
Резюмируем результаты этого параграфа. Пространное распределение поля в преобразованном излучений в отсутствие геометрических аберраций всегда имеет дифракционный характер. В схеме касательного синхронизма — это дифракция на эффективной диафрагме, определяемой формулами (3.7), (3.12). Фокусировка накачки при параметрическом преобразовании в схеме касательного синхронизма позволяет изменить как положение преобразованного изображения, так и разрешающую способность преобразователя.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
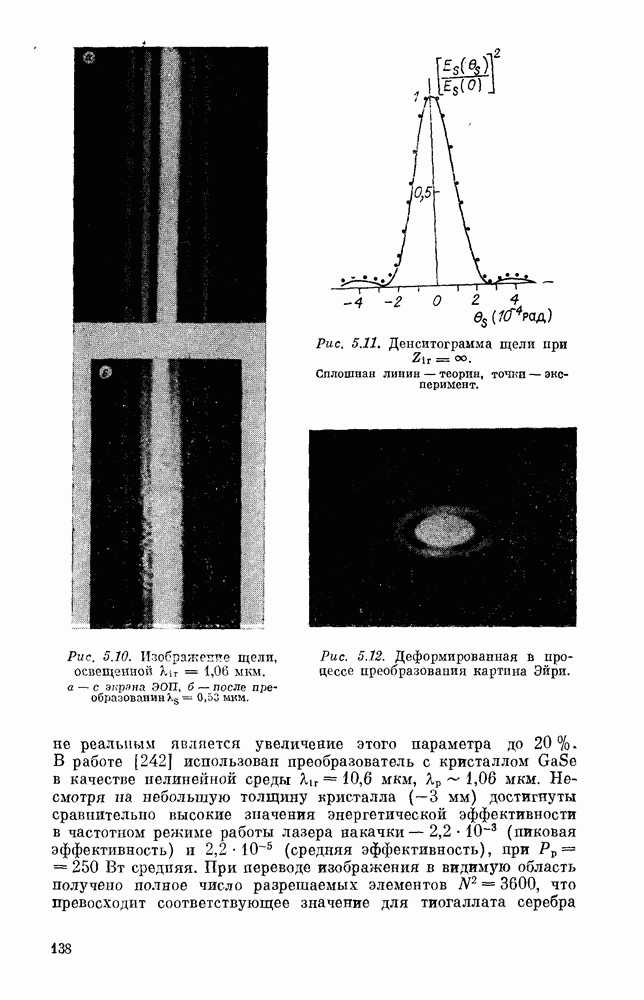
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
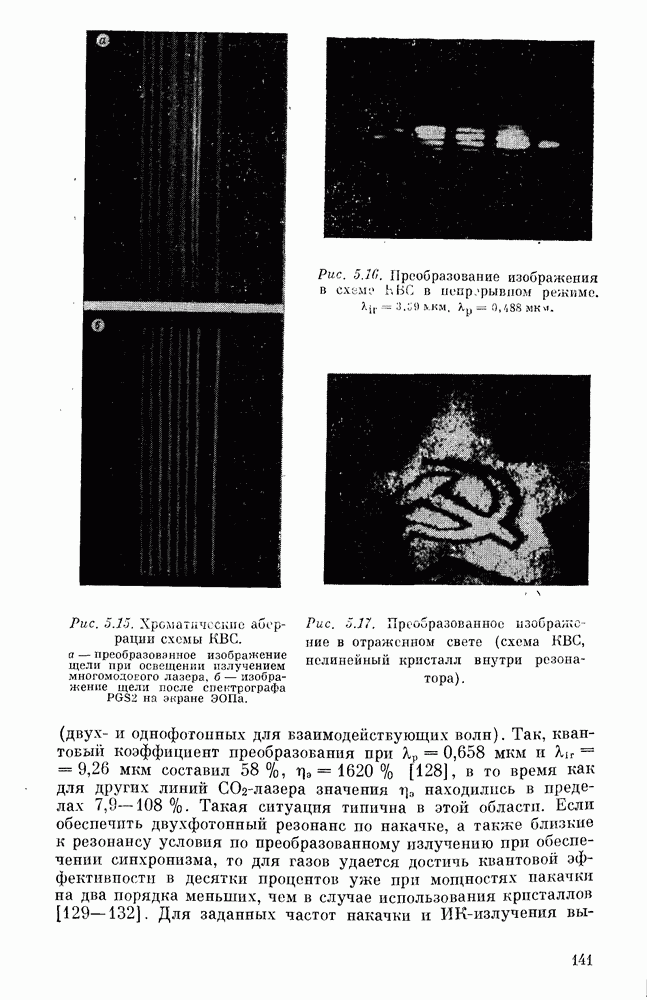
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)