| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
Для вычисления эффективности  преобразователя в схеме КВС удобно воспользоваться тем же подходом, что и в случае схемы касательного синхронизма (см. гл. 3, § 5). Определяющим, как и прежде, является то обстоятельство, что пространственное распределение интенсивности излучения
преобразователя в схеме КВС удобно воспользоваться тем же подходом, что и в случае схемы касательного синхронизма (см. гл. 3, § 5). Определяющим, как и прежде, является то обстоятельство, что пространственное распределение интенсивности излучения  в области формирования идеального изображения совпадает по форме с дифракционным распределением. Это позволяет выбрать амплитуду
в области формирования идеального изображения совпадает по форме с дифракционным распределением. Это позволяет выбрать амплитуду
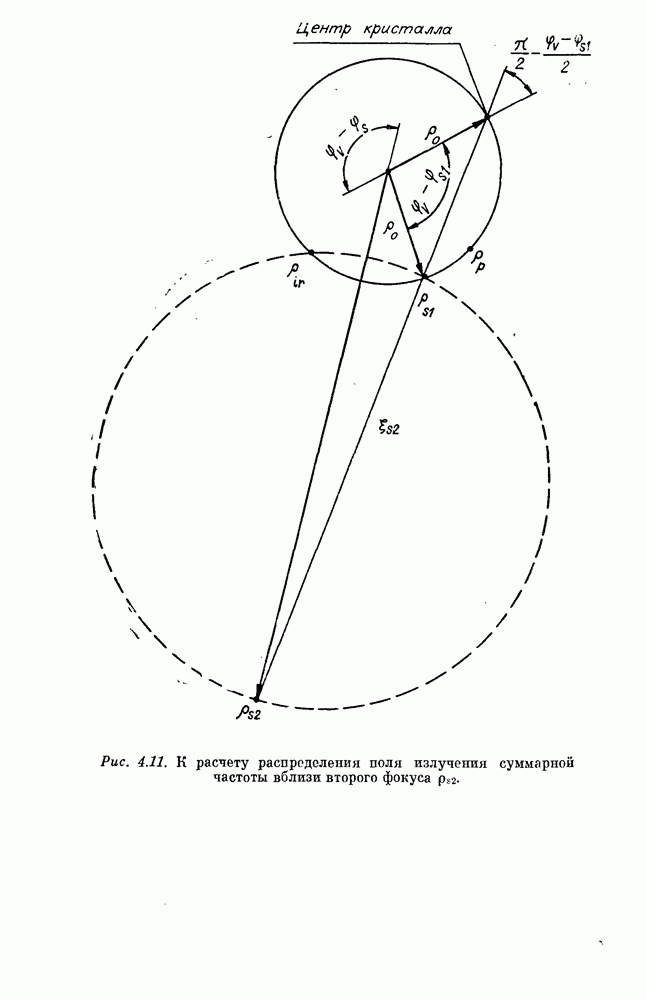
эквивалентного источника излучения суммарной частоты так, чтобы после прохождения через диафрагму (4.39) возникло поле, совпадающее с генерируемым в нелинейно-оптическом преобразователе. Эквивалентный источник имеет смысл поместить в точку формирования идеального изображения. В случае преобразования объекта, находящегося на конечном расстоянии от кристалла и, следовательно, при наличии астигматизма (4.18), будем считать, что в плоскости диафрагмы (4.39) (поверхность сихронизма) имеется преломляющая поверхность с различными радиусами кривизны в перпендикулярных нацравлениях (I и У). Такая поверхность превратит сферическую волну от точечного эквивалентного источника в астигматический пучок (см. Приложение 1), удобный для сравнения с полем выходного излучения преобразователя в схеме КВС.
Начнем с двумерной модели преобразователя. Эквивалентным источником в этом случае является источник цилиндрической волны, ось которого параллельна оси фокусировки накачки. С учетом (4.45) имеем

Отсюда следует:

Напряженность электрического поля волны  вблизи поверхности синхроннзма определяется выражением
вблизи поверхности синхроннзма определяется выражением

Формулы для энергетических коэффициентов преобразованы по интенсивности  и полной мощности
и полной мощности  и принимают вид:
и принимают вид:

где  апертура кристалла (луча накачки) в направлении оси фокусировки накачки.
апертура кристалла (луча накачки) в направлении оси фокусировки накачки.
В более интересной для практики модели преобразователя, где ИК-излучение имеет вид сферической волны, вместо (4.70) (полагая, что эквивалентный источник находится в точке  и в (4.58), (4.59) и
и в (4.58), (4.59) и  имеем
имеем

Из (4.73) следует, что соотношение между напряженностями электрических полей взаимодействующих волн, а также формулы для  остаются прежними (см. (4.71), (4.72)). Все сказанное сохраняет силу и для преобразования изображения бесконечно удаленного источника. Аналогичные вычисления приводят к следующей формуле, связывающей амплитуды
остаются прежними (см. (4.71), (4.72)). Все сказанное сохраняет силу и для преобразования изображения бесконечно удаленного источника. Аналогичные вычисления приводят к следующей формуле, связывающей амплитуды  плоских волн излучений частот
плоских волн излучений частот 

Из (4.74) с учетом направлений распространения волн относительно нормали к поверхности синхронизма снова приходим к формулам (4.72).
Из (4.72) следует, что как  так и
так и  обратно пропорциональны
обратно пропорциональны  тогда как число разрешаемых элементов прямо пропорционально этим параметрам (см. (4.64)). Отсюда следует, что, как и в схеме касательного синхронизма, требования высокой эффективности и возможно большего числа разрешаемых элементов являются здесь взаимно противоположными друг другу. Поэтому имеет смысл ввести инвариант, аналогичный (3.68):
тогда как число разрешаемых элементов прямо пропорционально этим параметрам (см. (4.64)). Отсюда следует, что, как и в схеме касательного синхронизма, требования высокой эффективности и возможно большего числа разрешаемых элементов являются здесь взаимно противоположными друг другу. Поэтому имеет смысл ввести инвариант, аналогичный (3.68):

Условия применимости формул (4.69) — (4.76) определяются неравенствами (4.50). При  эти неравенства означают, что в случае преобразования бесконечно удаленного ИК-объекта источник накачки не должен находиться во фраунгоферовой зоне. Таким образом, (4.69) — (4.74) при
эти неравенства означают, что в случае преобразования бесконечно удаленного ИК-объекта источник накачки не должен находиться во фраунгоферовой зоне. Таким образом, (4.69) — (4.74) при  справедливы при уменьшении
справедливы при уменьшении  (увеличении
(увеличении  вплоть до значений
вплоть до значений  а формулы (4.75), (4.76) остаются в силе при уменьшении
а формулы (4.75), (4.76) остаются в силе при уменьшении  вплоть до
вплоть до  При меньших значениях
При меньших значениях  при расчете излучения суммарной частоты необходимо учесть все слагаемые в
при расчете излучения суммарной частоты необходимо учесть все слагаемые в
выражении для фазы (4.37), что дает при  переход от (4.69) -(4.76) к выражениям (1.70), (1.128), описывающим взаимодействие плоских волн при параметрическом сложении частот в нелинейной среде.
переход от (4.69) -(4.76) к выражениям (1.70), (1.128), описывающим взаимодействие плоских волн при параметрическом сложении частот в нелинейной среде.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
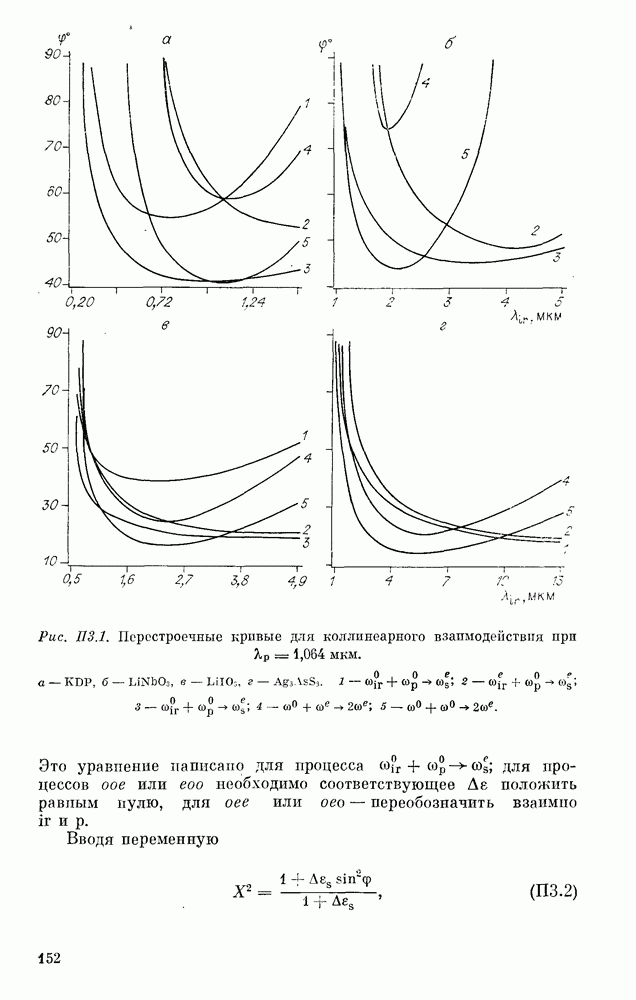
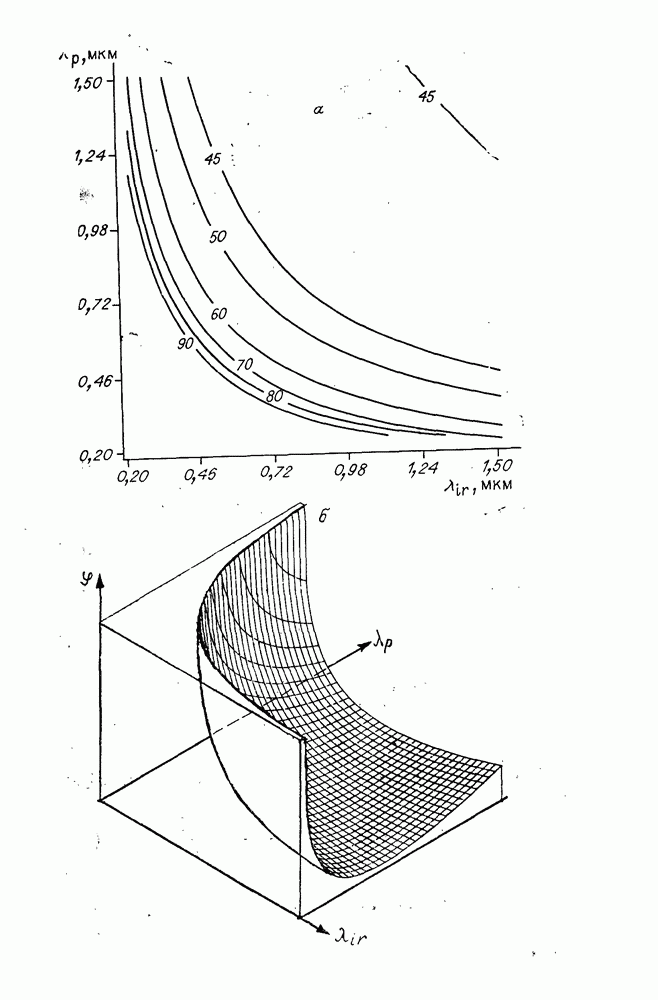
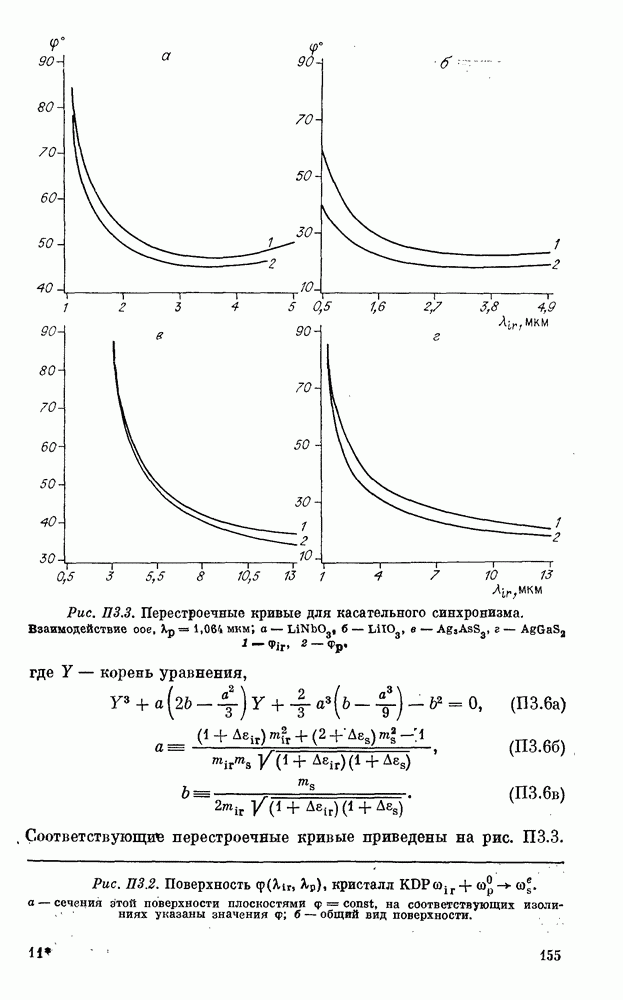
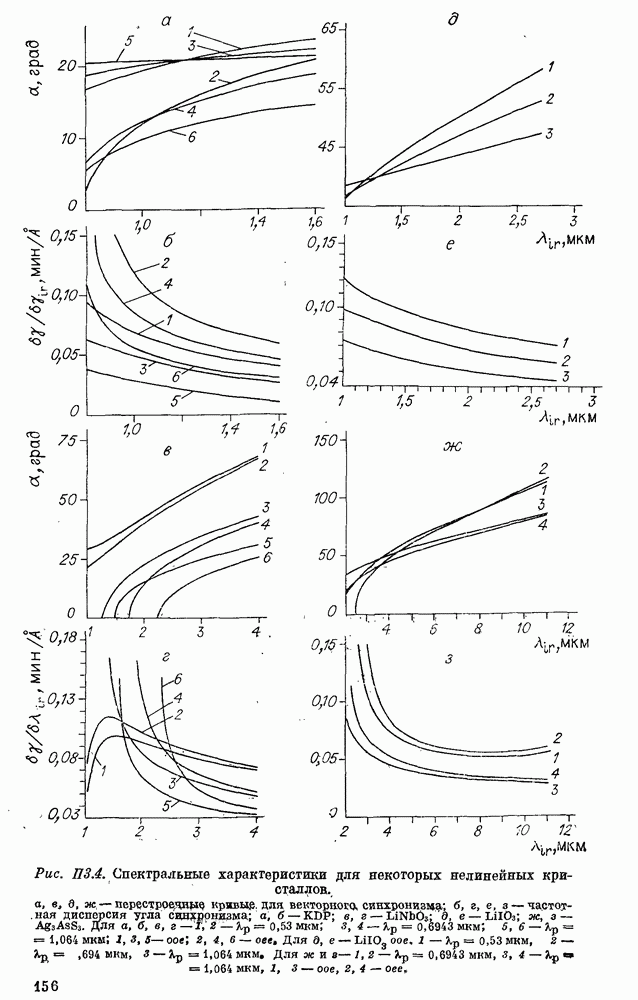
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)