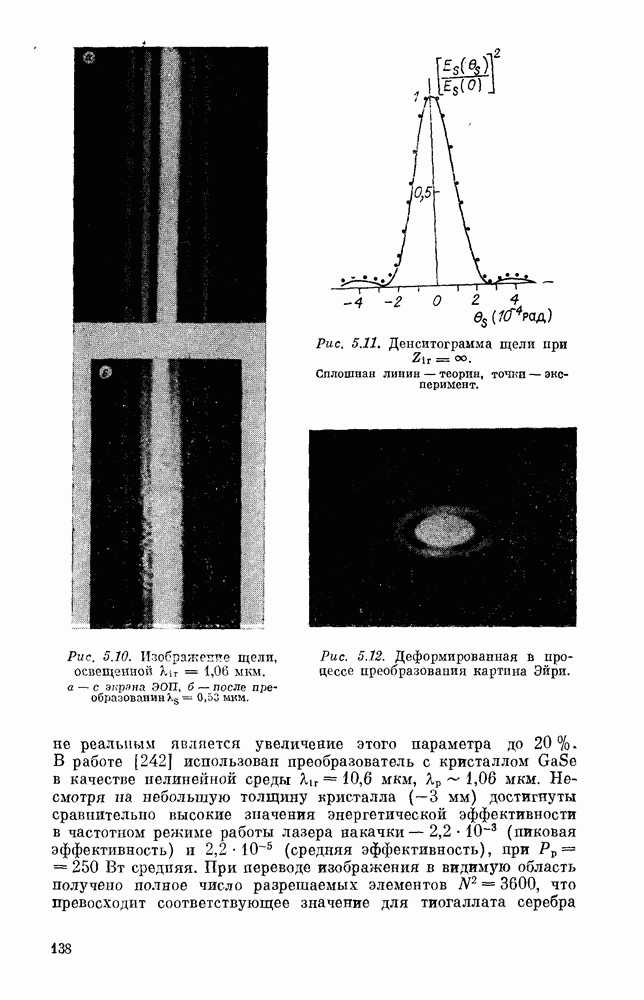
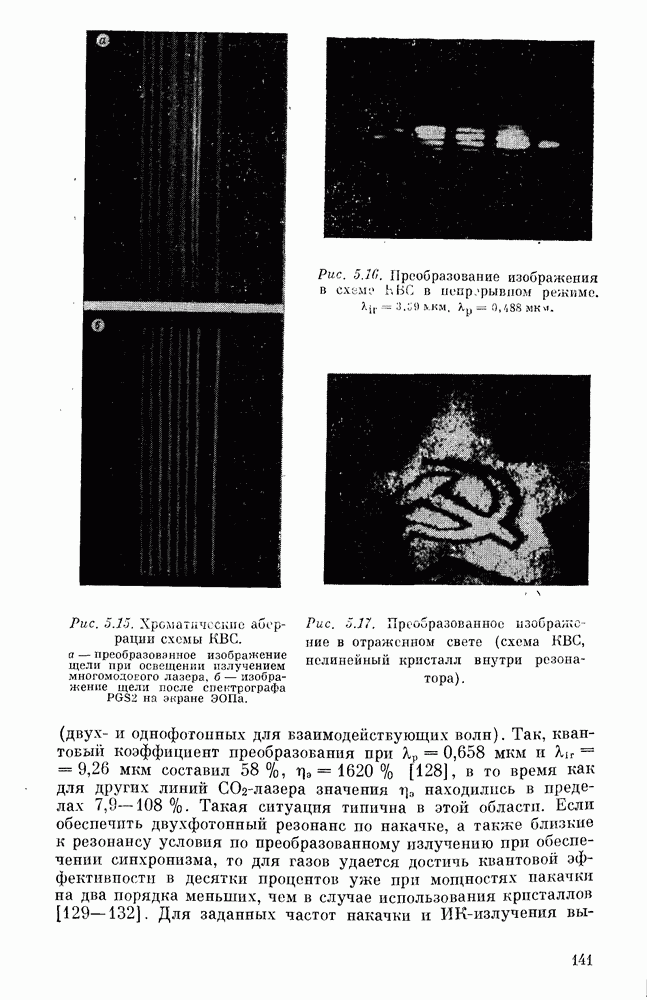
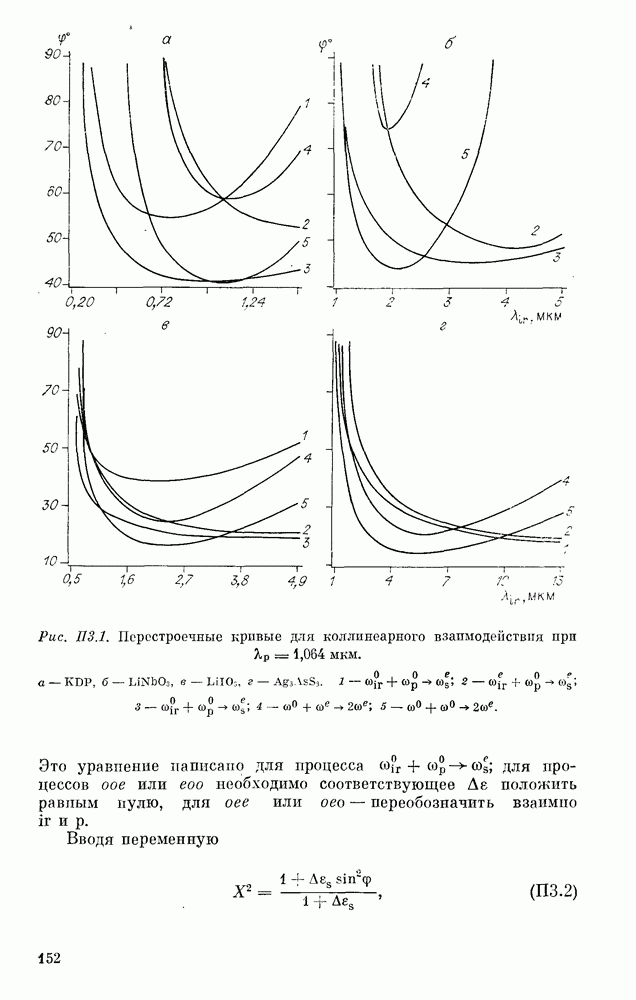
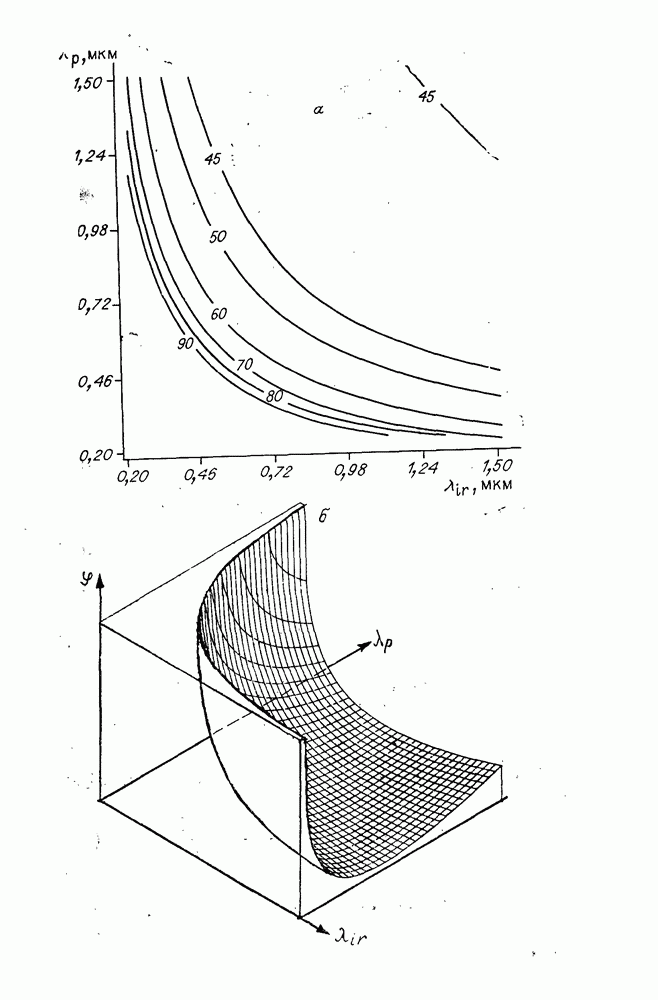
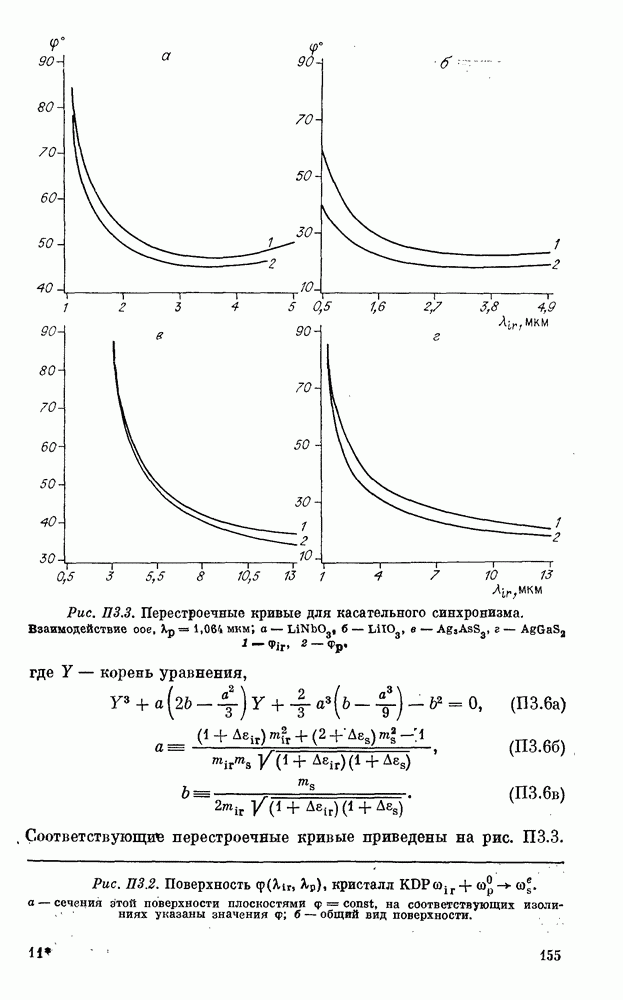
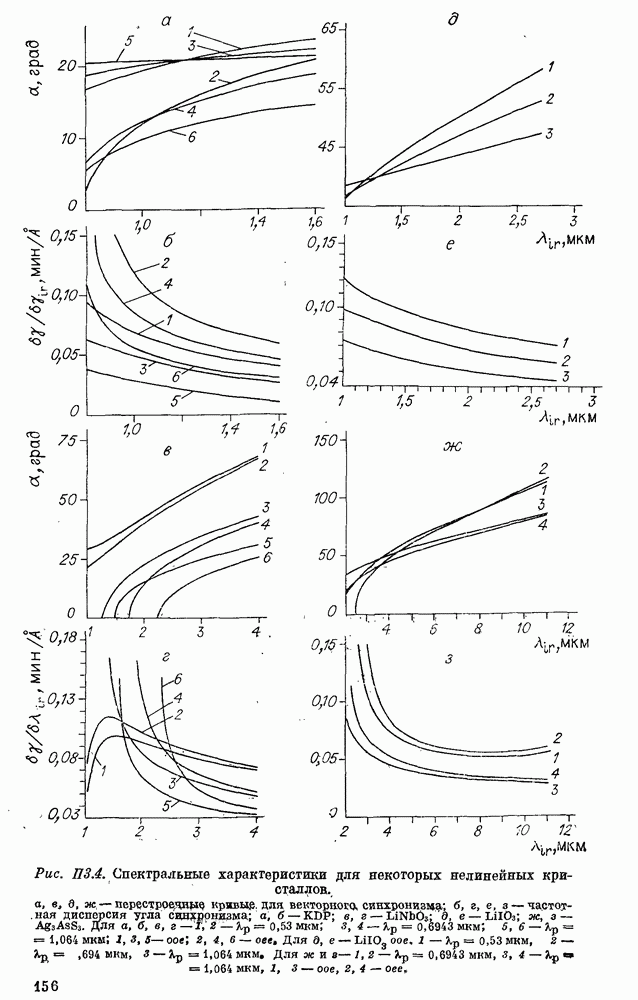
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
С ючки зрения практических применений наиболее интересны многоканальные приемники инфракрасного излучения с преобразованием частоты вверх (преобразователи изображения). Однако и одноканальные приемники, обеспечивающие только преобразование сигнала, также представляют большой интерес, поскольку обладают такими уникальными характеристиками, как малая инерционность, чувствительность, широкий спектральный диапазон [16].
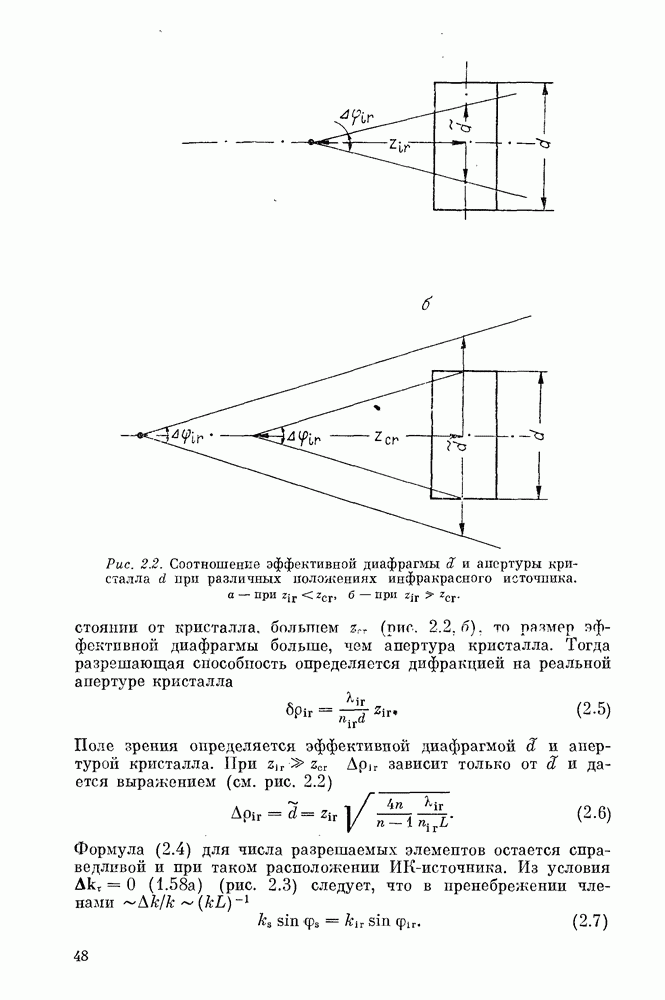
Оценим основные параметры преобразователей сигнала. Наиболее интересны их предельные возможности, возникающие из-за физических ограничений самого процесса сложения частот и никак не связанные с техническим несовершенством аппаратуры. Шумовые характеристики коротко рассмотрим далее, а здесь рассчитаем коэффициент преобразования. Поскольку в. такой задаче
не требуется сохранение информации о пространственной структуре инфракрасного излучения, то имеется возможность с помощью линейных оптических систем формировать не только это излучение, но и излучение накачки с целью получения максимальной эффективности преобразования. На первый взгляд (см. (1.130) - (1.134)) коэффициент преобразования по числу квантов всегда может быть увеличен до единицы посредством фокусировки ИК-излучения и накачки. Имеется, однако, два эффекта, ограничивающие эффективность преобразования при фокусировке. Первый связан с выносом излучения из области взаимодействия из-за двулучерреломления. Он проявляется для пучков конечной апертуры. Другой эффект связан с дифракцией, которая приводит к обогащению углового спектра взаимодействующих пучков. При этом в точном синхронизме преобразуются лишь центральные угловые компоненты и, таким образом, при фокусировке излучения эффективная длина когерентности уменьшается. Отсюда ясно, что существует оптимальная степень фокусировки, которая увеличивает интенсивность взаимодействующих волн, но не приводит еще к существенному выносу излучения и к уменьшению длины когерентности вплоть до длины самого нелинейного кристалла. Для определения оптимальной степени фокусировки рассмотрим взаимодействие в нелинейной анизотропной среде гауссовых пучков накачки и ИК-излучения, воспользовавшись методом функций Грина. Распределение поля в пучках накачки и инфракрасного излучения в приближении слабой анизотропии с учетом  запишется в виде
запишется в виде

где  размеры гауосового пучка в х и у направлениях соответственно. В силу анизотропии кристалла очевидно, что степень оптимальной фокусировки в х и у направлениях может быть различной (эллиптическая фокусировка [41]). Используя выражения (2.27), (5.5) и (П2.11), можно вычислить распределение электрического поля суммарной частоты в произвольной плоскости наблюдения
размеры гауосового пучка в х и у направлениях соответственно. В силу анизотропии кристалла очевидно, что степень оптимальной фокусировки в х и у направлениях может быть различной (эллиптическая фокусировка [41]). Используя выражения (2.27), (5.5) и (П2.11), можно вычислить распределение электрического поля суммарной частоты в произвольной плоскости наблюдения  (для упрощения выражений мы, как и ранее, пренебрегли отражением и преломлением на входной и выходной гранях кристалла):
(для упрощения выражений мы, как и ранее, пренебрегли отражением и преломлением на входной и выходной гранях кристалла):


 мнимая часть
мнимая часть  координата среды, с которой начинается поглощение (например, входяая грань кристаллов). Интегрирование в (5.6а) ведется по длине нелинейной среды. В формулах (5.6) все три волны (накачки, ИК-излучения и суммарной частоты) считаются необыкновенными. Это позволяет все возможные типы синхронизма описать едиными формулами. При расчете конкретного варианта
координата среды, с которой начинается поглощение (например, входяая грань кристаллов). Интегрирование в (5.6а) ведется по длине нелинейной среды. В формулах (5.6) все три волны (накачки, ИК-излучения и суммарной частоты) считаются необыкновенными. Это позволяет все возможные типы синхронизма описать едиными формулами. При расчете конкретного варианта  обыкновенной волны нужно положить равным нулю.
обыкновенной волны нужно положить равным нулю.
Для наших целей достаточно найти полную мощность суммарного излучения на выходе нелинейной среды. Поэтому для упрощения выражений можно воспользоваться (5.6) при 

Равенства (5.6), (5.7) позволяют вычислить интенсивность излучения суммарной частоты. Интегрируя затем полученное выражение по  получим формулу для полной мощности
получим формулу для полной мощности 


означает комплексное сопряжение с одновременной заменой в соответствующих выражениях  на
на 
Для синхронизма типа  или
или  в (5.8) нужно положить
в (5.8) нужно положить  или
или 

При  выражение (5.8) с фазой (5.9) совпадает с выражением, полученным в работе [41] разложением но плоским волнам.
выражение (5.8) с фазой (5.9) совпадает с выражением, полученным в работе [41] разложением но плоским волнам.
В случае генерации второй гармоники, когда  существенно упрощается и принимает вид
существенно упрощается и принимает вид

Отличие (5.10) от соответствующего выражения работы [33] связано с нестрогостью развитого в ней подхода (выбора в качестве функции Грина вместо выражений  или
или  экспоненты
экспоненты  При пренебрежении дифракционными эффектами
При пренебрежении дифракционными эффектами  по сравнению с
по сравнению с  это отличие исчезает.
это отличие исчезает.
Ввиду громоздкости (5.6) имеет смысл анализировать его в двух предельных случаях:
4. Если отграничения на степень фокусировки определяются главным образом анизотропией кристалла, то дифракционными
эффектами можно пренебречь, т. е. всюду в (5.6) пренебречь  но сравнению с
но сравнению с  В этом пределе в работе [41] оптимальное отношение радиусов фокусировки в
В этом пределе в работе [41] оптимальное отношение радиусов фокусировки в  -направлении найдено в явном виде:
-направлении найдено в явном виде:

и численными методами определено оптимальное значение каждого радиуса фокусировки для 

Выражения (5.12) позволяют оценить пределы применимости подхода с пренебрежением дифракцией 

Таким образом, условия пренебрежения дифракцией хорошо выполнены. Оптимальная фокусировка в  -направлении определяется, очевидно, только дифракционными эффектами. В приближении слабой фокусировки в [41] приведено оптимальное значение отношения радиусов
-направлении определяется, очевидно, только дифракционными эффектами. В приближении слабой фокусировки в [41] приведено оптимальное значение отношения радиусов

которое показывает, что при оптимальной фокусировке должны быть равны конфокальные параметры пучков накачки и
ИК-излучения. Оптимальное значение расстройки  также приведено в [41]:
также приведено в [41]:

При этом в пределе слабой фокусировки оптимум по абсолютной величине  отсутствует, т. е. чем меньше
отсутствует, т. е. чем меньше  тем лучше. Качественные рассуждения и результаты работы [41] позволяют предположить: соотношения (5.14) и (5.15) по порядку величины сохраняется и при нарушении условия (5.14). Можно ожидать, что оптимальные значения
тем лучше. Качественные рассуждения и результаты работы [41] позволяют предположить: соотношения (5.14) и (5.15) по порядку величины сохраняется и при нарушении условия (5.14). Можно ожидать, что оптимальные значения  определяются условием совпадения конфокального параметра и длины нелинейного кристалла
определяются условием совпадения конфокального параметра и длины нелинейного кристалла

2. Другой предельный случай имеет место, когда дифракционные ограничения играют определяющую роль. Полагая  в (5.6) и, как следует из соображений симметрии,
в (5.6) и, как следует из соображений симметрии,  имеем
имеем

Выражение  допускает, по-видимому, только численный анализ. Можно, однако, полагать, что соотношения (5.14) — (5.16) сохранятся, по крайней мере, приближенно и в этом случае.
допускает, по-видимому, только численный анализ. Можно, однако, полагать, что соотношения (5.14) — (5.16) сохранятся, по крайней мере, приближенно и в этом случае.
Соотношения (1.133) и (5.16) позволяют оценить предельный для данной мощности накачки и заданной длине кристалла коэффициент преобразования

где  энергетическая, а
энергетическая, а  фотонная эффективности.
фотонная эффективности.
В отсутствие поглощения оптимальная фокусировка реализуется при  и фокальная плоскость находится в центре кристалла. Качественный анализ (5.17) показывает, что при
и фокальная плоскость находится в центре кристалла. Качественный анализ (5.17) показывает, что при
фокальная плоскость должна быть смещена в направлении входной грани кристалла [33].
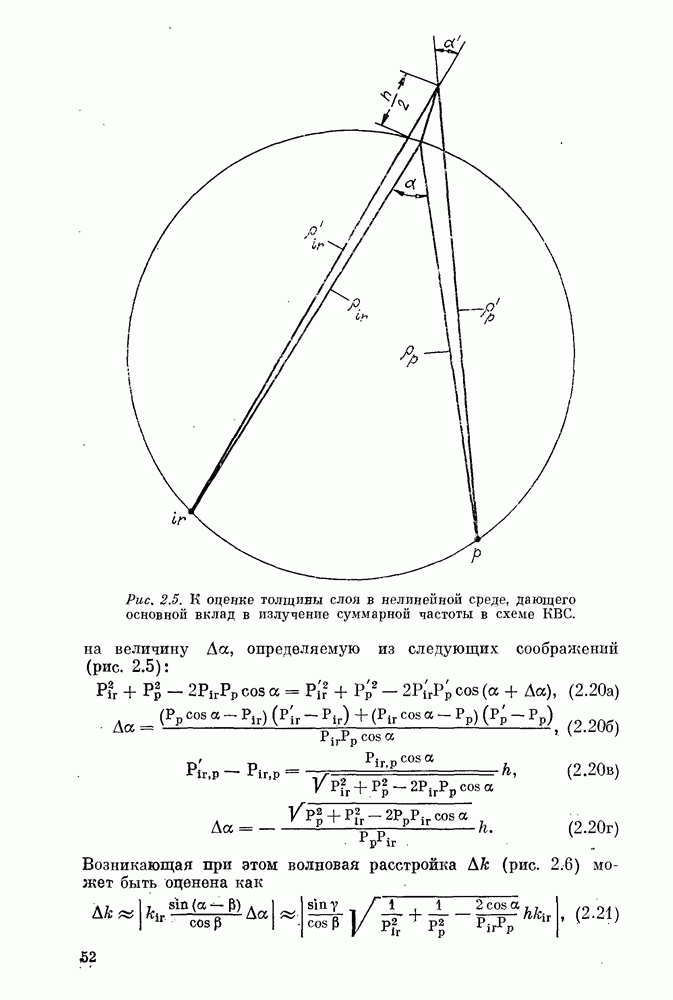
Проведенный анализ относился к взаимодействию идеальных по качеству волн — гауссовых пучков. Если же волны представляют собой не полностью пространственно-когерентное излучение (тепловой источник или лазер в режиме многих поперечных мод), то максимальный коэффициент преобразования уменьшается. Меняются и условия оптимальной фокусировки [234]. Это объясняется более богатым пространственным спектром излучения и выходом из синхронизма боковых спектральных компонент. Основные соображения относительно фокусировки остаются прежними: нужно максимально увеличивать плотность мощности во взаимодействующих волнах, не допуская существенного увеличения их расходимости и, как следствия, выхода их из синхронизма. Данные соображения приводят к выводу о целесообразности использования анаморфной оптической системы (цилиндрической угла фокусировки), поскольку условия синхронизма критичны к изменению в главном сечении одноосного кристалла и некритичны к изменению угла в перпендикулярном направлении [235]. Оптимальная фокусировка с помощью анаморфных оптических систем в некоторых конкретных случаях позволила более чем на порядок повысить коэффициент преобразований  во вторую гармонику по сравнению со случаем без фокусировки [234].
во вторую гармонику по сравнению со случаем без фокусировки [234].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)