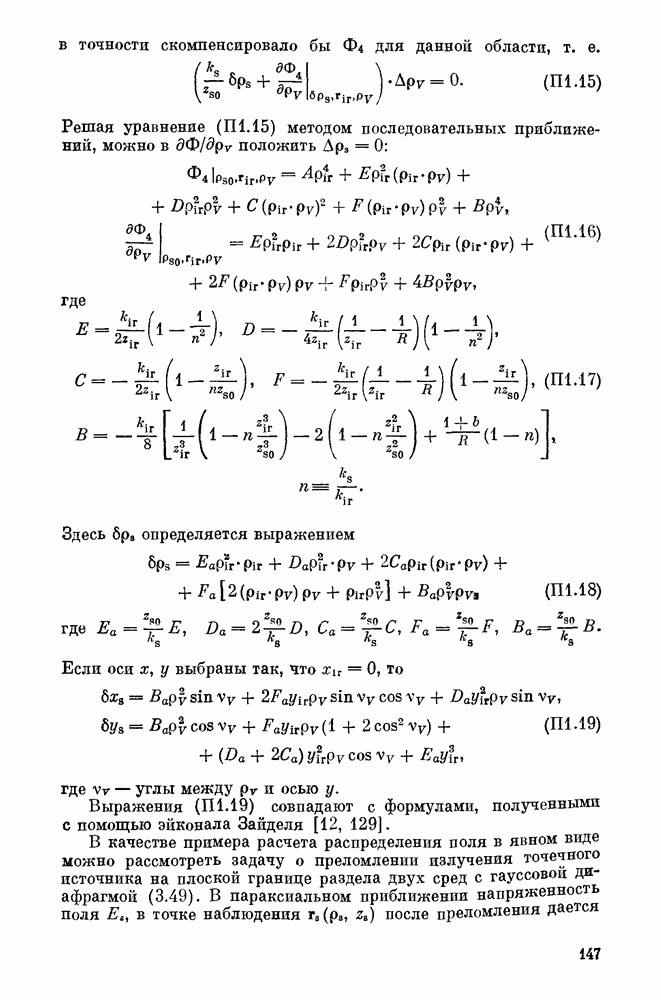| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
Интегральные принципы описания распространения электромагнитных волн широко применяются в теории оптических приборов [7, 8]. В линейной оптике основой такого описания является принцип Гюйгенса — Френеля, позволяющий с единой точки зрения построить геометрическую (см. Приложение 1) и дифракционную [7, 8] теории прибора. Имеющиеся в литературе расчеты нелинейно-оптических преобразователей основаны, как правило, на непосредственном решении укороченных волновых уравнений [1-6] с использованием различных упрощающих предположений [159—160]. Подход функций Грина, аналогичный подходу Гюйгенса — Френеля, может эффективно применяться в теории параметрического преобразования изображения из ИК-области в видимую [175—177, 219, 223, 224].
Пространственное распределение поля суммарной частоты можно найти, решая уравнения Максвелла, содержащие  при заданном пространственном распределении полей накачки и инфракрасного излучения (приближение заданного поля, см. гл. 1). В оптике при рассмотрении процесса распространения волн принято вместо решения уравнения Максвелла пользоваться скалярной теорией распространения волн, охватывающей все основные закономерности [7]. В этой теории поле суммарной частоты описывается уравнением
при заданном пространственном распределении полей накачки и инфракрасного излучения (приближение заданного поля, см. гл. 1). В оптике при рассмотрении процесса распространения волн принято вместо решения уравнения Максвелла пользоваться скалярной теорией распространения волн, охватывающей все основные закономерности [7]. В этой теории поле суммарной частоты описывается уравнением

где  волновое число,
волновое число,  длина волны,
длина волны,  показатель преломления на частоте
показатель преломления на частоте  нелинейная константа, пропорциональная свертке тензора
нелинейная константа, пропорциональная свертке тензора  с единичными векторами поляризации взаимодействующих волн, включающая в себя поправочные коэффициенты Лоренца.
с единичными векторами поляризации взаимодействующих волн, включающая в себя поправочные коэффициенты Лоренца.
Для произвольной замкнутой гладкой поверхности 2 внутри кристалла решение уравнения (2.25) можно представить в виде

где V — объем, ограниченный поверхностью 2. Формула (2.26) содержит два члена. Первый определяется значением поля и его нормальными производными на поверхности 2. Второй описывает вклад объемных источников, находящихся внутри поверхности 2. Пренебрежем отражением и преломлением волн суммарной частоты на гранях кристалла. Данные эффекты с учетом указанных выше приближений можно рассмотреть уже после решения нелинейной задачи. При этом грани кристалла рассматриваются как линейные оптические системы, находящиеся на входе и выходе преобразователя, каждая из которых представляет собой преломляющую поверхность (как правило, плоскую), по форме совпадающую с соответствующей частью границы нелинейного кристалла. Дополнительно будем считать, что внешние поля на суммарной частоте отсутствуют. В указанных предположениях в правой части формулы (2.26) остается только второе слагаемое. Действительно, непосредственным вычислением можно убедиться, что для поля

первый интеграл справа в формуле (2.26) тождественно равен нулю.
Формула (2.27) представляет собой модифицированный принцип Гюйгенса — Френеля в нелинейной оптике. Физический смысл интеграла (2.27) довольно прост. Поле излучения является суммой полей когерентных источников, распределенных в объеме, в то время как в линейной оптике эти источники всегда расположены на поверхности [7, 8].
Для понимания того, как работает формула (2.27), проанализируем с ее помощью взаимодействие плоских волн накачки и ИК-излучения:

Вычислим распределение суммарного излучения в дальней зоне. Тогда

Как видно из (2.27) и (2.29), условие применимости (2.30) можно записать следующим образом:

где  наибольший размер нелинейной среды. Интеграл (2.30) вычисляется непосредственно:
наибольший размер нелинейной среды. Интеграл (2.30) вычисляется непосредственно:

При  выражение (2.32) с точностью до амплитудного множителя
выражение (2.32) с точностью до амплитудного множителя  совпадает с главной при А частью формулы (1.70), полученной из непосредственного анализа волнового уравнения полубесконечной задачи. Наличие амплитудного множителя связано, очевидно, с разницей в постановках задачи — формула (1.70) дает амплитуду плоской волны суммарного излучения в области, где поперечные размеры кристалла можно считать бесконечными, а
совпадает с главной при А частью формулы (1.70), полученной из непосредственного анализа волнового уравнения полубесконечной задачи. Наличие амплитудного множителя связано, очевидно, с разницей в постановках задачи — формула (1.70) дает амплитуду плоской волны суммарного излучения в области, где поперечные размеры кристалла можно считать бесконечными, а  -угловое распределение в области, где справедливо условие (2.31), и отсюда множитель
-угловое распределение в области, где справедливо условие (2.31), и отсюда множитель  Если рассмотреть дифракцию волны, определяемой формулой (1.70) на прямоугольном отверстии размерами
Если рассмотреть дифракцию волны, определяемой формулой (1.70) на прямоугольном отверстии размерами  иными словами, если подставить поле (1.70) в интеграл Френеля — Крихгофа (см.
иными словами, если подставить поле (1.70) в интеграл Френеля — Крихгофа (см.  без второго слагаемого в правой части, то в дальней зоне (дифракция Фраунгофера) после интегрирования получится выражение, совпадающее с (2.32). Таким образом, если пренебречь поверхностными эффектами, т. е. членами или
без второго слагаемого в правой части, то в дальней зоне (дифракция Фраунгофера) после интегрирования получится выражение, совпадающее с (2.32). Таким образом, если пренебречь поверхностными эффектами, т. е. членами или  то формула (2.32) правильно описывает точное решение волнового уравнения. С другой стороны, с ее помощью сравнительно просто удалось решить задачу о пространственном распределении суммарного излучения, генерируемого средой с конечными поперечными размерами. Непосредственный анализ волнового уравнения в такой задаче достаточно сложен. Приведенный пример позволяет думать, что использование подхода функций Грина вместо непосредственного нахождения решений волнового уравнения эффективно, когда нужно найти приближенное решение задачи с достаточно сложной пространственной конфигурацией.
то формула (2.32) правильно описывает точное решение волнового уравнения. С другой стороны, с ее помощью сравнительно просто удалось решить задачу о пространственном распределении суммарного излучения, генерируемого средой с конечными поперечными размерами. Непосредственный анализ волнового уравнения в такой задаче достаточно сложен. Приведенный пример позволяет думать, что использование подхода функций Грина вместо непосредственного нахождения решений волнового уравнения эффективно, когда нужно найти приближенное решение задачи с достаточно сложной пространственной конфигурацией.
В случае преобразования сигнала конфигурации полей  в значительной степени произвольны и определяются конкретными оптическими схемами, в которых используется преобразователь. При переводе изображения достаточно знать преобразованное поле от точечного источника ИК-излучения. В этом случае
в значительной степени произвольны и определяются конкретными оптическими схемами, в которых используется преобразователь. При переводе изображения достаточно знать преобразованное поле от точечного источника ИК-излучения. В этом случае

Здесь  волновое число,
волновое число,  длина волны,
длина волны,  показатель преломления ИК-излучения
показатель преломления ИК-излучения  радиус-вектор, характеризующий положение ИК-источника. Распределение поля накачки определяет тип преобразователя [14, 204]. Представим поле накачки в виде
радиус-вектор, характеризующий положение ИК-источника. Распределение поля накачки определяет тип преобразователя [14, 204]. Представим поле накачки в виде

где — медленно меняющаяся по сравнению с фазой  функция. Выберем следующий порядок интегрирования в формуле (2.27): сначала интегрируем по поверхностям постоянной фазы накачки
функция. Выберем следующий порядок интегрирования в формуле (2.27): сначала интегрируем по поверхностям постоянной фазы накачки  а затем суммируем излучение от всех фазовых поверхностей. В результате получаем
а затем суммируем излучение от всех фазовых поверхностей. В результате получаем

Здесь  параметр, характеризующий интенсивность инфракрасной волны и нелинейность кристалла;
параметр, характеризующий интенсивность инфракрасной волны и нелинейность кристалла;  координата пересечения поверхности постоянной фазы
координата пересечения поверхности постоянной фазы  с осью
с осью  Интеграл по в формуле (2.35) по форме совпадает с интегралом Френеля—Кирхгофа для преломляющей поверхности
Интеграл по в формуле (2.35) по форме совпадает с интегралом Френеля—Кирхгофа для преломляющей поверхности  с показателем преломления
с показателем преломления  Таким образом, нелинейный кристалл ведет себя как система непрерывно расположенных вдоль оси z и когерентно излучающих поверхностей с апертурными диафрагмами с амплитудными прозрачпостями
Таким образом, нелинейный кристалл ведет себя как система непрерывно расположенных вдоль оси z и когерентно излучающих поверхностей с апертурными диафрагмами с амплитудными прозрачпостями  [175, 176, 223].
[175, 176, 223].
Следует подчеркнуть, что когерентность источников, принадлежащих к различным поверхностям, весьма существенна. Даже когда для каждой из преломляющих поверхностей применимо приближение геометрической оптики, суммарное поле зачастую имеет дифракционный характер.
Расчет конкретных схем преобразования изображения основан на приближенном вычислении интеграла Грина (2.27), что позволяет выделить часть нелинейного кристалла, дающую основной вклад в излучение на суммарной частоте, и пренебречь влиянием остальной части. Излучатели, интерферирующие точно в фазе, определяют лучи, соответствующие геометрической оптике. Оставшиеся излучатели описывают эффекты, аналогичные дифракционным. Таким образом, удается построить отдельно геометрическую оптику нелинейно-оптических преобразователей (гл. 2, 4), а затем дать дифракционную теорию разрешающей способности (гл. 3, 4).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
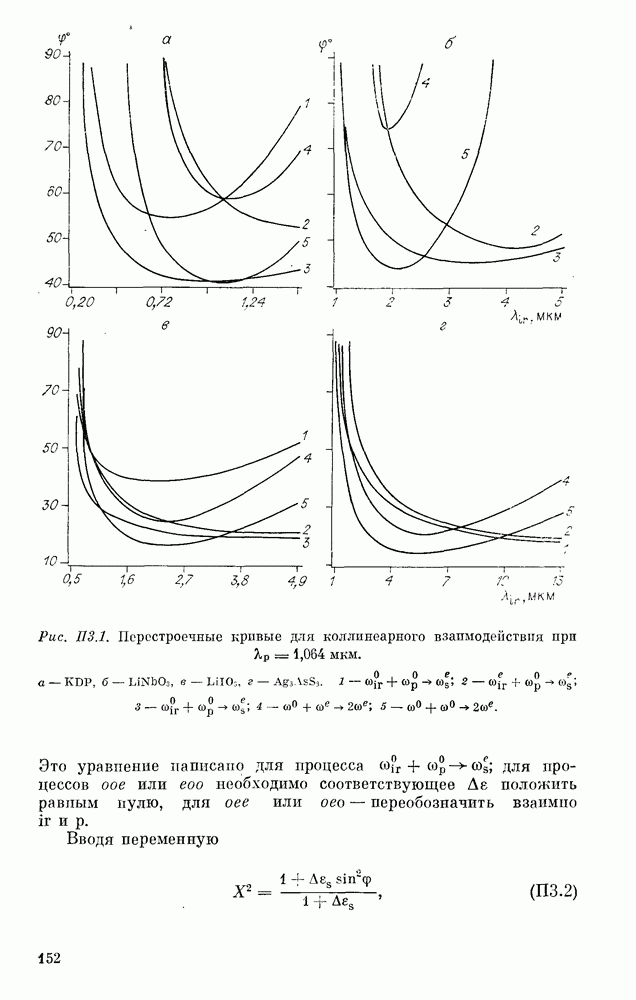
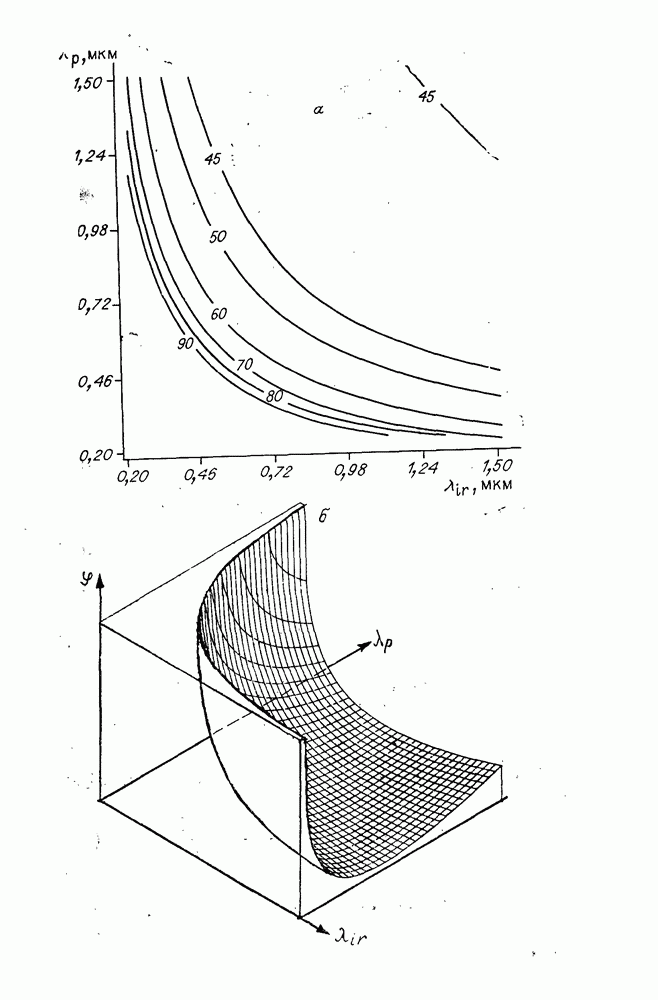
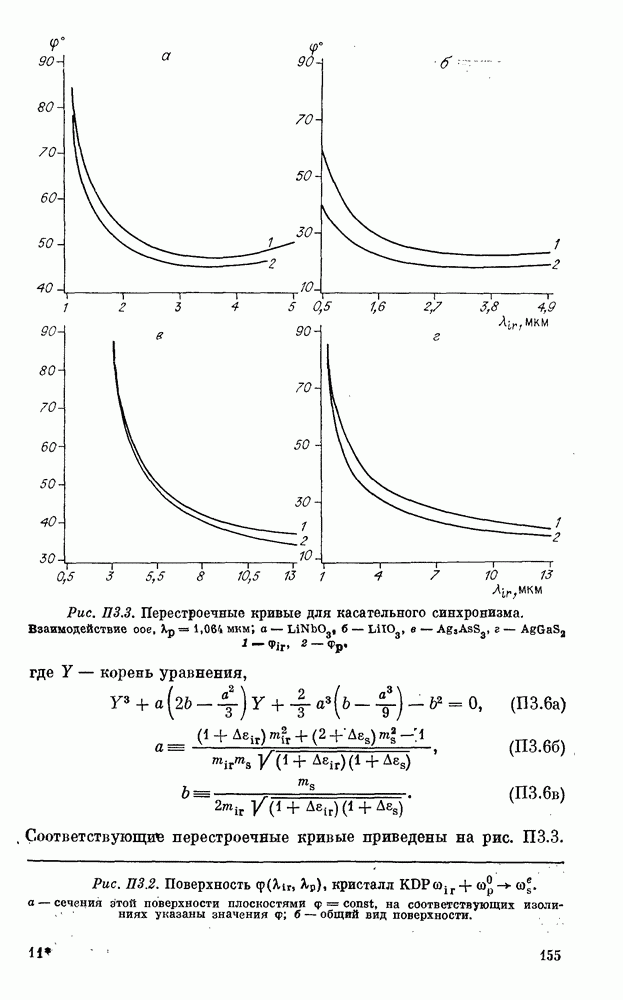
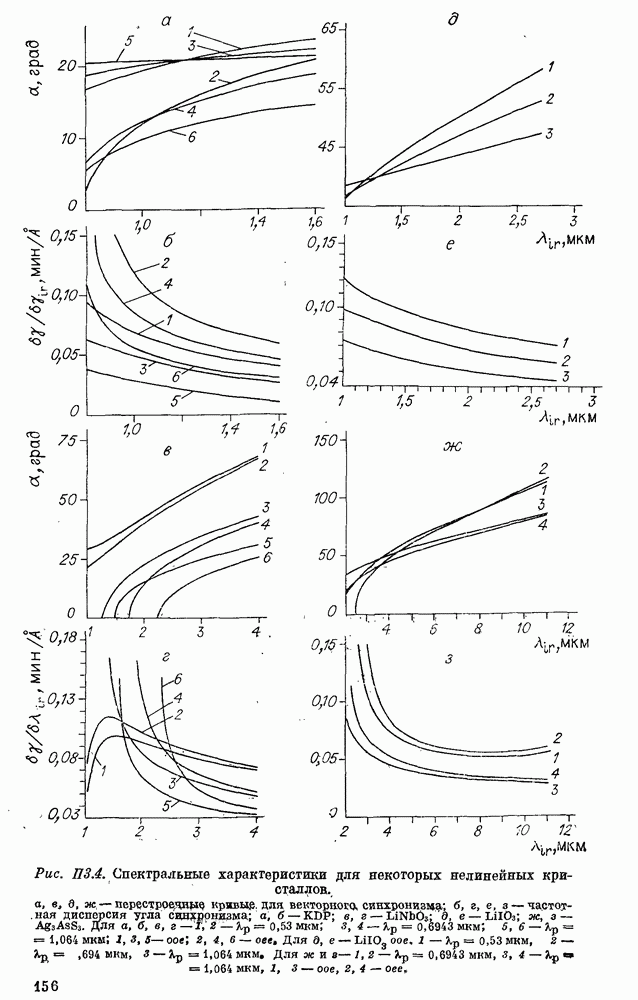
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)