| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
Рассмотрим взаимодействие двух бесконечно узких астигматических пучков [225] в нелинейной среде. Предположим, что центральные лучи пучков пересекаются под углом а. В собственной системе координат пучка, когда ось z совпадает с центральным лучом, а оси х и у направлены по осям симметрии, уравнения астигматического пучка имеют вид

здесь  текущие координаты в собственной системе;
текущие координаты в собственной системе;  координаты пересечения данного луча с плоскостью
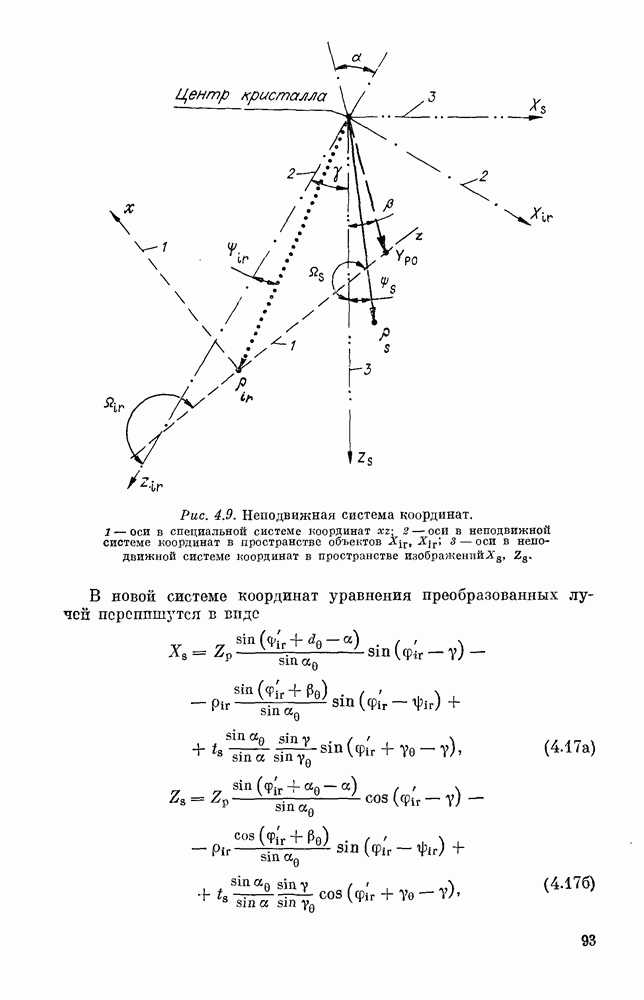
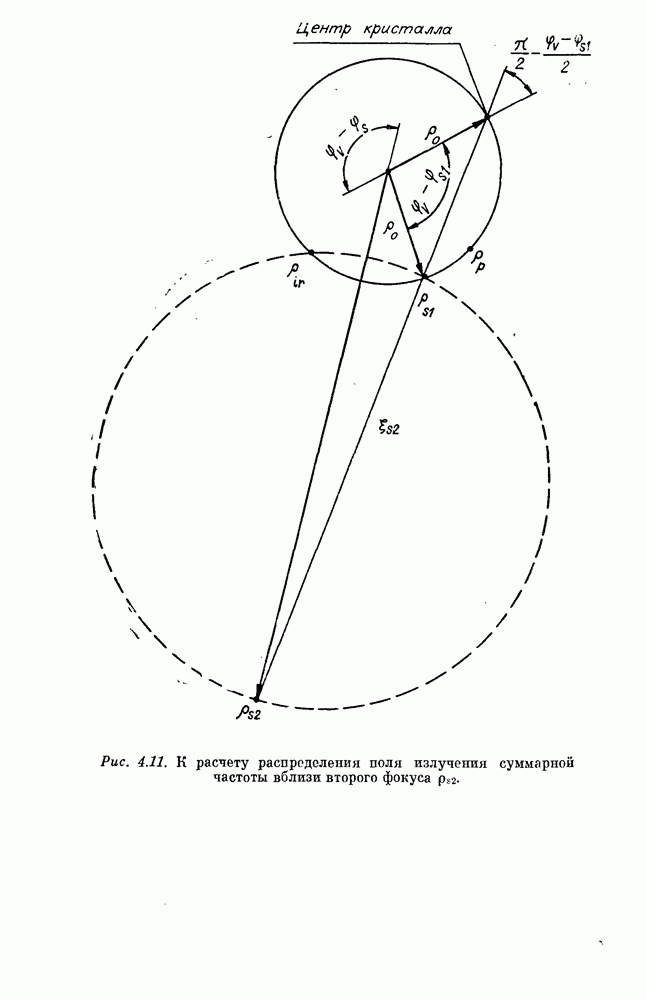
координаты пересечения данного луча с плоскостью  координаты обоих фокусов. Вычисления удобно проводить в системе координат, начало которой лежит в точке пересечения центральных лучей, ось z направлена вдоль центрального луча суммарной частоты, ось х лежит в плоскости, включающей центральные лучи взаимодействующих пучков, ось у перпендикулярна указанной плоскости. Переход в эту систему координат для ИК-пучка состоит в повороте вокруг оси
координаты обоих фокусов. Вычисления удобно проводить в системе координат, начало которой лежит в точке пересечения центральных лучей, ось z направлена вдоль центрального луча суммарной частоты, ось х лежит в плоскости, включающей центральные лучи взаимодействующих пучков, ось у перпендикулярна указанной плоскости. Переход в эту систему координат для ИК-пучка состоит в повороте вокруг оси  на угол —
на угол —  и затем в повороте вокруг оси у на угол у; для пучка накачки — в повороте вокруг оси
и затем в повороте вокруг оси у на угол у; для пучка накачки — в повороте вокруг оси  угол —
угол —  и затем повороте
и затем повороте
вокруг оси у на угол  углы между осями
углы между осями  соответствующих собственных систем координат пучков и плоскостью
соответствующих собственных систем координат пучков и плоскостью  включающей центральные лучи. После вычислений получим уравнение поверхности синхронизма с точностью до членов первого порядка по
включающей центральные лучи. После вычислений получим уравнение поверхности синхронизма с точностью до членов первого порядка по 

где индекс  означает, что данная точка лежит на поверхности синхронизма:
означает, что данная точка лежит на поверхности синхронизма:

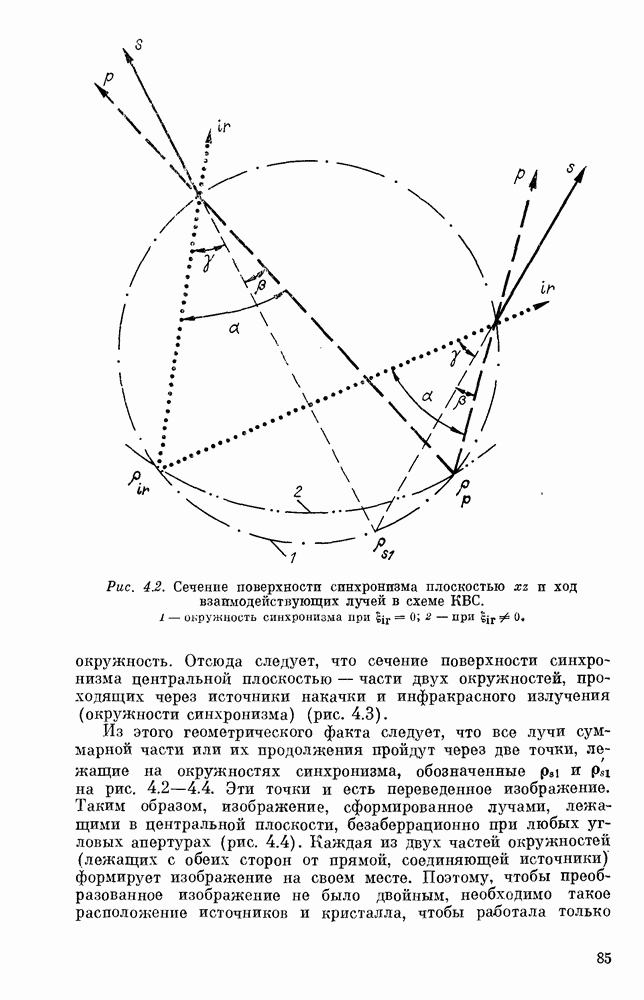
Уравнения (2.44) — (2.46) показывают, что поверхность синхронизма в рассматриваемом случае — плоскость, проходящая через начало координат.
Направляющие косинусы луча суммарной частоты, идущего из точки  поверхности синхронизма, т. е. рожденного ИК-лучом с параметрами
поверхности синхронизма, т. е. рожденного ИК-лучом с параметрами  определяются выражениями (справедливыми также с точностью
определяются выражениями (справедливыми также с точностью 

Используя приведенный в [225] критерий, можно убедиться, что формулы (2.44) — (2.49) описывают так называемую нормальную конгруэнцию лучей [7, 225]. Математически нормальная конфигурация — это такое семейство лучей, когда

Равенство (2.50) свидетельствует о том, что существует совокупность поверхностей (волновых фронтов), нормали к которым в каждой точке совпадают с направлением лучей  Отсюда следует возможность построения линейной оптической системы, преобразующей инфракрасный астигматический пучок (2.42), (2.43) в пучок, определяемый формулами (2.44) — (2.49). Этот факт
Отсюда следует возможность построения линейной оптической системы, преобразующей инфракрасный астигматический пучок (2.42), (2.43) в пучок, определяемый формулами (2.44) — (2.49). Этот факт
означает, что по крахней мере в приближении геометрической оптики параметрический преобразователь можно рассматривать как линейную оптическую систему (вообще говоря, зависящую от положения ИК-источника) и, в частности, устранять геометрические аберрации корректирующей оптикой.
Приведем, наконец, формулы связи параметров  узкого астигматического пучка преобразованного излучения с параметрами
узкого астигматического пучка преобразованного излучения с параметрами  ИК-пучка и
ИК-пучка и  пучка накачки. В силу громоздкости выражений в общем случае ограничимся ситуацией, когда
пучка накачки. В силу громоздкости выражений в общем случае ограничимся ситуацией, когда  Из выражений (2.44) — (2.49) в данном случае следует:
Из выражений (2.44) — (2.49) в данном случае следует:

Эти соотношения можно рассматривать как аналог формулы тонкой линзы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
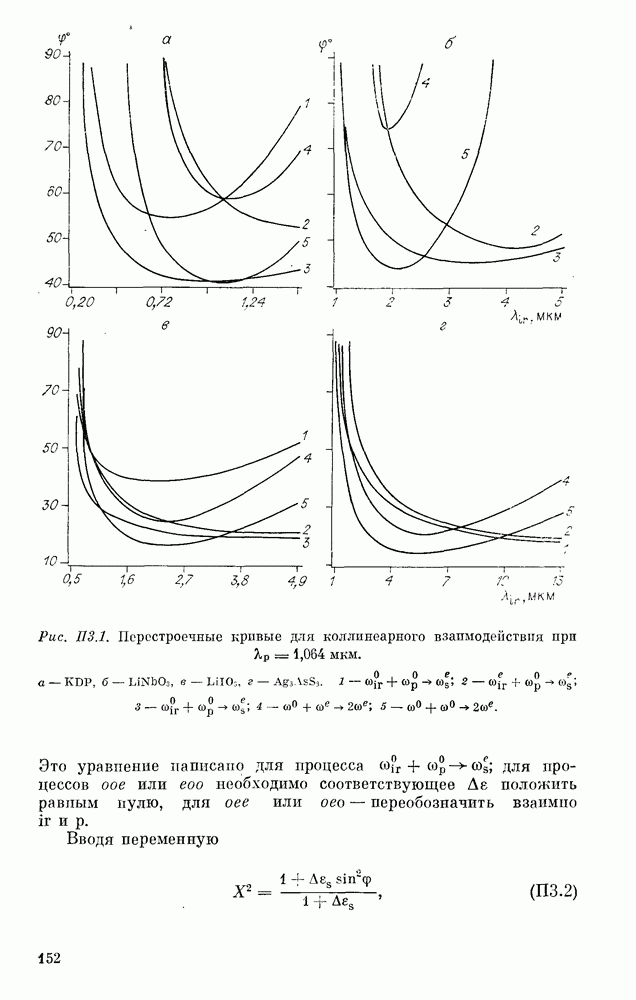
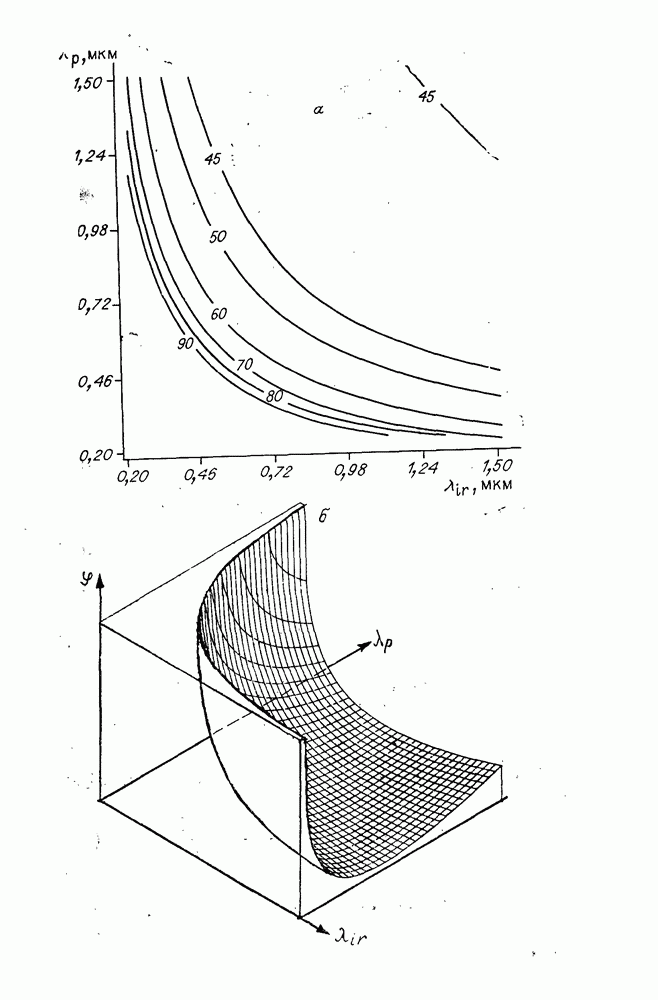
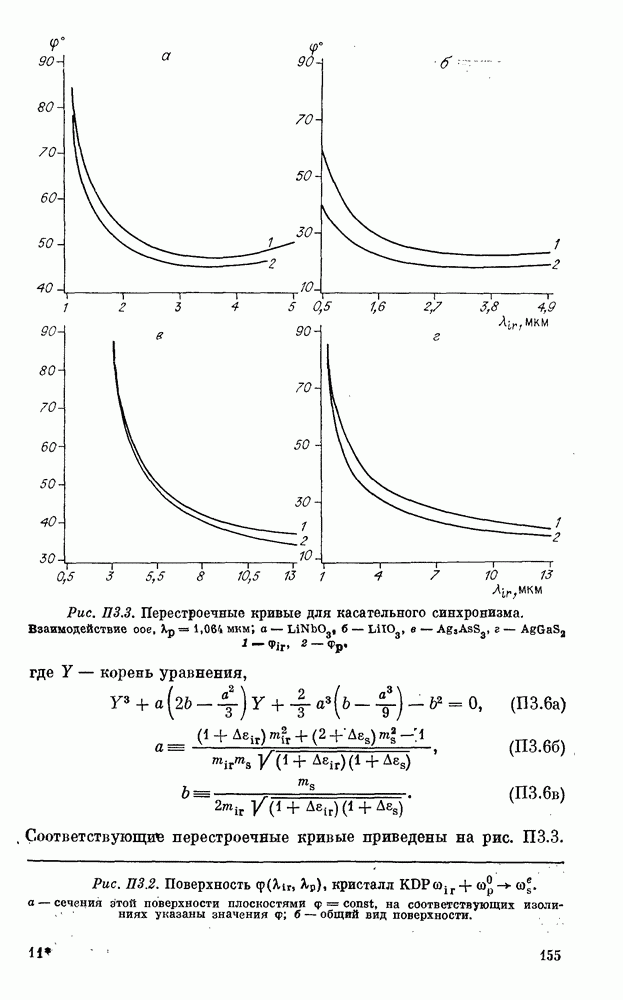
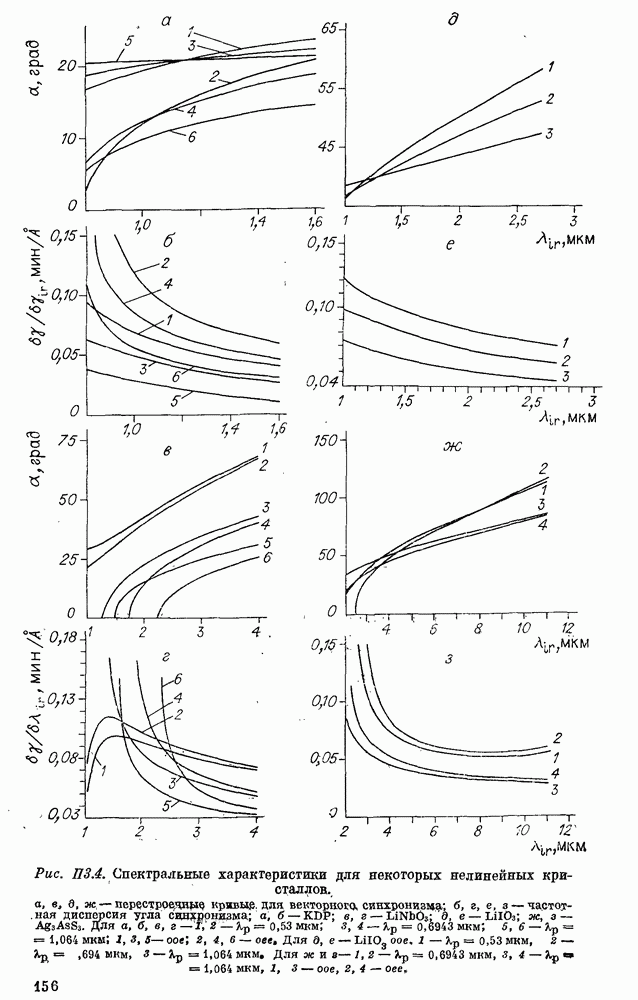
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)