| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
Преобразуем закон Ома применительно к дифференциально малым участкам цепи. Для этого введем в формулу (4) закона Ома напряженность электрического поля внутри проводника, по которому течет электрический ток.

Рис. 86
Выделим элементарно малый по длине  участок проводника. Падение напряжения на его концах обозначим через
участок проводника. Падение напряжения на его концах обозначим через  (рис. 86). Тогда закон Ома для этого участка проводника напишется так:
(рис. 86). Тогда закон Ома для этого участка проводника напишется так:

Напряженность электрического поля определяется градиентом потенциала

Подставив это выражение в вышеприведенную формулу, получим:

Перепишем это соотношение, введя плотность тока, под которой будем понимать в случае равномерного распределения тока вектор, направленный по полю и численно равный отношению величины тока к площади поперечного сечения проводника,

Вместо удельного сопротивления введем удельную электропроводность  Таким образом, получаем следующее, часто применяемое выражение закона Ома:
Таким образом, получаем следующее, часто применяемое выражение закона Ома:

или в векторной форме:

Можно доказать, что  выражение остается справедливым и для случая неравномерного распределения тока по поперечному сечению проводника, когда плотность тока
выражение остается справедливым и для случая неравномерного распределения тока по поперечному сечению проводника, когда плотность тока  неодинакова в различных точках сечения проводника.
неодинакова в различных точках сечения проводника.
В указанной дифференциальной форме (18) закон Ома связывает вектор плотности тока с напряженностью электрического поля внутри проводника. В проводящей цепи замкнутые линии тока совпадают с линиями электрического поля. Плотность электрического тока в любой точке проводника вычисляется как произведение удельной электропроводности среды на напряженность электрического поля в этой точке.
Подобно закону Ома, - закон Джоуля — Ленца тоже можно представить в дифференциальной форме. По закону Джоуля— Ленца количество тепла  которое ежесекундно выделяется в элементарно малом объеме
которое ежесекундно выделяется в элементарно малом объеме  пропорционально квадрату падения напряжения
пропорционально квадрату падения напряжения  на концах рассматриваемого участка проводника и обратно пропорционально сопротивлению рассматриваемого участка проводника; если
на концах рассматриваемого участка проводника и обратно пропорционально сопротивлению рассматриваемого участка проводника; если  и выражены в одинаковых единицах энергии, то
и выражены в одинаковых единицах энергии, то

Падение напряжения  на элементарно малой длине проводника А/связано с напряженностью поля
на элементарно малой длине проводника А/связано с напряженностью поля  соотношением
соотношением  Сопротивление рассматриваемого участка проводника равно:
Сопротивление рассматриваемого участка проводника равно:

Следовательно,

Обозначая количество тепла, ежесекундно выделяющегося в единице объема (т. е. «объемную плотность секундного выделения тепла»), через  получаем:
получаем:

Это выражение закона Джоуля — Ленца можно переписать еще следующим образом, приняв во внимание (18):

Мы видим, таким образом, что объемная плотность секундного выделения тепла электрическим током равна произведению плотности тока на напряженность электрического поля в рассматриваемом участке проводника.
Здесь уместно отметить аналогию между дифференциальной формой закона Ома (18) и выражением для вектора электрической индукции:

Обе величины — вектор электрической индукции в диэлектрике и вектор плотности тока в проводнике — пропорциональны напряженности поля, но коэффициентом пропорциональности для вектора индукции является диэлектрическая постоянная среды, а для вектора плотности тока — удельная электропроводность среды.

Рис. 87. Линии тока в тонкой металлической пластине
На рис. 87 показано распределение линий тока в весьма тонкой металлической пластине. Точка, из которой выходят эти линии, и точка, где они сходятся, соответствуют местам, в которых токонесущие провода прикасаются к пластине. Эта картина аналогична виду силовых линий поля, образованного разноименными зарядами.
Подобно преломлению линий электрической индукции на границе двух диэлектриков, линии тока также испытывают преломление на границе соприкосновения двух сред, имеющих неодинаковую удельную электропроводность. Такое преломление линий тока можно видеть на рис. 88. Здесь показано распределение линий тока в круглой пластине, спаянной из двух половин — медной и свинцовой; электроды помещены на окружности.
Указанное выше сходство формул для вектора плотности тока и вектора электрической индукции и соответствие в распределении линий токами линий электрической индукции дополняются практически важной аналогией формул для вычисления проводимости и электроемкости.
По закону Ома электрическое сопротивление слоя, имеющего толщину  и площадь поперечного сечения 5, равно
и площадь поперечного сечения 5, равно


Рис. 88. Преломление линий тока на поверхности раздела меди и свинца.
Следовательно, проводимость слоя

где у — удельная проводимость среды. Вспомним, что электроемкость плоского конденсатора выражается формулой

 диэлектрическая постоянная среды, разделяющей пластины конденсатора, I — толщина слоя этой среды и
диэлектрическая постоянная среды, разделяющей пластины конденсатора, I — толщина слоя этой среды и  площадь поперечного сечения слоя (площадь пластин конденсатора). Мы видим, что геометрические размеры I и 5 входят в указанные формулы совершенно аналогично. Поэтому отношение проводимости слоя среды к электроемкости плоского конденсатора, заключающего слой той же толщины и сечения, не зависит от геометрических характеристик и равно
площадь поперечного сечения слоя (площадь пластин конденсатора). Мы видим, что геометрические размеры I и 5 входят в указанные формулы совершенно аналогично. Поэтому отношение проводимости слоя среды к электроемкости плоского конденсатора, заключающего слой той же толщины и сечения, не зависит от геометрических характеристик и равно

Это соотношение между электропроводностью слоя и электроемкостью конденсатора, охватывающего слой, оказывается справедливым во всех случаях, для слоев какой угодно формы Возможность обобщения формулы (20), полученной нами для чястного случая емкости плоского конденсатора и проводимости плоского слоя, объясняется следующим образом. Во-первых, в сложных случаях любой слой можно представить как совокупность элементарных почти плоских слоев. Во-вторых, закон суммирования емкостей тождествен закону суммирования прэводимостей: при параллельном соединении емкости, так же как и проводимости, складываются; при последовательном соединении складываются их обратные величины.
Применим формулу (20) для определения сопротивления цилиндрического слоя изоляции в экранированном проводе, имеющем радиус сечения металлической жилы  радиус металлического экрана
радиус металлического экрана  и удельное сопротивление изоляции
и удельное сопротивление изоляции  Электроемкость цилиндрического конденсатора как было упомянуто в § 14, выражается формулой
Электроемкость цилиндрического конденсатора как было упомянуто в § 14, выражается формулой

где  - длина, а
- длина, а  и
и  - радиусы обкладок. Стало быть, по формуле (20) сопротивление цилиндрического слоя изоляции
- радиусы обкладок. Стало быть, по формуле (20) сопротивление цилиндрического слоя изоляции

Точно таким же способом из формулы для электроемкости двух цилиндрических проводников, приведенной в § 15, и формулы (20) находим, что сопротивление слоя изолирующей среды между двумя проводами, имеющими радиусы  при расстояний а между их осями (когда оно значительно больше радиусов проводов) равно
при расстояний а между их осями (когда оно значительно больше радиусов проводов) равно

где  длина каждого из параллельных проводов и
длина каждого из параллельных проводов и  удельное сопротивление среды.
удельное сопротивление среды.
Применим соотношение аналогии между емкостью  проводимостью для вычисления так называемого «переходного сопротивления» полусферического электрода, помещенного в среду с удельным сопротивлением
проводимостью для вычисления так называемого «переходного сопротивления» полусферического электрода, помещенного в среду с удельным сопротивлением  (рис. 89). Емкость шара радиуса
(рис. 89). Емкость шара радиуса  равна
равна  Для рассматриваемой задачи вследствие симметрии можно принять в формуле (20) емкость полушария равной
Для рассматриваемой задачи вследствие симметрии можно принять в формуле (20) емкость полушария равной 
Таким образом, находим, что «переходное сопротивление» полусферического электрода


Рис. 89. Полусферический электрод в среде (с удельным сопротивлением 
Наконец, тем же способом из формулы для электроемкости двух шаров, имеющих радиусы  и расположенных друг от друга на расстоянии а, которое значительно больше их радиусов (§ 14), получаем, что сопротивление промежутка между этими шарами при удельном сопротивлении среды
и расположенных друг от друга на расстоянии а, которое значительно больше их радиусов (§ 14), получаем, что сопротивление промежутка между этими шарами при удельном сопротивлении среды  равно
равно

Нередко соотношение аналогии между проводимостью и емкостью применяется для вычисления электроемкости на основании результатов измерения проводимости. Этим методом пользуются, например, для определения весьма малых емкостей между электродами радиоламп. Погружая изготовленный металлический каркас сетчатых электродов радиолампы в жидкость с небольшой и точно измеренной проводимостью, измеряют сопротивление между электродами и по формуле (20) вычисляют их взаимную электроемкость.
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
- § 42. Аккумуляторы
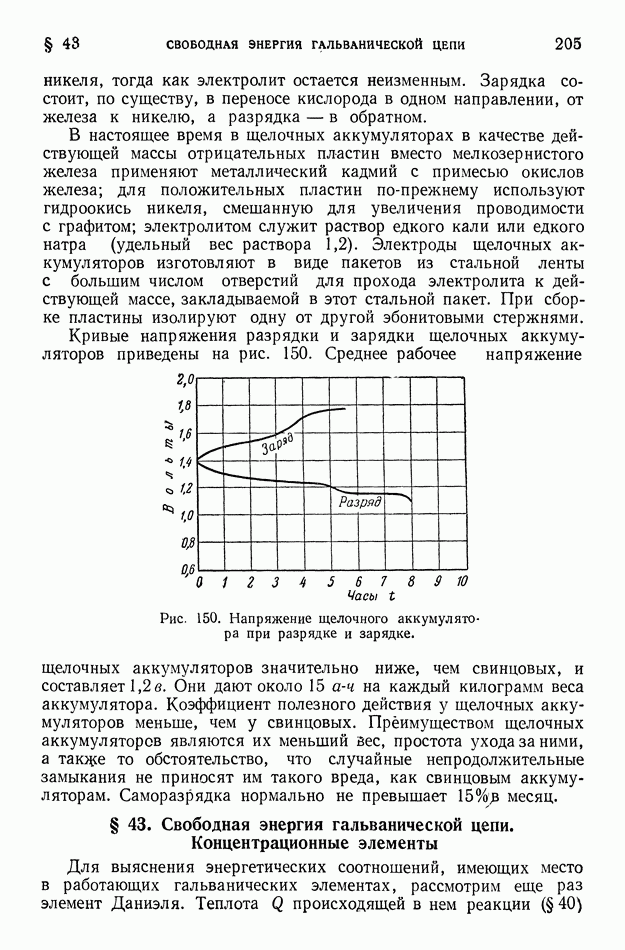
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
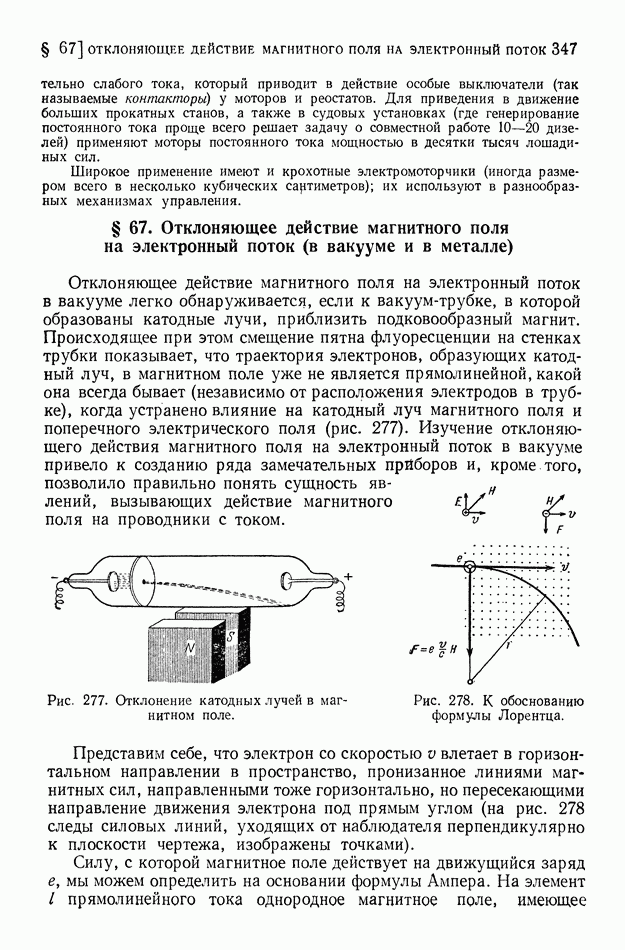
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
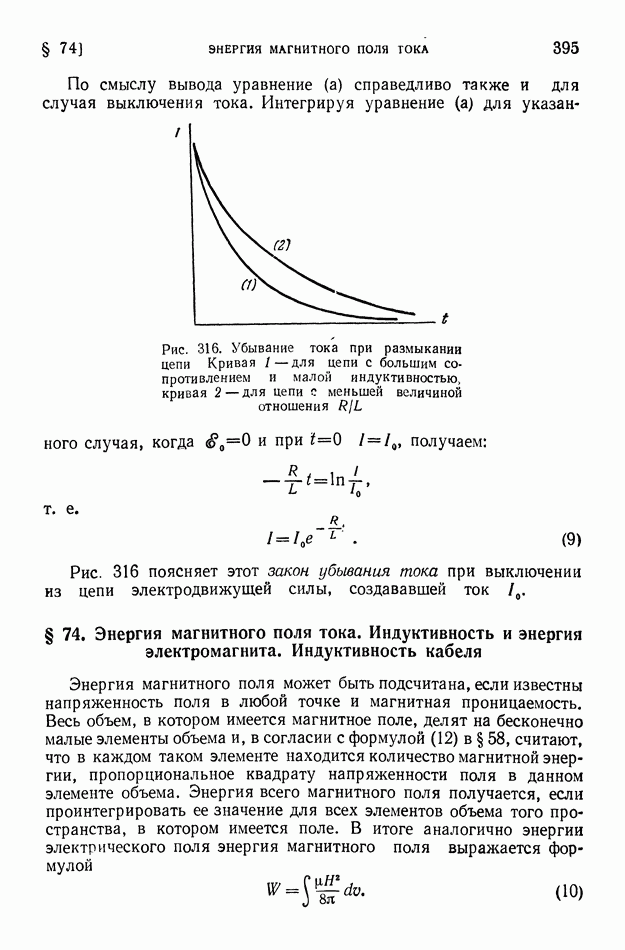
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
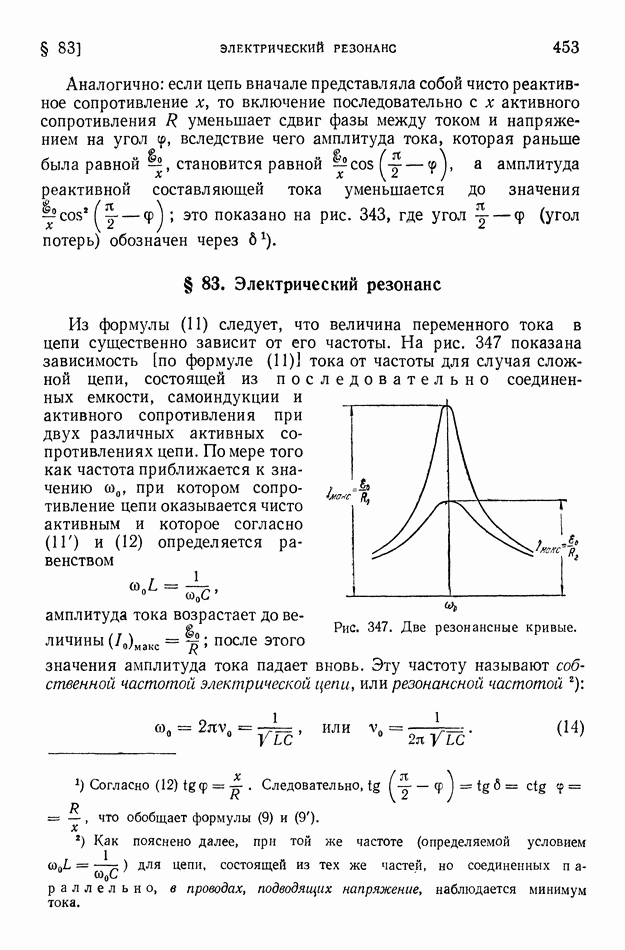
- § 83. Электрический резонанс
- § 84. Трансформация тока
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)