| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
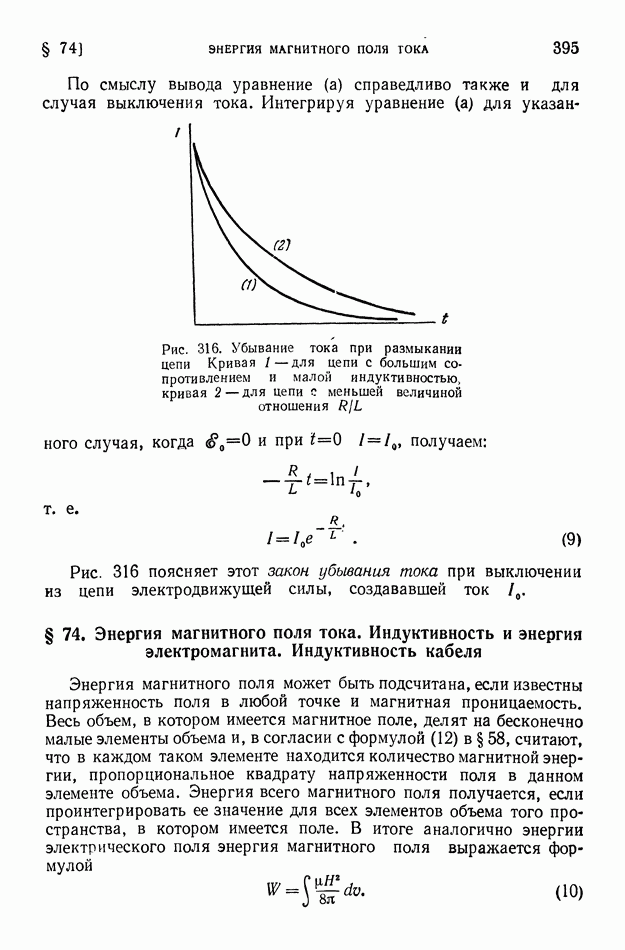
§ 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
Энергия магнитного поля может быть подсчитана, если известны напряженность поля в любой точке и магнитная проницаемость. Весь объем, в котором имеется магнитное поле, делят на бесконечно малые элементы объема и, в согласии с формулой (12) в § 58, считают, что в каждом таком элементе находится количество магнитной энергии, пропорциональное квадрату напряженности поля в данном элементе объема. Энергия всего магнитного поля получается, если проинтегрировать ее значение для всех элементов объема того пространства, в котором имеется поле. В итоге аналогично энергии электрического поля энергия магнитного поля выражается формулой

Но что представляет собой магнитное поле и за счет чего создается его энергия?
Магнитное поле является одним из неотъемлемых проявлений электрического тока. Вместе с возникновением тока возникает магнитное поле, и оно неизбежно уничтожается при прекращении тока.
Процесс трансформации энергии электрического тока в энергию магнитного поля глубоко отличен от процессов преобразования электрической энергии в другие виды энергии. Действительно, мы можем по желанию увеличить или уменьшить, замедлить или ускорить переход энергии электрического тока в теплоту или химическую энергию, изменяя сопротивление проводников выбором произвольно малого или большого поперечного сечения, варьируя их длину, включая в цепь электролиты и т. д. Мы можем избежать преобразования электрической энергии в механическую, закрепив неподвижно все проводники, образующие электрическую цепь; но мы не в состоянии предотвратить трансформацию энергии тока в период его возникновения в энергию магнитного поля. Магнитное поле является неразлучным спутником электрического тока.
Стационарному (постоянному) току соответствует статическое состояние магнитного поля. Изменение величины тока неизбежно влечет за собой изменение напряженности магнитного поля, и обратно: любое нарушение статического состояния магнитного поля, связанное, например, с перемещением магнитов, с движением посторонних проводников, окруженных собственным магнитным полем, или с изменением величины тока в этих проводниках, немедленно отражается на величине тока в основной цепи. В этой сопряженности магнитного поля и тока друг с другом и заключается физическая сущность явления электромагнитной индукции и, в частности, самоиндукции.
Стальные, или постоянные, магниты, сохраняющие свои поля как бы независимо от движения электричества, в действительности, как уже говорилось, представляют собой лишь более сложный случай, подтверждающий эту неразрывную связь магнитного поля и движения электричества: их магнитные поля обусловлены вращением электронов внутри атомов ферромагнетиков.
Факт неразрывного существования магнитного поля и движения электричества побуждает думать, что энергия магнитного поля представляет собой не что иное, как энергию движения электричества, или так называемую электрокинетическую энергию.
Когда мы включаем ток в проводе или в системе проводов, то в момент включения создается магнитное поле; оно нарастает на протяжении короткого, однако вполне измеримого промежутка времени. В течение того же промежутка времени и скорость урегулированного (преобладающего) движения электронов в направлении тока возрастает от нуля до той скорости, которая соответствует
току установившейся величины  , т. е. стационарному току, напряжение которого мы определяем, основываясь на законе Ома:
, т. е. стационарному току, напряжение которого мы определяем, основываясь на законе Ома: 
Когда в цепь включается какой-нибудь проводник с сопротивлением  то под действием разности потенциалов заряды (например, электроны), находящиеся внутри провода, приобретают преобладающее движение в направлении действующих на них электрических сил. При этом создается магнитное поле, являющееся наглядным выражением приобретенной этими зарядами электрокинетической энергии урегулированного движения. Положим, что через
то под действием разности потенциалов заряды (например, электроны), находящиеся внутри провода, приобретают преобладающее движение в направлении действующих на них электрических сил. При этом создается магнитное поле, являющееся наглядным выражением приобретенной этими зарядами электрокинетической энергии урегулированного движения. Положим, что через  секунд (или долей секунды) ток достиг такой величины, когда оказываемое проводником сопротивление движению электронов становится равным действующей на них силе, находящейся в зависимости от разности потенциалов
секунд (или долей секунды) ток достиг такой величины, когда оказываемое проводником сопротивление движению электронов становится равным действующей на них силе, находящейся в зависимости от разности потенциалов  на концах проводника. Теперь электроны приобрели запас электрокинетической энергии, который в среднем уже не будет изменяться, так как ток останется постоянным. Вся работа, совершаемая током, теперь нацело будет превращаться в тепло, количество которого, выделяемое ежесекундно, пропорционально мощности тока
на концах проводника. Теперь электроны приобрели запас электрокинетической энергии, который в среднем уже не будет изменяться, так как ток останется постоянным. Вся работа, совершаемая током, теперь нацело будет превращаться в тепло, количество которого, выделяемое ежесекундно, пропорционально мощности тока 
До наступления этого момента, пока магнитное поле и движение зарядов еще не достигли своего стационарного состояния, работа тока расходовалась: 1) на тепло и 2) на увеличение электрокинетической энергии потока электронов в проводе, т. е. на создание магнитного поля тока.
Работа тока, расходуемая на создание магнитного поля, направлена на преодоление электродвижущей силы самоиндукции Если величина тока в данный момент есть  то мощность тока, расходуемая на преодоление электродвижущей силы самоиндукции, будет
то мощность тока, расходуемая на преодоление электродвижущей силы самоиндукции, будет  а работа тока, превращающаяся за дифференциально малый промежуток времени
а работа тока, превращающаяся за дифференциально малый промежуток времени  в энергию магнитного поля
в энергию магнитного поля  будет равна
будет равна 
Воспользовавшись формулой (7), определяющей величину электродвижущей силы самоиндукции (умножив обе части этой формулы на  находим, что
находим, что

следовательно,

Запас энергии  магнитного поля тока равен работе, израсходованной током на преодоление электродвижущей силы самоиндукции за весь тот промежуток времени, пока ток возрастает от нуля до некоторого стационарного значения. Значит,
магнитного поля тока равен работе, израсходованной током на преодоление электродвижущей силы самоиндукции за весь тот промежуток времени, пока ток возрастает от нуля до некоторого стационарного значения. Значит,

откуда

Здесь, если  выражено в амперах,
выражено в амперах,  в генри, то энергия получается выраженной в джоулях; если же I выражено в единицах
в генри, то энергия получается выраженной в джоулях; если же I выражено в единицах  в сантиметрах, то энергия получается выраженной в эргах.
в сантиметрах, то энергия получается выраженной в эргах.
Эта формула является одной из важнейших формул электродинамики. Она равносильна формуле (10) [когда формула (10) применяется к вычислению энергии поля уединенного тока], но в сравнении с формулой (10) формула (11) имеет преимущество простоты.
Выражение  является особенно наглядным, так как оно совпадает по форме с выражениями
является особенно наглядным, так как оно совпадает по форме с выражениями  для кинетической энергии поступательного движения и для кинетической энергии вращательного движения.
для кинетической энергии поступательного движения и для кинетической энергии вращательного движения.
Величина тока является обобщенной скоростью движения электричества (§ 25); в самоиндукции проявляется инерция тока; мы вправе поэтому рассматривать формулу (11) как прямое указание на единство магнитной и электрокинетической энергии.
Когда проводник имеет форму компактной катушки, пронизываемой  линиями магнитной индукции, то каждая линия магнитной индукции столько раз охватывает контур проводника, каково число витков
линиями магнитной индукции, то каждая линия магнитной индукции столько раз охватывает контур проводника, каково число витков  в катушке. Это равносильно тому, что контур проводника охватывается по одному разу
в катушке. Это равносильно тому, что контур проводника охватывается по одному разу  линиями магнитной индукции.
линиями магнитной индукции.
Сопоставляя формулу потока магнитной индукции (когда  измерено в генри, I в амперах,
измерено в генри, I в амперах,  максвеллах)
максвеллах)

с формулой Гопкинсона (§ 62)

находим коэффициент самоиндукции (индуктивность) электромагнита:

Здесь I — длина магнитной цепи в железе,  длина воздушного зазора,
длина воздушного зазора,  и
и  поперечные сечения (эти величины должны
поперечные сечения (эти величины должны
быть выражены в сантиметрах);  есть магнитная проницаемость материала сердечника (при заданной величине тока),
есть магнитная проницаемость материала сердечника (при заданной величине тока),  число витков.
число витков.
При пользовании этой формулой не следует забывать, что  зависит от напряженности поля (§ 63), а поэтому для различных величин тока коэффициент самоиндукции тоже будет различным.
зависит от напряженности поля (§ 63), а поэтому для различных величин тока коэффициент самоиндукции тоже будет различным.
Для электромагнита, полюсы которого замкнуты железным якорем, точнее — для тороида (рис. 317), приведенная формула упрощается 


Рис. 317. Тороид
Мы видим отсюда, что индуктивность действительно имеет размерность длины, умноженной на магнитную проницаемость.
Зная индуктивность электромагнита, мы легко можем вычислить его энергию по формуле (11):

Заменив в этой формуле произведение  через поток магнитной индукции
через поток магнитной индукции  выраженный в максвеллах, из (5) или из (6), получим:
выраженный в максвеллах, из (5) или из (6), получим:

Заметим, что обмотку катушки проводом можно осуществить и так, что индуктивность катушки, несмотря на большое число витков, будет близкой к нулю. Для этого провод складывают вдвое и осуществляют обмотку, как показано на рис. 318. Благодаря противоположному направлению тока в смежных витках создаваемые этими витками магнитные поля взаимно почти уничтожаются.

Рис. 318 Безындукционная двухнитная («бифилярная») обмотка.
Вычисление индуктивности проводников в общем случае сопряжено со значительными математическими трудностями. При вычислении индуктивности электромагнита мы воспользовались найденным ранее выражением для магнитного потока, что сразу и привело нас к решению задачи. В большинстве случаев при вычислении индуктивности приходится исходить из уравнения (10) для магнитной энергии тока и, проведя интегрирование, сопоставлять результат с выражением энергии тока через индуктивность, т. е. с формулой  Поясним этот метод расчета на простейшем примере.
Поясним этот метод расчета на простейшем примере.
Вычислим индуктивность кабеля, состоящего из двух коаксиальных цилиндров (рис. 319), по которым ток равной величины идет в противоположны направлениях. Заметим, что когда ток протекает по полому цилиндру (с равномерной по окружности цилиндра плотностью), то магнитное поле тока внутри цилиндра равно нулю, а вне цилиндра оно таково же, как поле тока той же величины, идущего по оси цилиндра. Это следует из соображений симметрии и из выражения для магнитодвижущей силы:  Действительно, для любого замкнутого контура, который не охватывает тока (например, для окружности, проведенной вокруг оси цилиндра в плоскости, перпендикулярной к оси и имеющей радиус
Действительно, для любого замкнутого контура, который не охватывает тока (например, для окружности, проведенной вокруг оси цилиндра в плоскости, перпендикулярной к оси и имеющей радиус  меньший, чем радиус
меньший, чем радиус  цилиндра), магнитодвижущая сила равна нулю; но
цилиндра), магнитодвижущая сила равна нулю; но  стало быть, поскольку
стало быть, поскольку  то и
то и  Из выражения магнитодвижущей силы для окружности, охватывающей цилиндр
Из выражения магнитодвижущей силы для окружности, охватывающей цилиндр  находим, что
находим, что 

Рис. 319. Кабель из двух коаксиальных цилиндров
Таким образом, в интересующем нас случае все магнитное поле равных и противоположных токов сосредоточивается в пространстве между коаксиальными цилиндрами и создается здесь током, идущим по внутреннему цилиндру (по сказанному выше поле обоих токов внутри меньшего цилиндра равно нулю, а вне большего цилиндра поля противоположно направленных токов взаимно уничтожаются). Следовательно, в рассматриваемом случае, разбив весь объем между цилиндрами на бесконечно тонкие слои  для энергии токов мы получаем выражение, которое легко интегрируется:
для энергии токов мы получаем выражение, которое легко интегрируется:

Сопоставляя найденную величину энергии магнитного поля токов с выражением энергии тока через индуктивность  получаем формулу для индуктивности кабеля длиной
получаем формулу для индуктивности кабеля длиной  состоящего из двух коаксиальных цилиндров с радиусами
состоящего из двух коаксиальных цилиндров с радиусами 

Аналогичные вычисления для случая двух параллельных проводников длиной  с радиусом сечения
с радиусом сечения  удаленных друг от друга на расстояние а
удаленных друг от друга на расстояние а  дают для величины индуктивности двухпроводной линии:
дают для величины индуктивности двухпроводной линии:

Для индуктивности круглой петли провода при радиусе петли  и радиусе сечения провода
и радиусе сечения провода  получается:
получается:

При  оборотах провода индуктивность кольцевой катушки в
оборотах провода индуктивность кольцевой катушки в  раз превышает индуктивность круглой петли.
раз превышает индуктивность круглой петли.
Индуктивность соленоида длиной I при  витках провода с радиусом витков
витках провода с радиусом витков  (и площадью сечения соленоида
(и площадью сечения соленоида  равна
равна

Индуктивность одиночного провода длиной  имеющего радиус сечения
имеющего радиус сечения  и расположенного на высоте
и расположенного на высоте  над землей:
над землей:

Приведенные формулы определяют индуктивность в сантиметрах, если в сантиметрах выражены  и другие величины.
и другие величины.
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
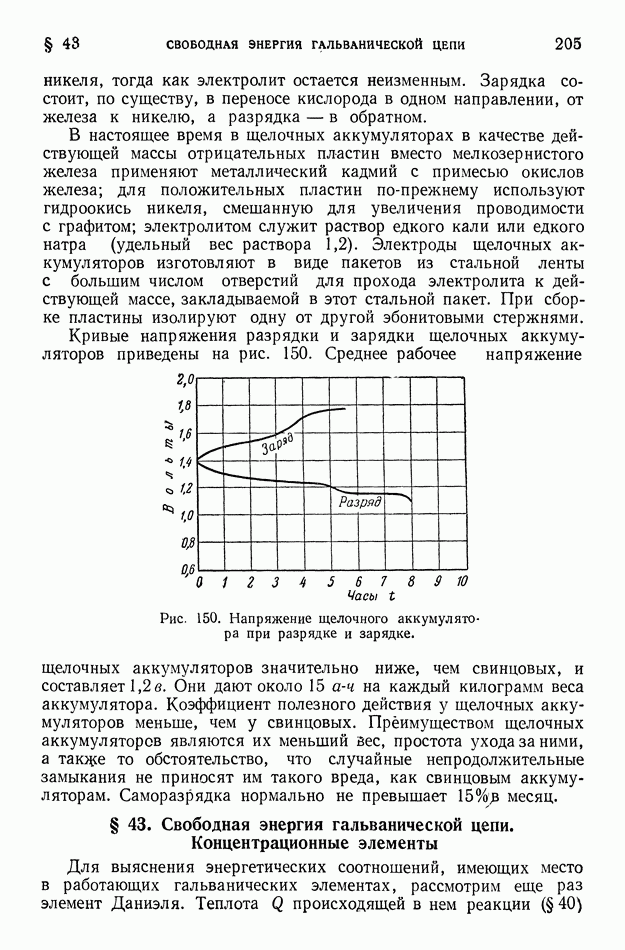
- § 42. Аккумуляторы
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
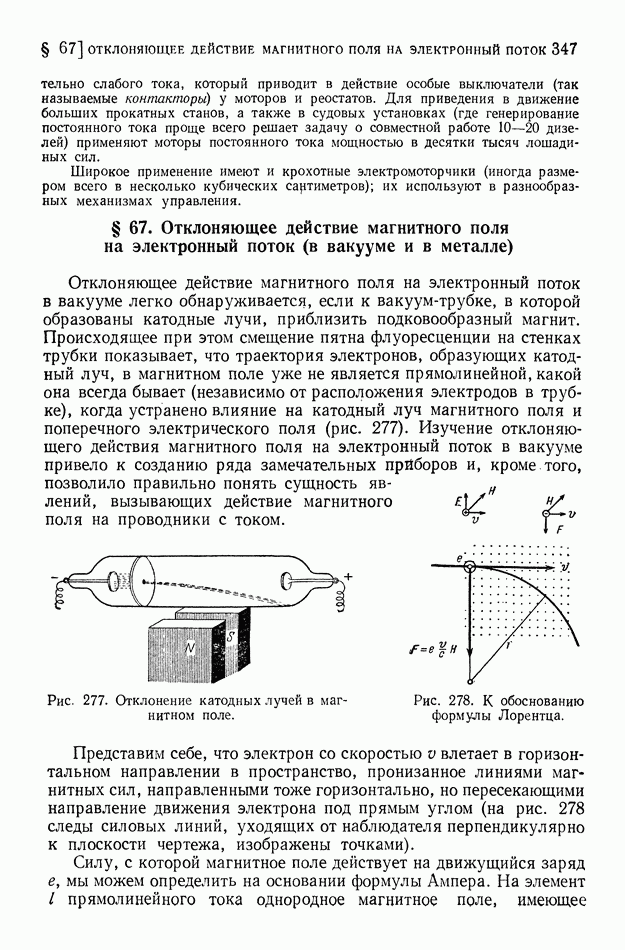
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
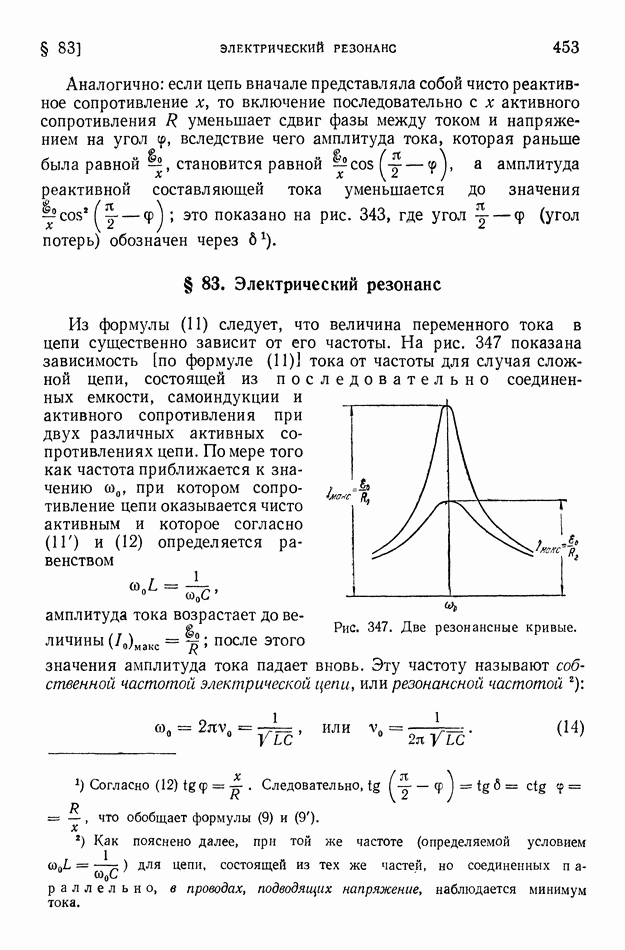
- § 83. Электрический резонанс
- § 84. Трансформация тока
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)