| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 61. Закон Био и Савара
В основе всех расчетов магнитных действий тока и многих других расчетов, связанных с теорией электромагнитного поля, лежит закон, открытый в 1820 г. французскими учеными Био и Саваром, сделавшими измерения, и Лапласом, который обобщил результаты измерений. Эти ученые показали, что во всех случаях силу магнитного поля тока можно вычислить, геометрически суммируя (по правилу многоугольника) силы, вызываемые отдельными малыми участками тока.

Рис. 231. К закону Био и Савара. Действие элемента тока на магнитный полюс.
Био, Савар и Лаплас установили, что если тонкий проводник, по которому течет ток, представлять себе разбитым на отдельные малые участки (рис. 231), то силу  с которой взаимодействует каждый участок тока с магнитным полюсом, надо считать, во-первых, пропорциональной длине участка
с которой взаимодействует каждый участок тока с магнитным полюсом, надо считать, во-первых, пропорциональной длине участка  во-вторых, силу эту надо считать прямо пропорциональной произведению величины полюса
во-вторых, силу эту надо считать прямо пропорциональной произведению величины полюса  на величину тока
на величину тока  в проводнике и обратно пропорциональной квадрату расстояния
в проводнике и обратно пропорциональной квадрату расстояния  от данного участка проводника до полюса.
от данного участка проводника до полюса.
В этой (еще неполной) формулировке закон Био и Савара напоминает собой законы Кулона для электрических зарядов и магнитных полюсов. Дело осложняется, однако, тем, что величина  зависит еще от угла между направлением элемента тока и
зависит еще от угла между направлением элемента тока и
направлением радиуса-вектора, проведенного от элемента тока к магнитному полюсу. А именно, сила взаимодействия элемента тока и магнитного полюса является наибольшей, когда ток направлен под прямым углом к радиусу-вектору, проведенному от элемента тока к магнитному полюсу. Когда же указанный угол равен нулю (т. е. направления элемента тока и радиуса-вектора совпадают), то сила взаимодействия между элементом тока и магнитным полюсом обращается в нуль. Вообще же магнитная сила, определяемая законом Био и Савара, пропорциональна синусу упомянутого угла, так что в общем случае закон Био и Савара выражается формулой

Каждая такая элементарная сила  направлена перпендикулярно к плоскости, проведенной через полюс и элемент тока, в сторону, определяемую правилом буравчика. Если в приведенной формуле
направлена перпендикулярно к плоскости, проведенной через полюс и элемент тока, в сторону, определяемую правилом буравчика. Если в приведенной формуле  измерено в абсолютных магнитных единицах,
измерено в абсолютных магнитных единицах,  в абсолютных электромагнитных единицах величины тока,
в абсолютных электромагнитных единицах величины тока,  в сантиметрах, то
в сантиметрах, то  будет выражена в динах.
будет выражена в динах.
Пользуясь понятием о векторном произведении (т. I, стр. 39) и рассматривая элемент  тока и расстояние
тока и расстояние  от него до магнитного полюса
от него до магнитного полюса  векторы, закон Био и Савара можно представить в следующем виде:
векторы, закон Био и Савара можно представить в следующем виде:

Для демонстрации действия тока на магнитный полюс, казалось бы, необходимо изолировать магнитный полюс от другого, противоположного по знаку магнитного полюса, что, конечно, невозможно. Однако это затруднение, как показано Фарадеем в 1821 г., можно обойти, расположив магнит относительно тока таким образом, чтобы один из полюсов магнита оказался на оси вращения другого полюса. На рис. 232 изображен прибор Фарадея, позволяющий одновременно демонстрировать действие тока на магнитный полюс и действие магнитного полюса на ток (которое рассмотрено в § 65). В этом приборе имеются два сосуда (они показаны в разрезе), в которые наливают ртуть. Цепь тока указана стрелками. В левом

Рис. 232. Прибор Фарадея для демонстрации действия тока на магнитный полюс (левая часть) и действия магнитного полюса на ток (правая часть).
сосуде стержневой магнит удерживается от всплывания в ртути гибкой нитью, причем нижний полюс магнита находится на  вокруг которой при пропускании тока через прибор начинает вращаться другой полюс магнита. В правом сосуде оба полюса магнита расположены на оси, вокруг которой при пропускании тока вращается гибкий проводник (один его конец закреплен наверху, а другой скользит по поверхности ртути).
вокруг которой при пропускании тока через прибор начинает вращаться другой полюс магнита. В правом сосуде оба полюса магнита расположены на оси, вокруг которой при пропускании тока вращается гибкий проводник (один его конец закреплен наверху, а другой скользит по поверхности ртути).
Заметим, что магнитные свойства среды не оказывают никакого влияния на напряженность магнитного поля, создаваемого током: в закон Био и Савара магнитная проницаемость среды  вовсе не входит.
вовсе не входит.
Выражение (13), представляющее закон Био и Савара в дифференциальной форме, показывает, что элементарная сила  с которой бесконечно малый участок тела действует на магнитный полюс, обратно пропорциональна квадрату расстояния между ними. Отсюда совсем не следует, что ивсясила
с которой бесконечно малый участок тела действует на магнитный полюс, обратно пропорциональна квадрату расстояния между ними. Отсюда совсем не следует, что ивсясила  с которой ток конечной длины действует на магнитный полюс, также обратно пропорциональна квадрату расстояния. Сила
с которой ток конечной длины действует на магнитный полюс, также обратно пропорциональна квадрату расстояния. Сила  может быть найдена геометрический суммированием бесконечно малых воздействий
может быть найдена геометрический суммированием бесконечно малых воздействий  для всех элементов тока, причем мы, вообще говоря, получим иную степень расстояния.
для всех элементов тока, причем мы, вообще говоря, получим иную степень расстояния.

Рис. 233.
Так, например, напряженность поля, создаваемого прямолинейным током, обратно пропорциональна первой степени расстояния от линии тока. Очевидно, что когда все элементы тока лежат на одной прямой, то все обусловленные этими элементами тока силы  в какой-либо рассматриваемой точке поля, где находится полюс
в какой-либо рассматриваемой точке поля, где находится полюс  направлены в одну сторону (на рис. 233 перпендикулярно к плоскости чертежа, к читателю), и, стало быть, в данном случае геометрическое суммирование сил
направлены в одну сторону (на рис. 233 перпендикулярно к плоскости чертежа, к читателю), и, стало быть, в данном случае геометрическое суммирование сил  сводится к их простому арифметическому сложению:
сводится к их простому арифметическому сложению:

Легко видеть, что  а следовательно,
а следовательно,  но
но  и поэтому
и поэтому  Таким образом,
Таким образом,

где  углы, определяющие предельное положение радиусов-векторов, проведенных из концов проводника в рассматриваемую точку поля.
углы, определяющие предельное положение радиусов-векторов, проведенных из концов проводника в рассматриваемую точку поля.
Для бесконечно длинного прямолинейного проводника  следовательно,
следовательно,  т. е.
т. е.

Если величина тока  выражена в амперах, то
выражена в амперах, то

Мы видим, что напряженность поля прямого тока в любой точке прямо пропорциональна величине тока и обратно пропорциональна первой степени - расстояния между этой точкой и током.

Рис. 234.
Задача геометрического суммирования сил, с которыми действуют на магнитный полюс отдельные участки тока, наиболее легко разрешается для случая, когда магнитный полюс помещен в центре кругового тока (рис. 234). Представим себе, что круговой ток разделен на весьма большое число малых участков  Сила
Сила  с которой каждый такой участок действует на магнитный полюет, помещенный в центре кругового тока, для всех участков одинакова и направлена в одну и ту же сторону. Синус угла между направлением тока в каждом из этих участков и радиусом равен единице. Следовательно, по закону Био и Савара
с которой каждый такой участок действует на магнитный полюет, помещенный в центре кругового тока, для всех участков одинакова и направлена в одну и ту же сторону. Синус угла между направлением тока в каждом из этих участков и радиусом равен единице. Следовательно, по закону Био и Савара

Вынося за знак интеграла одинаковую для всех участков величину -у и учитывая, что суммарная длина всех участков кругового тока равна  находим:
находим:

Отсюда заключаем, что напряженность поля в центре кругового тока выражается такой формулой:

где  выражено в
выражено в  в сантиметрах.
в сантиметрах.
Если величина тока выражена в амперах, то

Исследуя расчетом напряженность магнитного поля кругового тока в различных точках пространства, Ампер доказал замечательную теорему о том, что магнитное поле кругового тока таково же, как поле магнитного листка. А именно:
Круговой ток, имеющий величину  единиц CGSM, создает такое же магнитное поле, как если бы площадь, обтекаемая током, представляла собой бесконечно тонкий магнит (магнитный листок) с магнитным моментом, равным произведению величины тока I на площадь
единиц CGSM, создает такое же магнитное поле, как если бы площадь, обтекаемая током, представляла собой бесконечно тонкий магнит (магнитный листок) с магнитным моментом, равным произведению величины тока I на площадь  обтекаемую током (выраженную в квадратных сантиметрах):
обтекаемую током (выраженную в квадратных сантиметрах):

На основании сказанного Ампер и высказал догадку, что намагничивание тел объясняется внутримолекулярными круговыми токами. Как упоминалось в § 57, природа этих амперовых молекулярных токов была установлена только в XX в.
Ампер первый изучил магнитное взаимодействие токов и разработал математические основы электродинамики. Замечательный трактат Андре Мари Ампера «Теория электродинамических явлений, выведенная из опыта» был опубликован в 1827 г. Максвелл называл Ампера «Ньютоном электричества». Ампер проявил исключительную прозорливость не только в вопросах физики. Он с большой убежденностью защищал идею об эволюции организмов — идею, которая в те годы, задолго до работ Дарвина, вызывала только насмешки.
Когда имеется  витков кругового тока (сжатый соленоид), то магнитный момент эквивалентного магнита равен
витков кругового тока (сжатый соленоид), то магнитный момент эквивалентного магнита равен

Соотношения (17) и (17) были проверены экспериментально и подтверждены Вебером.
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
- § 42. Аккумуляторы
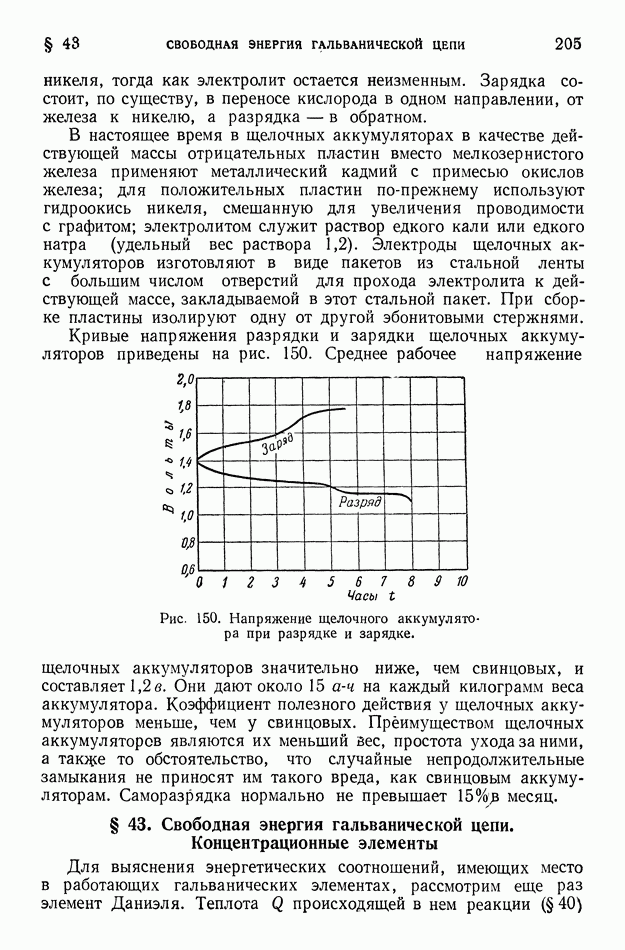
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
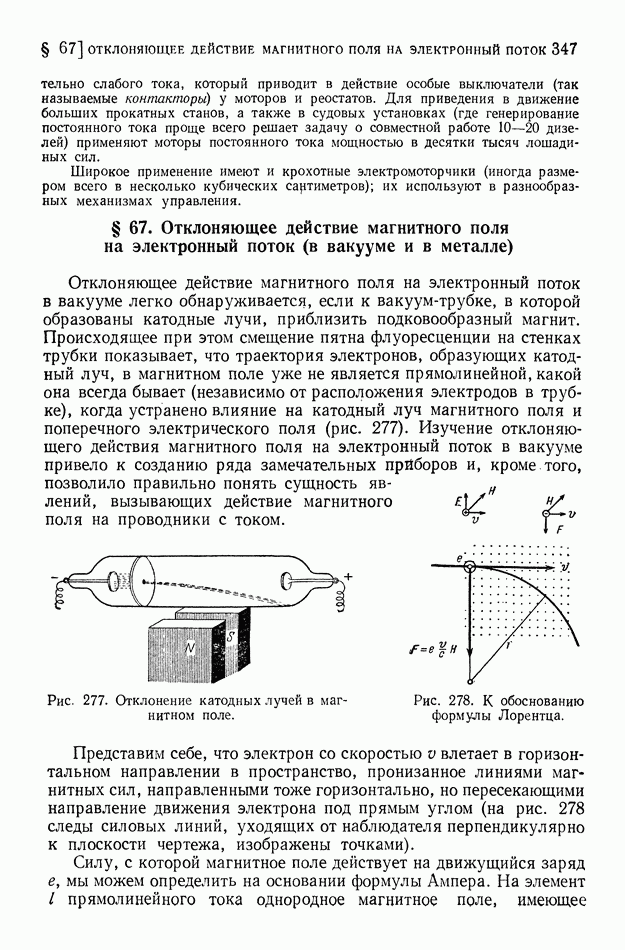
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
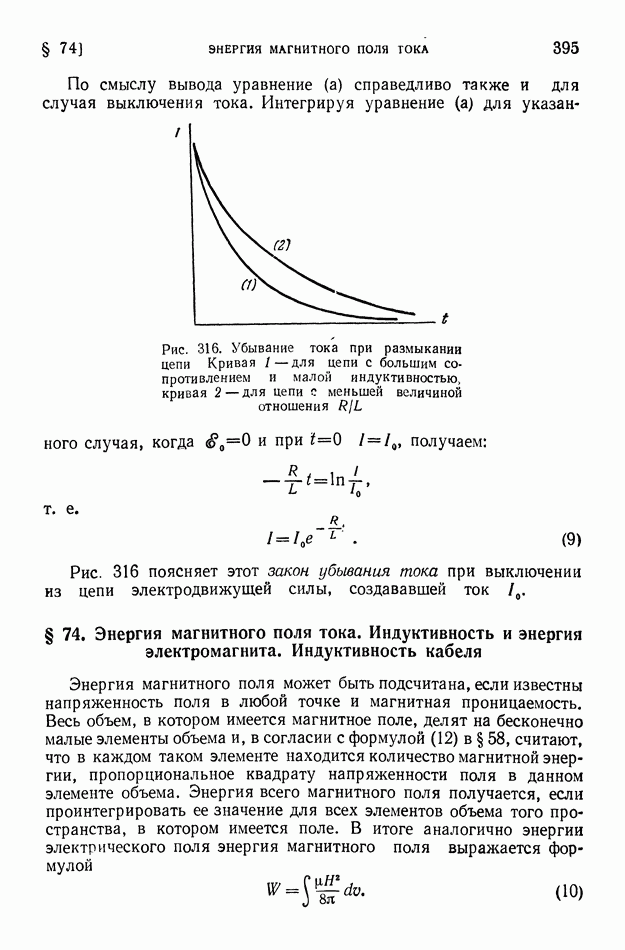
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
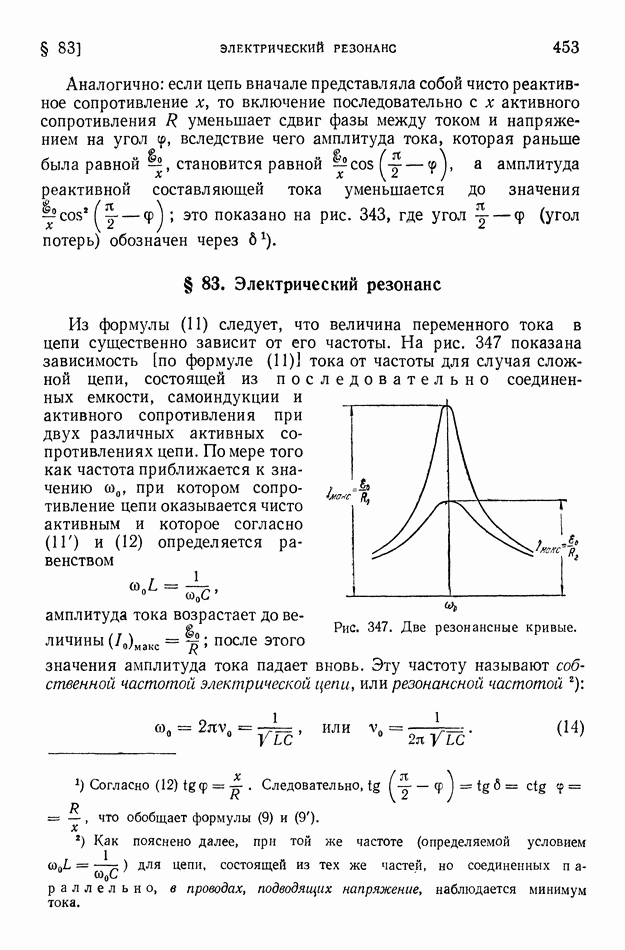
- § 83. Электрический резонанс
- § 84. Трансформация тока
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)