| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Теорема Острогдадского — Гаусса
Представление о силовых линиях позволяет внести наглядность и простоту в изучение электрических явлений.
Через каждую точку поля можно провести силовую линию. Число силовых линий ничем не ограничено; вычерчивая поле, их можно было бы рисовать и очень густо и, наоборот, на больших расстояниях друг от друга. Сделаем соглашение выбирать густоту линий, изображающих поле, так, чтобы эта густота определяла величину напряженности поля: будем проводить столько линий, чтобы через каждый квадратный сантиметр сечения, перпендикулярного к линиям, проходило число линий, равное численному значению напряженности поля. Если напряженность поля равна  единиц, то через
единиц, то через  поперечного сечения нужно провести
поперечного сечения нужно провести  линий.
линий.
Этот способ изображения электрических полей обладает весьма важным достоинством: одни и те же линии изображают поле на всем его протяжении, причем по общему числу линий, выходящих наружу из какой-либо замкнутой поверхности, можно судить о количестве электричества, содержащегося в пространстве, ограниченном этой поверхностью.
В самом деле, окружим какой-либо точечный заряд  шаровой поверхностью с радиусом и Так как силовые линии поля направлены по радиусам, а поверхность шара везде перпендикулярна к радиусу, то через каждый квадратный сантиметр поверхности шара, по условию, должно проходить число линий, равное напряженности поля на этой поверхности, т. е. линий, где
шаровой поверхностью с радиусом и Так как силовые линии поля направлены по радиусам, а поверхность шара везде перпендикулярна к радиусу, то через каждый квадратный сантиметр поверхности шара, по условию, должно проходить число линий, равное напряженности поля на этой поверхности, т. е. линий, где  есть диэлектрическая постоянная среды (мы предполагаем, что среда однородна). Поверхность шара равна
есть диэлектрическая постоянная среды (мы предполагаем, что среда однородна). Поверхность шара равна  Следовательно, общее число линий
Следовательно, общее число линий  выходящих наружу из всей шаровой поверхности, равно
выходящих наружу из всей шаровой поверхности, равно

Для положительного заряда число линий  положительно, для отрицательного заряда
положительно, для отрицательного заряда  отрицательно, т. е. линии входят в поверхность шара.
отрицательно, т. е. линии входят в поверхность шара.
Это число, как видим, не зависит от  Как на близких расстояниях, так и на далеких избранное нами изображение поля, при котором густота силовых линий выражает напряженность поля, осуществляется при помощи одних и тех же линий. Линии начинаются или кончаются только на зарядах.
Как на близких расстояниях, так и на далеких избранное нами изображение поля, при котором густота силовых линий выражает напряженность поля, осуществляется при помощи одних и тех же линий. Линии начинаются или кончаются только на зарядах.
Остроградский и Гаусс доказали, что приведенная выше формула для числа линий  может быть распространена на любое число как угодно расположенных зарядов.
может быть распространена на любое число как угодно расположенных зарядов.
Теорему Остроградского — Гаусса можно сформулировать следующим образом: при сделанном соглашении, что густота силовых линий в каждом месте изображает напряженность поля, из всякой замкнутой поверхности, охватывающей заряды  выходит алгебраическое число линий
выходит алгебраическое число линий

Если мы проведем замкнутую поверхность, не содержащую внутри себя зарядов или же содержащую внутри себя равное число положительных и отрицательных зарядов, то алгебраическое число линий, выходящих из этой поверхности, будет равно нулю: из поверхности будет выходить столько же линий, сколько входит в нее.

Рис. 3. Силовая трубка.
Рассмотрим ту часть электрического поля, где нет зарядов и где диэлектрическая среда однородна. В этой части поля представим себе пучок силовых линий. Ограничим эти силовые линии поверхностью, которая всюду касательна к направлению поля, и двумя плоскостями, перпендикулярными к силовым линиям (рис. 3). Выделенная таким образом часть поля представляет собой «трубку силовых линий», или, иначе, «фараде-еву силовую трубку». Так как внутри лиловой трубки нет электрических зарядов, то согласно теореме Остроградского — Гаусса число силовых линий, входящих в трубку через сечение  будет равно числу силовых линий, выходящих из нее через сечение
будет равно числу силовых линий, выходящих из нее через сечение  Иными словами, ни одна из силовых линий не кончается внутри трубки и не начинается там, а все силовые линии, не прерываясь, пронизывают оба поперечных сечения трубки. При этом согласно сделанному соглашению густота силовых линий (измеряемая их числом на
Иными словами, ни одна из силовых линий не кончается внутри трубки и не начинается там, а все силовые линии, не прерываясь, пронизывают оба поперечных сечения трубки. При этом согласно сделанному соглашению густота силовых линий (измеряемая их числом на  сечения, перпендикулярного к линиям) всюду по длине силовой трубки равна напряженности поля. Если площадь сечения
сечения, перпендикулярного к линиям) всюду по длине силовой трубки равна напряженности поля. Если площадь сечения  в
в  раз больше, чем площадь сечения
раз больше, чем площадь сечения  то это означает, что напряженность поля вдоль силовой трубки уменьшается так, что в сечении
то это означает, что напряженность поля вдоль силовой трубки уменьшается так, что в сечении  напряженность поля в
напряженность поля в  раз меньше, чем в сечении
раз меньше, чем в сечении 
Следует отметить, однако, что для случаев, когда диэлектрическая среда неоднородна, изображение поля посредством силовых
линий и силовых трубок утрачивает свою простоту. Из уравнения (7) видно, что число силовых линий зависит от диэлектрической постоянной. Стало быть, в неоднородной среде число линий в силовой трубке может измениться вследствие изменения диэлектрической постоянной среды. В неоднородной среде изображение поля, как показано в следующем параграфе, нужно строить иначе.
При графическом изображении поля густота силовых линий, пересекающих перпендикулярную к ним прямую в любом месте поля, изображает напряженность поля. Это позволяет вычерчивать сложные поля, образованные несколькими зарядами, по способу, указанному Максвеллом: сначала вычерчивают два уже известных поля, например поля точечных зарядов (рис. 4);

Рис. 4. Вычерчивание поля по способу Максвелла.
получается сетка четырехугольных ячеек, в которых одна диагональ пропорциональна геометрической сумме напряженностей полей, а другая — их разности; соединяя соответственные углы этих ячеек, получают картину суммарного поля. Затем так же суммируют полученное поле с полем третьего, четвертого и т. д. зарядов. Во многих случаях этот графический метод анализа поля оказывается практически наиболее удобным.
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
- § 42. Аккумуляторы
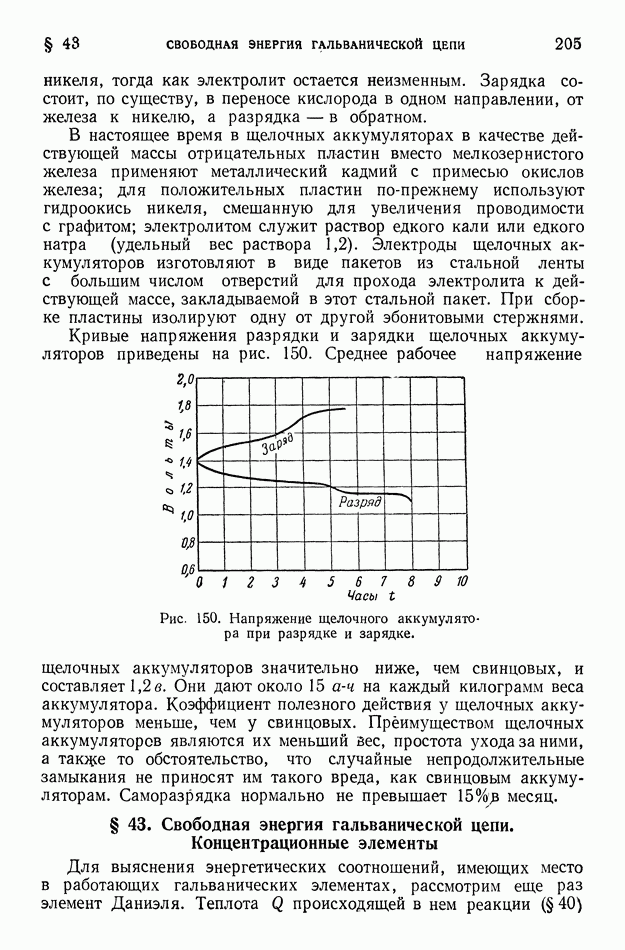
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
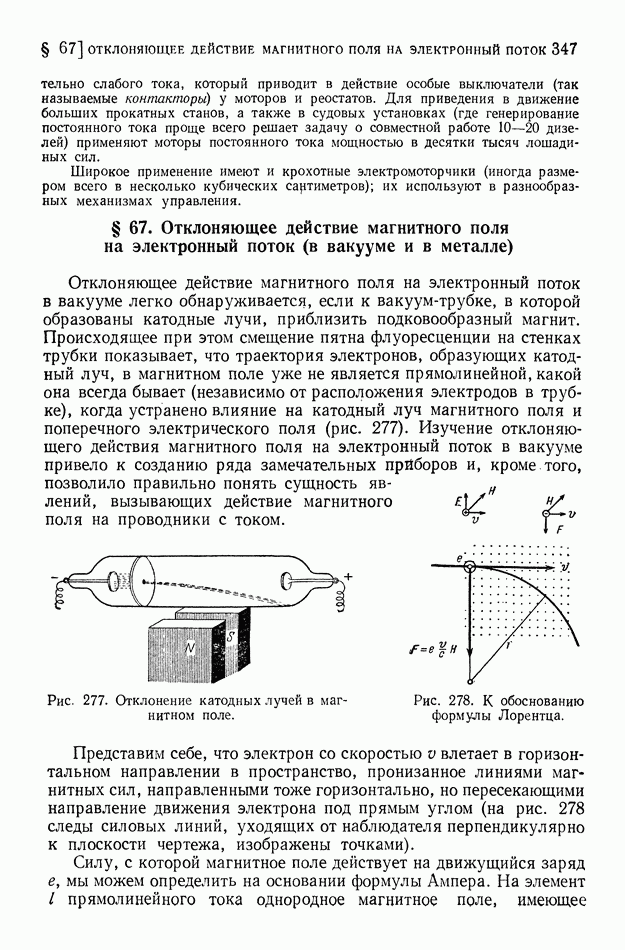
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
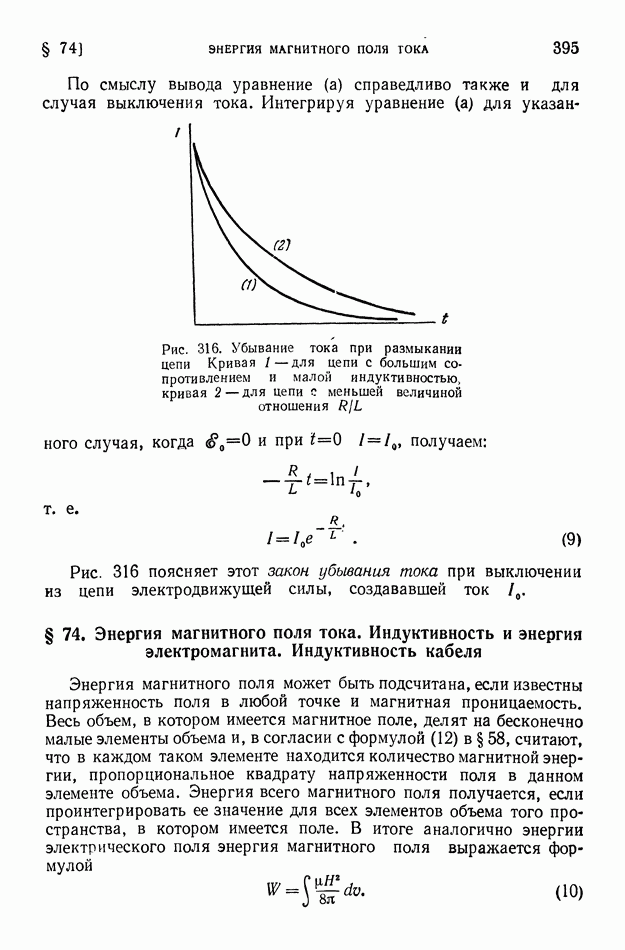
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
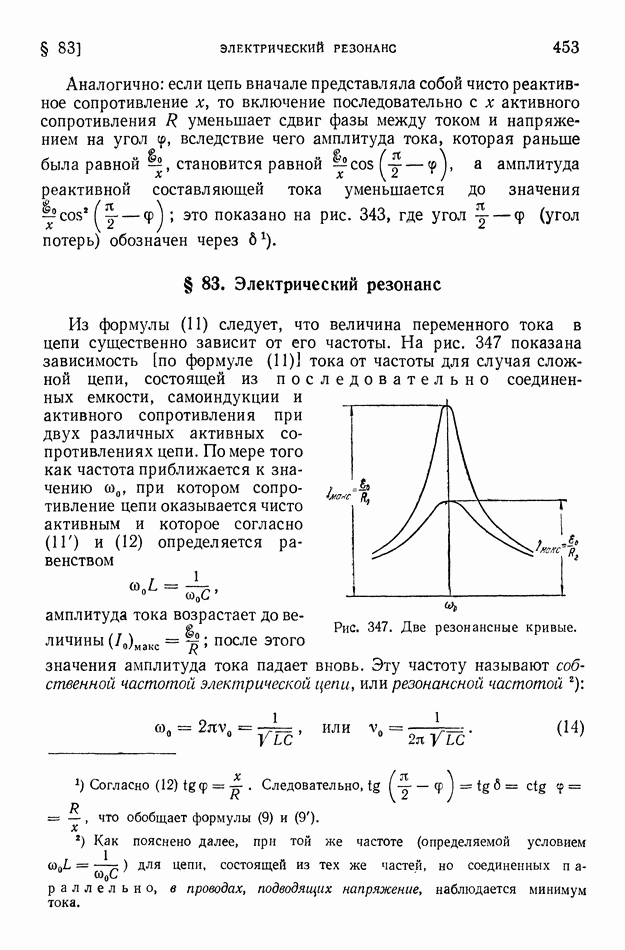
- § 83. Электрический резонанс
- § 84. Трансформация тока
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)