| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 83. Электрический резонанс
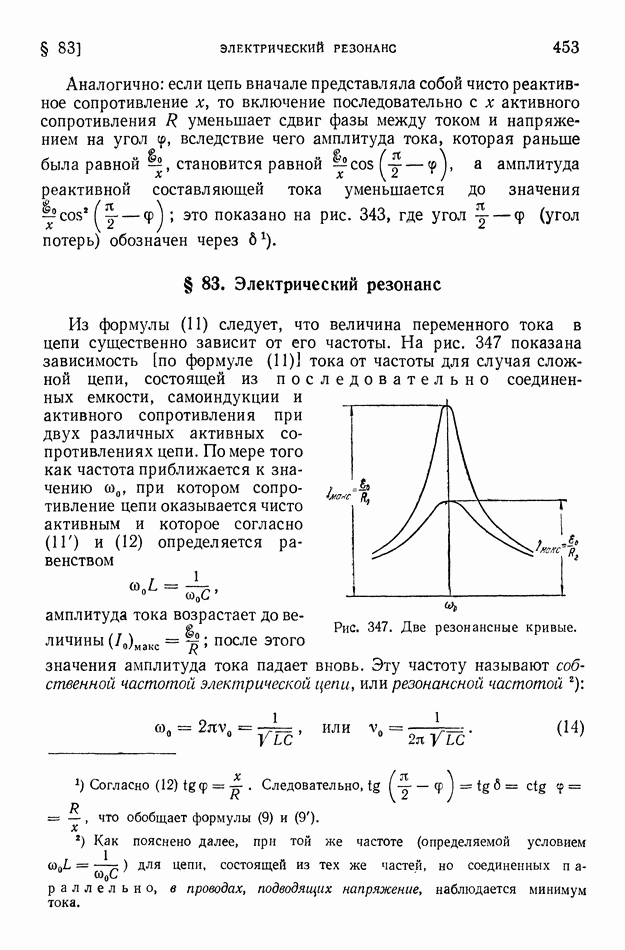
Из формулы (11) следует, что величина переменного тока в цепи существенно зависит от его частоты. На рис. 347 показана зависимость [по формуле (11)] тока от частоты для случая сложной цепи, состоящей из последовательно соединенных емкости, самоиндукции и активного сопротивления при двух различных активных сопротивлениях цепи. По мере того как частота приближается к значению  при котором сопротивление цепи оказывается чисто активным и которое согласно
при котором сопротивление цепи оказывается чисто активным и которое согласно  и (12) определяется равенством
и (12) определяется равенством

амплитуда тока возрастает до величины  после этого значения амплитуда тока падает вновь. Эту частоту называют собственной частотой электрической цепи, или резонансной частотой:
после этого значения амплитуда тока падает вновь. Эту частоту называют собственной частотой электрической цепи, или резонансной частотой:


Рис. 347. Две резонансные кривые.
Величина тока при резонансе получается, следовательно, тем большей, чем меньше омическое сопротивление цепи. При весьма малом омическом сопротивлении ток при резонансе соответственно обычному закону Ома велик и кривая резонанса имеет острый горб; чем больше омическое сопротивление цепи, тем меньше подъем тока при резонансе и тем менее резко выражен максимум на кривой резонанса.
Напряжения на конденсаторе  и индуктивной катушке
и индуктивной катушке  при резонансе могут быть очень велики; но (поскольку при резонансе
при резонансе могут быть очень велики; но (поскольку при резонансе  они одинаковы по величине и, вместе с тем, противоположны по знаку; поэтому все подведенное напряжение
они одинаковы по величине и, вместе с тем, противоположны по знаку; поэтому все подведенное напряжение  падает на активном сопротивлении
падает на активном сопротивлении 

Заменяя в этих формулах собственную частоту цепи  через
через  их часто записывают так:
их часто записывают так:

По сопоставлении с законом Ома очевидно, что величина  имеет физический смысл сопротивления цепи при резонансе. Эту величину называют волновым сопротивлением цепи (как пояснено подробнее на стр. 502, указанная величина определяет отношение напряжения к току в электромагнитной волне, распространяющейся вдоль проводящей линии).
имеет физический смысл сопротивления цепи при резонансе. Эту величину называют волновым сопротивлением цепи (как пояснено подробнее на стр. 502, указанная величина определяет отношение напряжения к току в электромагнитной волне, распространяющейся вдоль проводящей линии).
Мы видим, таким образом, что при резонансе в последовательной цепи амплитуды напряжения на катушке и конденсаторе равны напряжению, которое резонансный ток амплитудной величины создает на волновом сопротивлении:

Полезно отметить, что, вообще говоря, при какой-либо частоте, отличной от резонансной, волновое сопротивление цепи представляет собой величину среднегармоническую по отношению к индуктивному и емкостному сопротивлениям цепи. Действительно,

Следовательно,

При резонансной частоте  и
и

Заметим, что если  выражено не в генри, а в микрогенри или же в сантиметрах, а С не в фарадах, а в пикофарадах или тоже в сантиметрах, то
выражено не в генри, а в микрогенри или же в сантиметрах, а С не в фарадах, а в пикофарадах или тоже в сантиметрах, то

По формуле (15) в цепи, которая состоит из последовательно включенных омического сопротивления  ом и реактивных сопротивлений
ом и реактивных сопротивлений  ом, электродвижущая сила, имеющая амплитуду 100 в, дает при резонансе амплитуду тока в 10 а (при частоте, в четыре раза большей или меньшей, чем резонансная, ток в указанной цепи не превышает
ом, электродвижущая сила, имеющая амплитуду 100 в, дает при резонансе амплитуду тока в 10 а (при частоте, в четыре раза большей или меньшей, чем резонансная, ток в указанной цепи не превышает  напряжения на конденсаторе и катушке при резонансе будут иметь амплитуду
напряжения на конденсаторе и катушке при резонансе будут иметь амплитуду  в.
в.

Рис. 348. Параллельное соединение элементов цепи.
Мы видим, таким образом, что цепь, состоящая  последовательно соединенных индуктивности, емкости и сопротивления, представляет для проходящего через нее переменного тока тем меньшее сопротивление, чем ближе частота тока к резонансной частоте цепи; при резонансе напряжения на конденсаторе и катушке, равные друг другу, но противоположные по направлению, могут во много раз превышать электродвижущую силу, действующую на цепь в целом.
последовательно соединенных индуктивности, емкости и сопротивления, представляет для проходящего через нее переменного тока тем меньшее сопротивление, чем ближе частота тока к резонансной частоте цепи; при резонансе напряжения на конденсаторе и катушке, равные друг другу, но противоположные по направлению, могут во много раз превышать электродвижущую силу, действующую на цепь в целом.

Рис. 349. Векторная диаграмма токов для параллельного соединения элементов цепи
Обратимся к ряс. 348, на котором схематически изображена цепь, состоящая из параллельно соединенных индуктивности  емкости С и активного сопротивления
емкости С и активного сопротивления  к которым приложена синусоидальная электродвижущая сила.
к которым приложена синусоидальная электродвижущая сила.
Понятно, что общий ток в такой цепи является суммой трех токов: активного и двух реактивных. Построим систему векторов для этих трех токов (рис. 349). Векторы индуктивного и емкостного токов направлены противоположно друг другу (так как первый на 90 отстает от вектора напряжения, а второй на  опережает напряжение); вектор же активного тока расположен к ним под прямым углом. Чтобы найти правило слежения амплитуд тока, вспомним, что нам нужно найти вектор, проекция которого равнялась бы сумме проекций отдельных составляющих векторов; очевидно, что в качестве вектора суммарного тока мы должны взять
опережает напряжение); вектор же активного тока расположен к ним под прямым углом. Чтобы найти правило слежения амплитуд тока, вспомним, что нам нужно найти вектор, проекция которого равнялась бы сумме проекций отдельных составляющих векторов; очевидно, что в качестве вектора суммарного тока мы должны взять
равнодействующую (геометрическую сумму) активного, индуктивного и емкостного токов.
На рис. 349 произведено сложение трех векторов тока для электрической сети, которая схематически представлена на рис. 348. Мы видим, что угол между вектором суммарного тока и вектором напряжения (угол  ) определяется соотношением между активной составляющей тока и алгебраической суммой реактивных составляющих. Вектор тока может как опережать, так и отставать от вектора напряжения в зависимости от того, что больше: индуктивное сопротивление или же емкостное сопротивление.
) определяется соотношением между активной составляющей тока и алгебраической суммой реактивных составляющих. Вектор тока может как опережать, так и отставать от вектора напряжения в зависимости от того, что больше: индуктивное сопротивление или же емкостное сопротивление.
Наиболее выгодный случай получается тогда, когда оба реактивных тока, противоположных один другому, уравновесят друг друга. Тогда источник электроэнергии, генератор, будет загружен только полезным активным током.
Векторы емкостного и индуктивного токов компенсируют друг друга, когда

Мы получаем в этом случае явление резонанса при частоте, которая определяется той же формулой (14) (если участки цепи, содержащие  не обладают заметным активным сопротивлением).
не обладают заметным активным сопротивлением).
Однако в этом случае суммарный ток  во внешней цепи при резонансе имеет уже не наибольшее, а наименьшее значение, так как реактивные токи, компенсируя друг друга в цепи емкости и индуктивности, во внешней цепи отсутствуют.
во внешней цепи при резонансе имеет уже не наибольшее, а наименьшее значение, так как реактивные токи, компенсируя друг друга в цепи емкости и индуктивности, во внешней цепи отсутствуют.
Аналогично выводу формулы (11) по диаграмме рис. 345 и учитывая, что для параллельной цепи  из диаграммы рис. 349 получаем:
из диаграммы рис. 349 получаем:  Отсюда полная проьодимость параллельной цепи определяется формулой
Отсюда полная проьодимость параллельной цепи определяется формулой

При резонансе  и полное сопротивление цепи равно активному сопротивлению
и полное сопротивление цепи равно активному сопротивлению  которое шунтирует катушку и конденсатор. При частоте, отличной от резонансной, когда
которое шунтирует катушку и конденсатор. При частоте, отличной от резонансной, когда  полная проводимость становится больше, т. е. уменьшается сопротивление цепи; тогда через внешнюю цепь протекает не только активный ток, но и часть реактивного тока, циркулирующего в контуре катушка — конденсатор.
полная проводимость становится больше, т. е. уменьшается сопротивление цепи; тогда через внешнюю цепь протекает не только активный ток, но и часть реактивного тока, циркулирующего в контуре катушка — конденсатор.
Таким образом, контур, состоящий из параллельно подключенных индуктивности и емкости, представляет собой тем большее сопротивление для подведенного к этому контуру переменного тока, чем ближе частота тока к резонансной частоте контура.
Реактивные токи (рис. 350) образуют в цепи кольцевой переменный ток, который при резонансной частоте минует внешнюю цепь; этот реактивный ток может быть очень велик, в то время как ток во внешней цепи определяется в момент резонанса только сопротивлением  и может быть относительно небольшим.
и может быть относительно небольшим.
Амплитуда реактивного тока в цепи параллельно включенных катушки и конденсатора при резонансе равна частному от деления амплитуды подведенного к ним напряжения на реактивное сопротивление катушки или конденсатора или, что для резонансной частоты согласно (16) то же самое, на волновое сопротивление контура:

Поскольку при собственной частоте  в цепи, состоящей из последовательно включенных сопротивления, катушки и конденсатора, напряжения на клеммах катушки и конденсатора могут во много раз превышать подведенное напряжение, этот случай часто (но не вполне удачно) называют резонансом напряжений; по аналогичной причине резонанс в цепи, состоящей из тех же элементов, соединенных параллельно, называют резонансом токов. [Правильнее относить понятие резонанса к совокупности явлений, происходящих в цепи; кроме того, как раз в последовательной цепи ток при резонансе максимален. Наиболее характерно, что при резонансе сопротивление становится чисто активным и что в зависимости от частоты тока сопротивление последовательной цепи при резонансе имеет более или менее остро выраженный минимум, а параллельной цепи — максимум.]
в цепи, состоящей из последовательно включенных сопротивления, катушки и конденсатора, напряжения на клеммах катушки и конденсатора могут во много раз превышать подведенное напряжение, этот случай часто (но не вполне удачно) называют резонансом напряжений; по аналогичной причине резонанс в цепи, состоящей из тех же элементов, соединенных параллельно, называют резонансом токов. [Правильнее относить понятие резонанса к совокупности явлений, происходящих в цепи; кроме того, как раз в последовательной цепи ток при резонансе максимален. Наиболее характерно, что при резонансе сопротивление становится чисто активным и что в зависимости от частоты тока сопротивление последовательной цепи при резонансе имеет более или менее остро выраженный минимум, а параллельной цепи — максимум.]

Рис. 350. Резонанс в параллельной цепи.
Прохождение переменного тока через катушку и конденсатор всегда сопряжено с некоторыми потерями мощности (стр. 449). В совокупности эти потери равносильны активным сопротивлениям  включенным последовательно с катушкой и конденсатором, которые тогда можно считать идеальными, т. е. не имеющими потерь и обладающими только чисто реактивными сопротивлениями
включенным последовательно с катушкой и конденсатором, которые тогда можно считать идеальными, т. е. не имеющими потерь и обладающими только чисто реактивными сопротивлениями  В связи со сказанным ясно, что когда катушка и конденсатор включены в цепь последовательно без
В связи со сказанным ясно, что когда катушка и конденсатор включены в цепь последовательно без
дополнительного активного сопротивления R (рис. 344), то в такой последовательной цепи все же нельзя считать  равным нулю, но нужно принять
равным нулю, но нужно принять  равным сопротивлению суммарных потерь в катушке и конденсаторе:
равным сопротивлению суммарных потерь в катушке и конденсаторе:  В этом случае сопротивление цепи при резонансе согласно (11)
В этом случае сопротивление цепи при резонансе согласно (11)

т. е. при малых потерях оно мало.
Для цепи, состоящей из параллельно включенных катушки и конденсатора (рис. 350), без дополнительного шунтирующего сопротивления (т. е. когда  дело обстоит несколько сложнее.
дело обстоит несколько сложнее.

Рис. 351. Резонанс в параллельной цепи.
Казалось бы, что если нет шунтирующего сопротивления, то согласно (17) проводимость параллельной цепи при резонансе равна нулю, т. е. резонансное сопротивление контура бесконечно велико. Однако и в этом случае, когда никакого дополнительного шунтирующего сопротивления к катушке и конденсатору не подключено, все же нельзя считать  потому что, как мы сейчас убедимся, наличие
потому что, как мы сейчас убедимся, наличие  в цепи катушки и конденсатора (рис. 351) равносильно существованию некоторого шунтирующего сопротивления
в цепи катушки и конденсатора (рис. 351) равносильно существованию некоторого шунтирующего сопротивления  По формуле (17) это эквивалентное шунтирующее сопротивление и является в данном случае резонансным сопротивлением цепи.
По формуле (17) это эквивалентное шунтирующее сопротивление и является в данном случае резонансным сопротивлением цепи.
При резонансе в контуре  циркулирует реактивный ток с амплитудой
циркулирует реактивный ток с амплитудой  В связи с этим на каком-либо сопротивлении
В связи с этим на каком-либо сопротивлении  включенном в указанный контур (в частности, на сопротивлении
включенном в указанный контур (в частности, на сопротивлении  рассеивается мощность
рассеивается мощность

Через сопротивление  проходит ток с амплитудой
проходит ток с амплитудой  следовательно, рассеивается мощность
следовательно, рассеивается мощность

Эти рассеиваемые мощности равны и, стало быть, замена сопротивления  сопротивлением
сопротивлением  (или же обратная замена
(или же обратная замена  )
)
допустима, когда

т. е. когда

или, что то же, когда

Мы видим, таким образом, что катушку и конденсатор можно считать идеальными (не создающими потерь мощности тока), если представить себе, что при воображаемой замене реальной катушки и конденсатора идеальными параллельно им подключено шунтирующее сопротивление, определяемое формулой (19). При резонансе сопротивление контура  если катушка и конденсатор не создают потерь, бесконечно велико, и поэтому резонансное сопротивление реальной цепи, не имеющей дополнительного шунта сверх создаваемого фактическими потерями в катушке и конденсаторе по формулам (17) и (19),
если катушка и конденсатор не создают потерь, бесконечно велико, и поэтому резонансное сопротивление реальной цепи, не имеющей дополнительного шунта сверх создаваемого фактическими потерями в катушке и конденсаторе по формулам (17) и (19),

Эта формула показывает, что резонансное сопротивление контура из параллельно включенных катушки и конденсатора тем более велико, чем меньше сопротивление потерь катушки и конденсатора и чем больше волновое сопротивление цепи, т. е. чем больше отношение индуктивности контура к емкости. Реально в радиотехнических устройствах  для частот порядка
для частот порядка  т. е. для длинных радиоволн (когда
т. е. для длинных радиоволн (когда  значительно), может иметь величину порядка сотен тысяч омов, а для более высоких частот (когда
значительно), может иметь величину порядка сотен тысяч омов, а для более высоких частот (когда  невелико) — десятков тысяч омов.
невелико) — десятков тысяч омов.
Если контур из параллельно включенных катушки и конденсатора дополнительно шунтирован сопротивлением  шунт, то понятно, что это соответственно уменьшает резонансное сопротивление контура, которое тогда вычисляется по обычному правилу сложения проводимостей для параллельно включенных сопротивлений:
шунт, то понятно, что это соответственно уменьшает резонансное сопротивление контура, которое тогда вычисляется по обычному правилу сложения проводимостей для параллельно включенных сопротивлений:

Действие сопротивления, дополнительно шунтирующего контур, равносильно тому, что в контур  вносится дополнительное активное сопротивление, равное по формуле (19)
вносится дополнительное активное сопротивление, равное по формуле (19)

Поэтому предыдущее уравнение можно переписать так:

Стало быть, введя полное активное сопротивление контура, равное сумме сопротивления потерь и сопротивления, вносимого шунтом, можно, как это обычно и делают, вычислять резонансное сопротивление шунтированной цепи по формуле, аналогичной формуле (20):

где

Поясненная выше формула (19) для пересчета шунтирующего сопротивления в сопротивление, включенное последовательно, широко применяется в радиотехнических расчетах; получаемые такой заменой  на
на  (или обратной заменой) схемы электрических цепей называют эквивалентными схемами.
(или обратной заменой) схемы электрических цепей называют эквивалентными схемами.
Для характеристики резонансных свойств цепи, состоящей из катушки и конденсатора (а также и отдельно ее элементов), вместо сопротивления потерь часто пользуются представлением о добротности  цепи (или отдельно ее элементов):
цепи (или отдельно ее элементов):

Запас энергии в катушке равен половине произведения индуктивности на квадрат амплитуды реактивного тока, а потеря энергии в катушке за 1 сек. равна половине произведения сопротивления потерь в катушке тоже на квадрат амплитуды реактивного тока. Поэтому добротность катушки получается равной отношению  (т. е. реактивного сопротивления) к сопротивлению потерь в катушке. В случае конденсатора запас энергии в цепи равен
(т. е. реактивного сопротивления) к сопротивлению потерь в катушке. В случае конденсатора запас энергии в цепи равен  и поэтому также
и поэтому также  Аналогичное выражение получается и для цепи катушка — конденсатор (в соответствии со сказанным на стр. 449):
Аналогичное выражение получается и для цепи катушка — конденсатор (в соответствии со сказанным на стр. 449):

Согласно формуле (16) при резонансе  а сопротивление потерь возрастает на величину потерь, вносимых шунтом (если он имеется) и, следовательно, добротность контура из
а сопротивление потерь возрастает на величину потерь, вносимых шунтом (если он имеется) и, следовательно, добротность контура из
катушки и конденсатора

Совмещая (21) и (22), получаем удобную для запоминания формулу резонансного сопротивления:

Индуктивные катушки, применяемые в высокочастотных контурах радиотехнической аппаратуры, обычно имеют добротность, равную для длинных волн 40—60, для коротких 150—200. Добротность слюдяных конденсаторов высока (при емкости более 50 см — порядка 1000, при малых емкостях 300—500). Добротность электролитических конденсаторов весьма мала (для низких частот 5—10). Волновое сопротивление резонансных контуров, рассчитанных на усиление средних радиочастот ( т. е. волн длиной
т. е. волн длиной  обычно составляет около 1000 ом, для более длинных волн 2000—3000 ом, а для высоких частот
обычно составляет около 1000 ом, для более длинных волн 2000—3000 ом, а для высоких частот  т. е. волн длиной
т. е. волн длиной  приблизительно 500—600 ом; удовлетворительной добротностью контура считают
приблизительно 500—600 ом; удовлетворительной добротностью контура считают 
Итак, контур, состоящий из параллельно подключенных емкости и индуктивности, оказывает переменному току резонансной частоты тем большее сопротивление, чем меньше активное сопротивление контура [формула (21)], или, что то же, чем больше добротность контура [формула (23)]. На этом основано применение
резонансных контуров для фильтрации токов; если к схеме, изображенной на рис. 351, одновременно подведены токи различных частот, то (при большом сопротивлении шунта  все токи, имеющие частоту, отличную от резонансной, пойдут через контур
все токи, имеющие частоту, отличную от резонансной, пойдут через контур  представляющий для них малое сопротивление; напротив, ток, имеющий резонансную частоту, вследствие большого
представляющий для них малое сопротивление; напротив, ток, имеющий резонансную частоту, вследствие большого  пойдет преимущественно через шунт и, таким образом, он окажется выделенным, отфильтрованным
пойдет преимущественно через шунт и, таким образом, он окажется выделенным, отфильтрованным  токов всех остальных частот.
токов всех остальных частот.

Рис. 352. Резонансные кривые при разных значениях добротности. Для параллельного соединения конденсатора и катушки  где
где  сопротивление контура при частоте
сопротивление контура при частоте  для последовательного соединения
для последовательного соединения 
Резонансные кривые, определяющие зависимость сопротивления контура 1—2—3—4 переменному току, при разных добротностях имеют такой же вид, как и резонансные кривые тока в последовательной цепи емкости и индуктивности при разных активных сопротивлениях цепи. На рис, 352 эти кривые построены для относительных значений ординат  Здесь ясно видно, что чем больше
Здесь ясно видно, что чем больше
добротность, тем уже резонансная кривая (тем больше избирательность контура). Если на оси абсцисс откладывать не величину  где
где  резонансная частота, а произведение величины
резонансная частота, а произведение величины  на добротность, то все кривые для значений добротности от 25 до 500 почти совпадают (рис. 353).
на добротность, то все кривые для значений добротности от 25 до 500 почти совпадают (рис. 353).

Рис. 353. Обобщенная резонансная кривая. Пунктиром показана «полоса пропускания».
Для характеристики избирательности контура условно принято называть полосой пропускания, или шириной резонансной кривой, тот интервал частот  вблизи резонансной частоты, на границах которого амплитуды тока или напряжения уменьшаются до
вблизи резонансной частоты, на границах которого амплитуды тока или напряжения уменьшаются до  их резонансного значения, что соответствует уменьшению мощности в два раза. Из рис. 353 видно, что для указанного интервала частот
их резонансного значения, что соответствует уменьшению мощности в два раза. Из рис. 353 видно, что для указанного интервала частот

т. е. обратная величина добротности как раз указывает относительную полосу пропускания (этим обычно и пользуются для измерения добротности).
В теории колебаний, когда эту теорию развивают на основе анализа колебательных движений в механических системах  глава X), под резонансной частотой понимают ту частоту, при которой амплитуда смещений достигает максимума; с собственной частотой
глава X), под резонансной частотой понимают ту частоту, при которой амплитуда смещений достигает максимума; с собственной частотой  резонансная частота связана соотношением [т. I, стр. 239, формула (24)]
резонансная частота связана соотношением [т. I, стр. 239, формула (24)]

где а — коэффициент затухания.
В связи с этим может возникнуть недоумение: почему даже при наличии значительного затухания резонанс в электрической цепи определяется совпадением частоты подведенного напряжения с собственной частотой цепи  а не соответственно формуле (а), причем надо отметить, что для последовательной цепи формула
а не соответственно формуле (а), причем надо отметить, что для последовательной цепи формула

является точной независимо от величины потерь, тогда как для резонанса в параллельной цепи она, как показано ниже, нуждается в уточнении.
Дело в том, что если руководствоваться аналогией между колебаниями тока и механическими колебаниями, то в дифференциальных уравнениях колебаний соответствие между механическими системами и электрическими цепями обнаруживается, когда величина смещения уподоблена напряжению на конденсаторе. При частоте  сопротивление последовательной цепи становится чисто активным и амплитуда тока достигает максимума, но это не означает, как иногда думают, что и амплитуды напряжения на конденсаторе или катушке тоже максимальны. В полном согласии с формулой (а) и величиной коэффициента затухания, указанной в примечании на стр. 461, амплитуда напряжения на конденсаторе в последовательной цепи становится максимальной не при частоте
сопротивление последовательной цепи становится чисто активным и амплитуда тока достигает максимума, но это не означает, как иногда думают, что и амплитуды напряжения на конденсаторе или катушке тоже максимальны. В полном согласии с формулой (а) и величиной коэффициента затухания, указанной в примечании на стр. 461, амплитуда напряжения на конденсаторе в последовательной цепи становится максимальной не при частоте  а при частотех)
а при частотех)

Амплитуда напряжения на катушке достигает максимума, напротив, при частоте большей, чем собственная частота цепи, причем

Для технических применений важны, однако, не эти (тоже резонансные) явления, а резонансный минимум (для последовательной цепи) и максимум (для параллельной цепи) сопротивления, которое оказывает цепь подведенному к ней переменному току; при этом особенно существенно, что при резонансе сопротивление цепи становится чисто активным.
В случае параллельной цепи, чтобы ее сопротивление было чисто активным, должны взаимно компенсироваться реактивные составляющие токов через катушку и конденсатор. При неодинаковых потерях в катушке и конденсаторе компенсация реактивных токов происходит при частоте, немного отличающейся от  Действительно, согласно сказанному в конце предыдущего параграфа и по рис. 343 амплитуда реактивного тока через катушку равна а через конденсатор — равна
Действительно, согласно сказанному в конце предыдущего параграфа и по рис. 343 амплитуда реактивного тока через катушку равна а через конденсатор — равна  где
где  углы потерь. Стало быть,
углы потерь. Стало быть,

Обычно потери в конденсаторе весьма малы  тогда, если принять во внимание, что
тогда, если принять во внимание, что  следовательно,
следовательно,

получится:

Эта формула показывает, что даже при небольшой добротности катушки, порядка  частота резонанса в параллельной цепи меньше собственной частоты цепи всего на пять сотых долей процента.
частота резонанса в параллельной цепи меньше собственной частоты цепи всего на пять сотых долей процента.
При возбуждении резонансных колебаний тока в электрической цепи в ней наряду с вынужденными колебаниями возникают свободные колебания, происходящие с частотой

где а — коэффициент затухания, который для электрической цепи (как было показано в примечании на стр. 461) равен  или, что тоже, Таким образом,
или, что тоже, Таким образом,

Чем больше величина потерь и меньше индуктивность цепи, тем быстрее затухают свободные колебания тока в цепи, уступая место стационарному режиму вынужденных резонансных колебаний.
Из сказанного и формулы (24) ясно, что при слишком большой величине добротности резонансный контур может оказаться для некоторых применений непригодным, так как чрезмерно сужается ширина резонансной кривой и возрастает время установления резонансного режима.
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
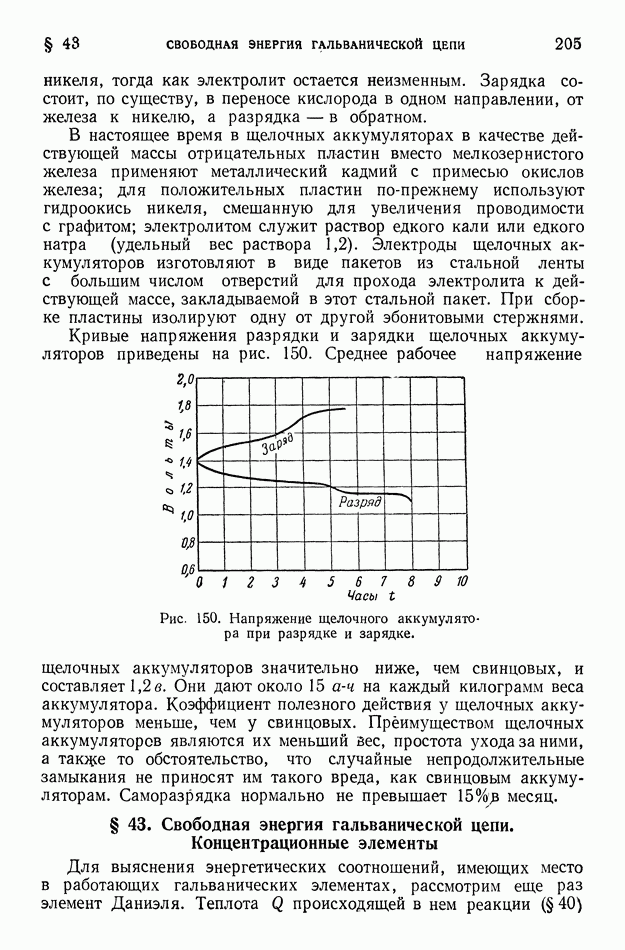
- § 42. Аккумуляторы
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
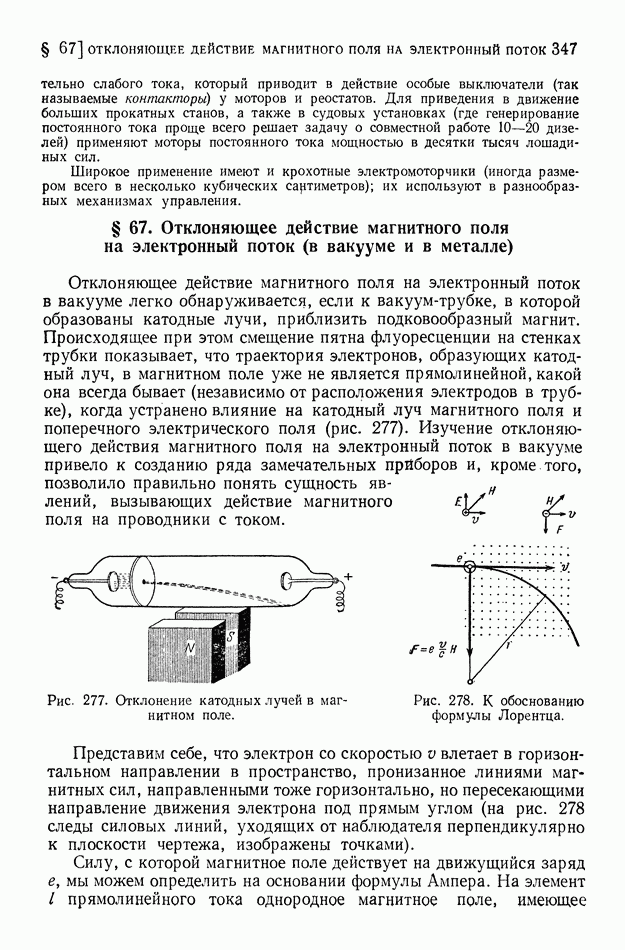
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
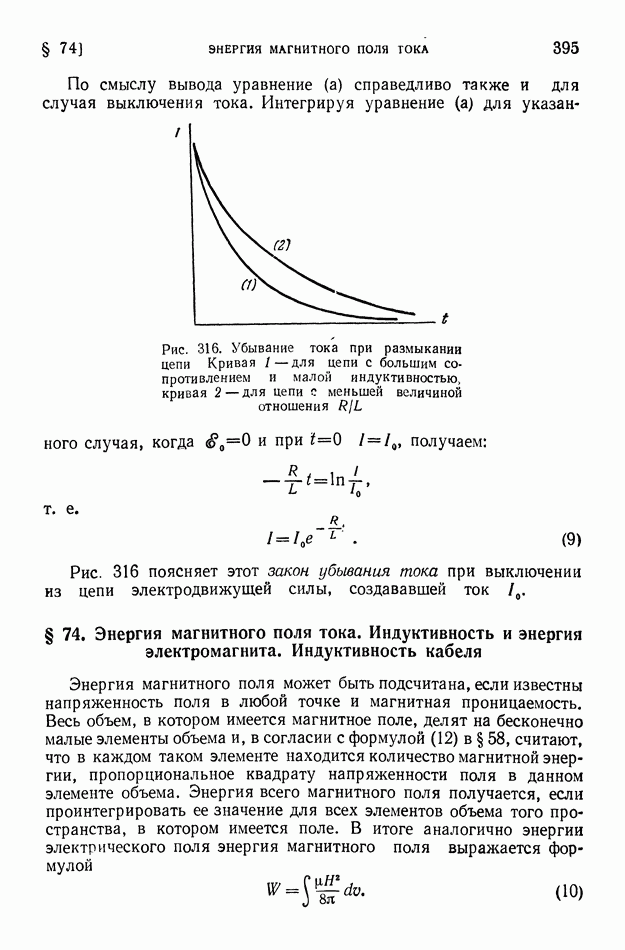
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
- § 83. Электрический резонанс
- § 84. Трансформация тока
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)