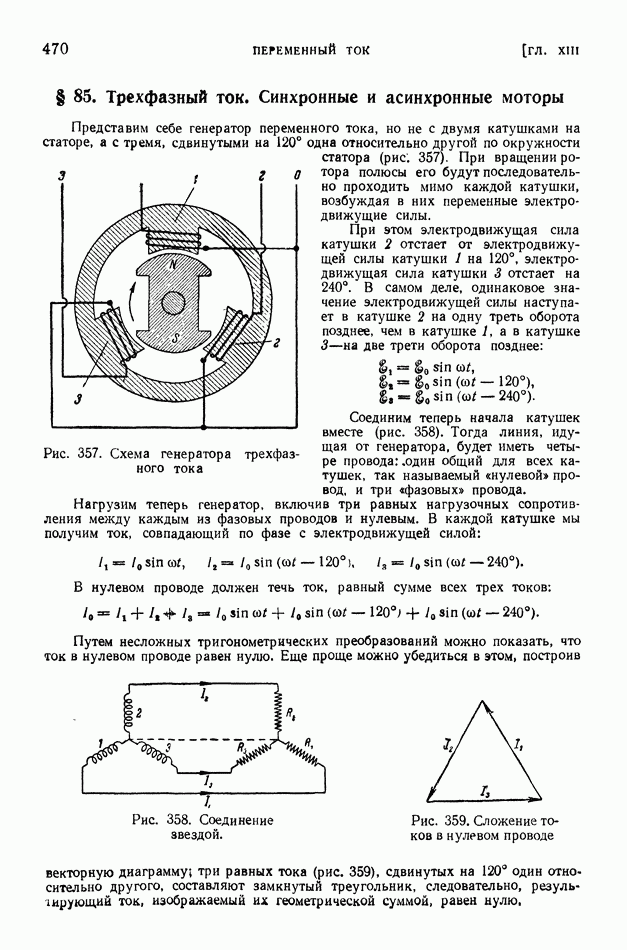
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 76. Уравнения Максвелла и уравнения Лорентца
Обобщение всех основных законов электродинамики было осуществлено в 60-х годах прошлого столетия Максвеллом. Максвелл выразил в математической форме картину электромагнитного поля, разработанную Фарадеем (и уже поясненную нами в ряде параграфов: 16, 18, 58, 65, 71).
Свойства электрического поля и поля магнитов определяются, как мы видели, теоремой Остроградского — Гаусса (§§ 5, 6, 7, 58). Свойства электромагнитного поля определяются законами Био и Савара (§ 61) и Фарадея (§ 72).
Фарадеев закон электромагнитной индукции и закон Био и Савара можно сформулировать так, что вскроется глубокое математическое сходство этих законов.
Сделаем нижеследующее соглашение: число «входящих» в замкнутый контур линий индукции, т. е. пересекающих замкнутый контур в направлении извне, будем обозначать как число положительное; число «выходящих» из замкнутого контура линий индукции, т. е. пересекающих замкнутый контур в направлении изнутри, будем обозначать как число отрицательное. Тогда закон Фарадея можно сформулировать так: выраясенная в вольтах электродвижущая сила, индуцируемая магнитным полем, равна одной стомиллионной части алгебраического числа линий магнитной индукции (т. е. магнитного потока в максвеллах), пересекаемых контуром в одну секунду. Точнее,

 означает алгебраическое число линий магнитной индукции.
означает алгебраическое число линий магнитной индукции.
пересекаемых контуром за время  а число
а число  указывает, сколько оборотов делает контур тока вокруг охватываемых им линий индукции.
указывает, сколько оборотов делает контур тока вокруг охватываемых им линий индукции.
Учитывая, что 1 в составляет  абсолютной электростатической единицы потенциала (§ 8), и введя скорость света с, измеренную в сантиметрах в секунду
абсолютной электростатической единицы потенциала (§ 8), и введя скорость света с, измеренную в сантиметрах в секунду  можно вышеприведенную формулу для электродвижущей силы написать так:
можно вышеприведенную формулу для электродвижущей силы написать так:

Закон Био и Савара (если от дифференциальной формулировки этого закона перейти к его интегральному выражению) устанавливает, что магнитодвижущая сила  пропорциональна току (§ 62):
пропорциональна току (§ 62):

Мы убедимся сейчас, что это интегральное выражение закона Био и Савара можно представить в форме, аналогичной закону Фарадея.
Величина тока определяется количеством электричества, протекающим через поперечное сечение проводника в единицу времени:

Чтобы ток был выражен в единицах системы  должно быть выражено в абсолютных электромагнитных единицах заряда и
должно быть выражено в абсолютных электромагнитных единицах заряда и  в секундах. Вспомним, что по теореме Остроградского — Гаусса (§ 6) одна электростатическая единица заряда связана с
в секундах. Вспомним, что по теореме Остроградского — Гаусса (§ 6) одна электростатическая единица заряда связана с  линиями электрической индукции. Так как одна электромагнитная единица заряда содержит с электростатических единиц, где с есть численное значение скорости света, измеренной в сантиметрах в секунду
линиями электрической индукции. Так как одна электромагнитная единица заряда содержит с электростатических единиц, где с есть численное значение скорости света, измеренной в сантиметрах в секунду  то число линий электрической индукции, связанных с зарядом в
то число линий электрической индукции, связанных с зарядом в  электромагнитных единиц, равно
электромагнитных единиц, равно

Движущийся заряд несет с собой свои линии электрической индукции. Любой замкнутый контур, охватывающий проводник, по которому протекает ток, будет за время  пересечен
пересечен  линиями электрической индукции. Сопоставляя три вышеприведенных уравнения, получаем формулу для магнитодвижущей силы:
линиями электрической индукции. Сопоставляя три вышеприведенных уравнения, получаем формулу для магнитодвижущей силы:

где с есть значение скорости света, измеренной в сантиметрах в секунду.
Сходство этого уравнения, выражающего в преобразованном виде закон Био и Савара, с законом Фарадея (21) является очевидным.
По смыслу вывода уравнение (22) справедливо не только для случая движения зарядов в проводнике, но вообще для любого перемещения зарядов, например для смещения зарядов при поляризации диэлектрика. Сопоставляя уравнение (22) с обычным выражением магнитодвижущей силы  мы видим, что для величины тока смещения зарядов при поляризации диэлектрика (когда ток измерен в электромагнитных единицах) получается формула
мы видим, что для величины тока смещения зарядов при поляризации диэлектрика (когда ток измерен в электромагнитных единицах) получается формула

а для плотности тока

(так как величина  представляет собой электрическую индукцию D).
представляет собой электрическую индукцию D).

Рис 322. Схема магнитных силовых линий вокруг изменяющегося во времени потока электрической индукции,  «тока смещения» (для случая, когда изменяется только величина, а не направление
«тока смещения» (для случая, когда изменяется только величина, а не направление 

Рис. 323. Схема электрических силовых линий вокруг изменяющегося во времени потока магнитной индукции (для случая, когда изменяется только величина а не направление 
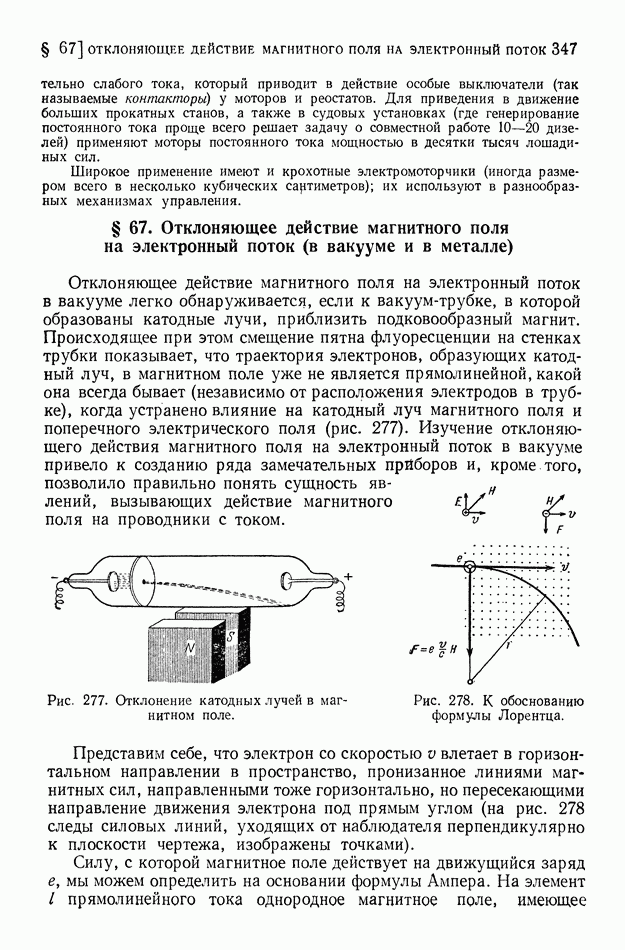
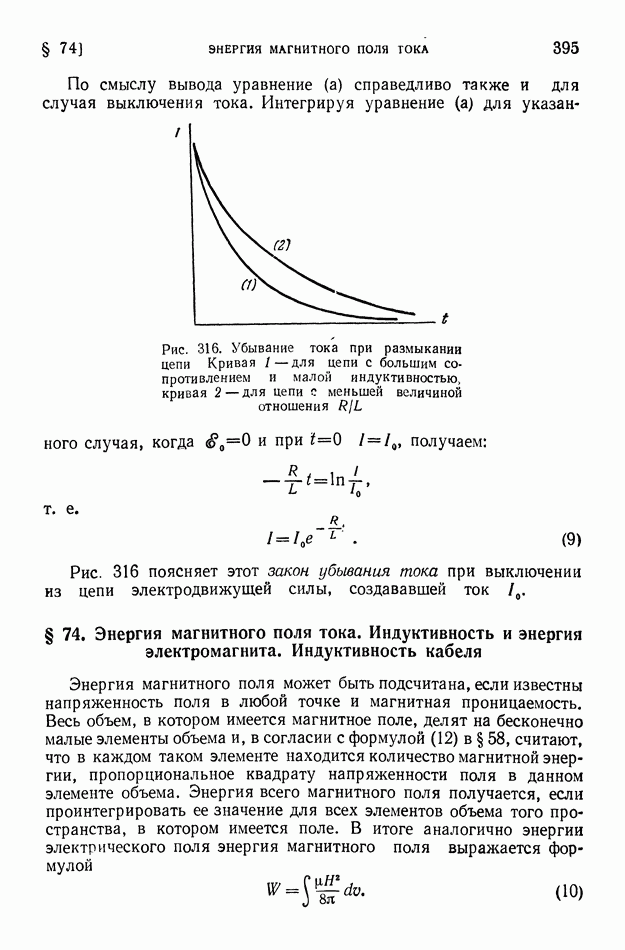
Как уже было пояснено выше (в §§ 70 и 71), по трактовке электромагнитного поля, разработанной Фарадеем, любое изменение электрического поля (хотя бы и в вакууме) приводит к образованию в том же месте (или к изменению существовавшего там) магнитного поля. Это означает, что изменение электрической напряженности (или электрической индукции) равносильно электрическому току. Такой процесс Максвелл назвал током смещения (в вакууме и в диэлектриках). По Максвеллу, уравнения (23) и (24) должны рассматриваться как справедливые во всех случаях, включая ток смещения в вакууме, и являются применимыми, так же как и уравнения  и (22), для любых сколь угодно малых участков поля.
и (22), для любых сколь угодно малых участков поля.
По трактовке Максвелла, согласно уравнению (22) изменение во времени потока электрической индукции в любой точке поля (т. е. ток смещения в этом месте поля) сопровождается возникновением здесь же магнитных силовых линий (рис. 322). Этот процесс
индуцирования магнитного поля при изменении электрического поля является глубоко аналогичным тому, как изменение магнитного поля индуцирует [по уравнению (21)] электрическое поле (рис. 323). Полная симметрия нарушается только различием знаков в уравнениях (21) и (22). Если смотреть по направлению возрастающего потока, то положительным считают направление силовых линий по движению часовой стрелки; в соответствии с этим в уравнении (21) мы имеем знак «минус», а на рис. 323 — обратное направление силовых линий в сравнении с рис. 322.
Два уравнения: уравнение (22), выражающее в преобразованном виде закон Био и Савара, и уравнение (21), выражающее закон Фарадея, являются основными в электродинамике, все остальные уравнения электродинамики могут быть получены из них и из теоремы Остроградского — Гаусса как следствия.
Уравнения Максвелла представляют собой обобщение этих основных законов электродинамики.
Чтобы получить достаточно полное представление о сущности сделанного Максвеллом обобщения, нужно воспользоваться некоторыми понятиями векторного анализа.
В векторном анализе под термином «поле» подразумевают часть пространства, в каждой точке которого некоторая интересующая нас величина имеет определенное значение. О величине этой говорят, что она является функцией точки. Эта величина может быть скаляром или вектором.
Скалярное поле определено однозначно, коль скоро скаляр задан как функция точки. В этом случае, следовательно, исчерпывающее описание поля может быть представлено в форме одного уравнения, связывающего скалярную величину с тремя пространственными координатами. Чтобы однозначно определить векторное поле, необходимо, помимо численного значения вектора, указать также и его направление. По существу, это сводится к требованию, чтобы были заданы численные значения компонентов (проекций) вектора для трех координатных осей; исчерпывающее описание векторного поля слагается, таким образом, из трех уравнений, из которых каждое связывает численное значение проекции вектора на одну из координатных осей с тремя пространственными координатами произвольной точки поля.
Существует, однако, один распространенный тип векторных полей, который представляет собой исключение из этого общего правила. Представим себе совершенно произвольное поле некоторого скаляра, например распределение температуры в неравномерно нагретой среде, распределение плотности или концентрации и т.д. Назовем градиентом вектор, направленный в каждой точке поля в сторону наибольшего возрастания скаляра и равный по величине приращению, которое испытывает скаляр при перемещении в этом направлении на единицу расстояния.
Точнее, градиентом А скаляра  мы называем вектор, направленный в сторону возрастания
мы называем вектор, направленный в сторону возрастания  по нормали
по нормали  к поверхности
к поверхности  проведенной через рассматриваемую точку, и равный пространственной производной
проведенной через рассматриваемую точку, и равный пространственной производной
Вектор  являющийся градиентом скаляра
являющийся градиентом скаляра  обозначают символом
обозначают символом  (сокращение от слова gradient):
(сокращение от слова gradient):

Для каждой точки скалярного поля мы можем построить вектор-градиент А. Мы получим таким образом векторное поле. Оно является простейшим из всех возможных векторных полей, так как может быть исчерпывающе описано, как это явствует из способа его построения, всего одним уравнением, связывающим скаляр с координатами точки. О значении этого типа векторных полей можно судить уже по одному тому, что к нему принадлежат поля гравитационное и электростатическое. Их объединяют под общим названием потенциальных полей, подразумевая под именем потенциала тот скаляр, градиентом которого служит исследуемый вектор А — вектор, определяющий напряженность поля.
Можно доказать, что электростатическое поле, вызванное какой угодно совокупностью электрических зарядов  как угодно расположенных, в какой угодно неоднородной диэлектрической среде, всегда является полем потенциальным, причем потенциалом поля, т. е. тем скаляром, по отношению к которому вектор напряженности электрического поля
как угодно расположенных, в какой угодно неоднородной диэлектрической среде, всегда является полем потенциальным, причем потенциалом поля, т. е. тем скаляром, по отношению к которому вектор напряженности электрического поля  играет роль градиента (взятого с обратным знаком, т. е. направленного в сторону убывания, а не возрастания потенциала), служит работа V, которую силы поля могли бы совершить при перемещении пробного точечного заряда величиной в единицу положительного электричества из рассматриваемой точки в бесконечность:
играет роль градиента (взятого с обратным знаком, т. е. направленного в сторону убывания, а не возрастания потенциала), служит работа V, которую силы поля могли бы совершить при перемещении пробного точечного заряда величиной в единицу положительного электричества из рассматриваемой точки в бесконечность:

В электростатическом поле не может быть замкнутых силовых линий. Линии электрической индукции начинаются на положительных зарядах и кончаются на отрицательных зарядах. Число линий электрической индукции определяется теоремой Остроградского — Гаусса:

Выделим мысленно внутри поля вокруг некоторой точки бесконечно малый объем  Пусть в нем содержится алгебраическое количество электричества
Пусть в нем содержится алгебраическое количество электричества  Отношение представляет собой алгебраическую плотность электрического заряда в данной точке поля; обозначим эту плотность электрического заряда через
Отношение представляет собой алгебраическую плотность электрического заряда в данной точке поля; обозначим эту плотность электрического заряда через 
Через поверхность, ограничивающую выделенный нами бесконечно малый объем  выходит наружу тем больше линий электрической индукции, чем больше плотность заряда. Число их по теореме Остроградского — Гаусса равно
выходит наружу тем больше линий электрической индукции, чем больше плотность заряда. Число их по теореме Остроградского — Гаусса равно

Отношение алгебраического числа линий индукции, выходящих из бесконечно малого объема  к величине этого объема
к величине этого объема  называют расхождением вектора электрической индукции
называют расхождением вектора электрической индукции  наряду с этим названием часто (а в сокращенном обозначении — всегда) употребляют другое название той же величины — дивергенция (divergenz); сокращенно пишут
наряду с этим названием часто (а в сокращенном обозначении — всегда) употребляют другое название той же величины — дивергенция (divergenz); сокращенно пишут 
Если мы разделим предыдущее уравнение на  то в левой части будем иметь расхождение электрической индукции
то в левой части будем иметь расхождение электрической индукции  а в правой части — плотность электрического заряда
а в правой части — плотность электрического заряда  умноженную на
умноженную на 

Так называемое «магнитостатическое» поле, т. е. поле, образованное неподвижными относительно друг друга магнитами, в действительности представляет собой поле элементарных (внутримолекулярных) токов. Линии магнитной индукции всегда являются замкнутыми: они нигде «не начинаются» и «не кончаются». Это означает, что не существует магнитных зарядов, подобных электрическим зарядам, на которых начинаются или кончаются линии электрической индукции. В этом смысле говорят, что не существует свободного магнетизма. Если мы выделим в пол-е какой-либо объем (все равно — большой или бесконечно малый), то в этом объеме всегда будет иметься равное количество положительных и отрицательных магнитных полюсов, так что их алгебраическая сумма будет равна нулю. Ту же самую мысль можно высказать так: алгебраическая плотность магнетизма в любой точке поля равна нулю. В каком бы участке поля мы ни выделили объем  (хотя бы и внутри магнита), через поверхность, ограничивающую этот объем, будет выходить наружу всегда такое же число линий магнитной индукции, какое входит внутрь, так как они только пересекают этот объем, но не начинаются и не кончаются в нем. Следовательно, в отличие от уравнения (25), применяя представление о расхождении вектора магнитной индукции
(хотя бы и внутри магнита), через поверхность, ограничивающую этот объем, будет выходить наружу всегда такое же число линий магнитной индукции, какое входит внутрь, так как они только пересекают этот объем, но не начинаются и не кончаются в нем. Следовательно, в отличие от уравнения (25), применяя представление о расхождении вектора магнитной индукции  получаем:
получаем:

С точки зрения математического анализа электростатическое поле в некоторой мере родственно полю тяготения. Это, однако, только внешнее сходство. По сути дела, оно ограничивается аналогией, существующей между законом тяготения Ньютона и законом Кулона. В отличие от поля тяготения в электростатическом поле, во-первых, имеются не только силы притяжения, но и силы отталкивания. Во-вторых, в электростатическом поле сказывается влияние среды, которая в случае гравитационного поля роли не играет (закон тяготения Ньютона не содержит коэффициента, численно зависящего от свойств среды, аналогичного диэлектрической постоянной, которая входит в формулу Кулона). В-третьих, в электрическом поле обнаруживается своеобразная деформация поля, вызываемая присутствием проводников.
Всякая аналогия между электрическим и гравитационным полем исчезает, когда мы обращаемся к сопоставлению поля движущихся относительно друг друга зарядов с полем тяготения движущихся масс.
Движение тяготеющих масс ничем не нарушает обычной картины гравитационного поля; гравитационное поле всегда, при сколь угодно быстром движении масс остается таким же «однозначно потенциальным» полем, как и поле, образованное взаимно неподвижными массами.
В противоположность ему поле электрических сил резко меняется, если создающие его заряды приходят в состояние относительного движения. Тогда наряду с электростатическим взаимодействием зарядов возникают электрокинетические силы, и поле в целом утрачивает характер «однозначно потенциального» поля. Попутно с этой трансформацией, которая сводится к образованию замкнутых электросиловых линий, внутри электродинамического поля возникают магнитные силовые линии. Они замкнутыми кольцами охватывают линии электрического тока.
В теории Максвелла под именем электрического тока объединены четыре группы электродинамических явлений, эквивалентных друг другу с точки зрения возникновения магнитного поля. Сюда относится прежде всего обычный ток проводимости, т. е. движение электрических зарядов внутри проводника. Вторую форму тока, открытую (вернее, теоретически предугаданную) Фарадеем и Максвеллом, составляет ток смещения, который имеет место тогда, когда в вакууме или в диэлектрике изменяется напряженность электрического поля. В диэлектрике ток смещения представляет собой распространяющийся импульс поляризации среды, ориентирующий элементарные диполи в направлении силовых линий. Мы не имеем, однако, какой-либо конкретной картины тока смещения в вакууме.
Согласно теории Максвелла электрический ток всегда образует замкнутые линии; в тех случаях, когда ток проводимости не дает
замкнутой линии (примером может служить зарядка конденсатора), ток смещения замыкает линию тока.
Третьей формой электрического тока является конвекционный ток. Это — движение электрических зарядов, связанное с перемещением наэлектризованного тела, а также движение потоков свободных электронов или ионов в пустоте или в разреженной диэлектрической среде. Четвертая форма электрического тока наблюдается при движении электрически нейтрального, но поляризованного диэлектрика.
Любой вид тока имеет две стороны: во-первых, перемещение или смещение зарядов или же в случае тока смещения в вакууме, какие-то неизвестные нам явления, физически эквивалентные смещению зарядов, и, во-вторых, существование магнитного поля, замкнутые линии которого охватывают линию тока. Поскольку имеется движение зарядов, то, очевидно, имеется также движение связанных с ними (выходящих из них) линий электрической индукции. Встав на почву представлений, развитых Фарадеем, мы должны представлять себе линии электрической индукции как обозначение некоторого реального возбуждения среды, равносильного ее натяжению. Движение линий электрической индукции, один конец которых скользит по поверхности проводника, где перемещаются заряды, проявляется в возбуждении магнитного поля. Какое-либо изменение, происшедшее в магнитном поле, указывает на изменившийся характер движения линий электрической индукции.
С этой точки зрения, фиксирующей наше внимание на явлениях, происходящих в среде (во всем пространстве, а не только в проводнике), ток имеется всюду, где имеется движение линий электрической индукции.
Как уже упоминалось, главными законами электродинамики, из которых все уравнения электродинамики могут быть получены как следствия, являются (наряду с теоремой Остроградского - Гаусса) закон Фарадея и (в преобразованной форме) закон Био и Савара:

Здесь  означает электродвижущую силу. Электродвижущая сила измеряется работой, которую способны произвести электрические силы поля, действующие на единицу положительного заряда, когда этот заряд мы обводим по какому-либо замкнутому контуру вокруг пучка
означает электродвижущую силу. Электродвижущая сила измеряется работой, которую способны произвести электрические силы поля, действующие на единицу положительного заряда, когда этот заряд мы обводим по какому-либо замкнутому контуру вокруг пучка  линий магнитной индукции. Аналогично магнитодвижущая сила
линий магнитной индукции. Аналогично магнитодвижущая сила  измеряется работой, которую способны произвести магнитные силы поля, когда положительный магнитный полюс величиной в одну единицу мы обводим по
измеряется работой, которую способны произвести магнитные силы поля, когда положительный магнитный полюс величиной в одну единицу мы обводим по
какому-либо замкнутому контуру вокруг  линий электрической индукции. Указанные величины и
линий электрической индукции. Указанные величины и  как показывают вышеприведенные уравнения (21) и (22), отличны от нуля только тогда, когда поток индукции (
как показывают вышеприведенные уравнения (21) и (22), отличны от нуля только тогда, когда поток индукции ( или во втором случае
или во втором случае  изменяется во времени.
изменяется во времени.
Представим себе, что вокруг какой-либо точки электромагнитного поля проведено по поверхности сферы множество бесконечно малых замкнутых контуров, расположенных в различных плоскостях. Из всех этих контуров выберем один, а именно тот, по которому электродвижущая сила является наибольшей. Так как длина контура бесконечно мала, то и электродвижущая сила по этому контуру будет бесконечно мала; обозначим ее через  число линий магнитной индукции, пронизывающих этот контур, обозначим через
число линий магнитной индукции, пронизывающих этот контур, обозначим через 
Применим к этому контуру уравнение, формулирующее закон Фарадея, разделив обе части этого уравнения на площадь  ограниченную контуром:
ограниченную контуром:

Вспомним, что плотность (густота) линий магнитной индукции изображает величину вектора магнитной индукции В:

Следовательно, в правой части вышенаписанного уравнения мы имеем производную от вектора В по времени (для обозначения этой производной обычно пользуются символом  а не
а не  Обратимся теперь к левой части уравнения.
Обратимся теперь к левой части уравнения.
Предел, к которому стремится отношение электро- или магнитодвижущей силы элементарного контура, стягивающегося вокруг точки, к площади, ограниченной этим контуром, называют вихрем, или иначе ротором, электрической (или магнитной) силы. При этом имеют в виду контур, расположенный в той плоскости, для которой указанный предел является наибольшим. Ротор рассматривают как вектор, направленный по перпендикуляру к площади контура так, чтобы, смотря в направлении этого вектора, мы видели направление электро- или магнитодвижущей силы совпадающим с движением часовой стрелки. Сокращая слово rotor, в уравнениях пишут первые три буквы этого слова (rot Е). Нередко ту же величину называют керл 
Применяя представление о роторе электрической силы, мы видим, что вышеприведенное уравнение можно записать так:

Исходя из выражения для магнитодвижущей силы  будем рассуждать аналогично предыдущему. Из множества бесконечно малых контуров, проведенных по поверхности сферы вокруг той же рассматриваемой нами точки поля, выберем тот, для которого предел отношения магнитодвижущей силы
будем рассуждать аналогично предыдущему. Из множества бесконечно малых контуров, проведенных по поверхности сферы вокруг той же рассматриваемой нами точки поля, выберем тот, для которого предел отношения магнитодвижущей силы  к площади контура
к площади контура  при
при  является наибольшим. Предел этого отношения представит собой ротор магнитной силы
является наибольшим. Предел этого отношения представит собой ротор магнитной силы  Напишем для указанного бесконечно малого контура уравнение магнитодвижущей силы, разделенное на площадь
Напишем для указанного бесконечно малого контура уравнение магнитодвижущей силы, разделенное на площадь  ограниченную контуром:
ограниченную контуром:

Плотность (густота) линий электрической индукции изображается вектором электрической индукции 

Поэтому

Рис. 324 и 325 поясняют понятия ротора  и ротора
и ротора  Уравнения (25), (26), (27) и (28) представляют собой систему максвеллов
Уравнения (25), (26), (27) и (28) представляют собой систему максвеллов  уравнений:
уравнений:

В указанном виде система максвелловых уравнений применима для любой точки поля, где не происходит отдачи электромагнитной энергии в форме тепла.

Рис. 324. Схема, поясняющая (в дополнение к рис,  понятие ротора
понятие ротора  В общем случае
В общем случае  параллелен и пропорционален вектору плотности тока.
параллелен и пропорционален вектору плотности тока.

Рис. 325, Схема, поясняющая (в дополнение к рис, 323) понятие ротора  В общем случае
В общем случае  ангипараллелен и пропорционален вектору плотности потока магнитной индукции.
ангипараллелен и пропорционален вектору плотности потока магнитной индукции.
Для поля внутри проводников, где выделяется тепло, применяя ту же систему уравнений, к прсшой части уравнения (28), выражающей плотность тока смещения, умноженную на  нужно присоединить член, выражающий плотность тока проводимости (с коэффициентом
нужно присоединить член, выражающий плотность тока проводимости (с коэффициентом  т. е.
т. е.

где а — удельная проводимость. При наличии конвекционного и других видов тока то же уравнение должно быть дополнено членами, учитывающими плотность этих токов.
В системе максвелловых уравнений первые два уравнения [(25) и (26)] являются скалярными уравнениями, тогда как два других [(27] и (28)] представляют собой векторные уравнения. Каждое из них равносильно трем скалярным уравнениям, написанным для проекций векторов  на оси координат.
на оси координат.
Из всего сказанного выше мы видим: основная идея обобщения, сделанного Максвеллом в соответствии с представлениями Фарадея, заключалась в том, что главные макрофизические законы электродинамики, установленные для конечных контуров тока в проводниках и для конечных магнитных цепей, были признаны справедливыми для любого отдельно взятого участка поля и при этом для сколь угодно малого участка поля.
Такое обобщение оказалось возможным благодаря тому, что было предугадано существование тока электрического смещения и таким образом обнаружено, что линии тока всегда являются замкнутыми линиями.
В системе уравнений Максвелла уравнения (25) и (26) представляют собой преобразованные законы Кулона (с учетом, что не имеется «свободного» магнетизма), причем это преобразование сделано так, что законы Кулона приобрели смысл для любого взятого в отдельности бесконечно малого участка поля (для «точки» поля). Уравнение (27) является преобразованным законом Фарадея; чтобы сделать этот закон применимым к любой в отдельности взятой точке поля, величина, связанная с электродвижущей силой, здесь выражена в виде ротора (предел отношения электродвижущей силы по стягивающемуся вокруг точки контуру к бесконечно убывающей площади, ограниченной этим контуром). Уравнение (28) представляет собой аналогичное преобразование выражения для магнитодвижущей силы, получающегося из закона Био и Савара.
Уравнения Максвелла в вышеприведенном начертании написаны с применением общепринятых в физике символов векторного анализа. Для использования уравнений Максвелла при решении задач электродинамики приведем, не останавливаясь на математических подробностях, формулы векторного анализа, раскрывающие выражения дивергенции, градиента и ротора.
Если  представляет собой скалярную величину, изменяющуюся в пространстве от точки к точке, а вектор А является градиентом этого скаляра, то
представляет собой скалярную величину, изменяющуюся в пространстве от точки к точке, а вектор А является градиентом этого скаляра, то
проекции вектора на оси координат (т. е. его декартовы компоненты) выражаются формулами

Действительно, градиент  по определению представляет собой пространственную производную от
по определению представляет собой пространственную производную от  взятую в направлении наибольшего возрастания
взятую в направлении наибольшего возрастания  т. е. по нормали
т. е. по нормали  к поверхности
к поверхности  Представим себе, что вместо перемещения
Представим себе, что вместо перемещения  мы прослеживаем перемещение по какой-либо оси I (рис. 326). Учитывая, что
мы прослеживаем перемещение по какой-либо оси I (рис. 326). Учитывая, что  для производной от
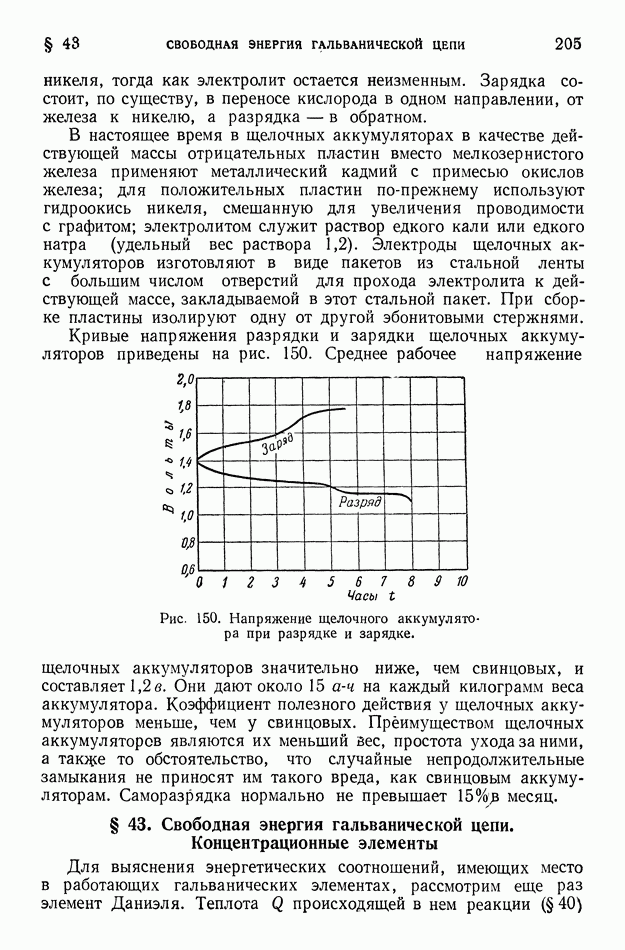
для производной от  по оси
по оси  получаем:
получаем:

т. е. убеждаемся, что проекция градиента на какую-либо ось равна производной от потенциала в направлении этой оси.
Для любого вектора А, изменяющегося в пространстве от точки к точке, дивергенция (расхождение) Ьектора определяется формулой


Рис. 326

Рис. 327. К пояснению формулы для расхождения (дивергенции) вектора А.
Рис. 327 поясняет эту формулу. Дивергенция вектора А по определению, которое приведено выше, представляет собой предел, к которому стремится отношение потока вектора А через замкнутую поверхность к объему, ограниченному этой поверхностью, когда поверхность стягивается вокруг рассматриваемой точки. От формы поверхностй этот предел не зависит. Руководствуясь рис. 327, рассмотрим поток вектора через поверхность элементарного параллелепипеда, грани которого параллельны координатным плоскостям. Поток вектора через первую грань, перпендикулярную к оси  равен
равен  а через вторую грань, также перпендикулярную к оси
а через вторую грань, также перпендикулярную к оси  что в сумме дает величину
что в сумме дает величину 
Аналогичные выражения мы получаем для потока вектора через другие пары граней. В итоге

что и приводит к формуле (30), так как 
Применяя формулу (30) к основному уравнению электрического поля (25) и заменяя  через
через  можно уравнение (25) переписать так:
можно уравнение (25) переписать так:

В случае однородной диэлектрической среды  вместо вектора электрической индукции можно поставить вектор напряженности поля, а диэлектрическую проницаемость вынести за знак дифференциала. Принимая во внимание, что вектор напряженности электрического поля является градиентом (взятым с обратным знаком) электрического потенциала
вместо вектора электрической индукции можно поставить вектор напряженности поля, а диэлектрическую проницаемость вынести за знак дифференциала. Принимая во внимание, что вектор напряженности электрического поля является градиентом (взятым с обратным знаком) электрического потенциала  и учитывая формулы (29), получаем:
и учитывая формулы (29), получаем:

Это уравнение называют уравнением Пуассона, а для случая, когда во всем рассматриваемом объеме поля нет зарядов (т. е. когда  уравнением Лапласа.
уравнением Лапласа.
Если вектор  является ротором вектора
является ротором вектора  представляют собой единичные векторы в направлении декартовых осей координат, то вектор
представляют собой единичные векторы в направлении декартовых осей координат, то вектор  определяется детерминантом
определяется детерминантом

т. е. компоненты вектора  определяются формулами
определяются формулами

Эти, на первый взгляд несколько сложные, формулы легко запомнить, если обратить внимание на то, что индексы, обозначающие проекции векторов, чередуются в круговой последовательности:

Рис. 328 поясняет формулы (34). В соответствии с вышеприведенным определением ротора проекция ротора вектора А на какую-либо ось, например ось  представляет собой предел, к которому стремится отношение циркуляции
представляет собой предел, к которому стремится отношение циркуляции 
линейного интеграла по замкнутому контуру) этого вектора  к площади, ограниченной контуром, когда упомянутый контур проведен в плоскости, перпендикулярной к оси
к площади, ограниченной контуром, когда упомянутый контур проведен в плоскости, перпендикулярной к оси  и стягивается вокруг рассматриваемой точки поля. От формы контура упомянутый предел не зависит.
и стягивается вокруг рассматриваемой точки поля. От формы контура упомянутый предел не зависит.

Рис. 328. К пояснению формулы для проекции ротора  на ось
на ось  которая считается направленной от плоскости чертежа к читателю (если смотреть в направлении оси
которая считается направленной от плоскости чертежа к читателю (если смотреть в направлении оси  то элементарный контур, показанный на чертеже, представится обводимым по ходу часовой стрелки).
то элементарный контур, показанный на чертеже, представится обводимым по ходу часовой стрелки).
На рис. 328 показан элементарный прямоугольник с площадью  Если вектор А представляет собой напряженность магнитного поля
Если вектор А представляет собой напряженность магнитного поля  то
то  есть магнитодвижущая сила, и отношение этой магнитодвижущей силы, вычисленной для указанного элементарного контура, к площади, ограниченной контуром, в пределе равно проекции ротора
есть магнитодвижущая сила, и отношение этой магнитодвижущей силы, вычисленной для указанного элементарного контура, к площади, ограниченной контуром, в пределе равно проекции ротора  на ось
на ось  по уравнению Максвелла (28), обобщающему закон Био и Савара, эта величина определяет плотность тока (тока смещения, тока проводимости
по уравнению Максвелла (28), обобщающему закон Био и Савара, эта величина определяет плотность тока (тока смещения, тока проводимости  ) в направлении оси
) в направлении оси  Руководствуясь рис. 328, легко видеть, что
Руководствуясь рис. 328, легко видеть, что

Таким образом, проекция плотности тока на ось  определяется в соответствии с векторным уравнением (28) нижеследующим скалярным уравнением:
определяется в соответствии с векторным уравнением (28) нижеследующим скалярным уравнением:

Заменив на рис. 328 вектор  на
на  и вычисляя аналогично отношение циркуляции
и вычисляя аналогично отношение циркуляции  (т. е. электродвижущей силы) к площади контура, мы получим проекцию ротора
(т. е. электродвижущей силы) к площади контура, мы получим проекцию ротора  на ось
на ось  По уравнению (27), обобщающему закон Фарадея, эта величина, взятая с обратным знаком, определяет быстроту изменения проекции вектора магнитной индукции на ось
По уравнению (27), обобщающему закон Фарадея, эта величина, взятая с обратным знаком, определяет быстроту изменения проекции вектора магнитной индукции на ось 

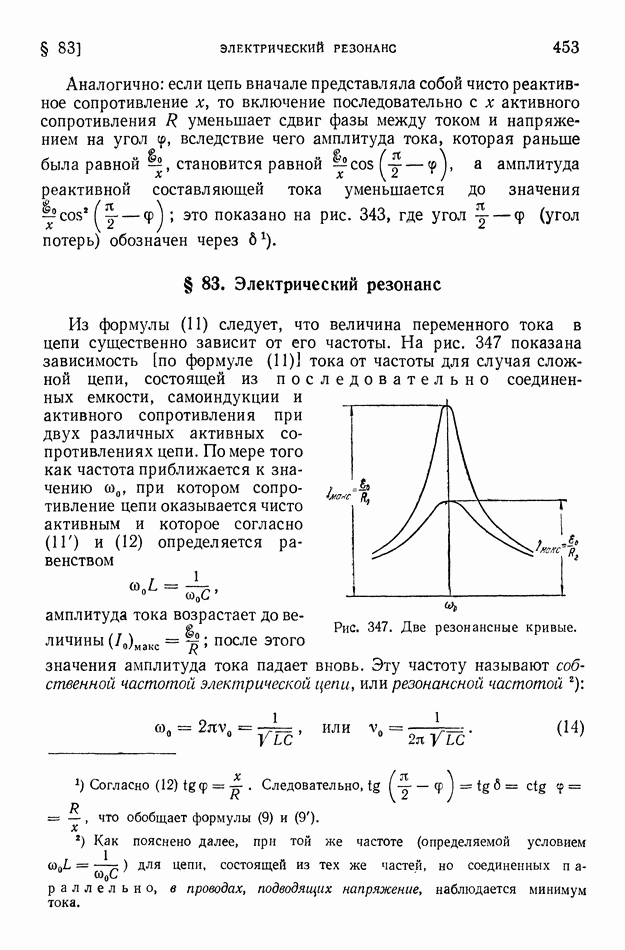
На рубеже XX в. теория Максвелла была существенно дополнена Лорентцом. Теория Максвелла не затрагивала вопроса о строении вещества, не учитывала дискретности вещества и ограничивалась чисто эмпирической характеристикой свойств среды. В уравнениях Максвелла свойства среды определяются тремя величинами: электрической проницаемостью среды  ее магнитной проницаемостью
ее магнитной проницаемостью  и удельной электропроводностью а. В противоположность этому главная задача теории Лорентца заключалась в выяснении действительной атомистической картины разнообразных электрических и магнитных процессов. В соответствии с такой задачей Лорентц исходил из уравнений Максвелла, написанных для вакуума, и рассматривал поле в любом веществе как поле в вакууме, усложненное микроскопическими полями молекулярных зарядов. При таком подходе, очевидно, необходимо учитывать, что в микроскопических областях между молекулами и внутри молекул напряженность электрического, а также и магнитного поля резко изменяется вследствие действия хотя и малых, но весьма близко расположенных внутримолекулярных зарядов. Поэтому вместо обычных макроскопических значений напряженностей электрического и магнитного полей
и удельной электропроводностью а. В противоположность этому главная задача теории Лорентца заключалась в выяснении действительной атомистической картины разнообразных электрических и магнитных процессов. В соответствии с такой задачей Лорентц исходил из уравнений Максвелла, написанных для вакуума, и рассматривал поле в любом веществе как поле в вакууме, усложненное микроскопическими полями молекулярных зарядов. При таком подходе, очевидно, необходимо учитывать, что в микроскопических областях между молекулами и внутри молекул напряженность электрического, а также и магнитного поля резко изменяется вследствие действия хотя и малых, но весьма близко расположенных внутримолекулярных зарядов. Поэтому вместо обычных макроскопических значений напряженностей электрического и магнитного полей  в среде Лорентц рассматривал усредненные значения истинных величин напряженностей этих полей в и А в вакууме, трактуя поле в веществе как геометрическую сумму поля внешних зарядов в вакууме и резко изменяющегося от точки к точке и быстро изменчивого во времени поля (тоже в вакууме), вызванного наличием и движением внутримолекулярных зарядов.
в среде Лорентц рассматривал усредненные значения истинных величин напряженностей этих полей в и А в вакууме, трактуя поле в веществе как геометрическую сумму поля внешних зарядов в вакууме и резко изменяющегося от точки к точке и быстро изменчивого во времени поля (тоже в вакууме), вызванного наличием и движением внутримолекулярных зарядов.
Чтобы сопоставить среднее значение введенных Лорентцом величин  и А (которые, понятно, не поддаются непосредственному измерению) с макрофизическими величинами, входящими в уравнения Максвелла, нужно произвести усреднение истинных напряженностей микроскопических полей: по пространству — для областей, достаточно больших в сравнении с величинами молекул, но малых с с макрофизической точки зрения, а по времени — для промежутков времени, достаточно больших в сравнении с периодами внутримолекулярных движений, но малых по отношению к длительности изучаемых макрофизических процессов. Такое усреднение истинных величин напряженностей микрофизических полей
и А (которые, понятно, не поддаются непосредственному измерению) с макрофизическими величинами, входящими в уравнения Максвелла, нужно произвести усреднение истинных напряженностей микроскопических полей: по пространству — для областей, достаточно больших в сравнении с величинами молекул, но малых с с макрофизической точки зрения, а по времени — для промежутков времени, достаточно больших в сравнении с периодами внутримолекулярных движений, но малых по отношению к длительности изучаемых макрофизических процессов. Такое усреднение истинных величин напряженностей микрофизических полей  и А обеспечивает тождественность средних величин
и А обеспечивает тождественность средних величин  и А с обычными макрофизическими напряженностями
и А с обычными макрофизическими напряженностями  Поэтому уравнения Максвелла в
Поэтому уравнения Максвелла в
теории Лорентца преобразуются в нижеследующую систему уравнений: 

где  представляет собой плотность электрического тока
представляет собой плотность электрического тока  плотность зарядов и
плотность зарядов и  скорость их движения).
скорость их движения).
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
- § 42. Аккумуляторы
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
- § 83. Электрический резонанс
- § 84. Трансформация тока
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)