| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Примеры применения теоремы Остроградского — Гаусса
Применим теорему Остроградского — Гаусса к вычислению вектора электрической индукции в некоторых частных случаях.
Рассмотрим электрическое поле сферы с зарядом  равномерно распределенным по поверхности. Из соображений симметрии замечаем, что силовые линии направлены по радиусам. Для определения индукции в точке
равномерно распределенным по поверхности. Из соображений симметрии замечаем, что силовые линии направлены по радиусам. Для определения индукции в точке  удаленной от центра на расстояние
удаленной от центра на расстояние  проведем через
проведем через  концентрическую сферическую поверхность (рис. 10). Тогда по теореме Остроградского — Гаусса
концентрическую сферическую поверхность (рис. 10). Тогда по теореме Остроградского — Гаусса

откуда


Рис. 10. Электрическое поле заряженной проводящей сферы радиуса 
Следовательно, электрическое поле, создаваемое сферой, равномерно заряженной по поверхности, тождественно вне этой сферы полю точечного заряда, помещенного в центре сферы и равного заряду сферы.
Наибольшее значение индукции и напряженности поля наблюдается на поверхности сферы (при  где
где  радиус сферы):
радиус сферы):

Введя поверхностную плотность заряда  получим:
получим:

В любой точке  внутри заряженной сферы электрическое поле равно нулю. Поток индукции через любую замкнутую поверхность внутри сферы равен нулю, поскольку внутри этой поверхности нет зарядов (они расположены только на поверхности сферы).
внутри заряженной сферы электрическое поле равно нулю. Поток индукции через любую замкнутую поверхность внутри сферы равен нулю, поскольку внутри этой поверхности нет зарядов (они расположены только на поверхности сферы).
В качестве второго примера рассмотрим поле, образованное весьма длинным заряженным цилиндром (например, заряженной проволокой) с радиусом сечения  В этом случае линии индукции, как и силовые линии, направлены по радиусам
В этом случае линии индукции, как и силовые линии, направлены по радиусам
круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. Очевидно, что поток индукции через боковую поверхность коаксиального цилиндра радиуса  и длиной
и длиной  равен
равен  поток индукции через основания этого цилиндра равен нулю, так как вектор
поток индукции через основания этого цилиндра равен нулю, так как вектор  параллелен основаниям. Если поверхностную плотность электричества на заряженном цилиндре обозначить через а, то суммарный заряд на отрезке
параллелен основаниям. Если поверхностную плотность электричества на заряженном цилиндре обозначить через а, то суммарный заряд на отрезке  заряженного цилиндра будет равен
заряженного цилиндра будет равен 
По теореме Остроградского — Гаусса

Следовательно,

т. е. напряженность поля весьма длинного заряженного цилиндра обратно пропорциональна расстоянию от оси цилиндра.

Рис. 11. К вычислению напряженности поля заряженного цилиндра

Рис. 12. К вычислению напряженности поля между заряженными пластинами,
Рассмотрим теперь поле между двумя бесконечно большими параллельными пластинами, заряженными разноименно, с поверхностной плотностью электричества  (одна пластина) и — и (другая пластина). Поток индукции через боковую поверхность цилиндра, показанного на рис. 12, равен нулю, так как линии индукции, как и силовые линии, между пластинами направлены перпендикулярно к плоскости пластин и, следовательно, параллельны образующим цилиндра. Во внешнем пространстве поля нет, так как действие двух разноименно заряженных пластин (при их бесконечно большой величине и численно одинаковой плотности электризации) взаимно компенсируется. Следовательно, поток индукции через всю замкнутую поверхность цилиндра, показанного на рис. 12, равен
(одна пластина) и — и (другая пластина). Поток индукции через боковую поверхность цилиндра, показанного на рис. 12, равен нулю, так как линии индукции, как и силовые линии, между пластинами направлены перпендикулярно к плоскости пластин и, следовательно, параллельны образующим цилиндра. Во внешнем пространстве поля нет, так как действие двух разноименно заряженных пластин (при их бесконечно большой величине и численно одинаковой плотности электризации) взаимно компенсируется. Следовательно, поток индукции через всю замкнутую поверхность цилиндра, показанного на рис. 12, равен  где
где  — площадь основания этого цилиндра,
— площадь основания этого цилиндра,  вектор индукции в точке А (у того основания цилиндра, которое находится между пластинами). Количество электричества на отсекаемой цилиндром части пластины равно
вектор индукции в точке А (у того основания цилиндра, которое находится между пластинами). Количество электричества на отсекаемой цилиндром части пластины равно  По теореме Остроградского — Гаусса
По теореме Остроградского — Гаусса

Следовательно,

т. е. напряженность поля между двумя параллельными, бесконечно большими, разноименно заряженными пластинами во всех точках между пластинами имеет не только одинаковое направление, но и одинаковую величину.
В случае параллельных пластин ограниченного размера соотношение  остается справедливым для центральной части поля между пластинами (по мере приближения к краям пластин оно становится неточным, но погрешность является тем меньшей, чем меньше расстояние между пластинами в сравнении с размерами пластин).
остается справедливым для центральной части поля между пластинами (по мере приближения к краям пластин оно становится неточным, но погрешность является тем меньшей, чем меньше расстояние между пластинами в сравнении с размерами пластин).
Соотношением  можно воспользоваться при экспериментальном изучении любого электростатического поля. Если внести в изучаемое поле две тонкие металлические пластины, укрепленные на изоляторе (рис. 13 и 14), а затем, слегка раздвинув их, вынести из поля, то нетрудно измерить индуцированный на них заряд.
можно воспользоваться при экспериментальном изучении любого электростатического поля. Если внести в изучаемое поле две тонкие металлические пластины, укрепленные на изоляторе (рис. 13 и 14), а затем, слегка раздвинув их, вынести из поля, то нетрудно измерить индуцированный на них заряд.

Рис. 13. Измерение электрической индукции поля посредством пластинок 

Рис. 14. Пластинки 
Если пластины расположены перпендикулярно к линиям индукции, то плотность заряда (его отношение к площади пластин) пропорциональна величине вектора индукции. Если же пластины в момент разделения их в поле были расположены под острым углом к направлению линий индукции, то индуцированный на них заряд будет меньше, а именно, плотность заряда будет пропорциональна проекции вектора  на нормаль к поверхности пластин.
на нормаль к поверхности пластин.
Описанный опыт придает наглядность потоку вектора электрической индукции как величине, пропорциональной плотности электричества, которое может быть индуцировано полем.
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
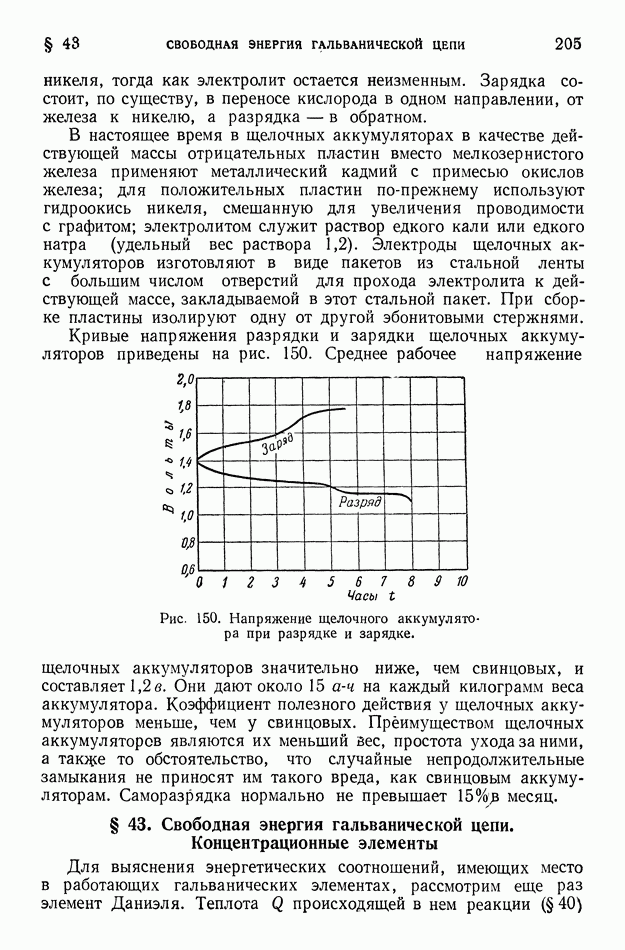
- § 42. Аккумуляторы
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
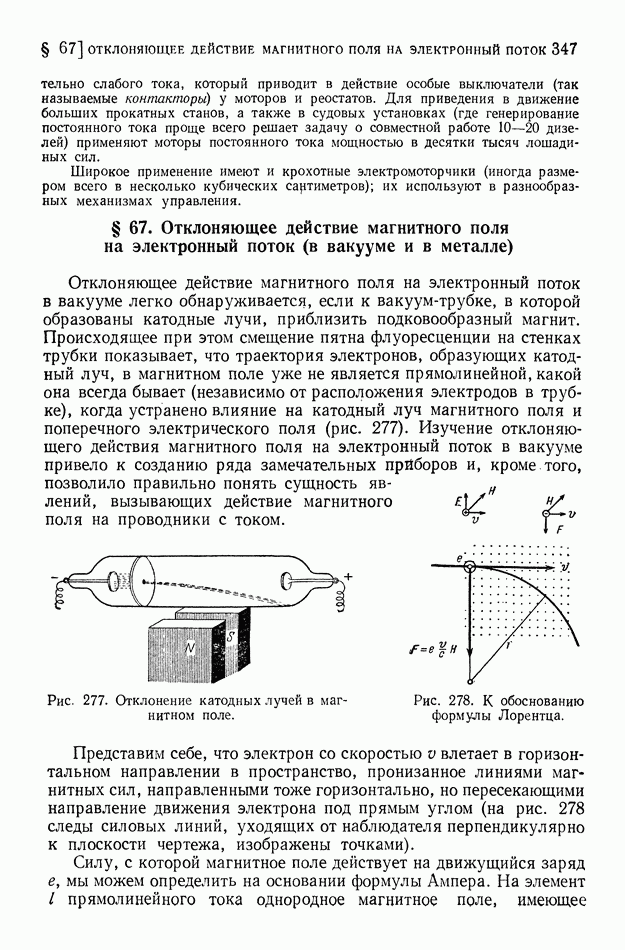
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
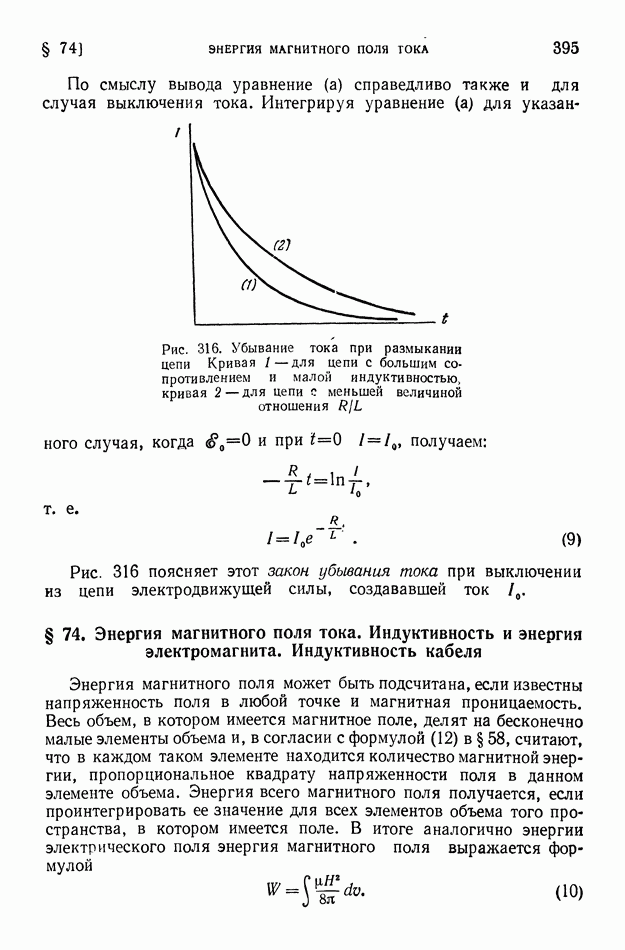
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
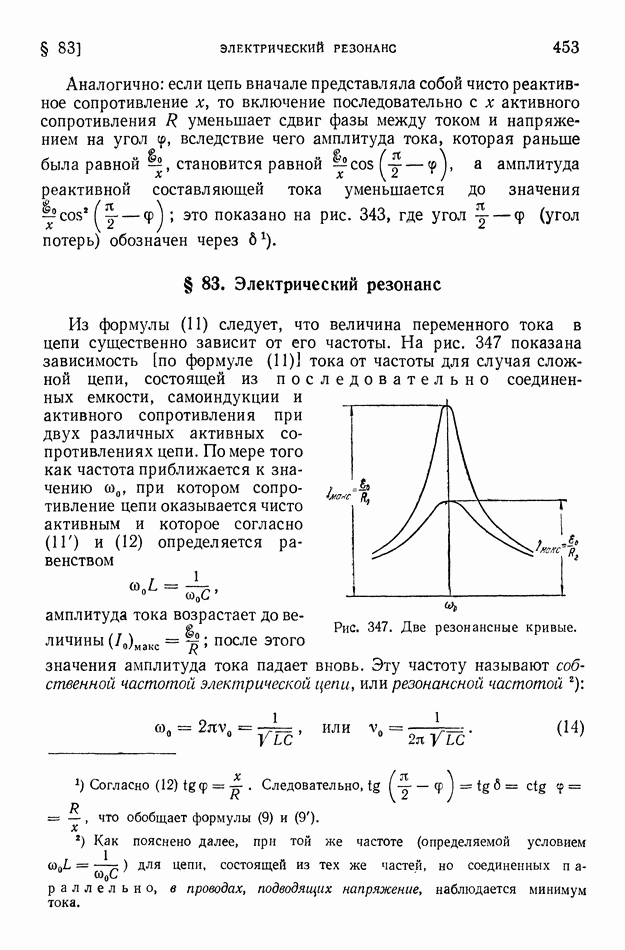
- § 83. Электрический резонанс
- § 84. Трансформация тока
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)