| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Вектор электрической индукции
Если электрическое поле заполнено различными диэлектриками, то в этих случаях теорема Остроградского — Гаусса в приведенной выше формулировке для расчетов непригодна.
Так, например, представим себе, что точечный заряд  помещен в центре воздушного пузырька, который находится, скажем, в масле с диэлектрической постоянной
помещен в центре воздушного пузырька, который находится, скажем, в масле с диэлектрической постоянной  (диэлектрическая постоянная
(диэлектрическая постоянная
воздуха близка к единице). Тогда вокруг заряда в воздухе имеются  линий и густота их у самой поверхности воздушного пузырька, имеющего форму шара с радиусом
линий и густота их у самой поверхности воздушного пузырька, имеющего форму шара с радиусом  равна
равна  . По другую сторону этой поверхности, в масле, напряженность поля и густота линий равны
. По другую сторону этой поверхности, в масле, напряженность поля и густота линий равны  в
в  раз меньше, и общее число выходящих из поверхности линий тоже в
раз меньше, и общее число выходящих из поверхности линий тоже в  раз меньше: оно равно вместо
раз меньше: оно равно вместо  При переходе через границу раздела диэлектриков, таким образом, потеряно некоторое число линий (рис. 5).
При переходе через границу раздела диэлектриков, таким образом, потеряно некоторое число линий (рис. 5).

Рис. 5. Электрический заряд расположен в центре воздушного пузырька, находящегося в масле. На поверхности раздела воздух — масло часть силовых линий прерывается.
В нашем случае силовые линии перпендикулярны к поверхности раздела. В общем случае, когда силовые линии проходят под углом к поверхности раздела, нормальные составляющие векторов напряженностей электрического поля испытывают такой же скачок, как и в разобранном случае, т.е. нормальная составляющая напряженности всегда уменьшается во столько раз, во сколько возрастает диэлектрическая постоянная.

Рис. 6. Преломление силовых линий на границе двух диэлектриков — керосина (1) и воздуха (2), Поскольку  то по уравнению
то по уравнению  тогда как
тогда как  Вследствие этого вектор
Вследствие этого вектор  больше, чем
больше, чем  и имеет другое направление.
и имеет другое направление.
Если одна среда имеет диэлектрическую постоянную  а другая
а другая  то скачок нормальных составляющих напряженностей поля определяется следующим уравнением:
то скачок нормальных составляющих напряженностей поля определяется следующим уравнением:

где  нормальная составляющая напряженности поля в первой среде, а
нормальная составляющая напряженности поля в первой среде, а  нормальная составляющая напряженности поля во второй среде Тангенциальные составляющие
нормальная составляющая напряженности поля во второй среде Тангенциальные составляющие  параллельные границе раздела, при переходе из одной среды в другую изменяются непрерывно, без скачка. Благодаря этому происходит «преломление» силовых линий на границе двух сред (рис. 6). Чтобы сохранить все
параллельные границе раздела, при переходе из одной среды в другую изменяются непрерывно, без скачка. Благодаря этому происходит «преломление» силовых линий на границе двух сред (рис. 6). Чтобы сохранить все
преимущества, которые вытекают из теоремы Остроградского — Гаусса, вместо напряоюенности, которая испытывает скачок на поверхности раздела двух сред, надо ввести новую величину, для которой такого скачка не имелось бы. Нетрудно указать такую величину. Так как при переходе в среду с диэлектрической постоянной  сила поля
сила поля  и число линий, ее изображающих, уменьшаются в
и число линий, ее изображающих, уменьшаются в  раз, то введем векторную величину для электрического поля:
раз, то введем векторную величину для электрического поля:  Очевидно, что эта величина остается неизменной при переходе в новую среду (
Очевидно, что эта величина остается неизменной при переходе в новую среду ( уменьшается во столько же раз, во сколько раз возрастает
уменьшается во столько же раз, во сколько раз возрастает  Вектор
Вектор  называют электрической индукцией.
называют электрической индукцией.

Рис. 7. Индукция поля в диэлектрике измеряется силой, действующей на заряд  в узком поперечном зазоре.
в узком поперечном зазоре.
Каков физический смысл вектора электрической индукции? Чтобы разобраться в этом, вспомним, что вектор напряженности  в любой точке электрического поля и в любой среде представляет собой силу, которая действовала бы на единицу положительного электричества, помещенную в этой точке поля. Теперь представим себе, что в среде с диэлектрической постоянной
в любой точке электрического поля и в любой среде представляет собой силу, которая действовала бы на единицу положительного электричества, помещенную в этой точке поля. Теперь представим себе, что в среде с диэлектрической постоянной  образован бесконечно тонкий вакуумный зазор, грани которого перпендикулярны к направлению поля в рассматриваемом месте (рис. 7). Если в эту вакуумную щель поместить точечный «пробный» заряд величиной в единицу положительного электричества, то сила, с которой поле будет действовать на этот заряд, окажется равной не
образован бесконечно тонкий вакуумный зазор, грани которого перпендикулярны к направлению поля в рассматриваемом месте (рис. 7). Если в эту вакуумную щель поместить точечный «пробный» заряд величиной в единицу положительного электричества, то сила, с которой поле будет действовать на этот заряд, окажется равной не  а индукции
а индукции  Действительно, на гранях раздела среды, имеющей диэлектрическую постоянную
Действительно, на гранях раздела среды, имеющей диэлектрическую постоянную  и вакуума, диэлектрическая постоянная которого равна единице, напряженность поля испытывает скачок согласно уравнению (8):
и вакуума, диэлектрическая постоянная которого равна единице, напряженность поля испытывает скачок согласно уравнению (8):

А так как, по определению,  то, стало быть,
то, стало быть,

Итак, вектор электрической индукции представляет собой силу, действующую на точечный заряд в единицу положительного электричества, когда этот заряд помещен в бесконечно узком зазоре, грани которого перпендикулярны к направлению поля.
Заметим, что если бы тонкий вакуумный зазор был расположен не перпендикулярно к силовым линиям, а параллельно им (рис. 8), то сила, действующая на пробный заряд, помещенный в такую параллельную щель, была бы равна Е:

Это объясняется тем, что, как отмечено выше, тангенциальные составляющие напряженности поля не испытывают скачка на границе раздела двух сред.
Название вектора («вектор индукции») указывает на связь этого вектора с явлением электризации по влиянию — с явлением электростатической индукции. И в самом деле, при определенных, и притом наипростейших, условиях электризация проводников по влиянию действительно пропорциональна величине вектора  Подробнее это пояснено в следующем параграфе.
Подробнее это пояснено в следующем параграфе.
(Вместо вектора электрической индукции нередко вводят в рассмотрение вектор электрического смещения, отличающийся от вектора электрической индукции коэффициентом так что  некоторые авторы называют этот вектор электрической возбужденностью.)
некоторые авторы называют этот вектор электрической возбужденностью.)

Рис. 8. Напряженность поля в диэлектрике измеряется силой, действующей на заряд  в узкой продольной щели.
в узкой продольной щели.
Так же как раньше поле изображалось при помощи силовых линий, густота которых измеряла силу поля, мы можем теперь изображать линии индукции, совпадающие по направлению с силовыми линиями (только в кристаллах индукция может не совпадать по направлению с силой поля). Чтобы изобразить величину индукции, мы опять условимся проводить через  поперечного сечения столько линий индукции, сколько абсолютных электростатических единиц в числе
поперечного сечения столько линий индукции, сколько абсолютных электростатических единиц в числе 
Главное преимущество индукции заключается в безусловной применимости теоремы Остроградского — Гаусса: общее алгебраическое число линий индукции  проходящих через любую замкнутую поверхность, не зависит от диэлектрических свойств среды и равно
проходящих через любую замкнутую поверхность, не зависит от диэлектрических свойств среды и равно

где  заряды, находящиеся внутри этой поверхности (см. предпоследний абзац предыдущего параграфа).
заряды, находящиеся внутри этой поверхности (см. предпоследний абзац предыдущего параграфа).
В пустоте число линий индукции и число силовых линий совпадают.
Число линий индукции, проходящих сквозь какую-либо поверхность, проведенную в поле, называют потоком индукции сквозь данную поверхность.
Очевидно, что в равномерном поле поток индукции через площадку в  расположенную перпендикулярно к направлению поля, равен численному значению вектора индукции
расположенную перпендикулярно к направлению поля, равен численному значению вектора индукции 
В неравномерном ноле поток индукции через бесконечно малую площадку  перпендикулярную к
перпендикулярную к  равен
равен 
Если площадка  расположена под острым углом к направлению поля и
расположена под острым углом к направлению поля и  есть проекция площадки
есть проекция площадки  (рис. 9), то поток индукции через площадку
(рис. 9), то поток индукции через площадку  будет таким же, как и через площадку
будет таким же, как и через площадку  равным
равным  Иначе говоря, он равен
Иначе говоря, он равен  как
как  Произведение
Произведение  можно записать и так:
можно записать и так:  где
где  проекция вектора
проекция вектора  на нормаль к площадке
на нормаль к площадке  Итак, поток индукции через площадку
Итак, поток индукции через площадку  равен произведению
равен произведению 
Для вычисления потока индукции через некоторую поверхность  нужно образовать сумму потоков индукции через все элементарно малые площадки, из которых состоит поверхность
нужно образовать сумму потоков индукции через все элементарно малые площадки, из которых состоит поверхность  Такая сумма бесконечно большого числа бесконечно малых слагаемых выражается интегралом, «распределенным по поверхности
Такая сумма бесконечно большого числа бесконечно малых слагаемых выражается интегралом, «распределенным по поверхности 


Рис. 9. Поток индукции через площадку  равен
равен 
По теореме Остроградского — Гаусса поток электрической индукции через любую замкнутую поверхность равен нулю, если внутри этой поверхности электрические заряды отсутствуют; поток электрической индукции равен нулю также и в том случае, если алгебраическая сумма зарядов, охватываемых поверхностью, равна нулю. Если же алгебраическая сумма зарядов в рассматриваемом объеме отлична от нуля и равна  то поток индукции через поверхность, охватывающую этот объем, равен
то поток индукции через поверхность, охватывающую этот объем, равен 
Внешние заряды не влияют на величину потока индукции через замкнутую поверхность (сколько линий индукции от внешних зарядов входит через эту поверхность, столько и выходит).
Основываясь на теореме Остроградского — Гаусса в форме (9), еще раз обратимся к характеристике поля в бесконечно тонкой вакуумной полости, имеющей вид узкой щели, грани которой перпендикулярны к направлению поля в диэлектрике. Вследствие непрерывности линий индукции густота линий индукции в такой щели при достаточной протяженности ее граней будет такой же, как и в Диэлектрике. Стало быть, если  есть вектор электрической индукции в диэлектрике,
есть вектор электрической индукции в диэлектрике,  же в указанном вакуумном зазоре, то
же в указанном вакуумном зазоре, то  Но индукция в вакууме совпадает по величине и направлению с напряженностью поля
Но индукция в вакууме совпадает по величине и направлению с напряженностью поля  следовательно,
следовательно,

| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
- § 42. Аккумуляторы
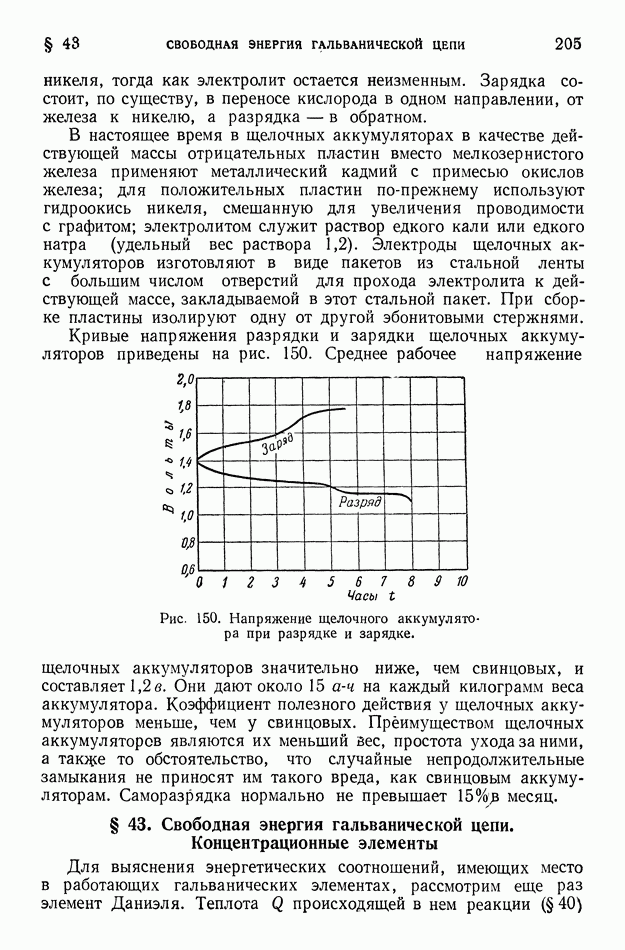
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
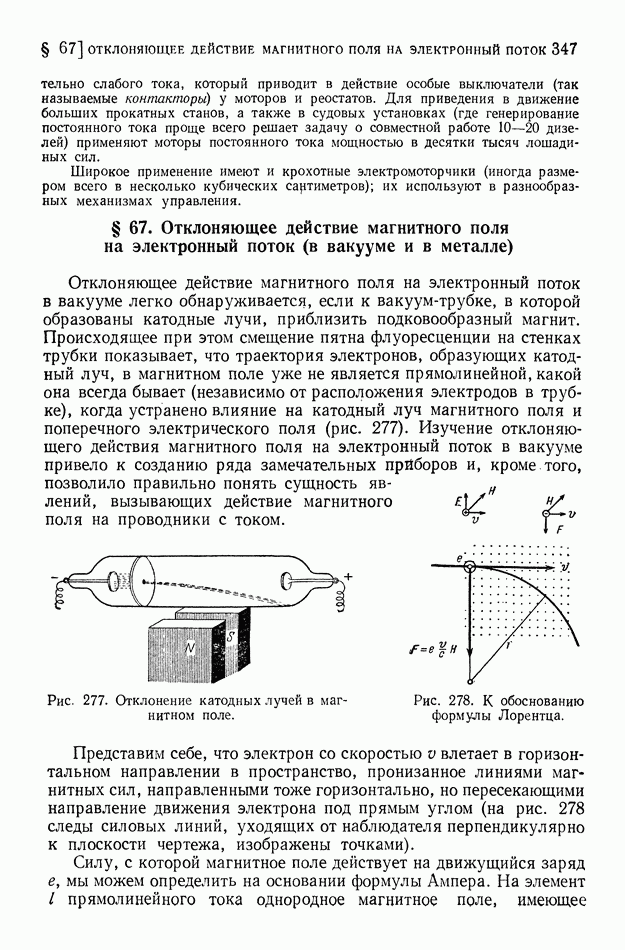
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
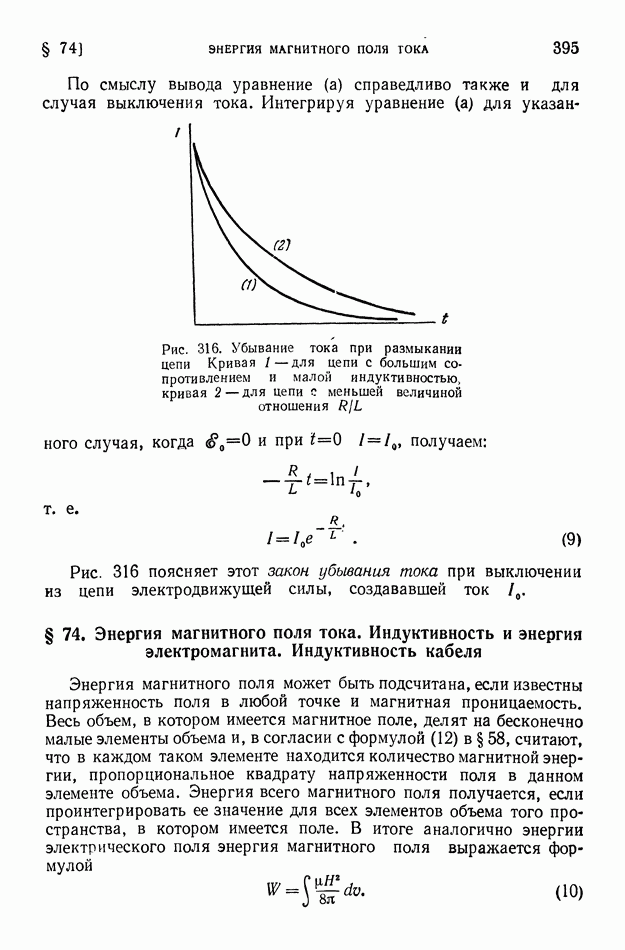
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
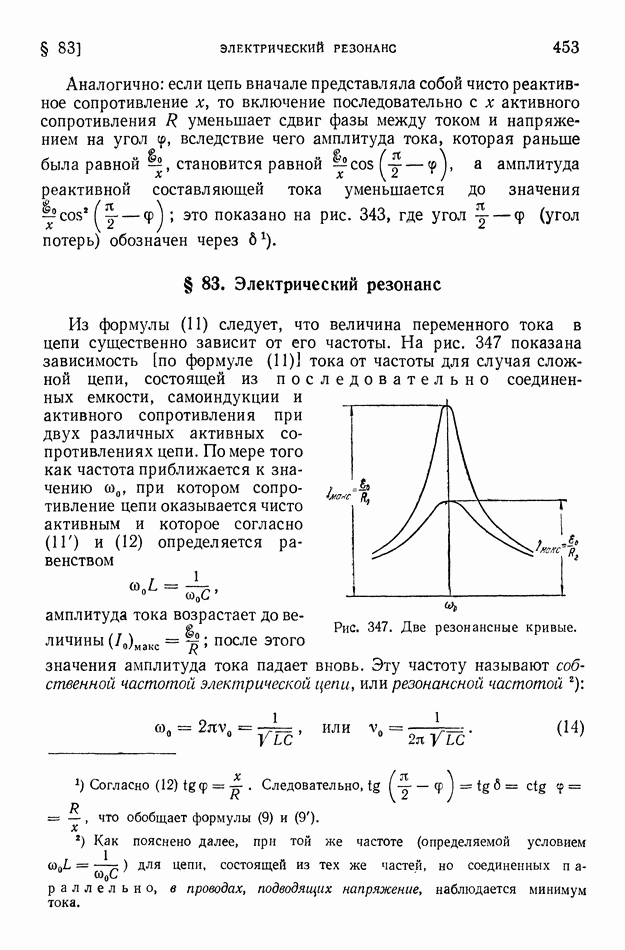
- § 83. Электрический резонанс
- § 84. Трансформация тока
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)