| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 82. Обобщенный закон Ома
Мы разобрали три простейшие электрические цепи: цепь, содержащую только емкость, только индуктивность и только активное сопротивление. Однако реальная электрическая цепь всегда представляет собой более или менее сложную комбинацию этих простейших элементов.
Обратимся к случаю поел едовател  соединения емкости, индуктивности и активного сопротивления, к которым приложена синусоидальная электродвижущая сила
соединения емкости, индуктивности и активного сопротивления, к которым приложена синусоидальная электродвижущая сила  (рис. 344). Очевидно, что здесь через всю цепь протекает один и тот же ток
(рис. 344). Очевидно, что здесь через всю цепь протекает один и тот же ток  Выберем его амплитуду в качестве основного вектора диаграммы.
Выберем его амплитуду в качестве основного вектора диаграммы.

Рис. 344. Последовательное соединение элементов цепи.

Рис. 345. Векторная диаграмма напряжений для последовательного соединения элементов цепи.
Вектор напряжения на сопротивлении  совпадает по направлению с вектором тока, вектор напряжения на емкости С отстает от вектора тока на
совпадает по направлению с вектором тока, вектор напряжения на емкости С отстает от вектора тока на  вектор напряжения на индуктивности
вектор напряжения на индуктивности  опережает вектор тока на
опережает вектор тока на  (рис. 345). Геометрическая сумма этих векторов изображает амплитуду внешней электродвижущей силы. Она равна по величине гипотенузе треугольника, построенного на
(рис. 345). Геометрическая сумма этих векторов изображает амплитуду внешней электродвижущей силы. Она равна по величине гипотенузе треугольника, построенного на  и на геометрической сумме
и на геометрической сумме 

Мы получили соотношение между амплитудой тока и амплитудой напряжения для случая последовательно включенных емкости, индуктивности и сопротивления. Перепишем это соотношение в такой форме:

Назвав 

полным сопротивлением цепи, мы приходим к обобщенному закону Ома:

Это соотношение справедливо, конечно, и для эффективных значений.
Легко видеть, что амплитуда тока будет наибольшей тогда, когда противоположно направленные векторы напряжений  будут равны по величине. При этом
будут равны по величине. При этом

и величина тока

т. е. в этом случае величина тока определяется только активным сопротивлением цепи.
Нетрудно определить угол  (рис. 345) — разность фаз векторов тока и электродвижущей силы. Очевидно, тангенс этого угла равен отношению катетов треугольника, составленного векторами
(рис. 345) — разность фаз векторов тока и электродвижущей силы. Очевидно, тангенс этого угла равен отношению катетов треугольника, составленного векторами

В зависимости от соотношения между и  изменяются как величина, так и знак
изменяются как величина, так и знак  При преобладании емкостной составляющей вектор тока опережает суммарный вектор напряжения, при преобладании индуктивной составляющей — отстает от него. При
При преобладании емкостной составляющей вектор тока опережает суммарный вектор напряжения, при преобладании индуктивной составляющей — отстает от него. При  угол
угол  становится равным нулю и вектор тока совпадает с вектором напряжения.
становится равным нулю и вектор тока совпадает с вектором напряжения.
Итак, когда к цепи (рис. 344) подведено напряжение

то это напряжение возбуждает ток

амплитуда и фаза которого определяются формулами (11) и (12),
Обозначим через х алгебраическую сумму индуктивного и емкостного сопротивлений цепи, считая, что одно из них, скажем емкостное сопротивление, должно быть взято в этой сумме с обратным знаком, так как на этих реактивных сопротивлениях создаются противоположные сдвиги фаз:

При таком обозначении суммарного реактивного сопротивления полное сопротивление цепи из последовательно включенных в нее элементов согласно  и (12) можно представить в следующем виде:
и (12) можно представить в следующем виде:

Стало быть, обобщенный закон Ома (11) можно записать так:

Если в выражении полного сопротивления цепи вынести за знак радикала не  то получается:
то получается:

и, следовательно,


Рис. 346. При включении последовательно с  реактивного сопротивления х амплитуда тока уменьшается до величины
реактивного сопротивления х амплитуда тока уменьшается до величины  а амплитуда активной составляющей тока — до величины
а амплитуда активной составляющей тока — до величины 
Мы видим, что если цепь вначале представляла собой чисто активное сопротивление  то, когда при неизменном подведенном к цепи напряжении в нее вводится последовательно с
то, когда при неизменном подведенном к цепи напряжении в нее вводится последовательно с  реактивное сопротивление
реактивное сопротивление  вектор, изображающий амплитуду тока, становится равным проекции вектора-амплитуды существовавшего ранее в цепи активного тока на ось, составляющую угол
вектор, изображающий амплитуду тока, становится равным проекции вектора-амплитуды существовавшего ранее в цепи активного тока на ось, составляющую угол  с вектором напряжения (рис. 346). Проходящий теперь в цепи ток можно представить как сумму активного тока с амплитудой, уменьшившейся до значения
с вектором напряжения (рис. 346). Проходящий теперь в цепи ток можно представить как сумму активного тока с амплитудой, уменьшившейся до значения  и возникшего реактивного тока с амплитудой
и возникшего реактивного тока с амплитудой 
Аналогично: если цепь вначале представляла собой чисто реактивное сопротивление  то включение последовательно с х активного сопротивления
то включение последовательно с х активного сопротивления  уменьшает сдвиг фазы между током и напряжением на угол
уменьшает сдвиг фазы между током и напряжением на угол  вследствие чего амплитуда тока, которая раньше была равной становится равной
вследствие чего амплитуда тока, которая раньше была равной становится равной  а амплитуда реактивной составляющей тока уменьшается до значения
а амплитуда реактивной составляющей тока уменьшается до значения  это показано на рис. 343, где угол
это показано на рис. 343, где угол  потерь) обозначен через
потерь) обозначен через 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
- § 42. Аккумуляторы
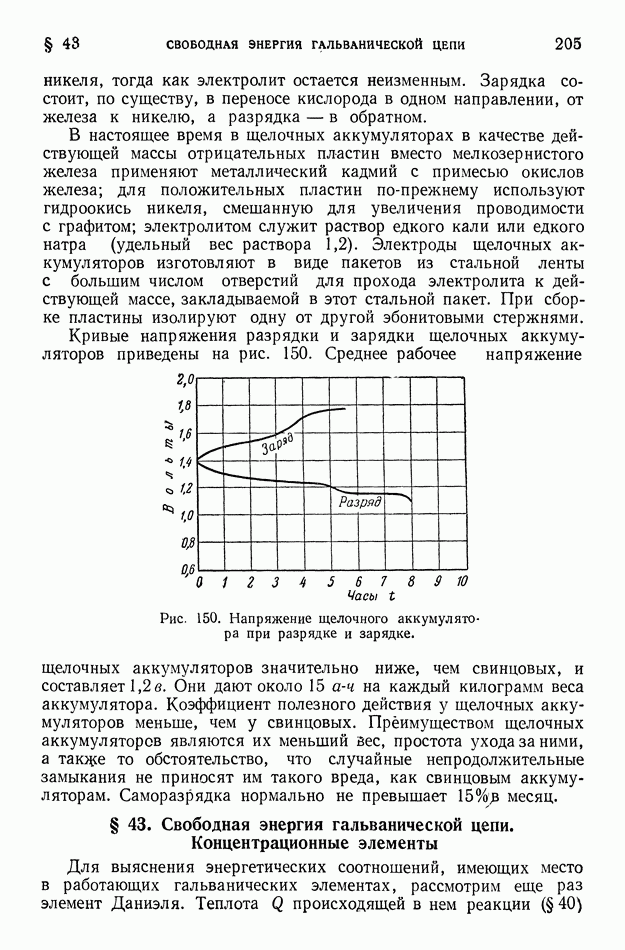
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
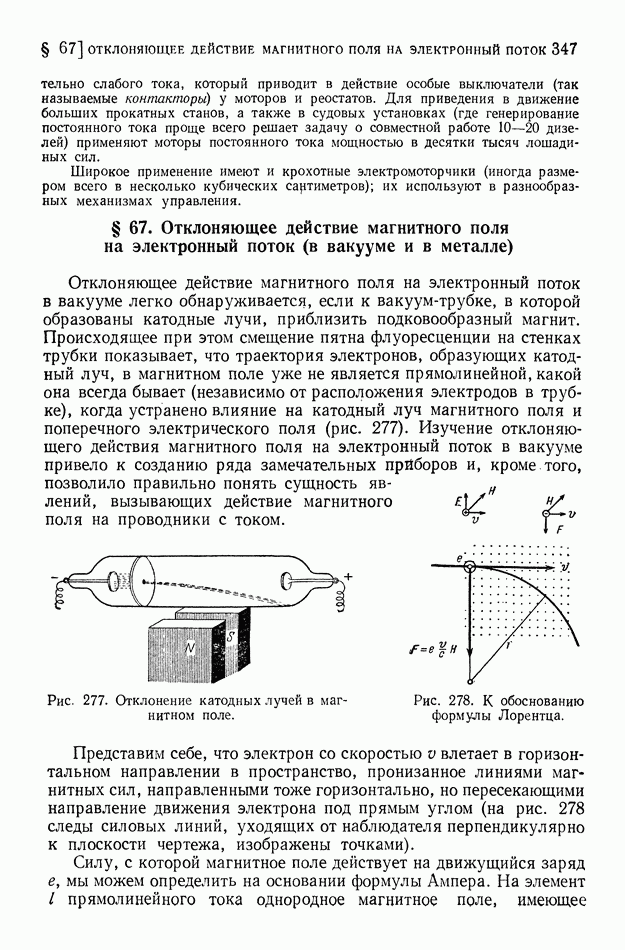
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
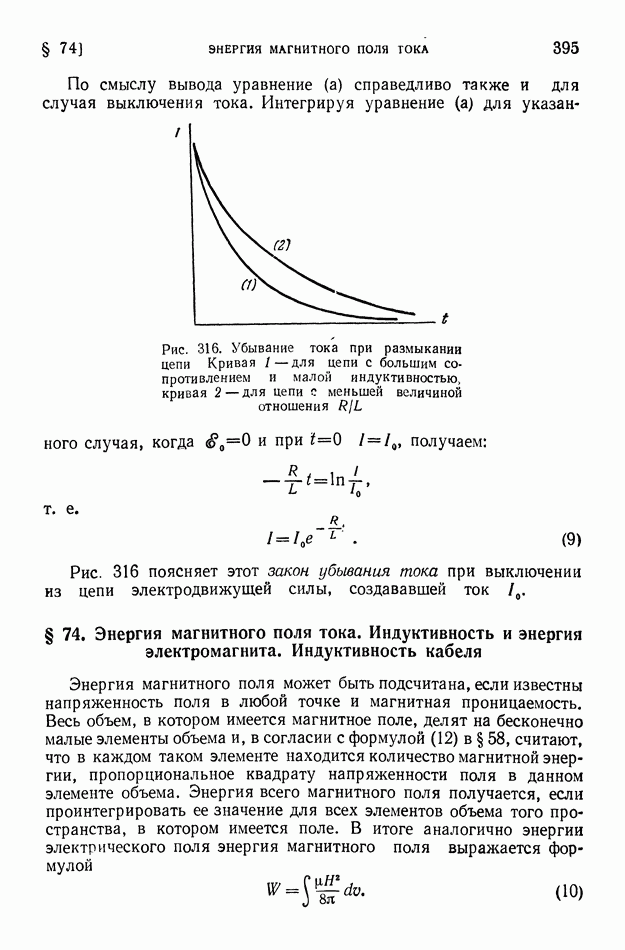
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
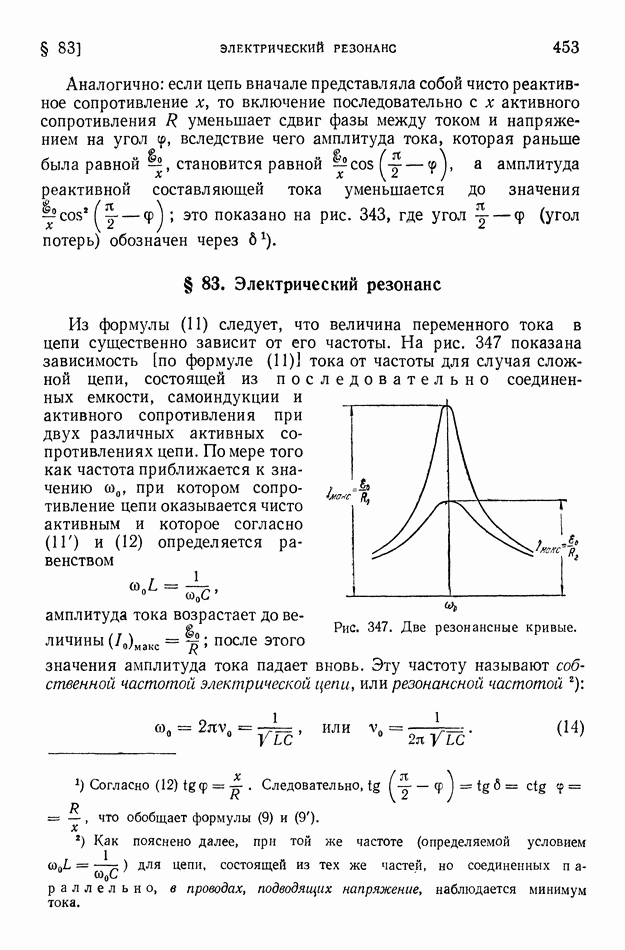
- § 83. Электрический резонанс
- § 84. Трансформация тока
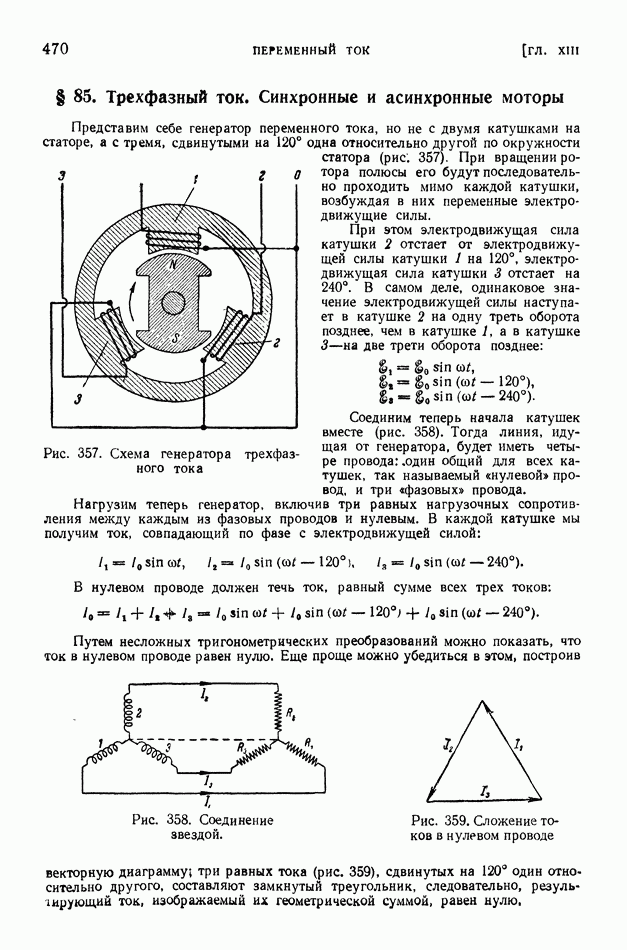
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)