| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
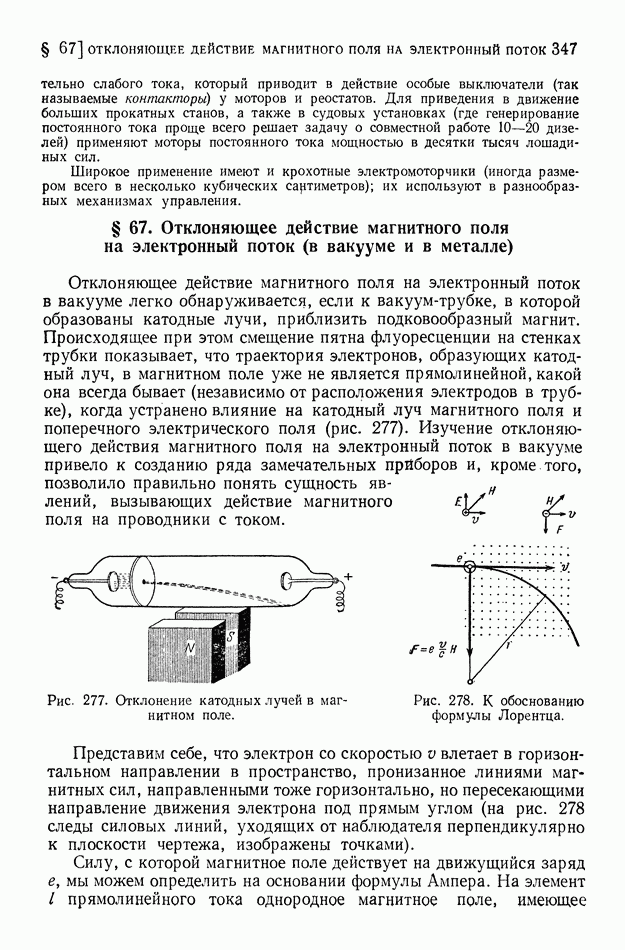
Отклоняющее действие магнитного поля на электронный поток в вакууме легко обнаруживается, если к вакуум-трубке, в которой образованы катодные лучи, приблизить подковообразный магнит. Происходящее при этом смещение пятна флуоресценции на стенках трубки показывает, что траектория электронов, образующих катодный луч, в магнитном поле уже не является прямолинейной, какой она всегда бывает (независимо от расположения электродов в трубке), когда устранено влияние на катодный луч магнитного поля и поперечного электрического поля (рис. 277). Изучение отклоняющего действия магнитного поля на электронный поток в вакууме привело к созданию ряда замечательных приборов и, кроме того, позволило правильно понять сущность явлений, вызывающих действие магнитного поля на проводники с током.

Рис. 277. Отклонение катодных лучей в магнитном поле.

Рис. 278. К обоснованию формулы Лорентца.
Представим себе, что электрон со скоростью  влетает в горизонтальном направлении в пространство, пронизанное линиями магнитных сил, направленными тоже горизонтально, но пересекающими направление движения электрона под прямым углом (на рис. 278 следы силовых линий, уходящих от наблюдателя перпендикулярно к плоскости чертежа, изображены точками).
влетает в горизонтальном направлении в пространство, пронизанное линиями магнитных сил, направленными тоже горизонтально, но пересекающими направление движения электрона под прямым углом (на рис. 278 следы силовых линий, уходящих от наблюдателя перпендикулярно к плоскости чертежа, изображены точками).
Силу, с которой магнитное поле действует на движущийся заряд  мы можем определить на основании формулы Ампера. На элемент I прямолинейного тока однородное магнитное поле, имеющее
мы можем определить на основании формулы Ампера. На элемент I прямолинейного тока однородное магнитное поле, имеющее
напряженность  действует с силой, равной
действует с силой, равной  Пусть рассматриваемый нами движущийся заряд
Пусть рассматриваемый нами движущийся заряд  за время
за время  передвинулся на расстояние
передвинулся на расстояние  это явление подобно элементу
это явление подобно элементу  тока, величина которого
тока, величина которого  Подставив указанное выражение для
Подставив указанное выражение для  в формулу Ампера, получим
в формулу Ампера, получим  ; здесь
; здесь  есть скорость движения
есть скорость движения  Учитывая далее, что заряд
Учитывая далее, что заряд  здесь выражен в абсолютных электромагнитных единицах (так как в формуле Ампера величина тока предполагается измеренной в единицах CGSM), и желая в дальнейшем подразумевать под
здесь выражен в абсолютных электромагнитных единицах (так как в формуле Ампера величина тока предполагается измеренной в единицах CGSM), и желая в дальнейшем подразумевать под  заряд, выраженный в электростатических единицах, мы должны разделить полученное выражение на скорость света с. Таким образом, окончательно находим, что однородное магнитное поле действует на частицу, движущуюся перпендикулярно к направлению поля, с силой
заряд, выраженный в электростатических единицах, мы должны разделить полученное выражение на скорость света с. Таким образом, окончательно находим, что однородное магнитное поле действует на частицу, движущуюся перпендикулярно к направлению поля, с силой

В более общем случае, когда вектор скорости движения электрона не перпендикулярен к вектору напряженности магнитного поля, формулу для силы, с которой магнитное поле действует на движущийся в нем электрон, можно представить, пользуясь понятием о векторном произведении и учитывая, что  в следующем виде:
в следующем виде:

Для определения направления этой, так называемой лорентцовой силы можно применять правило левой ладони, нов данном случае нужно располагать пальцы не по направлению электронного потока, а против движения электронов (так как электроны имеют отрицательный заряд, а направлением тока считается направление движения положительных зарядов).
Если на электрон одновременно действуют магнитное поле с напряженностью  и электрическое поле с напряженностью
и электрическое поле с напряженностью  то результирующая лорентцова сила будет представлять собой геометрическую сумму ускоряющего действия электрического поля
то результирующая лорентцова сила будет представлять собой геометрическую сумму ускоряющего действия электрического поля  в направлении
в направлении  отклоняющего действия магнитного поля
отклоняющего действия магнитного поля  в направлении, перпендикулярном к векторам
в направлении, перпендикулярном к векторам  и Н:
и Н:

Эта формула — одна из основных в физике; ее называют формулой Лорентца. Руководствуясь этой формулой, голландский ученый Гендрик Антоон Лорентц на рубеже XX в. в ряде статей (подытоженных им в монографии «Электронная теория»,
изданной в 1909 г.) объяснил многие электродинамические, магнитные и оптические явления.
Поскольку сила, действующая со стороны магнитного поля на движущийся электрон, направлена всегда перпендикулярно к вектору скорости движения электрона, то очевидно, что, отклоняя траекторию электрона (искривляя ее), магнитное поле не производит работы и не изменяет энергии движения электрона. Так как действие магнитного поля на движущийся электрон проявляется в центростремительном ускорении —  где
где  масса электрона и
масса электрона и  радиус кривизны траектории электрона в магнитном поле, то при перпендикулярности векторов
радиус кривизны траектории электрона в магнитном поле, то при перпендикулярности векторов  и
и 

Отсюда мы видим, что в однородном магнитном поле, где  т. е. траектория электрона в однородном магнитном поле, в которое электрон влетел перпендикулярно к линиям поля, всюду имеет одинаковую кривизну, стало быть, является окружностью, радиус которой равен
т. е. траектория электрона в однородном магнитном поле, в которое электрон влетел перпендикулярно к линиям поля, всюду имеет одинаковую кривизну, стало быть, является окружностью, радиус которой равен

Эту окружность называют (в честь Лармора, детально изучившего влияние магнитного поля на движение электронов) ларморовой орбитой.
Если начальная скорость электрона, попавшего в однородное магнитное поле, составляла некоторый острый угол с направлением линий поля, то этот угол сохраняется неизменным при движении электрона в магнитном поле, и поэтому в указанном случае траектория электрона приобретает форму винтовой линии (рис. 279).

Рис. 279. Винтовая траектория электрона в магнитном поле.
Влияние электрического поля на движение электрона существенно отличается от влияния магнитного поля; электрическое поле изменяет кинетическую энергию электрона, тогда как магнитное поле изменяет только направление, но не величину скорости. Движение электрона в электрическом поле в общем сходно с движением тела в гравитационном поле: когда начальная скорость электрона противоположна направлению линий сил однородного электрического поля, то для электрона, имеющего отрицательный заряд, это означает совпадение силы, действующей на него, с направлением
скорости — электрон движется равноускоренно; при обратном направлении скорости он движется равнозамедленно; в общем случае, когда начальная скорость электрона составляет некоторый угол с направлением однородного электрического поля, электрон движется по параболе. Электрическое поле, направленное перпендикулярно к скорости, электрона (рис. 280), в начальный момент действует на электрон только с центростремительной силой; поэтому радиус кривизны  траектории электрона, движущегося перпендикулярно к электрическому полю (для начальной точки параболы), может быть вычислен из соотношения
траектории электрона, движущегося перпендикулярно к электрическому полю (для начальной точки параболы), может быть вычислен из соотношения


Рис. 280. К выводу формулы, определяющей отклонение электронного потока в поперечном электрическом поле.
Таким образом, для катодных лучей, отклоняемых поперечным электрическим полем, радиус кривизны траектории электронов оказывается пропорциональным квадрату скорости и равным

тогда как при отклонении катодных лучей магнитным полем радиус кривизны траектории электронов согласно формуле (9) пропорционален первой степени скорости. Это обстоятельство используют для измерения скорости движения электронов методом взаимной компенсации электрического и магнитного отклонений электронного потока. Действительно, если накрестк пластинкам заряженного конденсатора расположить плоские полюсы электромагнита таким образом, чтобы поток заряженных частиц, например пучок катодных лучей, проходил одновременно и между полюсами электромагнита и между пластинками конденсатора, то можно, регулируя ток в обмотке электромагнита, добиться того, чтобы отклонение катодных лучей от прямолинейного пути, вызванное электрическим полем, было нацело уничтожено равным по величине, но противоположным по направлению отклонением, которое вызывается магнитным полем.
Сопоставляя приведенные выше формулы для радиусов кривизны траектории электронов в поперечном электрическом и в магнитном поле, мы видим, что отклонения могут быть взаимно компенсированы, когда напряженности полей удовлетворяют соотношению

или

Это простое соотношение, определяющее напряженности скрещенных полей (электрического и магнитного), когда их отклоняющие действия по величине одинаковы и по направлению противоположны, легко выводится прямо из формулы Лорентца. Действительно, из (8) при  имеем:
имеем:  при взаимной перпендикулярности векторов
при взаимной перпендикулярности векторов  сразу получается формула (11).
сразу получается формула (11).
Воспользовавшись формулой (11), проанализируем движение электрона, который с некоторой начальной скоростью  попадает в однородные скрещенные электрическое и магнитное поля. Пусть силовые линии магнитного поля направлены вертикально снизу вверх по оси
попадает в однородные скрещенные электрическое и магнитное поля. Пусть силовые линии магнитного поля направлены вертикально снизу вверх по оси  а электрического — горизонтально, причем так, что электрическая сила, действующая на электрон, ориентирована по оси X слева направо, и допустим, что вектор начальной скорости лежит в горизонтальной плоскости. Как уже было пояснено выше, магнитное поле будет отклонять электрон по дуге окружности с радиусом
а электрического — горизонтально, причем так, что электрическая сила, действующая на электрон, ориентирована по оси X слева направо, и допустим, что вектор начальной скорости лежит в горизонтальной плоскости. Как уже было пояснено выше, магнитное поле будет отклонять электрон по дуге окружности с радиусом  Электрическое поле будет уносить электрон в направлении оси X направо со скоростью, слагающая которой в направлении поля (по оси X) вследствие однородности поля будет возрастать с течением времени равномерно.
Электрическое поле будет уносить электрон в направлении оси X направо со скоростью, слагающая которой в направлении поля (по оси X) вследствие однородности поля будет возрастать с течением времени равномерно.
Допустим, что начальная скорость велика в сравнении со скоростью, создаваемой за рассматриваемый промежуток временй электрическим полем, и что напряженность магнитного поля существенно превышает напряженность электрического поля. В этом случае нетрудно дать наглядное представление о траектории электрона. Для этого вообразим, что вместо силы  на электрон действует равная ей сила магнитного происхождения —
на электрон действует равная ей сила магнитного происхождения —  вызванная тем, что электррн движется на нас (по оси
вызванная тем, что электррн движется на нас (по оси  со скоростью
со скоростью  Действительно, при такой дополнительной скорости движения (одной и той же для всех моментов времени)
Действительно, при такой дополнительной скорости движения (одной и той же для всех моментов времени)  стало быть, вследствие перпендикулярности векторов
стало быть, вследствие перпендикулярности векторов 

Таким образом, в указанном случае (большой начальной скорости и  траекторией электрона является ларморова орбита, центр которой перемещается перпендикулярно к векторам
траекторией электрона является ларморова орбита, центр которой перемещается перпендикулярно к векторам  с неизменной скоростью
с неизменной скоростью  Эту скорость и называют скоростью дрейфа электрона.
Эту скорость и называют скоростью дрейфа электрона.
Понятно, что радиус ларморовой орбиты не остается постоянным, так как с течением времени увеличивается составляющая скорости движения электрона в направлении электрического поля. Но поскольку радиус и длина ларморовой орбиты возрастают пропорционально скорости, то очевидно, что угловая частота электрона по ларморовой орбите остается, как и скорость дрейфа, неизменной и равной, согласно (9),

Лармор доказал, что для электронов, удерживаемых на орбите радиальным полем положительного заряда, расположенного в центре орбиты, действие магнитного поля сказывается в возникновении прецессионного вращения оси орбиты вокруг направления магнитного поля с частотой прецессии в два раза меньшей, чем указанная выше частота»
Формула (11) позволяет определить скорость заряженных частиц, например электронов, в катодных лучах путем измерения напряженностей электрического и магнитного полей, подобранных так, чтобы их отклоняющие действия взаимно компенсировались. Если после этого, устранив электрическое поле, измерить отклонения потока заряженных частиц в магнитном поле, то по величинам  и
и  можно вычислить отношение заряда частицы к ее массе. Формула для вычисления по указанным измерениям отношения заряда частицы к массе получается из формул (9) и (11):
можно вычислить отношение заряда частицы к ее массе. Формула для вычисления по указанным измерениям отношения заряда частицы к массе получается из формул (9) и (11):

Впервые точное измерение скорости катодных лучей выполнил в 1897 г. Дж. Дж. Томсон. Как и следовало ожидать (согласно формуле, приведенной на стр. 216), скорость электронов в катодных лучах в хорошо эвакуированной трубке оказалась в простой зависимости от вольтажа, приложенного к электродам трубки: 100 в сообщают электронам скорость  при 10 000 в скорость электронов достигает одной пятой скорости света (таблица на стр. 217).
при 10 000 в скорость электронов достигает одной пятой скорости света (таблица на стр. 217).
Исторически катодные лучи были первым явлением, обнаружившим существование свободных (не связанных с атомами) электронов. На основании точных измерений отклонения катодных лучей в электрическом и магнитном полях найдено:

Так как тщательные измерения (§ 3) показали, что заряд электрона равен

то из сопоставления этого числа с предыдущим получается, что масса электрона равна

Поясненный выше метод измерения отношения заряда частицы к ее массе был применен Дж. Дж. Томсоном и подробно разработан и усовершенствован Астоном как метод точного определения масс ионов различных химических веществ, что привело к открытию изотопов, т. е. химически простых веществ, тождественных по своим химическим свойствам, но различающихся по величине массы атомов. Приборы для такого измерения масс потока ионов в вакууме называют масс-спектрографами. Устройство этих приборов пояснено в третьем томе курса. Там же рассказано о методе фотографирования траекторий быстро движущихся частиц посредством так называемых камер Вильсона  (Быстро движущиеся частицы вызывают ионизацию газа. Если газ был пересыщен водяными парами и сразу после пролета частицы подвергнут резкому охлаждению, то след движения частицы отчетливо обозначается на снятой в этот момент фотографии капельками конденсировавшейся влаги.)
(Быстро движущиеся частицы вызывают ионизацию газа. Если газ был пересыщен водяными парами и сразу после пролета частицы подвергнут резкому охлаждению, то след движения частицы отчетливо обозначается на снятой в этот момент фотографии капельками конденсировавшейся влаги.)
Влияние магнитного поля на поток ионов в электролитах можно демонстрировать, как это делал Плантэ еще в 1860 г., посредством следующего опыта. В стеклянный плоский сосуд с раствором серной кислоты опускают в качестве анода медную заостренную проволоку. При напряжении на электродах в несколько десятков вольт быстрое электролитическое растворение меди становится видимым по образующимся хлопьям, которые завихряются при приближении магнита (рис. 281).

Рис. 281. Опыт Плантэ.
Отклоняющее действие магнитного поля на электронный поток в металле проявляется в силах, приложенных к проводнику с током. Чтобы пояснить, как лорентцовы силы, действующие на электроны проводимости, преобразуются в амперовы силы, действующие на токонесущий проводник, проанализируем явления, происходящие в примитивном прообразе современных электромоторов — в диске Барлоу (1822 г.).
Диск из латуни свободно вращается в подшипниках, находясь в межполюсном пространстве стального магнита. Нижняя часть диска погружена в желобок, наполненный ртутью. Ток от аккумулятора подводится через подшипник по оси к диску и затем направляется по диску и через ртуть (рис. 282).
Очевидно, что на радиус диска, по которому в некоторый данный момент идет ток, действует сила  [формула (3)] в направлении, определяемом по правилу левой ладони. Эта сила, вызывая поворот диска на некоторый угол, приводит в контакт со ртутью следующий участок окружности диска, вследствие чего ток направляется по другому радиусу, и т. д. В результате возникает непрерывное вращение диска.
[формула (3)] в направлении, определяемом по правилу левой ладони. Эта сила, вызывая поворот диска на некоторый угол, приводит в контакт со ртутью следующий участок окружности диска, вследствие чего ток направляется по другому радиусу, и т. д. В результате возникает непрерывное вращение диска.
Рассмотрим описанное явление с точки зрения движения действительных носителей электрического тока в металлах — электронов.
На рис. 283 пунктиром показано направление электронного потока. Если перпендикулярно к плоскости диска создано магнитное поле, направленное на нас, то траектории движения электронов искривляются, как показано на рисунке.

Рис. 282. Диск Барлоу.

Рис. 283. Движение электронов в диске Барлоу.
При движении электронов в металле между ними и атомами металла происходят частые столкновения, при которых атомы получают импульсы в направлении движения электронов.

Рис. 284. Схема опытов по изучению явления Холла.
Когда вследствие действия магнитного поля происходит отклонение траекторий электронов, атомы металла получают импульсы, дающие результирующую силу в направлении, перпендикулярном к радиусу диска. Эта результирующая и вызывает вращение диска в целом.
Что электроны, движущиеся в металле, действительно отклоняются от прямолинейного пути под действием перпендикулярно направленного магнитного поля, это доказывается существованием так называемого эффекта Холла (1879 г.). Эффект Холла состоит в следующем.
Пусть вдоль широкой металлической пластины, изображенной на рис. 284, идет ток в направлении от  к
к  электроны в металле, следовательно, движутся от В к
электроны в металле, следовательно, движутся от В к  На боковых сторонах пластины
На боковых сторонах пластины
всегда можно отыскать две такие точки  разность потенциалов между которыми равна нулю. Если к этим точкам
разность потенциалов между которыми равна нулю. Если к этим точкам  присоединить провода от чувствительного гальванометра, то стрелка гальванометра будет находиться в покое. Добившись такого положения, создадим при помощи электромагнита сильное магнитное поле, направленное перпендикулярно к плоскости пластины. Пусть над пластиной находится северный полюс электромагнита, а внизу — южный. В этом случае поток электронов, бегущих внутри пластины, должен отклониться к точке
присоединить провода от чувствительного гальванометра, то стрелка гальванометра будет находиться в покое. Добившись такого положения, создадим при помощи электромагнита сильное магнитное поле, направленное перпендикулярно к плоскости пластины. Пусть над пластиной находится северный полюс электромагнита, а внизу — южный. В этом случае поток электронов, бегущих внутри пластины, должен отклониться к точке 
Благодаря этому в области, прилежащей к  создается повышенная «концентрация электронов», а в области, прилежащей к с
создается повышенная «концентрация электронов», а в области, прилежащей к с  наоборот, пониженная концентрация. Другими словами, точка с приобретает некоторый положительный потенциал по сравнению, с точкой
наоборот, пониженная концентрация. Другими словами, точка с приобретает некоторый положительный потенциал по сравнению, с точкой  таким образом, разность потенциалов между
таким образом, разность потенциалов между  уже не будет равна нулю. Вследствие этого от с к
уже не будет равна нулю. Вследствие этого от с к  через провода, соединенные с гальванометром, потечет электрический ток и вызовет отклонение стрелки прибора. При уничтожении магнитного поля, т. е. после размыкания тока, питающего электромагнит, создающий это поле, пути электронов в пластине снова примут свое обычное направление и стрелка гальванометра возвратится в свое нулевое положение.
через провода, соединенные с гальванометром, потечет электрический ток и вызовет отклонение стрелки прибора. При уничтожении магнитного поля, т. е. после размыкания тока, питающего электромагнит, создающий это поле, пути электронов в пластине снова примут свое обычное направление и стрелка гальванометра возвратится в свое нулевое положение.
Многочисленные экспериментальные исследования явления Холла показали, что электродвижущая сила хол» возникающая в явлении Холла, отнесенная к ширине пластины а, пропорциональна произведению напряженности магнитного поля на плотность тока  в пластине и на синус угла между направлением тока и направлением поля, т. е., иначе говоря, электродвижущая сила эффекта Холла, если ее рассматривать как вектор и разделить на ширину пластины, пропорциональна векторному произведению вектора напряженности магнитного поля и вектора плотности тока:
в пластине и на синус угла между направлением тока и направлением поля, т. е., иначе говоря, электродвижущая сила эффекта Холла, если ее рассматривать как вектор и разделить на ширину пластины, пропорциональна векторному произведению вектора напряженности магнитного поля и вектора плотности тока:

Коэффициент пропорциональности  в этом уравнении называют постоянной Холла. Постоянная Холла не одинакова для различных металлов и, подобно проводимости, зависит от наличия в металле примесей. Наиболее велика постоянная Холла для теллура, висмута, сурьмы и мышьяка (для висмута она почти в
в этом уравнении называют постоянной Холла. Постоянная Холла не одинакова для различных металлов и, подобно проводимости, зависит от наличия в металле примесей. Наиболее велика постоянная Холла для теллура, висмута, сурьмы и мышьяка (для висмута она почти в  раз больше, чем для меди).
раз больше, чем для меди).
Весьма замечательно, что примерно для половины металлов постоянная Холла имеет нормальный знак [отрицательный при вышеприведенном начертании формулы (13)], тогда как для других металлов постоянная Холла имеет противоположный знак. В классической электронной теории этот факт оставался необъясненным. Согласно квантовой теории электропроводности, общее представление о которой дано в §§ 30 и 35, носителями тока в
металле являются «полусвободные» электроны, которые энергетически остаются в некоторой мере связанными с кристаллической решеткой положительных ионов, но находятся на высших квантовых уровнях так называемой «незаполненной зоны». Оказалось, как показал Пайерлс, что если число электронов на этих уровнях незаполненной зоны меньше половины общего числа всех уровней в ней, то электродвижущая сила эффекта Холла имеет нормальное направление (постоянная  отрицательна); если же число электронов в незаполненной зоне превышает половину числа уровней в ней, то электродвижущая сила эффекта Холла должна иметь противоположное направление (постоянная
отрицательна); если же число электронов в незаполненной зоне превышает половину числа уровней в ней, то электродвижущая сила эффекта Холла должна иметь противоположное направление (постоянная  положительна).
положительна).

Рис. 285. Схема опытов по изучению явления Нернста.
Строго говоря, электродвижущая сила эффекта Холла определяется, собственно, не вектором напряженности  магнитного поля, а вектором намагниченности
магнитного поля, а вектором намагниченности  проводника. Это было обнаружено опытами русского ученого
проводника. Это было обнаружено опытами русского ученого  Гольдгаммера, изучившего явление Холла в ферромагнитных телах в 1889 г., и с полной убедительностью показано советским физиком И. К. Кикоиным в 1936 г. Поэтому уравнение (13) правильнее писать в следующем виде:
Гольдгаммера, изучившего явление Холла в ферромагнитных телах в 1889 г., и с полной убедительностью показано советским физиком И. К. Кикоиным в 1936 г. Поэтому уравнение (13) правильнее писать в следующем виде:

Величина  в этом уравнении [постоянная Холла — Кикоина) для инструментальной стали пропорциональна содержанию аустенита в стали; это обстоятельство используют в заводских лабораторных установках для определения процентного содержания аустенита в стали измерением электродвижущей силы эффекта Холла.
в этом уравнении [постоянная Холла — Кикоина) для инструментальной стали пропорциональна содержанию аустенита в стали; это обстоятельство используют в заводских лабораторных установках для определения процентного содержания аустенита в стали измерением электродвижущей силы эффекта Холла.
Следует отметить, что в отсутствие электрического тока, но при наличии в проводнике теплового потока магнитное поле может возбудить электродвижущую силу, аналогичную электродвижущей силе эффекта Холла. А именно, если на концах пластинки, имеющей длину  поддерживать разность температур
поддерживать разность температур  и держать пластинку в магнитном поле, силовые линии которого перпендикулярны к пластинке (рис. 285). то на коаях пластинки (ширина
и держать пластинку в магнитном поле, силовые линии которого перпендикулярны к пластинке (рис. 285). то на коаях пластинки (ширина
которой а) обнаруживается электродвижущая сила, пропорциональная произведению напряженности магнитного поля на градиент температуры:

Это явление было открыто Нернстом в 1886 г. Величину  называют постоянной Нернста; она, как и постоянная Холла, не одинакова по величине и по знаку для разных металлов. Если учесть неодинаковую теплопроводность металлов, то между, численными значениями постоянной Холла и постоянной Нернста обнаруживается некоторый параллелизм (отношение постоянной Нернста к коэффициенту теплопроводности приблизительно пропорционально постоянной Холла).
называют постоянной Нернста; она, как и постоянная Холла, не одинакова по величине и по знаку для разных металлов. Если учесть неодинаковую теплопроводность металлов, то между, численными значениями постоянной Холла и постоянной Нернста обнаруживается некоторый параллелизм (отношение постоянной Нернста к коэффициенту теплопроводности приблизительно пропорционально постоянной Холла).
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
- § 42. Аккумуляторы
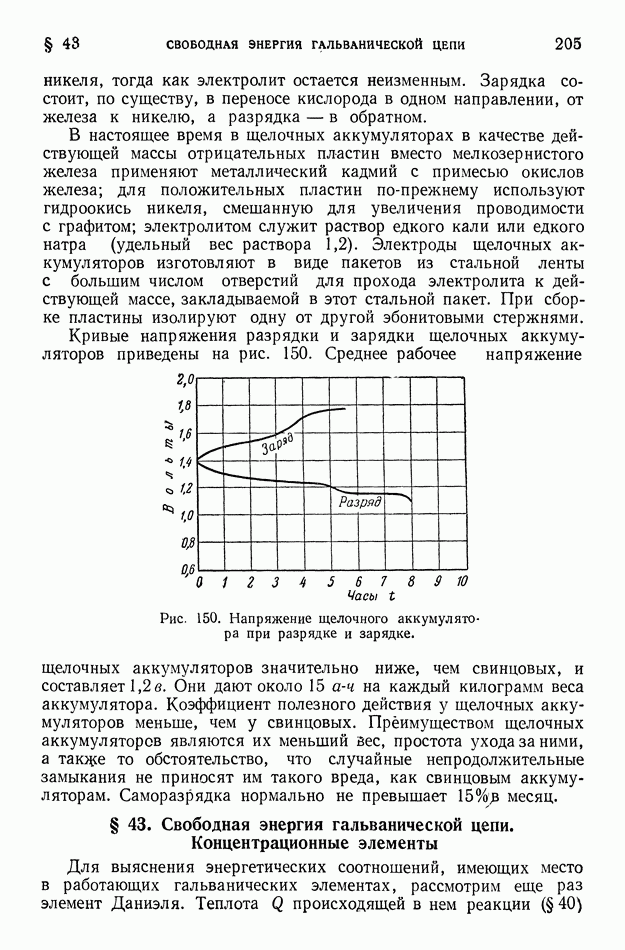
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
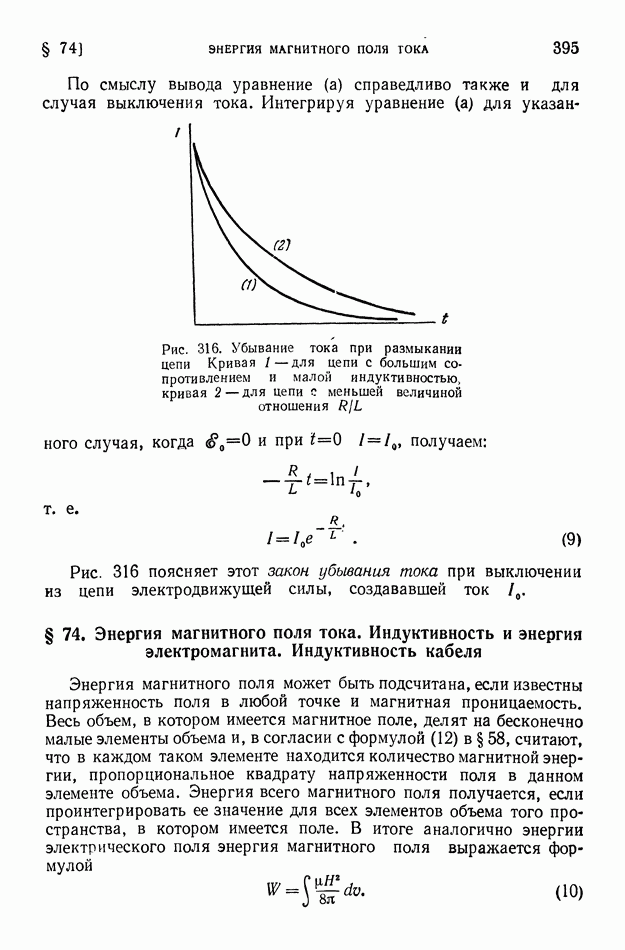
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
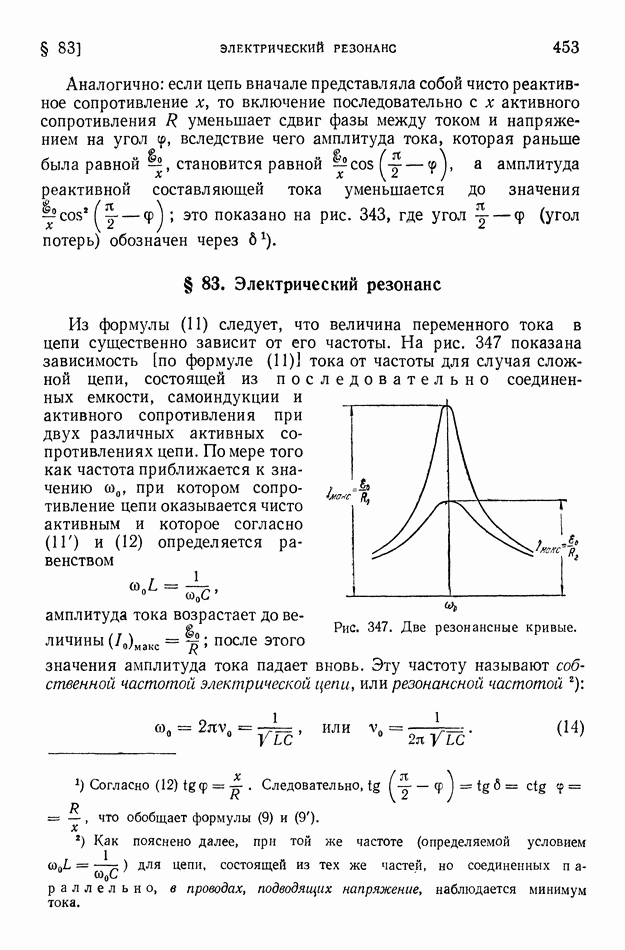
- § 83. Электрический резонанс
- § 84. Трансформация тока
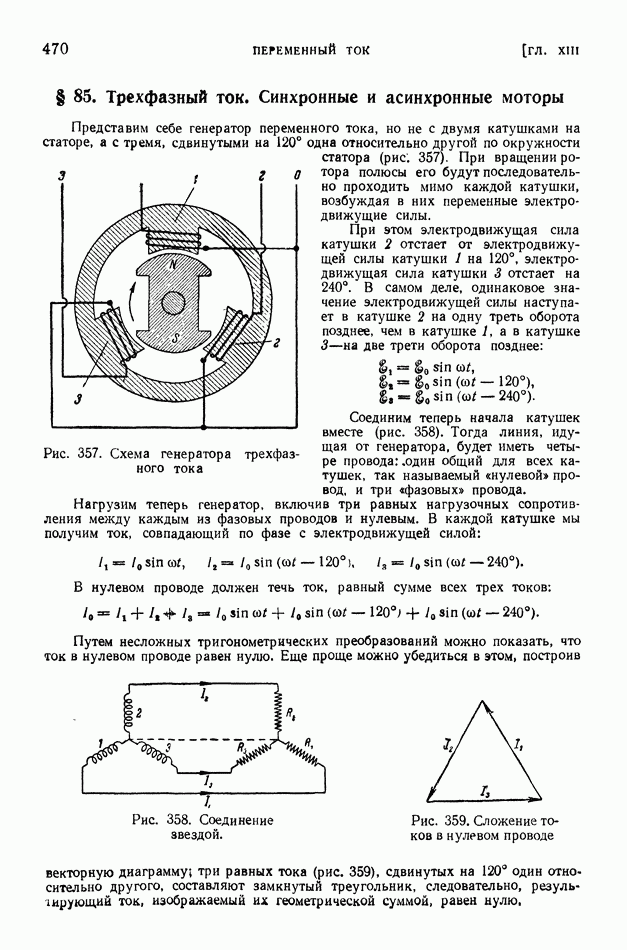
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)