| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
Причина рассмотрения этой темы в нашем курсе состоит в том, что нам предстоит построить модель магнитного поля в межпланетной среде. Для этого нужно знать электропроводность плазмы, так как диссипативные процессы рассеяния способны оказать сильное влияние на динамическое поведение магнитного поля (см. разд. 12.4).

Рис. 12.3. Схематическая диаграмма, иллюстрирующая понятие столкновения согласно а — модели Друде. б - взаимодействия посредством дальнодействующих электрических сил. в — в результате стохастического влияния большого числа далеких столкновений траектория частицы поворачивает на 90°.
Каждый хорошо знаком с электропроводностью. В средней школе это явление объясняют с помощью модели Друде, а в высших учебных заведениях — фононным рассеянием. Ни один из этих процессов не подходит в данном случае, потому что мы имеем дело с плазмой, т.е. полностью ионизованным газом, состоящим из свободных электронов и протонов. Поэтому наш случай ближе к задаче о свойствах проводимости и явлений переноса в газах, где носителями импульса, энергии и т.п. являются частицы, а перенос этих параметров осуществляется при столкновениях частиц. Этот случай идеально прост, если газ состоит из молекул, но здесь мы имеем дело с полностью ионизованным газом. Вспомните трудности, которые возникли в гл. 2, когда мы пытались определить, что подразумевается под столкновением между заряженными частицами.
В плазме столкновения осуществляются посредством дальнодействующих электростатических сил, возникающих между электронами и протонами. Динамика частицы в плазме схематически показана на рис. 12.3. Можно сформулировать тем не менее эквивалентное определение понятия столкновения, если вспомнить, что в классическом приближении столкновением считается взаимодействие, при котором частица полностью «забывает» о своем начальном направлении и начинает двигаться в новом случайном направлении.
В плазме заряженные частицы испытывают большое число слабых толчков, так же как и в случае ионизационных потерь, но результат усреднения по всем этим случайным импульсам не должен содержать результирующего поперечного импульса частицы. Статистически, как в «теории случайного блуждания», хотя среднего приращения поперечной скорости нет, среднеквадратичное значение  отлично от нуля, т.е.
отлично от нуля, т.е.
статистически в результате случайного рассеяния частица приобретает результирующий поперечный импульс. Если бы этот процесс был непрерывным, то никакого результирующего  было бы, но, поскольку
было бы, но, поскольку  передается в виде случайных дискретных порций,
передается в виде случайных дискретных порций,  Так же как при случайном блуждании, если среднеквадратичное значение поперечной скорости, приобретаемое за секунду, равно
Так же как при случайном блуждании, если среднеквадратичное значение поперечной скорости, приобретаемое за секунду, равно  то через промежуток времени
то через промежуток времени  поперечный импульс будет равен
поперечный импульс будет равен

т.е.  время, которое требуется частице на столкновение. К этому времени поперечная скорость будет по величине равна начальной, и поэтому можно считать, что частица забыла начальное направление движения. Этот расчет можно было бы упростить, положив, например, что протоны неподвижны, но в данном случае нас интересует динамика самих протонов, так как они несут весь импульс.
время, которое требуется частице на столкновение. К этому времени поперечная скорость будет по величине равна начальной, и поэтому можно считать, что частица забыла начальное направление движения. Этот расчет можно было бы упростить, положив, например, что протоны неподвижны, но в данном случае нас интересует динамика самих протонов, так как они несут весь импульс.
Выведем простое выражение для средней длины свободного пробега протона, имеющего скорость  и взаимодействующего с протонами и электронами плазмы. Для иллюстрации положим, что протоны и электроны в плазме неподвижны. Этот анализ покажет происхождение соотношений между физическими параметрами, входящими в полную теорию.
и взаимодействующего с протонами и электронами плазмы. Для иллюстрации положим, что протоны и электроны в плазме неподвижны. Этот анализ покажет происхождение соотношений между физическими параметрами, входящими в полную теорию.
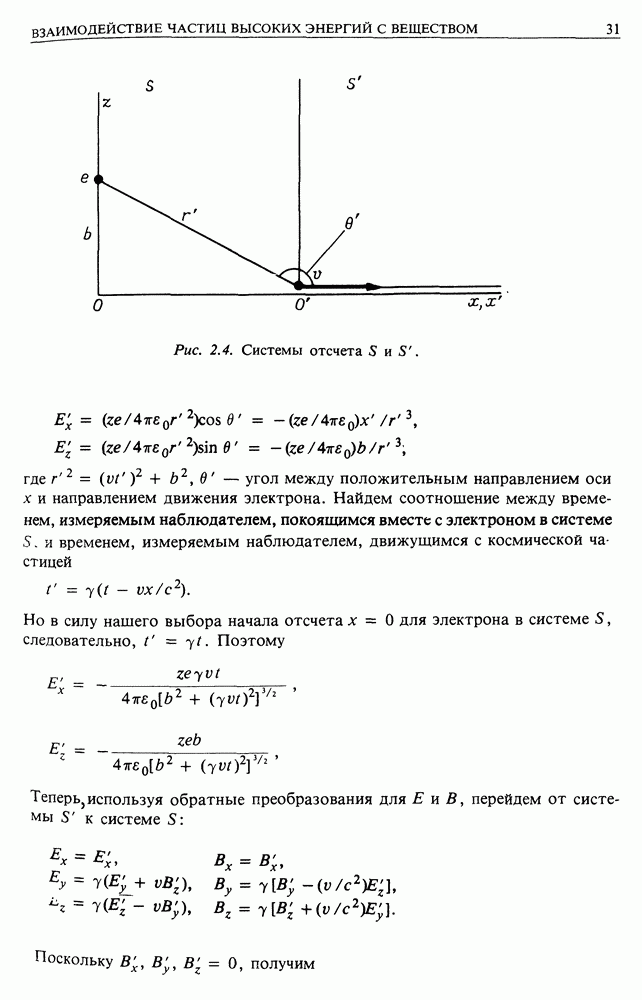
В одиночном столкновении протон получает импульс, перпендикулярный направлению движения

[см. уравнение (2.1)]. Следовательно,

Теперь вычислим среднеквадратичное отклонение скорости частицы от ее первоначального направления. Когда средний квадрат скорости будет равен  т.е. квадрату начальной скорости, частица отклонится на 90°, и можно будет считать, что столкновение произошло, т.е.
т.е. квадрату начальной скорости, частица отклонится на 90°, и можно будет считать, что столкновение произошло, т.е.  Как обычно,
Как обычно,

Поэтому

В формулу входит фактор Гаунта  поэтому возникают прежние трудности. В этом случае Ьтах — дебаевский радиус для тепловой плазмы
поэтому возникают прежние трудности. В этом случае Ьтах — дебаевский радиус для тепловой плазмы  обычное значение для низкотемпературной плазмы. Поэтому
обычное значение для низкотемпературной плазмы. Поэтому

Полная теория значительно сложнее, потому что все частицы находятся в движении, и, кроме того, имеет место максвелловское распределение по скоростям. Подробные, результаты можно найти в монографии Спитцера «Физика полностью ионизованного газа» [7].
Время соударения для протона в полностью ионизованной плазме дается формулой

где размерность  кельвины,
кельвины,  — массовое число частицы. Средняя длина свободного пробега частицы равна
— массовое число частицы. Средняя длина свободного пробега частицы равна  Для солнечного ветра примем
Для солнечного ветра примем  [7]. Тогда
[7]. Тогда  (для сравнения расстояние от Земли до Солнца, астрономическая единица, равно
(для сравнения расстояние от Земли до Солнца, астрономическая единица, равно  Итак, для протонов, которые несут весь импульс солнечного ветра, средняя длина свободного пробега для электростатических столкновений много больше, чем расстояние от Земли до Солнца, и поэтому для описания динамики частиц солнечного ветра с вмороженным магнитным полем можно рассматривать плазму без столкновений с бесконечной проводимостью.
Итак, для протонов, которые несут весь импульс солнечного ветра, средняя длина свободного пробега для электростатических столкновений много больше, чем расстояние от Земли до Солнца, и поэтому для описания динамики частиц солнечного ветра с вмороженным магнитным полем можно рассматривать плазму без столкновений с бесконечной проводимостью.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
- 4.4. ОБРАЗОВАНИЕ ПАР
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
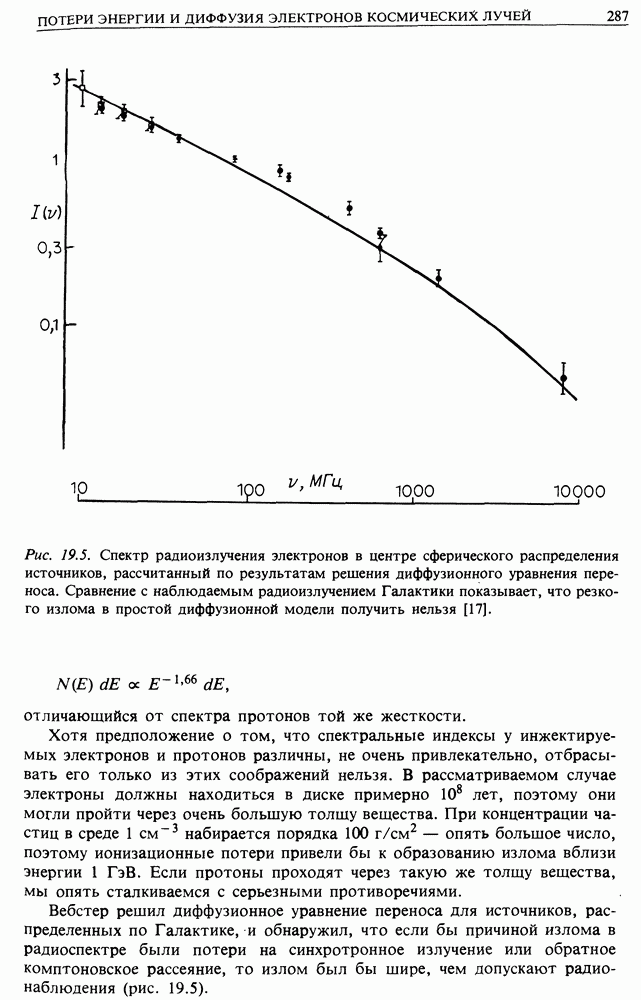
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
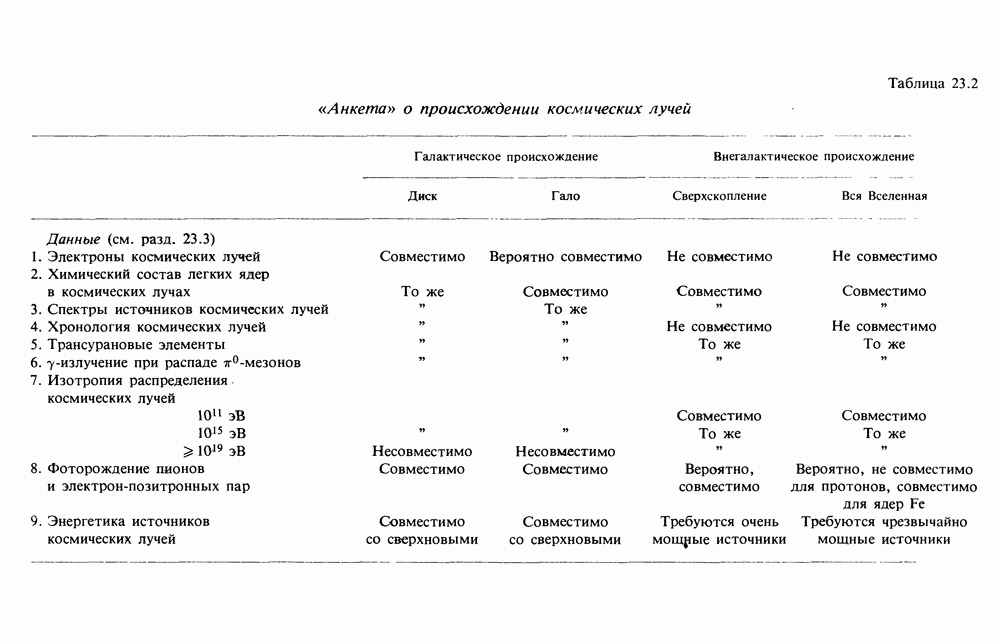
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ