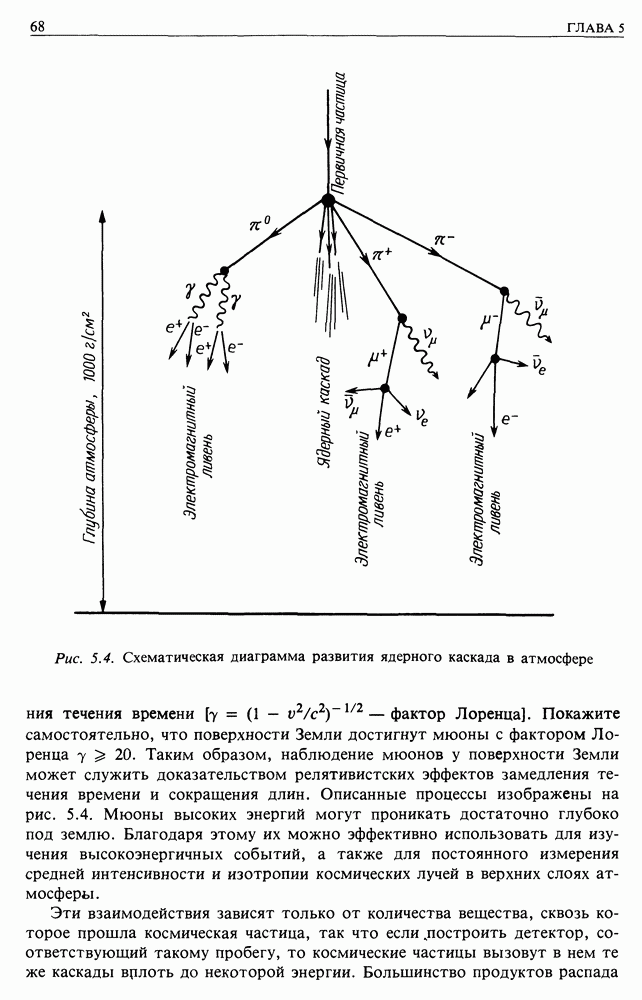
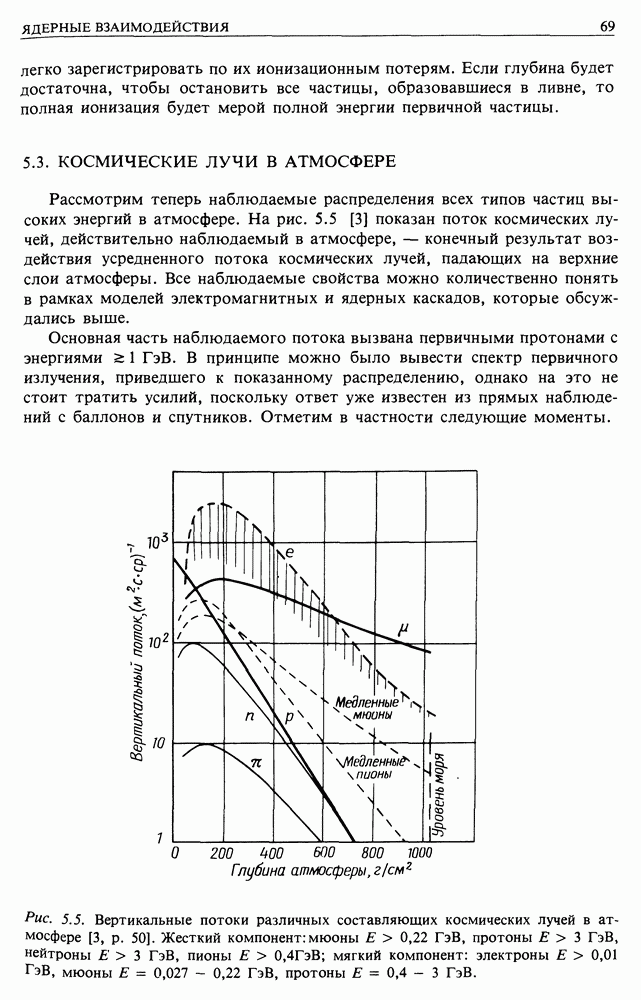
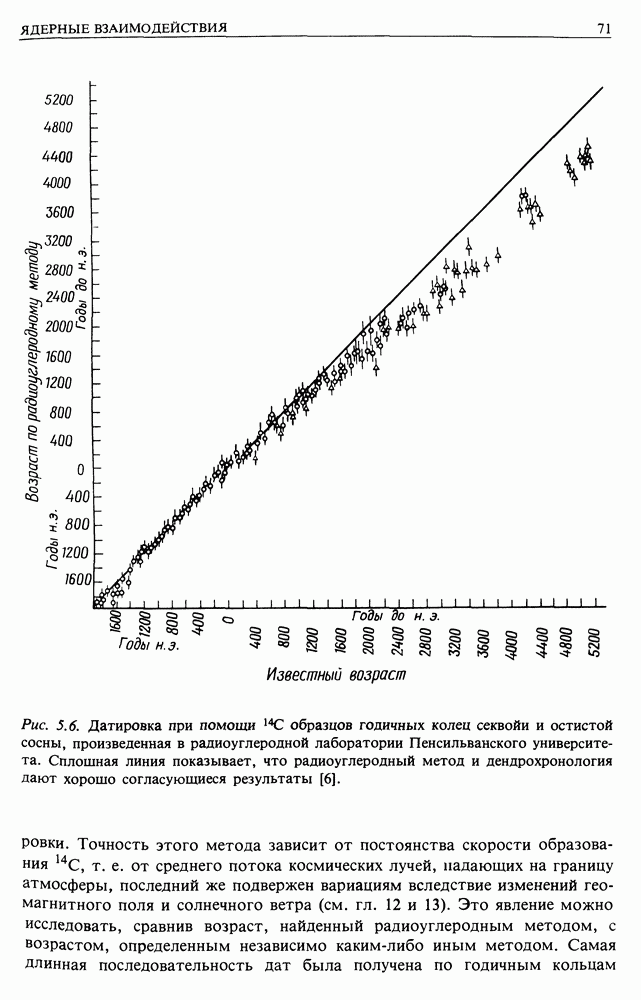
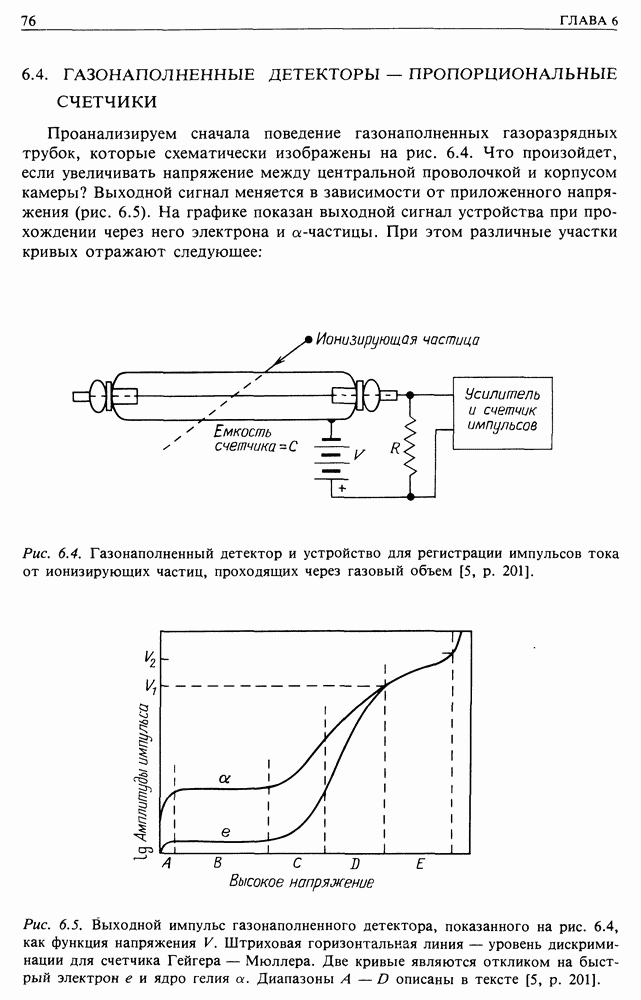
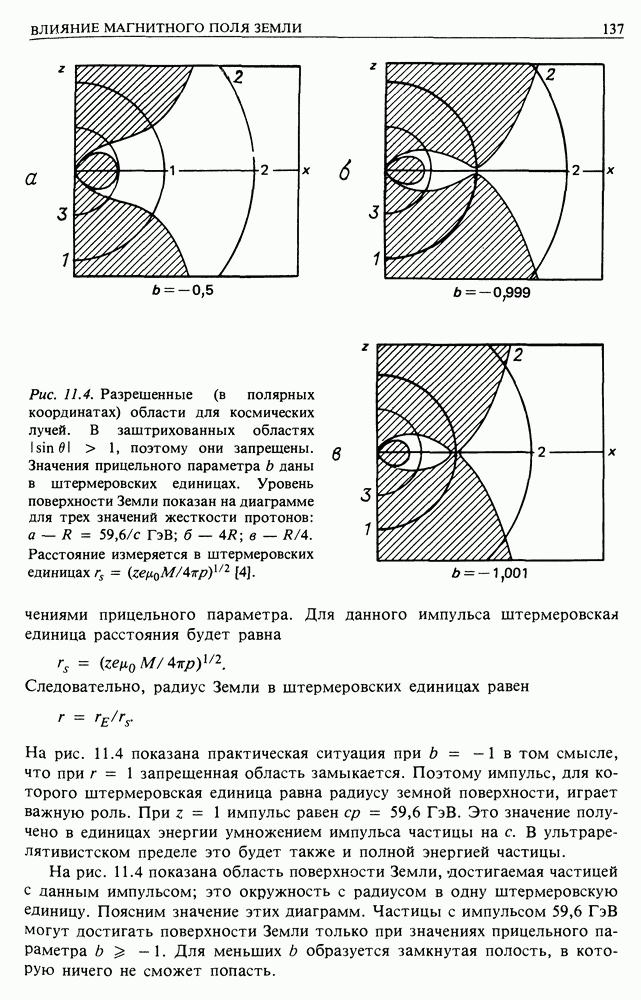
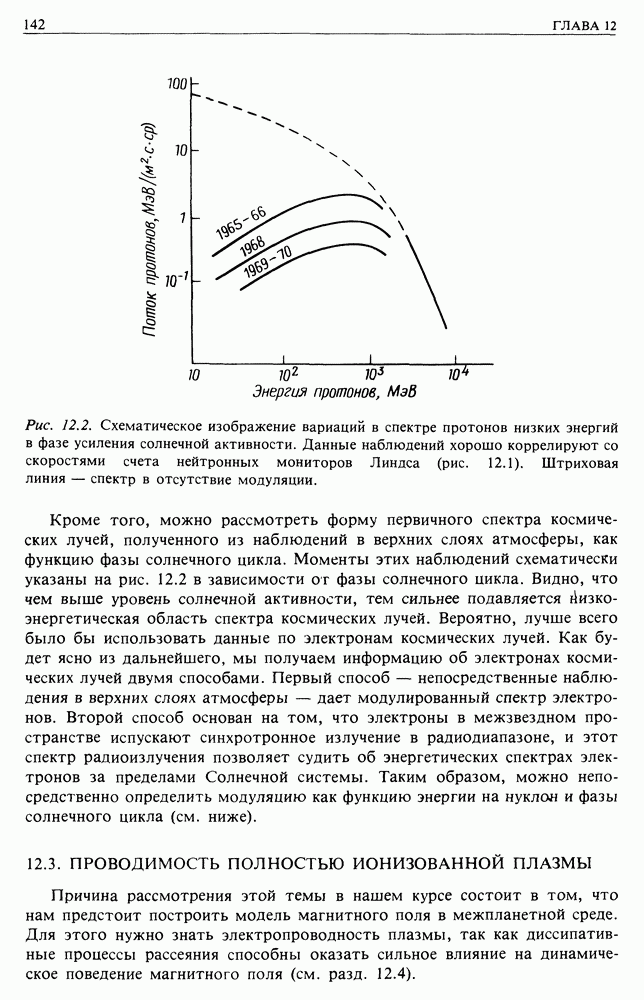
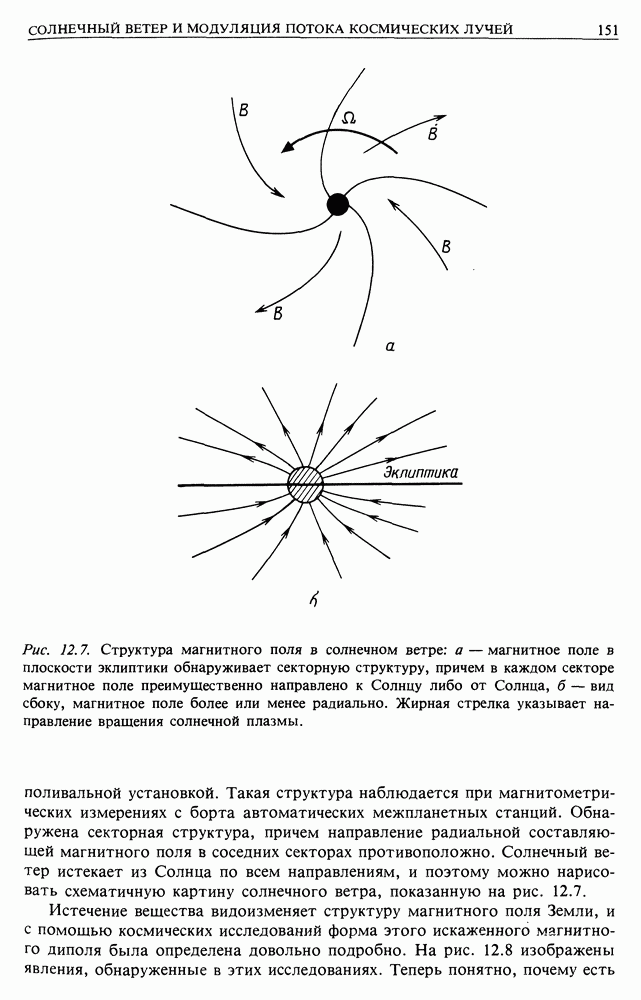
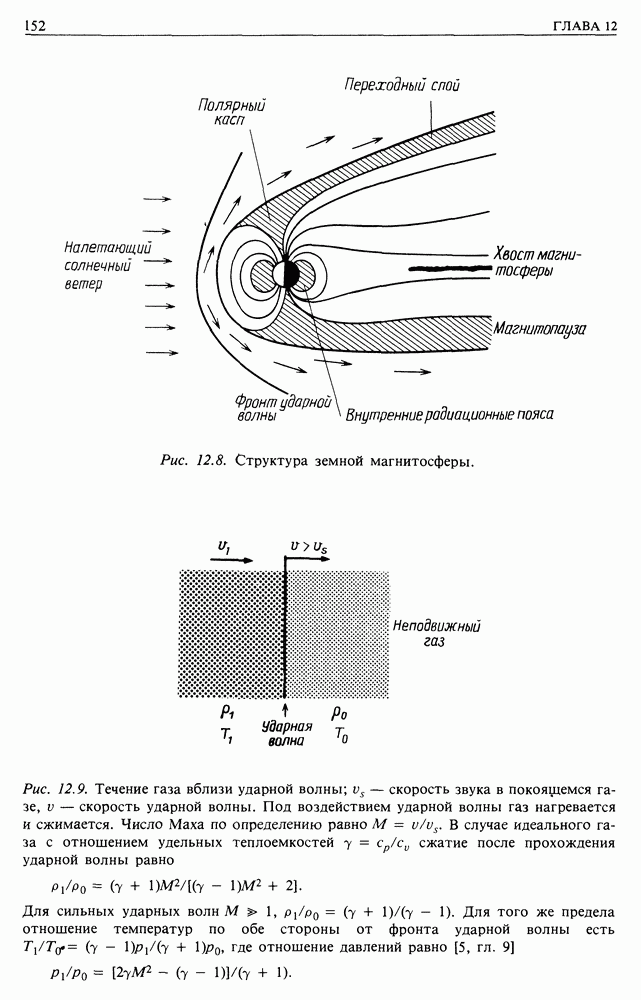
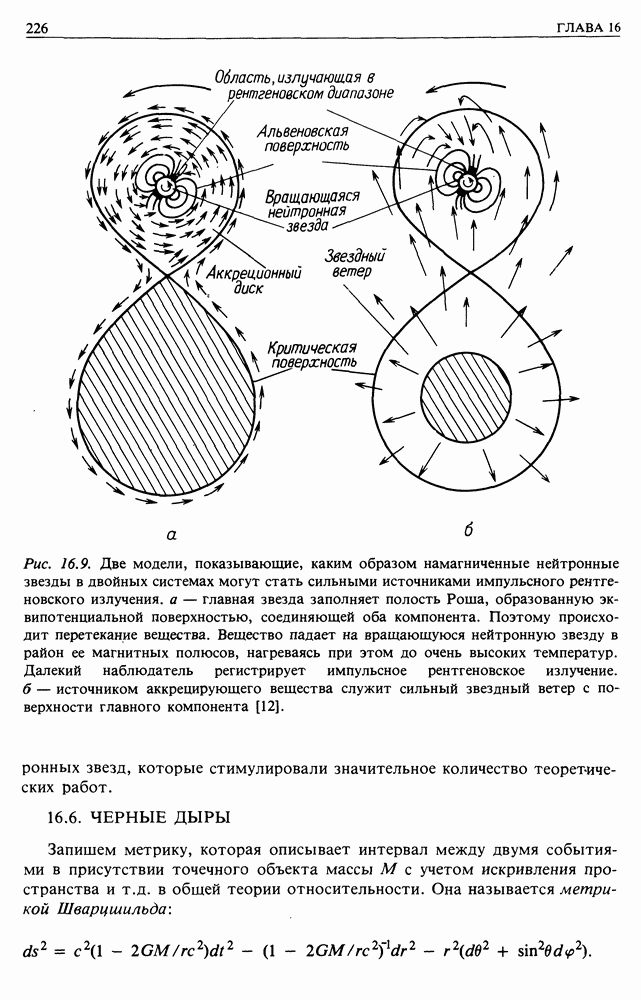
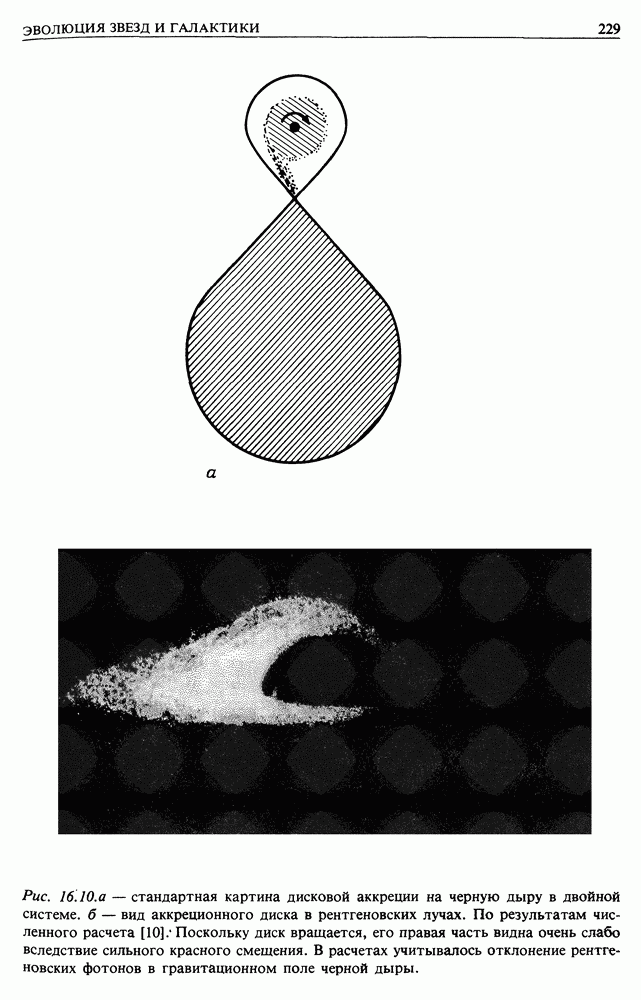
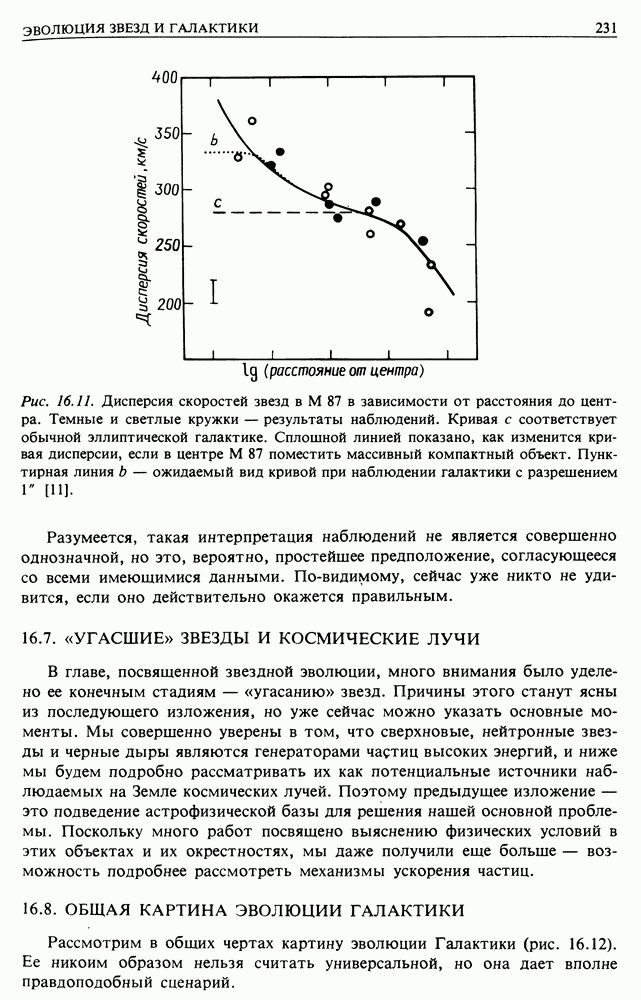
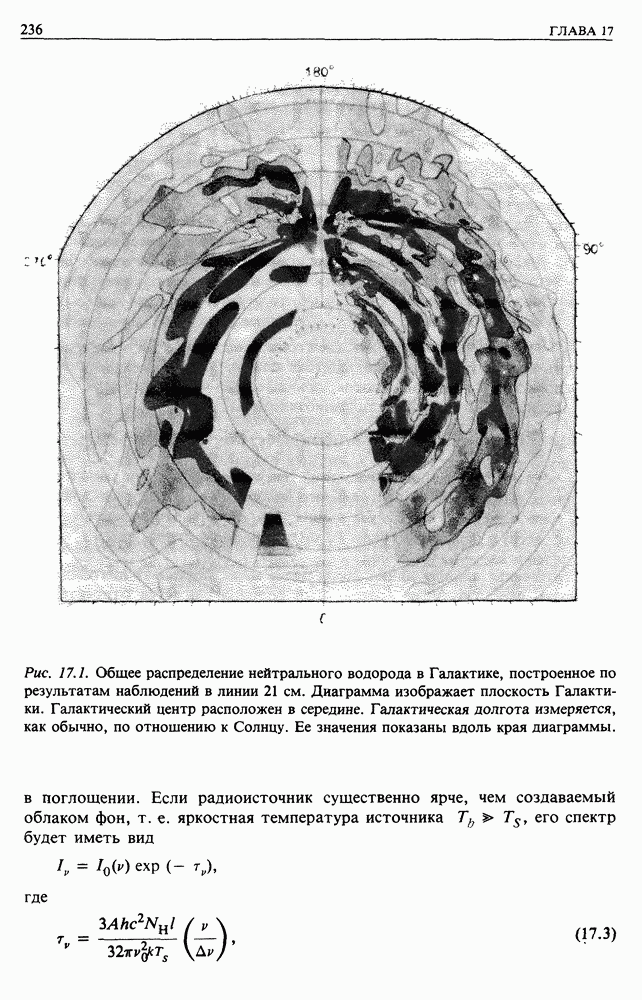
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
Рассмотрим влияние указанных механизмов потерь энергии на спектр электронов космических лучей при распространении от источников к Солнечной системе. Сразу ясно, что описывать распространение космических лучей в магнитных полях — дело сложное, и чтобы прийти хоть к какому-нибудь результату, необходимо сделать достаточно сильные приближения. Более подробные модели распространения космических лучей мы рассмотрим ниже  а сейчас воспользуемся, вероятно, простейшим способом описания динамики частиц — предположим, что они диффундируют в межзвездной среде. Обоснованием такого предположения служат многочисленные свидетельства нерегулярности структуры межпланетной среды, поэтому разумно считать, что и межзвездное магнитное поле является хаотическим. Тогда траектории частиц должны быть сильно запутанными, как в рассмотренном в разд. 13.3 случае межпланетных магнитных полей.
а сейчас воспользуемся, вероятно, простейшим способом описания динамики частиц — предположим, что они диффундируют в межзвездной среде. Обоснованием такого предположения служат многочисленные свидетельства нерегулярности структуры межпланетной среды, поэтому разумно считать, что и межзвездное магнитное поле является хаотическим. Тогда траектории частиц должны быть сильно запутанными, как в рассмотренном в разд. 13.3 случае межпланетных магнитных полей.
Для простоты и наглядности предположим, что динамика электронов описывается скалярным коэффициентом диффузии  Задача состоит в том, чтобы получить уравнение в частных производных для функции распределения частиц в различных точках межзвездной среды с учетом
Задача состоит в том, чтобы получить уравнение в частных производных для функции распределения частиц в различных точках межзвездной среды с учетом
непрерывных потерь энергии и постоянного притока новых частиц от источников. Оно называется диффузионным уравнением переноса для электронов космических лучей. Мы приведем два вывода; один «на пальцах», а второй более изящный.
19.2.1. Простой вывод. Пусть количество электронов, инжектируемых в единицу времени в элемент объема  равно
равно  Процесс приобретения и потерь энергии электроном будем описывать уравнением
Процесс приобретения и потерь энергии электроном будем описывать уравнением

так что если  положительно, то частица отдает энергию. Рассмотрим сначала обусловленное этим процессом изменение спектра электронов в отсутствие инжекции. В момент
положительно, то частица отдает энергию. Рассмотрим сначала обусловленное этим процессом изменение спектра электронов в отсутствие инжекции. В момент  число частиц в интервале энергий от
число частиц в интервале энергий от  до
до  равно
равно  В последующий момент
В последующий момент  эти частицы замещаются теми, энергия которых в момент
эти частицы замещаются теми, энергия которых в момент  попадала в интервал от
попадала в интервал от  до
до  где
где

Разлагая в ряд Тейлора по малым  и вычитая первое равенство из второго, получим
и вычитая первое равенство из второго, получим

 за время
за время  меняется на величину
меняется на величину

Совершая еще одно разложение в ряд Тейлора по малым  и подставляя
и подставляя  получим
получим

откуда получаем

Это уравнение описывает временную эволюцию спектра электронов, находящихся в элементарном объеме А К, в случае, когда изменяется только энергия каждого электрона. Теперь в это уравнение переноса можно ввести другие члены. Так, если происходит постоянная инжекция частиц со скоростью  в секунду на единицу объема, уравнение принимает вид
в секунду на единицу объема, уравнение принимает вид

В результате диффузии частицы входят в объем  и покидают его. Этот процесс определяется градиентом плотности частиц
и покидают его. Этот процесс определяется градиентом плотности частиц  Задаваясь скалярным коэффициентом диффузии
Задаваясь скалярным коэффициентом диффузии  можем обычным образом написать
можем обычным образом написать

Это уравнение называется диффузионным уравнением переноса релятивистских электронов.

Рис. 19.3. Фазовое пространство, используемое при выводе уравнения переноса космических лучей.
19.2.2. Элегантный вывод. Альтернативный более изящный вывод получится, если ввести фазовое пространство, в котором энергия откладывается по оси у, а пространственные координаты — по оси  Легко представить себе и более общий трехмерный случай (рис. 19.3). Обозначим потоки частиц через различные поверхности в фазовом пространстве через
Легко представить себе и более общий трехмерный случай (рис. 19.3). Обозначим потоки частиц через различные поверхности в фазовом пространстве через  В маленьком прямоугольнике частицы перемещаются вдоль оси х в результате диффузии, а вдоль оси у — когда теряют или приобретают энергию. Число частиц в бесконечно малом интервале
В маленьком прямоугольнике частицы перемещаются вдоль оси х в результате диффузии, а вдоль оси у — когда теряют или приобретают энергию. Число частиц в бесконечно малом интервале  с энергией от
с энергией от  до
до  равно
равно

Поэтому скорость изменения концентрации частиц в этой малой области фазового пространства равна

где  скорость образования электронов в единице объема фазового пространства. Разлагая в ряд Тейлора и опуская аргумент, получим
скорость образования электронов в единице объема фазового пространства. Разлагая в ряд Тейлора и опуская аргумент, получим

где  поток частиц в точке х с энергией
поток частиц в точке х с энергией  Он по определению равен
Он по определению равен

Отсюда получаем

Это уравнение можно очевидным образом обобщить:

Здесь  поток частиц через отрезок
поток частиц через отрезок  имеющих в момент
имеющих в момент  энергию
энергию  Если темп потерь энергии частицей равен
Если темп потерь энергии частицей равен  то число частиц, проходящих в единицу времени через поверхность
то число частиц, проходящих в единицу времени через поверхность  равно
равно

Отсюда получаем, как и выше  с формулой (19.21)],
с формулой (19.21)],

Заметим, что при необходимости в это уравнение можно ввести дополнительные члены. Если  описывает не электроны, а атомные ядра, то можно учесть рождение и уничтожение частиц в реакциях расщепления, радиоактивный распад, аннигиляцию и т.д.
описывает не электроны, а атомные ядра, то можно учесть рождение и уничтожение частиц в реакциях расщепления, радиоактивный распад, аннигиляцию и т.д.
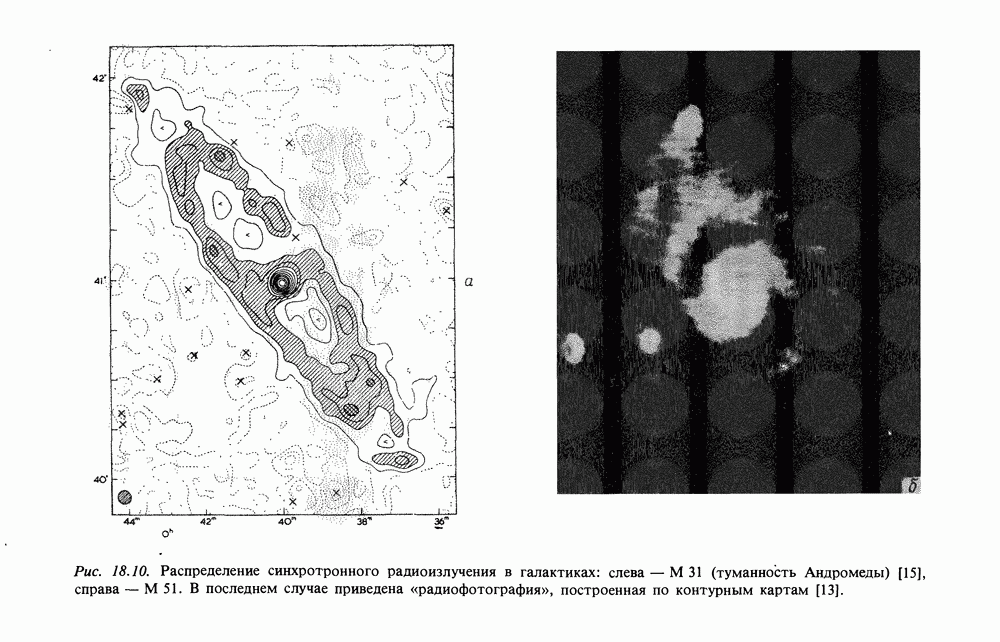
19.2.3. Решения уравнения диффузии электронов космических лучей. Можно решить уравнения переноса при конкретных распределениях источников и граничных условиях. Это делается, например, в классической монографии Гинзбурга и Сыроватского «Происхождение космических лучей» [4] и в последующих статьях Гинзбурга, Догеля и Сыроватского (см., например, [11]). Однако многие важнейшие результаты можно получить, рассмотрев несколько частных стационарных решений.
Сначала предположим, что источники электронов однородно заполняют все пространство, причем спектр инжектируемых электронов степенной  т.е.
т.е.  Тогда диффузия несущественна и уравнение переноса сводится к уравнению
Тогда диффузия несущественна и уравнение переноса сводится к уравнению

Предполагая, что  при
при  получим, выполнив интегрирование,
получим, выполнив интегрирование,

Выпишем теперь выражение для  в условиях межзвездной среды:
в условиях межзвездной среды:

Эта формула позволяет выявить, как постоянные потери энергии действуют на первоначальный спектр электронов космических лучей. Таким образом,

Рис. 19.4. Решение стационарного уравнения переноса в случае, когда спектр впрыскиваемых электронов степенной,  а потери энергии описываются соотношением
а потери энергии описываются соотношением 
если преобладают ионизационные потери, то  т.е. спектр становится более плоским;
т.е. спектр становится более плоским;
если преобладают тормозные или адиабатические потери, то  т.е. спектр не меняется;
т.е. спектр не меняется;
если преобладают синхротронные или комптоновские потери, то  т.е. спектр становится круче.
т.е. спектр становится круче.
Равновесные спектры должны получаться также всякий раз, когда постоянная инжекция частиц продолжается дольше, чем тормозится отдельный электрон. Например, если непрерывно в течение времени  впрыскивать электроны, а наиболее существенными являются синхротронные потери, то спектр электронов в системе будет различным для энергий, больших и меньших
впрыскивать электроны, а наиболее существенными являются синхротронные потери, то спектр электронов в системе будет различным для энергий, больших и меньших  энергии электронов, время жизни которых равно
энергии электронов, время жизни которых равно  Низкоэнергичные электроны не успевают отдать заметную долю своей энергии, поэтому их спектр совпадает с начальным,
Низкоэнергичные электроны не успевают отдать заметную долю своей энергии, поэтому их спектр совпадает с начальным,  При энергиях, превышающих, время торможения меньше поэтому мы видим только те частицы, которые были впрыснуты в систему в течение времени жизни частицы
При энергиях, превышающих, время торможения меньше поэтому мы видим только те частицы, которые были впрыснуты в систему в течение времени жизни частицы  Поэтому спектр получается круче:
Поэтому спектр получается круче:  в соответствии с решением стационарного уравнения переноса.
в соответствии с решением стационарного уравнения переноса.
Можно показать, что если потери имеют вид  а частицы инжектируются равномерно во всем пространстве с тем же, что и ранее, спектром
а частицы инжектируются равномерно во всем пространстве с тем же, что и ранее, спектром  то по прошествии времени
то по прошествии времени  спектр примет вид
спектр примет вид

Этот спектр показан на рис. 19.4.
19.2.4. Интерпретация наблюдаемого спектра электронов космических лучей. Применим эти результаты к спектру электронов в Галактике. Мы наблюдаем степенной спектр с изломом вблизи  Что можно сказать о распространении электронов и их начальном спектре? Вопрос заключается в том, сколько времени релятивистские электроны находятся в Галактике. Можно использовать два подхода: считать электроны молодыми,
Что можно сказать о распространении электронов и их начальном спектре? Вопрос заключается в том, сколько времени релятивистские электроны находятся в Галактике. Можно использовать два подхода: считать электроны молодыми,
тогда наблюдаемый спектр подобен начальному, или, наоборот, предположить, что электроны старые, а их спектр сформировался в результате действия различных механизмов торможения.
Молодые электроны космических лучей. В этом случае предполагается, что электроны впрыскиваются со спектром

Тогда отсутствие каких-либо наблюдаемых отклонений от степенной зависимости означает, что даже самые энергичные электроны не испытали заметных синхротронных потерь. Отсюда можно получить ограничение на время, в течение которого они двигались сквозь реликтовое излучение и галактическое магнитное поле.
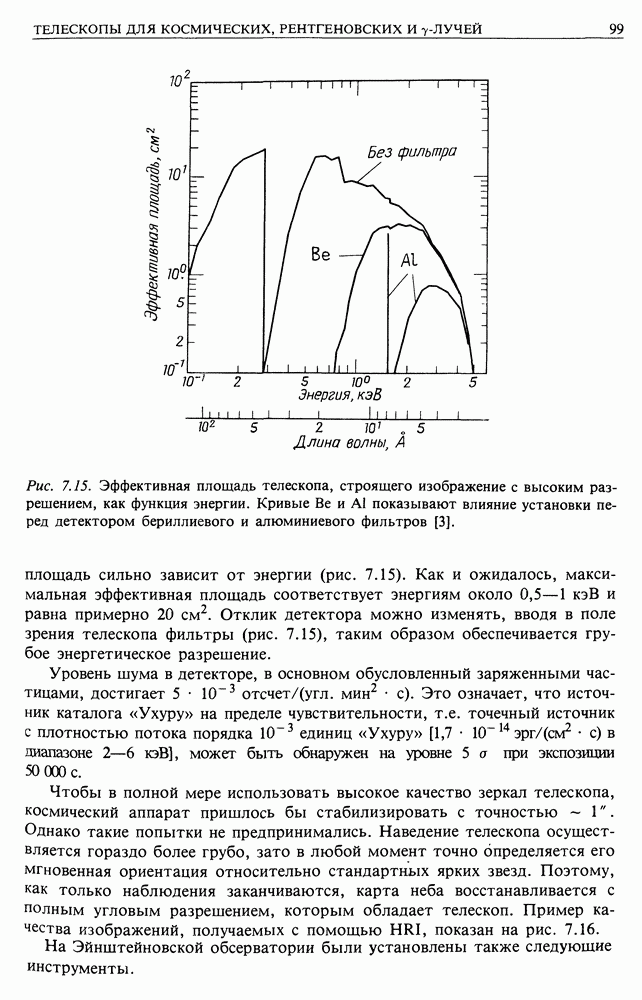
Формулу для времени жизни ультрарелятивистского электрона при наличии как синхротронных, так и комптоновских потерь можно записать следующим образом:

Здесь магнитное поле нормировано на величину  а плотность энергии излучения — на плотность энергии реликтового излучения
а плотность энергии излучения — на плотность энергии реликтового излучения  Для минимального значения
Для минимального значения  равного
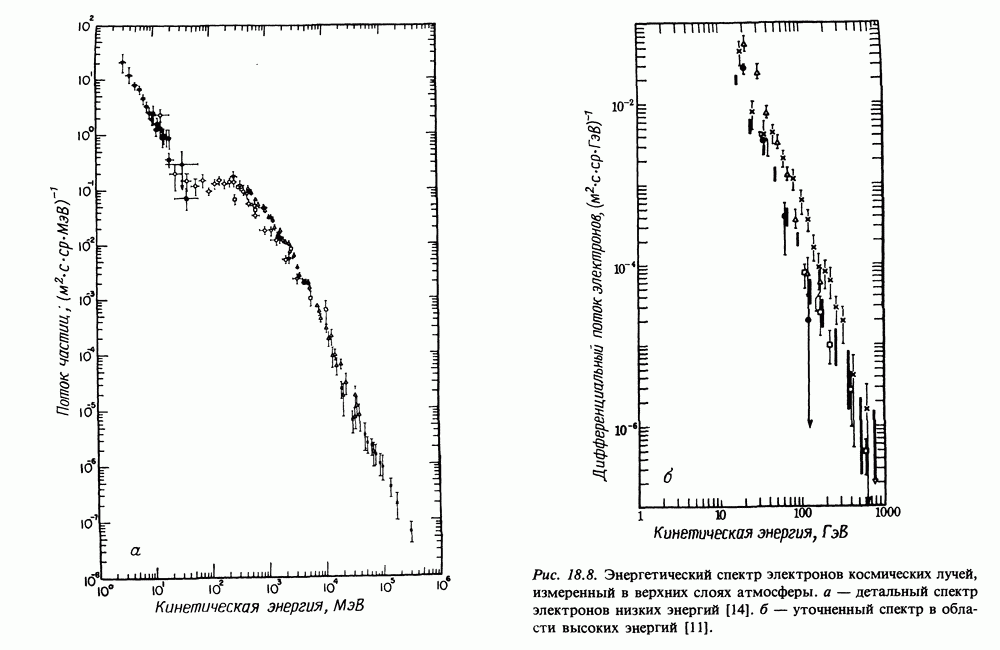
равного  (см. рис. 18.8), и
(см. рис. 18.8), и  получим, что частицы должны находится в магнитном поле Галактики меньше, чем примерно
получим, что частицы должны находится в магнитном поле Галактики меньше, чем примерно  лет. Это очень сильное ограничение.
лет. Это очень сильное ограничение.
Чтобы понять, насколько эта модель реальна, необходимо выяснить, может ли она объяснить излом в спектре электронов вблизи  В соответствии с предыдущим анализом, одна возможность состоит в том, что уплощение спектра ниже
В соответствии с предыдущим анализом, одна возможность состоит в том, что уплощение спектра ниже  возникло в результате действия ионизационных потерь. Чтобы этот процесс привел к заметным искажениям спектра, необходимо время порядка
возникло в результате действия ионизационных потерь. Чтобы этот процесс привел к заметным искажениям спектра, необходимо время порядка  лет (см. п. 19.1.1). Таким образом, электроны должны были бы двигаться в среде с концентрацией примерно
лет (см. п. 19.1.1). Таким образом, электроны должны были бы двигаться в среде с концентрацией примерно  что существенно выше плотности межзвездной среды. Другая сложность состоит в том, что электроны должны пройти толщу вещества
что существенно выше плотности межзвездной среды. Другая сложность состоит в том, что электроны должны пройти толщу вещества  но, как будет показано в п. 20.2.2, протоны и ядра такой же жесткости не могут пройти через такое количество вещества. Таким образом, если верна модель молодых космических лучей, то излом в спектре не мог возникнуть вследствие потерь энергии при движении в межзвездной среде, а должен был существовать изначально.
но, как будет показано в п. 20.2.2, протоны и ядра такой же жесткости не могут пройти через такое количество вещества. Таким образом, если верна модель молодых космических лучей, то излом в спектре не мог возникнуть вследствие потерь энергии при движении в межзвездной среде, а должен был существовать изначально.
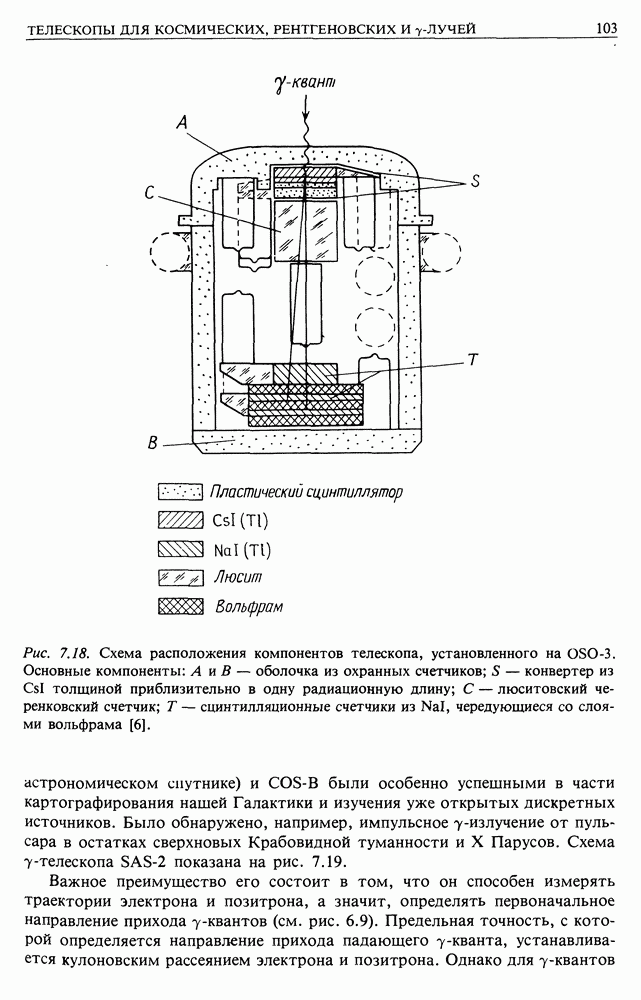
Старые электроны космических лучей. Можно предположить, что синхротронные и комптоновские процессы столь существенны, что излом, показанный на рис. 19.4, приходится на энергию  (рис. 18.8). В этом случае, принимая
(рис. 18.8). В этом случае, принимая  получим
получим  лет. Если учесть оптическое излучение Галактики, плотность энергии которого равна —
лет. Если учесть оптическое излучение Галактики, плотность энергии которого равна —  то
то  окажется меньше, около
окажется меньше, около  лет, т.е. электроны космических лучей должны быть старыми. Тогда спектр инжектируемых электронов должен иметь вид
лет, т.е. электроны космических лучей должны быть старыми. Тогда спектр инжектируемых электронов должен иметь вид
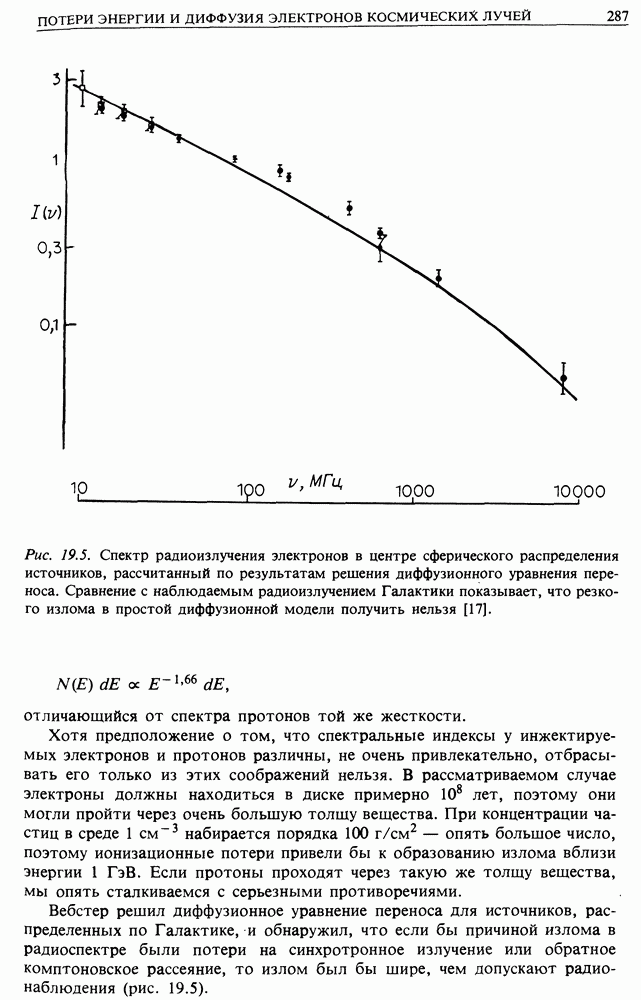
Рис. 19.5. (см. скан) Спектр радиоизлучения электронов в центре сферического распределения источников, рассчитанный по результатам решения диффузионного уравнения переноса. Сравнение с наблюдаемым радиоизлучением Галактики показывает, что резкого излома в простой диффузионной модели получить нельзя [17].

отличающийся от спектра протонов той же жесткости.
Хотя предположение о том, что спектральные индексы у инжектируемых электронов и протонов различны, не очень привлекательно, отбрасывать его только из этих соображений нельзя. В рассматриваемом случае электроны должны находиться в диске примерно 108 лет, поэтому они могли пройти через очень большую толщу вещества. При концентрации частиц в среде  набирается порядка
набирается порядка  опять большое число, поэтому ионизационные потери привели бы к образованию излома вблизи энергии
опять большое число, поэтому ионизационные потери привели бы к образованию излома вблизи энергии  Если протоны проходят через такую же толщу вещества, мы опять сталкиваемся с серьезными противоречиями.
Если протоны проходят через такую же толщу вещества, мы опять сталкиваемся с серьезными противоречиями.
Вебстер решил диффузионное уравнение переноса для источников, распределенных по Галактике, и обнаружил, что если бы причиной излома в радиоспектре были потери на синхротронное излучение или обратное комптоновское рассеяние, то излом был бы шире, чем допускают радионаблюдения (рис. 19.5).
Эти аргументы свидетельствуют в пользу модели молодых электронов. Заметим, что удовлетворительное объяснение излома в спектре электронов вблизи  отсутствует. Никакого убедительного объяснения этого факта модели распространения космических лучей дать не могут. По-видимому, излом следует приписать исходному спектру инжектируемых частиц. Это накладывает, серьезные ограничения на возможные механизмы ускорения.
отсутствует. Никакого убедительного объяснения этого факта модели распространения космических лучей дать не могут. По-видимому, излом следует приписать исходному спектру инжектируемых частиц. Это накладывает, серьезные ограничения на возможные механизмы ускорения.
Проведенное обсуждение весьма характерно для астрофизики. Здесь всегда существует широкий спектр возможностей и задача состоит в том, чтобы отобрать существенные данные, основываясь на которых можно исключить конкретные модели.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
- 4.4. ОБРАЗОВАНИЕ ПАР
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
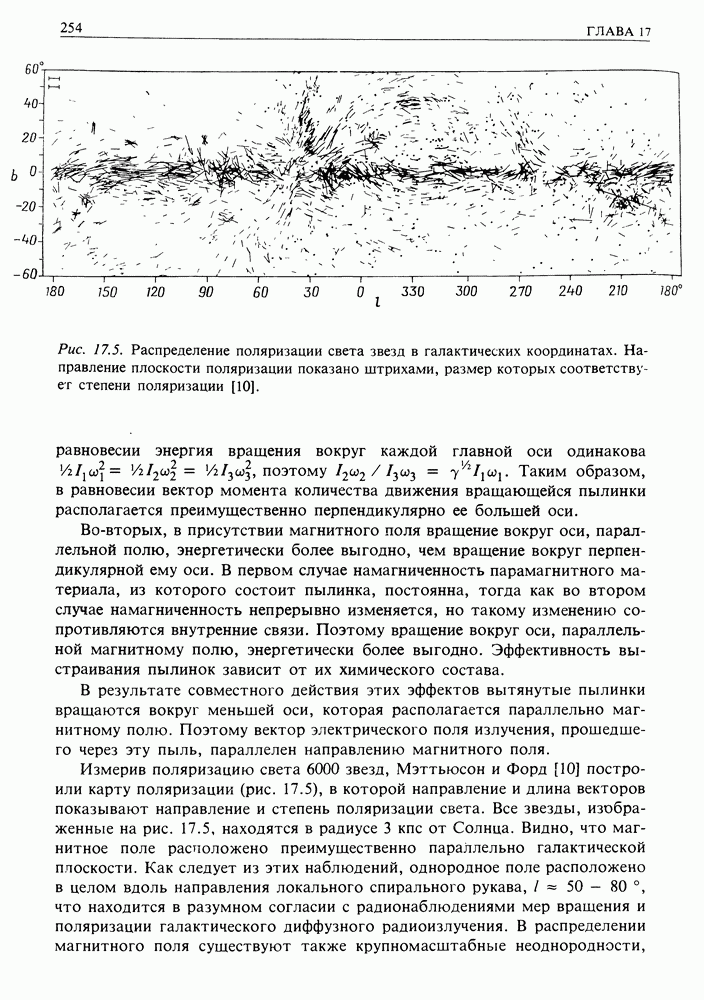
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
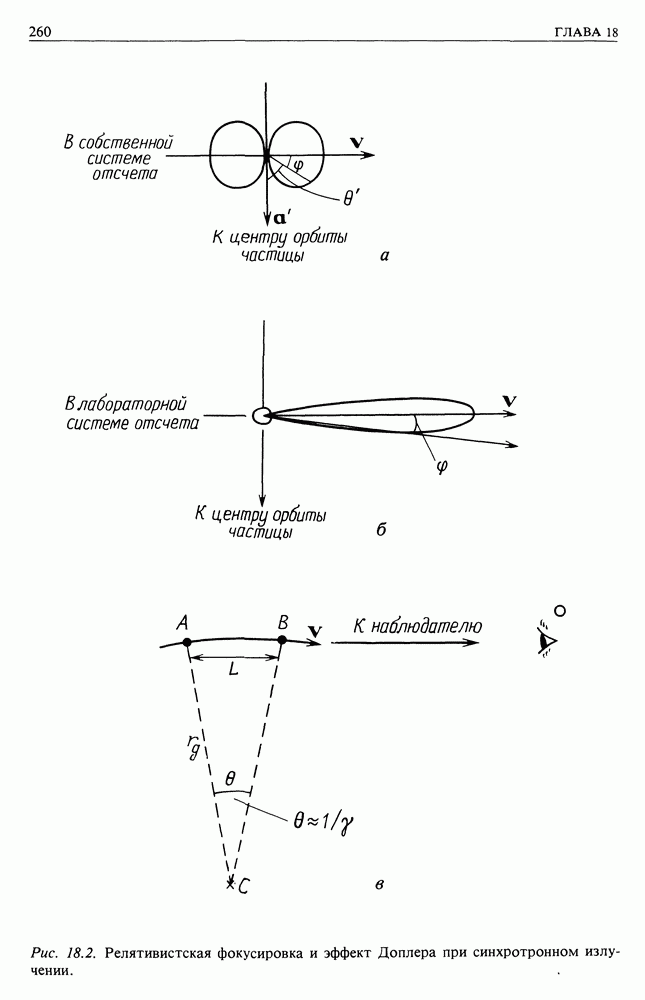
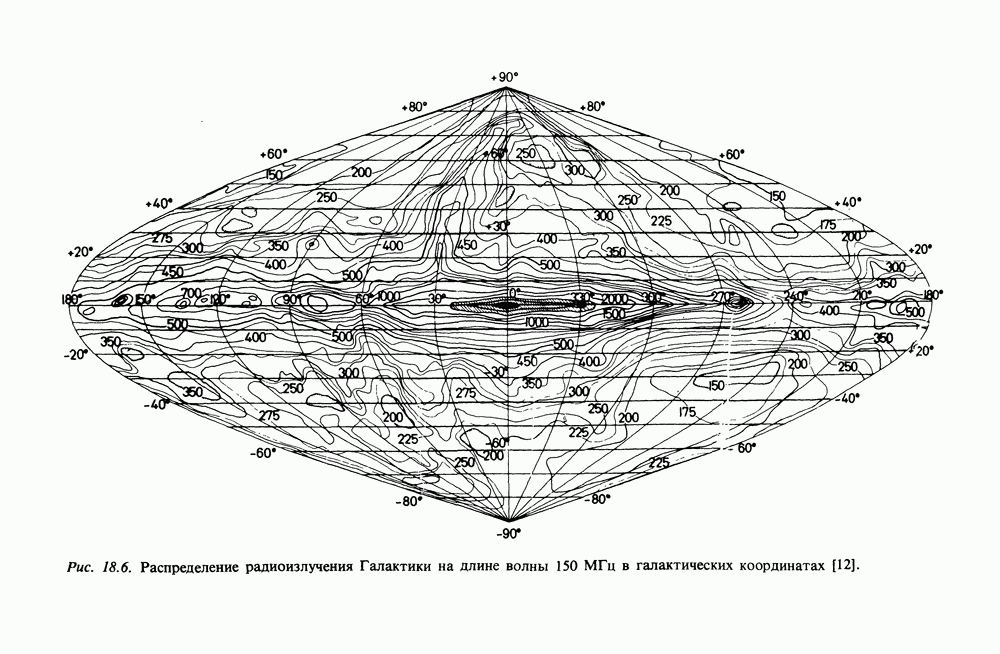
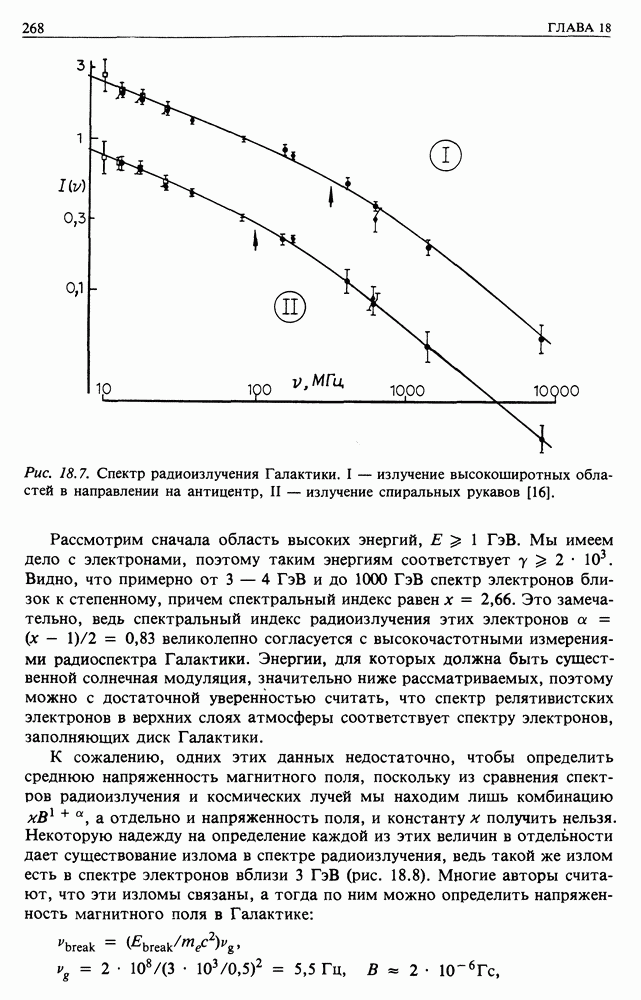
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
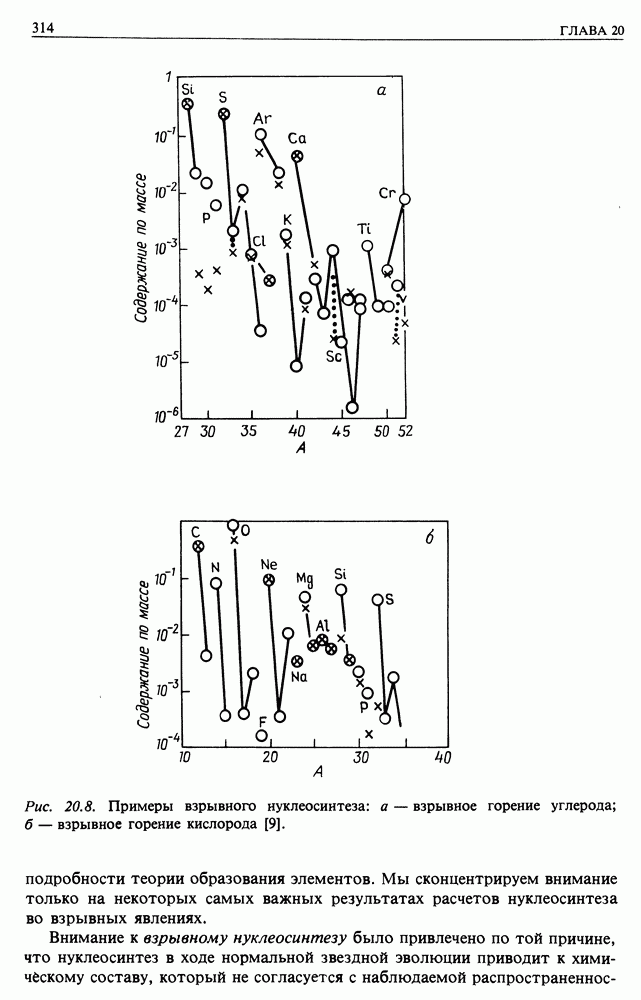
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
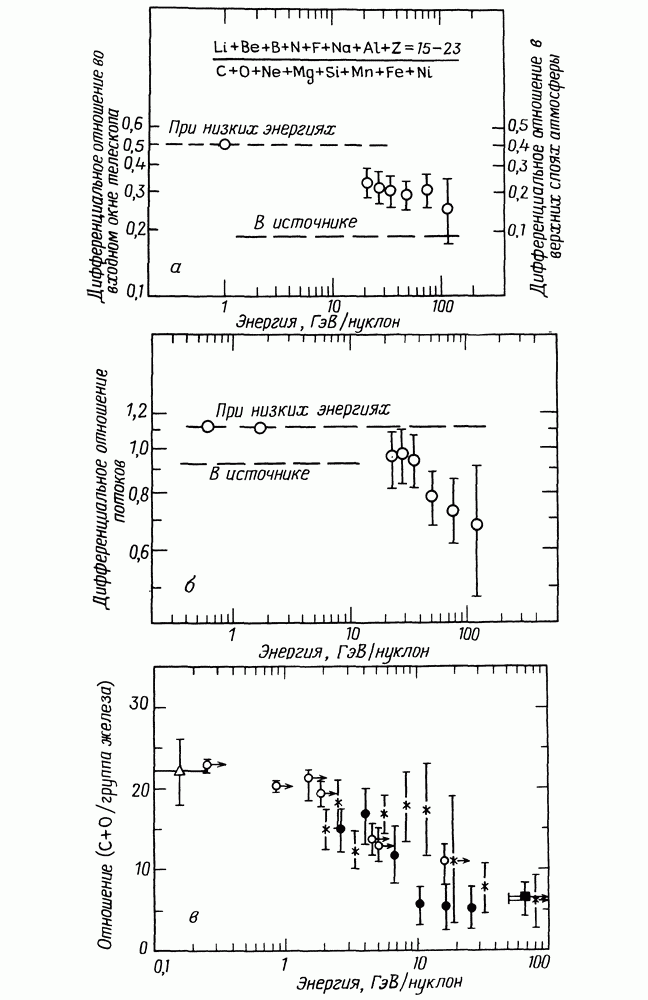
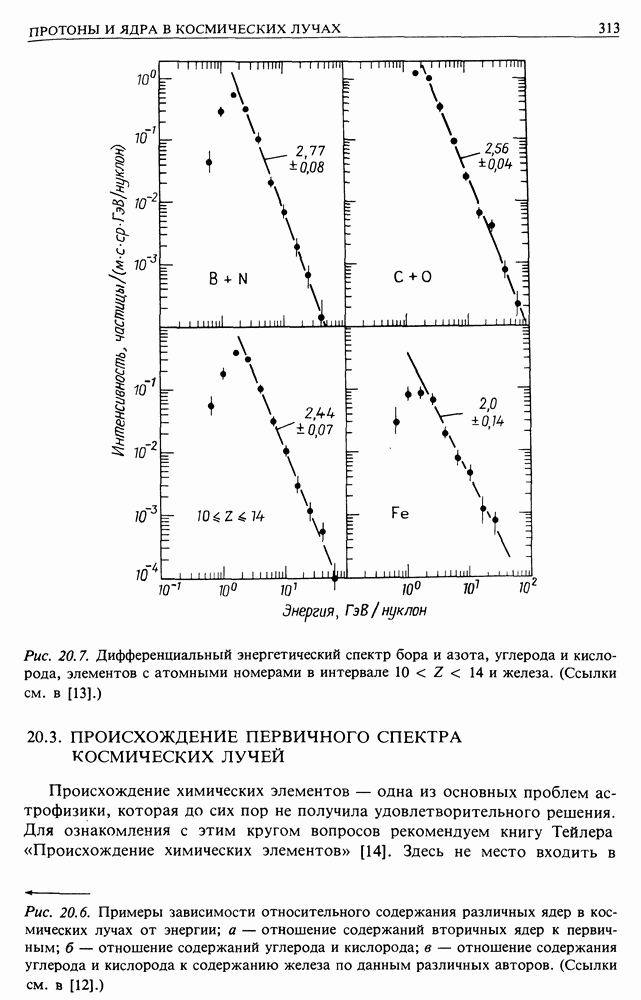
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
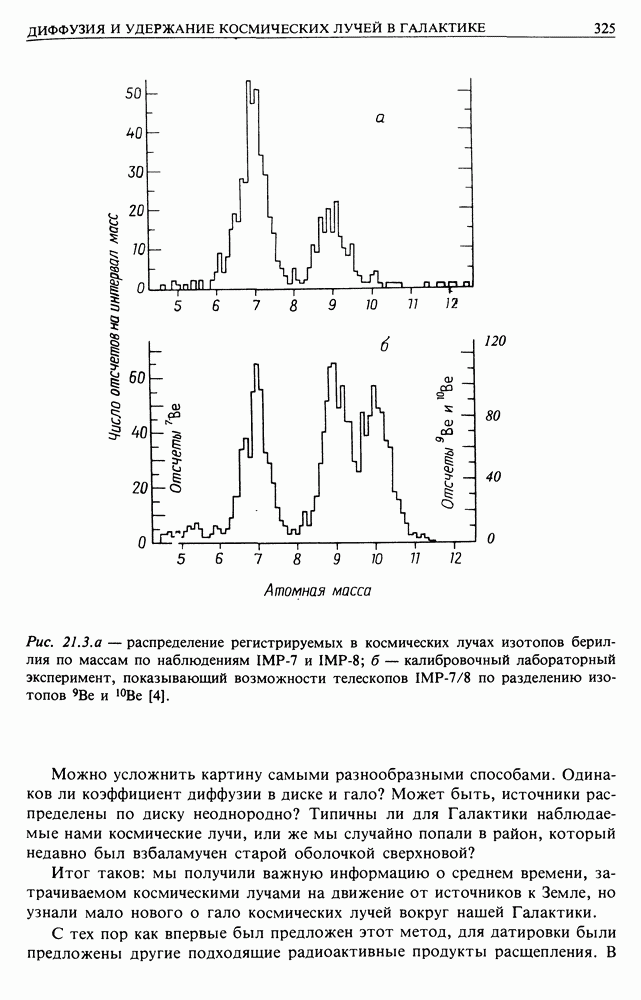
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
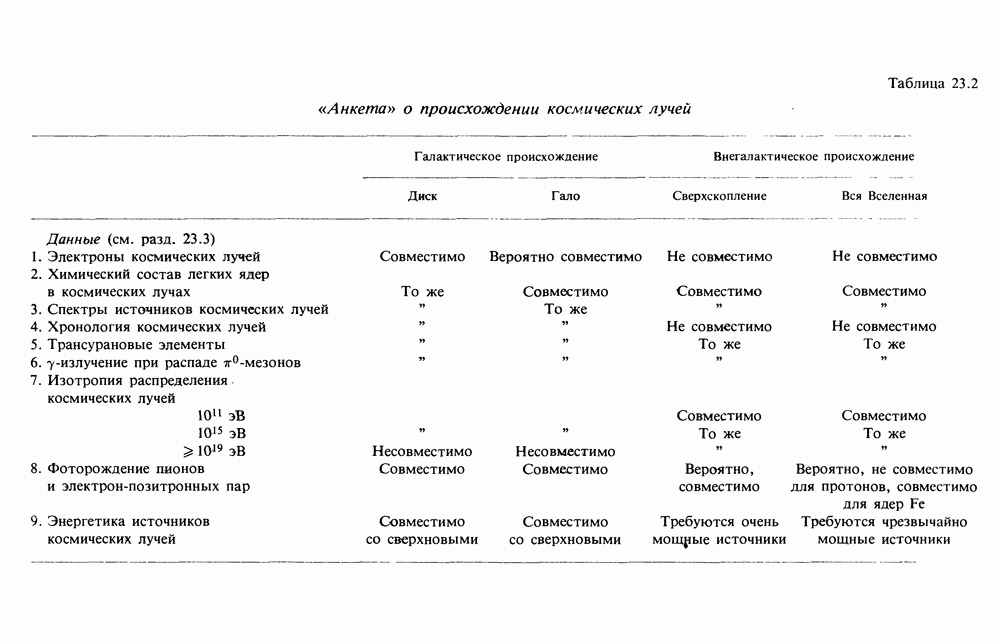
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
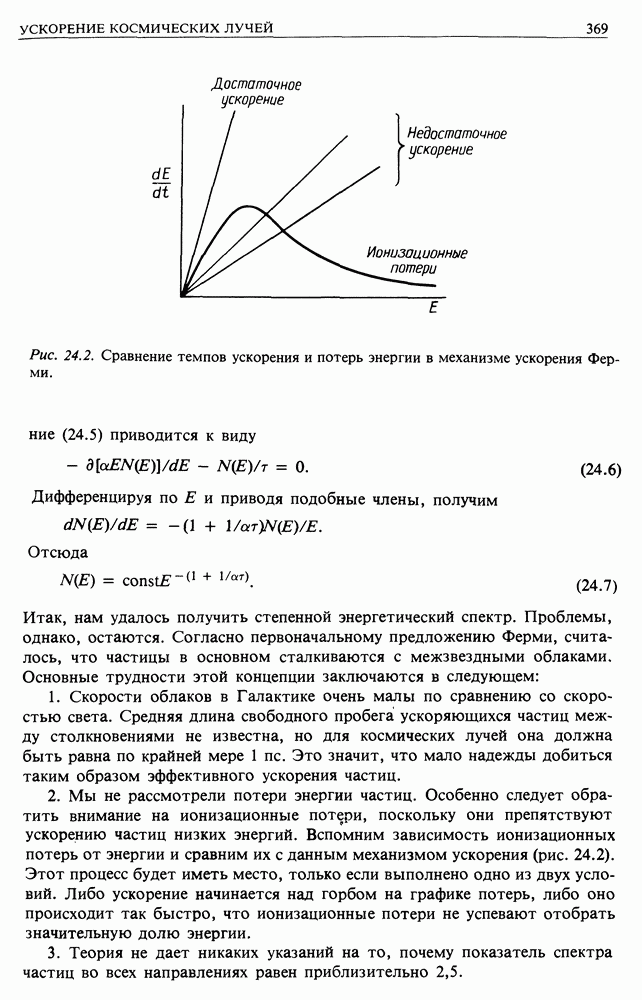
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ