| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
Распространение описанной процедуры на релятивистскую область осуществляется очень просто и совершенно строго. Хотя космические частицы и релятивистские, на электрон воздействуют нерелятивистские силы. Определим, как выглядит поле, создаваемое релятивистской частицей, с точки зрения неподвижного наблюдателя. Затем, проверив уравнения с точки зрения симметрии, будем двигаться дальше.
2.3.1. Релятивистские преобразования кулоновского поля. если вы можете проделать это в рамках теории относительности, то сразу переходите к следующему разделу.
Пусть космическая частица движется вдоль оси  а электрон находится на оси
а электрон находится на оси  Выберем начало отсчета таким образом, чтобы при
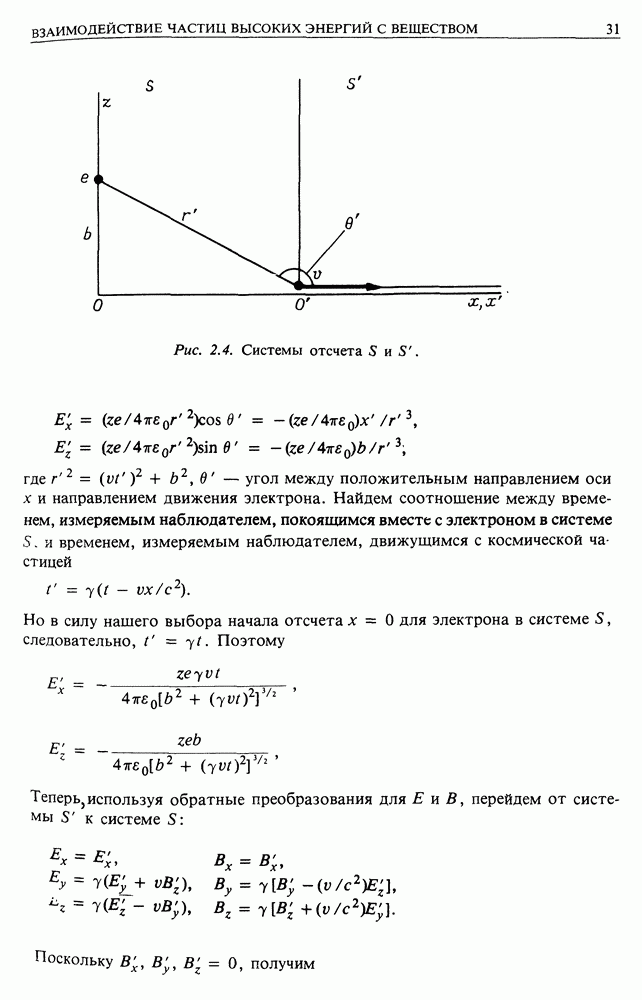
Выберем начало отсчета таким образом, чтобы при  космическая частица находилась на минимальном расстоянии от электрона (рис. 2.4). По истечении времени
космическая частица находилась на минимальном расстоянии от электрона (рис. 2.4). По истечении времени  космическая частица будет находиться в точке х в системе
космическая частица будет находиться в точке х в системе  . В системе
. В системе  координаты электрона равны
координаты электрона равны  . В системе
. В системе  электрическое поле космической частицы
электрическое поле космической частицы  осесимметрично относительно О и, следовательно, в точке нахождения электрона
осесимметрично относительно О и, следовательно, в точке нахождения электрона

Рис. 2.4. Системы отсчета  .
.

где  угол между положительным направлением оси х и направлением движения электрона. Найдем соотношение между временем, измеряемым наблюдателем, покоящимся вместе с электроном в системе
угол между положительным направлением оси х и направлением движения электрона. Найдем соотношение между временем, измеряемым наблюдателем, покоящимся вместе с электроном в системе  и временем, измеряемым наблюдателем, движущимся с космической частицей
и временем, измеряемым наблюдателем, движущимся с космической частицей

Но в силу нашего выбора начала отсчета  для электрона в системе
для электрона в системе  следовательно,
следовательно,  Поэтому
Поэтому

Теперь, используя обратные преобразования для  и В, перейдем от системы
и В, перейдем от системы  к системе
к системе 

Поскольку  получим
получим

(кликните для просмотра скана)

Отметим, что

2.3.2. Релятивистские ионизационные потери. Следствия уравнений (2.12) для электрических и магнитных полей, связанных с релятивистски движущимся зарядом, очень важны и полезны. При  космическая частица находится на минимальном расстоянии от электрона. При
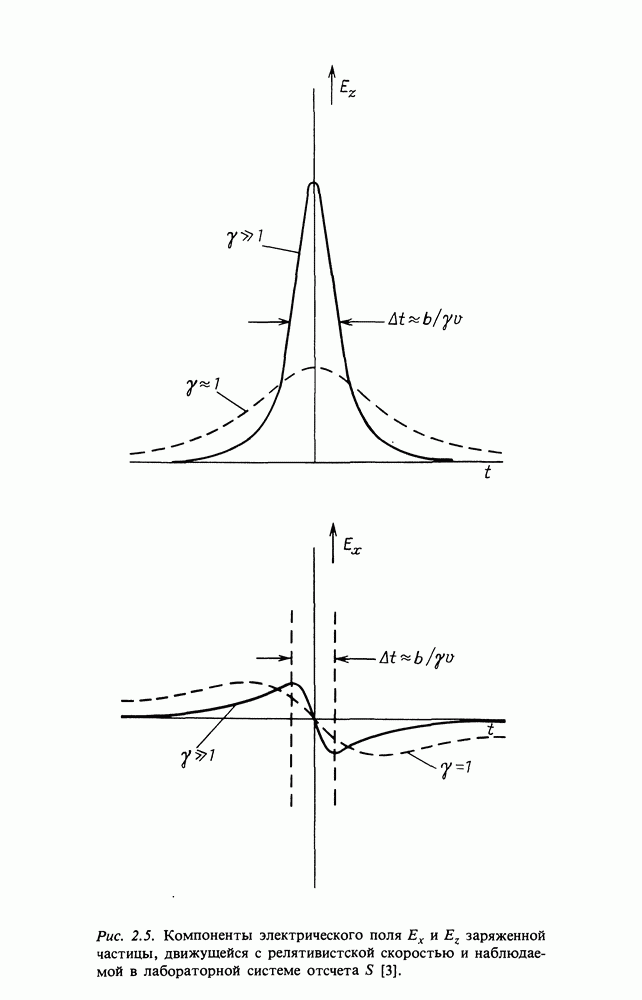
космическая частица находится на минимальном расстоянии от электрона. При  решение принимает обычную форму закона Кулона, как это и должно быть; когда частица релятивистская, поле электрона значительно усиливается, но на существенно более короткое время (рис. 2.5). Составляющая
решение принимает обычную форму закона Кулона, как это и должно быть; когда частица релятивистская, поле электрона значительно усиливается, но на существенно более короткое время (рис. 2.5). Составляющая  при
при  в релятивистском случае увеличивается в у раз, а ширина импульса
в релятивистском случае увеличивается в у раз, а ширина импульса  уменьшается в у раз. Компонент
уменьшается в у раз. Компонент  В ультрарелятивистском пределе
В ультрарелятивистском пределе  импульс похож на электромагнитную волну с
импульс похож на электромагнитную волну с  распространяющуюся в направлении
распространяющуюся в направлении 
Вследствие симметрии составляющей поля  электрон и в этом случае не получает от нее никакого импульса. Составляющая
электрон и в этом случае не получает от нее никакого импульса. Составляющая  дает
дает

Замена переменных  дает
дает

как и в уравнении (2.1). Этот результат, конечно, не должен быть для нас неожиданностью, поскольку уже из грубых прикидок следовало, что важную роль играет произведение  на время столкновения, причем один из сомножителей увеличивается в у раз, а другой уменьшается в у раз.
на время столкновения, причем один из сомножителей увеличивается в у раз, а другой уменьшается в у раз.
Интегрирование по прицельному параметру выполняется так же, как в нерелятивистском случае, поэтому нужно лишь определить, какие значения  поставить под знак логарифма. Правильное выражение можно найти, либо выяснив, как меняются значения
поставить под знак логарифма. Правильное выражение можно найти, либо выяснив, как меняются значения  при переходе к релятивистскому случаю, либо обобщив выражение
при переходе к релятивистскому случаю, либо обобщив выражение  на случай релятивистской космической частицы.
на случай релятивистской космической частицы.
В первом подходе Ьтах увеличивается в у раз, потому что длительность импульса во столько же раз сокращается. При определении  следует Учесть, что поперечный импульс электрона больше в у раз и поэтому
следует Учесть, что поперечный импульс электрона больше в у раз и поэтому
вследствие принципа неопределенности  Таким образом, можно принять, что логарифмический член имеет форму
Таким образом, можно принять, что логарифмический член имеет форму 
Второй подход — это полезное упражнение по теории относительности.
2.3.3. РЕЛЯТИВИСТСКИЕ СТОЛКНОВЕНИЯ МЕЖДУ КОСМИЧЕСКОЙ ЧАСТИЦЕЙ И СТАЦИОНАРНЫМ ЭЛЕКТРОНОМ. Используем обозначение Риндлера для записи  -вектора импульса космической частицы и электрона в лабораторной системе отсчета:
-вектора импульса космической частицы и электрона в лабораторной системе отсчета:

Компоненты  -векторов записаны таким образом, чтобы их преобразования осуществлялись по типу
-векторов записаны таким образом, чтобы их преобразования осуществлялись по типу  Затем мы преобразуем компоненты обоих векторов с тем, чтобы записать их в системе отсчета, движущейся со скоростью
Затем мы преобразуем компоненты обоих векторов с тем, чтобы записать их в системе отсчета, движущейся со скоростью  для этой системы
для этой системы  Удобно выбрать
Удобно выбрать  параллельно
параллельно  Следовательно,
Следовательно,

В системе центра инерции  и поэтому
и поэтому

В этой системе отсчета релятивистский  -импульс электрона равен
-импульс электрона равен  Приобретенная электроном энергия будет максимальна в том случае, если его направление после столкновения в точности противоположно первоначальному направлению движения. Поскольку столкновение упругое, импульс равен
Приобретенная электроном энергия будет максимальна в том случае, если его направление после столкновения в точности противоположно первоначальному направлению движения. Поскольку столкновение упругое, импульс равен  а полная энергия сохраняется. Теперь преобразуем этот импульс обратно в лабораторную систему отсчета:
а полная энергия сохраняется. Теперь преобразуем этот импульс обратно в лабораторную систему отсчета:  -импульс в системе
-импульс в системе  равен
равен  . Теперь найдем «временной» компонент
. Теперь найдем «временной» компонент  -вектора импульса в соответствии с обратным преобразованием Лоренца:
-вектора импульса в соответствии с обратным преобразованием Лоренца:

Следовательно, полная энергия в системе  равна
равна

Соответственно максимальная кинетическая энергия электрона есть

Теперь те  и поэтому
и поэтому

В ультрарелятивистском пределе максимальная энергия, переданная электрону, равна

Используя это выражение для  придем к тому же логарифмическому члену, что и прежде:
придем к тому же логарифмическому члену, что и прежде:

| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
- 4.4. ОБРАЗОВАНИЕ ПАР
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
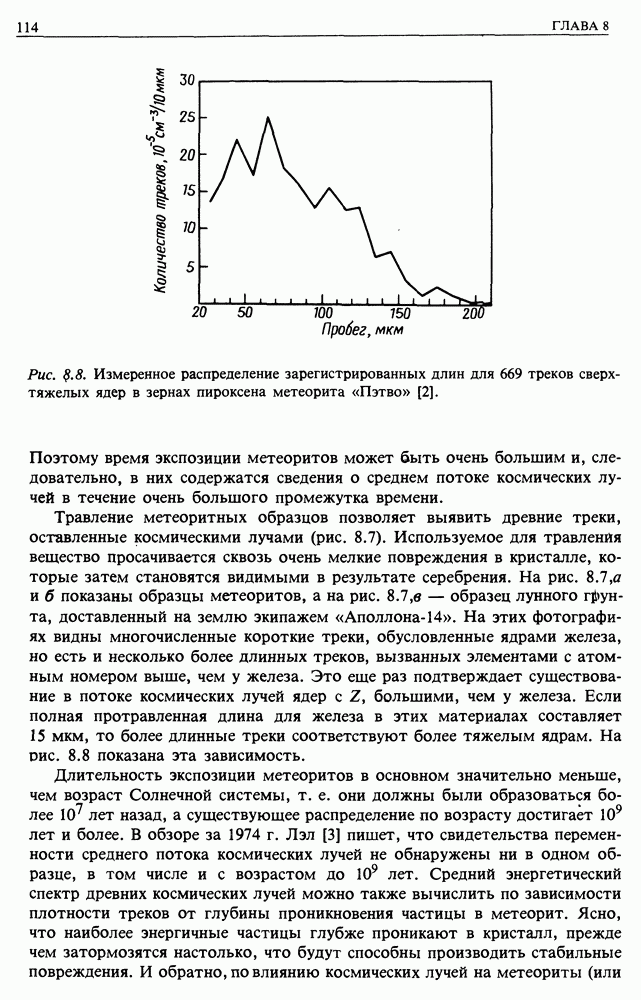
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
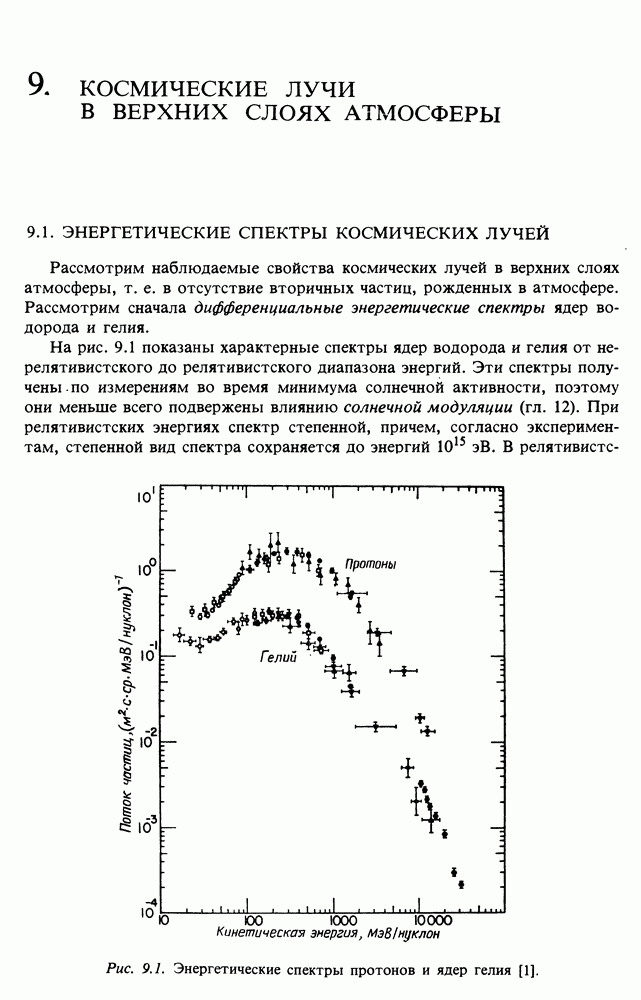
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
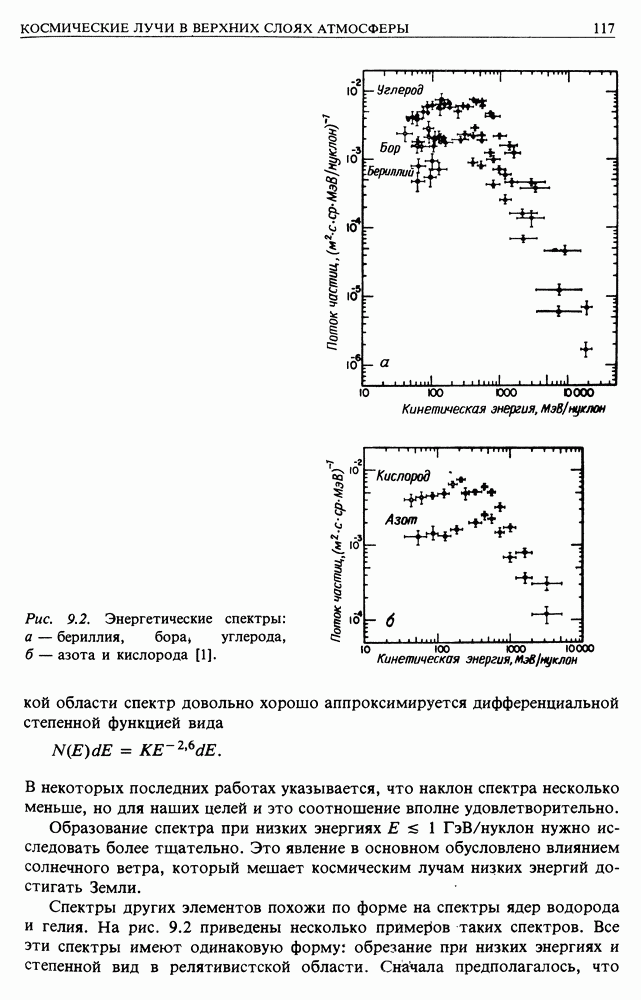
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
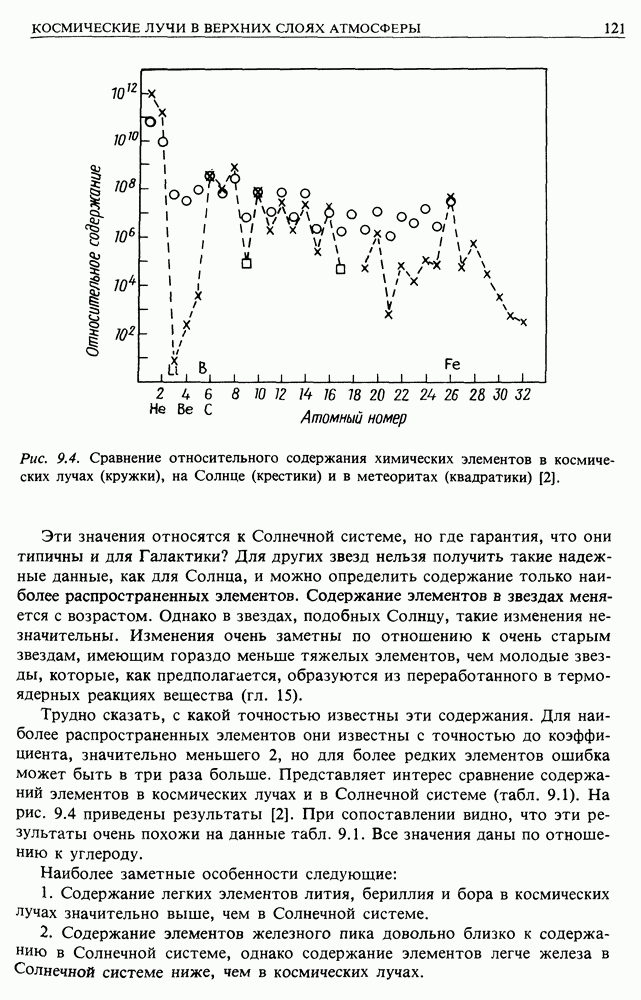
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
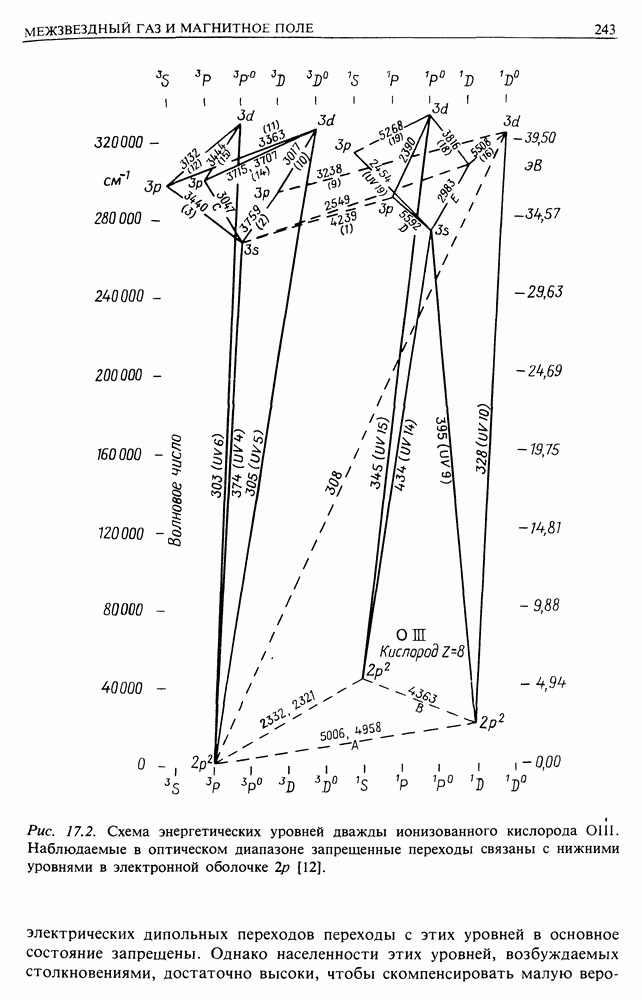
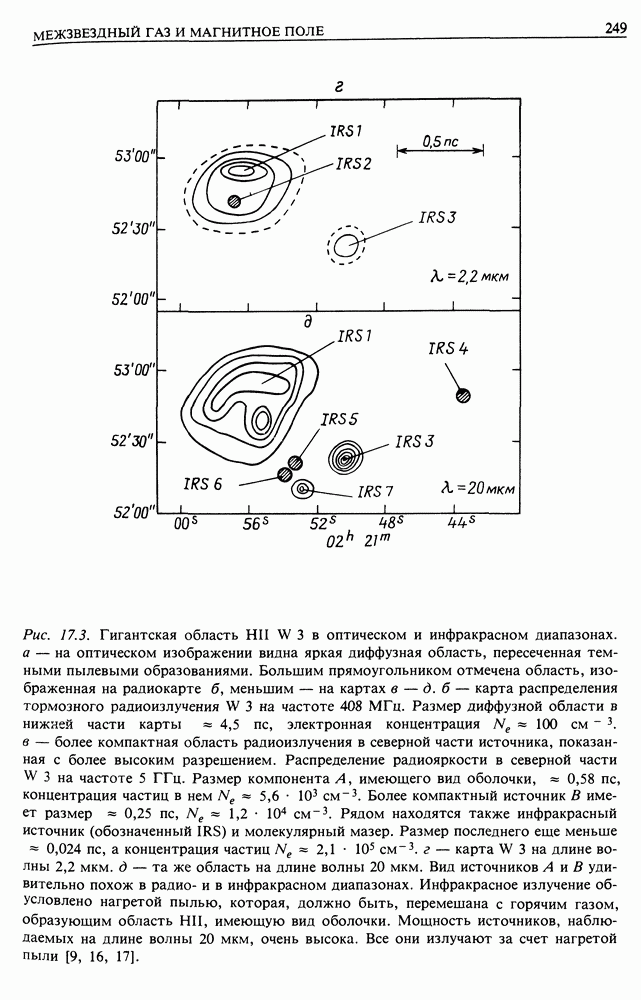
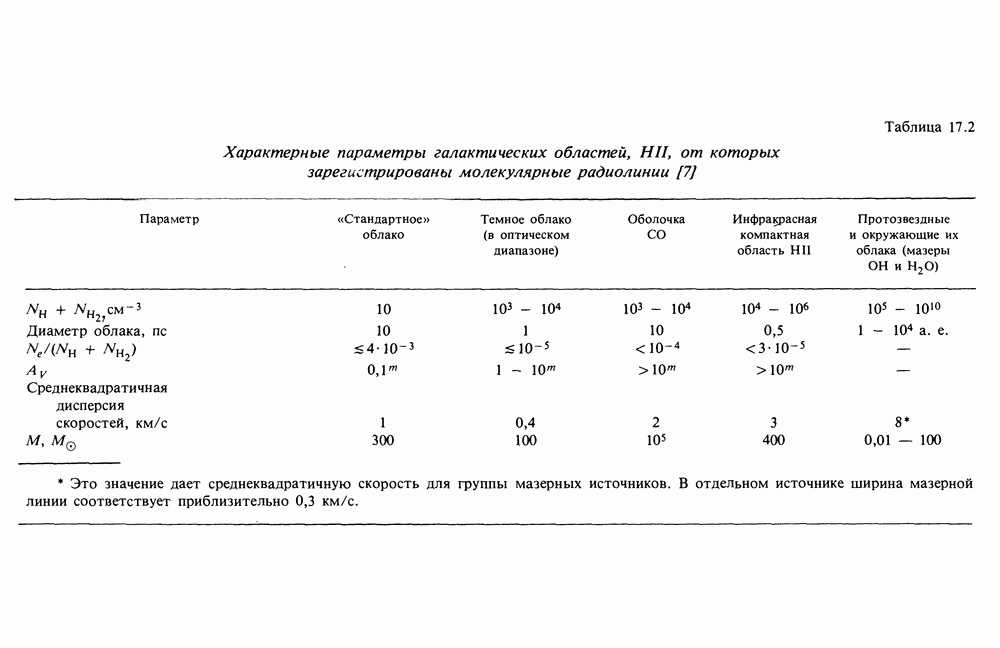
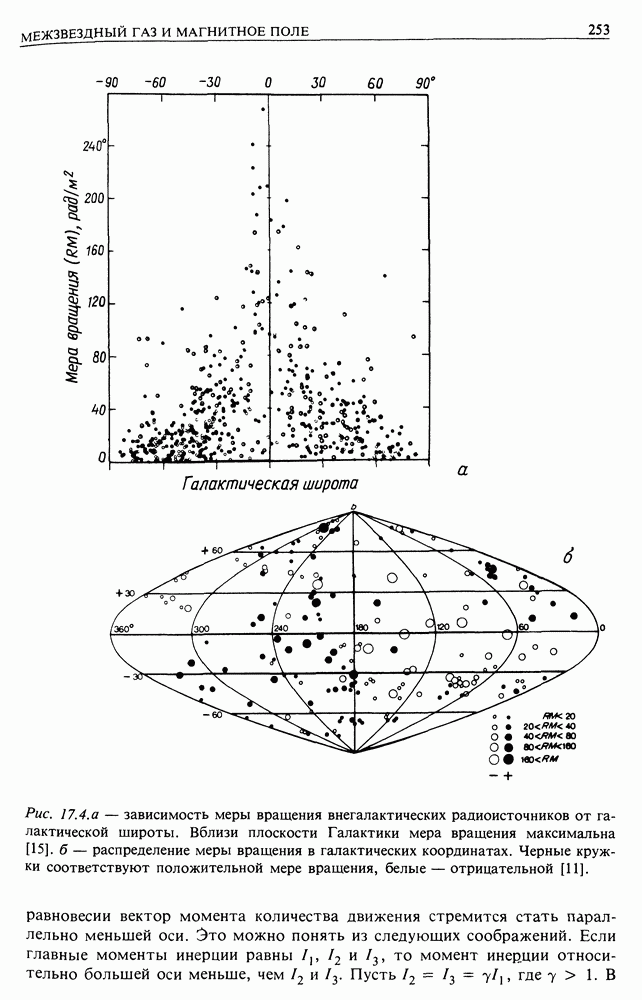
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
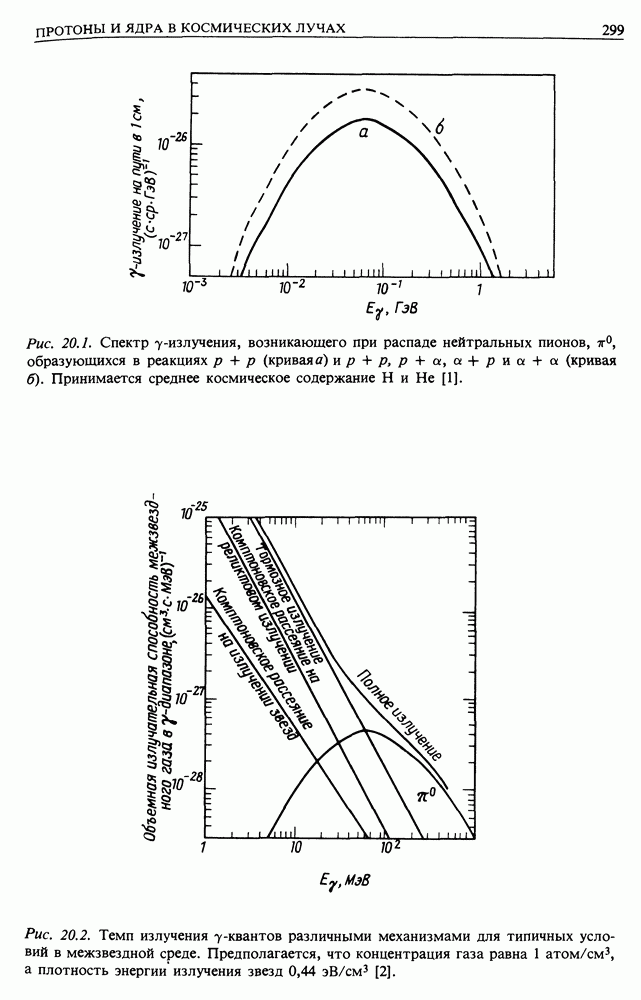
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ