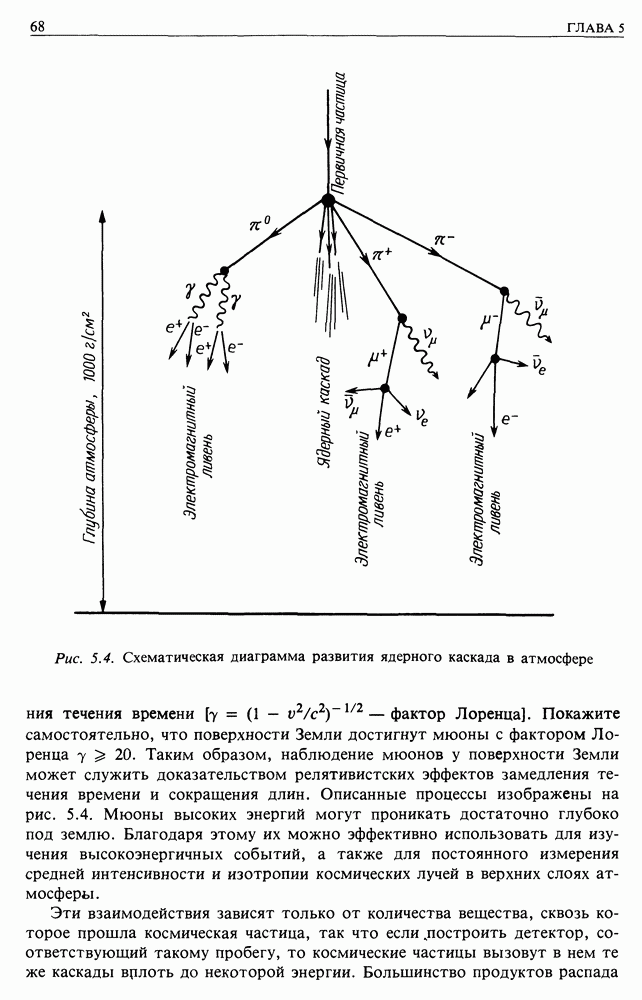
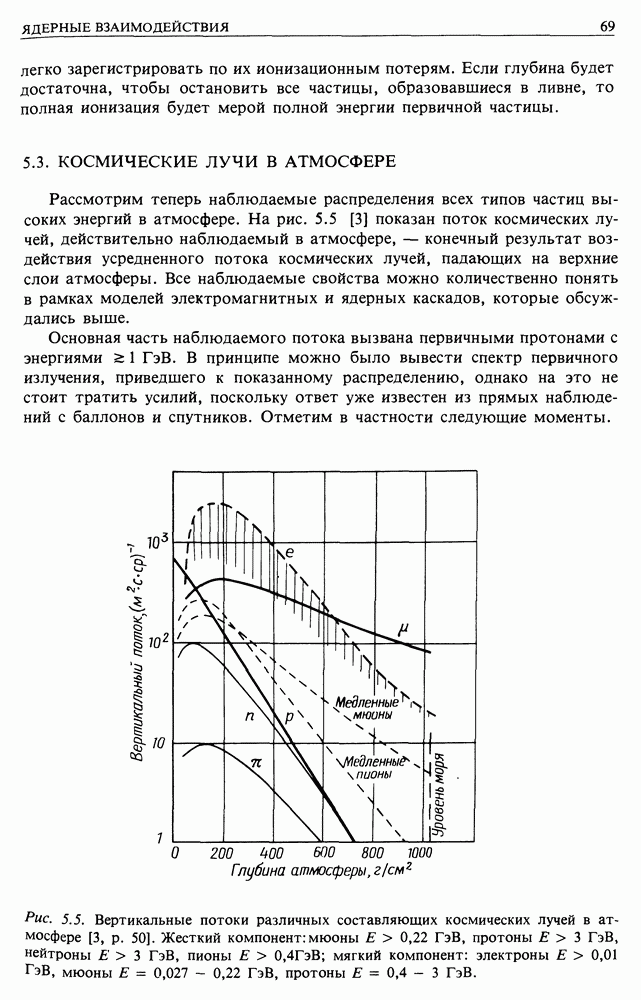
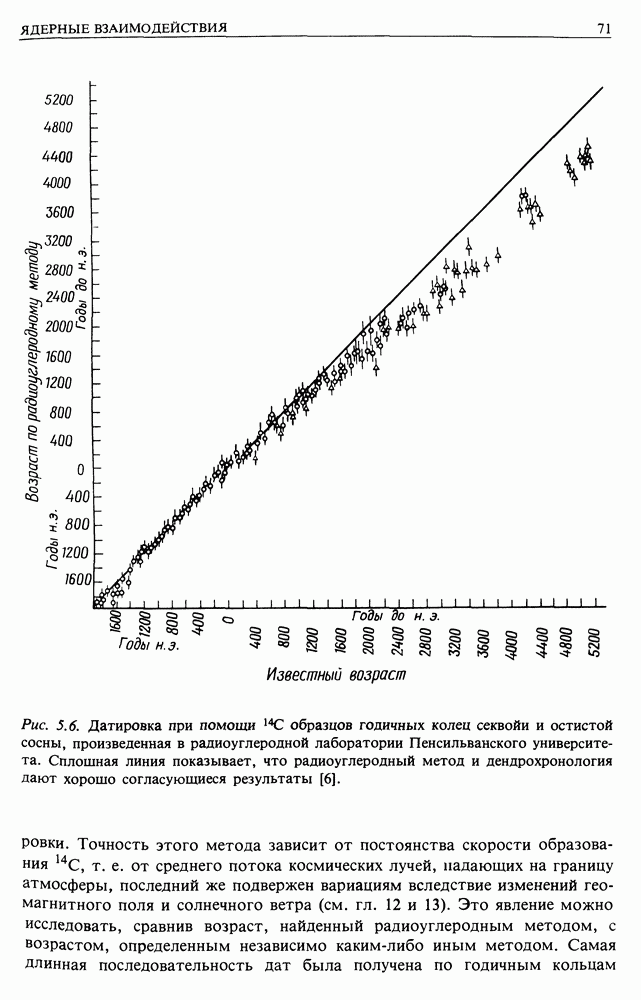
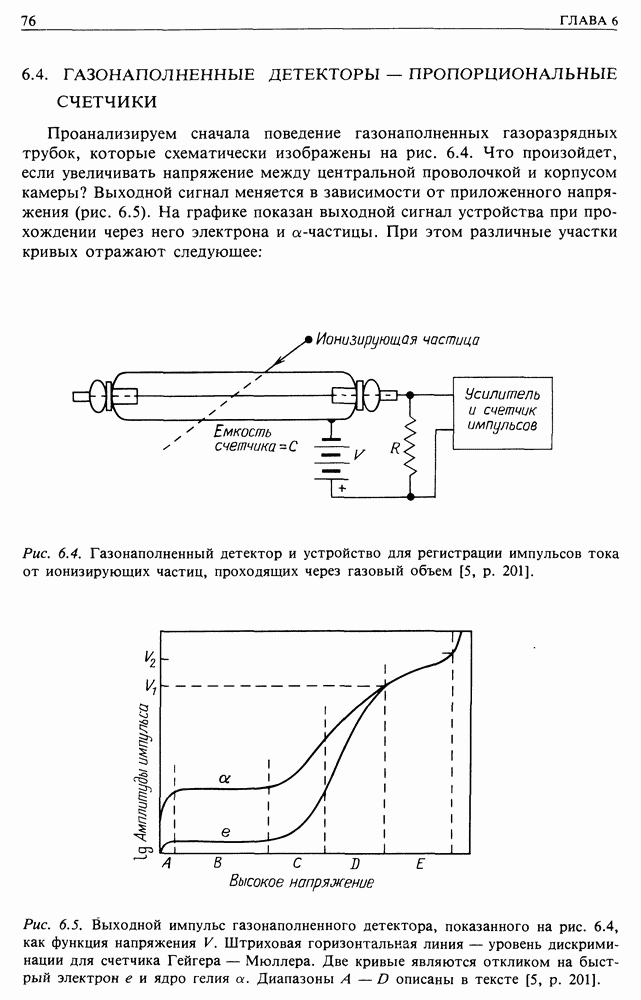
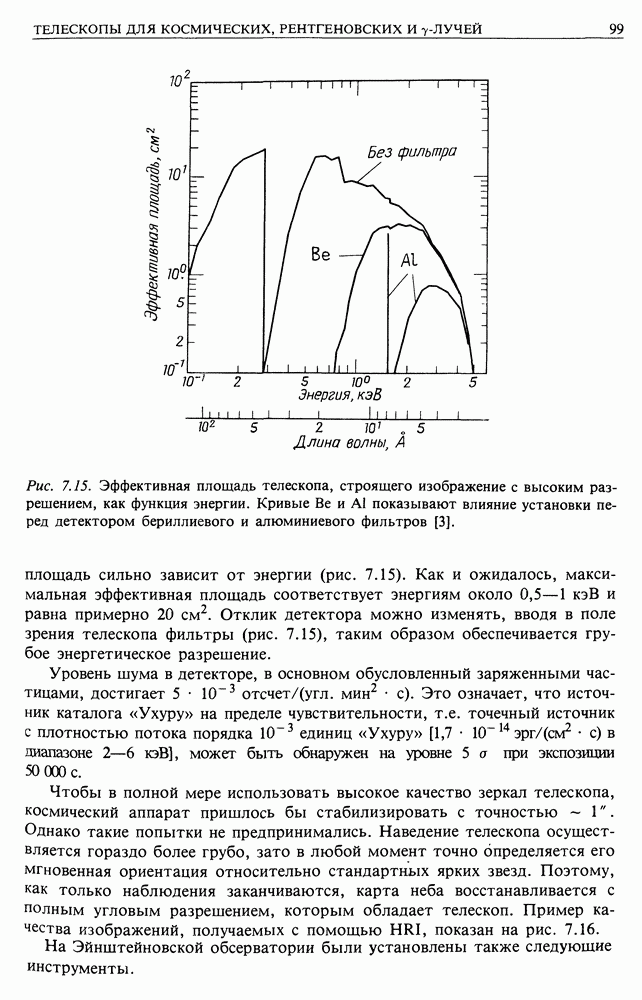
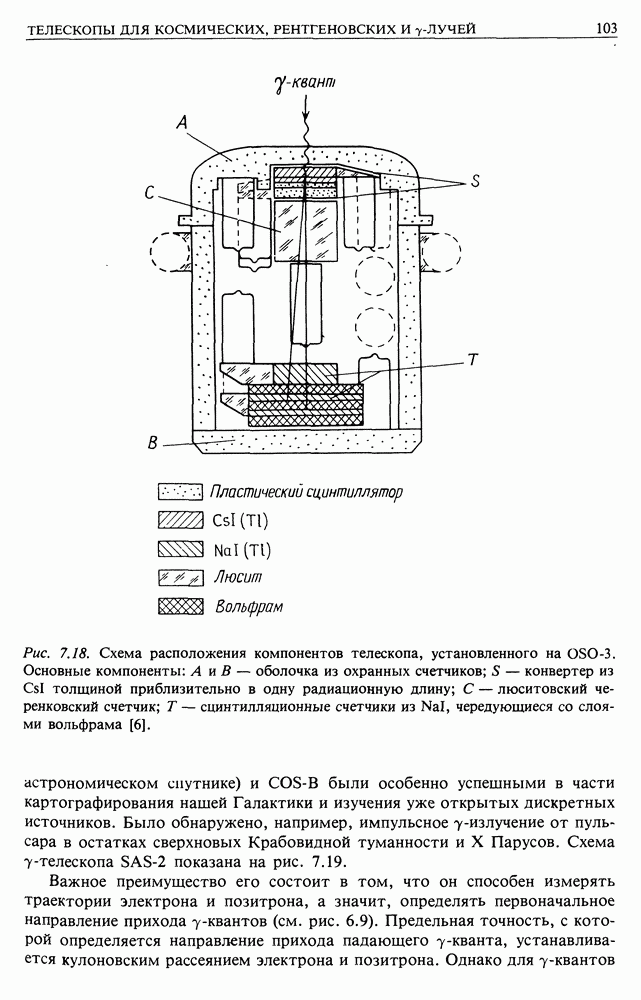
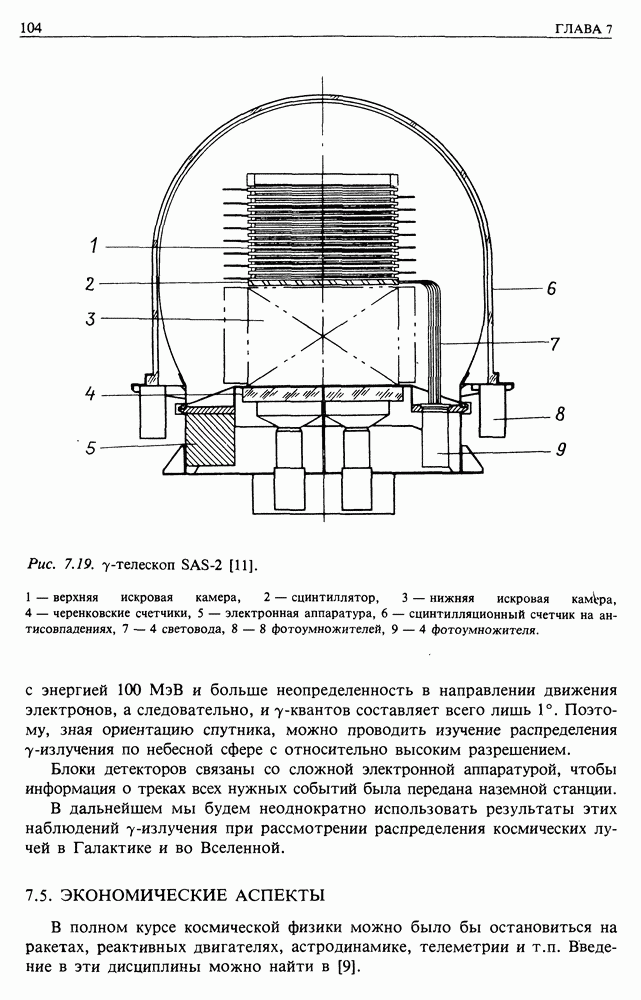
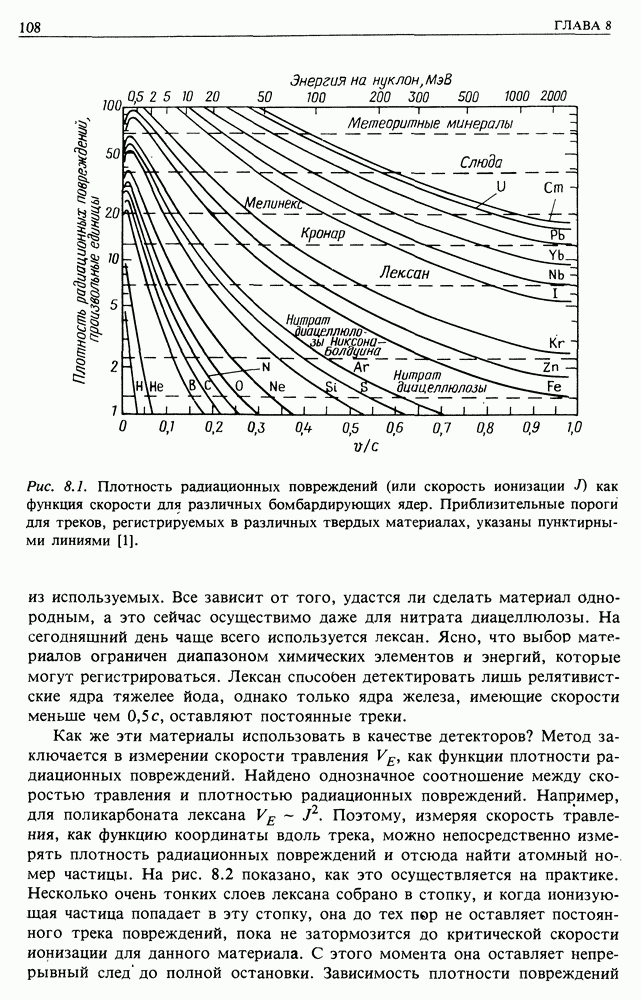
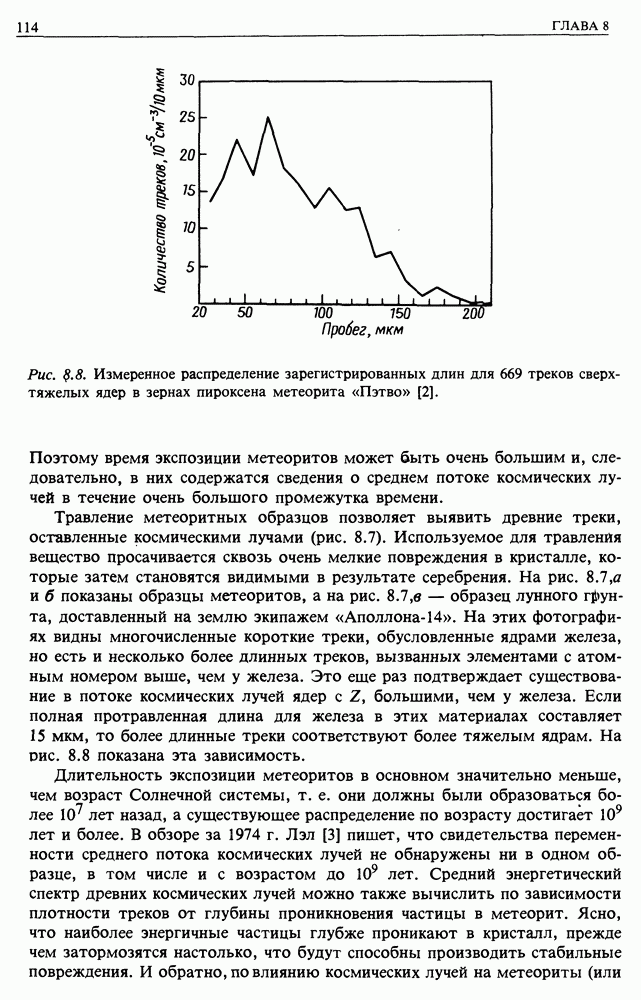
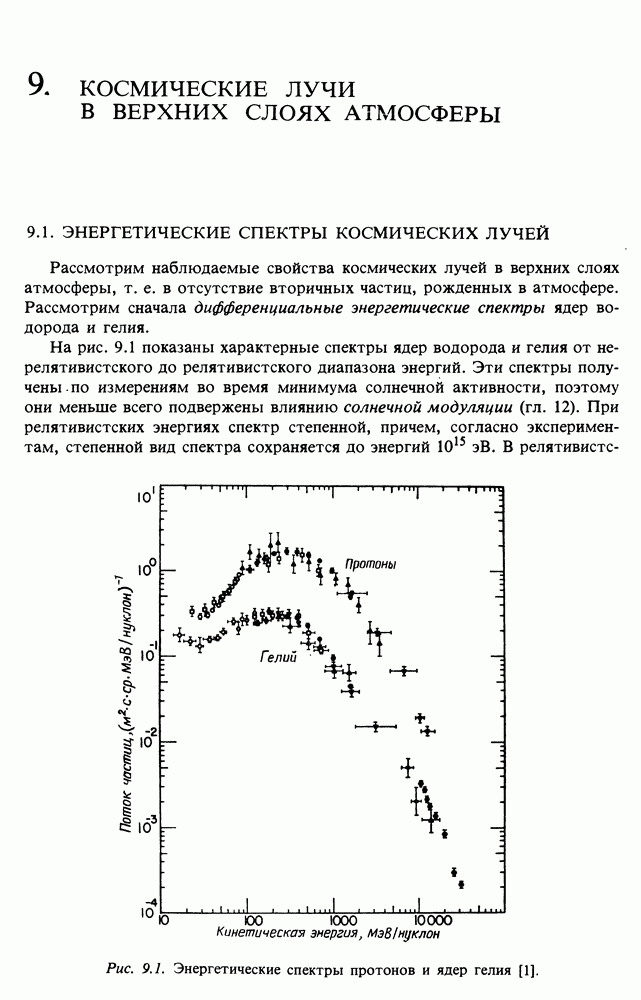
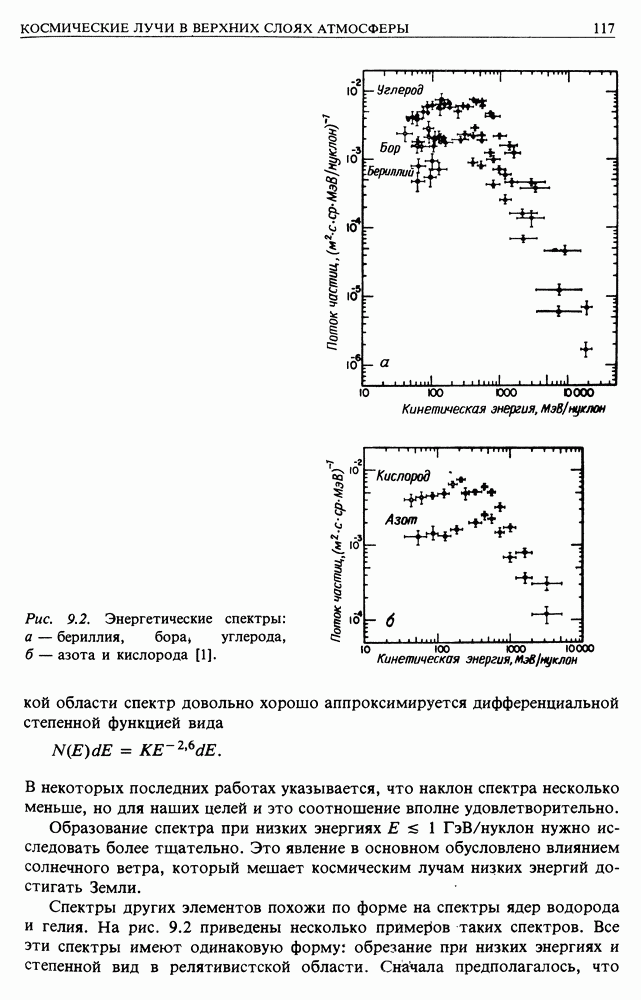
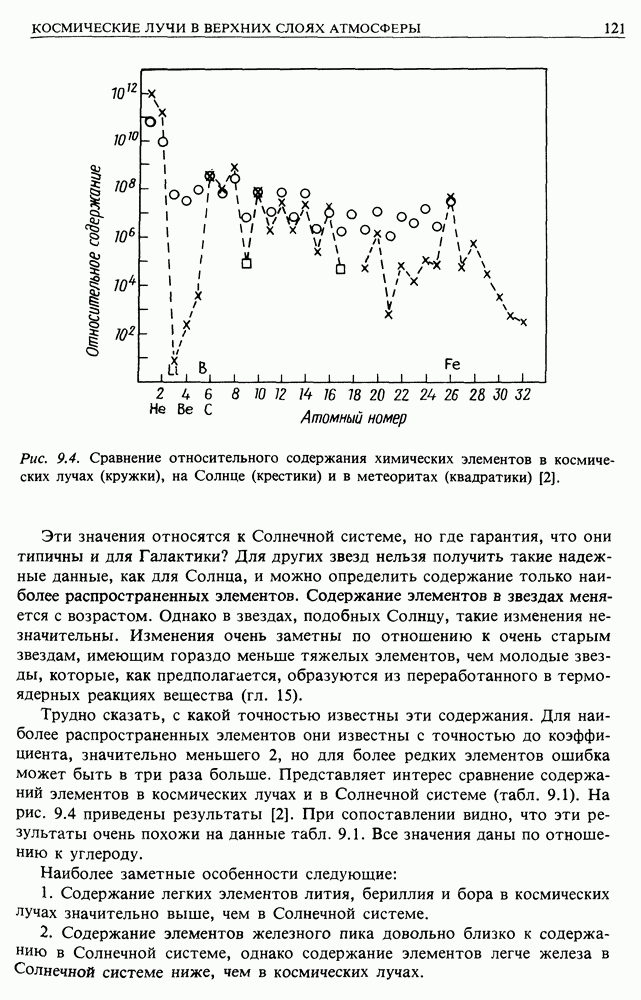
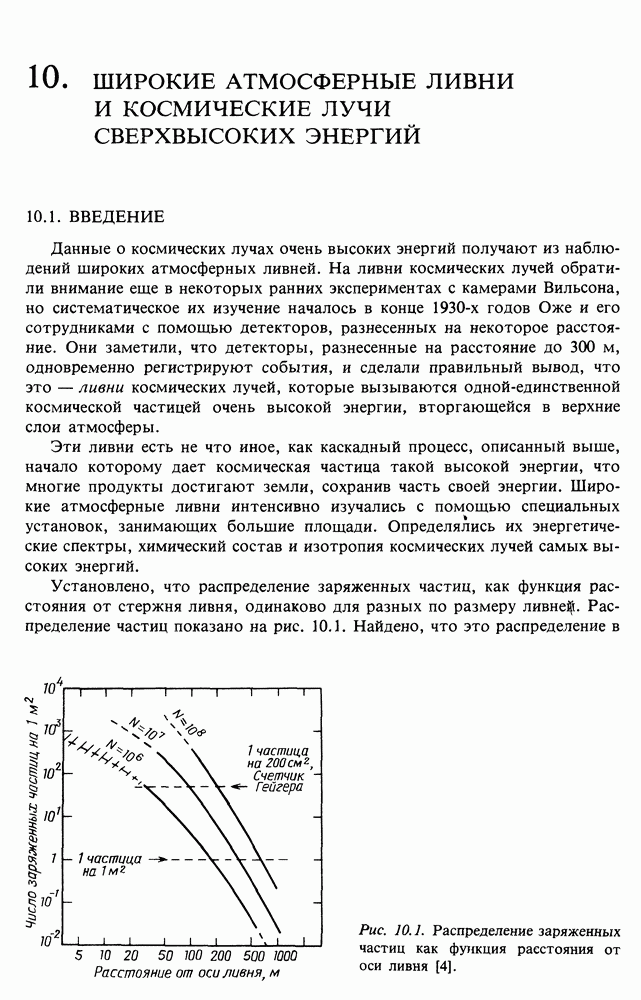
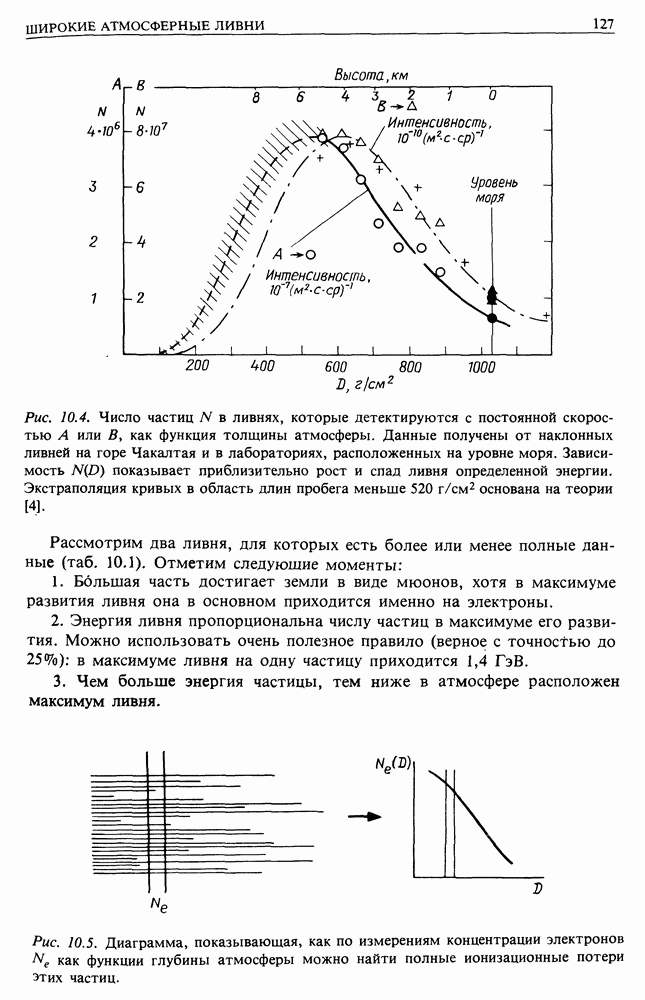
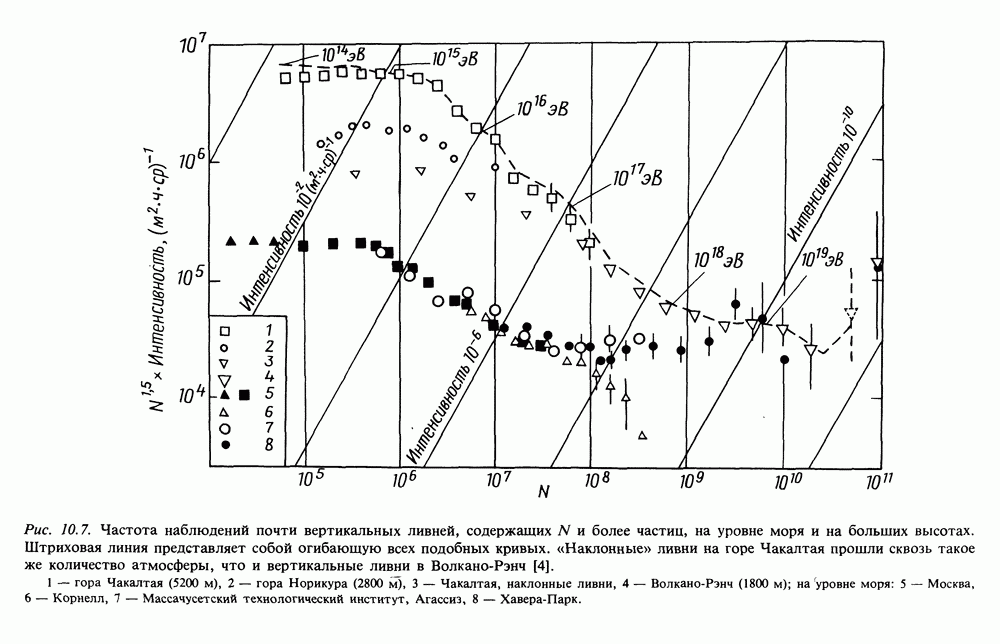
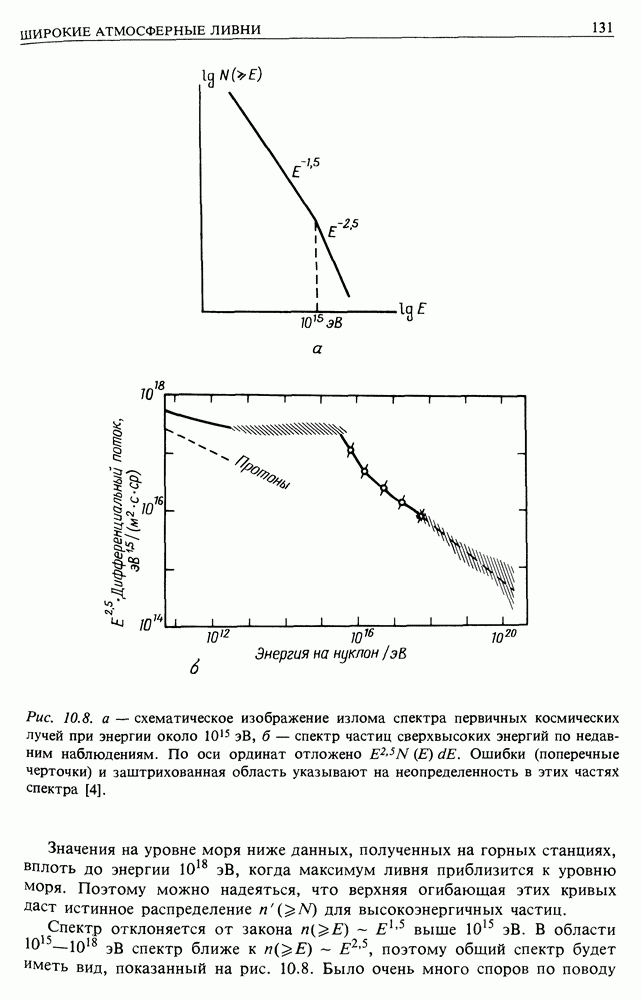
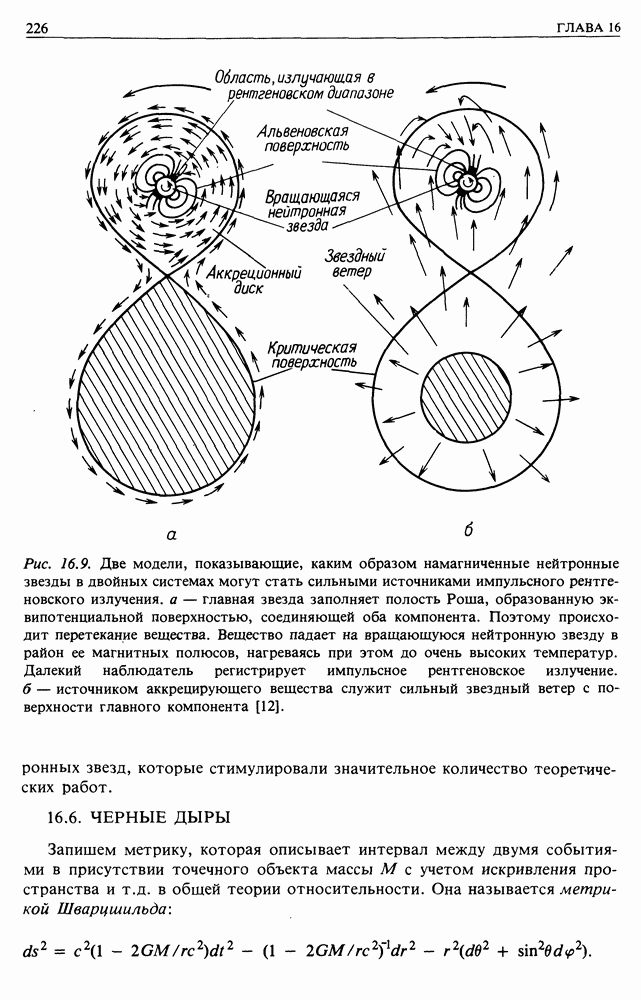
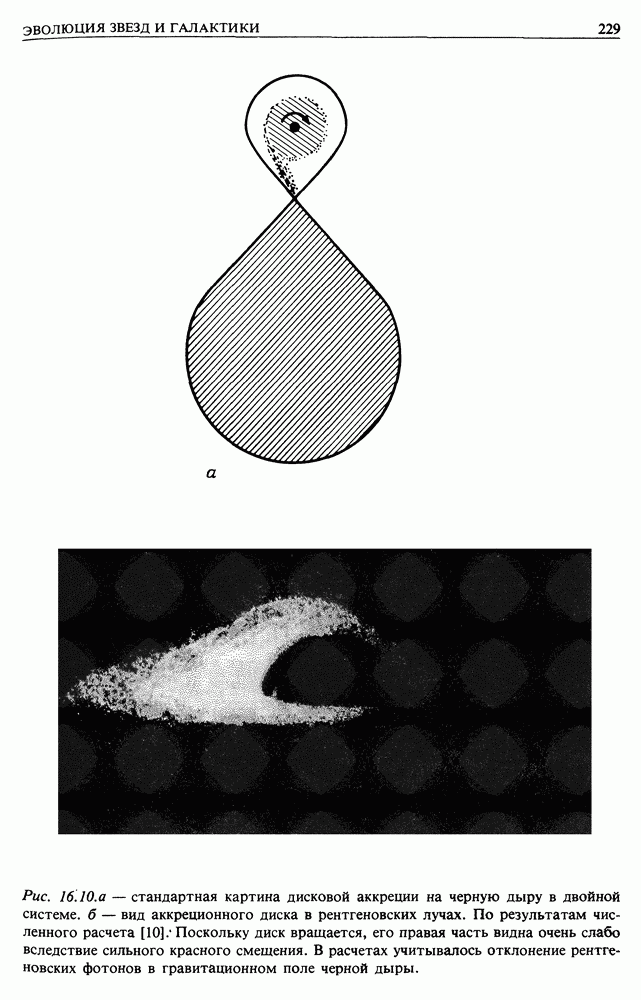
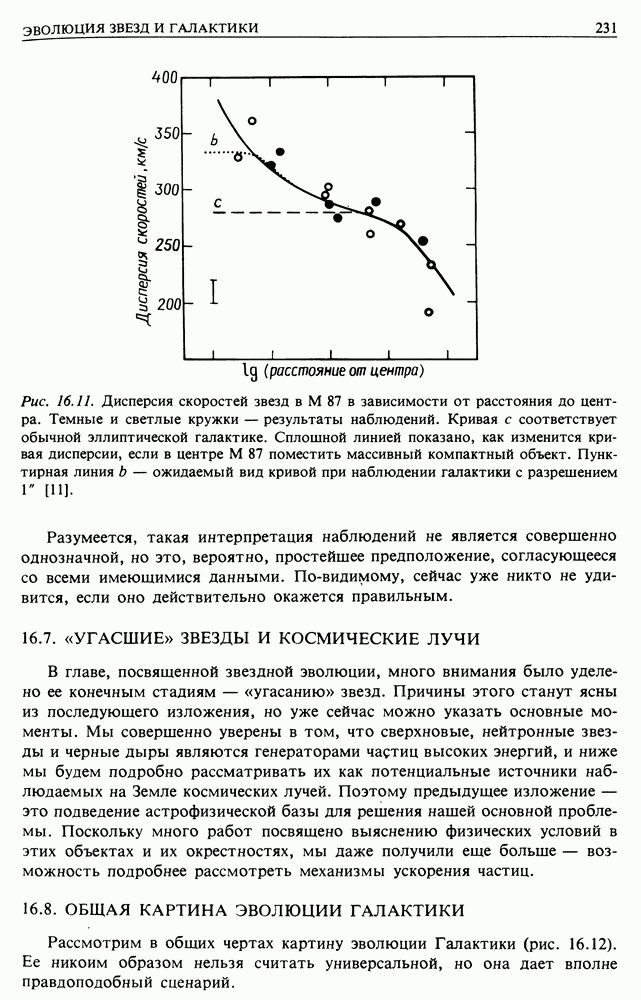
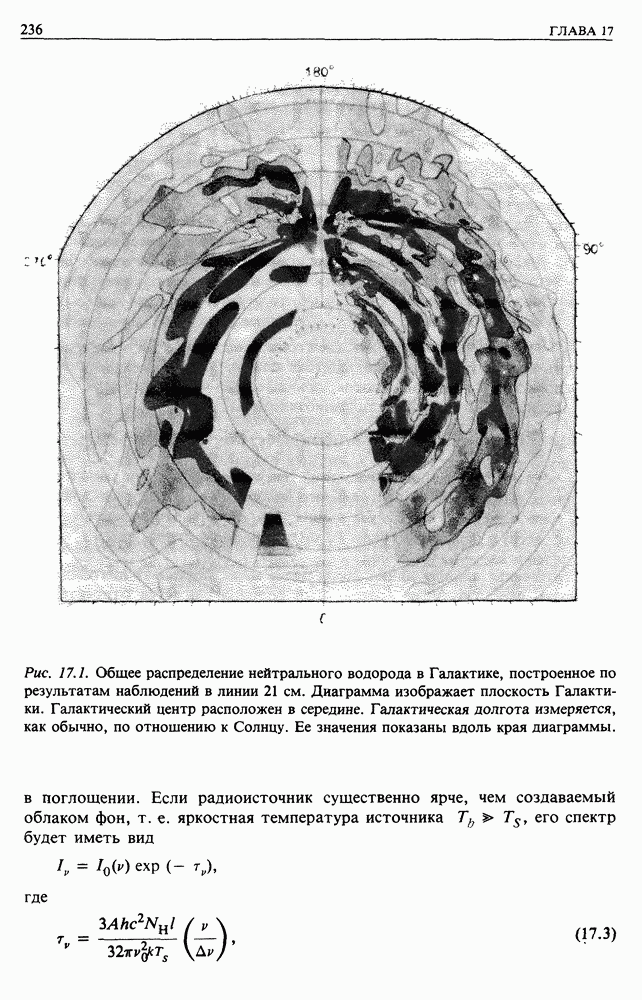
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
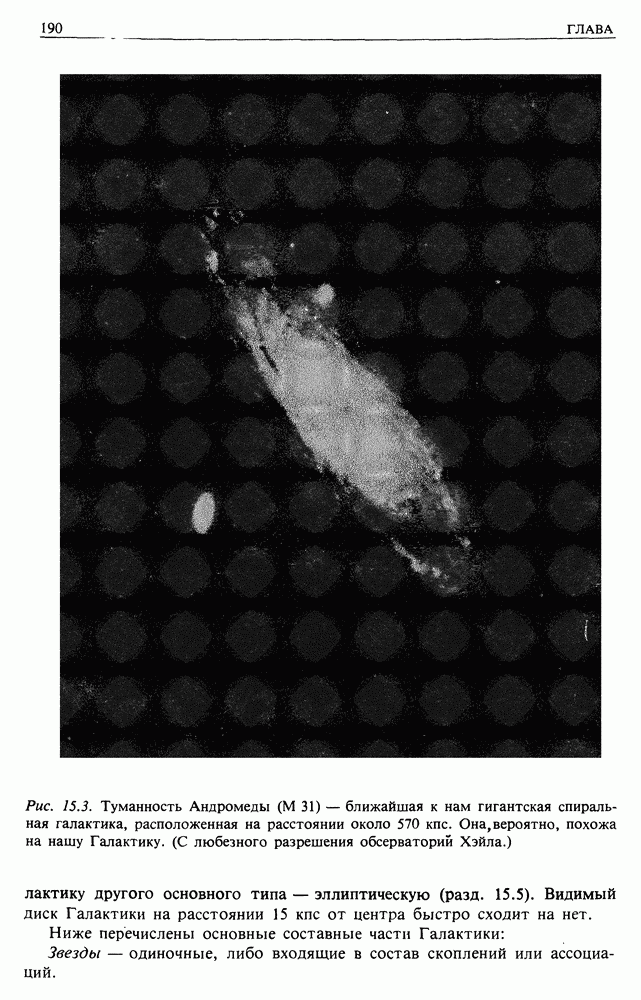
2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
Рассмотрим сначала случай столкновения протонов и ядер космических лучей с покоящимися электронами. В общем случае частицы космических лучей передают электронам очень малую долю своей кинетической энергии. Рассмотрим лобовое столкновение частицы космических лучей массой  с электроном массой те (рис. 2.1). Если считать их твердыми шарами, то максимальная скорость, приобретенная электроном, не может превышать
с электроном массой те (рис. 2.1). Если считать их твердыми шарами, то максимальная скорость, приобретенная электроном, не может превышать  в случае идеально упругого соударения. Убедитесь в том, что при нерелятивистском столкновении максимальная скорость равна
в случае идеально упругого соударения. Убедитесь в том, что при нерелятивистском столкновении максимальная скорость равна  Поскольку
Поскольку  это выражение приблизительно равно
это выражение приблизительно равно 
Следовательно, частица космических лучей теряет энергии меньше, чем  а относительная потеря кинетической энергии
а относительная потеря кинетической энергии

Рис. 2.1.
составляет менее  Таким образом, за исключением электрон-электронных столкновений, относительные потери энергии очень малы. Это означает, что в реальных столкновениях, когда взаимодействие происходит при посредстве электростатических полей частиц, налетающие частицы космических лучей практически не меняют направление движения. Электрон получает небольшой импульс в результате электростатического притяжения частицей или отталкивания. Приведем теперь первое решение — нерелятивистское, приняв, однако, что космическая частица движется достаточно быстро для того, чтобы электрон за время взаимодействия не успевал изменить свое положение на орбите. Приведенный ниже метод расчетов будет неоднократно повторяться на протяжении курса.
Таким образом, за исключением электрон-электронных столкновений, относительные потери энергии очень малы. Это означает, что в реальных столкновениях, когда взаимодействие происходит при посредстве электростатических полей частиц, налетающие частицы космических лучей практически не меняют направление движения. Электрон получает небольшой импульс в результате электростатического притяжения частицей или отталкивания. Приведем теперь первое решение — нерелятивистское, приняв, однако, что космическая частица движется достаточно быстро для того, чтобы электрон за время взаимодействия не успевал изменить свое положение на орбите. Приведенный ниже метод расчетов будет неоднократно повторяться на протяжении курса.
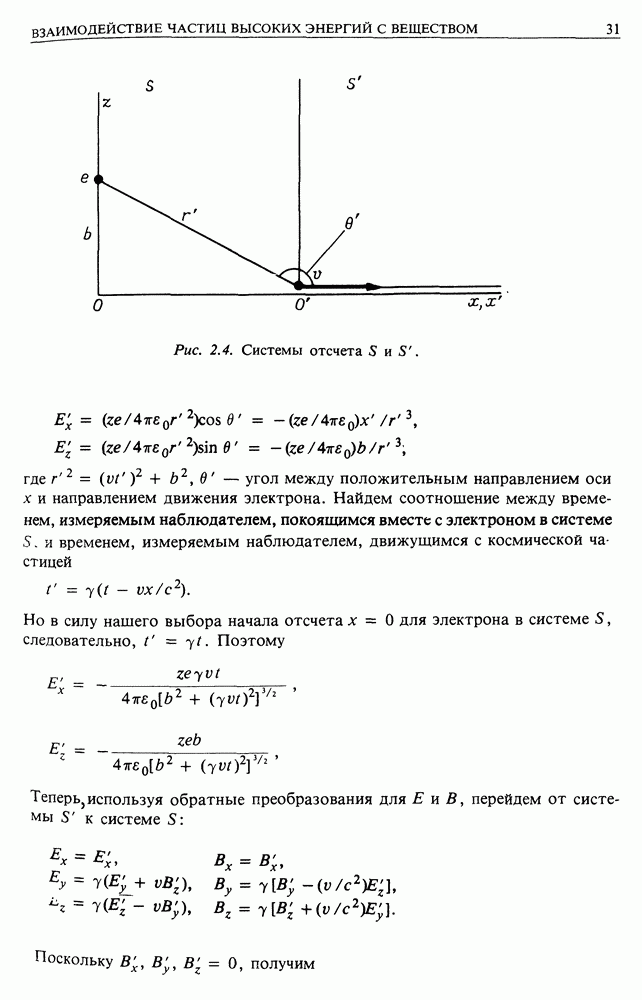
Динамику взаимодействия иллюстрирует рис. 2.2. Заряд космической частицы равен  и предполагается, что он не меняется в процессе взаимодействия;
и предполагается, что он не меняется в процессе взаимодействия;  прицельный параметр столкновения. Тогда полный импульс, передаваемый электрону за время взаимодействия, равен
прицельный параметр столкновения. Тогда полный импульс, передаваемый электрону за время взаимодействия, равен  Из соображений симметрии вклады сил, параллельных вектору скорости космической частицы, сокращаются, поэтому нужно учитывать лишь составляющую силы, перпендикулярную направлению пролета:
Из соображений симметрии вклады сил, параллельных вектору скорости космической частицы, сокращаются, поэтому нужно учитывать лишь составляющую силы, перпендикулярную направлению пролета:

Выражая переменные через  и принимая
и принимая  имеем
имеем


Рис. 2.2.

Рис. 2.3.
Следовательно, импульс

Отсюда кинетическая энергия, переданная электрону, равна

Энергетические потери частицы космических лучей
Теперь выразим эту величину через средние потери энергии на единицу длины. Для этого необходимо найти число соударений с прицельными параметрами от  до
до  и проинтегрировать по
и проинтегрировать по  (рис. 2.3). Поэтому полные потери энергии космической частицы
(рис. 2.3). Поэтому полные потери энергии космической частицы  в веществе на пути
в веществе на пути  равны
равны

где  число электронов в единице объема, или концентрация электронов. Теперь тщательно проверим правильность выбора пределов интегрирования. Возьмем сначала интеграл (2.2)
число электронов в единице объема, или концентрация электронов. Теперь тщательно проверим правильность выбора пределов интегрирования. Возьмем сначала интеграл (2.2)

Чем ближе частицы подходят друг к другу во время столкновения, тем больше импульс  Однако чем больше расстояние, тем больше электронов
Однако чем больше расстояние, тем больше электронов  Этим и объясняется логарифмическая зависимость полных энергетических потерь. Мы будем постоянно встречаться с такими явлениями в плазме, когда эффект, пропорциональный
Этим и объясняется логарифмическая зависимость полных энергетических потерь. Мы будем постоянно встречаться с такими явлениями в плазме, когда эффект, пропорциональный  дает в конечном счете логарифмический член. Можно спросить: «Зачем вводить пределы
дает в конечном счете логарифмический член. Можно спросить: «Зачем вводить пределы  вместо того, чтобы найти точный ответ?» Дело в том, что точное решение гораздо сложнее и для нахождений его пришлось бы учитывать ускорение электрона под действием космической частицы, а также квантовомеханические эффекты, возникающие в процессе взаимодействия. Риближенный метод дает достаточно хороший ответ, поскольку пределы
вместо того, чтобы найти точный ответ?» Дело в том, что точное решение гораздо сложнее и для нахождений его пришлось бы учитывать ускорение электрона под действием космической частицы, а также квантовомеханические эффекты, возникающие в процессе взаимодействия. Риближенный метод дает достаточно хороший ответ, поскольку пределы
 только в логарифмы и, следовательно, нет нужды энать их очень точно. Рассмотрим верхний и нижний пределы по отдельности.
только в логарифмы и, следовательно, нет нужды энать их очень точно. Рассмотрим верхний и нижний пределы по отдельности.
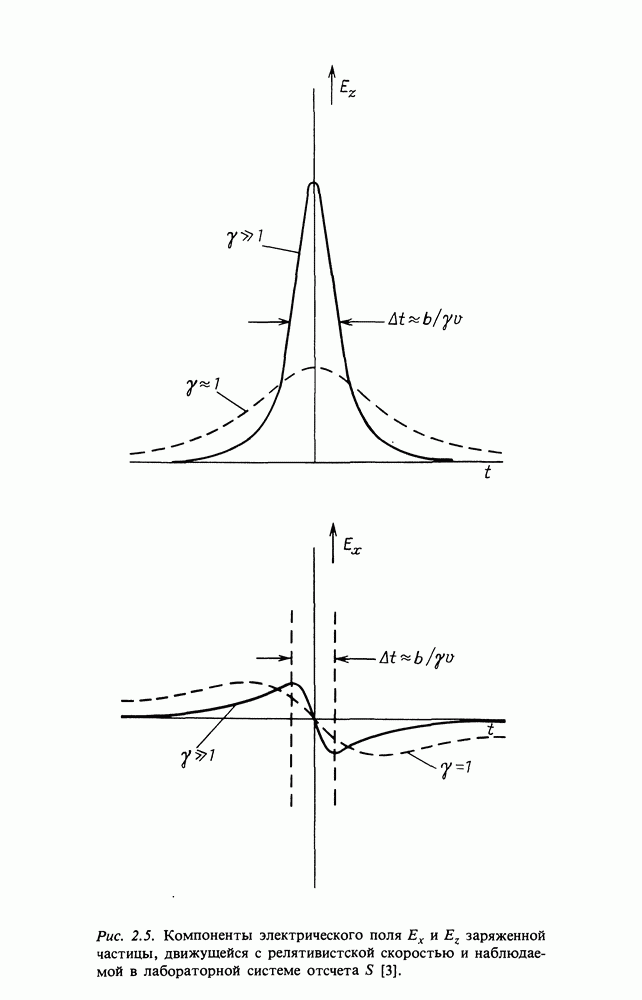
Верхний предел  Верхний предел прицельного параметра определяется длительностью столкновения того же порядка, что и период обращения электрона по своей орбите. В этом случае взаимодействие не носит более характера короткого импульса. Если длительность столкновения много больше орбитального периода, то электрон оказывается как бы в слегка возмущённом поле, или в рамках динамики частиц, которую мы рассмотрим ниже, он будет «сохранять свое движение» во время действия возмущения и ионизация не будет иметь места. Что понимается под длительностью столкновения? Полную энергию, переданную при столкновении, можно представить следующим образом. Пусть длительность столкновения равна
Верхний предел прицельного параметра определяется длительностью столкновения того же порядка, что и период обращения электрона по своей орбите. В этом случае взаимодействие не носит более характера короткого импульса. Если длительность столкновения много больше орбитального периода, то электрон оказывается как бы в слегка возмущённом поле, или в рамках динамики частиц, которую мы рассмотрим ниже, он будет «сохранять свое движение» во время действия возмущения и ионизация не будет иметь места. Что понимается под длительностью столкновения? Полную энергию, переданную при столкновении, можно представить следующим образом. Пусть длительность столкновения равна  Используем силу, действующую на расстоянии максимального сближения частицы и электрона, тогда
Используем силу, действующую на расстоянии максимального сближения частицы и электрона, тогда

Поэтому

Такой же результат был получен выше. Значит, «длительность» столкновения равна  Если длительность столкновения равна периоду обращения электрона в атоме, то можно получить оценку по порядку величины для Ьтах. Заметим, что коэффициент 2 не играет роли, поскольку
Если длительность столкновения равна периоду обращения электрона в атоме, то можно получить оценку по порядку величины для Ьтах. Заметим, что коэффициент 2 не играет роли, поскольку  и
и  войдут в логарифм. Следовательно, хорошим приближением для Ьтах является
войдут в логарифм. Следовательно, хорошим приближением для Ьтах является

где  частота обращения электрона на орбите. С учетом
частота обращения электрона на орбите. С учетом  получим
получим

Нижний предел  Здесь имеются две возможности:
Здесь имеются две возможности:
1. В классической физике минимальное сближение соответствует прицельному параметру, при котором потенциальная энергия электростатического взаимодействия космической частицы и электрона равна максимальному значению энергии, которое может быть передано электрону, т.е. в соответствии с проделанным выше расчетом  Таким образом,
Таким образом,

Если в ходе взаимодействия передается такое количество энергии, то электрон при столкновении отклоняется на расстояние, сравнимое с  следовательно, предположения, на которых основан расчет, не
следовательно, предположения, на которых основан расчет, не
справедливы Чтобы это продемонстрировать, заметим, что средняя скорость частицы равна  Поэтому расстояние, проходимое за время соударения
Поэтому расстояние, проходимое за время соударения  есть
есть  и имеет тот же порядок величины, что и
и имеет тот же порядок величины, что и 
2. Второе возможное значение  следует из применения квантовой механики для описания близких столкновений. Максимальная скорость, которую может приобрести электрон, равна
следует из применения квантовой механики для описания близких столкновений. Максимальная скорость, которую может приобрести электрон, равна  значит,
значит,  Поэтому имеется неопределенность положения электрона А, которая в соответствии с принципом Гейзенберга равна
Поэтому имеется неопределенность положения электрона А, которая в соответствии с принципом Гейзенберга равна  т.е.
т.е.

Если это подходящее значение  значит, при расчетах следует учитывать квантовую механику. Во всяком случае, полученное выражение показывает, каков разумный предел
значит, при расчетах следует учитывать квантовую механику. Во всяком случае, полученное выражение показывает, каков разумный предел  используемого при интегрировании.
используемого при интегрировании.
В каждом частном случае следует определить, какое из значений  больше, т.е. выбор зависит от отношения
больше, т.е. выбор зависит от отношения

где  постоянная тонкой структуры. Итак, если для частицы
постоянная тонкой структуры. Итак, если для частицы  то следует учитывать квантовомеханические поправки. Это ограничение будет использоваться в последующем изложении. Заметим, что такой же расчет применим для ионизационных потерь в горячем газе, например, полностью ионизованной водородной плазме. В этом случае типичные скорости частиц также много меньше
то следует учитывать квантовомеханические поправки. Это ограничение будет использоваться в последующем изложении. Заметим, что такой же расчет применим для ионизационных потерь в горячем газе, например, полностью ионизованной водородной плазме. В этом случае типичные скорости частиц также много меньше  поэтому классический предел здесь вполне применим.
поэтому классический предел здесь вполне применим.
Подставляя полученные значения пределов в уравнение (2.3), получим в нерелятивистском приближении скорость потерь на единицу длины для энергичных космических лучей

Если обратиться к модели атома Бора, то

есть энергия самого нижнего связанного состояния атома, и мы можем написать

где  потенциал ионизации атома. На практике
потенциал ионизации атома. На практике  должно быть некоторым хорошо вычисленным взвешенным средним по всем состояниям атома, т.е. следует писать
должно быть некоторым хорошо вычисленным взвешенным средним по всем состояниям атома, т.е. следует писать  , а не
, а не  Значение
Значение  учитывает тот факт, что электроны в атомах находятся на различных энергетических уровнях, с которых они могут быть выбиты космическими лучами. Даже в самых сложных расчетах невозможно определить точное значение
учитывает тот факт, что электроны в атомах находятся на различных энергетических уровнях, с которых они могут быть выбиты космическими лучами. Даже в самых сложных расчетах невозможно определить точное значение  и его приходится находить экспериментально. Обычно пишут
и его приходится находить экспериментально. Обычно пишут

где  максимальная кинетическая энергия, которая может быть передана электрону. Поэтому можно переписать логарифмический член в виде
максимальная кинетическая энергия, которая может быть передана электрону. Поэтому можно переписать логарифмический член в виде  .
.
В качестве упражнения покажите самостоятельно, что спектр выбитых электронов — степенной:

Интегрирование по всем энергиям от  до
до  даст такой же логарифмический член, как выведенный выше.
даст такой же логарифмический член, как выведенный выше.
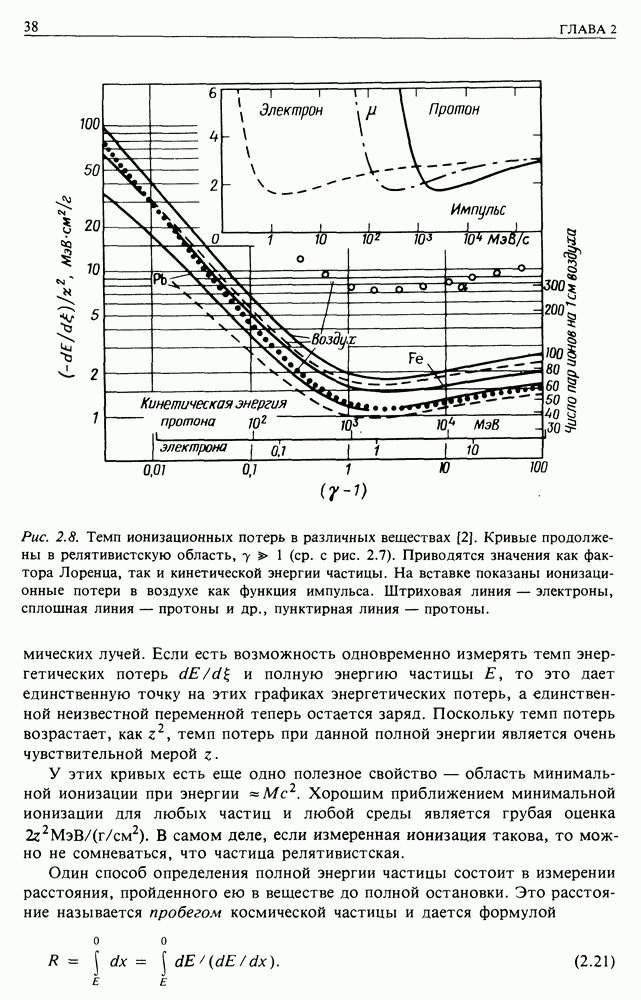
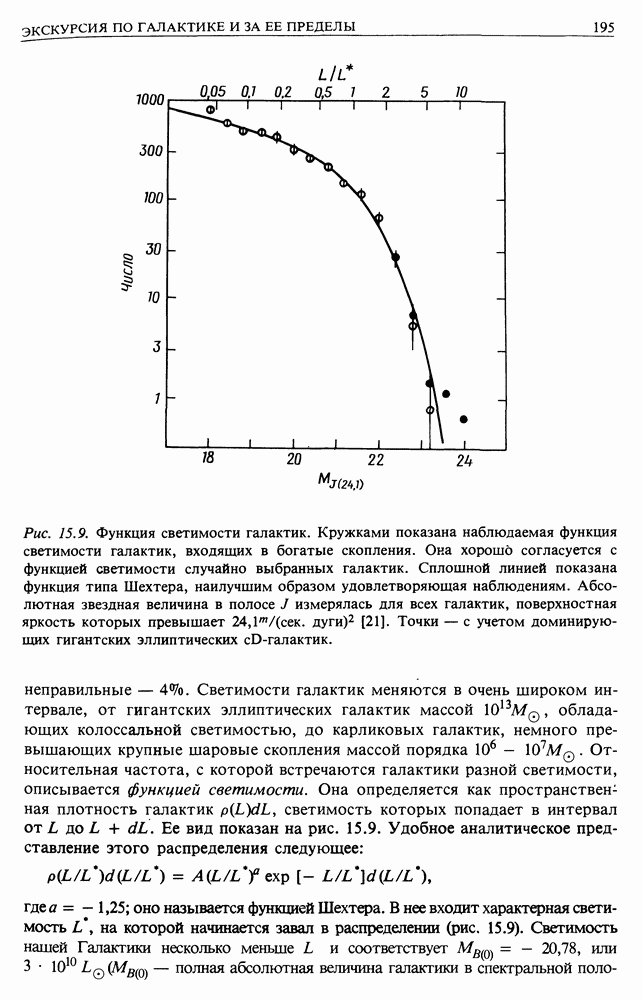
Итак, ионизационные потери не зависят от массы космической частицы  Измерение энергетических потерь на единицу длины,
Измерение энергетических потерь на единицу длины,  дает информацию
дает информацию  Мы также извлекаем информацию
Мы также извлекаем информацию  из энергетического спектра выбитых электронов [см. уравнение (2.11)]. Наконец, потери пропорциональны
из энергетического спектра выбитых электронов [см. уравнение (2.11)]. Наконец, потери пропорциональны  а отсюда немедленно следует, что ионизационными потерями при электростатических взаимодействиях с протонами и ядрами можно пренебречь.
а отсюда немедленно следует, что ионизационными потерями при электростатических взаимодействиях с протонами и ядрами можно пренебречь.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
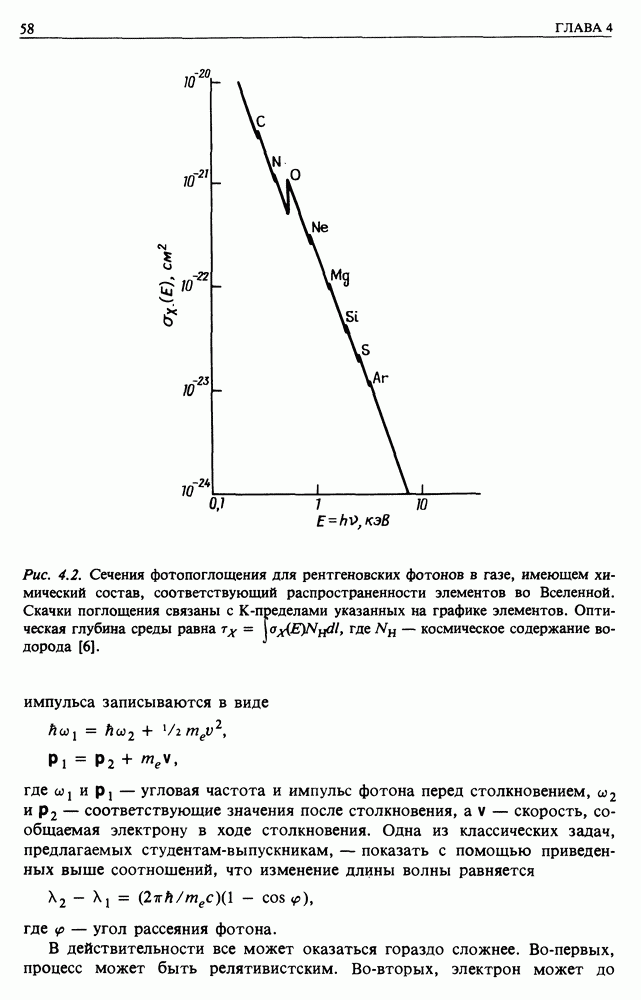
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
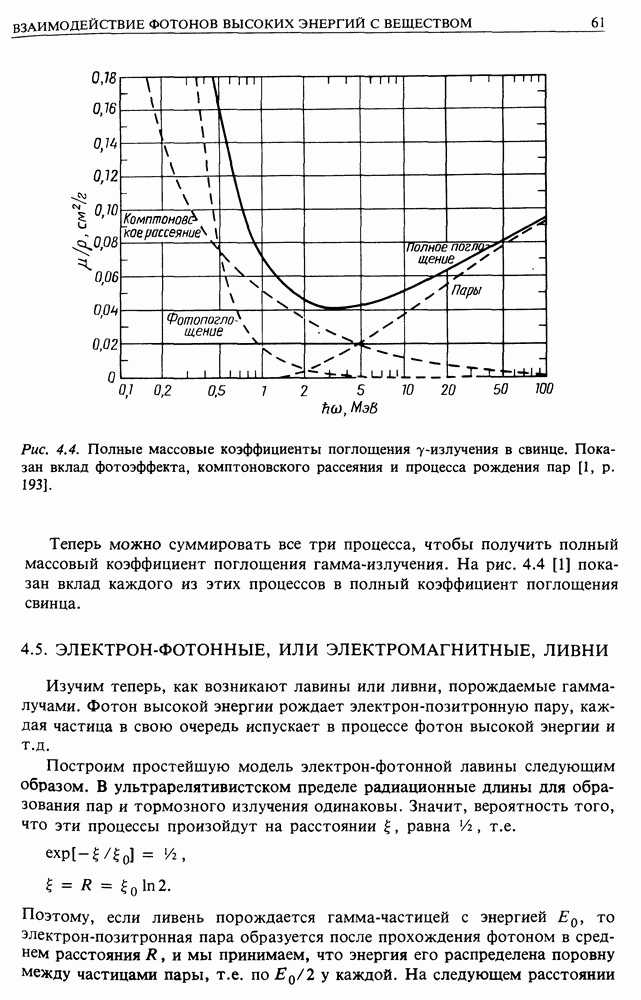
- 4.4. ОБРАЗОВАНИЕ ПАР
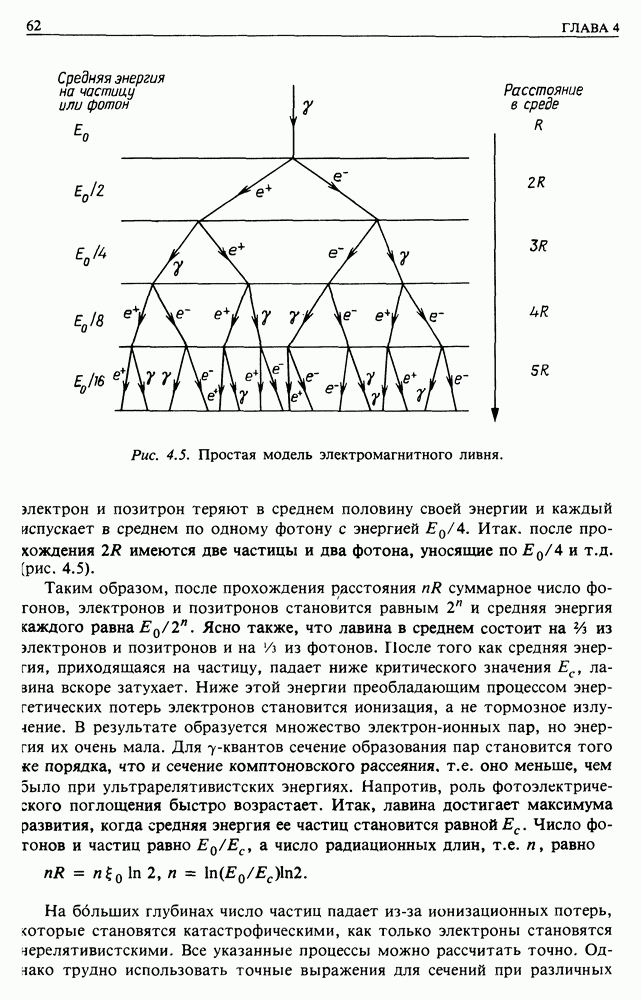
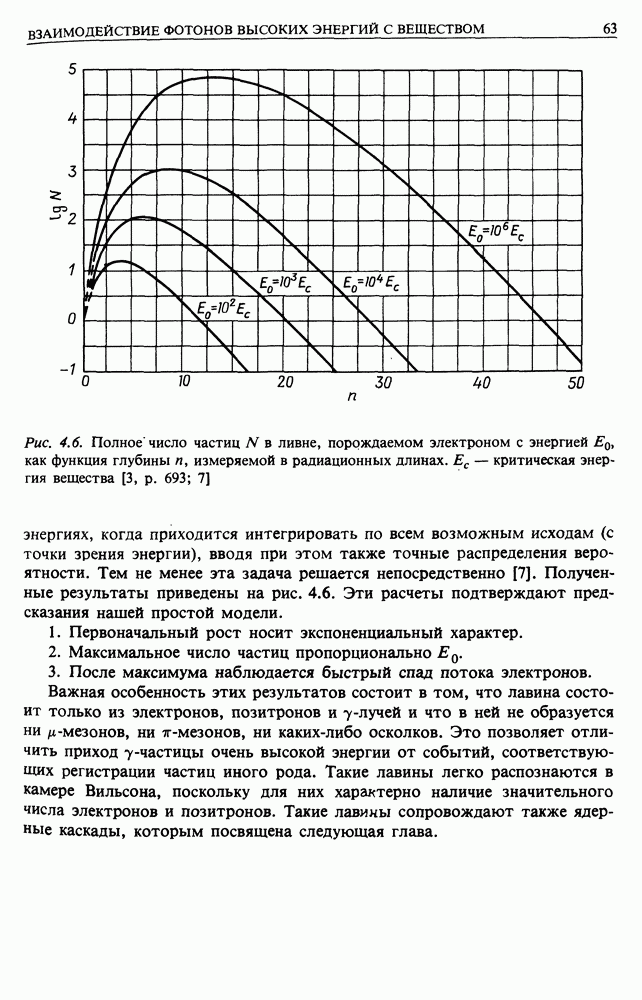
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
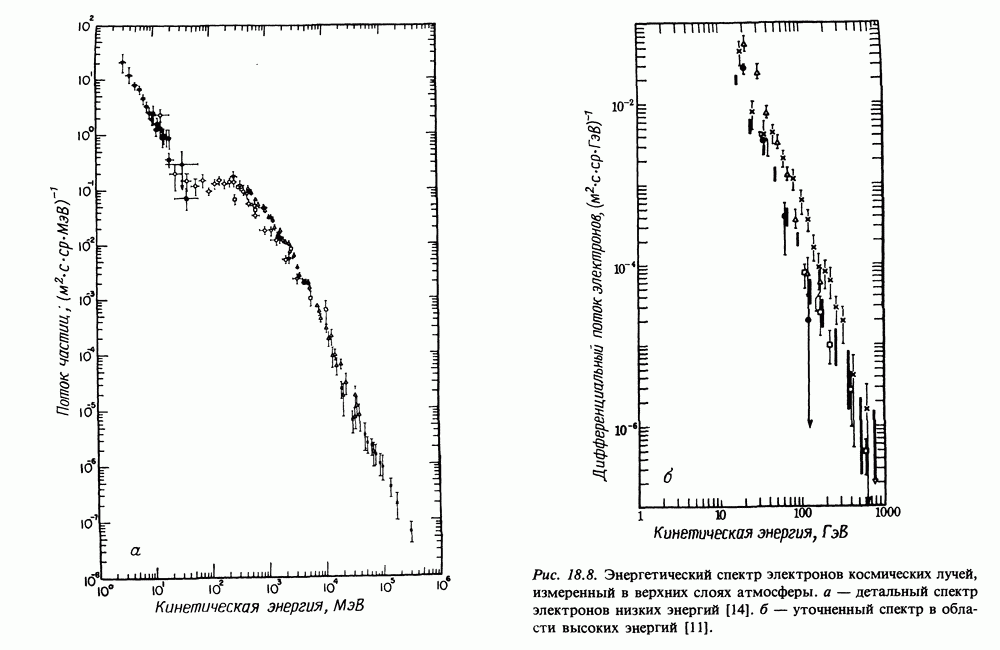
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
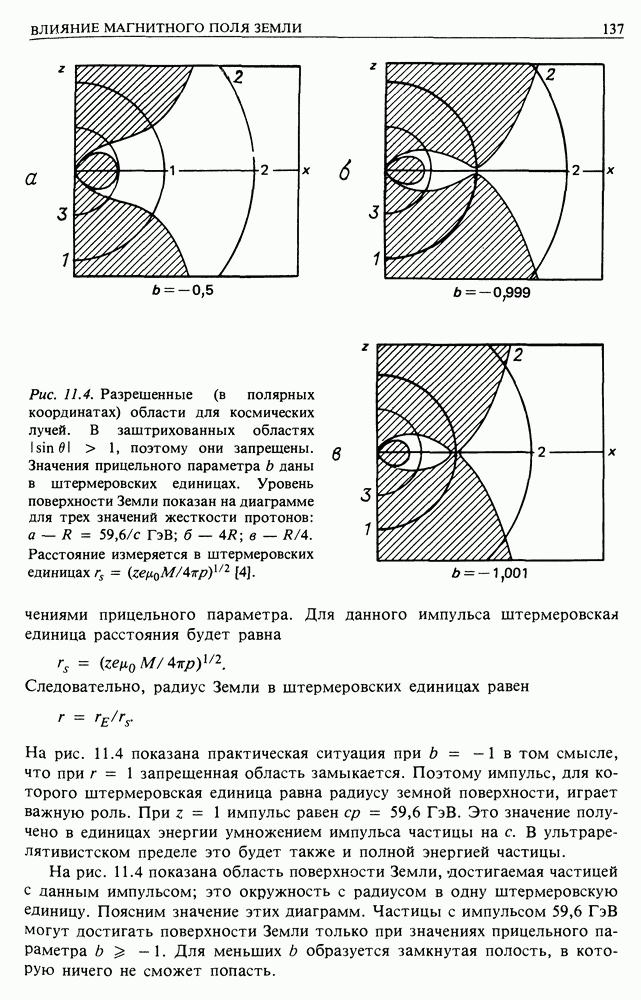
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
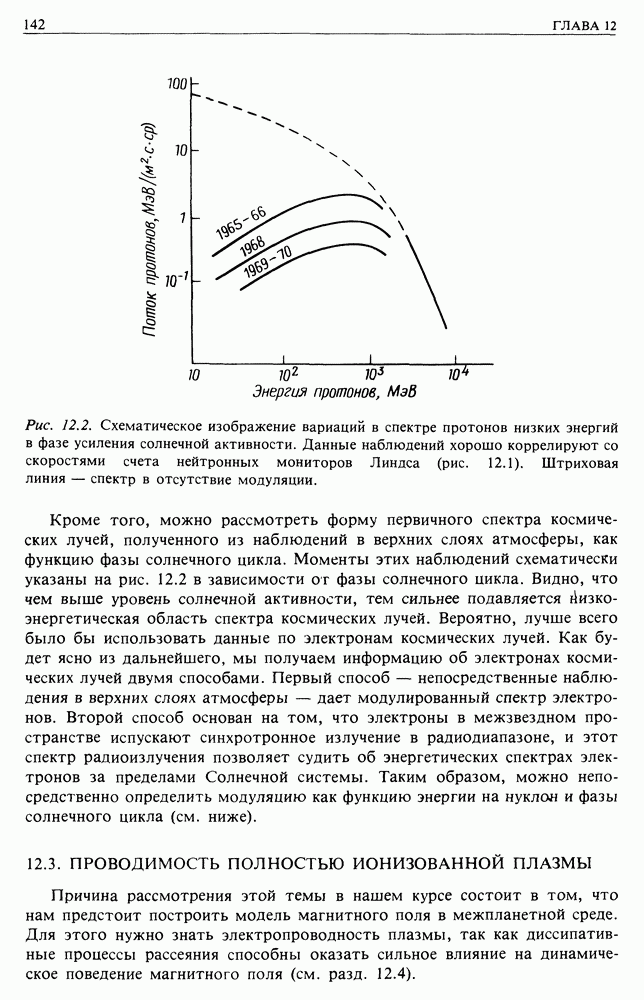
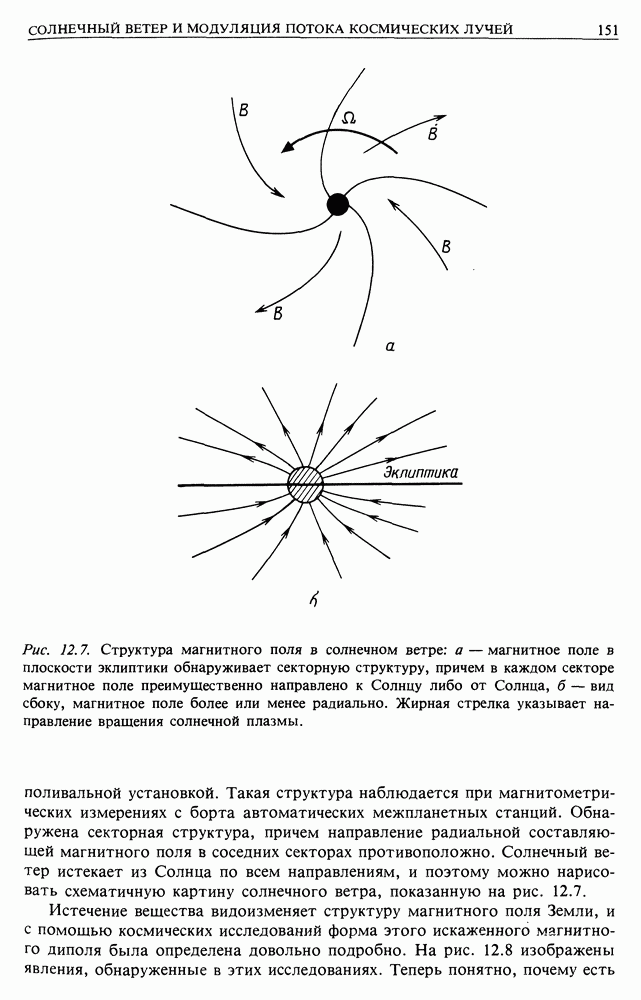
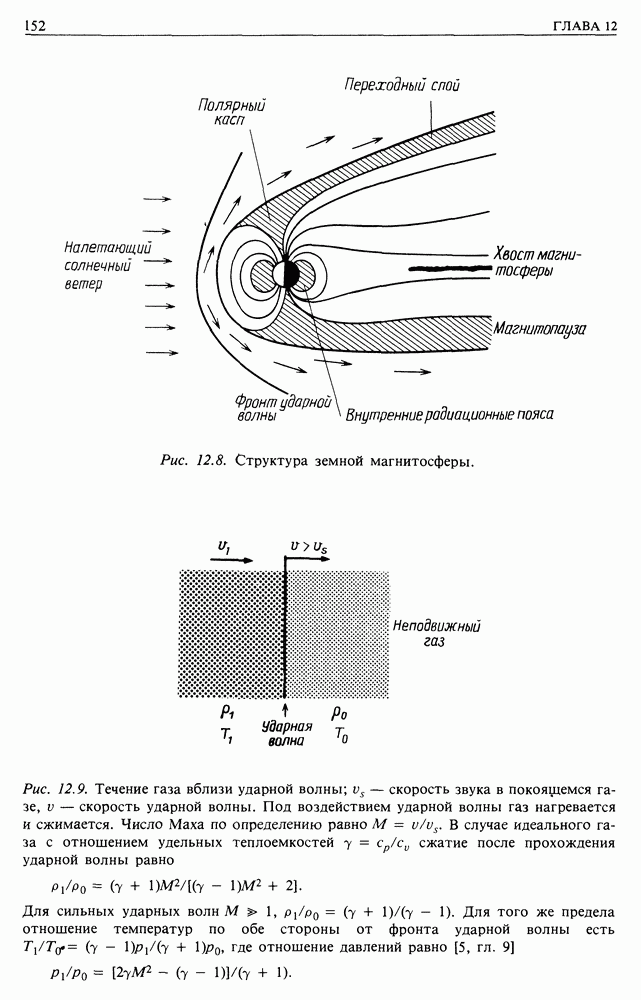
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
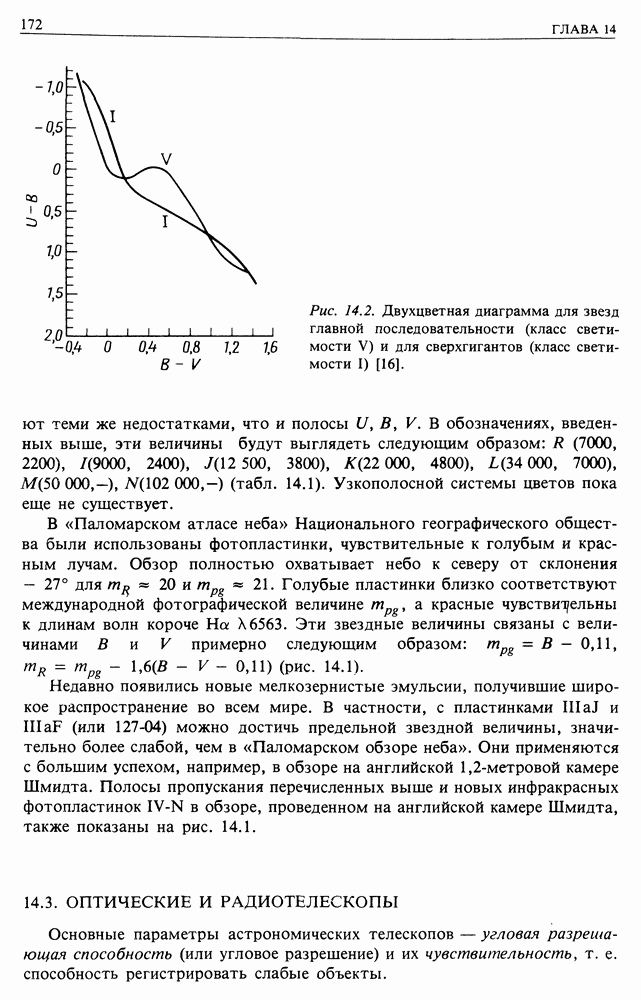
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
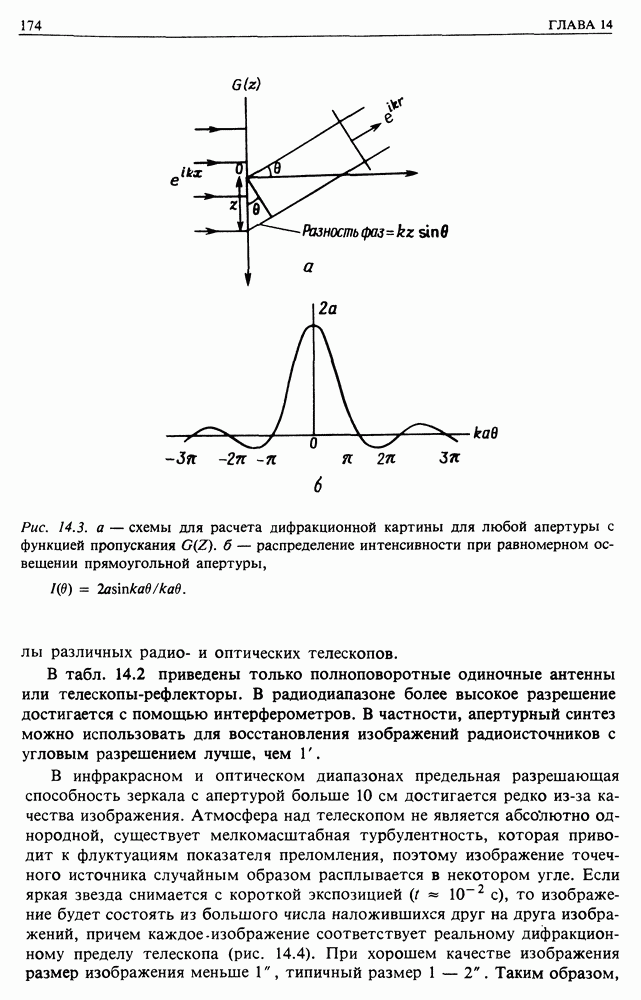
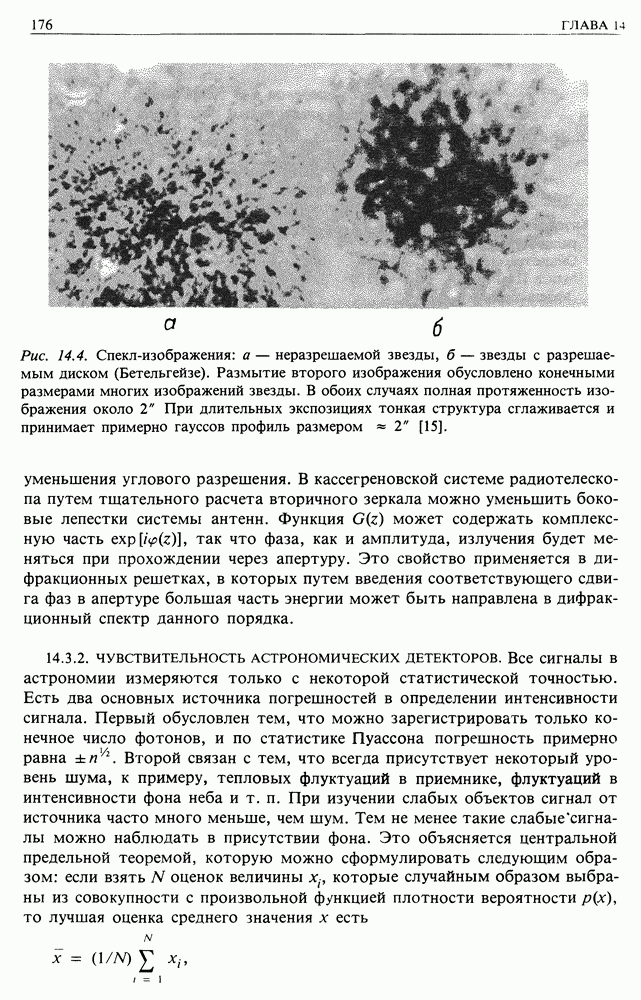
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
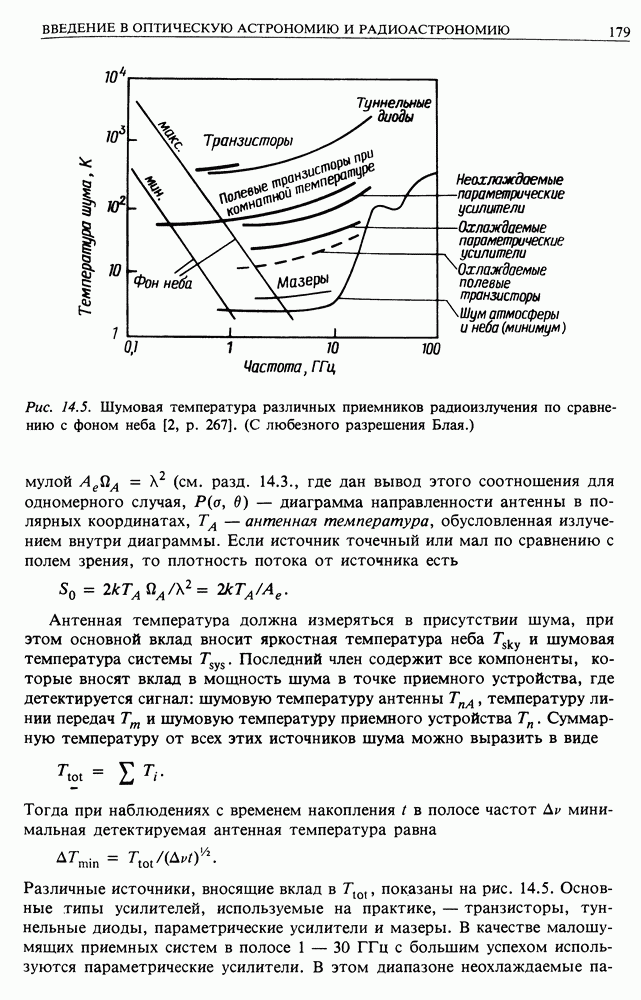
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
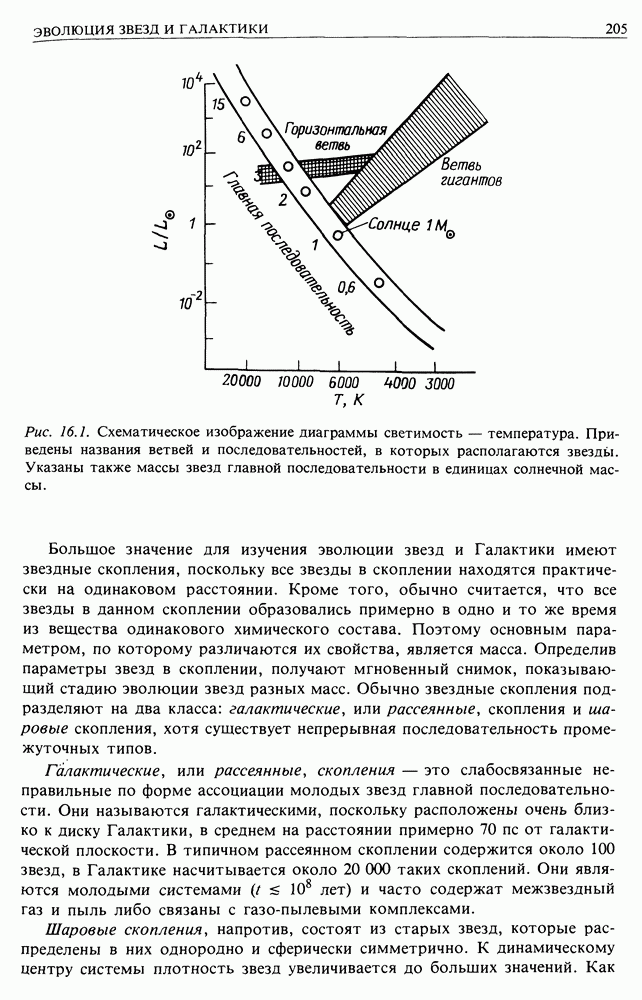
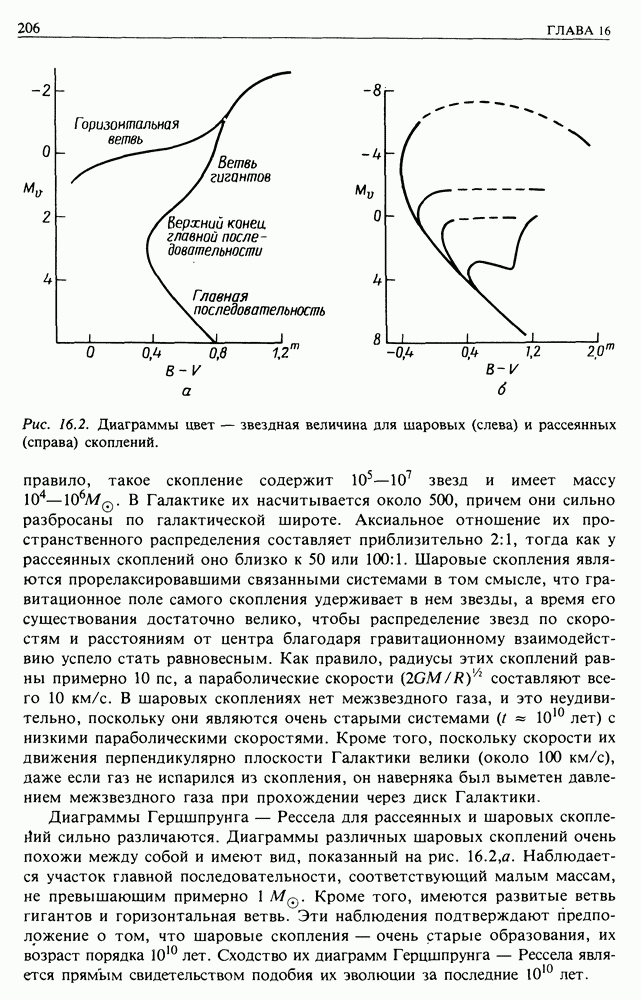
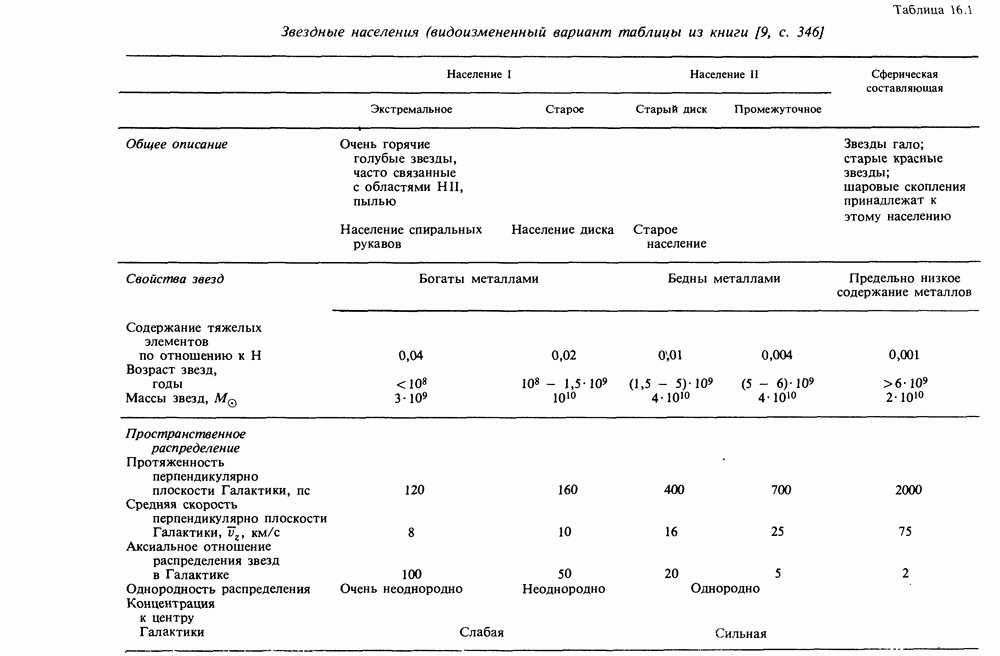
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
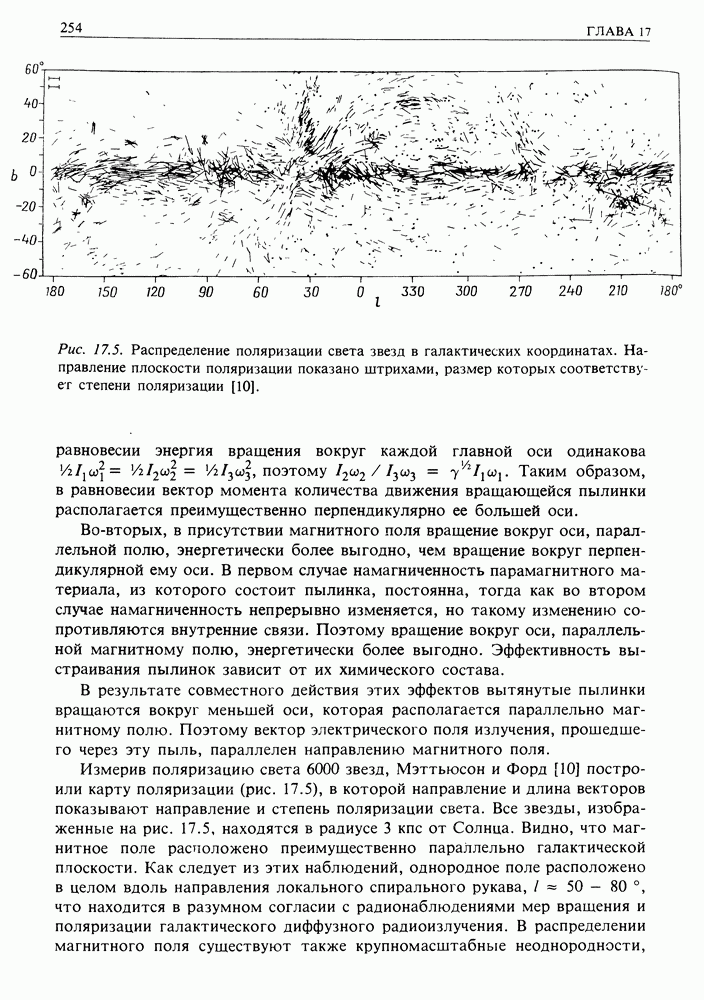
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
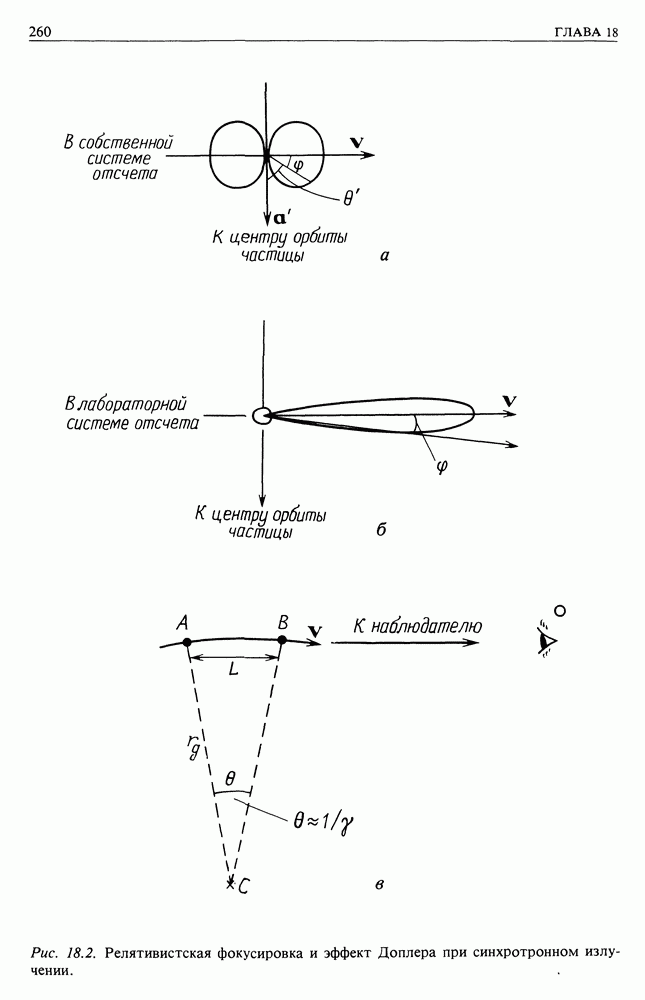
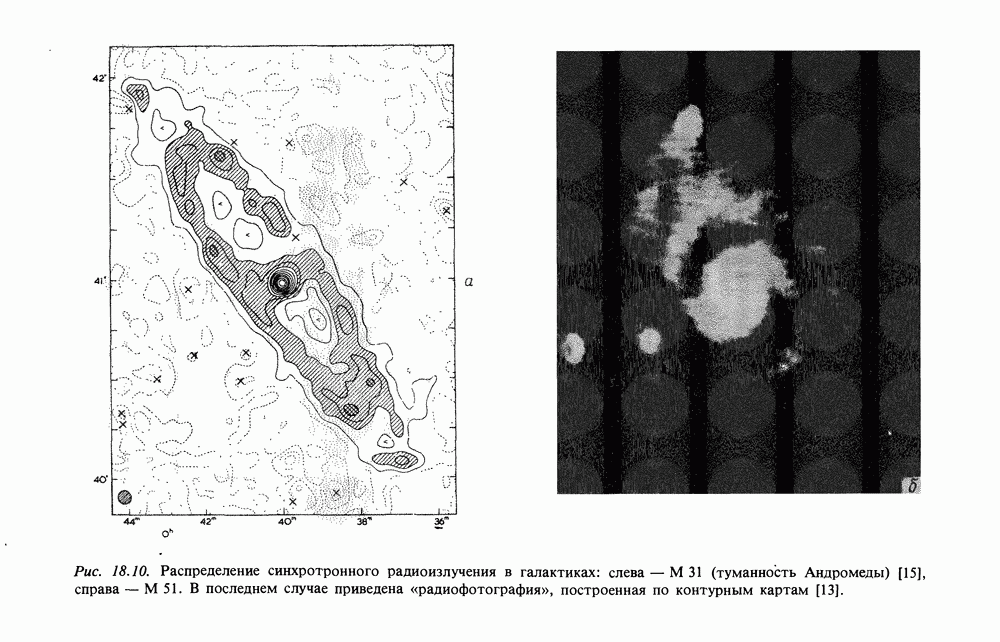
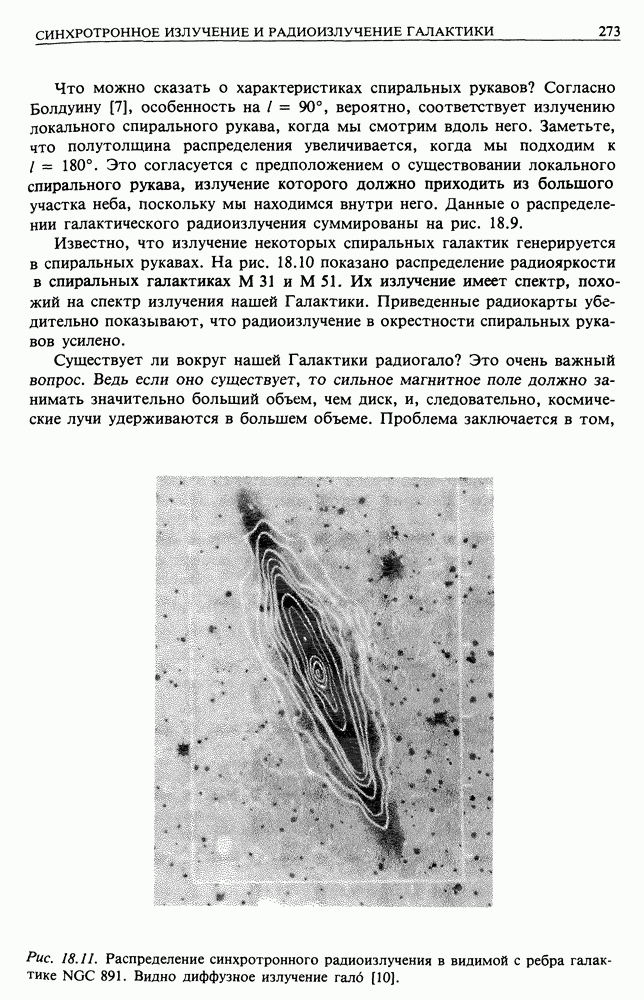
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
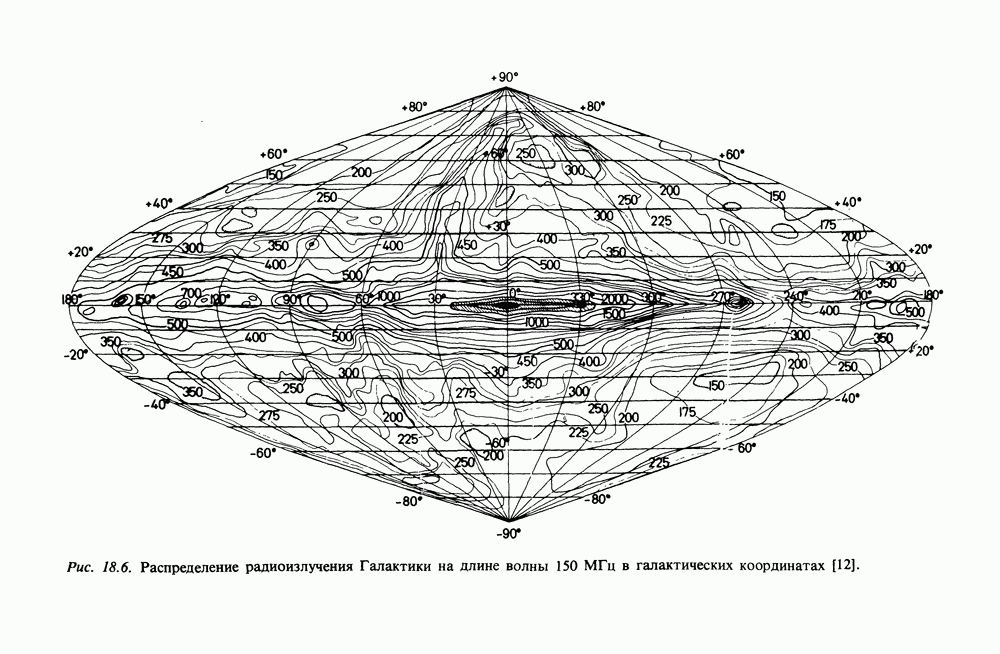
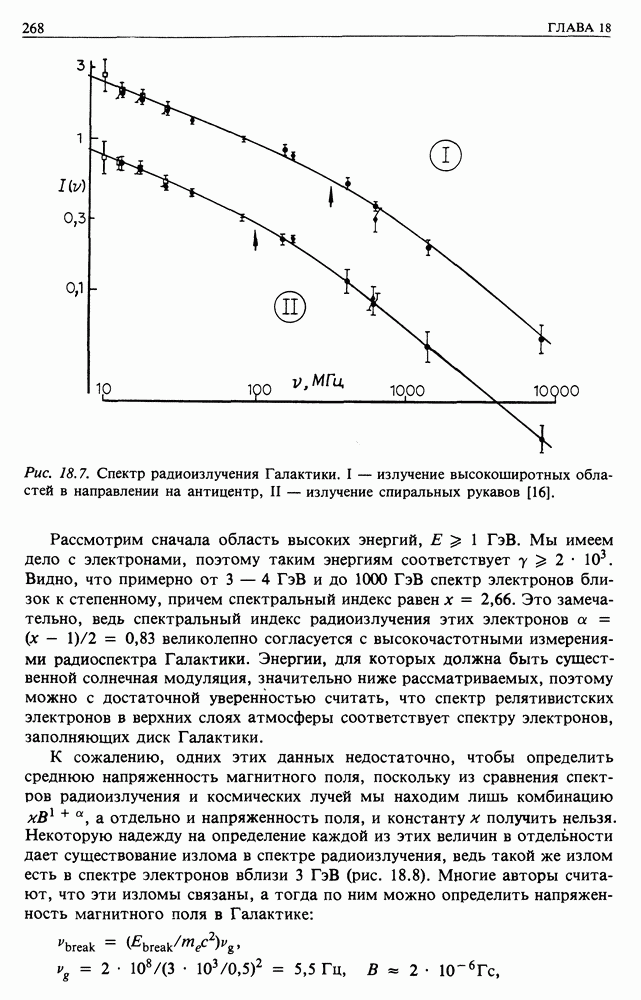
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
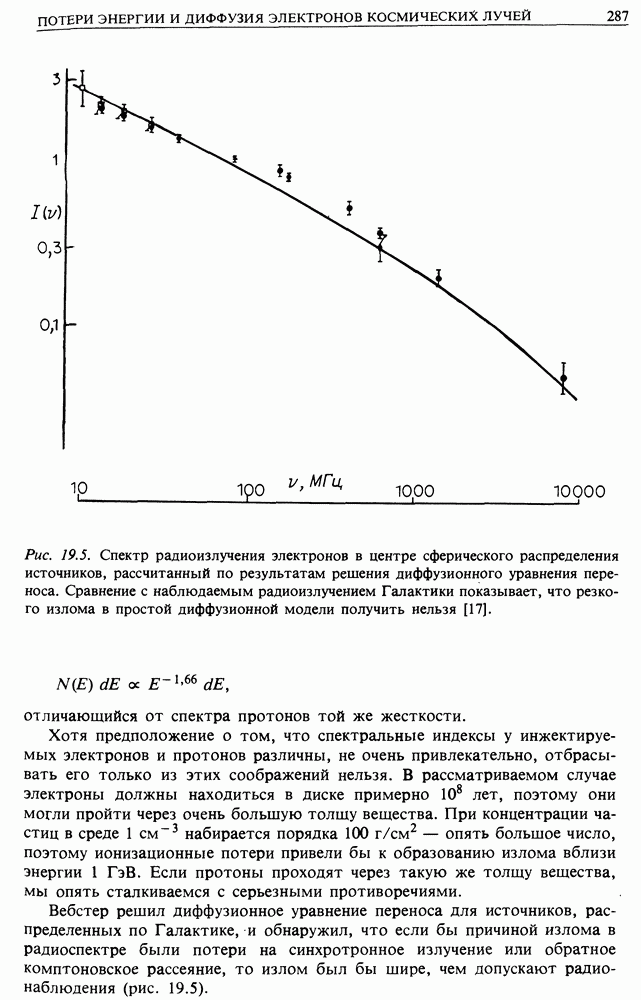
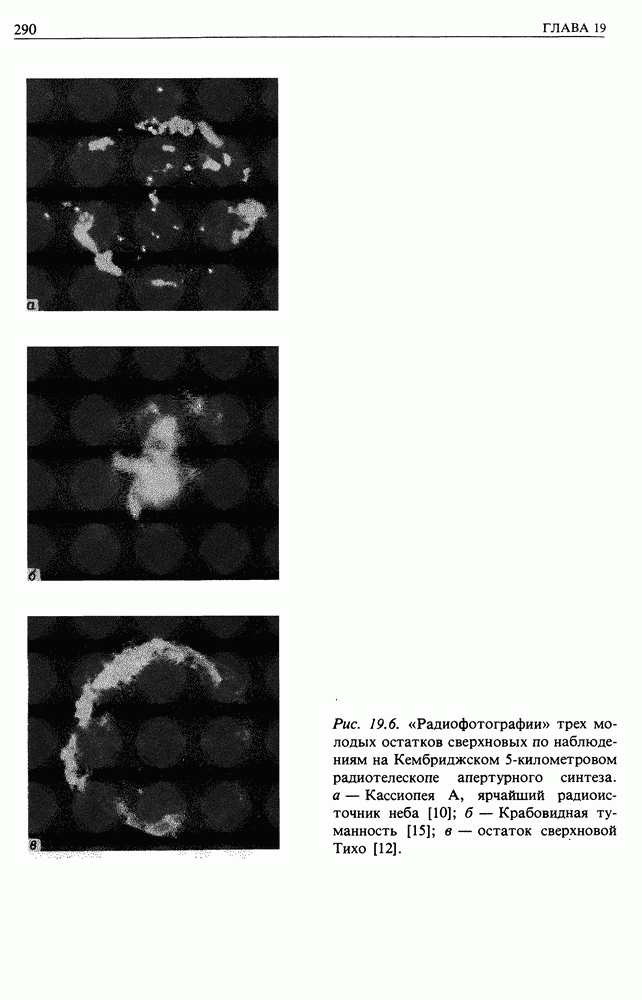
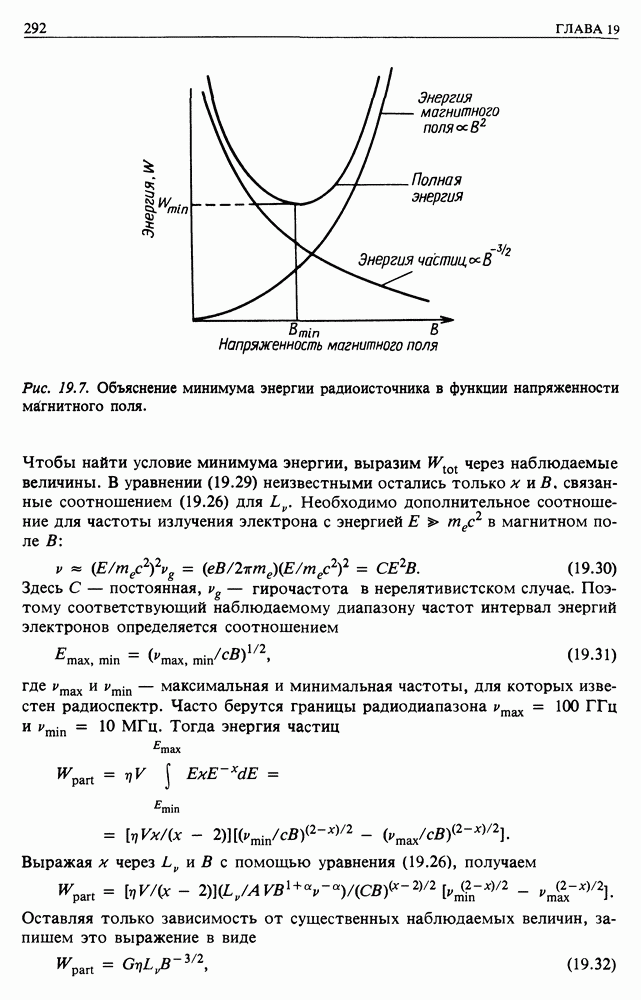
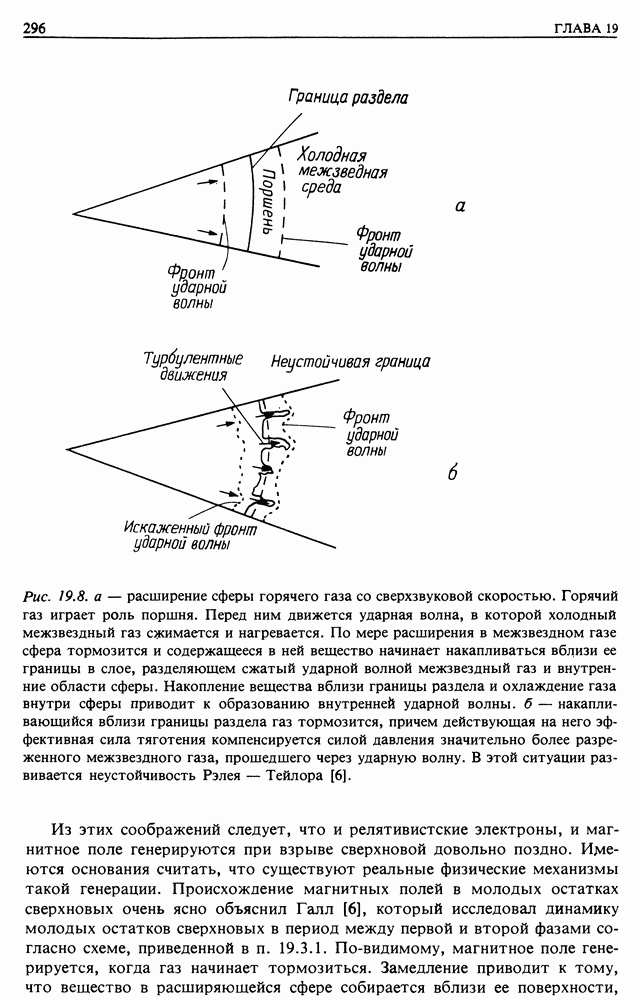
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
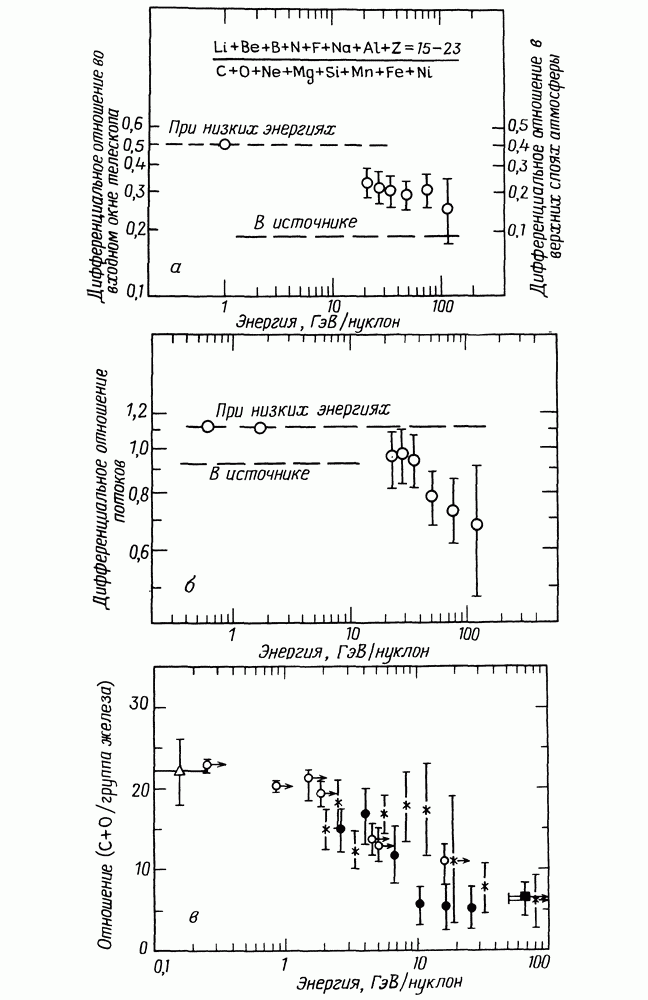
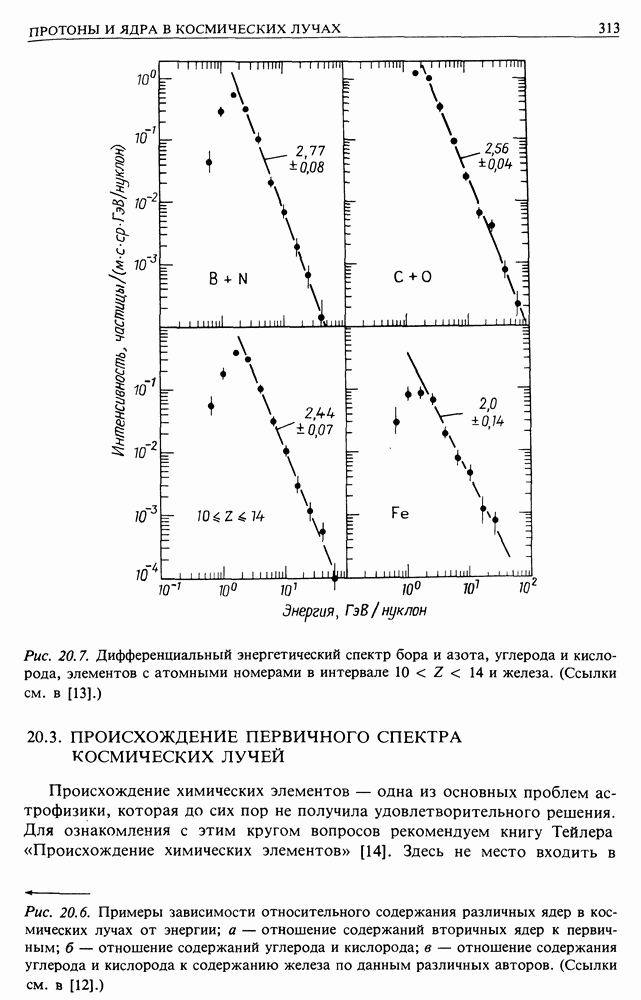
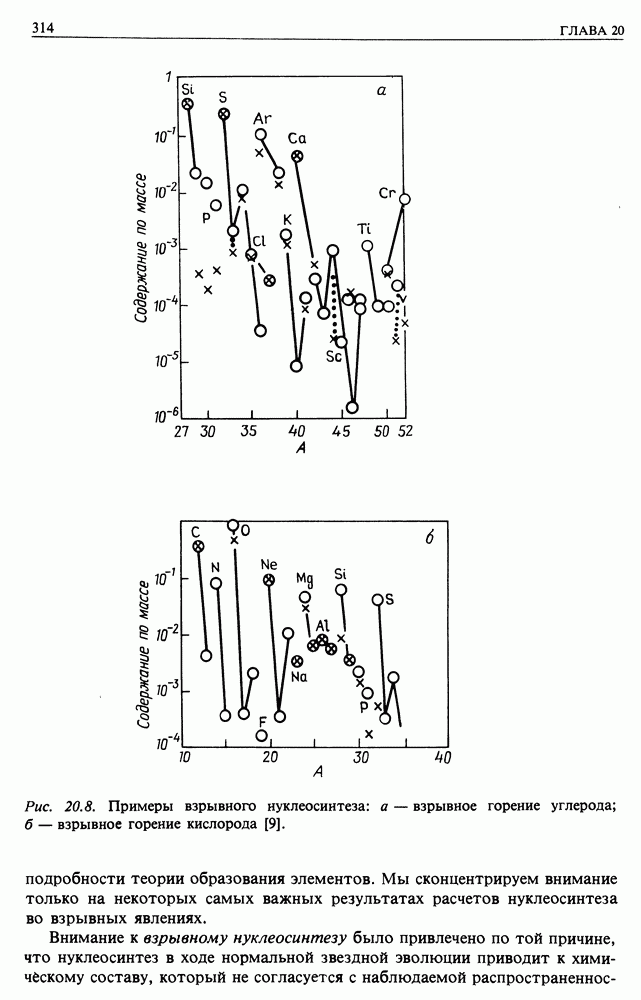
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
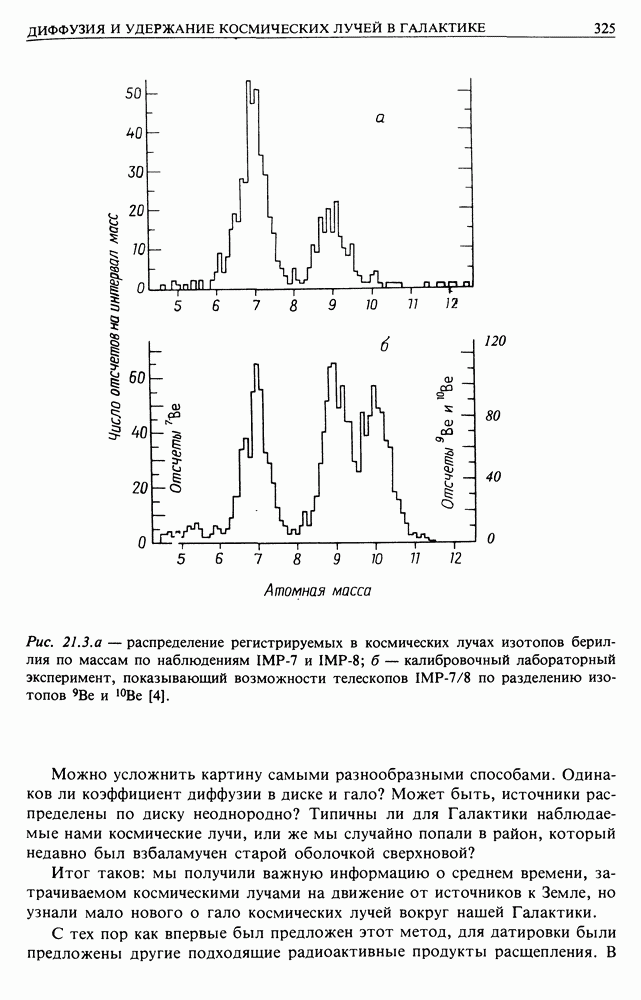
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
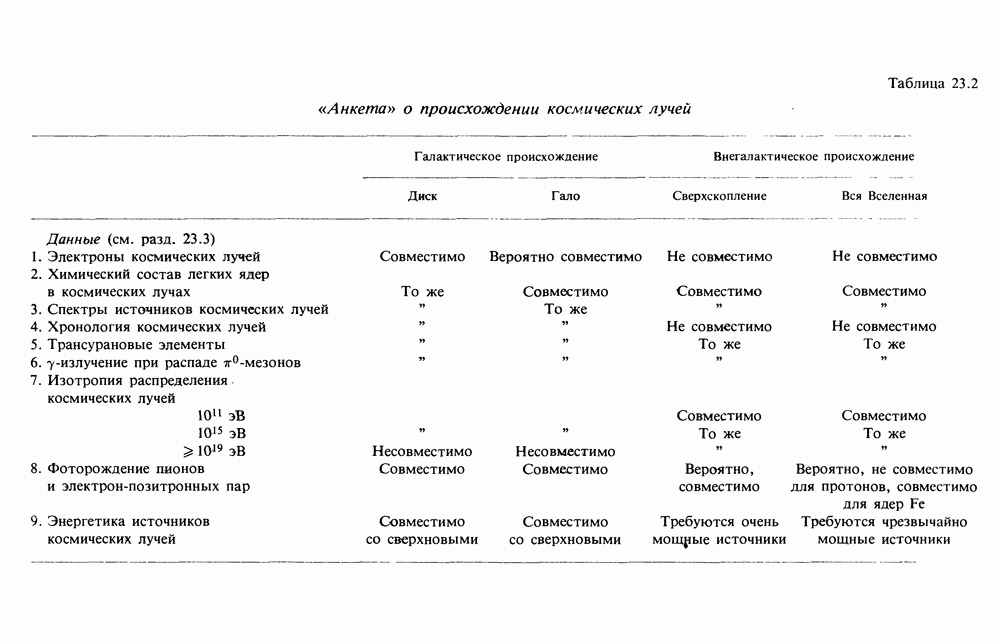
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
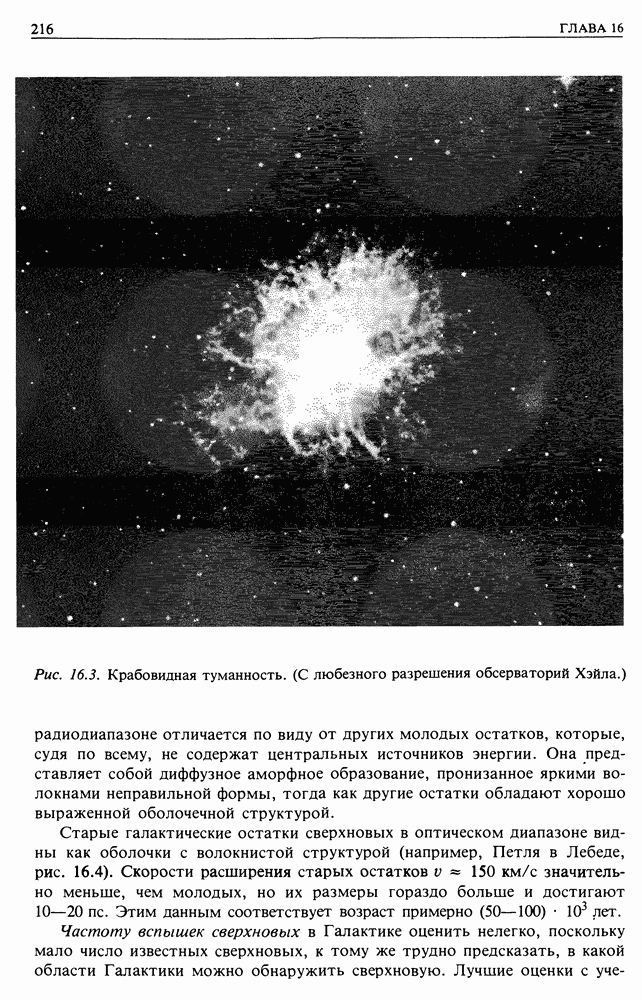
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
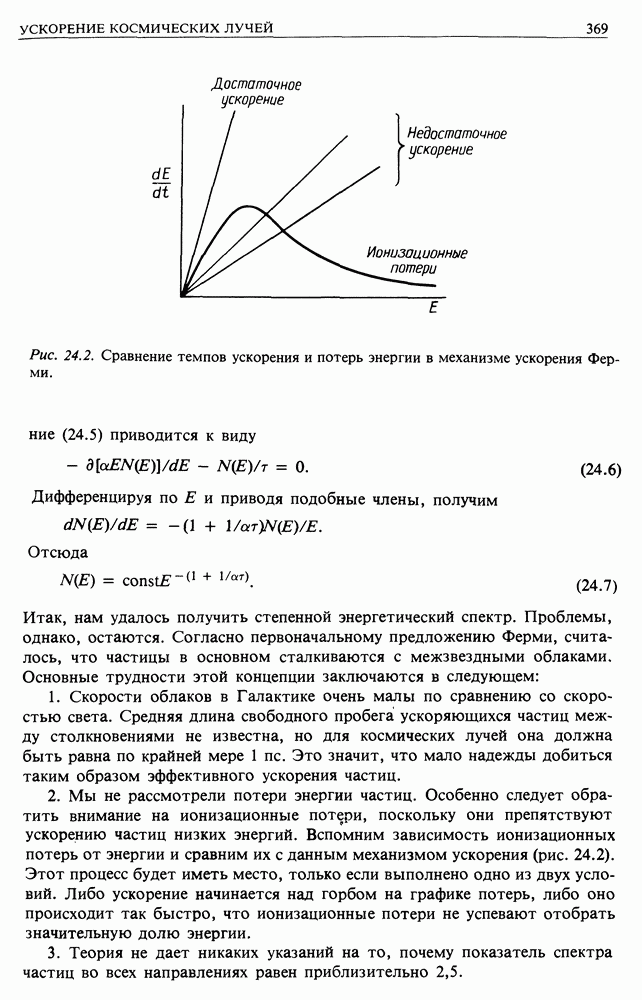
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ