13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ

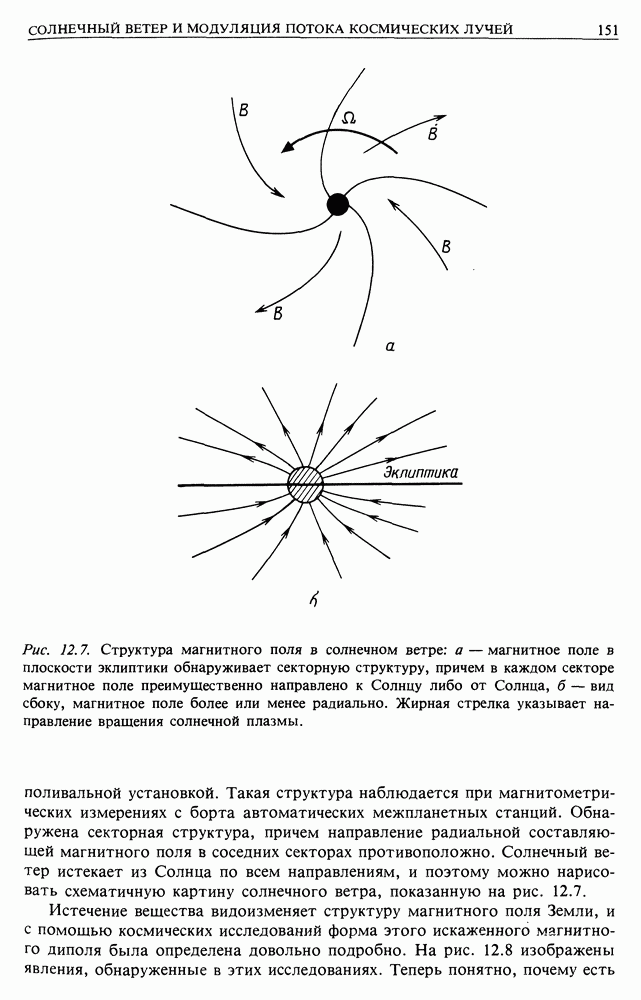
Казалось бы, теперь мы в состоянии понять, как космические лучи проникают в область земной орбиты из межзвездного пространства. Они движутся по винтовым траекториям вдоль силовых линий магнитного поля к Земле. Однако это не дает простого объяснения, почему существует корреляция между солнечной активностью и солнечной модуляцией потока космических лучей. Дело в том, что мы чрезмерно упростили картину структуры магнитного поля в солнечном ветре. Наблюдения с космических аппаратов показывают, что межпланетное поле обладает спиральной структурой, на которую накладывается нерегулярный компонент. Космические лучи могут рассеиваться по питч-углам на этих неоднородностях, и можно приближенно считать, что они диффундируют вдоль силовых линий магнитного поля с определенной средней длиной свободного пробега. Пройдя некоторое расстояние, эти частицы рассеиваются на большой угол и забывают свой начальный питч-угол. Это случайный процесс, имеющий тот же смысл, что и средняя длина свободного пробега для частиц в плазме (разд. 12.3). Значит, причина солнечной модуляции в том, что чем выше уровень солнечной модуляции, тем больше энергетическая плотность неоднородностей в солнечном ветре, тем короче средняя длина свободного пробега частиц и тем меньше поток космических лучей, достигающих Земли.

Рассмотрим одномерную радиальную диффузию против общего конвективного движения, направленного наружу и определяемого полным распределением солнечного ветра. Результирующий поток через единицу

площади на расстоянии от Солнца есть

где коэффициент диффузии, скорость солнечного ветра на расстоянии В устойчивом состоянии результирующий поток равен нулю. Таким образом,

Поэтому

где некоторый радиус относительно центра Солнца. Поэтому

Все «мелочи» включены в формулы, чтобы показать, что нужно по возможности ввести в подынтегральное выражение. Член межзвездный поток частиц; может быть функцией времени, т.е. в максимуме солнечной активности солнечный ветер может выметать межзвездный газ прочь от Земли, коэффициент диффузии может быть функцией жесткости, скорости частицы и (или фактора Лоренца 7), расстояния до Солнца, времени и т.д.

На этом этапе выявляются два альтернативных подхода. Можно аппроксимировать данные наблюдений эмпирически выбранной функцией что и делалось многими авторами. Это наиболее простой путь, так как альтернативой к нему является разработка полной теории модуляционных процессов.

В первом подходе пробную функцию упрощают до вида

(где индексы относятся к расстоянию от Земли до Солнца и к очень удаленнойг области межзвездной среды соответственно) и пытаются найти подходящие функции Здесь неявно предполагается, что скорость солнечного ветра постоянна, и коэффициент диффузии можно записать в виде

где средняя длина свободного пробега частицы с жесткостью эмпирическая функция времени. В ранних работах функция бралась в виде

где что давало довольно хорошие результаты. Последующие авторы исследовали, можно ли разделить переменные указанным образом, и использовали более сложные формы

Во втором подходе стараются связать коэффициент диффузии с наблюдаемым спектром неоднородностей в межпланетном магнитном поле. Это более интересно, и мы покажем, как вывести основные результаты методом, с которым мы сейчас познакомимся.