| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
18.1. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ
Наконец, мы приступаем к изучению основного физического механизма генерации нетеплового излучения частицами высоких энергий — синхротронного излучения релятивистских и ультрарелятивистских электронов, т. е. электронов космических лучей. Термин «нетепловое излучение» часто используется в астрофизике высоких энергий. Он весьма неудачен, поскольку все механизмы излучения в некотором смысле «тепловые». Этот термин традиционно обозначает «непрерывное излучение частиц, распределение которых по энергиям отличается от максвелловского», иначе говоря, непрерывное излучение, спектр которого не похож ни на спектр тормозного излучения, ни на спектр абсолютно черного тела.
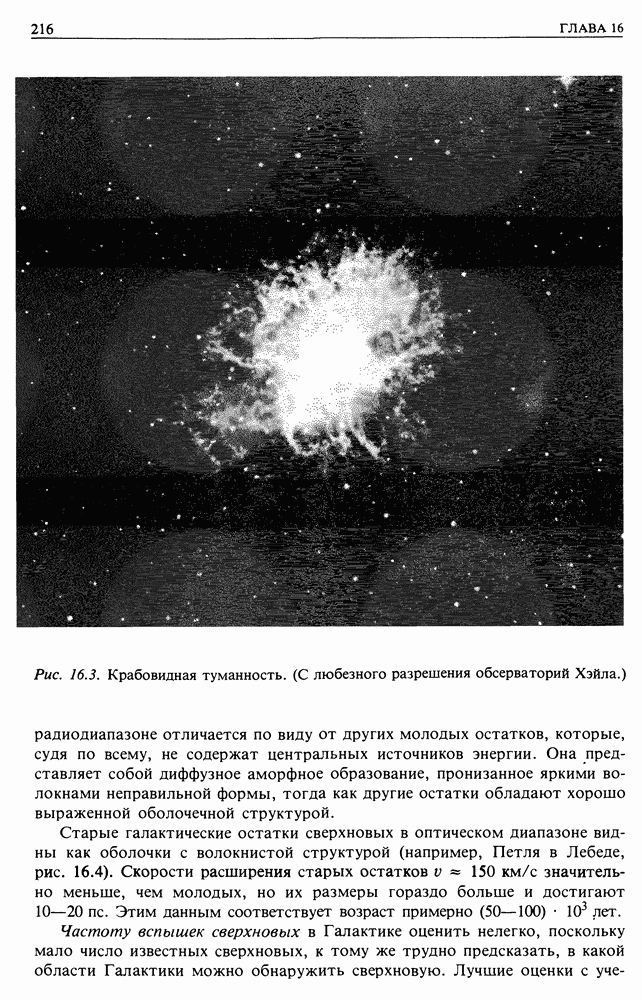
Синхротронным называется излучение частиц высоких энергий, движущихся по винтовым траекториям вдоль силовых линий магнитного поля. Сначала оно было обнаружено в ускорителях бетатронах, где впервые частицы были разогнаны до ультрарелятивистских скоростей. Этот же механизм ответствен за радиоизлучение Галактики, остатков сверхновых и внегалактических радиоисточников. Им также обусловлено непрерывное оптическое излучение Крабовидной туманности и, возможно, квазаров.
Прежде всего рассмотрим потери энергии на излучение.
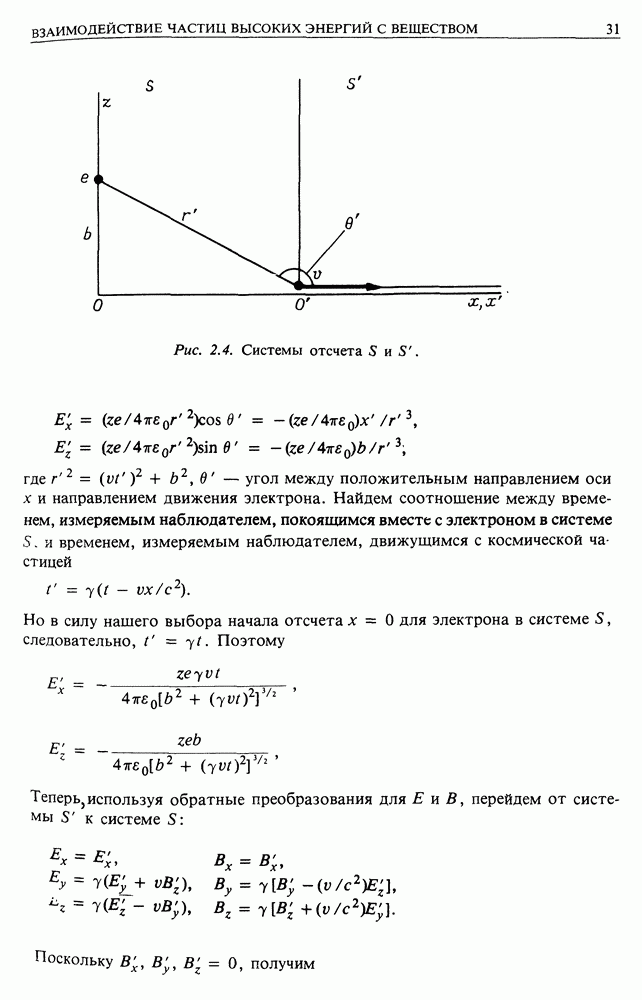
18.1.1. Потери энергии на излучение. Снова воспользуемся тем обстоятельством, что в собственной системе отсчета электрона его ускорение мало и поэтому применима нерелятивистская теория излучения. Выберем оси координат, как показано на рис. 18.1.
Пусть питч-угол частицы равен в. Для простоты зададим систему координат так, чтобы ось х совпадала с мгновенным направлением скорости частицы в лабораторной системе отсчета (т. е. в системе, где задано В). Чтобы найти действующую на частицу силу, перейдем к собственной системе отсчета электрона. В системе  действующая на электрон сила равна
действующая на электрон сила равна

поскольку частица в данный момент покоится. Чтобы найти  необходимо совершить преобразование напряженности магнитного поля В в систему
необходимо совершить преобразование напряженности магнитного поля В в систему 


Рис. 18.1. Система координат, используемая для вычисления потерь энергии на синхротронное излучение.
Отсюда

Следовательно, в собственной системе отсчета электрона скорость потерь энергии на излучение равна

(см. п. 3.3.1). Перепишем это выражение следующим образом:

Мы использовали соотношение  Величина в первой скобке в правой части формулы — томсоновское сечение (разд. 4.3). Поэтому
Величина в первой скобке в правой части формулы — томсоновское сечение (разд. 4.3). Поэтому

где  плотность энергии магнитного поля. Теперь нам осталось только совершить преобразование Лоренца назад в лабораторную систему отсчета, и мы окончательно получим темп потерь энергии частицей. Воспользуемся доказанным в п. 3.3.5 утверждением о том, что
плотность энергии магнитного поля. Теперь нам осталось только совершить преобразование Лоренца назад в лабораторную систему отсчета, и мы окончательно получим темп потерь энергии частицей. Воспользуемся доказанным в п. 3.3.5 утверждением о том, что  является инвариантом относительно преобразования Лоренца. Тогда (18.5) дает также скорость потерь энергии в лабораторной системе отсчета:
является инвариантом относительно преобразования Лоренца. Тогда (18.5) дает также скорость потерь энергии в лабораторной системе отсчета:

В ультрарелятивистском пределе  с это выражение сводится к
с это выражение сводится к

Этот результат получен в предположении, что питч-угол в задан. Чтобы усреднить полученное выражение по питч-углам, необходимо домножить его на  и проинтегрировать
и проинтегрировать

Заметим также, что, если питч-угол электрона случайным образом меняется во время движения, формула (18.7) остается верной в среднем.
18.1.2. Спектр излучения одного электрона. Приведенный вывод был совершенно строгим. Далее нам необходимо найти спектр излучения. Точный анализ здесь требует существенно больших усилий, поэтому мы только покажем в общих чертах, как спектр зависит от основных параметров.
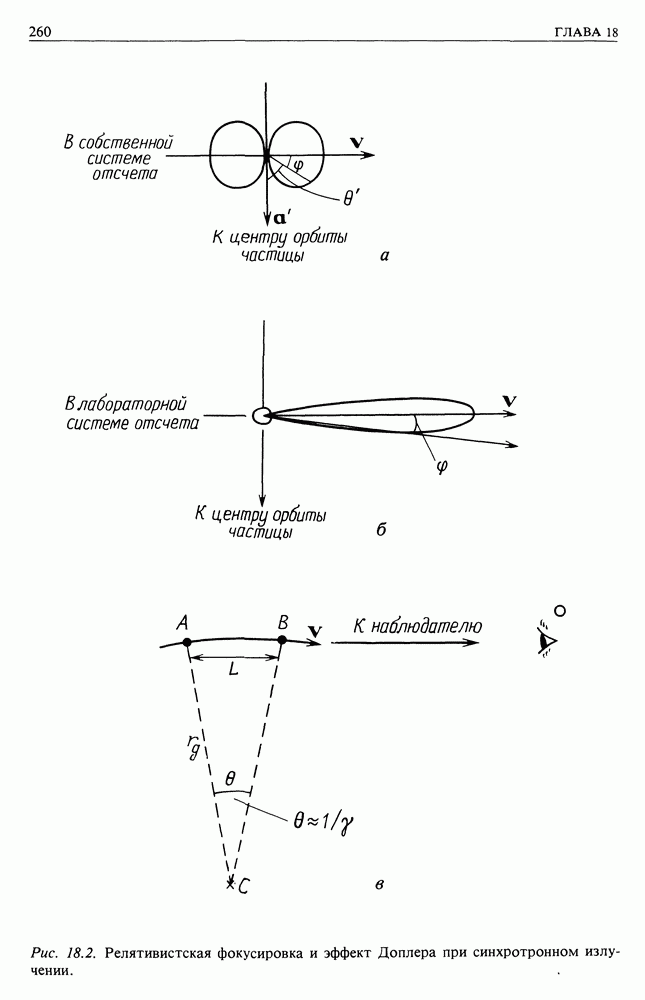
Прежде всего, что именно видит наблюдатель в лабораторной системе отсчета? Поскольку в собственной системе отсчета диаграмма направленности излучения относительно вектора ускорения имеет обычный дипольный вид, угловое распределение излучения с точки зрения внешнего наблюдателя получается с помощью формулы для аберрации (рис.  Излучение распределено относительно вектора скорости по закону
Излучение распределено относительно вектора скорости по закону  В лабораторной системе отсчета диаграмма сильно вытянута в соответствии с формулой для релятивистской аберрации. Зависимость интенсивности излучения от угла
В лабораторной системе отсчета диаграмма сильно вытянута в соответствии с формулой для релятивистской аберрации. Зависимость интенсивности излучения от угла  показана на рис. 18.2,6. Углы
показана на рис. 18.2,6. Углы  связаны соотношением
связаны соотношением

Например, в направлении  в собственной системе отсчета интенсивность составляет половину максимальной, приходящейся на
в собственной системе отсчета интенсивность составляет половину максимальной, приходящейся на  тогда как в лабораторной системе соответствующий угол
тогда как в лабораторной системе соответствующий угол  определяется соотношением
определяется соотношением

Таким образом, излучение в интервале углов —  фокусируется в направлении движения электрона в луч полушириной
фокусируется в направлении движения электрона в луч полушириной  Наблюдатель регистрирует значительный поток, только когда луч проходит через него. Поэтому он видит яркие «вспышки» каждый раз, когда вектор скорости электрона попадает в конус с раствором
Наблюдатель регистрирует значительный поток, только когда луч проходит через него. Поэтому он видит яркие «вспышки» каждый раз, когда вектор скорости электрона попадает в конус с раствором  с осью вдоль луча зрения. Анализ Фурье этого импульса дает частотный спектр синхротронного излучения. Очевидно, что, поскольку
с осью вдоль луча зрения. Анализ Фурье этого импульса дает частотный спектр синхротронного излучения. Очевидно, что, поскольку  должны быть задействованы очень высокие гармоники гирочастоты электрона.
должны быть задействованы очень высокие гармоники гирочастоты электрона.
Наблюдатель регистрирует значительное излучение только от участка орбиты частицы, соответствующего интервалу углов в  но наблюдаемая длительность импульса меньше, чем
но наблюдаемая длительность импульса меньше, чем  часть периода обращения, поскольку задний фронт импульса догоняет передний, т. е. наблюдаемая частота излучения очень сильно возрастает вследствие эффекта Доплера. Правильный результат можно получить с помощью рис. 18.2, в. Разность времен прибытия в точку О излучения из точек
часть периода обращения, поскольку задний фронт импульса догоняет передний, т. е. наблюдаемая частота излучения очень сильно возрастает вследствие эффекта Доплера. Правильный результат можно получить с помощью рис. 18.2, в. Разность времен прибытия в точку О излучения из точек  составляет
составляет

Это время равнялось бы  только если скорость света была бы бесконечной! Далее,
только если скорость света была бы бесконечной! Далее,


(кликните для просмотра скана)
где  нерелятивистская угловая гирочастота,
нерелятивистская угловая гирочастота,  Кроме того,
Кроме того,

Поэтому

т. е. длительность импульса в лабораторной системе отсчета составляет примерно долю  от периода обращения
от периода обращения  Максимальная фурье-компонента спектрального распределения наблюдаемого излучения приходится на частоту
Максимальная фурье-компонента спектрального распределения наблюдаемого излучения приходится на частоту  т. е.
т. е.

где  гирочастота в нерелятивистском случае.
гирочастота в нерелятивистском случае.
В приведенном выводе предполагается, что частица движется по круговой орбите вокруг силовой линии магнитного поля, т. е. питч-угол в равен 90°. При произвольном питч-угле подобные же вычисления приводят к результату

Этот простой пример был разобран так подробно потому, что направленность вообще характерна для излучения ультрарелятивистских частиц вне зависимости от природы сил, приводящих к ускорению. Возвращаясь к предыдущим вычислениям, запишем наблюдаемую частоту в виде

где  гирочастота в релятивистском случае,
гирочастота в релятивистском случае,  радиус кривизны орбиты частицы. Заметим, что вообще можно интерпретировать
радиус кривизны орбиты частицы. Заметим, что вообще можно интерпретировать  как мгновенный радиус кривизны орбиты частицы,
как мгновенный радиус кривизны орбиты частицы,  дает связанную с ним эффективную частоту. Наблюдается излучение с частотой примерно в
дает связанную с ним эффективную частоту. Наблюдается излучение с частотой примерно в  раз больше.
раз больше.
Подробные расчеты приводят к следующему точному результату: полная излучательная способность электрона с энергией  движущегося под углом
движущегося под углом  к направлению магнитного поля В, при
к направлению магнитного поля В, при  равна
равна

где  функция Бесселя порядка 5/3. Критическая частота определяется соотношением
функция Бесселя порядка 5/3. Критическая частота определяется соотношением

Спектр показан на рис. 18.3. Максимум излучательной способности приходится на частоту


Рис. 18.3. Спектр синхротронного излучения ультрарелятивистских электронов. Максимум интенсивности приходится на частоту  где критическая частота
где критическая частота 
На высоких частотах  функция Бесселя асимптотически стремится к экспоненте и излучательная способность имеет вид
функция Бесселя асимптотически стремится к экспоненте и излучательная способность имеет вид

На низких частотах 

Выражение (18.11) нужно проинтегрировать по питч-углам и энергиям электронов, т. е. по  Тогда получим полную излучательную способность
Тогда получим полную излучательную способность

Часто распределение по питч-углам можно считать изотропным

а энергетический спектр электрона — степенным

где  число частиц в единице объема. Прежде чем привести точный результат, получим правильную функциональную зависимость значительно более простым способом.
число частиц в единице объема. Прежде чем привести точный результат, получим правильную функциональную зависимость значительно более простым способом.
18.1.3. Излучение электронов со степенным спектром. Очень часто спектр космических лучей аппроксимируется степенным законом. Ниже будет показано, что спектр электронного компонента космических лучей хорошо описывается законом  Примем более общее выражение
Примем более общее выражение  Спектр излучения электронов с энергией
Спектр излучения электронов с энергией  имеет узкий пик вблизи критической частоты
имеет узкий пик вблизи критической частоты  (см. рис. 18.3), причем ширина этого
(см. рис. 18.3), причем ширина этого
пика значительно меньше, чем ширина распределения электронов по энергиям. Поэтому с хорошей точностью можно считать, что электроны с энергией  излучают только на критической частоте
излучают только на критической частоте  которая приближенно равна
которая приближенно равна

где  Тогда мощность
Тогда мощность  излучаемая в интервале частот от
излучаемая в интервале частот от  до
до  равна скорости потерь энергии электронами с энергиями от
равна скорости потерь энергии электронами с энергиями от  до
до  т. е.
т. е.

Далее,

Подставляя эти выражения в (18.15), получим зависимость светимости от  и фундаментальных констант
и фундаментальных констант

В этом приближении постоянная равна

Точный расчет приводит к такой же функциональной зависимости. Важное правило состоит в том, что если спектр электронов степенной с индексом х, то спектральный индекс синхротронного излучения этих электронов равен 
Точный расчет приводит к следующей формуле:

Здесь V — объем излучающей области, В — напряженность магнитного поля в гауссах. Значения постоянной  приведены в табл. 18.1.
приведены в табл. 18.1.
Таблица 18.1 (см. скан) Значения функции 
18.1.4. ПОЛЯРИЗАЦИЯ СИНХРОТРОННОГО ИЗЛУЧЕНИЯ. Механизм поляризации синхротронного излучения можно понять с помощью принципов, изложенных в п. 3.3.1. Полезно ввести представление о конусе скоростей. Это конус, который описывает вектор скорости электрона  при движении по винтовой траектории в магнитном поле. Ось конуса совпадает с направлением магнитного поля, вокруг которого прецессирует с циклотронной частотой вектор скорости. В соответствии с выводами п. 18.1.2, наблюдатель регистрирует значительное излучение, только когда направление движения электрона составляет с направлением на наблюдателя угол, не превышающий
при движении по винтовой траектории в магнитном поле. Ось конуса совпадает с направлением магнитного поля, вокруг которого прецессирует с циклотронной частотой вектор скорости. В соответствии с выводами п. 18.1.2, наблюдатель регистрирует значительное излучение, только когда направление движения электрона составляет с направлением на наблюдателя угол, не превышающий 
Рассмотрим сначала случай, когда образующая конуса скоростей электрона совпадает с лучом зрения (рис. 18.4). Вектор ускорения а параллелен вектору  поэтому наблюдаемое излучение будет линейно поляризовано в направлении
поэтому наблюдаемое излучение будет линейно поляризовано в направлении  Таким образом, в этом случае вектор электрического поля волны
Таким образом, в этом случае вектор электрического поля волны  перпендикулярен проекции вектора В на картинную плоскость, как показано на рис. 18.4.
перпендикулярен проекции вектора В на картинную плоскость, как показано на рис. 18.4.
Однако вклад в измеряемую интенсивность вносят также те электроны, конусы скоростей которых подходят к направлению на наблюдателя ближе, чем на угол  Они дают эллиптически поляризованное излучение, поскольку вектор ускорения электрона поворачивается при его движении. Для ультрарелятивистских частиц,
Они дают эллиптически поляризованное излучение, поскольку вектор ускорения электрона поворачивается при его движении. Для ультрарелятивистских частиц,  полная результирующая поляризация находится интегрированием по всем частицам, вносящим вклад в излучение в направлении на наблюдателя. При этом, поскольку ширина луча
полная результирующая поляризация находится интегрированием по всем частицам, вносящим вклад в излучение в направлении на наблюдателя. При этом, поскольку ширина луча  очень мала, компоненты с поляризацией, параллельной проекции В, также малы и результирующая поляризация оказывается линейной. Теория показывает, что в однородном магнитном поле степень линейной поляризации для изотропно распределенных электронов со степенным спектром
очень мала, компоненты с поляризацией, параллельной проекции В, также малы и результирующая поляризация оказывается линейной. Теория показывает, что в однородном магнитном поле степень линейной поляризации для изотропно распределенных электронов со степенным спектром  равна
равна


Рис. 18.4. К рассмотрению поляризации синхротронного излучения.
Таким образом, при  степень поляризации составляет 72%. Вектор электрического поля излучения перпендикулярен проекции магнитного поля на небесную сферу.
степень поляризации составляет 72%. Вектор электрического поля излучения перпендикулярен проекции магнитного поля на небесную сферу.
При не очень больших у может наблюдаться некоторая круговая поляризация. Доля поляризованного по кругу излучения по порядку величины равна 
18.1.5. СИНХРОТРОННОЕ САМОПОГЛОЩЕНИЕ. Наконец, посмотрим, что происходит, когда плотность энергии синхротронного излучения в излучающем объеме становится очень большой. Для радиоисточников со степенным спектром  яркостная температура
яркостная температура  пропорциональна
пропорциональна  поэтому на достаточно низких частотах яркостная температура излучения должна приближаться к кинетической температуре излучающих электронов, а тогда становятся существенными эффекты самопоглощения.
поэтому на достаточно низких частотах яркостная температура излучения должна приближаться к кинетической температуре излучающих электронов, а тогда становятся существенными эффекты самопоглощения.
Интенсивность синхротронного излучения движущихся в магнитном поле В релятивистских электронов со степенным спектром  при изотропном распределении по питч-углам равна
при изотропном распределении по питч-углам равна

где А — постоянная, слабо зависящая от  Сложность состоит в том, что распределение излучающих частиц по энергиям нетепловое, т. е. в данном случае оно не является релятивистским распределением Максвелла. Следующие рассуждения показывают, каким образом можно ввести понятие температуры. Во-первых, спектр излучения частицы с энергией
Сложность состоит в том, что распределение излучающих частиц по энергиям нетепловое, т. е. в данном случае оно не является релятивистским распределением Максвелла. Следующие рассуждения показывают, каким образом можно ввести понятие температуры. Во-первых, спектр излучения частицы с энергией  имеет максимум вблизи критической частоты
имеет максимум вблизи критической частоты  где
где  нерелятивистская гирочастота. Таким образом, процессы излучения и поглощения на частоте
нерелятивистская гирочастота. Таким образом, процессы излучения и поглощения на частоте  приближенно определяются только электронами с энергией
приближенно определяются только электронами с энергией  . Во-вторых, время релаксации спектра релятивистских электронов к равновесному громадно, поскольку вследствие низкой концентрации частиц очень велики времена взаимодействия с веществом. Поэтому можно приписать электронам данной энергии температуру Те по релятивистской формуле, связывающей энергию частиц и температуру,
. Во-вторых, время релаксации спектра релятивистских электронов к равновесному громадно, поскольку вследствие низкой концентрации частиц очень велики времена взаимодействия с веществом. Поэтому можно приписать электронам данной энергии температуру Те по релятивистской формуле, связывающей энергию частиц и температуру,

Эта эффективная температура частиц зависит от их энергии. Тогда, поскольку  В источнике с самопоглощением яркостная температура излучения должна быть равна кинетической температуре излучающих частиц
В источнике с самопоглощением яркостная температура излучения должна быть равна кинетической температуре излучающих частиц  , поэтому в пределе Рэлея — Джинса
, поэтому в пределе Рэлея — Джинса

где  телесный угол, под которым виден источник,
телесный угол, под которым виден источник, 
Эти расчеты демонстрируют физическую причину низкочастотного завала в спектре  в источниках с самопоглощением. Спектр не удовлетворяет закону Рэлея — Джинса, поскольку эффективная кинетическая
в источниках с самопоглощением. Спектр не удовлетворяет закону Рэлея — Джинса, поскольку эффективная кинетическая

Рис. 18.5.
температура электронов зависит от частоты. Отметим, что в источниках с самопоглощением спектр имеет вид  независимо от спектра излучающих частиц. Типичный спектр радиоисточника с самопоглощением показан на рис. 18.5.
независимо от спектра излучающих частиц. Типичный спектр радиоисточника с самопоглощением показан на рис. 18.5.
Спектры примерно такого вида наблюдаются у ядер активных галактик и квазаров. Согласно общепринятой точке зрения, они возникают вследствие синхротронного самопоглощения. Во многих случаях угловые размеры источников также измерялись посредством интерферометрии со сверхдлинными базами. Они в целом согласуются с оценками физических размеров, полученными по переменности источников (т. е.  где
где  характерное время переменности) и из соображений, связанных с самопоглощением.
характерное время переменности) и из соображений, связанных с самопоглощением.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
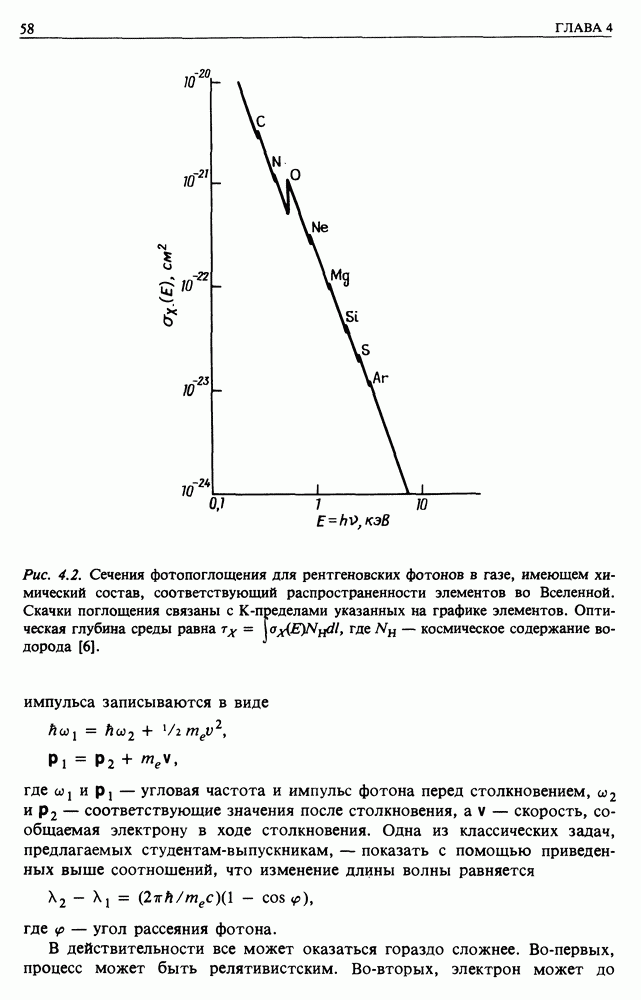
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
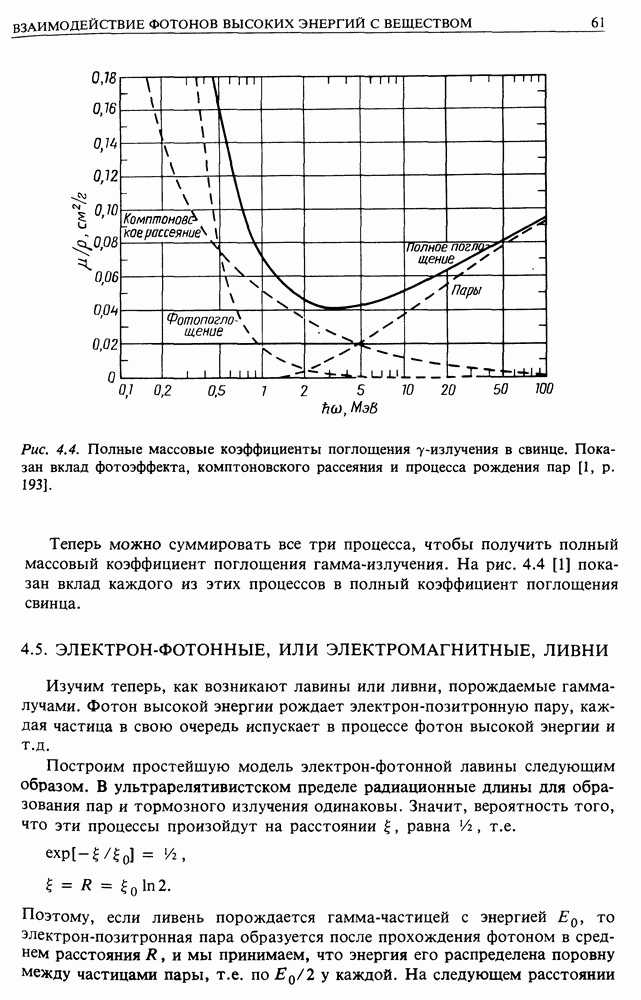
- 4.4. ОБРАЗОВАНИЕ ПАР
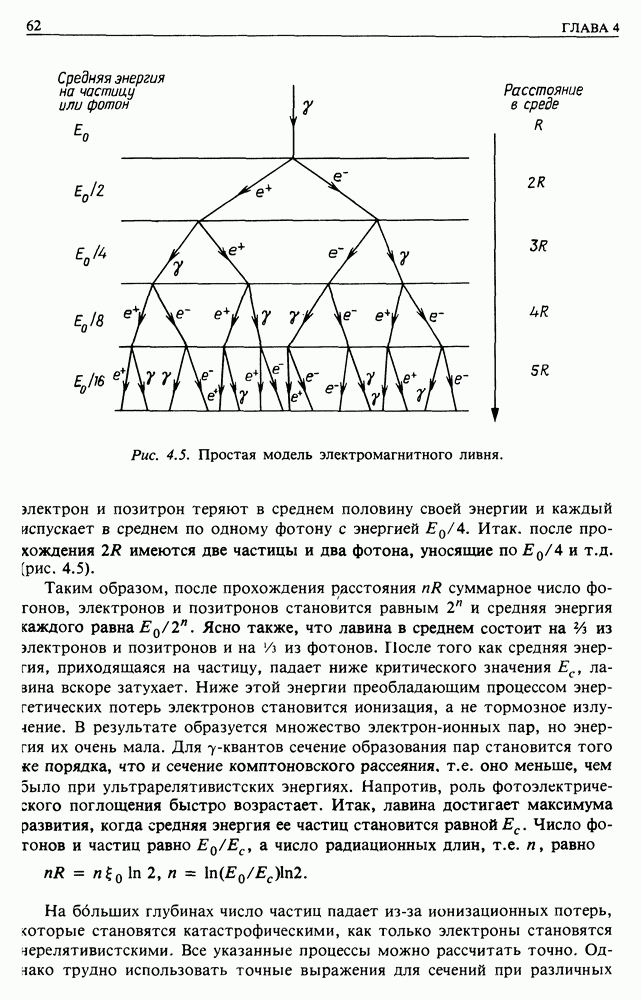
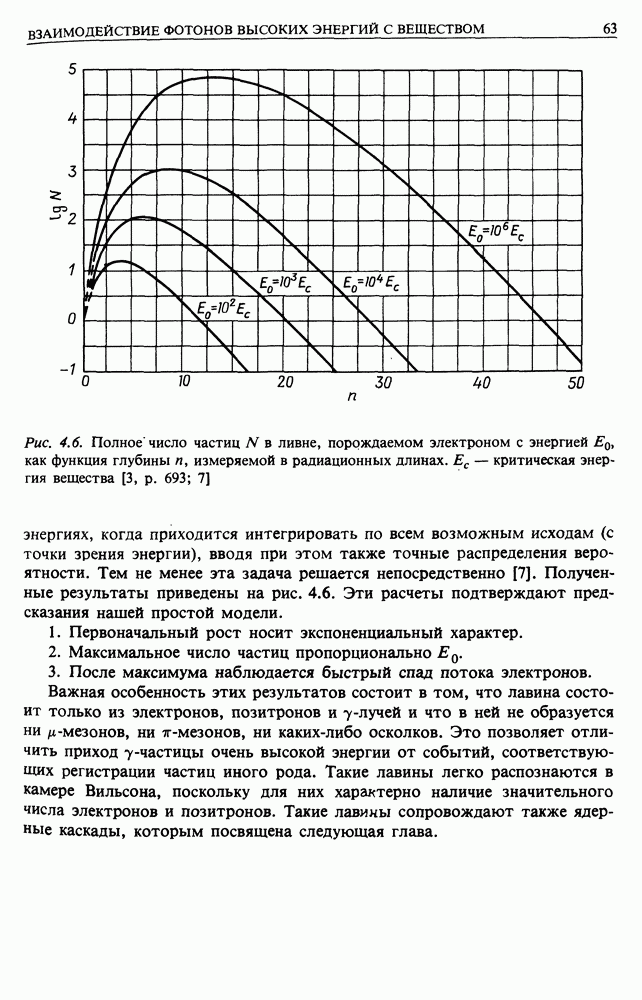
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
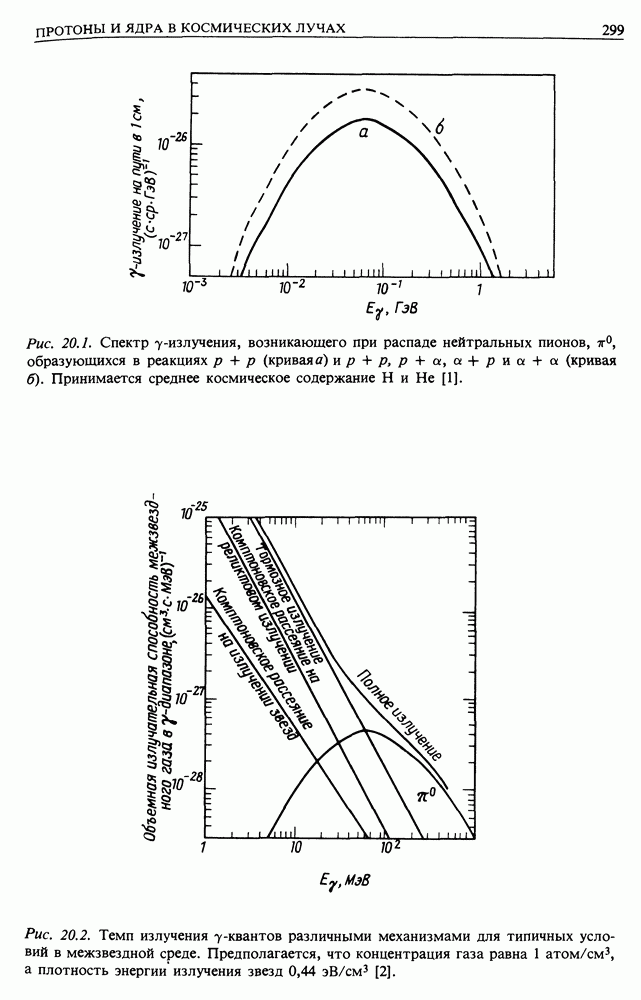
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ