| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
Основные параметры астрономических телескопов — угловая разрешающая способность (или угловое разрешение) и их чувствительность, т. е. способность регистрировать слабые объекты.
В радио-, инфракрасном, оптическом и ультрафиолетовом диапазонах фундаментальное ограничение, накладываемое на угловое разрешение, определяется дифракцией оптической системы инструмента. На более коротких волнах, действующих в телескопах, дифракционные эффекты неважны, а ограничения обусловлены техническими причинами, например размерами коллиматоров (см. разд. 7.3).
14.3.1. Дифракционные ограничения. В основе теории, необходимой для понимания свойств телескопов, лежит преобразование Фурье. Угловое разрешение телескопа (или дифракционной решетки) определяется как диаграмма телескопа. Основной результат этой теории состоит в том, что дифракционное изображение апертуры телескопа есть преобразование Фурье распределения яркости по апертуре. Этот результат можно истолковать следующим образом. Пусть имеется одномерная апертура, и пусть функция пропускания этой апертуры есть  т. е. часть электромагнитного излучения, падающего на участок длиной
т. е. часть электромагнитного излучения, падающего на участок длиной  и с координатой
и с координатой  пропускаемая диафрагмой, равна
пропускаемая диафрагмой, равна  Согласно схеме Гюйгенса, можно заменить любой волновой фронт суперпозицией точечных источников сферических волн. Таким образом, если освещать диафрагму
Согласно схеме Гюйгенса, можно заменить любой волновой фронт суперпозицией точечных источников сферических волн. Таким образом, если освещать диафрагму  однородным плоскопараллельным пучком света, то можно представить прошедший в точке
однородным плоскопараллельным пучком света, то можно представить прошедший в точке  свет от точечного источника сферических волн с интенсивностью
свет от точечного источника сферических волн с интенсивностью  Если свет падает на диафрагму под углом
Если свет падает на диафрагму под углом  к ее оси, то будет иметь место разность фаз по отношению к волнам, проходящим через центр апертуры, при
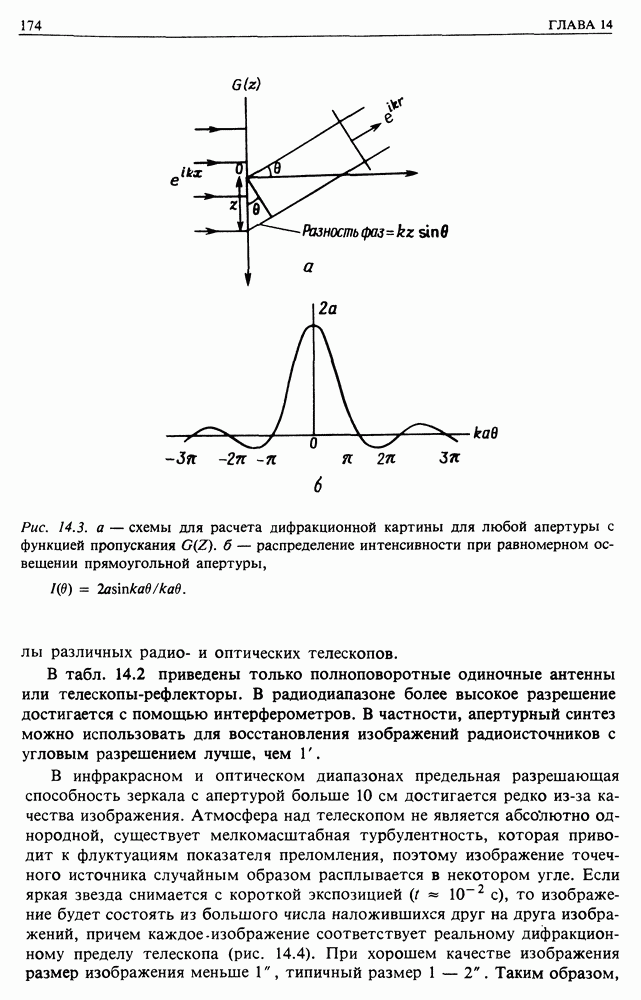
к ее оси, то будет иметь место разность фаз по отношению к волнам, проходящим через центр апертуры, при  (рис. 14.3, а). Поэтому интенсивность, получаемая в направлении 6 от малого участка апертуры
(рис. 14.3, а). Поэтому интенсивность, получаемая в направлении 6 от малого участка апертуры  есть
есть  и полная интенсивность равна
и полная интенсивность равна

Таким образом, диаграмма телескопа  есть преобразование Фурье распределения
есть преобразование Фурье распределения  Это общее выражение, и его можно использовать для отдельных телескопов, интерферометров, дифракционных решеток и т. п.
Это общее выражение, и его можно использовать для отдельных телескопов, интерферометров, дифракционных решеток и т. п.
Рассмотрим простейший пример однородно освещенной апертуры, например зеркала большого оптического или радиотелескопа. Тогда  если -
если -  в остальных случаях. Поэтому диаграмма приема есть
в остальных случаях. Поэтому диаграмма приема есть

Для малых углов  и тогда
и тогда

Распределение интенсивности показано на рис.  Первый нуль этой функции лежит в точке каб
Первый нуль этой функции лежит в точке каб  т. е.
т. е.  Это выражение похоже на критерий Рэлея для разрешения двух точечных объектов, разделенных углом 6, т. е.
Это выражение похоже на критерий Рэлея для разрешения двух точечных объектов, разделенных углом 6, т. е.  Полезное приближение
Полезное приближение  где
где  диаметр апертуры. В табл. 14.2 приведены дифракционные
диаметр апертуры. В табл. 14.2 приведены дифракционные

Рис. 14.3. а — схемы для расчета дифракционной картины для любой апертуры с функцией пропускания  распределение интенсивности при равномерном освещении прямоугольной апертуры,
распределение интенсивности при равномерном освещении прямоугольной апертуры, 
пределы различных радио- и оптических телескопов.
В табл. 14.2 приведены только полноповоротные одиночные антенны или телескопы-рефлекторы. В радиодиапазоне более высокое разрешение достигается с помощью интерферометров. В частности, апертурный синтез можно использовать для восстановления изображений радиоисточников с угловым разрешением лучше, чем 1.
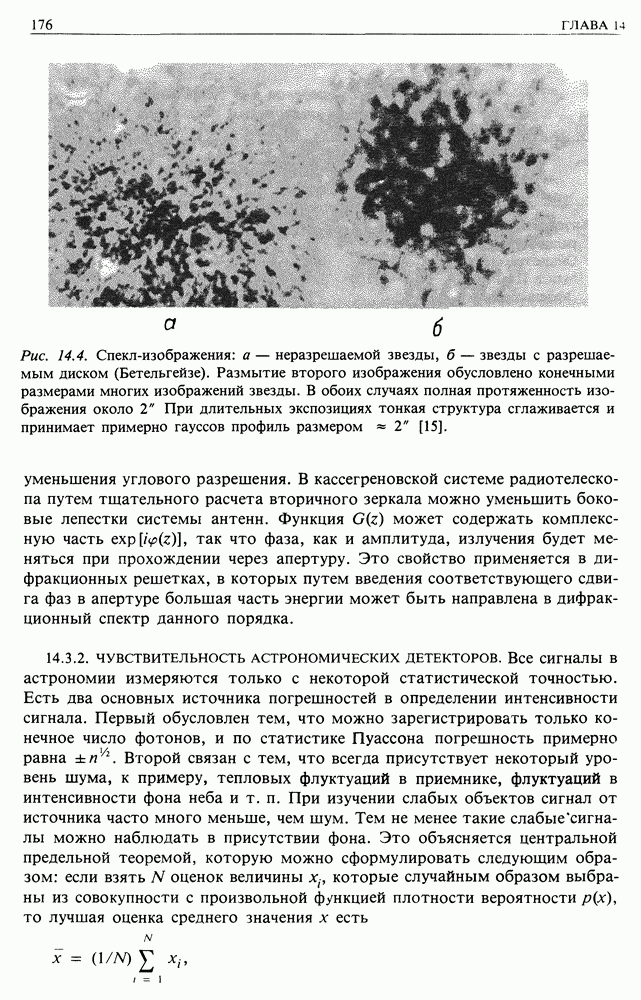
В инфракрасном и оптическом диапазонах предельная разрешающая способность зеркала с апертурой больше 10 см достигается редко из-за качества изображения. Атмосфера над телескопом не является абсолютно однородной, существует мелкомасштабная турбулентность, которая приводит к флуктуациям показателя преломления, поэтому изображение точечного источника случайным образом расплывается в некотором угле. Если яркая звезда снимается с короткой экспозицией  то изображение будет состоять из большого числа наложившихся друг на друга изображений, причем каждое изображение соответствует реальному дифракционному пределу телескопа (рис. 14.4). При хорошем качестве изображения размер изображения меньше
то изображение будет состоять из большого числа наложившихся друг на друга изображений, причем каждое изображение соответствует реальному дифракционному пределу телескопа (рис. 14.4). При хорошем качестве изображения размер изображения меньше  типичный размер
типичный размер  Таким образом,
Таким образом,
Таблица 14.1 (см. скан) Примеры дифракционных пределов для телескопов в радио-, миллиметровом и оптическом диапазонах
разрешающая способность крупнейших наземных телескопов в 20 — 40 раз хуже теоретического значения.
Чтобы достичь предельного разрешения больших рефлекторов, нужно вынести их за пределы земной атмосферы. Впервые это было осуществлено в принстонском эксперименте с телескопом «Стратоскоп-2», установленным на баллоне. Был достигнут дифракционный предел  -сантиметрового телескопа, построенного компанией «Перкин-Элмер». Следующим высокоточным телескопом данного типа будет космический телескоп
-сантиметрового телескопа, построенного компанией «Перкин-Элмер». Следующим высокоточным телескопом данного типа будет космический телескоп  который должен быть запущен космическим кораблем многоразового использования «Шатлл» в конце 1984 или в 1985 г. Он будет иметь апертуру
который должен быть запущен космическим кораблем многоразового использования «Шатлл» в конце 1984 или в 1985 г. Он будет иметь апертуру 
И наконец, сделаем некоторые замечания о функции пропускания  чтобы проиллюстрировать возможности метода Фурье. Ясно, что, меняя форму функции
чтобы проиллюстрировать возможности метода Фурье. Ясно, что, меняя форму функции  можно изменять диаграмму телескопа. К примеру, если функция пропускания телескопа описывается гауссовой кривой, то диаграмма должна также иметь гауссову форму, но только без отрицательных боковых лепестков. Таким образом, в процессе отладки апертуры уровень боковых лепестков можно значительно уменьшить за счет небольшого
можно изменять диаграмму телескопа. К примеру, если функция пропускания телескопа описывается гауссовой кривой, то диаграмма должна также иметь гауссову форму, но только без отрицательных боковых лепестков. Таким образом, в процессе отладки апертуры уровень боковых лепестков можно значительно уменьшить за счет небольшого

Рис. 14.4. Спекл-изображения: а — неразрешаемой звезды, б - звезды с разрешаемым диском (Бетельгейзе). Размытие второго изображения обусловлено конечными размерами многих изображений звезды. В обоих случаях полная протяженность изображения около  При длительных экспозициях тонкая структура сглаживается и принимает примерно гауссов профиль размером
При длительных экспозициях тонкая структура сглаживается и принимает примерно гауссов профиль размером 
уменьшения углового разрешения. В кассегреновской системе радиотелескопа путем тщательного расчета вторичного зеркала можно уменьшить боковые лепестки системы антенн. Функция  может содержать комплексную часть
может содержать комплексную часть  так что фаза, как и амплитуда, излучения будет меняться при прохождении через апертуру. Это свойство применяется в дифракционных решетках, в которых путем введения соответствующего сдвига фаз в апертуре большая часть энергии может быть направлена в дифракционный спектр данного порядка.
так что фаза, как и амплитуда, излучения будет меняться при прохождении через апертуру. Это свойство применяется в дифракционных решетках, в которых путем введения соответствующего сдвига фаз в апертуре большая часть энергии может быть направлена в дифракционный спектр данного порядка.
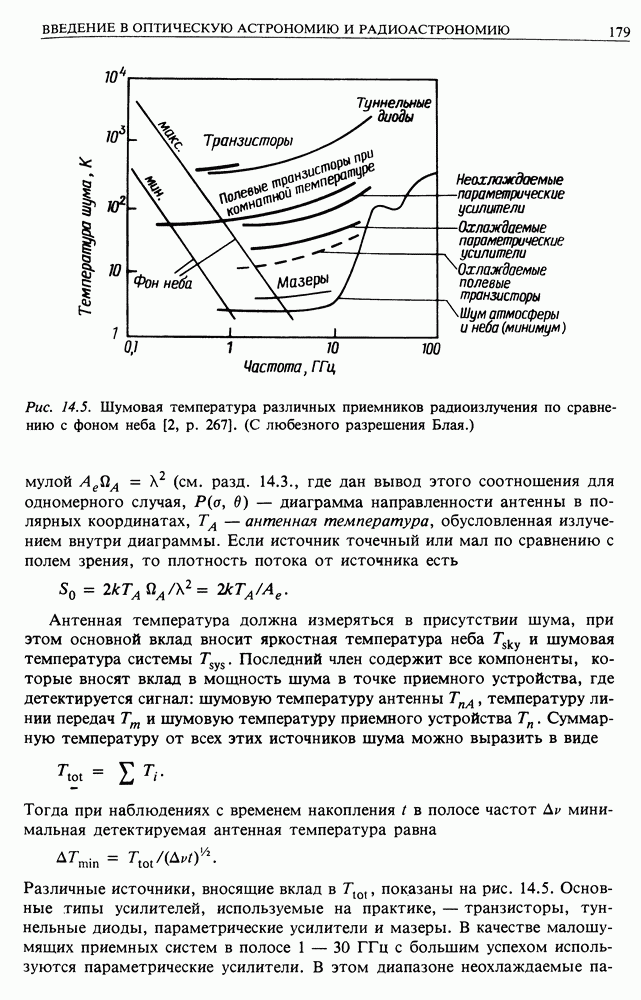
14.3.2. Чувствительность астрономических детекторов. Все сигналы в астрономии измеряются только с некоторой статистической точностью. Есть два основных источника погрешностей в определении интенсивности сигнала. Первый обусловлен тем, что можно зарегистрировать только конечное число фотонов, и по статистике Пуассона погрешность примерно равна  Второй связан с тем, что всегда присутствует некоторый уровень шума, к примеру, тепловых флуктуаций в приемнике, флуктуаций в интенсивности фона неба и т. п. При изучении слабых объектов сигнал от источника часто много меньше, чем шум. Тем не менее такие слабые сигналы можно наблюдать в присутствии фона. Это объясняется центральной предельной теоремой, которую можно сформулировать следующим образом: если взять
Второй связан с тем, что всегда присутствует некоторый уровень шума, к примеру, тепловых флуктуаций в приемнике, флуктуаций в интенсивности фона неба и т. п. При изучении слабых объектов сигнал от источника часто много меньше, чем шум. Тем не менее такие слабые сигналы можно наблюдать в присутствии фона. Это объясняется центральной предельной теоремой, которую можно сформулировать следующим образом: если взять  оценок величины
оценок величины  которые случайным образом выбраны из совокупности с произвольной функцией плотности вероятности
которые случайным образом выбраны из совокупности с произвольной функцией плотности вероятности  то лучшая оценка среднего значения х есть
то лучшая оценка среднего значения х есть

а распределение вероятности для этого значения  относительно истинного среднего будет гауссовым со стандартным уклонением
относительно истинного среднего будет гауссовым со стандартным уклонением  где
где  стандартное уклонение (негауссово) функции плотности вероятности
стандартное уклонение (негауссово) функции плотности вероятности  Этой теоремы вместе с правилом, что дисперсия суммы двух величин, дисперсии каждой
Этой теоремы вместе с правилом, что дисперсия суммы двух величин, дисперсии каждой  которых есть
которых есть  равна
равна  достаточно для понимания большинства вопросов теории регистрации сигналов в присутствии шума.
достаточно для понимания большинства вопросов теории регистрации сигналов в присутствии шума.
Существенный момент заключается в том, что при астрономических наблюдениях осуществляется усреднение но большому числу независимых оценок шума  Следовательно, можно с уверенностью предположить, что распределение вероятностей оценок х гауссово. Кроме того, чем больше
Следовательно, можно с уверенностью предположить, что распределение вероятностей оценок х гауссово. Кроме того, чем больше  тем выше относительная точность определения среднего уровня шума и стандартное уклонение среднего уменьшается как
тем выше относительная точность определения среднего уровня шума и стандартное уклонение среднего уменьшается как  так что если взять произвольно большое число оценок, флуктуации относительного среднего уровня шума можно уменьшить до нуля. Рассмотрим два примера.
так что если взять произвольно большое число оценок, флуктуации относительного среднего уровня шума можно уменьшить до нуля. Рассмотрим два примера.
Во многих случаях наблюдения производятся в узкой полосе частот  в которой плотность потока от источника можно считать постоянной. Пусть плотность потока равна
в которой плотность потока от источника можно считать постоянной. Пусть плотность потока равна  и он должен регистрироваться в присутствии случайного фонового сигнала со средней плотностью потока 5 и со стандартным уклонением
и он должен регистрироваться в присутствии случайного фонового сигнала со средней плотностью потока 5 и со стандартным уклонением  Пусть сделано
Пусть сделано  оценок потока от источника и фона. Полная энергия, принятая от источника, есть
оценок потока от источника и фона. Полная энергия, принятая от источника, есть  В то же время интенсивность от фона равна
В то же время интенсивность от фона равна  но стандартное уклонение шума от этого значения есть
но стандартное уклонение шума от этого значения есть  Значит, отношение сигнала к шуму есть
Значит, отношение сигнала к шуму есть

т. е. уровень шума падает как  Теперь получим более независимые от фонового сигнала оценки, увеличив либо время
Теперь получим более независимые от фонового сигнала оценки, увеличив либо время  измерения, либо полосу частот, в которой ведутся наблюдения,
измерения, либо полосу частот, в которой ведутся наблюдения,  Тогда
Тогда

Теперь предположим, что наблюдения проводятся со счетчиком фотонов, например, с прибором с зарядовой связью или с работающей в режиме счета фотонов системой, строящей изображение  в присутствии фона неба, темнового тока в детекторе и шума системы считывания. Тогда отношение сигнала к шуму равно
в присутствии фона неба, темнового тока в детекторе и шума системы считывания. Тогда отношение сигнала к шуму равно

где  время интегрирования,
время интегрирования,  эффективная площадь телескопа (площадь зеркала, которая соответствует регистрируемому детектором числу фотонов относительно плоскости потока источника) с учетом потерь, обусловленных отражением и квантовой эффективностью детектора;
эффективная площадь телескопа (площадь зеркала, которая соответствует регистрируемому детектором числу фотонов относительно плоскости потока источника) с учетом потерь, обусловленных отражением и квантовой эффективностью детектора;  плотность потока от источника, число
плотность потока от источника, число  интенсивность фона неба, число
интенсивность фона неба, число  — телесный угол, равный полю зрения детектора;
— телесный угол, равный полю зрения детектора;  темновой ток (среднеквадратичное
темновой ток (среднеквадратичное
число электронов в секунду);  шум считывания — среднеквадратичное число электронов, т. е. амплитуда шума в усилителе при считывании сигнала.
шум считывания — среднеквадратичное число электронов, т. е. амплитуда шума в усилителе при считывании сигнала.
Обратите внимание на то, что в знаменателе дисперсии отдельных независимых вкладов в неопределенность общего сигнала складываются. Если сигнал очень сильный, то член  больше, чем все члены, описывающие шум, и
больше, чем все члены, описывающие шум, и  Если наблюдения ограничены фоном неба, то член
Если наблюдения ограничены фоном неба, то член  преобладает
преобладает

В этом и состоит преимущество использования малых элементов детектора, т. е.  следует выбирать как можно меньше.
следует выбирать как можно меньше.
Наблюдению самых слабых источников с поверхности Земли мешает свечение ночного неба. Для грубых расчетов можно принять, что свечение ночного неба соответствует  (секунда
(секунда  Именно статистические флуктуации определяют предельную звездную величину регистрации слабого объекта. В уравнении для ограничения плотности потока, наблюдаемого детектором, работающим в режиме счета фотонов, интенсивность, соответствующая
Именно статистические флуктуации определяют предельную звездную величину регистрации слабого объекта. В уравнении для ограничения плотности потока, наблюдаемого детектором, работающим в режиме счета фотонов, интенсивность, соответствующая  равна
равна  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
- 4.4. ОБРАЗОВАНИЕ ПАР
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
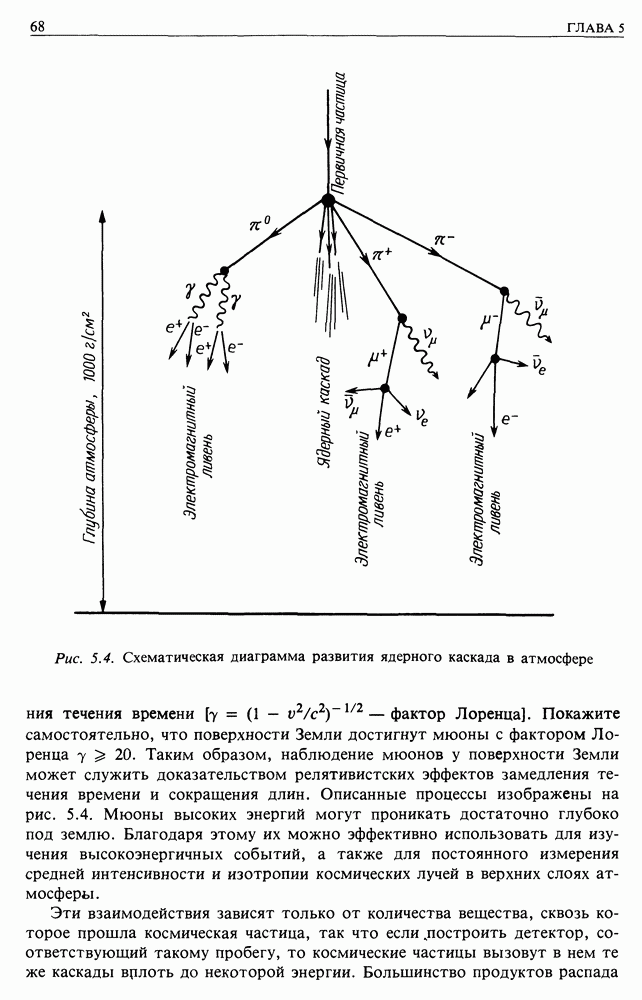
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
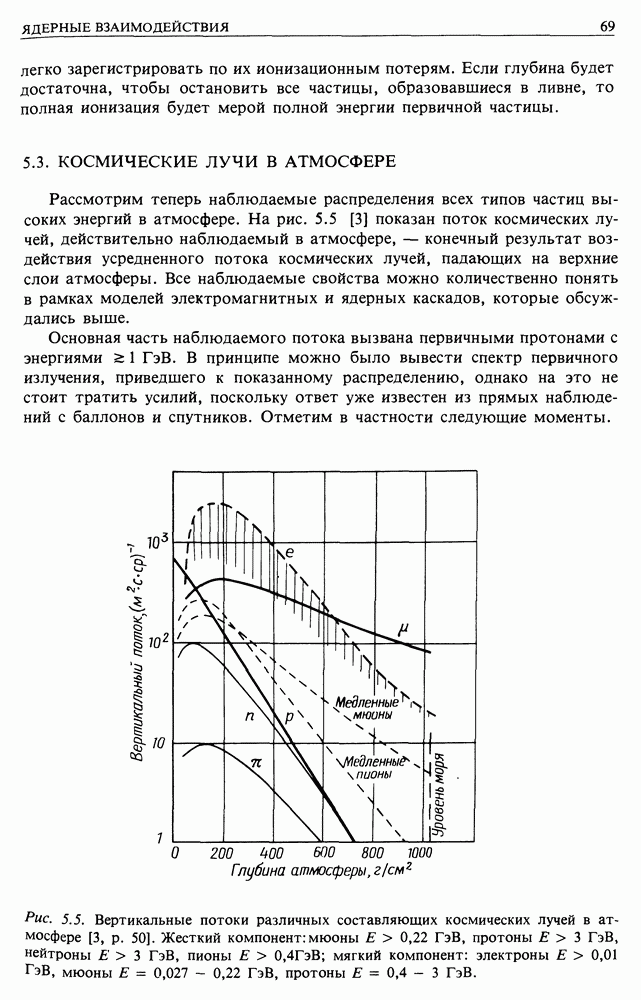
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
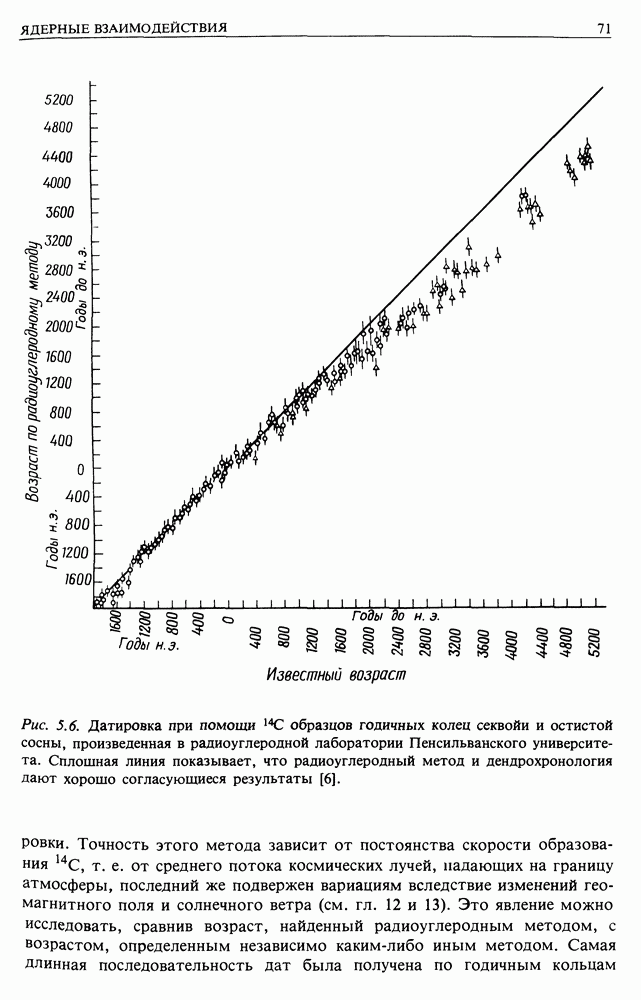
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
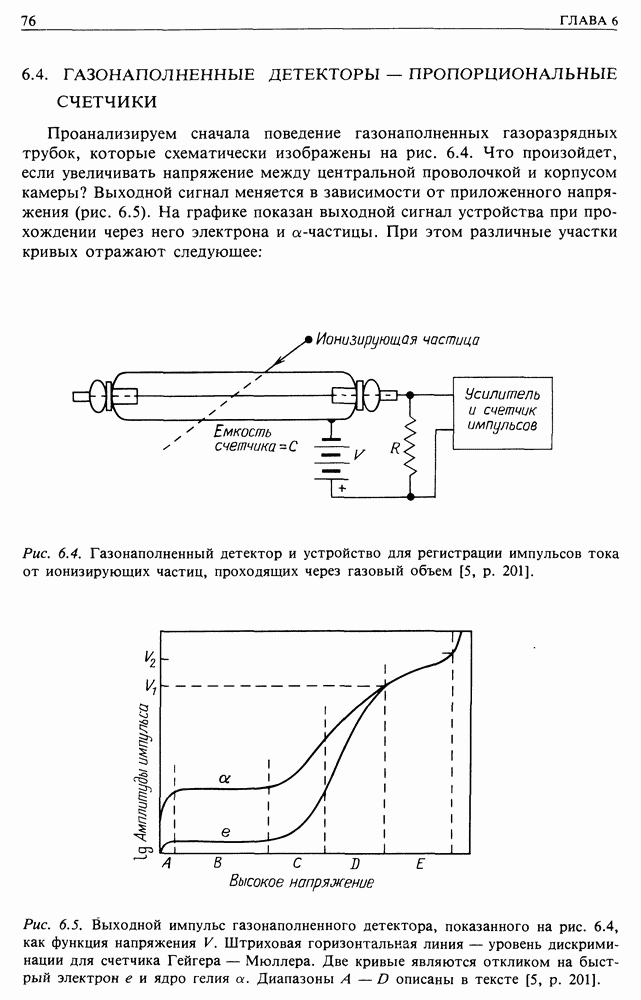
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
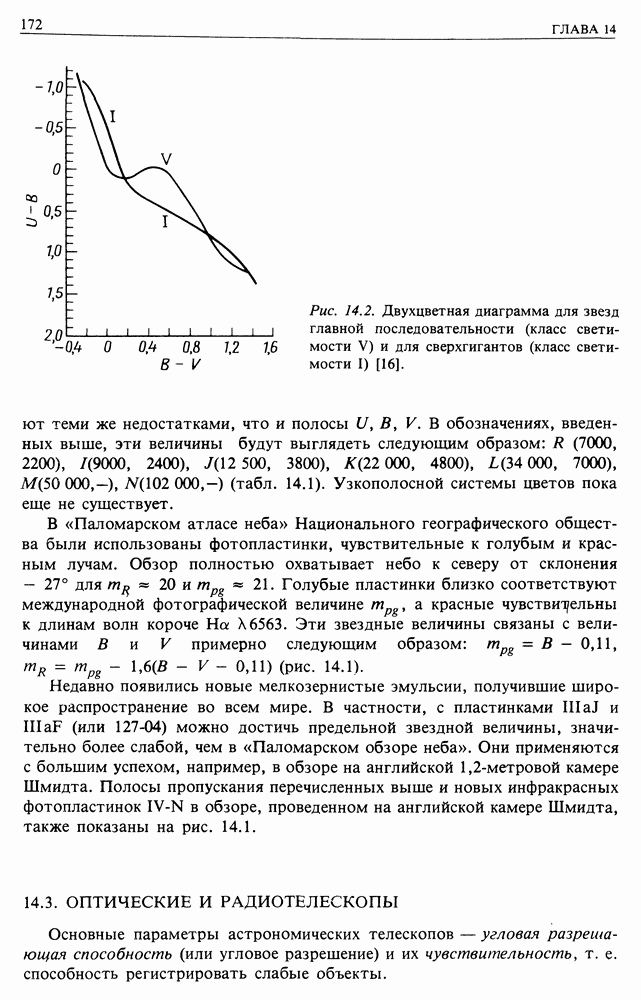
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
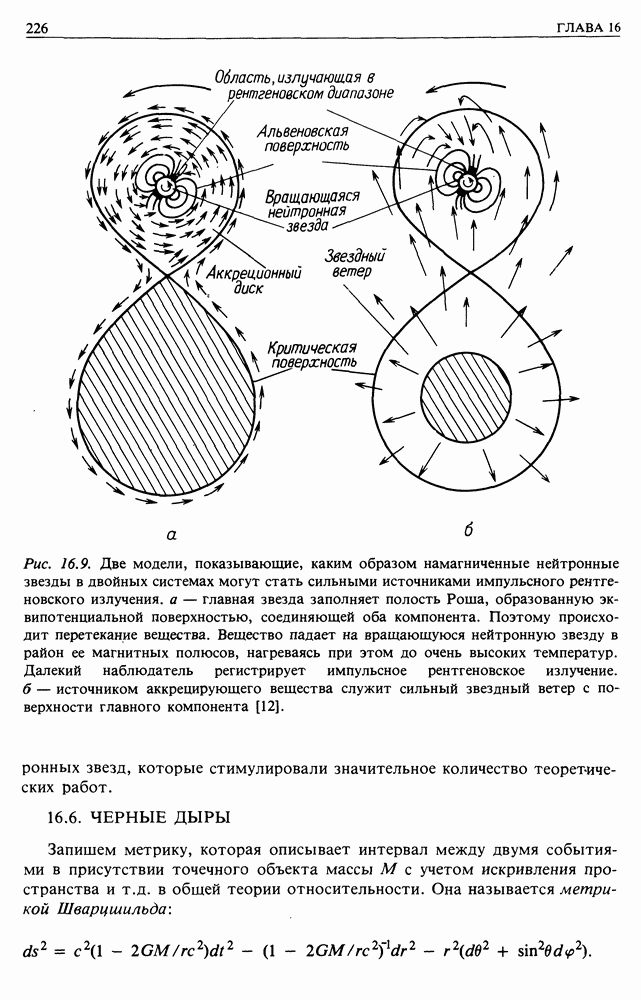
- 16.6. ЧЕРНЫЕ ДЫРЫ
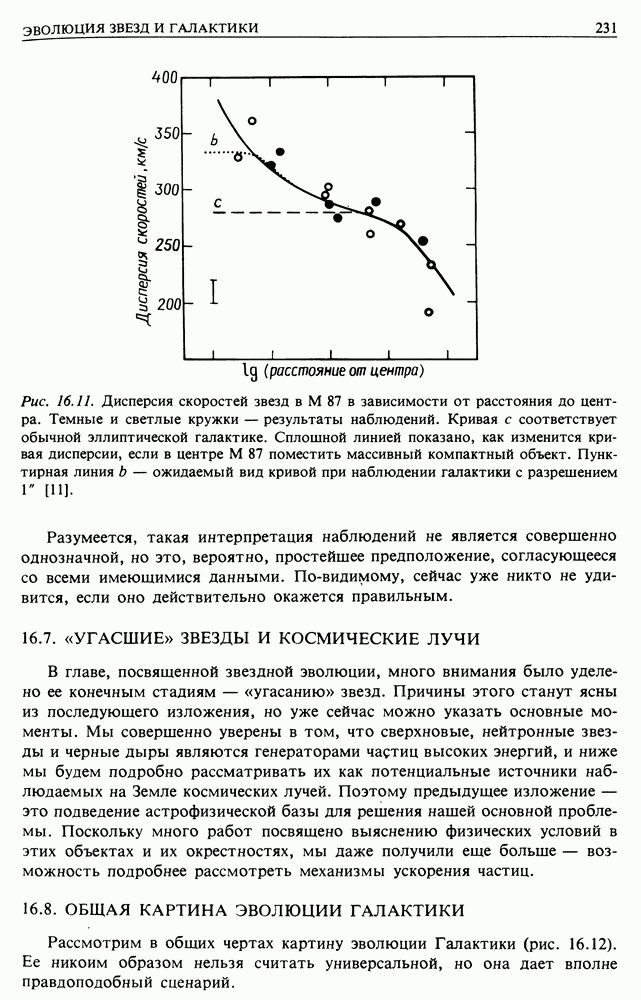
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
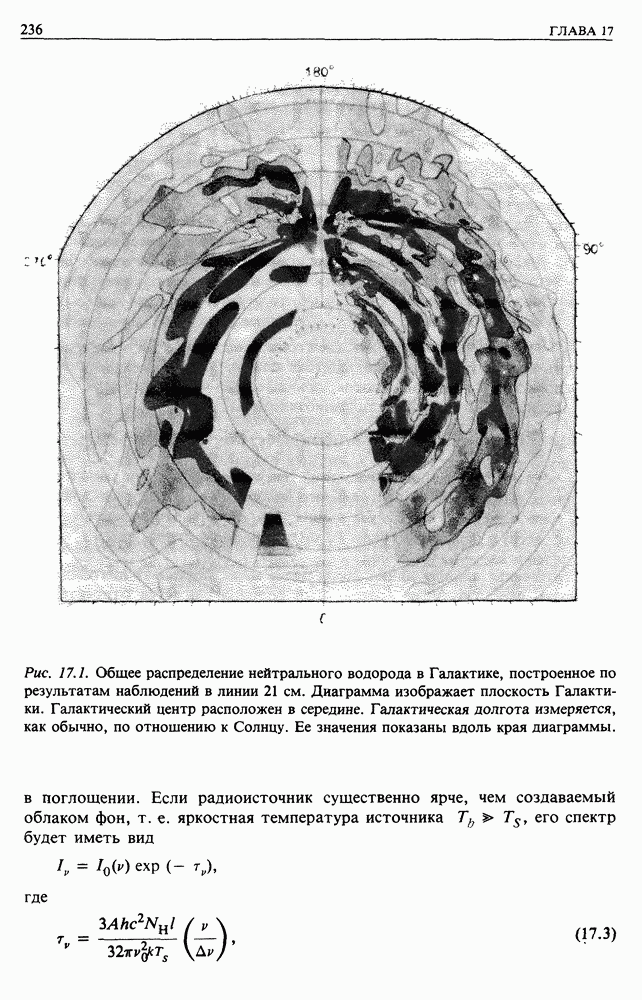
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
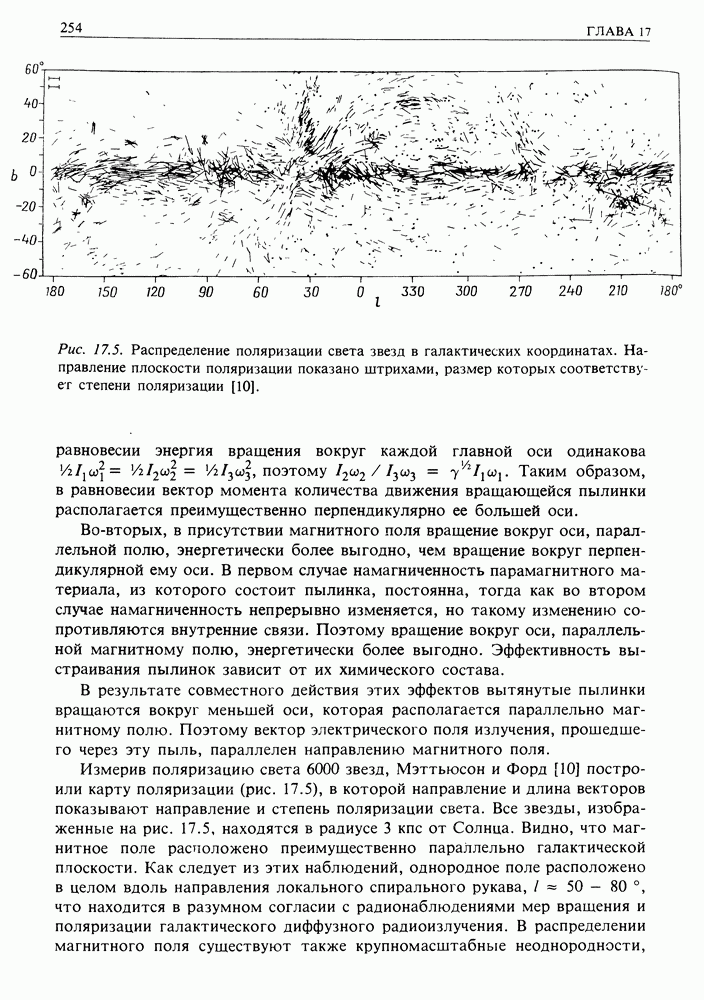
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
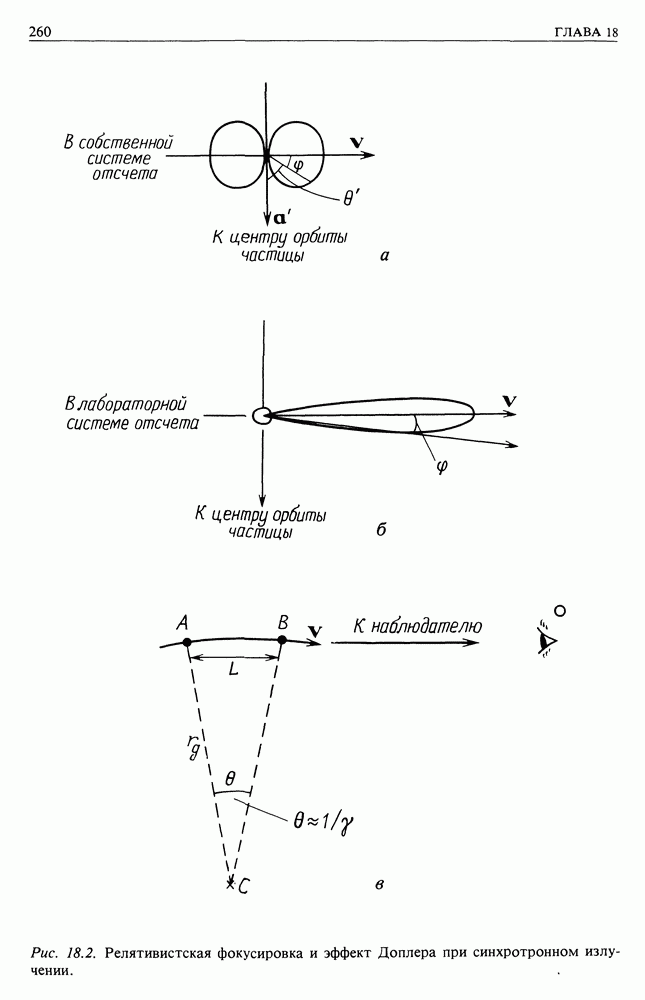
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
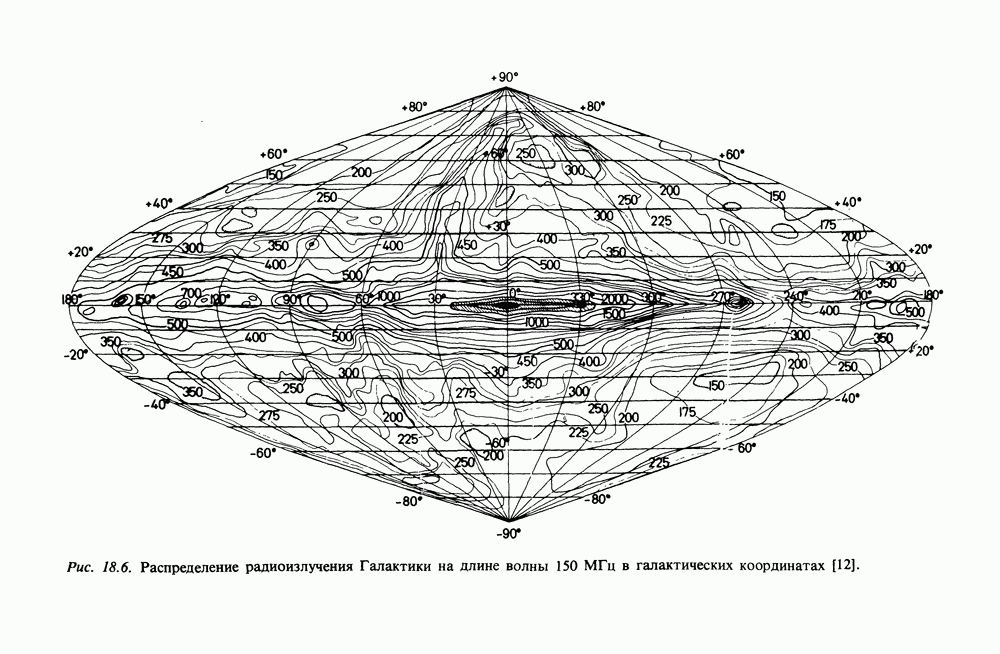
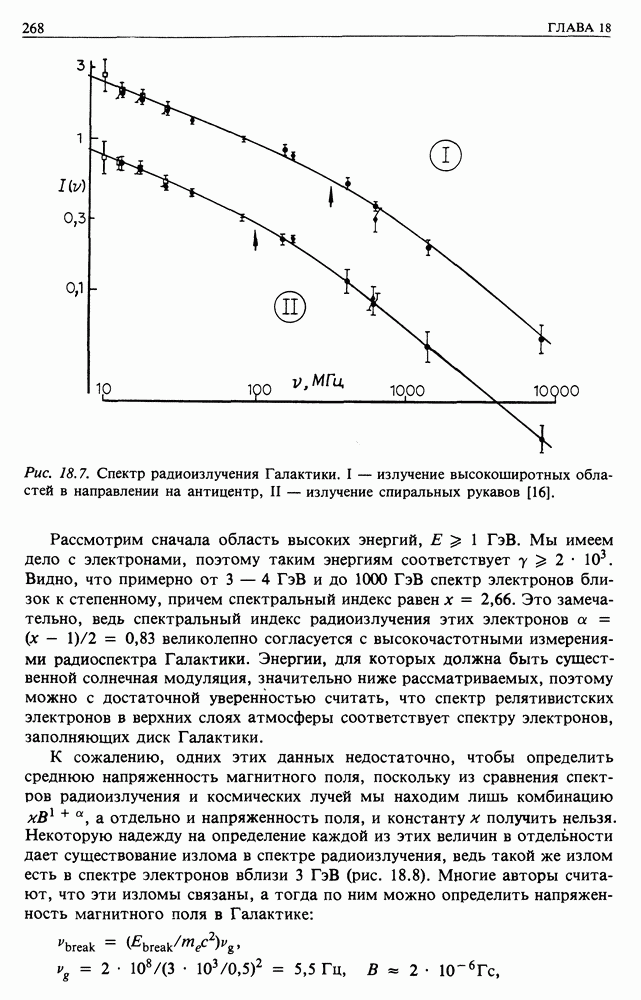
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ