| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
Как отмечалось выше, легкие элементы могут образовываться в результате фрагментации ядер космических лучей с большими  при их взаимодействии с холодным веществом, т.е. в результате реакций расщепления. Мы в основном будем интересоваться тремя видами продуктов этого процесса: 1) образованием легких элементов — лития, бериллия и бора, 2) наблюдаемым отношением содержаний
при их взаимодействии с холодным веществом, т.е. в результате реакций расщепления. Мы в основном будем интересоваться тремя видами продуктов этого процесса: 1) образованием легких элементов — лития, бериллия и бора, 2) наблюдаемым отношением содержаний  избыточным содержанием в космических лучах элементов немного легче железа.
избыточным содержанием в космических лучах элементов немного легче железа.
Чтобы как следует разобраться в этих вопросах, очевидно, необходима колоссальная таблица вероятностей различных каналов, по которым могут идти реакции расщепления ядер космических лучей, когда они сталкиваются с ядрами межзвездного водорода и гелия. Естественно, существует много вариантов, но практически невозможно рассчитать все из них с одинаковой точностью.
20.2.1. СЕЧЕНИЯ РЕАКЦИЙ РАСЩЕПЛЕНИЯ. Для решения задачи лучше всего было бы определить сечения образования каждого химического элемента в зависимости от энергии экспериментально на ускорителях. Очевидно, это невероятно обширная программа, но довольно значительная ее часть уже выполнена.
Завершив ее, можно попытаться составить полуэмпирические соотношения, как в капельной модели ядра, описывающие зависимость сечений от свойств первичной частицы. Это очень важно, поскольку могут образовываться редкие изотопы, которые еще не изучались в ускорителях.
Наконец, можно смоделировать процесс расщепления, воспроизводя условия, при которых происходит столкновение. Это осуществляется с помощью так называемого метода Монте-Карло. На ЭВМ рассчитывают одну траекторию протона в ядре при случайно выбранных начальных условиях. Этот протон случайным образом взаимодействует с нуклонами. В зависимости от того, какие частицы выбиваются и какова энергия возбужденного ядра, родительское ядро будет раскалываться разными способами, каждый из которых имеет определенную вероятность. В методе Монте-Карло такой расчет повторяется много раз и после, скажем,  циклов выводится усредненный спектр образовавшихся продуктов данного типа взаимодействия протона с ядром. Подобный метод часто используется в физике при изучении сложных систем, которые не поддаются
циклов выводится усредненный спектр образовавшихся продуктов данного типа взаимодействия протона с ядром. Подобный метод часто используется в физике при изучении сложных систем, которые не поддаются
Таблица 20.1 (см. скан) Парциальные сечения (в миллибарнах) столкновений тяжелых ядер с водородом, 
аналитическому описанию. Сейчас его применяют во всех областях науки. Что касается реакций расщепления, то подобные расчеты позволяют довольно успешно предсказывать их сечения и наблюдаемые продукты.
Объединяя все эти методы, можно построить таблицу сечений для всех типов ядер при любых энергиях. В табл. 20.1, взятой из работы [3], приведены парциальные сечения столкновений различных тяжелых ядер с водородом. В обзоре [3] описано, как получены эти величины. Также очень полезна книга [5].
В этих экспериментах вещество облучается протонами, поэтому энергия протона равна энергии нуклона из ядра-мишени в системе отсчета протона. Внизу каждой колонки приведено полное сечение разрушения ядра-мишени
Таблица 20.2 (см. скан)
при неупругом столкновении. Можно убедиться, что оно оказывается довольно близким к его геометрическому сечению.
Из приведенных в табл. 20.1 данных следует, что особенно велико сечение отщепления одного нуклона. Если дочернее ядро нестабильно, изучение парциальных сечении показывает, что вероятность расщепления на две равные части не так уж велика. Такой же эффект обнаружен при синтезе ядер.
Заметим, что приведенные в табл. 20.1 парциальные сечения в сумме дают только часть полного сечения. Недостающие сечения в основном описывают дробление ядра на протоны и  -частицы. Например, если одним из дочерних элементов является
-частицы. Например, если одним из дочерних элементов является  то он спонтанно распадается на две
то он спонтанно распадается на две  -частицы.
-частицы.
Именно такие таблицы необходимы для решения вопроса о фрагментации ядер космических лучей в межзвездной среде. Посмотрим, как далеко они позволяют продвинуться.
Удобно ввести полные сечения неупругих столкновений и с их помощью рассчитать средние длины свободного пробега в водороде в единицах  поскольку результаты будут применяться к реакциям в межзвездном газе. Средние значения сечений приведены в табл. 20.2. С каждой длиной свободного пробега можно связать вероятность фрагментации
поскольку результаты будут применяться к реакциям в межзвездном газе. Средние значения сечений приведены в табл. 20.2. С каждой длиной свободного пробега можно связать вероятность фрагментации  (т.е. среднее число вторичных ядер, образующихся при фрагментации первичных ядер). Здесь индекс
(т.е. среднее число вторичных ядер, образующихся при фрагментации первичных ядер). Здесь индекс  относится к первичному,
относится к первичному,  к вторичному ядрам. Теперь нужно решить диффузионное уравнение для этой задачи. Тогда станет ясно, насколько хорошо можно объяснить наблюдаемое распределение продуктов фрагментации.
к вторичному ядрам. Теперь нужно решить диффузионное уравнение для этой задачи. Тогда станет ясно, насколько хорошо можно объяснить наблюдаемое распределение продуктов фрагментации.
20.2.2. УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЛЕГКИХ ЯДЕР. Можно было бы решать диффузионные уравнения переноса с учетом реакций расщепления, но на это потребовалось бы слишком много времени. Некоторые примеры таких решений привели Гинзбург и Сыроватский. Исследуем лишь самый простой возможный случай и посмотрим, как его преобразовать, чтобы получить согласие с экспериментом.
Если не учитывать диффузию и потери энергии, то уравнение переноса примет вид

где  поток ядер типа 5 после прохождения через толщу вещества
поток ядер типа 5 после прохождения через толщу вещества  Первый член в правой части уравнения описывает разрушение ядер сорта
Первый член в правой части уравнения описывает разрушение ядер сорта  в результате реакций расщепления,
в результате реакций расщепления,  средняя длина свободного пробега относительно неупругих столкновений, выраженная в
средняя длина свободного пробега относительно неупругих столкновений, выраженная в  Второй член описывает образование ядер 5-го сорта при расщеплении более тяжелых ядер сорта
Второй член описывает образование ядер 5-го сорта при расщеплении более тяжелых ядер сорта 
Ясно, что для изучения эволюции всей системы необходимо написать такое уравнение для каждого изотопа каждого элемента периодической системы элементов, поэтому даже без учета диффузии и других усложняющих процессов (ионизационные потери и т.д.) мы оказываемся перед необходимостью обратить довольно сложную матрицу. Конечно, следует учесть расщепление конечных продуктов и т.д.
Отметим, что при выводе этого уравнения переноса было сделано одно важное предположение. Считалось, что все частицы проходят через одну и ту же толщу вещества от  до х, т.е. существует взаимно-однозначное соответствие между длиной пройденного пути и образованием новых элементов. Такая модель часто называется слоевой. Это, конечно, слишком сильное упрощение, но можно потом уточнить результат.
до х, т.е. существует взаимно-однозначное соответствие между длиной пройденного пути и образованием новых элементов. Такая модель часто называется слоевой. Это, конечно, слишком сильное упрощение, но можно потом уточнить результат.
Обратимся снова к таблице состава космических лучей (табл. 9.1). Видно, что углерод, азот и кислород по содержанию значительно превосходят другие тяжелые элементы, поэтому имеет смысл сначала попробовать рассмотреть только расщепление  или промежуточной
или промежуточной  группы, поскольку они служат сырьем, из которого образуются
группы, поскольку они служат сырьем, из которого образуются  или элементы легкой
или элементы легкой  группы. Мы будем говорить соответственно о группах
группы. Мы будем говорить соответственно о группах  для обозначения совокупности химических элементов.
для обозначения совокупности химических элементов.
Будем считать, что изначально при  группы
группы  в космических лучах не было. Тогда мы получим два дифференциальных уравнения, описывающих связь между группами
в космических лучах не было. Тогда мы получим два дифференциальных уравнения, описывающих связь между группами  :
:

Начальные условия таковы:

Уравнения легко решаются и дают содержание элементов группы  после прохождения через толщу
после прохождения через толщу  Уравнение (20.2) интегрируется непосредственно:
Уравнение (20.2) интегрируется непосредственно:

Умножая (20.3) на интегрирующий множитель  получим
получим

Таблица 20.3 (см. скан)
Решение этого уравнения:

Теперь подставим наблюдаемое значение  а также соответствующие вероятности фрагментации и средние длины свободного пробега
а также соответствующие вероятности фрагментации и средние длины свободного пробега  (среднее значение суммы парциальных сечений). Получим, что для образования наблюдаемого количества легких элементов космические лучи группы
(среднее значение суммы парциальных сечений). Получим, что для образования наблюдаемого количества легких элементов космические лучи группы  должны были пройти толщу вещества
должны были пройти толщу вещества 
Можно также убедиться в том, что детальное распределение элементов в группе  оказывается правильным. Полные неупругие сечеция образования
оказывается правильным. Полные неупругие сечеция образования  и В отдельно приведены в табл. 20.3. С точностью до ошибок отношение парциальных сечеций и наблюдаемого содержания элементов находятся в отличном согласии.
и В отдельно приведены в табл. 20.3. С точностью до ошибок отношение парциальных сечеций и наблюдаемого содержания элементов находятся в отличном согласии.
Более подробные расчеты дали результат  [7]. Заметим, что это среднее количество вещества, через которое должны пройти космические лучи.
[7]. Заметим, что это среднее количество вещества, через которое должны пройти космические лучи.
Точно таким же образом можно рассчитать образование  из
из  при расщеплении
при расщеплении  в межзвездном газе. В этом случае важны следующие реакции:
в межзвездном газе. В этом случае важны следующие реакции:

Есть особая группа реакций с участием  Проведенный для нее анализ также дает значение
Проведенный для нее анализ также дает значение  в предположении, что ядра гелия проходят через то же количество вещества, что и ядра
в предположении, что ядра гелия проходят через то же количество вещества, что и ядра 
Остается рассмотреть продукты расщепления железа. Это более сложная задача, так как средняя длина свободного пробега ядра железа меньше, чем ядер группы  поэтому железо должно значительно быстрее фрагментировать. Это очень странно, поскольку даже для
поэтому железо должно значительно быстрее фрагментировать. Это очень странно, поскольку даже для  пройденная толща вещества порядка средней длины свободного пробега. В этом случае отношение содержаний продуктов расщепления и оставшегося железа должно быть равно
пройденная толща вещества порядка средней длины свободного пробега. В этом случае отношение содержаний продуктов расщепления и оставшегося железа должно быть равно

При  отношение содержаний продуктов расщепления и непереработанного железа равно 3,7.
отношение содержаний продуктов расщепления и непереработанного железа равно 3,7.
Смысл этого значения легко понять из таблицы состава космических лучей (табл. 9.1), которая показывает, что значительную часть продуктов составляют ядра только немногим более легкие, чем родительские. Изучение таблицы парциальных сечений подтверждает, что примерно треть полного сечения соответствует образованию таких ядер, как  Поэтому можно было бы ожидать, что содержание этих элементов в целом должно быть таким же, как железа. Но это не так. Расхождение можно продемонстрировать иначе, если сравнить отношение
Поэтому можно было бы ожидать, что содержание этих элементов в целом должно быть таким же, как железа. Но это не так. Расхождение можно продемонстрировать иначе, если сравнить отношение  поскольку большая часть продуктов расщепления железа попадает в этот интервал атомных чисел. Наблюдаемое значение много меньше 3,7 и равно 1,5. Эти расхождения подтверждаются более подробными расчетами. Заметим, что хотя для астрофизики нетипично делать выводы на основании различия в два раза, но приведенные отношения являются относительными величинами, зависящими от физических параметров, которые известны с хорошей точностью. Поэтому в данном случае имеются серьезные основания считать теорию неудовлетворительной.
поскольку большая часть продуктов расщепления железа попадает в этот интервал атомных чисел. Наблюдаемое значение много меньше 3,7 и равно 1,5. Эти расхождения подтверждаются более подробными расчетами. Заметим, что хотя для астрофизики нетипично делать выводы на основании различия в два раза, но приведенные отношения являются относительными величинами, зависящими от физических параметров, которые известны с хорошей точностью. Поэтому в данном случае имеются серьезные основания считать теорию неудовлетворительной.
К счастью, эту трудность легко преодолеть следующим образом. Мы предполагали, что все частицы космических лучей, прежде чем достичь Земли, проходят одну и ту же толщу вещества, т.е. мы не учитывали того факта, что наблюдаемые космические лучи проходят самые разные расстояния. Для построения модели распределения по длинам пути можно использовать уравнение диффузии

Если движение от источников к наблюдателю чисто диффузионное, то получается примерно гауссово распределение по пройденным расстояниям. Если же принять модель, согласно которой в течение некоторого характерного времени  частицы остаются в диске Галактики, а затем покидают его, то получается экспоненциальное распределение. Уравнение
частицы остаются в диске Галактики, а затем покидают его, то получается экспоненциальное распределение. Уравнение

приводит к распределению

Обе модели физически правдоподобны и соответствуют различным представлениям о том, как частицы покидают Галактику. Сначала рассмотрим проблему с эмпирической точки зрения: какое распределение по пройденным расстояниям может привести к наблюдаемому химическому составу космических лучей?
Окончательный ответ можно получить только после подробного анализа с использованием полной системы уравнений переноса. Мы же ограничимся простой иллюстрацией влияния распределения по пройденным расстояниям на конечный результат. Предположим, например, что треть частиц прошла толщу  а две трети прошли через пренебрежимо малое количество вещества. Тогда с помощью уравнений (20.4) и (20.5) можно
а две трети прошли через пренебрежимо малое количество вещества. Тогда с помощью уравнений (20.4) и (20.5) можно

Рис. 20.4. Модели распределения космических лучей по расстояниям, пройденным в межзвездном газе; а — «слоевая» модель, согласно которой все частицы проходят одно и то же расстояние; б - модель, согласно которой частицы на пути к Земле проходят разные расстояния; она позволяет объяснить более широкий набор продуктов фрагментации; в — гауссово распределение, которое возникает в диффузионной модели, и экспоненциальное распределение, обрезанное на малых энергиях.
получить ожидаемое отношение содержаний элементов группы  к группе
к группе  и соответственно отношение количества продуктов расщепления железа к оставшемуся железу. Очевидно, химический состав той части, которая прошла толщу
и соответственно отношение количества продуктов расщепления железа к оставшемуся железу. Очевидно, химический состав той части, которая прошла толщу  основательно изменился. Из уравнения (20.4) следует, что
основательно изменился. Из уравнения (20.4) следует, что  тогда как уравнение (20.5) показывает, что железо расщепилось практически полностью. Оставшиеся две трети частиц не подверглись изменениям. Объединяя результаты обоих вариантов, получим
тогда как уравнение (20.5) показывает, что железо расщепилось практически полностью. Оставшиеся две трети частиц не подверглись изменениям. Объединяя результаты обоих вариантов, получим  продукты
продукты  что примерно согласуется с наблюдениями. Таким образом, мы модифицировали слоевую модель с учетом распределения по пройденным расстояниям. Отметим, что в приведенной простой модели средний путь, пройденный космическими лучами, составляет
что примерно согласуется с наблюдениями. Таким образом, мы модифицировали слоевую модель с учетом распределения по пройденным расстояниям. Отметим, что в приведенной простой модели средний путь, пройденный космическими лучами, составляет  Полный анализ требует рассмотрения расщепления вторичных элементов, образовавшихся из железа, но принцип ясен уже сейчас. Некоторые модели распределения по пройденным расстояниям, включая описанную, показаны на рис. 20.4.
Полный анализ требует рассмотрения расщепления вторичных элементов, образовавшихся из железа, но принцип ясен уже сейчас. Некоторые модели распределения по пройденным расстояниям, включая описанную, показаны на рис. 20.4.
В свете вышеизложенного не является неожиданным тот факт, что результаты подробных расчетов свидетельствуют в пользу экспоненциального распределения по пройденным расстояниям с обрезанием на малых расстояниях (рис. 20.4). Средняя толща вещества, сквозь которую проходят космические лучи, остается равной приблизительно 
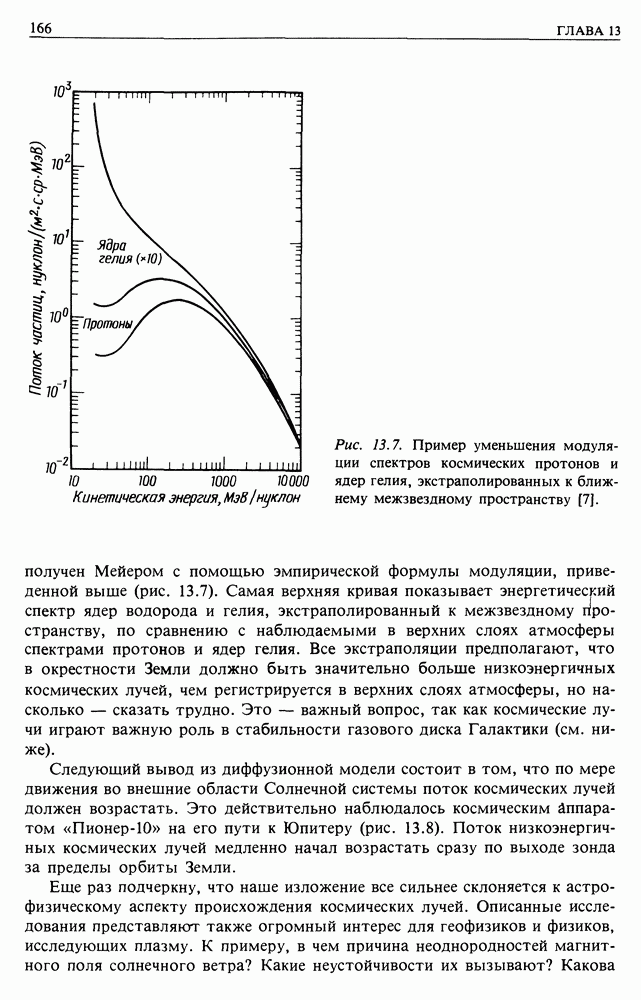
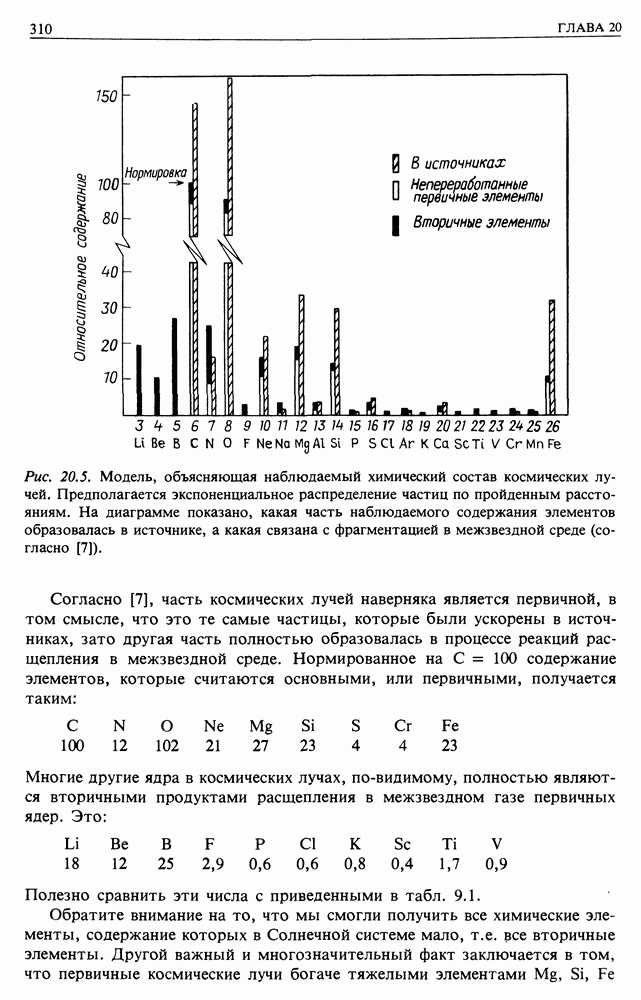
Самое полное обсуждение вопроса дано, по-видимому, в [7]. Задавался некоторый начальный химический состав космических лучей, а затем анализировалось их прохождение через нужную среднюю толщу вещества в Галактике. Это позволило получить наблюдаемое распределение компонентов космических лучей во всех деталях методом итераций. Удалось подробно проследить за всеми многократными процессами превращения химических элементов и использовалась подходящая модель распределения по пройденным расстояниям. Результаты показаны на рис. 20.5.

Рис. 20.5. Модель, объясняющая наблюдаемый химический состав космических лучей. Предполагается экспоненциальное распределение частиц по пройденным расстояниям. На диаграмме показано, какая часть наблюдаемого содержания элементов образовалась в источнике, а какая связана с фрагментацией в межзвездной среде (согласно [7]).
Согласно [7], часть космических лучей наверняка является первичной, в том смысле, что это те самые частицы, которые были ускорены в источниках, зато другая часть полностью образовалась в процессе реакций расщепления в межзвездной среде. Нормированное на  содержание элементов, которые считаются основными, или первичными, получается таким:
содержание элементов, которые считаются основными, или первичными, получается таким:

Многие другие ядра в космических лучах, по-видимому, полностью являются вторичными продуктами расщепления в межзвездном газе первичных ядер. Это:

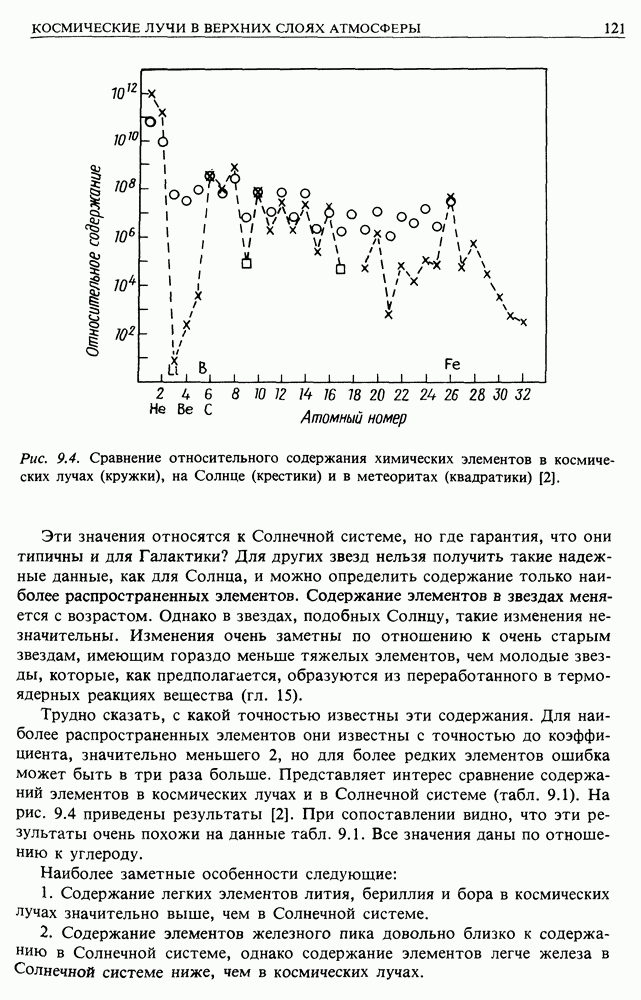
Полезно сравнить эти числа с приведенными в табл. 9.1.
Обратите внимание на то, что мы смогли получить все химические элементы, содержание которых в Солнечной системе мало, т.е. все вторичные элементы. Другой важный и многозначительный факт заключается в том, что первичные космические лучи богаче тяжелыми элементами 
по сравнению с Солнечной системой (ср. с табл. 9.1). Это является веским аргументом в пользу предположения, что источником космических лучей являются сильно проэволюционировавшие звезды, в которых к моменту взрыва, выбросившего в межзвездное пространство космические лучи, содержание тяжелых элементов было повышено. Сверхновые как раз и являются тем типом объектов, в которых это происходит.
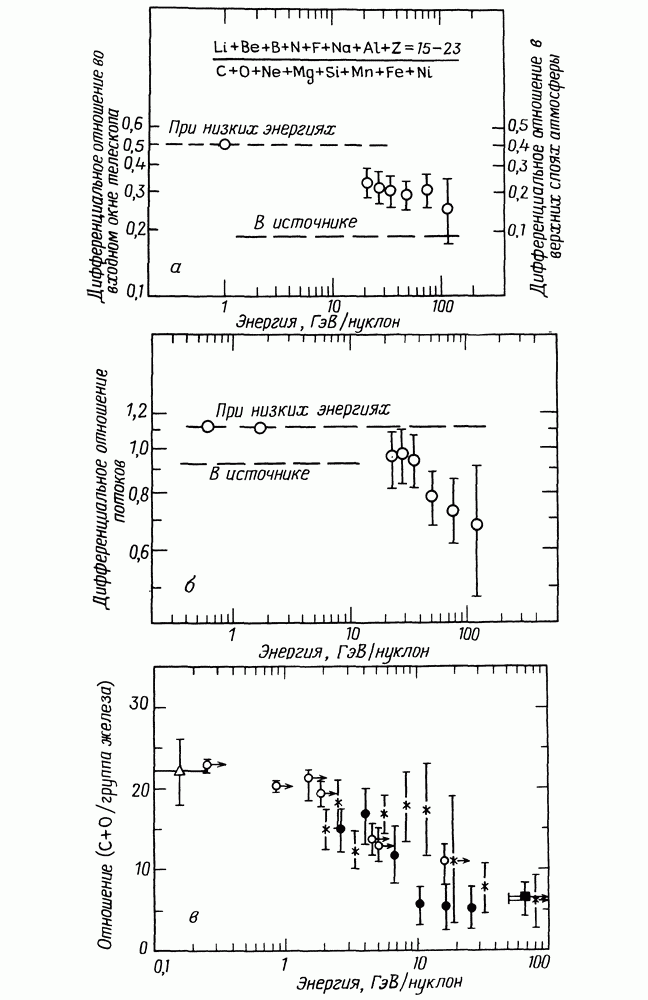
20.2.3. ЗАВИСИМОСТЬ ХИМИЧЕСКОГО СОСТАВА КОСМИЧЕСКИХ ЛУЧЕЙ ОТ ЭНЕРГИИ. К сожалению, мы не можем поставить здесь точку, поскольку имеются некоторые усложняющие обстоятельства. Еще в разд. 9.1 отмечалось, что сейчас известна зависимость химического состава космических лучей от энергии. Наличие такой зависимости требует усложнения модели, которую мы так тщательно разрабатывали, поэтому нам необходимо разобраться в этом вопросе. Указанная зависимость иллюстрируется рис. 20.6.
При энергиях, превышающих  а весьма вероятно, и более низких, отношение содержаний вторичных ядер к первичным, по-видимому, уменьшается с ростом энергии (рис. 20.6, а). Кроме того, имеются данные, указывающие на изменение с энергией отношения содержаний углерода к кислороду (рис. 20.6, б). Создается впечатление, что отношение
а весьма вероятно, и более низких, отношение содержаний вторичных ядер к первичным, по-видимому, уменьшается с ростом энергии (рис. 20.6, а). Кроме того, имеются данные, указывающие на изменение с энергией отношения содержаний углерода к кислороду (рис. 20.6, б). Создается впечатление, что отношение  О к
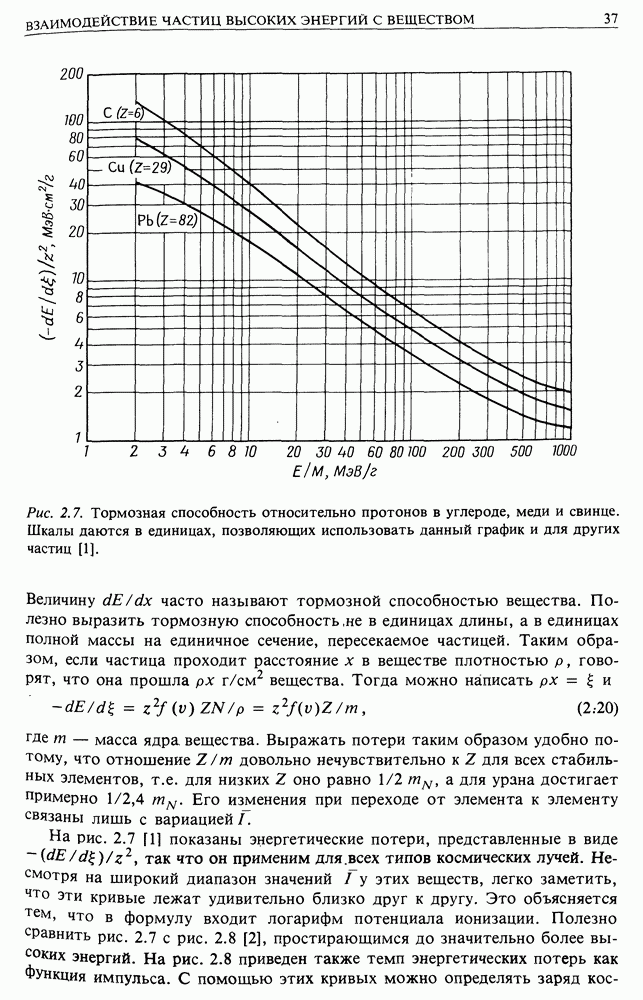
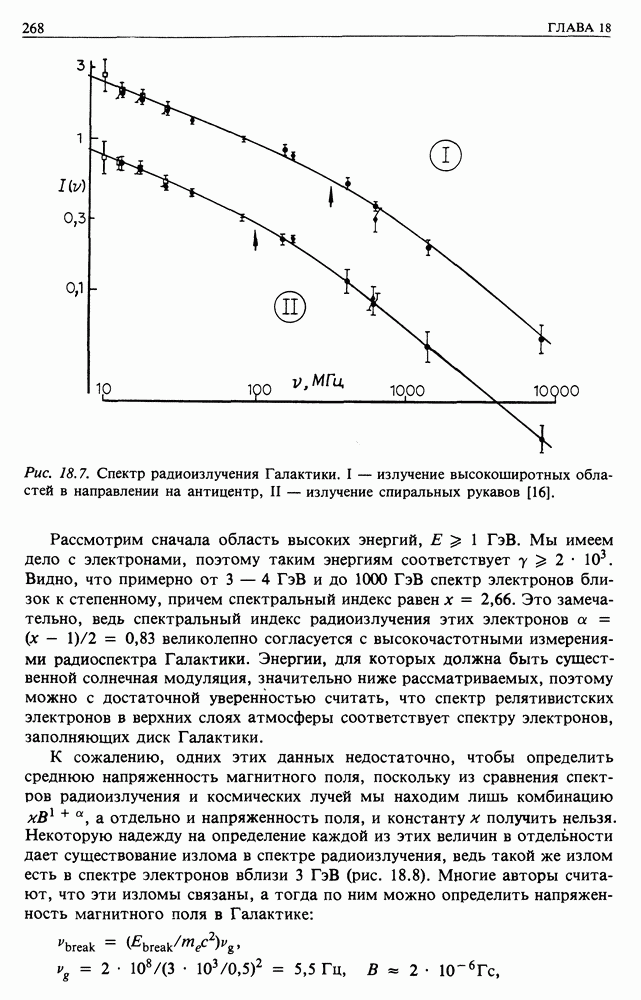
О к  уменьшается в результате того, что энергетический спектр железа более плоский, чем у кислорода и углерода (рис. 20.6, в). Все эти эффекты отражены в спектрах, приведенных на рис. 20.7. Отметим, что на существование этих зависимостей независимо указывали многие авторы.
уменьшается в результате того, что энергетический спектр железа более плоский, чем у кислорода и углерода (рис. 20.6, в). Все эти эффекты отражены в спектрах, приведенных на рис. 20.7. Отметим, что на существование этих зависимостей независимо указывали многие авторы.
Впечатление такое, как будто имеется несколько эффектов, действующих одновременно. Прежде всего зависимость от энергии отношения содержаний вторичных элементов к первичным, по-видимому, означает, что коэффициенты диффузии первичных элементов зависят от энергии. Количественно принято, что коэффициент диффузии (или средняя длина свободного пробега) меняется с энергией как  Вспомните, что у нас не вызвало особых затруднений получение зависимости подобного вида в теории солнечной модуляции (п. 13.3.2). По-видимому, какая-либо теория такого же типа могла бы объяснить зависимость коэффициента диффузии от энергии. Не исключено, что она даст возможность получать информацию о спектре неоднородностей межзвездной среды или о взаимодействии волн и частиц в ней.
Вспомните, что у нас не вызвало особых затруднений получение зависимости подобного вида в теории солнечной модуляции (п. 13.3.2). По-видимому, какая-либо теория такого же типа могла бы объяснить зависимость коэффициента диффузии от энергии. Не исключено, что она даст возможность получать информацию о спектре неоднородностей межзвездной среды или о взаимодействии волн и частиц в ней.
С другой стороны, зависимость от энергии для космических лучей, которые считаются первичными, должна отражать энергетическую зависимость механизмов ускорения различных компонентов космических лучей. Единого мнения о причинах такой зависимости пока нет.
Есть тем не менее одно важное обстоятельство. Если бы энергетический спектр железа продолжался с тем же наклоном до очень больших энергий, то большая часть энергии космических лучей (скажем, при  могла бы оказаться сосредоточенной в ядрах железа. Общепринятого мнения о том, верно ли это, нет.
могла бы оказаться сосредоточенной в ядрах железа. Общепринятого мнения о том, верно ли это, нет.
Решение перечисленных проблем должно пролить свет на природу ускорения частиц, но мы пока еще мало продвинулись в выяснении того, как все происходит.

(кликните для просмотра скана)
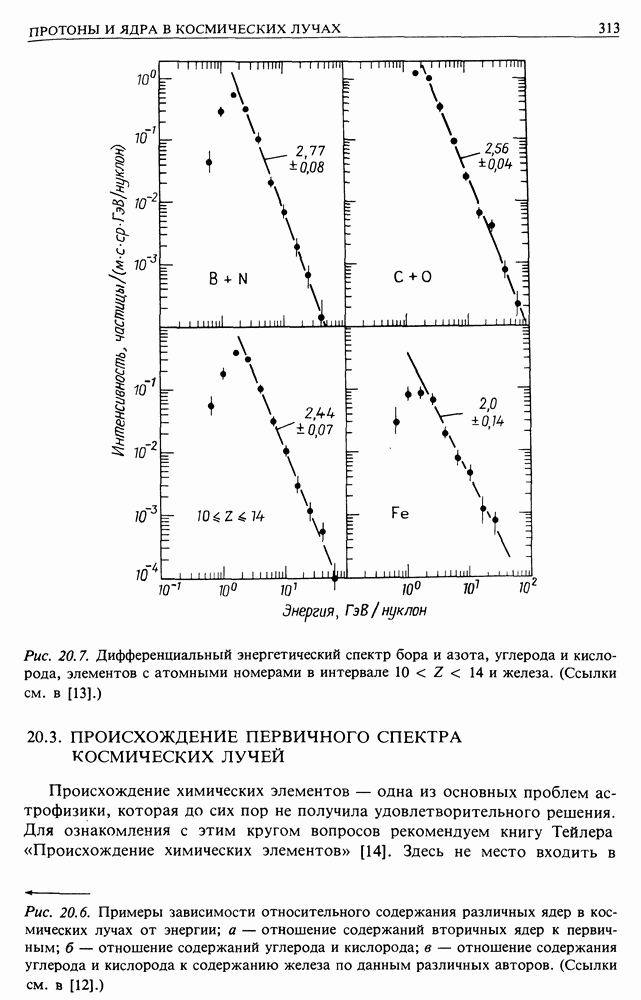
Рис. 20.7. (см. скан) Дифференциальный энергетический спектр бора и азота, углерода и кислорода, элементов с атомными номерами в интервале  и железа. (Ссылки см. в [13].)
и железа. (Ссылки см. в [13].)
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
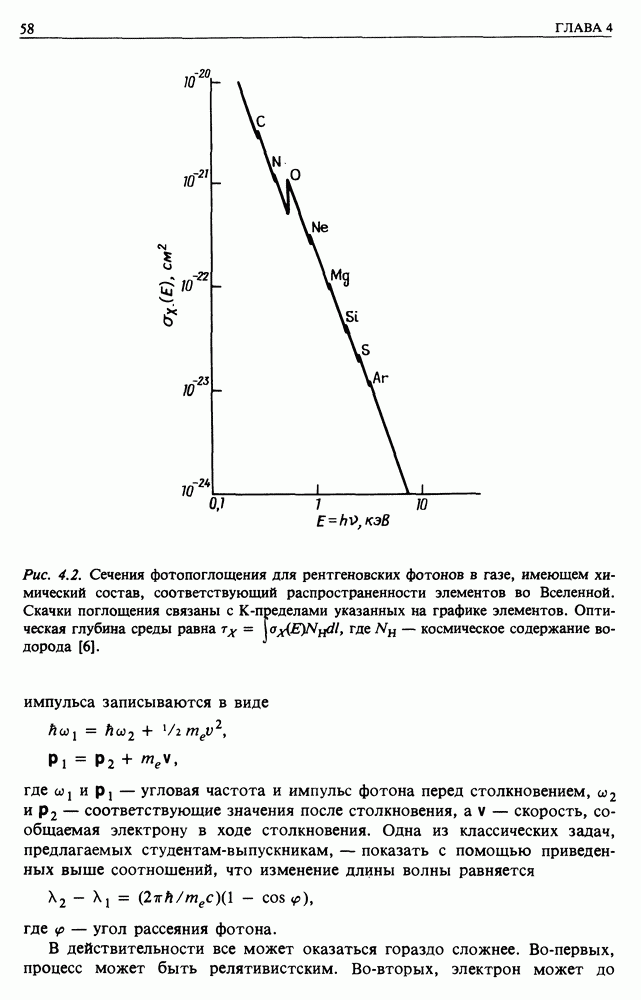
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
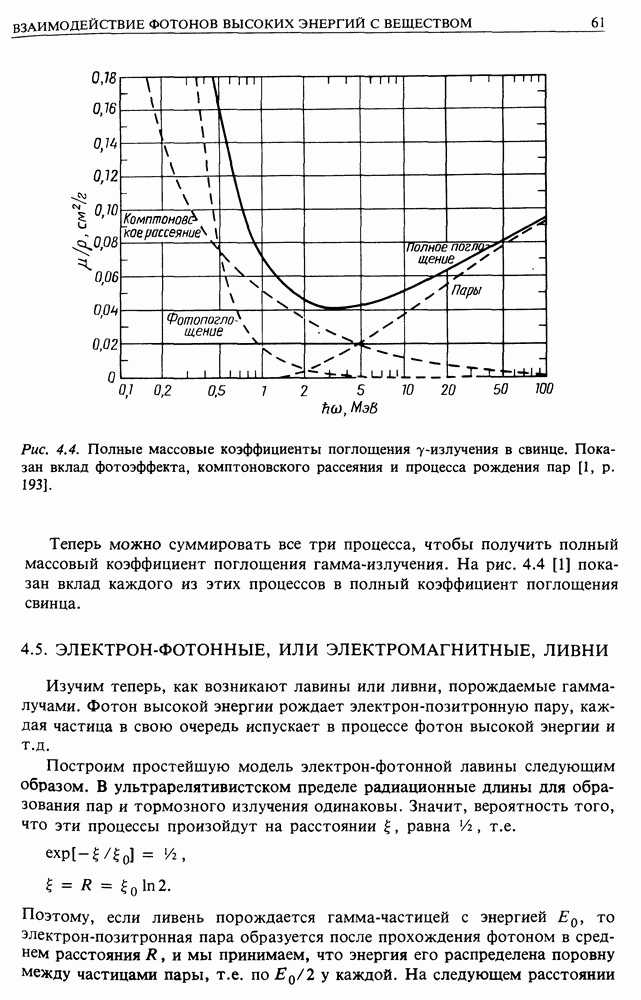
- 4.4. ОБРАЗОВАНИЕ ПАР
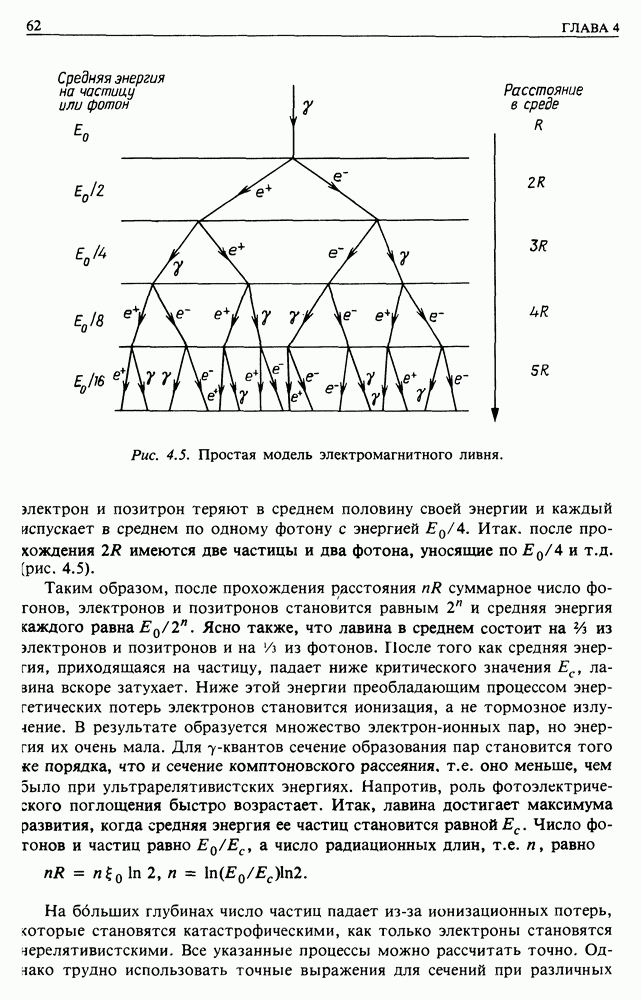
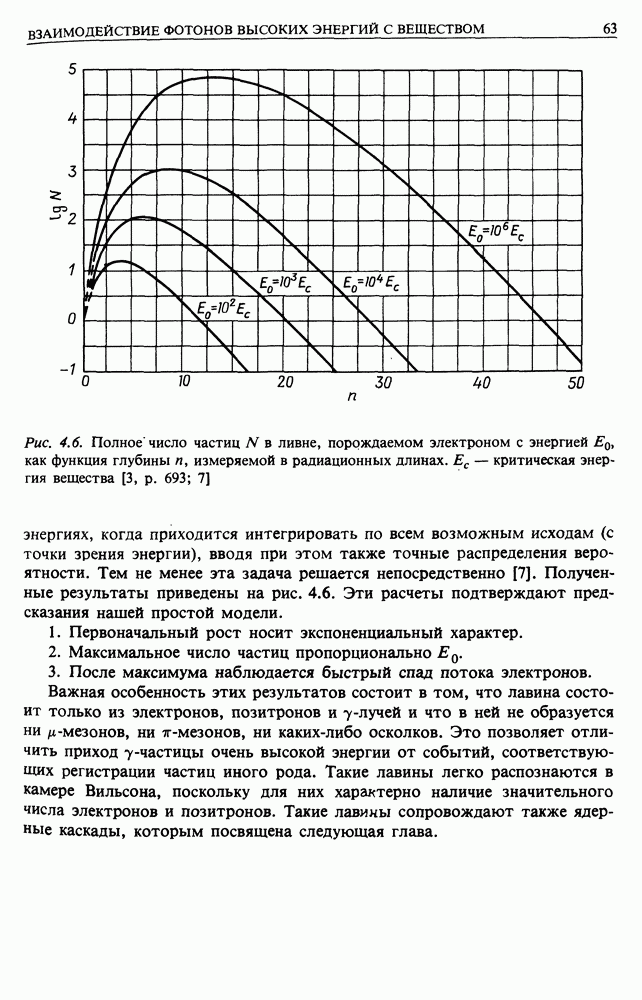
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
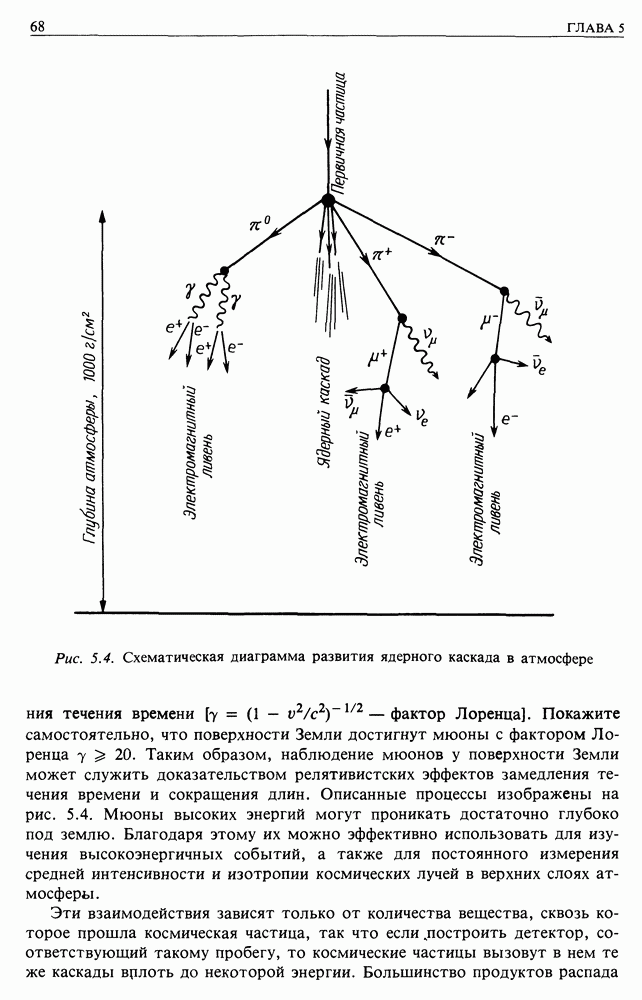
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
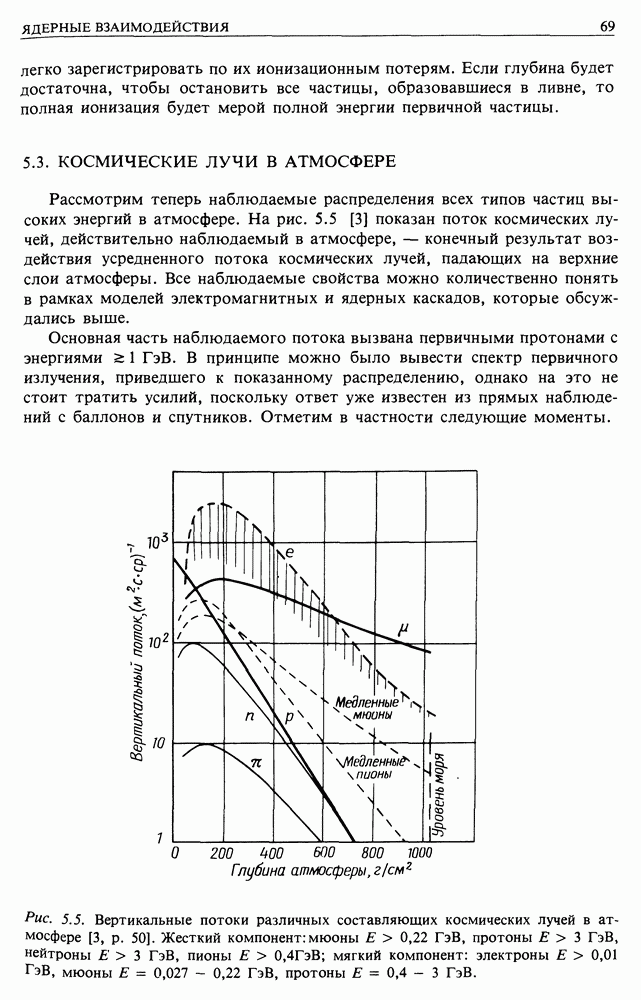
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
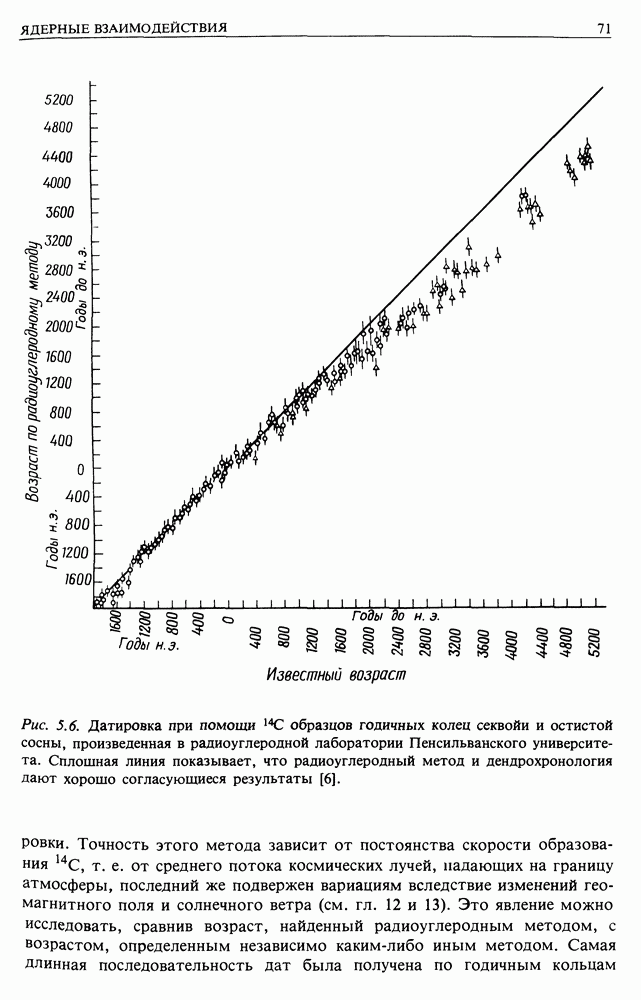
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
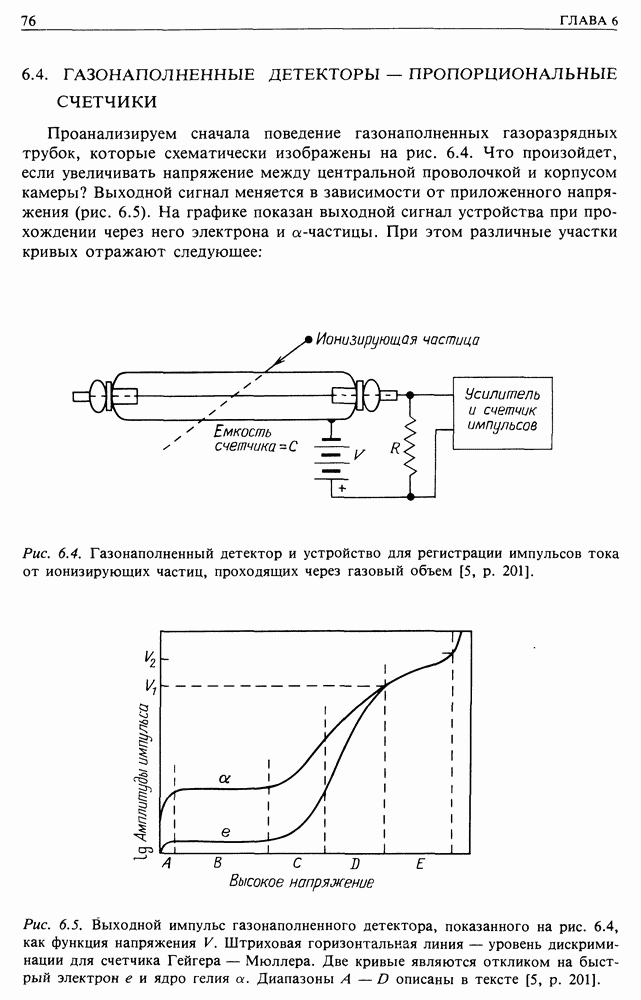
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
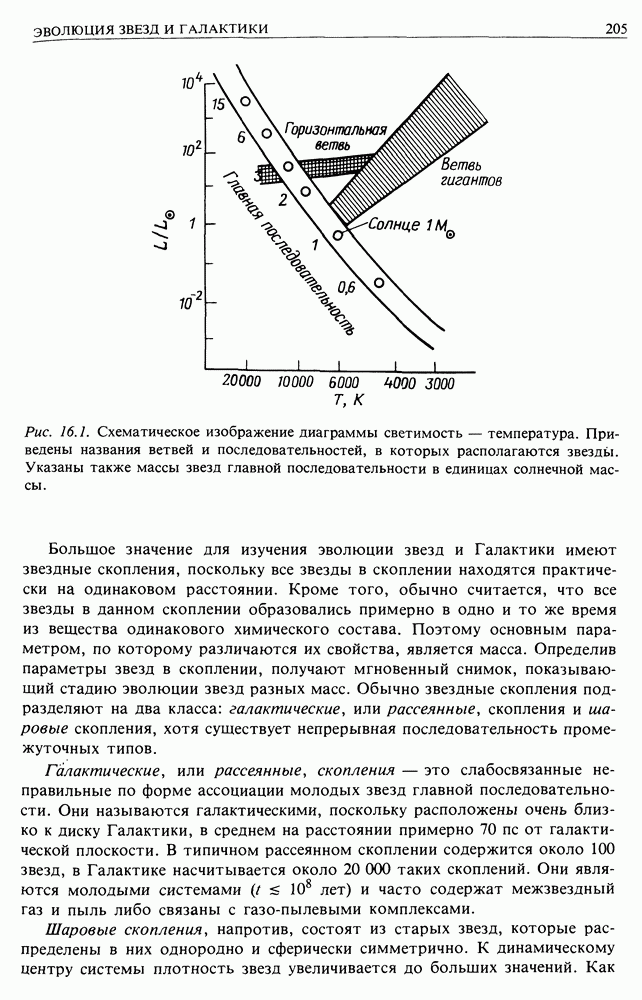
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
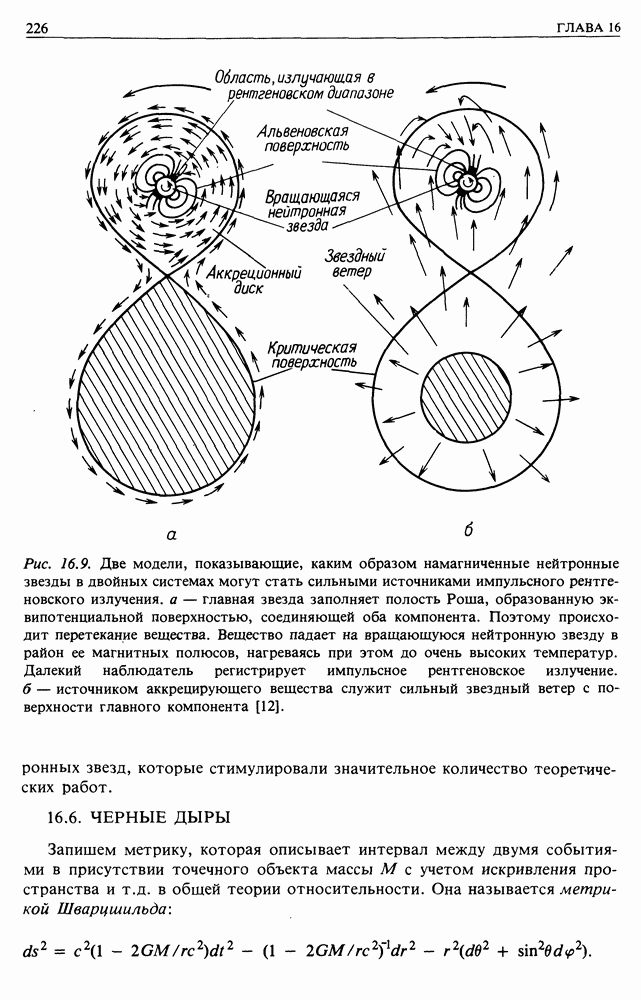
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
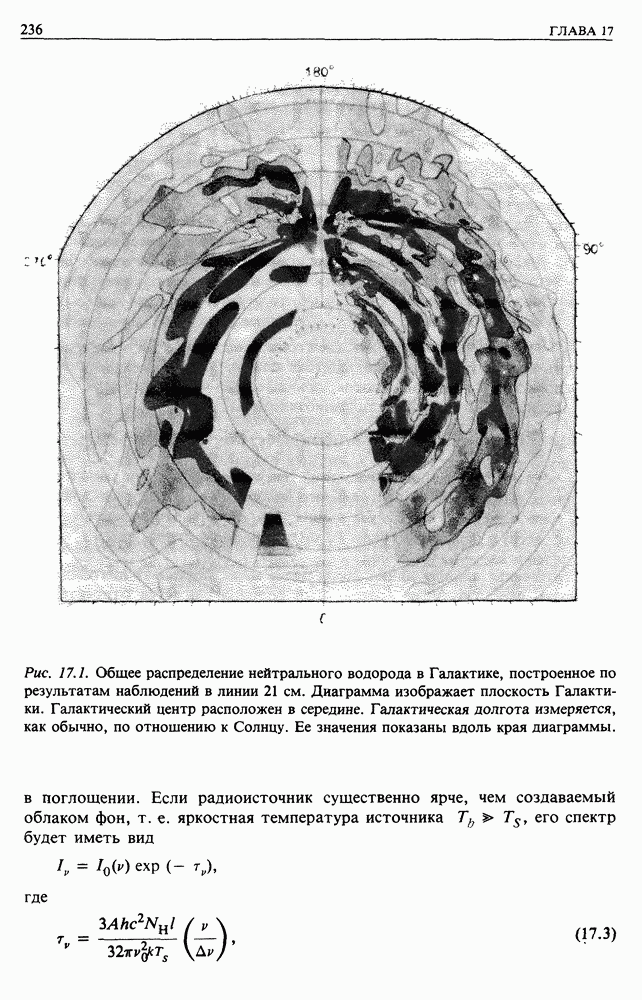
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ