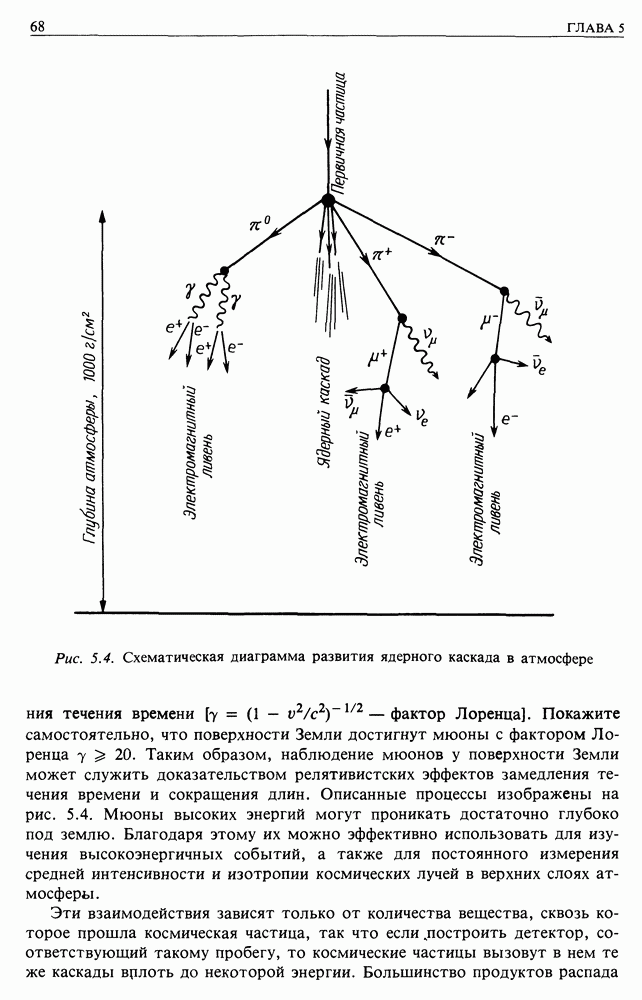
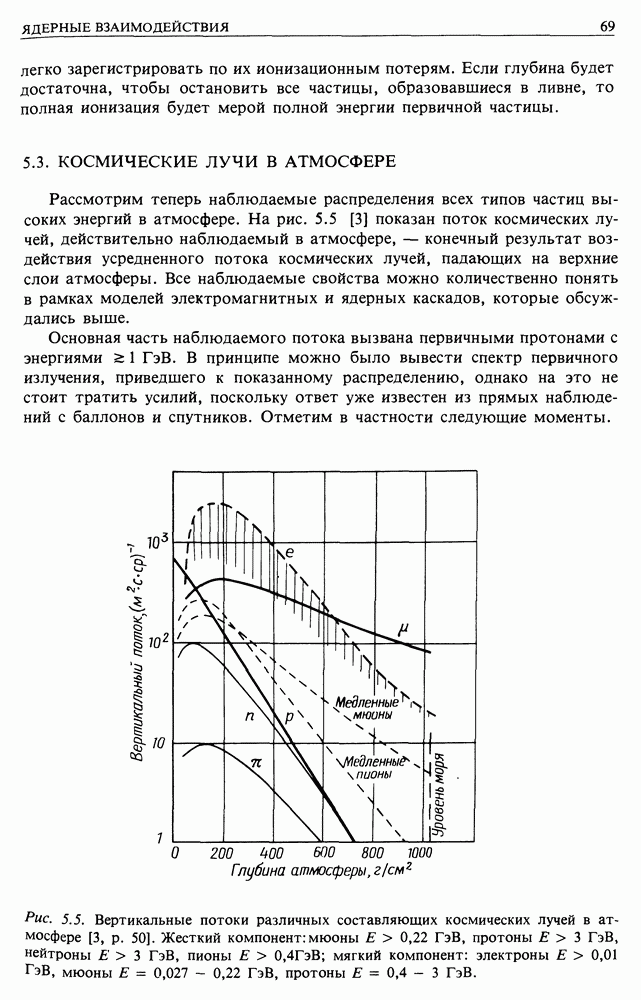
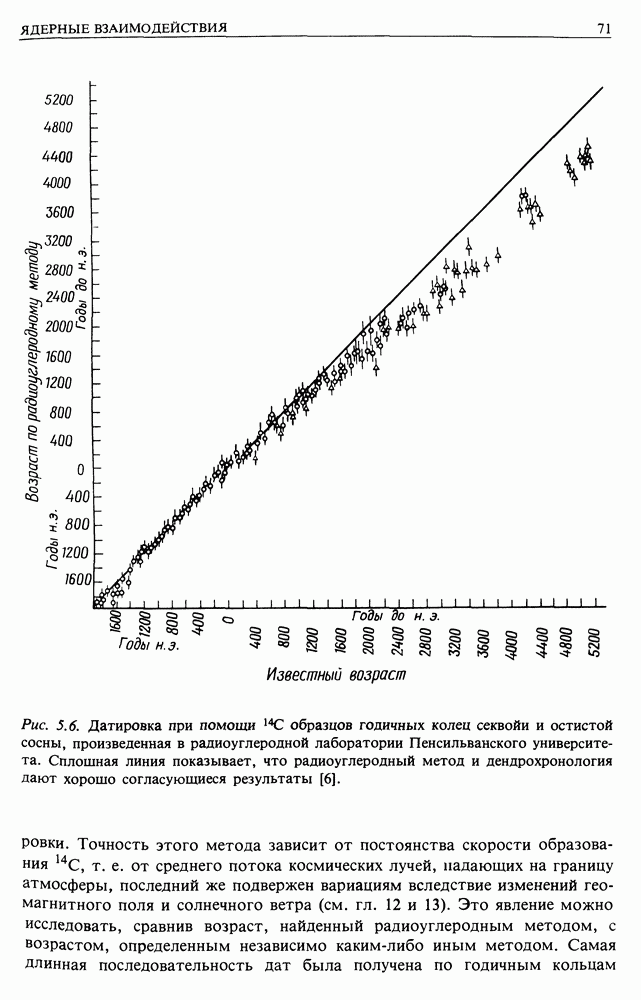
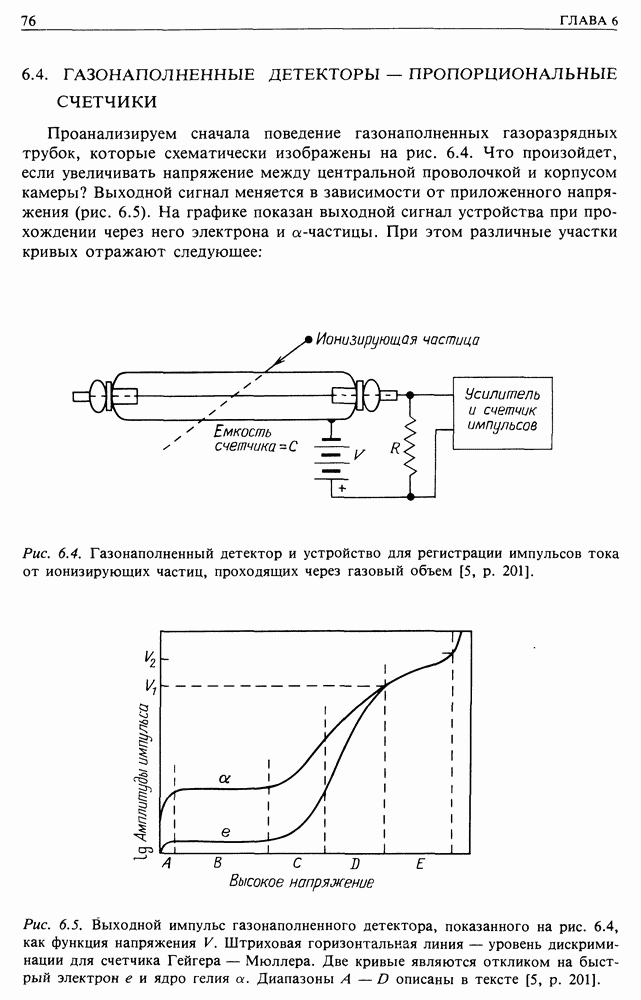
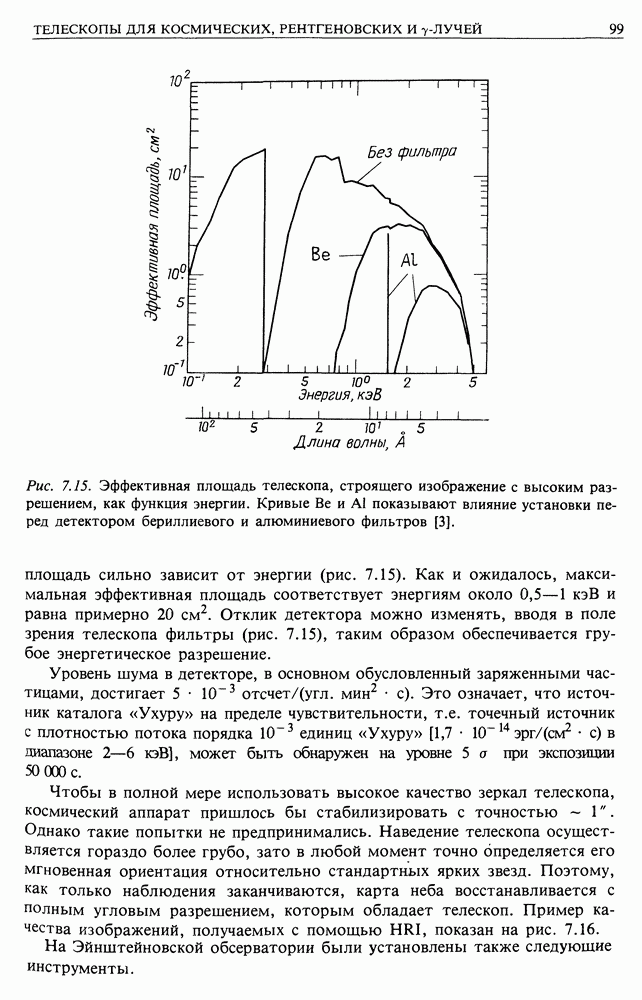
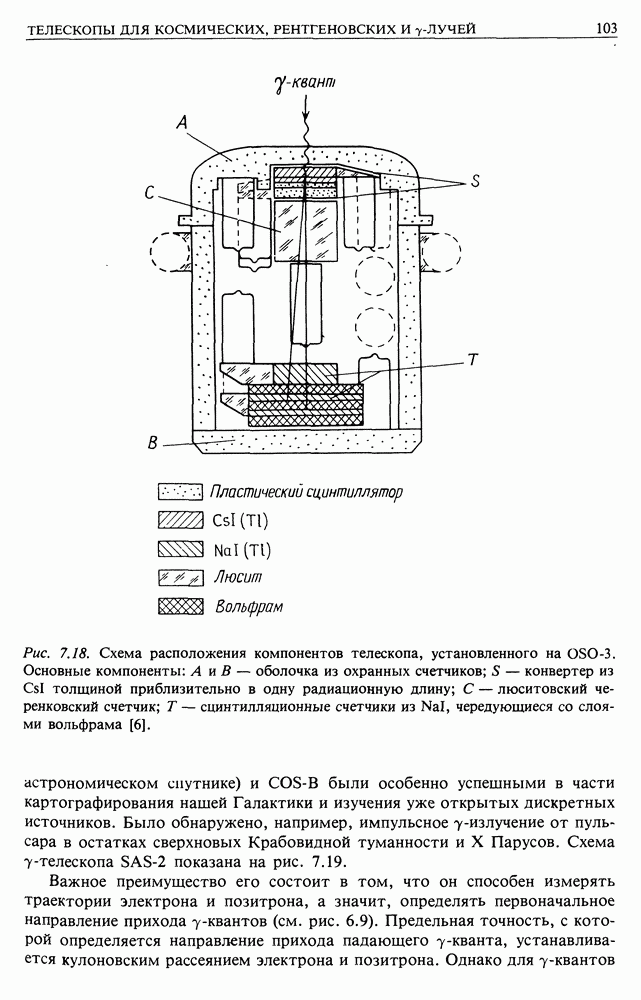
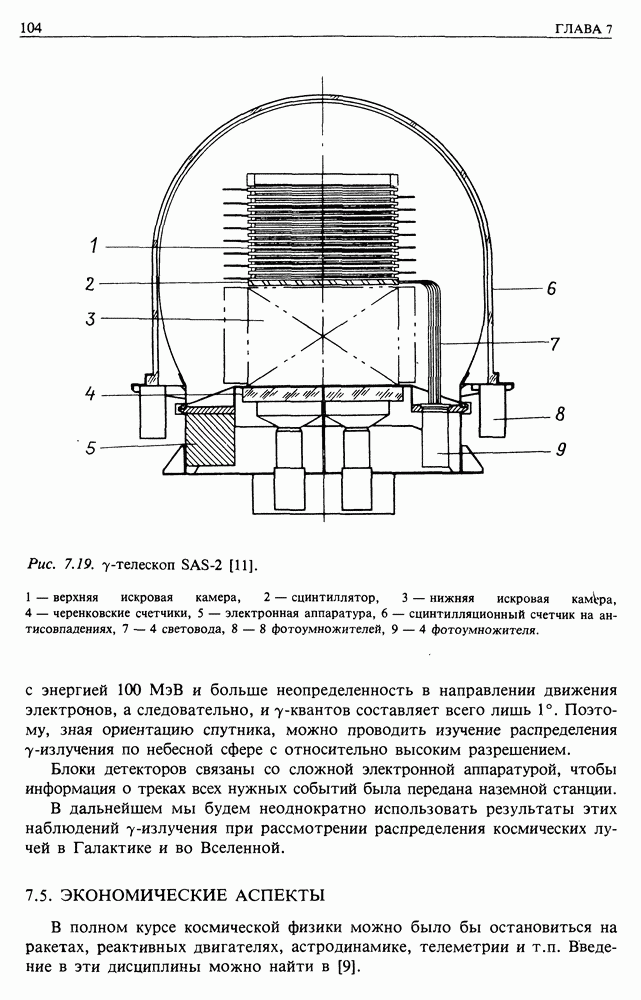
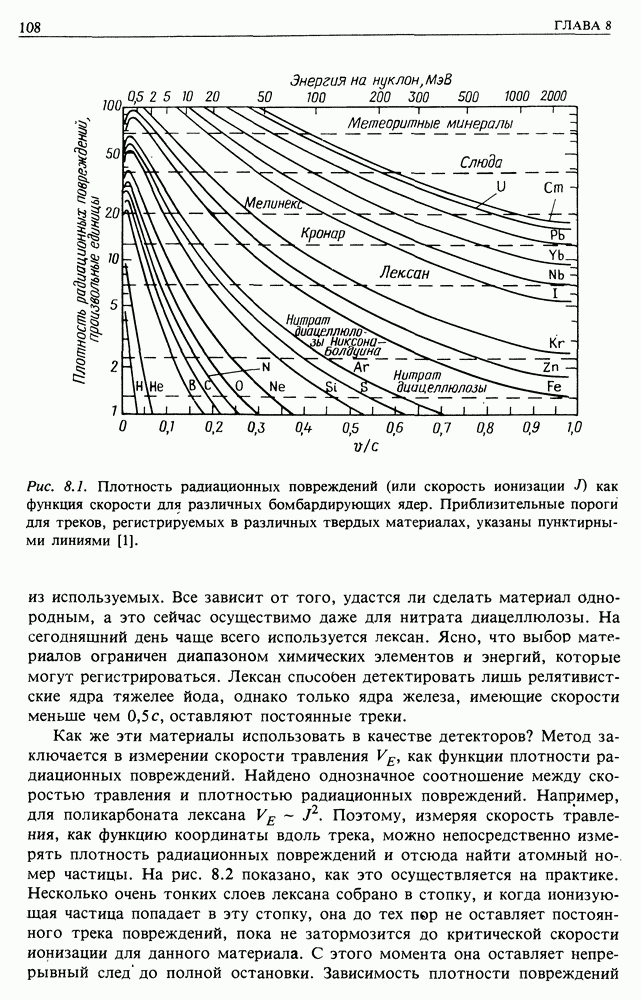
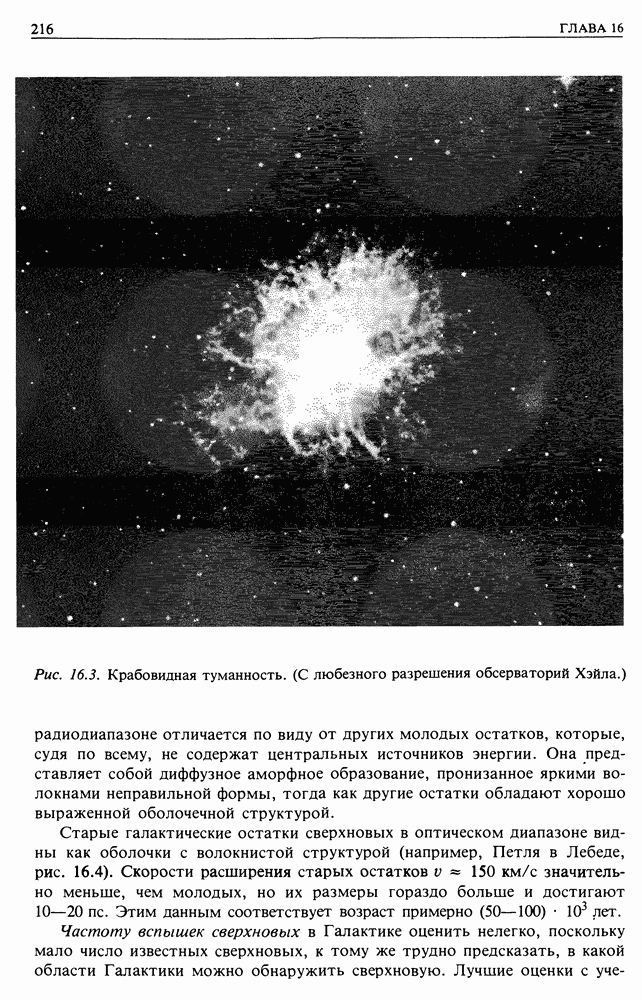
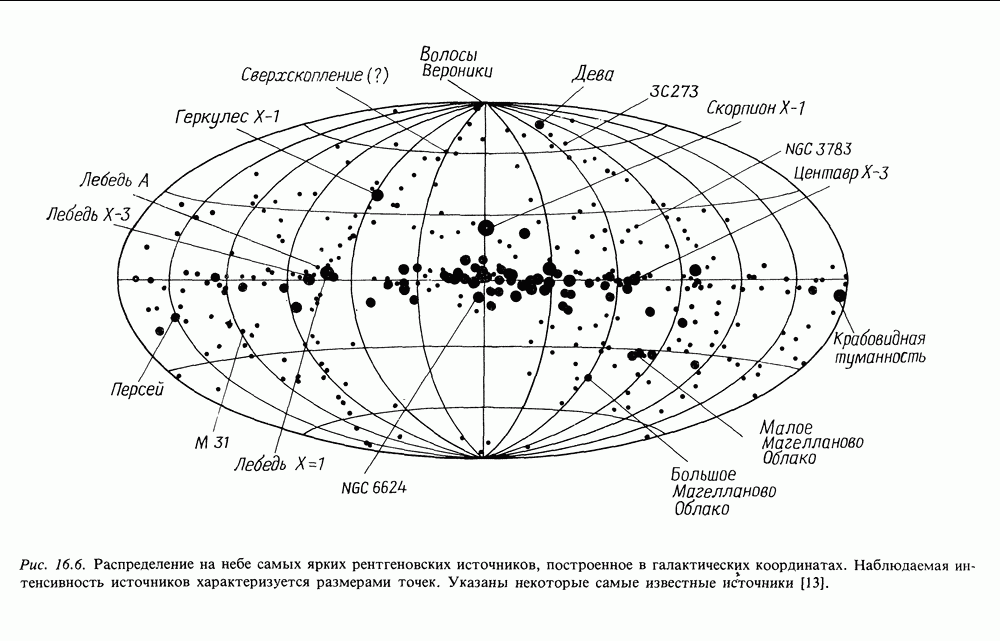
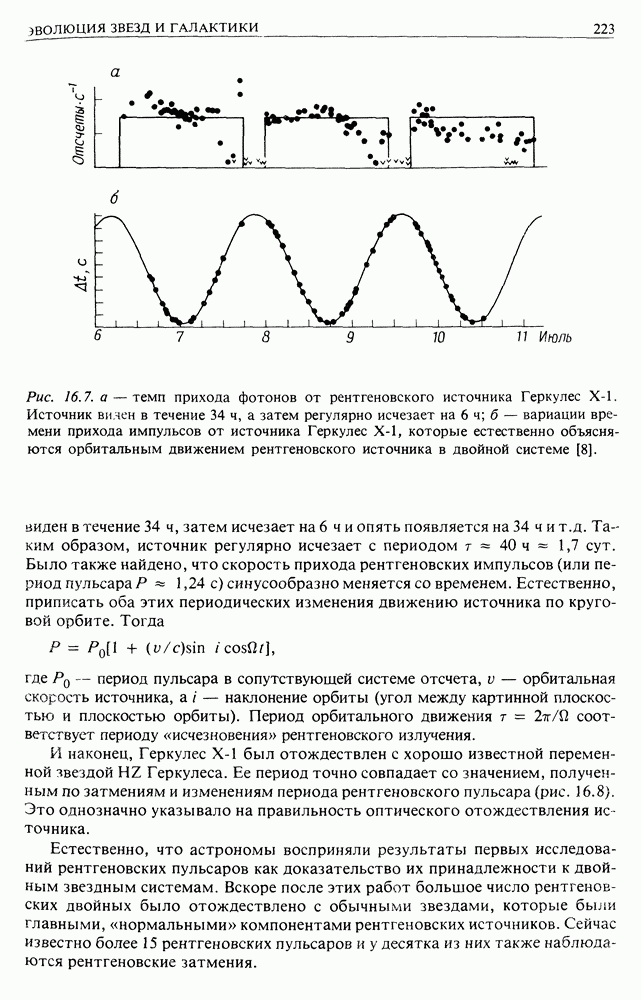
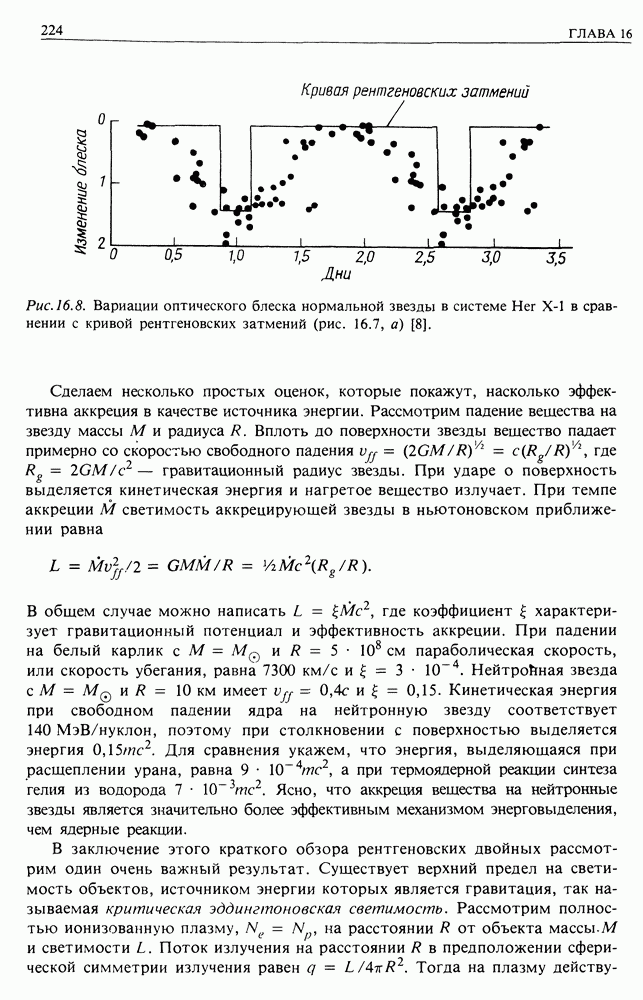
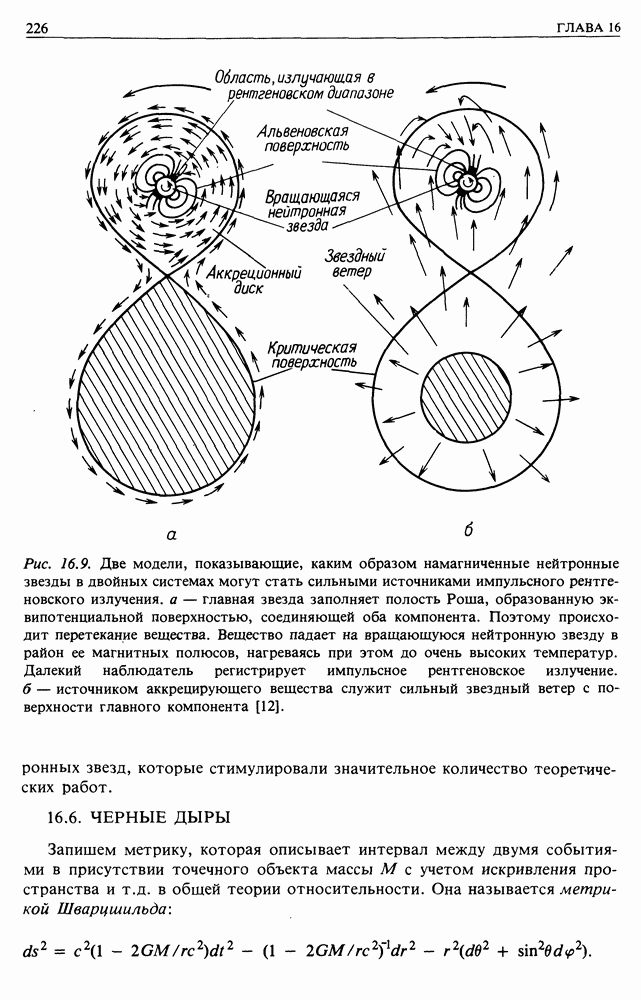
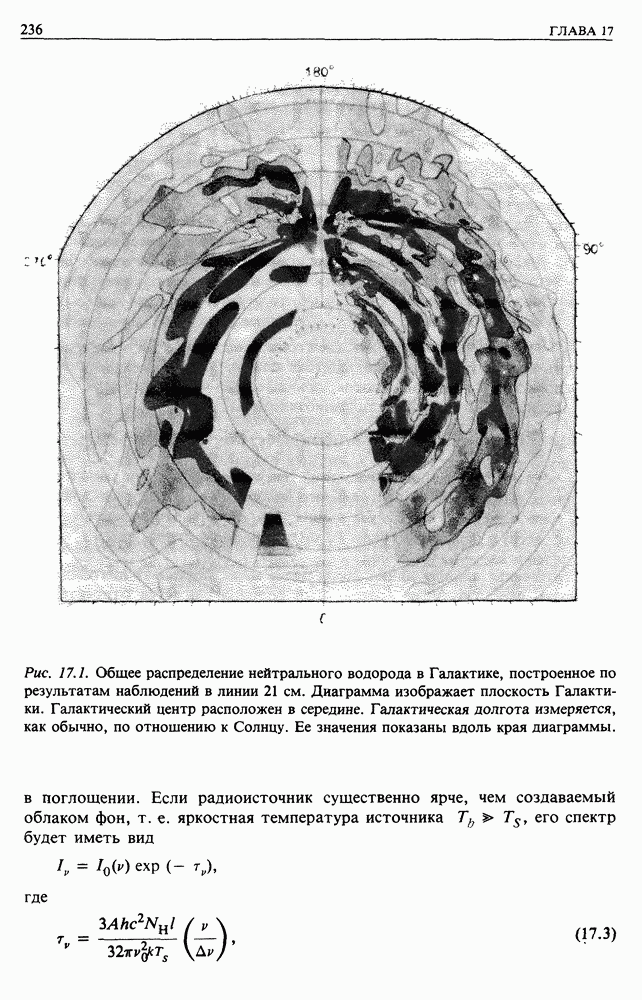
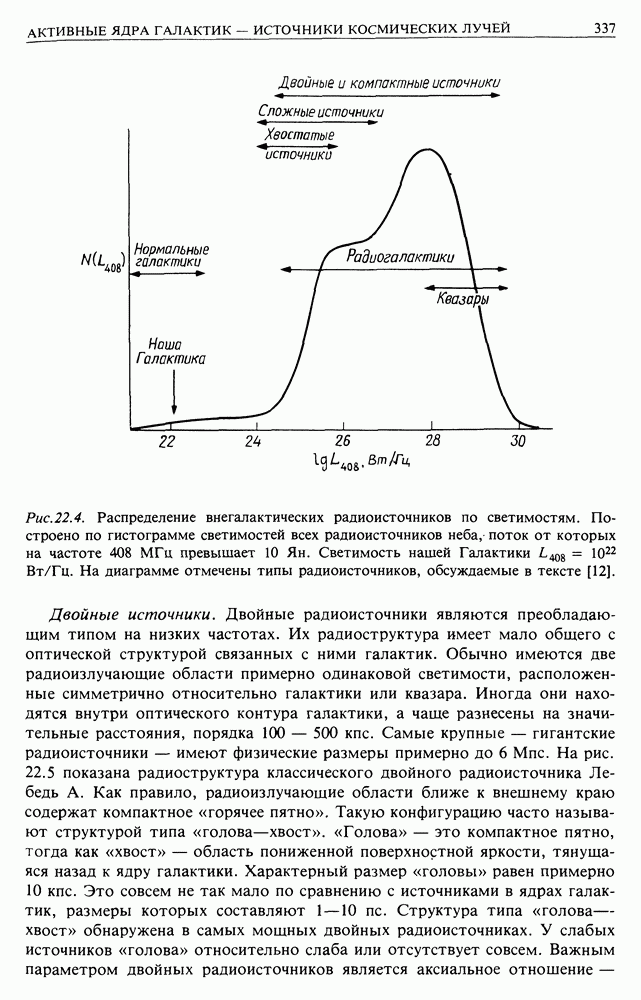
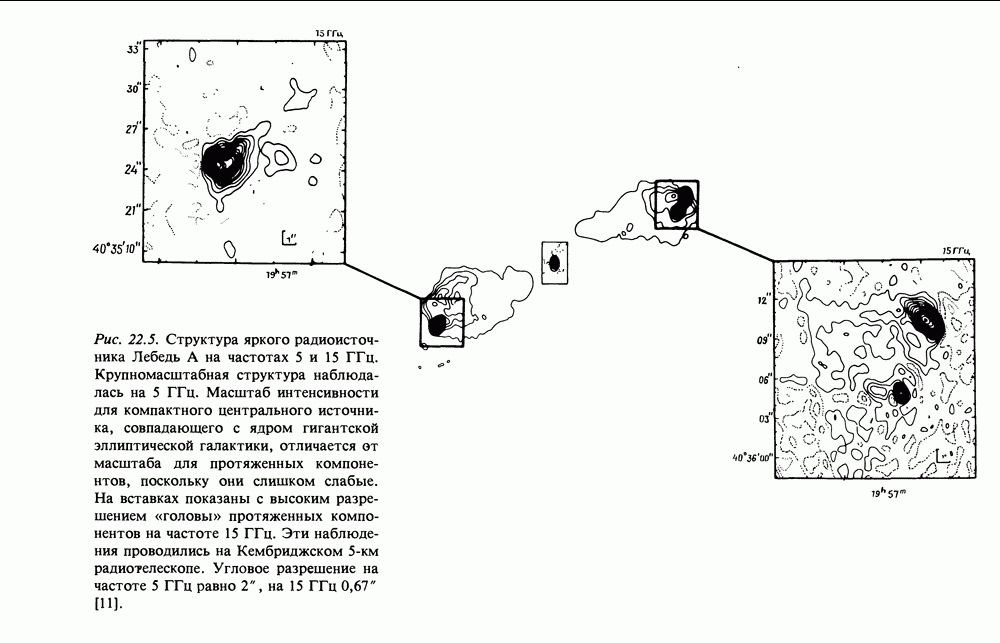
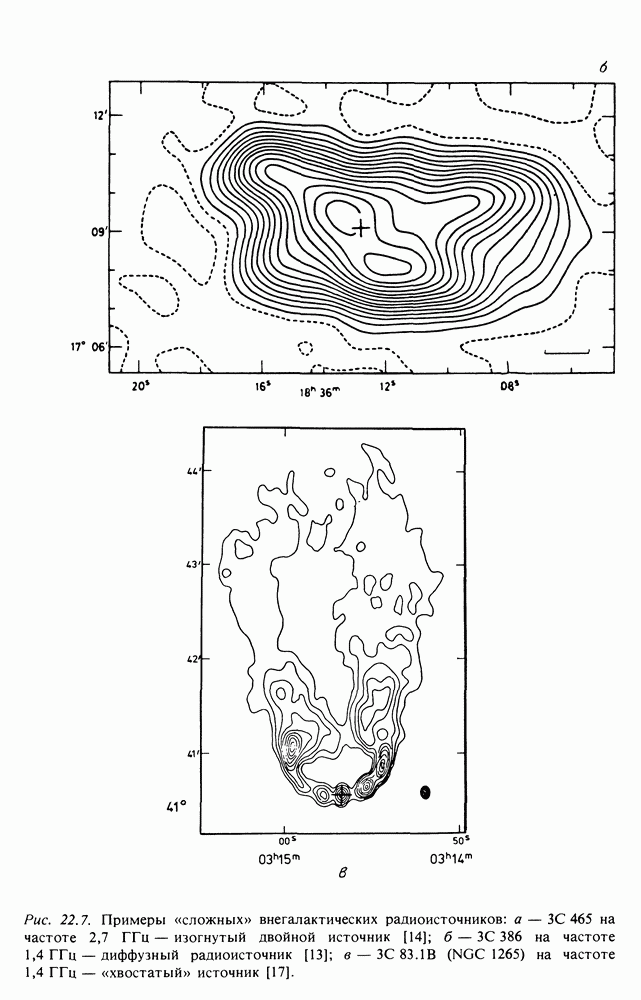
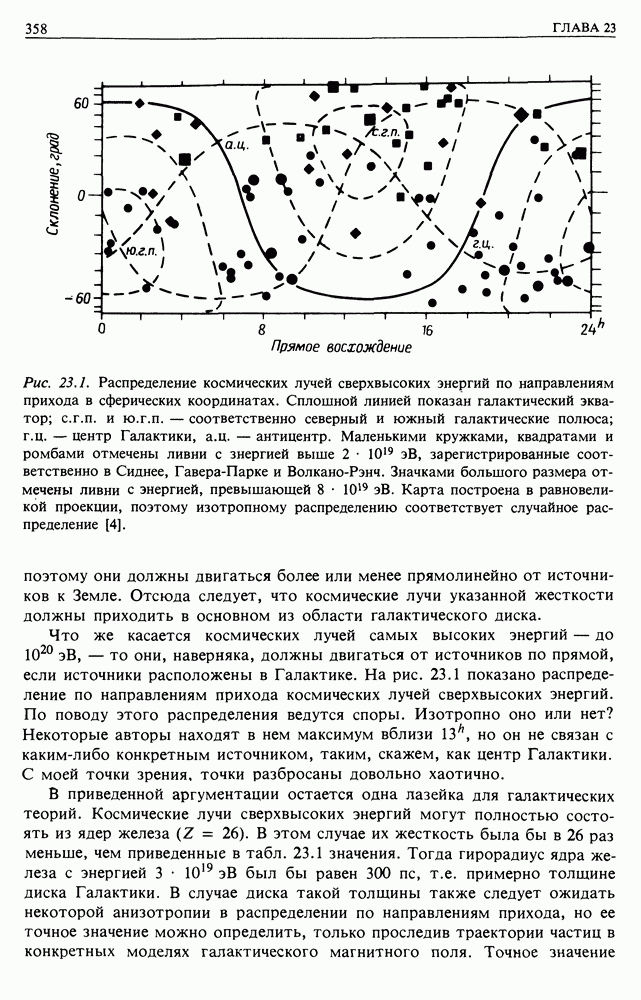
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
16.6. ЧЕРНЫЕ ДЫРЫ
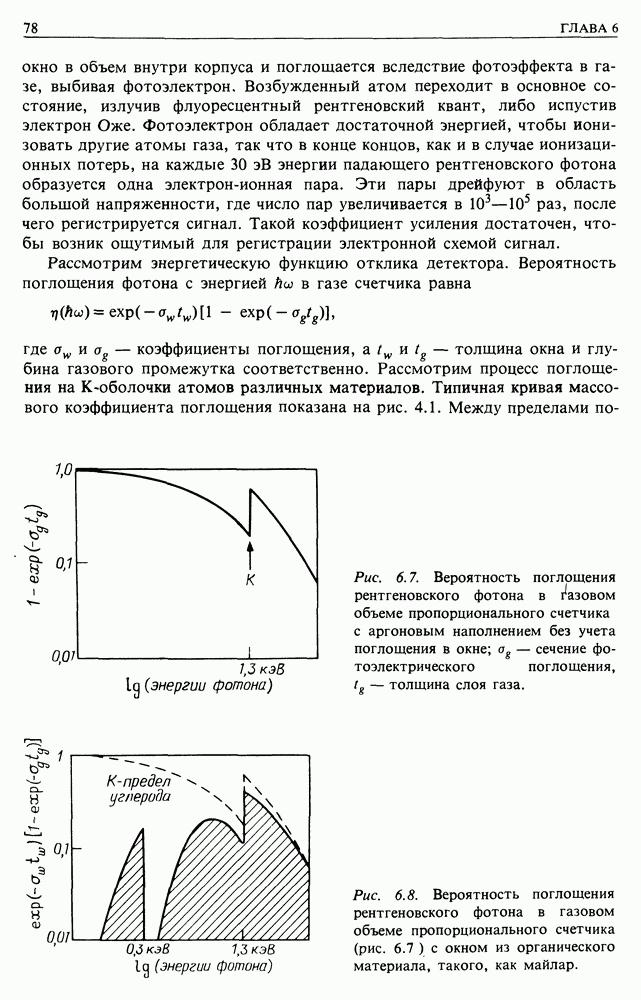
Запишем метрику, которая описывает интервал между двумя событиями в присутствии точечного объекта массы  с учетом искривления пространства и т.д. в общей теории относительности. Она называется метрикой Шварцшилъда:
с учетом искривления пространства и т.д. в общей теории относительности. Она называется метрикой Шварцшилъда:

На больших расстояниях она переходит в интервал специальной теории относительности

Интерпретация пространственно-временных координат в этой метрике нетривиальна. Как нетрудно заметить,  определено таким образом, что отрезок, перпендикулярный лучу зрения, связан со стягивающим его углом по формуле, совпадающей с евклидовой. В радиальной части метрики
определено таким образом, что отрезок, перпендикулярный лучу зрения, связан со стягивающим его углом по формуле, совпадающей с евклидовой. В радиальной части метрики

один из коэффициентов неограниченно возрастает по мере приближения к радиусу Шварцшильда  Обычно в астрофизических ситуациях он значительно меньше размеров тела. Подставив соответствующие значения величин, получим
Обычно в астрофизических ситуациях он значительно меньше размеров тела. Подставив соответствующие значения величин, получим

Таким образом, для Солнца радиусом  релятивистские эффекты несущественны, поскольку в радиусе
релятивистские эффекты несущественны, поскольку в радиусе  находится слишком маленькая масса. С другой стороны, у нейтронных звезд
находится слишком маленькая масса. С другой стороны, у нейтронных звезд  и поправки, учитывающие общую теорию относительности, важны при определении устойчивости таких объектов.
и поправки, учитывающие общую теорию относительности, важны при определении устойчивости таких объектов.
Нетрудно понять, что если радиус станет еще немного меньше, то начнется катастрофический гравитационный коллапс, в ходе которого усиление эффектов гравитации и увеличение гравитационного потенциала будут приводить к возрастанию эффективной гравитационной массы, а это в свою очередь будет увеличивать силу тяжести и т.д. Другими словами, если гравитация становится настолько мощной, что  то никакими силами нельзя предотвратить сжатие под сферу Шварцшильда.
то никакими силами нельзя предотвратить сжатие под сферу Шварцшильда.
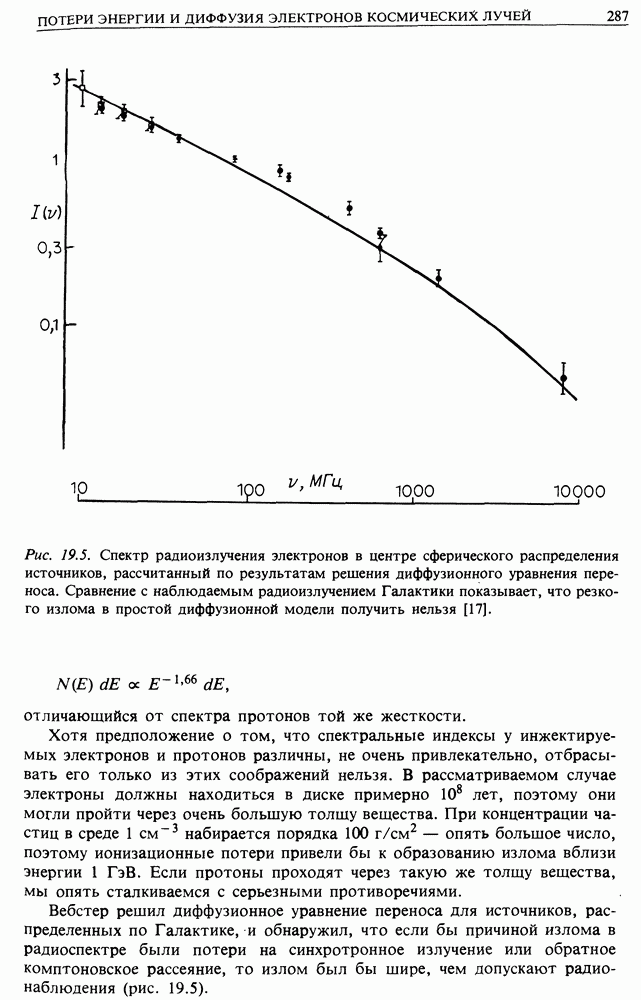
На первый взгляд эти рассуждения свидетельствуют о существовании сингулярности на радиусе Шварцшильда. Однако можно показать, что никакой физической особенности там нет, это просто результат конкретного выбора системы координат. Такую сингулярность нетрудно создать искусственно. В координатах Крускала или Финкельштейна она пропадает. Поэтому с падающим веществом на радиусе Шварцшильда, ничего страшного не происходит. Что происходит дальше? Конечно, никаким способом нельзя избавиться от реальной физической сингулярности при  т.е. когда вещество сжимается в точку. Избежать этого в любой теории гравитации можно, только если ввести законы физики, отличные от тех, какие мы наблюдаем во Вселенной. Например, можно использовать уравнение состояния с отрицательной энергией, но это крайняя мера. Большинство астрономов считают, что здесь есть реальная проблема и ее нужно решать. На изучение природы этих сингулярностей было потрачено много труда. По-видимому, самые многообещающие перспективы сулит квантование гравитационного поля. Возможно, таким путем удастся решить проблему сингулярности. Но квантовые эффекты становятся существенными на
т.е. когда вещество сжимается в точку. Избежать этого в любой теории гравитации можно, только если ввести законы физики, отличные от тех, какие мы наблюдаем во Вселенной. Например, можно использовать уравнение состояния с отрицательной энергией, но это крайняя мера. Большинство астрономов считают, что здесь есть реальная проблема и ее нужно решать. На изучение природы этих сингулярностей было потрачено много труда. По-видимому, самые многообещающие перспективы сулит квантование гравитационного поля. Возможно, таким путем удастся решить проблему сингулярности. Но квантовые эффекты становятся существенными на
предельно малых расстояниях в сильном гравитационном поле, когда комптоновская длина волны протона становится сравнимой с радиусом Шварцшильда.
Каковы свойства черных дыр? Я перечислю только некоторые из них, отсылая за подробностями к книге Мизнера, Торна и Уилера «Гравитация» [6].
Ни в какой системе координат свет не может выйти из-под сферы Шварцшильда, поэтому они черные. То, что оказалось под сферой Шварцшильда, не сможет выйти наружу. Поэтому они дыры. Тела, падающие извне, достигают сингулярности за конечное собственное время, однако внешнему наблюдателю вследствие замедления течения времени длительность падения кажется бесконечной. Правда, из-за сильного красного смещения он будет видеть падающее тело совсем недолго.
Все свойства черной дыры определяются всего тремя параметрами: ее массой, зарядом и моментом количества движения.
Сферически симметричная черная дыра на сфере Шварцшильда становится одновременно и «черной» и «дырой». Для вращающейся черной дыры, к которой применима метрика Керра, области действия этих свойств совпадают не полностью.
Естественно спросить, каким образом можно наблюдать черную дыру, если все падает в нее и ничего не выходит наружу? Ответ заключается в том, что нужно более внимательно наблюдать за характером падения вещества в черную дыру. Очевидно, если вещество обладает даже маленьким моментом количества движения, то поскольку он сохраняется, угловая скорость должна увеличиваться при падении. Поэтому, хотя ничто не препятствует коллапсу вдоль оси вращения, центробежные силы в конце концов остановят падение перпендикулярно ей. Естественно, что вокруг черной дыры образуется аккреционный диск.
Для пробных частиц, вращающихся по круговым орбитам вокруг черной дыры, существует последняя устойчивая орбита. У черной дыры с метрикой Шварцшильда ее радиус равен  а у предельной, т.е. вращающейся с максимально возможной скоростью, черной дыры с метрикой Керра он составляет
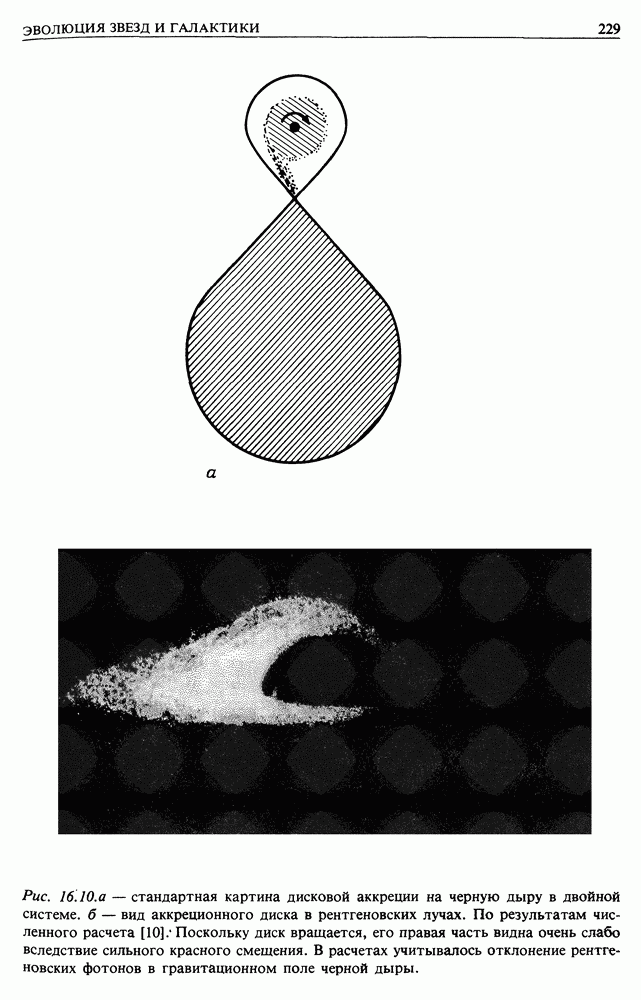
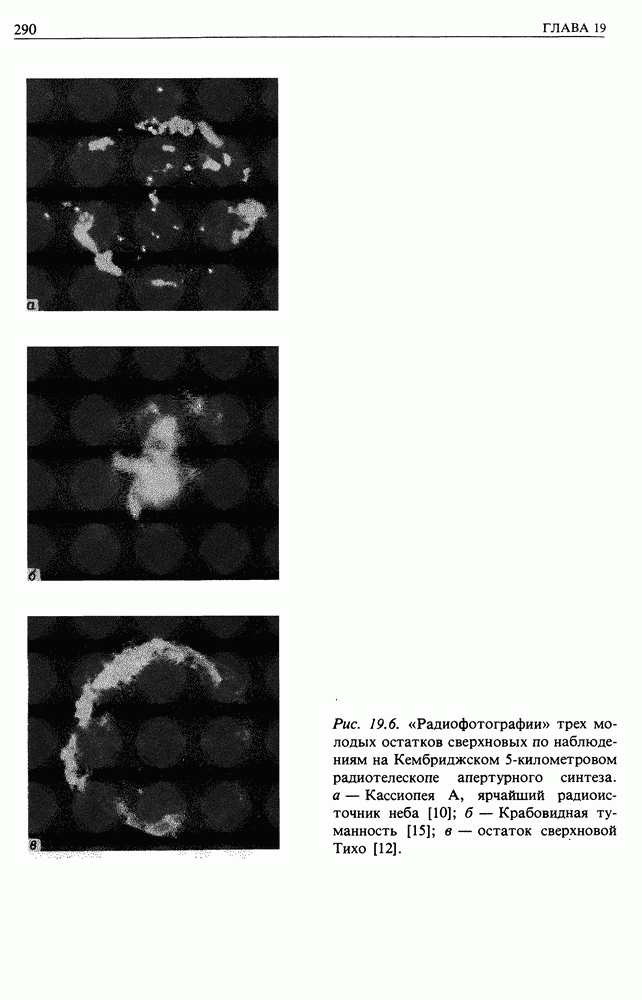
а у предельной, т.е. вращающейся с максимально возможной скоростью, черной дыры с метрикой Керра он составляет  Но, чтобы проникнуть до таких малых радиусов, частицы в диске должны избавиться от момента количества движения. Это возможно за «чет вязкого переноса момента по диску наружу. Действие вязких сил сопровождается диссипацией кинетической энергии, в результате чего вещество в диске нагревается до высоких температур. Такова стандартная картина дисковой аккреции вещества, обладающего моментом количества движения, на компактный объект. Ясно, что она реализуется, если одним из компонентов двойной системы является черная дыра (рис. 16.10).
Но, чтобы проникнуть до таких малых радиусов, частицы в диске должны избавиться от момента количества движения. Это возможно за «чет вязкого переноса момента по диску наружу. Действие вязких сил сопровождается диссипацией кинетической энергии, в результате чего вещество в диске нагревается до высоких температур. Такова стандартная картина дисковой аккреции вещества, обладающего моментом количества движения, на компактный объект. Ясно, что она реализуется, если одним из компонентов двойной системы является черная дыра (рис. 16.10).
Эта тема неисчерпаема. Как черные дыры могут выдать свое присутствие? Их можно изучать двумя основными способами: наблюдая, во-первых, рентгеновские двойные, а во-вторых, ядра галактик. В конечном итоге в обоих случаях необходимо уметь измерять массы объектов по их динамике.
В случае двойных рентгеновских источников задача состоит в том, чтобы отождествить объект с двойной системой и извлечь максимум информации об орбитах обеих звезд. Изучив орбиты, можно определить массы

(кликните для просмотра скана)
звезд. В частности, подобная процедура оказалась успешной для такой двойной системы, как Геркулес  В этом случае динамический анализ показал, что нормальная звезда имеет массу примерно
В этом случае динамический анализ показал, что нормальная звезда имеет массу примерно  а рентгеновский источник
а рентгеновский источник  Последнее значение явно свидетельствует в пользу гипотезы нейтронной звезды. В источнике Центавр
Последнее значение явно свидетельствует в пользу гипотезы нейтронной звезды. В источнике Центавр  нормальный компонент — это горячая звезда спектрального класса В массой
нормальный компонент — это горячая звезда спектрального класса В массой  тогда как масса рентгеновского источника
тогда как масса рентгеновского источника  согласуется с предположением о нейтронной звезде.
согласуется с предположением о нейтронной звезде.
Источник Лебедь  особенно интересен, поскольку здесь динамический анализ неполон, измерен только период нормальной звезды. По кривой лучевых скоростей можно найти функцию масс
особенно интересен, поскольку здесь динамический анализ неполон, измерен только период нормальной звезды. По кривой лучевых скоростей можно найти функцию масс

Для завершения анализа нужна дополнительная информация. По типу нормальной звезды можно заключить, что ее масса лежит в интервале  Известно также, что оптическая светимость системы меняется с частотой, равной удвоенной частоте орбитального движения. Это связано с приливными искажениями формы нормального компонента, в результате которых звезда из сферической становится яйцеобразной. Объединение этих данных может дать информацию об угле наклона орбиты и о массах звезд. Проведенный анализ показал, что масса рентгеновского источника должна лежать между
Известно также, что оптическая светимость системы меняется с частотой, равной удвоенной частоте орбитального движения. Это связано с приливными искажениями формы нормального компонента, в результате которых звезда из сферической становится яйцеобразной. Объединение этих данных может дать информацию об угле наклона орбиты и о массах звезд. Проведенный анализ показал, что масса рентгеновского источника должна лежать между  В этом случае единственным возможным рентгеновским источником является черная дыра, поскольку масса белых карликов и нейтронных звезд должна быть порядка солнечной. Лебедь
В этом случае единственным возможным рентгеновским источником является черная дыра, поскольку масса белых карликов и нейтронных звезд должна быть порядка солнечной. Лебедь  является лучшим, но не единственным из зарегистрированных кандидатов в двойные системы с черными дырами.
является лучшим, но не единственным из зарегистрированных кандидатов в двойные системы с черными дырами.
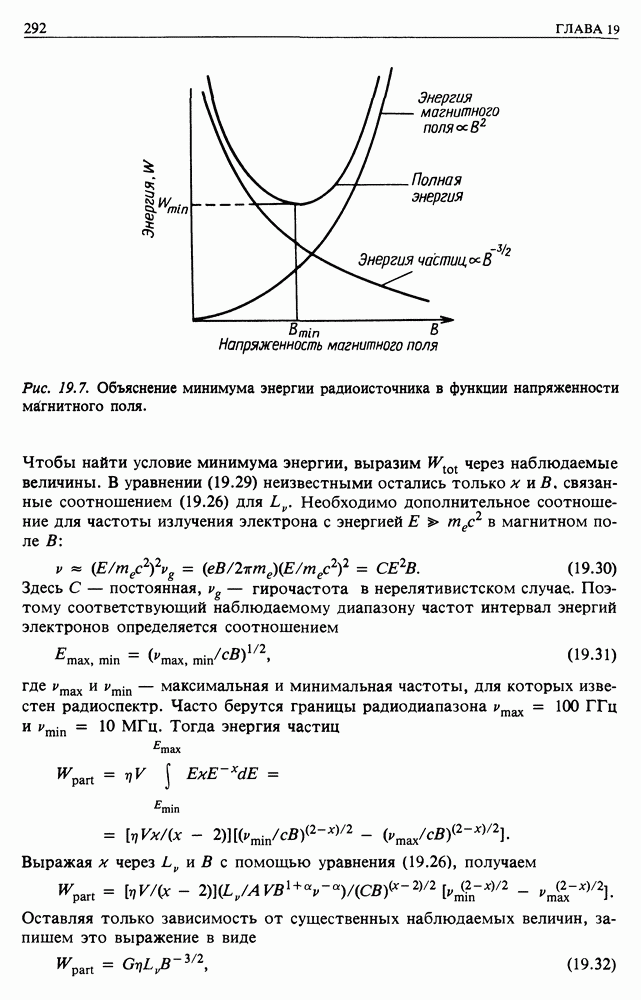
Кроме того, в ядрах галактик могут находиться массивные черные дыры. Существуют серьезные основания считать, что в процессе эволюции галактических ядер должна образоваться черная дыра. Лучше всего изучена ближайшая к Солнечной системе гигантская эллиптическая галактика  расположенная вблизи центра скопления галактик в созвездии Девы на расстоянии около
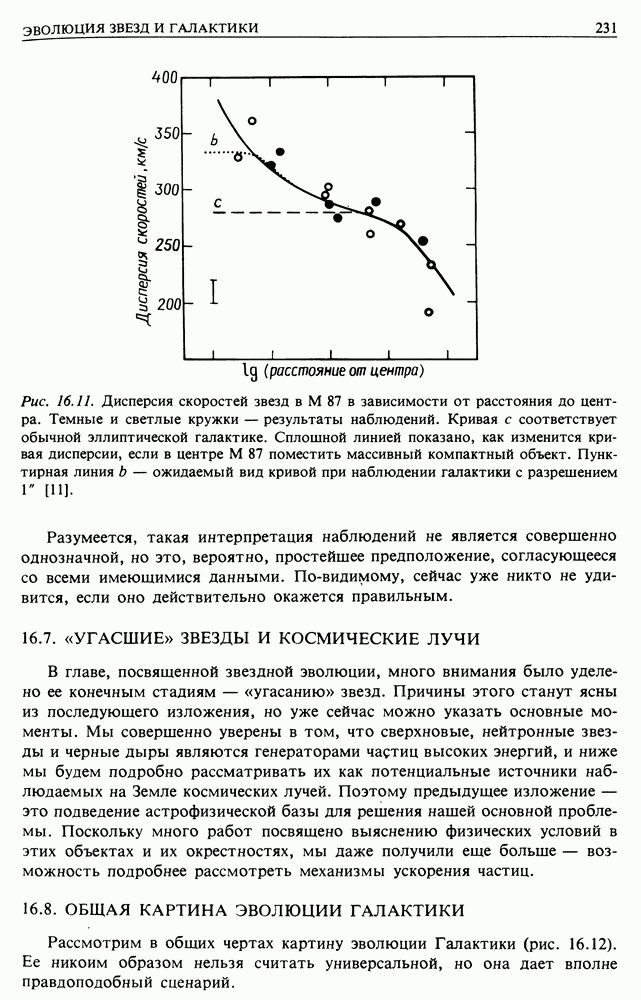
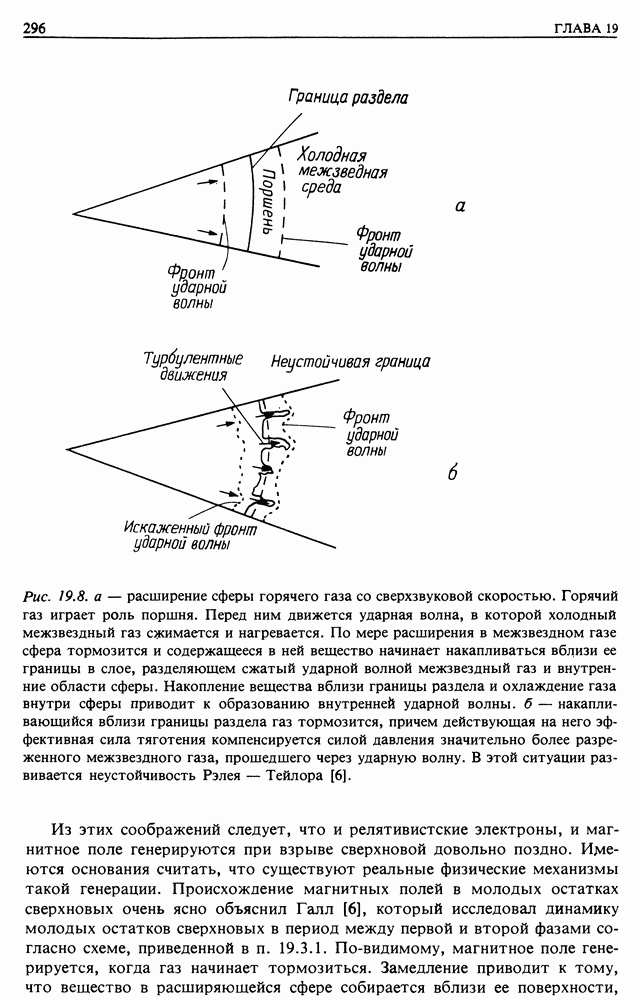
расположенная вблизи центра скопления галактик в созвездии Девы на расстоянии около  (рис. 15.8). Важное значение имеют измерения дисперсии скоростей звезд в галактике в зависимости от расстояния до ее центра, а также очень точная фотометрия распределения яркости. На рис. 16.11 показана зависимость дисперсии скоростей от радиуса для типичной гигантской эллиптической галактики, в ядре которой нет массивного объекта. Показанная кружками наблюдаемая дисперсия явно возрастает к центру быстрее. Следующие простые соображения показывают, что это можно объяснить наличием в ядре компактного массивного объекта. Если звезды (или пробные частицы) вращаются по стационарным орбитам вокруг ядра, то гравитационная и центробежная силы должны быть равны друг другу
(рис. 15.8). Важное значение имеют измерения дисперсии скоростей звезд в галактике в зависимости от расстояния до ее центра, а также очень точная фотометрия распределения яркости. На рис. 16.11 показана зависимость дисперсии скоростей от радиуса для типичной гигантской эллиптической галактики, в ядре которой нет массивного объекта. Показанная кружками наблюдаемая дисперсия явно возрастает к центру быстрее. Следующие простые соображения показывают, что это можно объяснить наличием в ядре компактного массивного объекта. Если звезды (или пробные частицы) вращаются по стационарным орбитам вокруг ядра, то гравитационная и центробежная силы должны быть равны друг другу  т. е. должно быть
т. е. должно быть  . Таким образом, гравитационное поле массивного центрального тела должно привести к наблюдаемому распределению скоростей. Это ткже согласуется с подробной фотометрией поверхности, которая показывает, что реальный профиль яркости искажен, причем именно так, как должно быть, если бы в ядре
. Таким образом, гравитационное поле массивного центрального тела должно привести к наблюдаемому распределению скоростей. Это ткже согласуется с подробной фотометрией поверхности, которая показывает, что реальный профиль яркости искажен, причем именно так, как должно быть, если бы в ядре  находилась черная дыра массой
находилась черная дыра массой 

Рис. 16.11. Дисперсия скоростей звезд в  в зависимости от расстояния до центра. Темные и светлые кружки — результаты наблюдений. Кривая с соответствует обычной эллиптической галактике. Сплошной линией показано, как изменится кривая дисперсии, если в центре
в зависимости от расстояния до центра. Темные и светлые кружки — результаты наблюдений. Кривая с соответствует обычной эллиптической галактике. Сплошной линией показано, как изменится кривая дисперсии, если в центре  поместить массивный компактный объект. Пунктирная линия
поместить массивный компактный объект. Пунктирная линия  ожидаемый вид кривой при наблюдении галактики с разрешением
ожидаемый вид кривой при наблюдении галактики с разрешением 
Разумеется, такая интерпретация наблюдений не является совершенно однозначной, но это, вероятно, простейшее предположение, согласующееся со всеми имеющимися данными. По-видимому, сейчас уже никто не удивится, если оно действительно окажется правильным.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
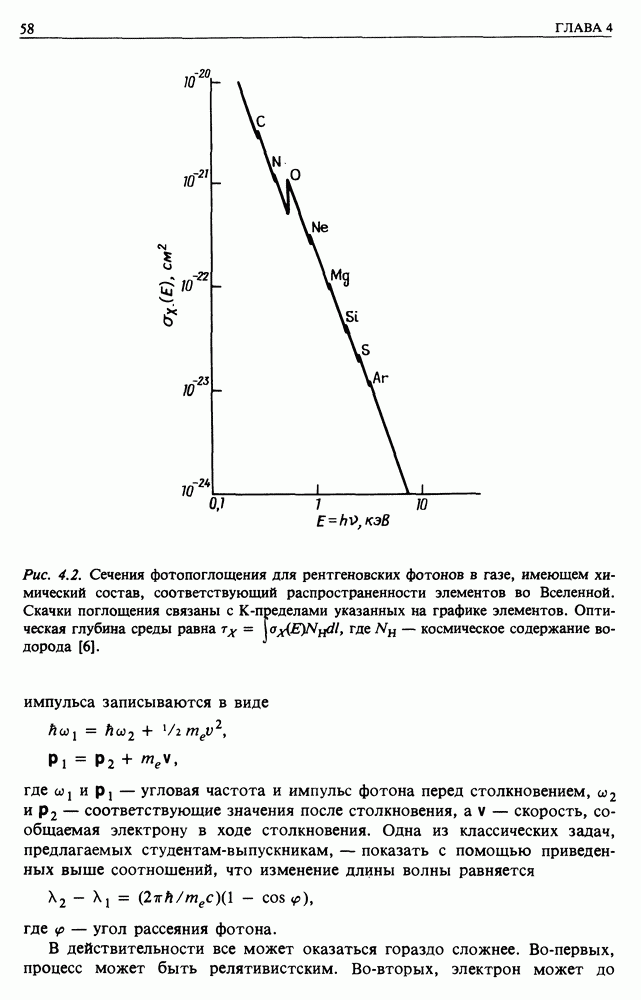
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
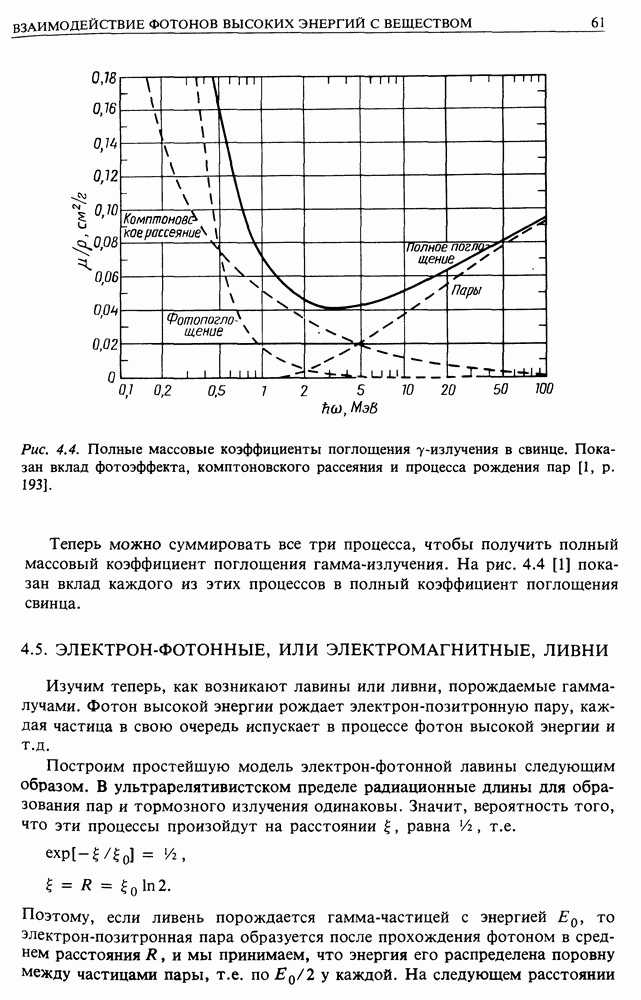
- 4.4. ОБРАЗОВАНИЕ ПАР
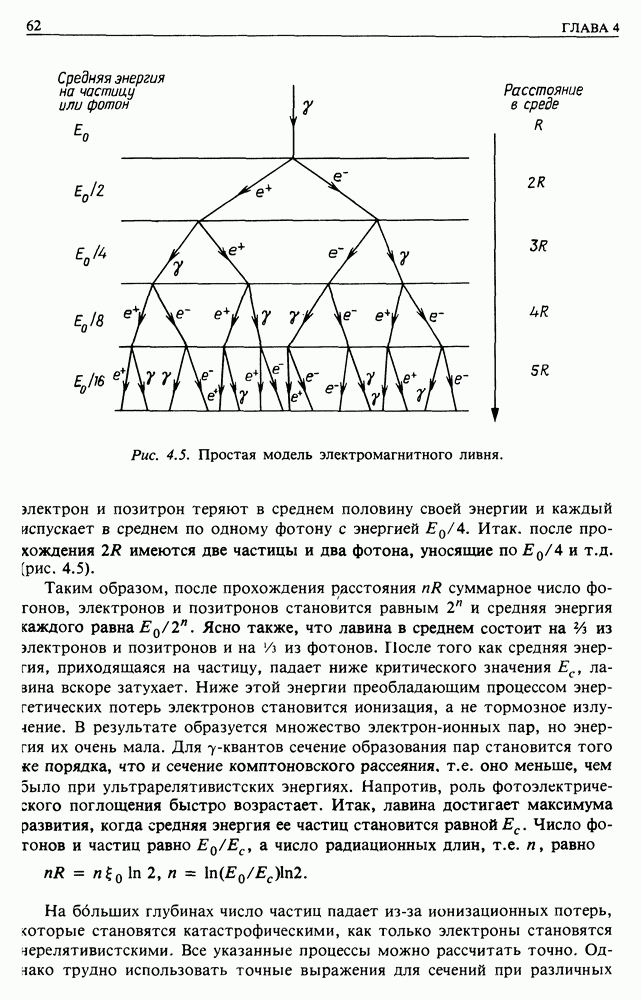
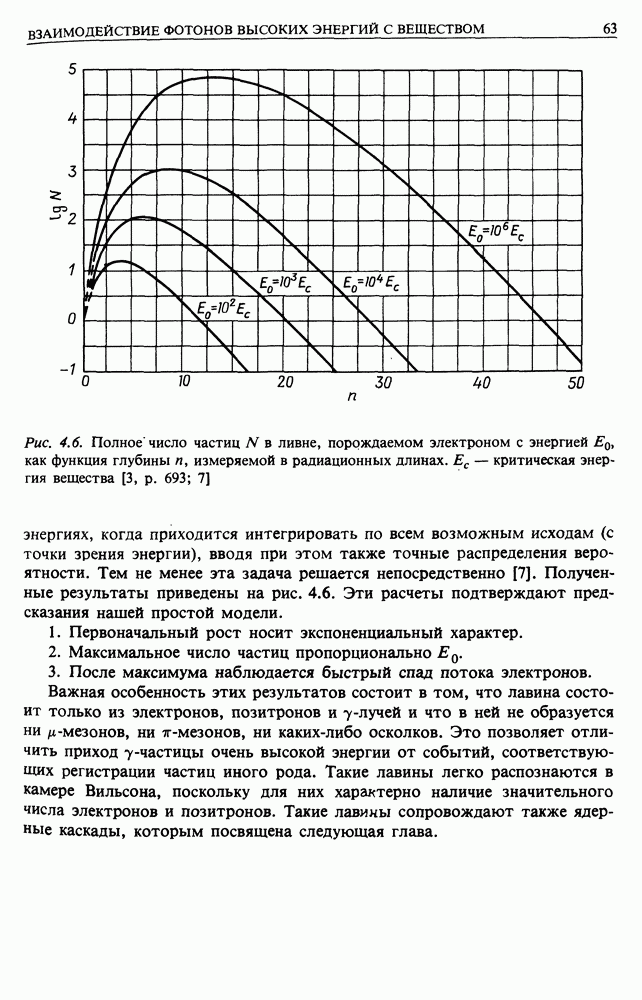
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
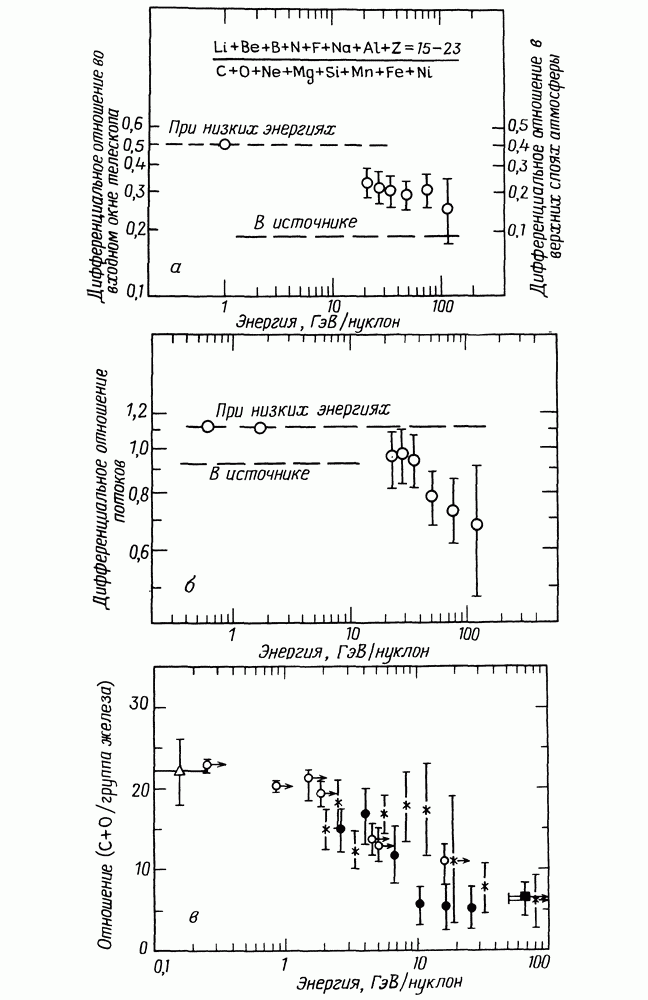
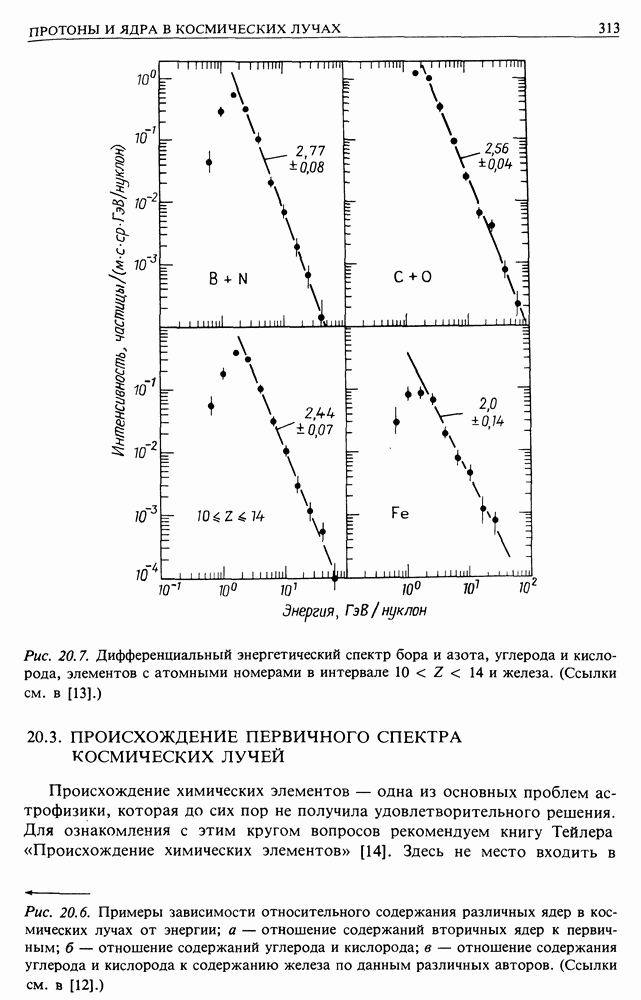
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
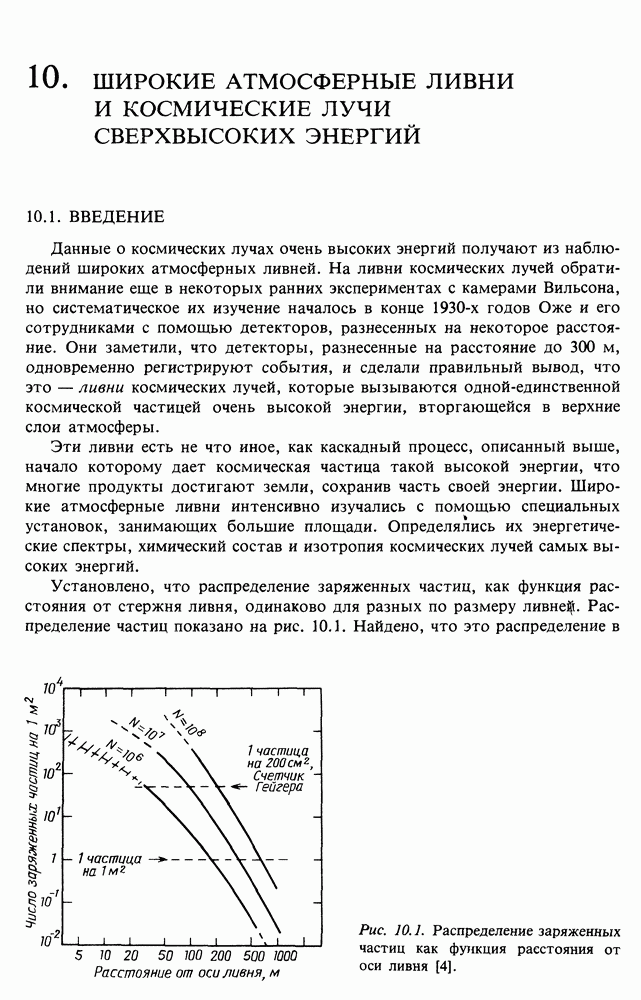
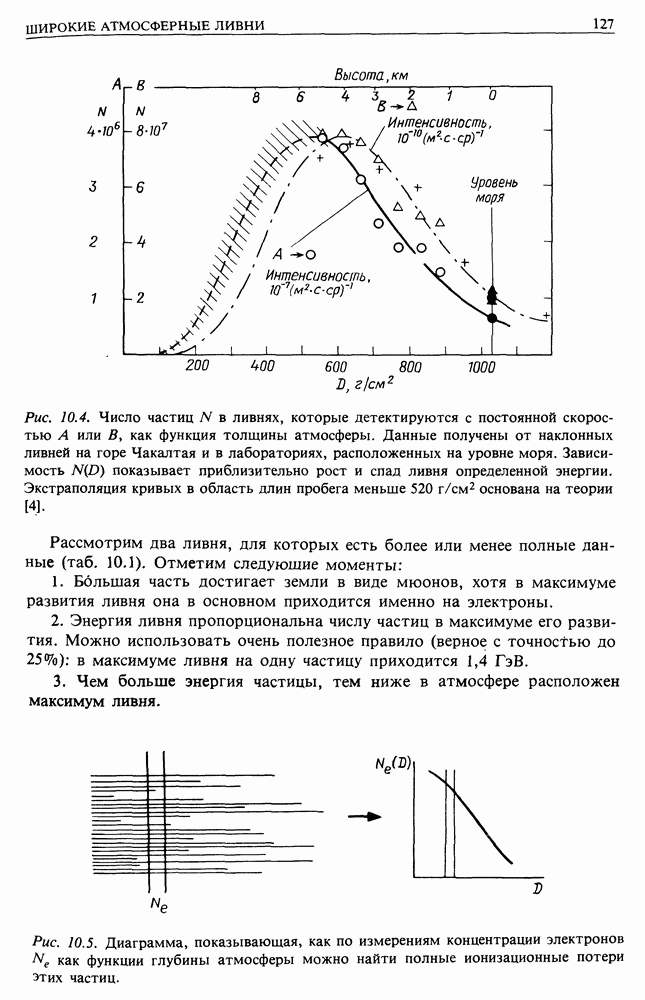
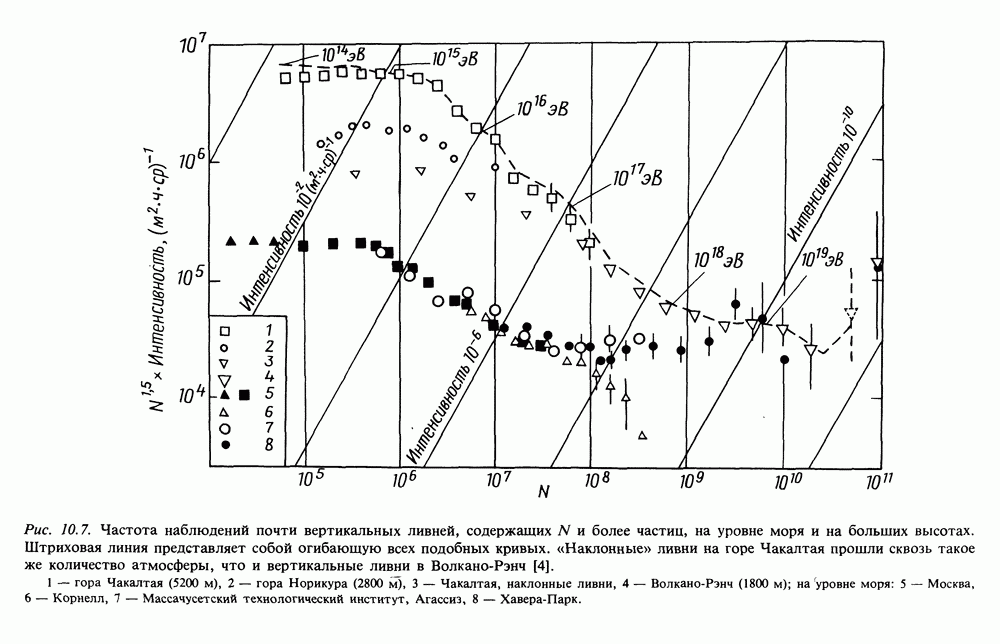
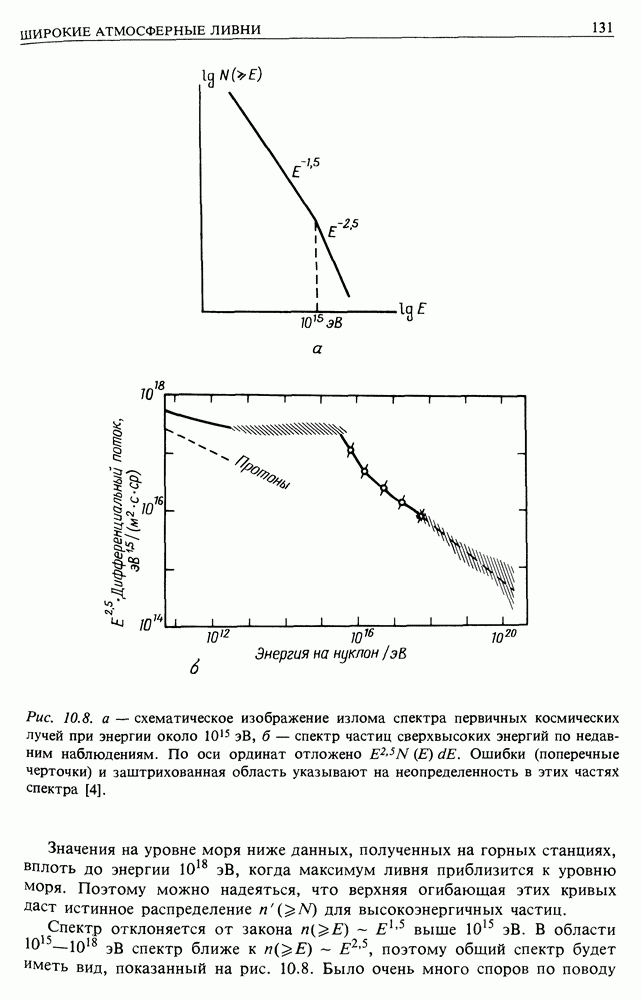
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
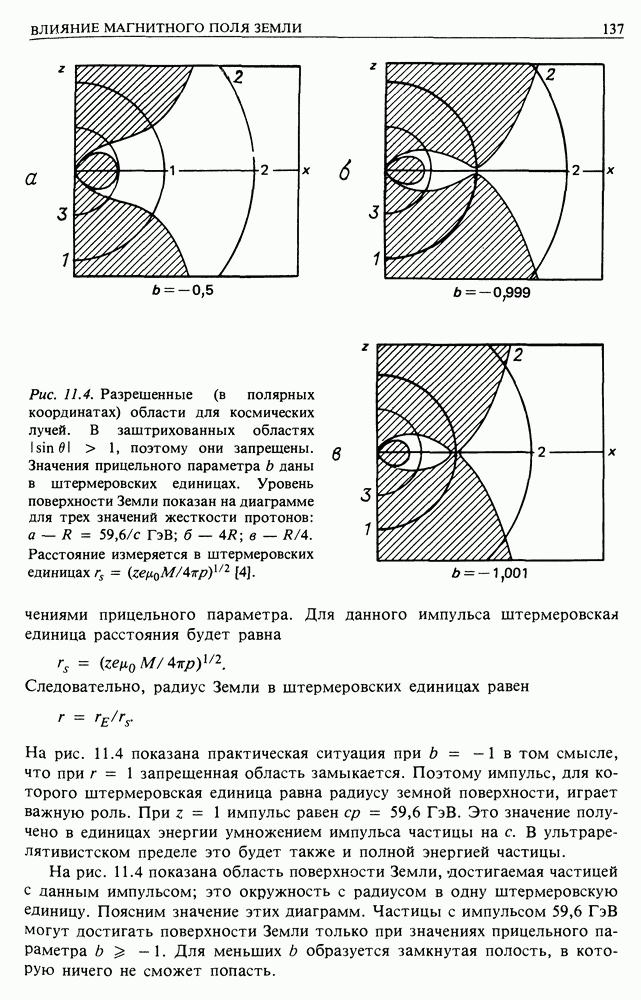
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
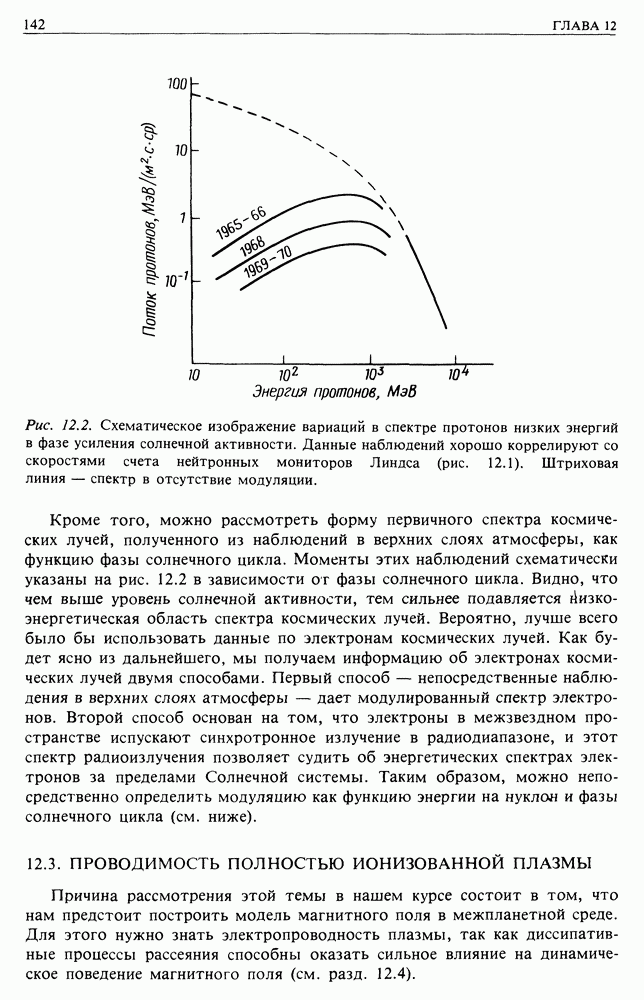
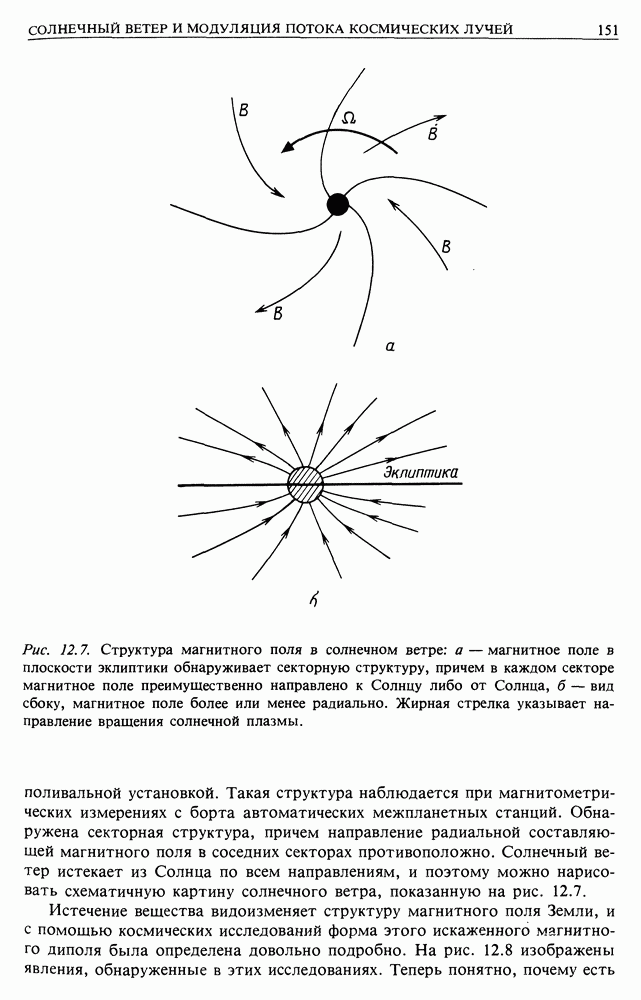
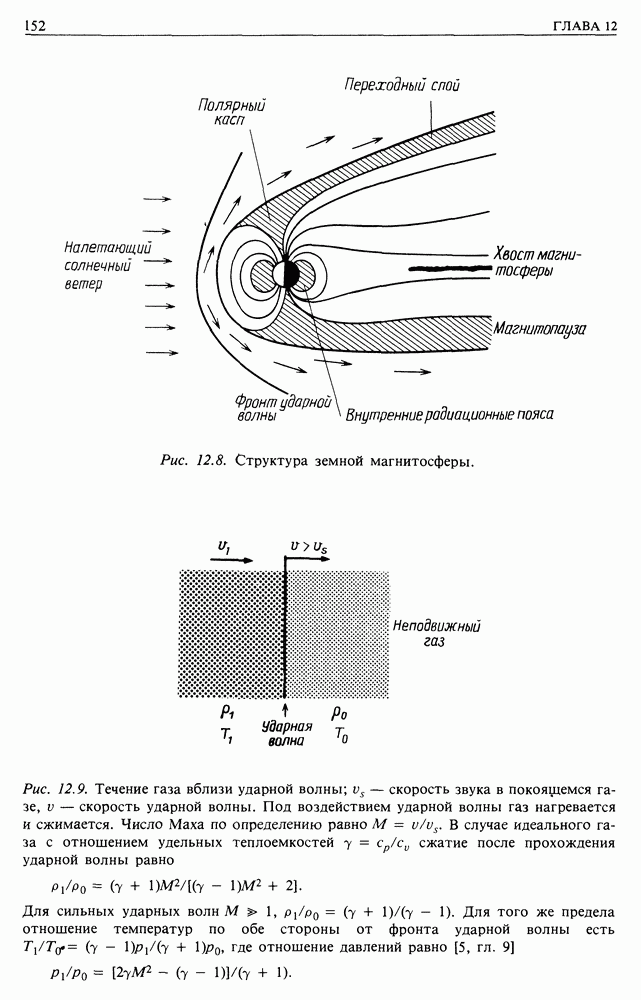
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
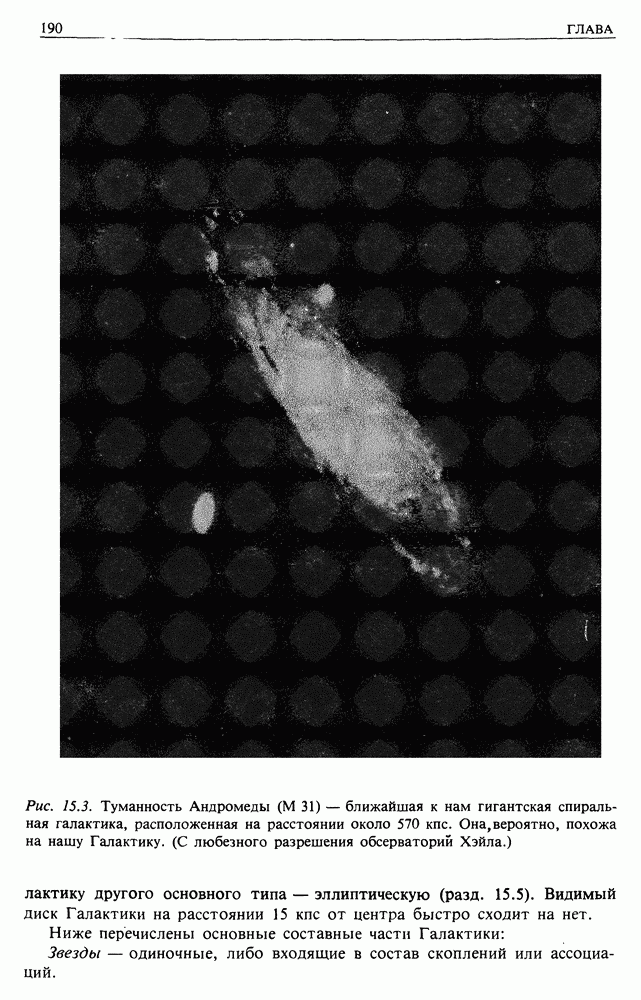
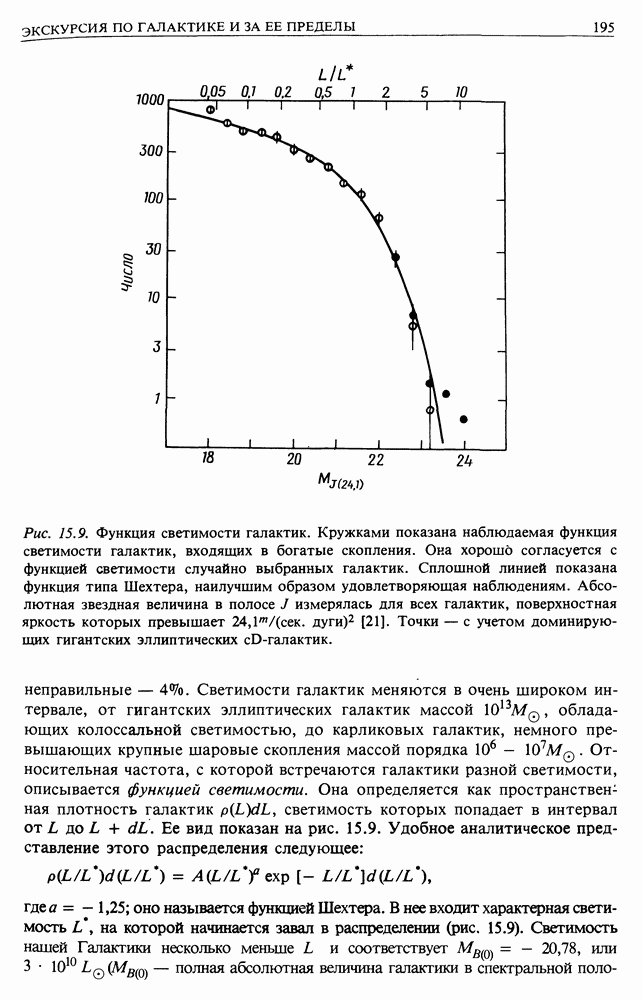
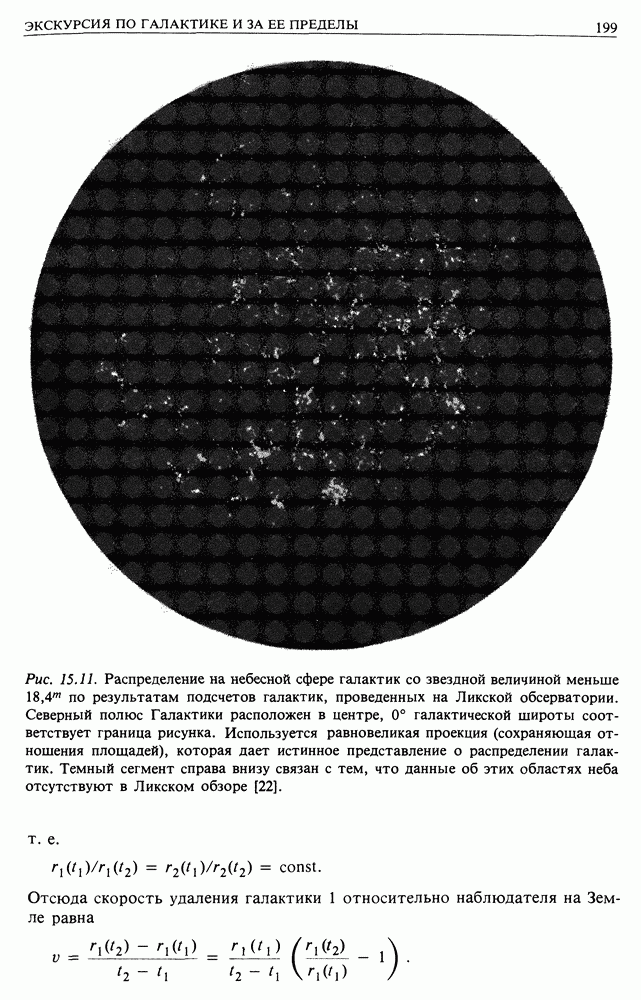
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
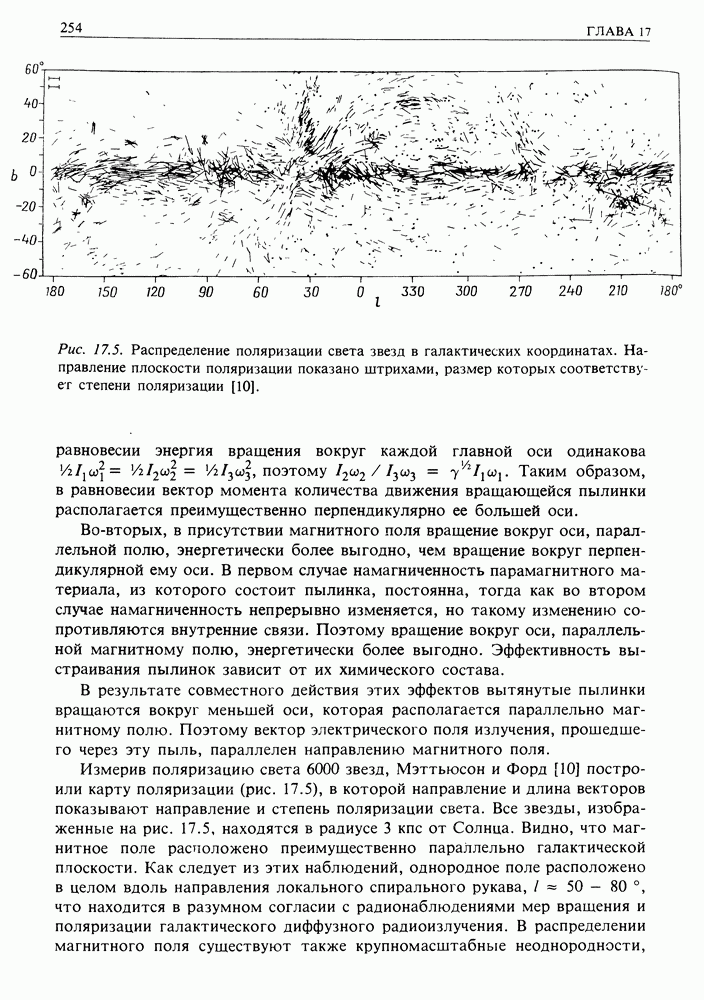
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
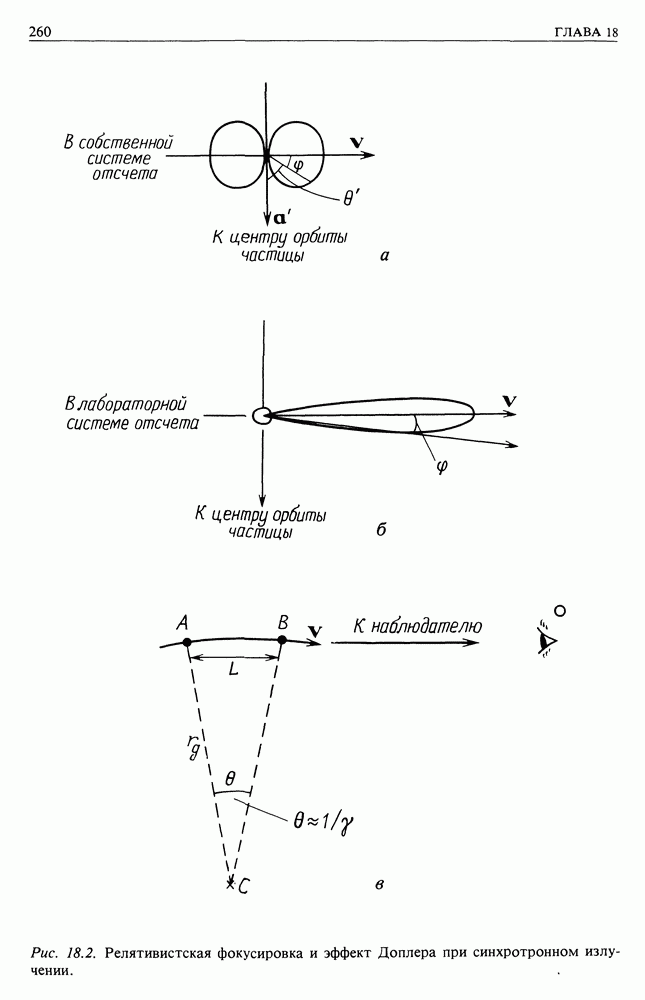
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
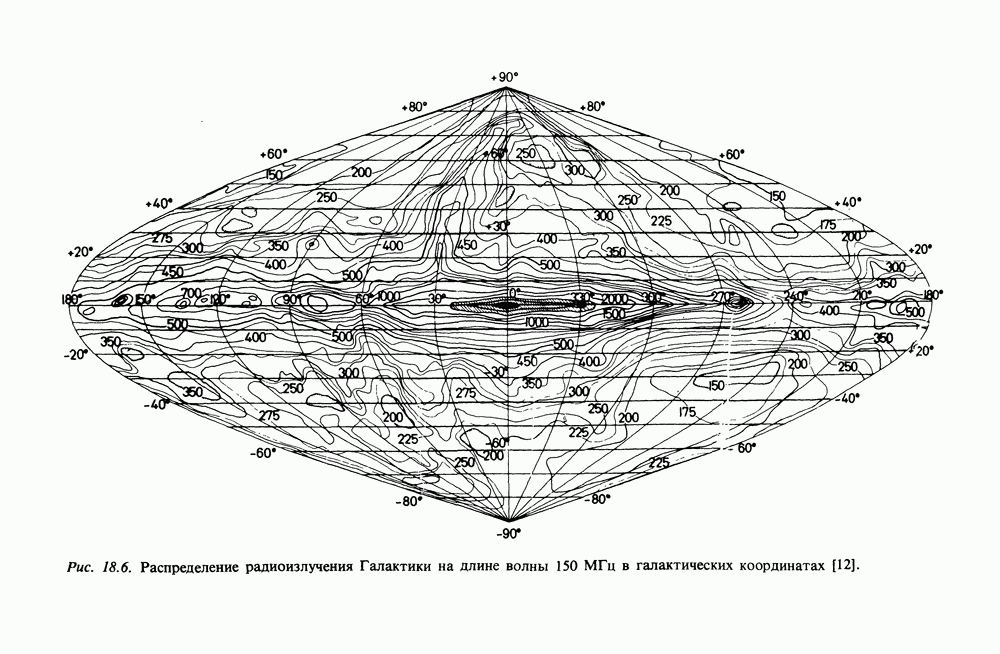
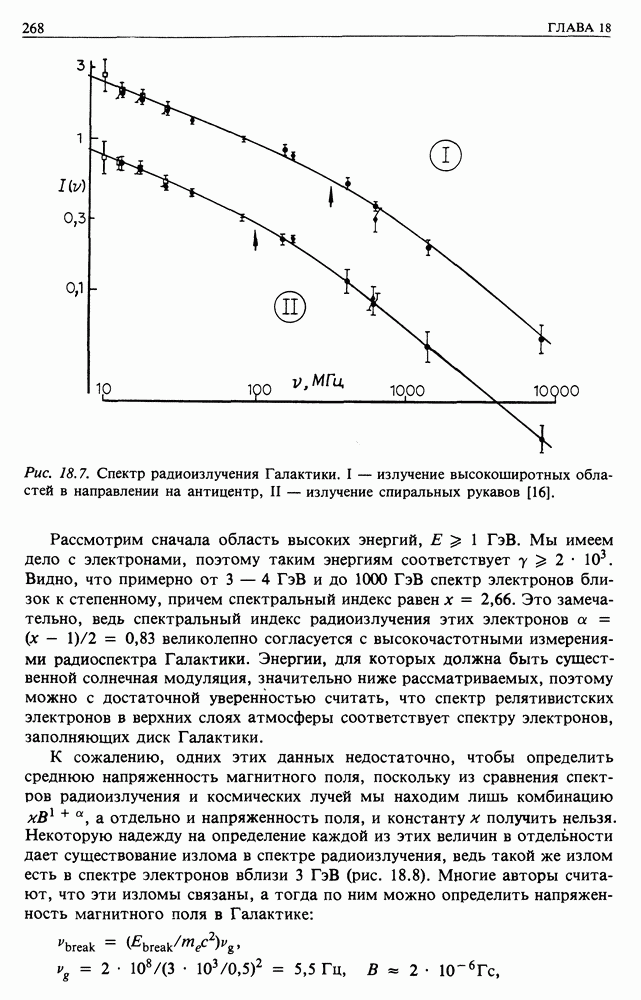
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
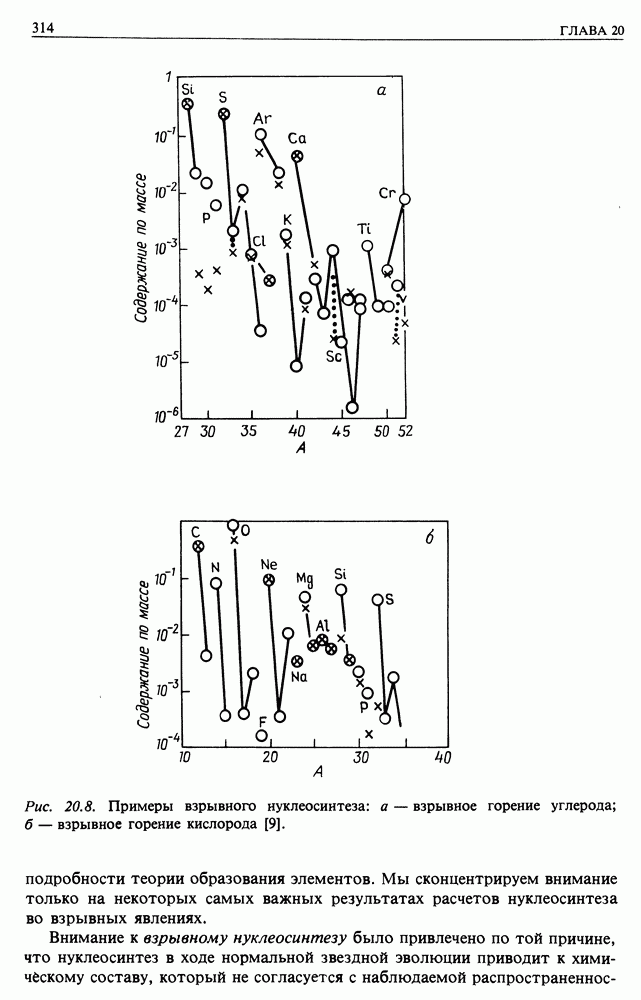
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
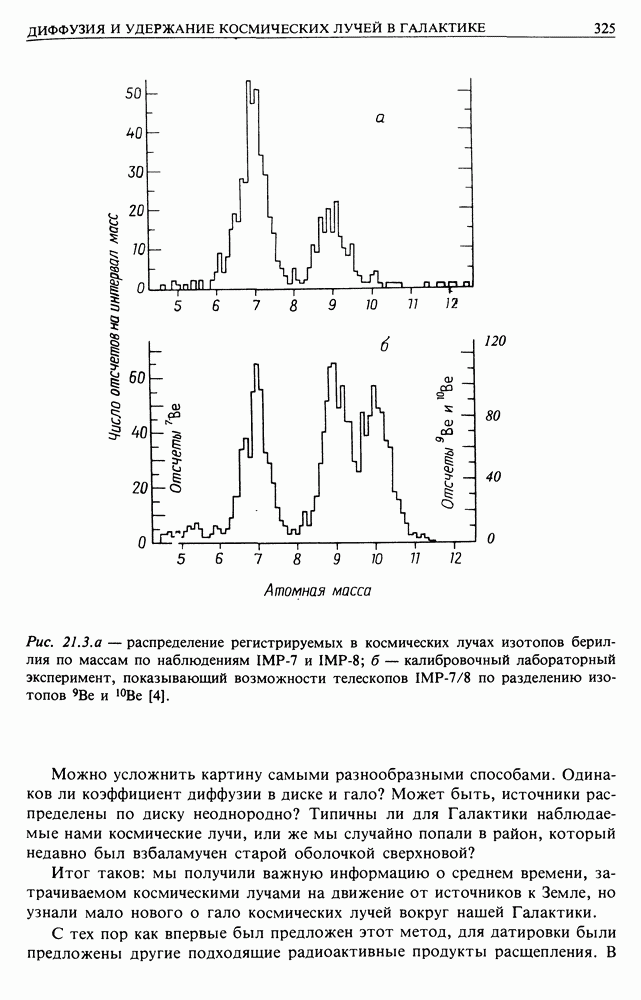
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
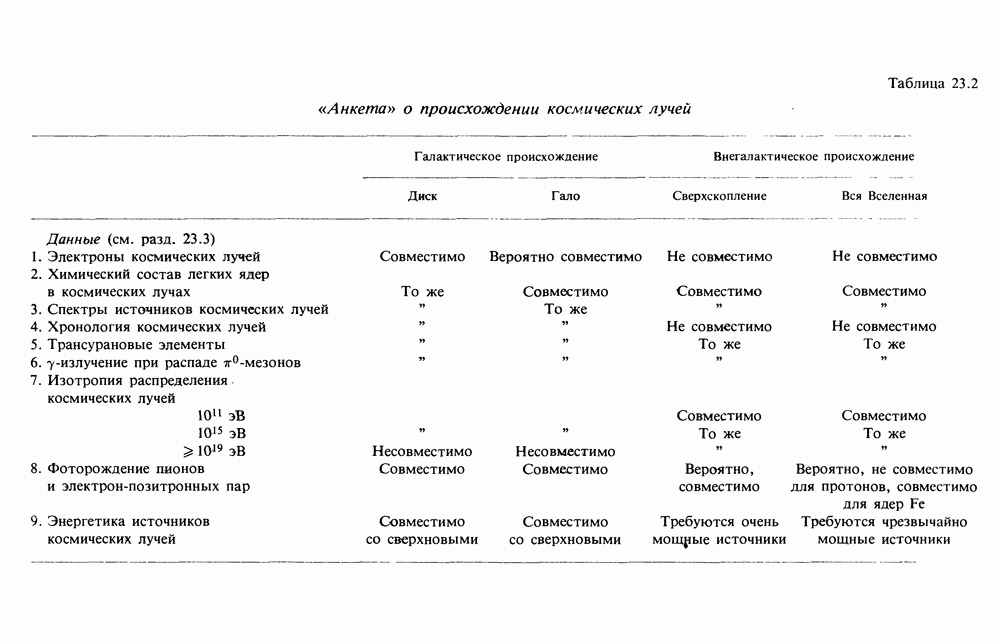
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
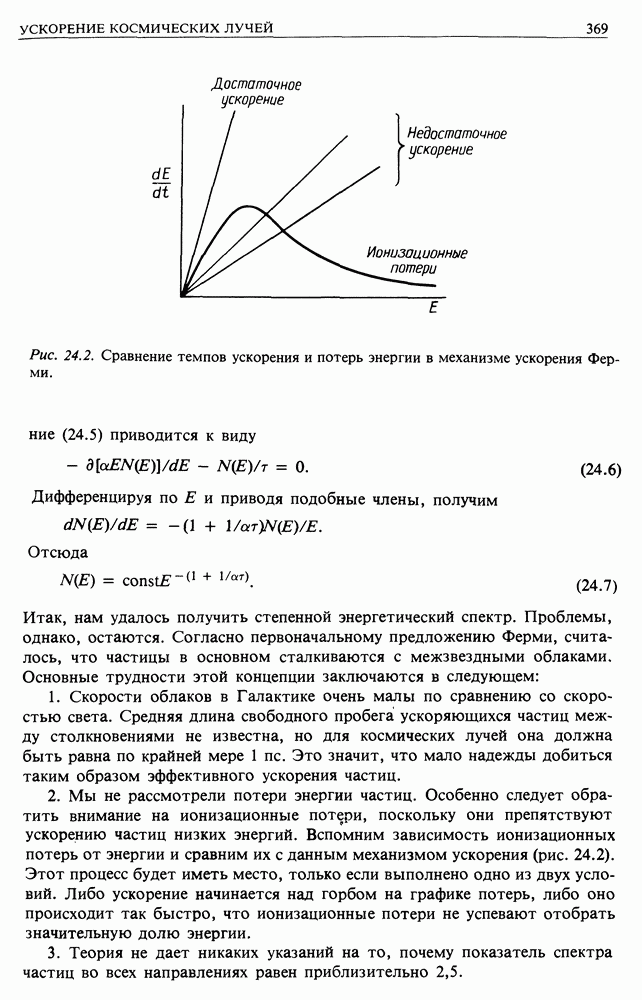
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ