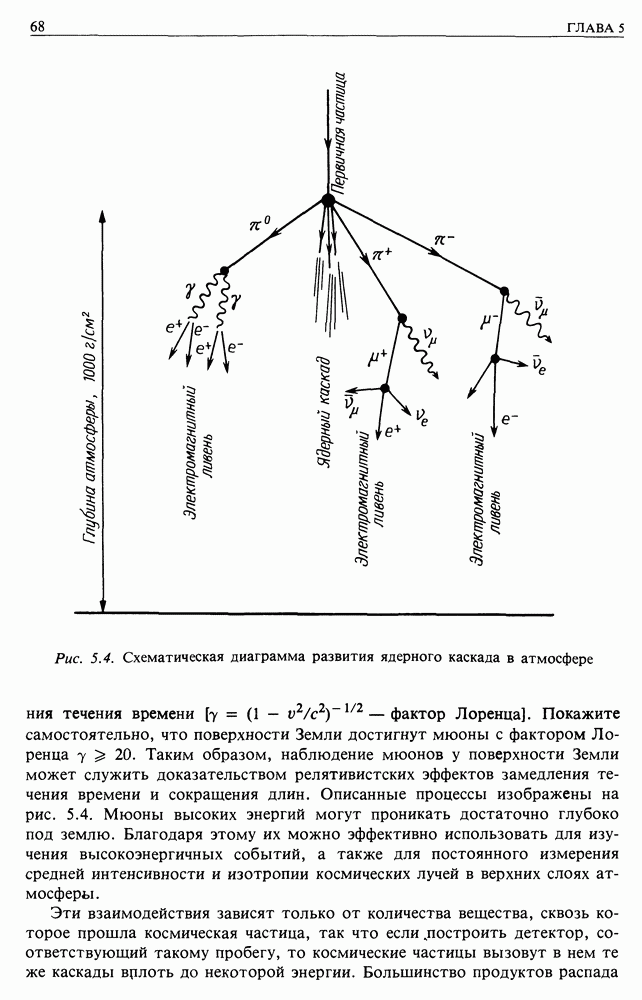
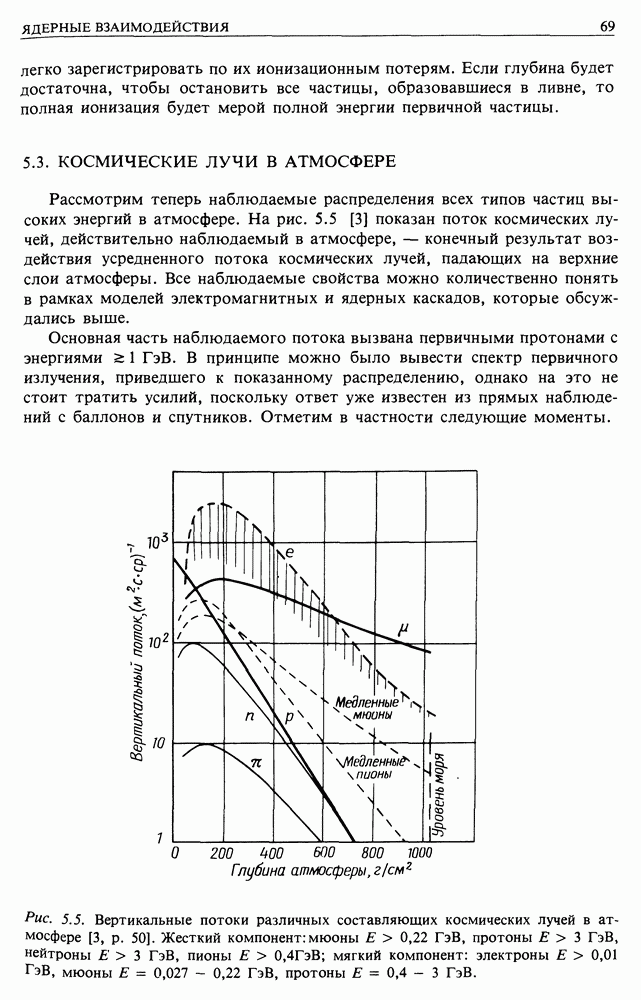
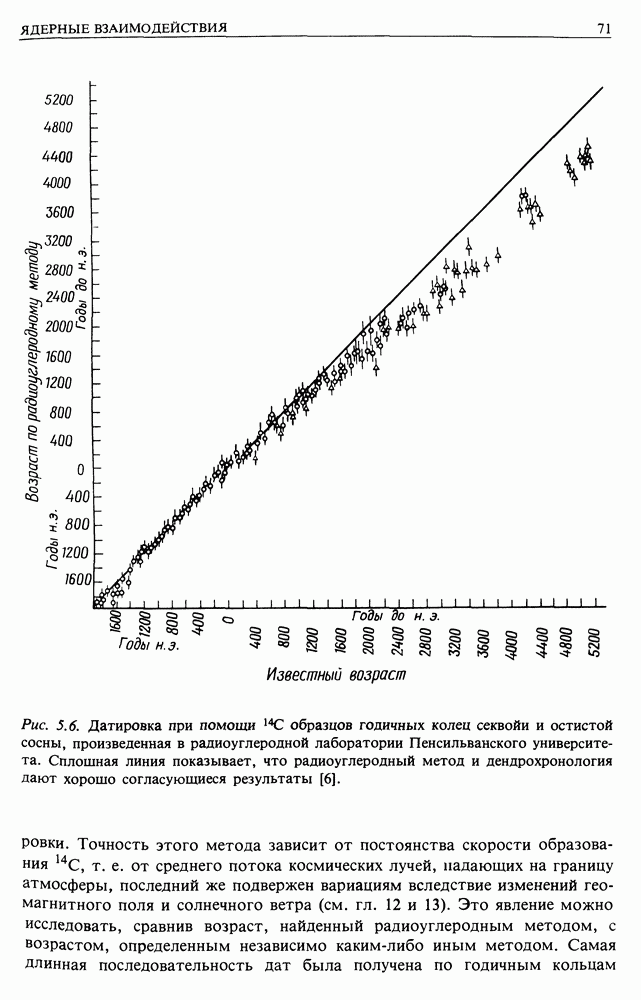
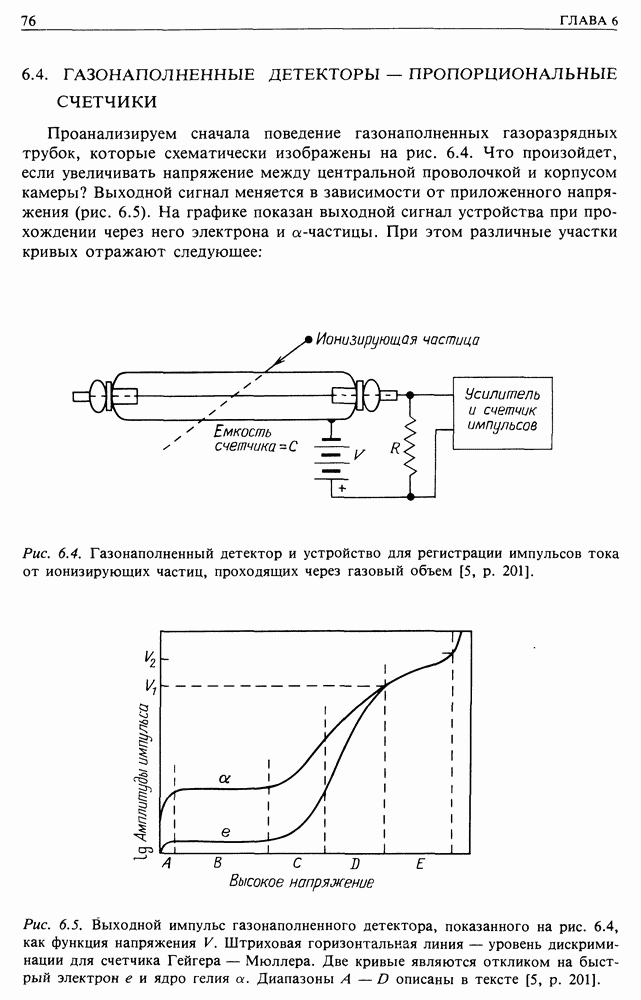
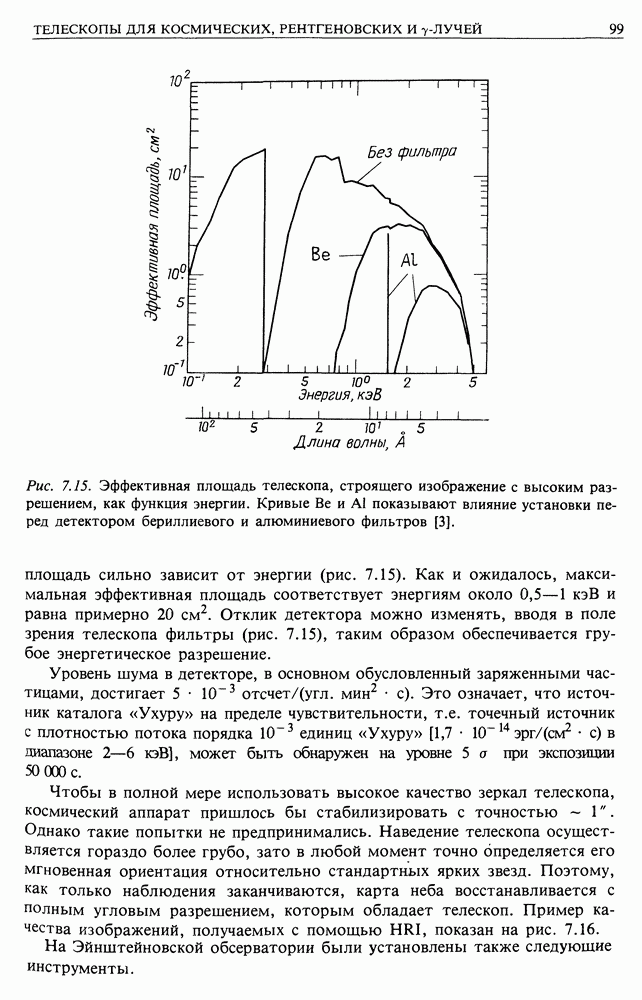
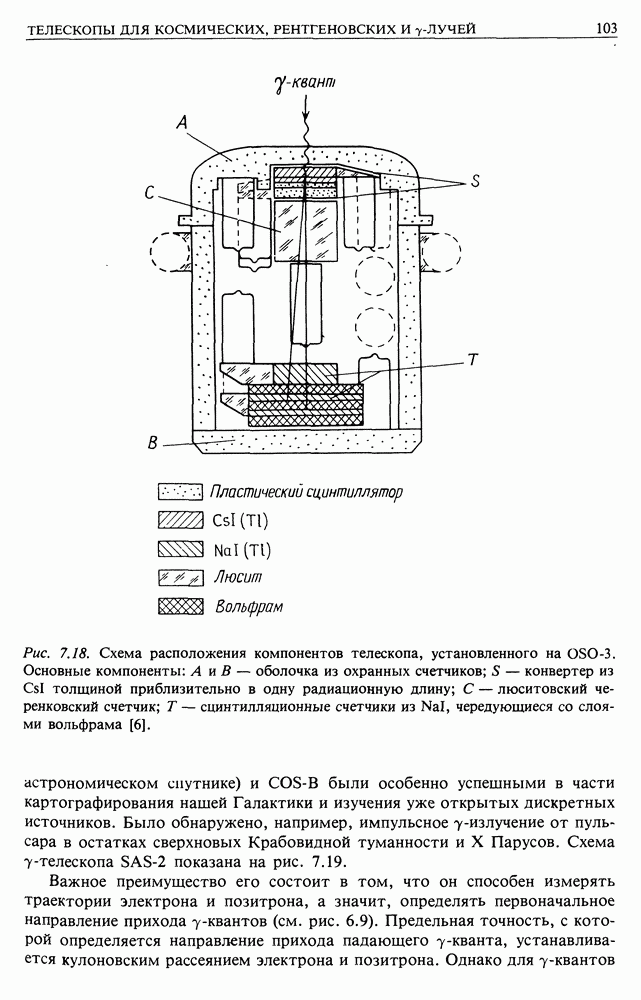
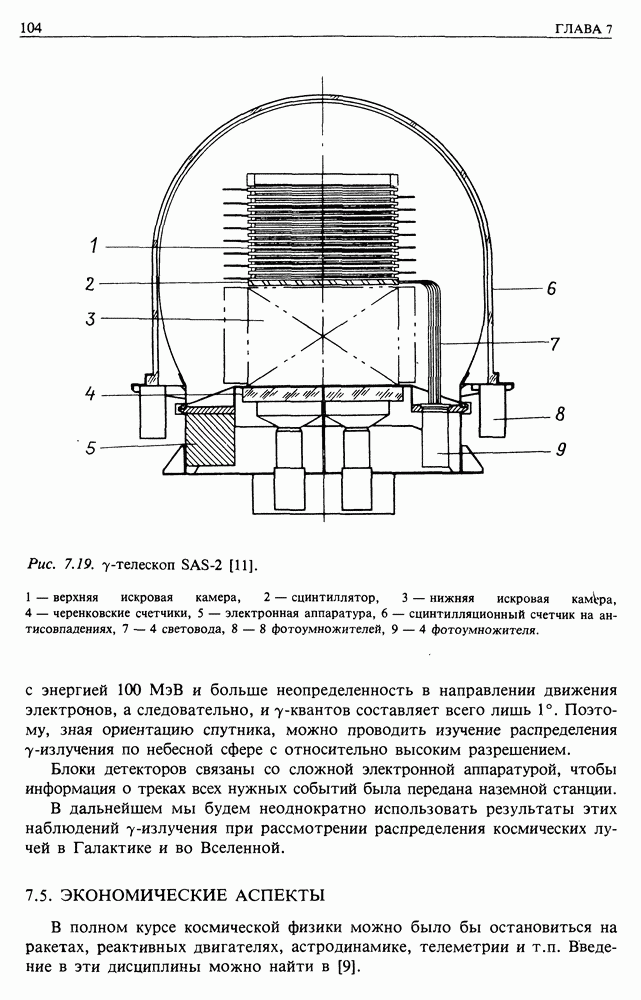
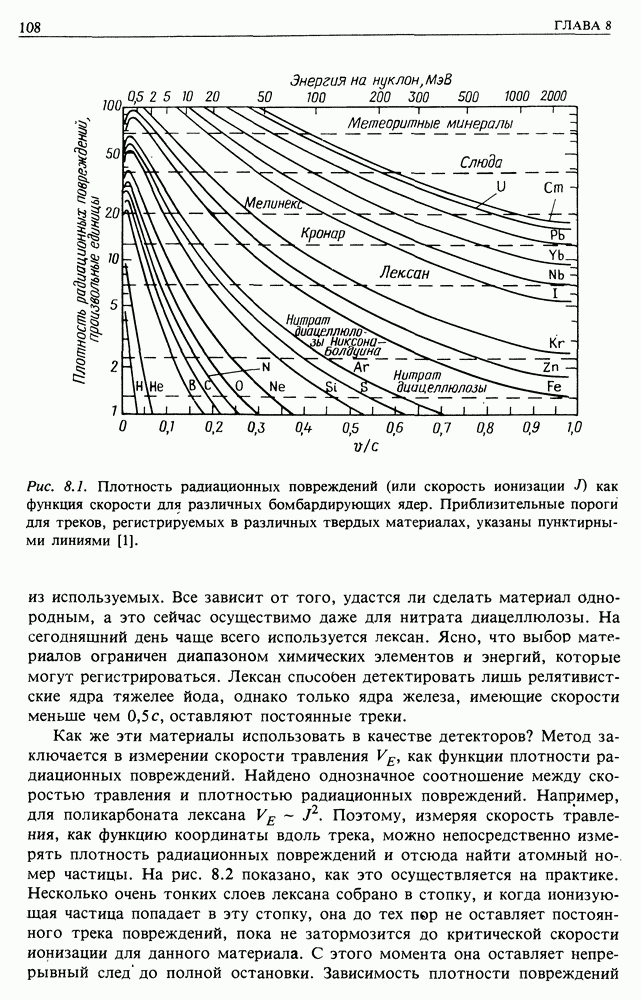
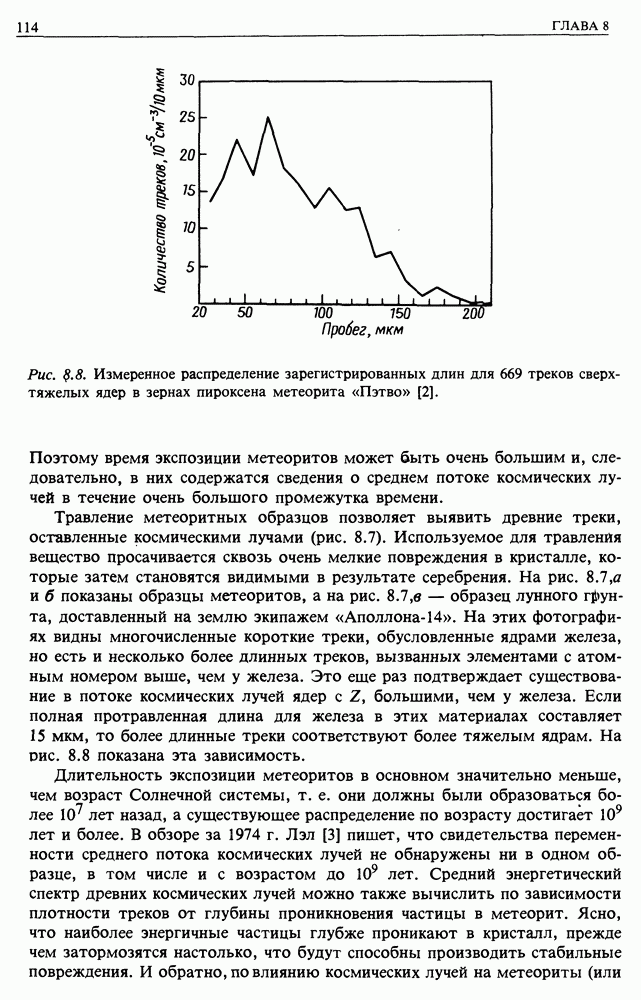
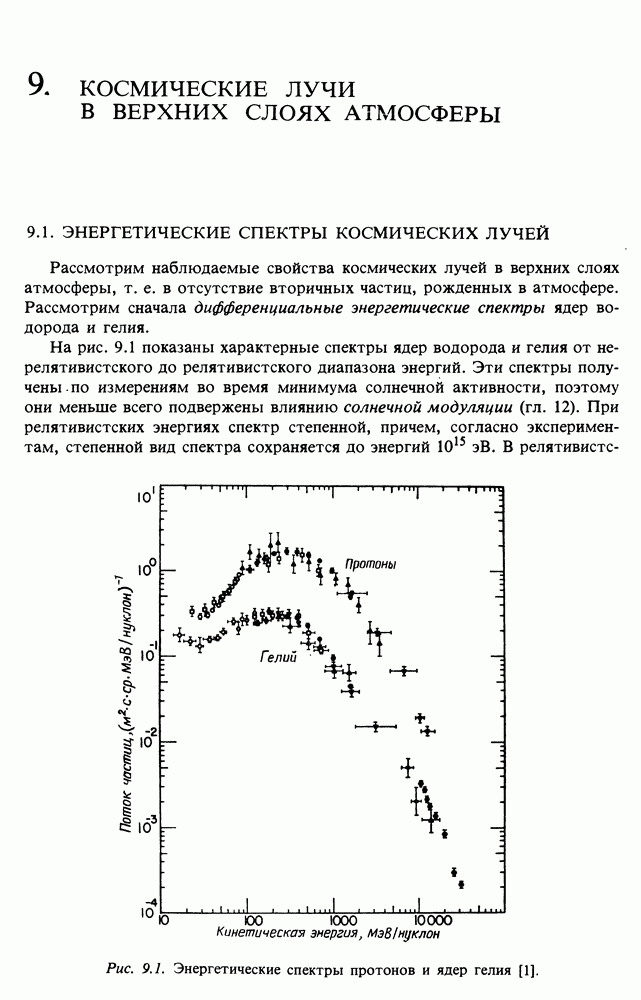
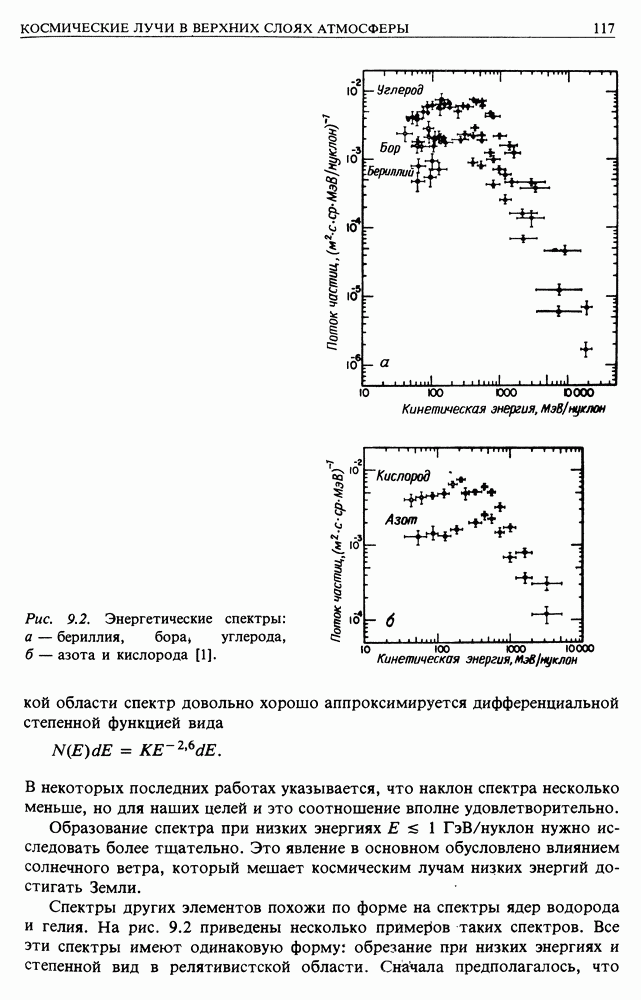
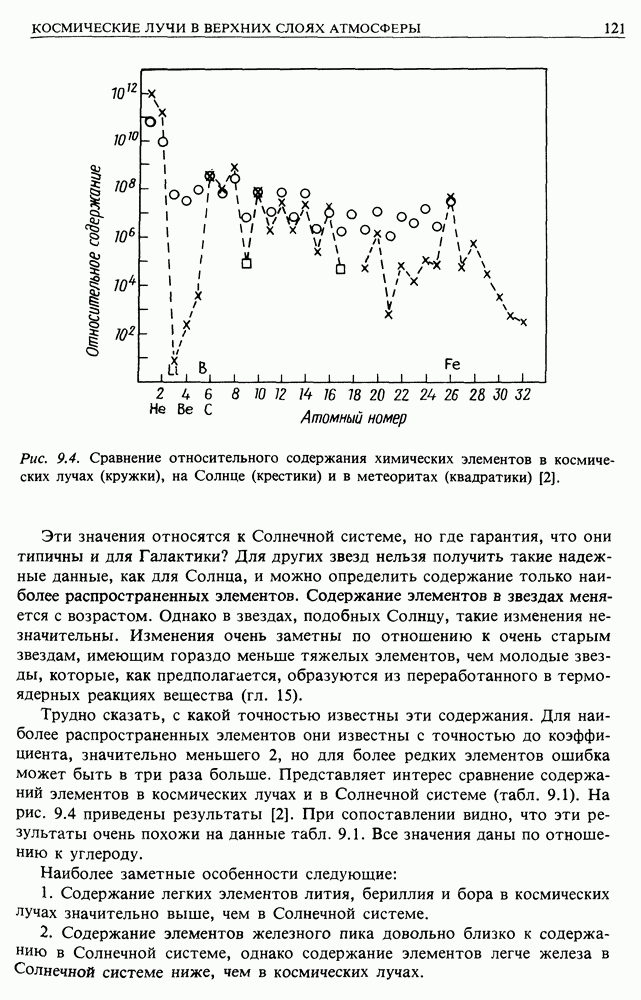
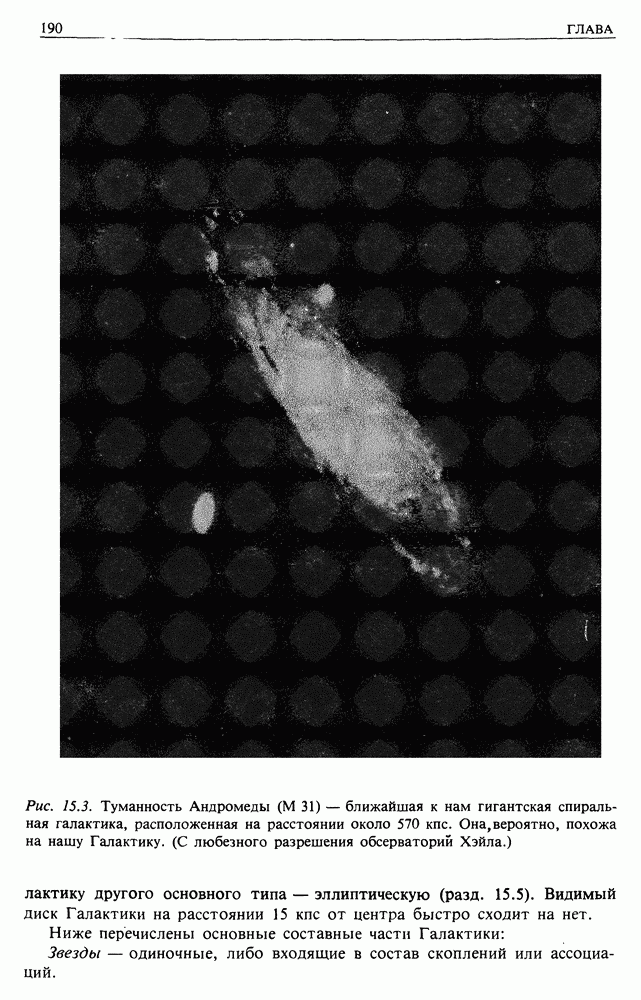
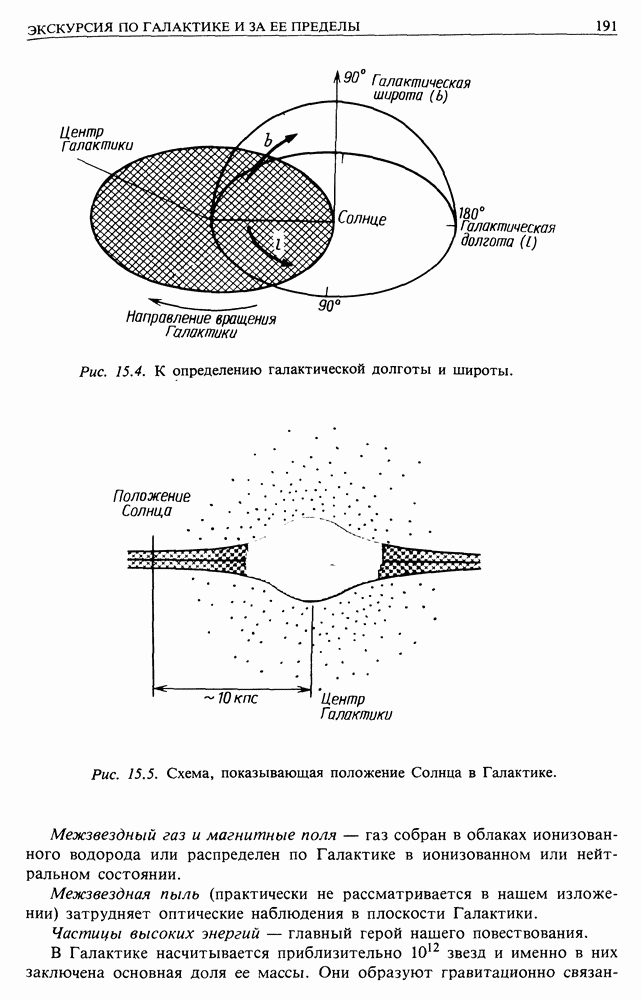
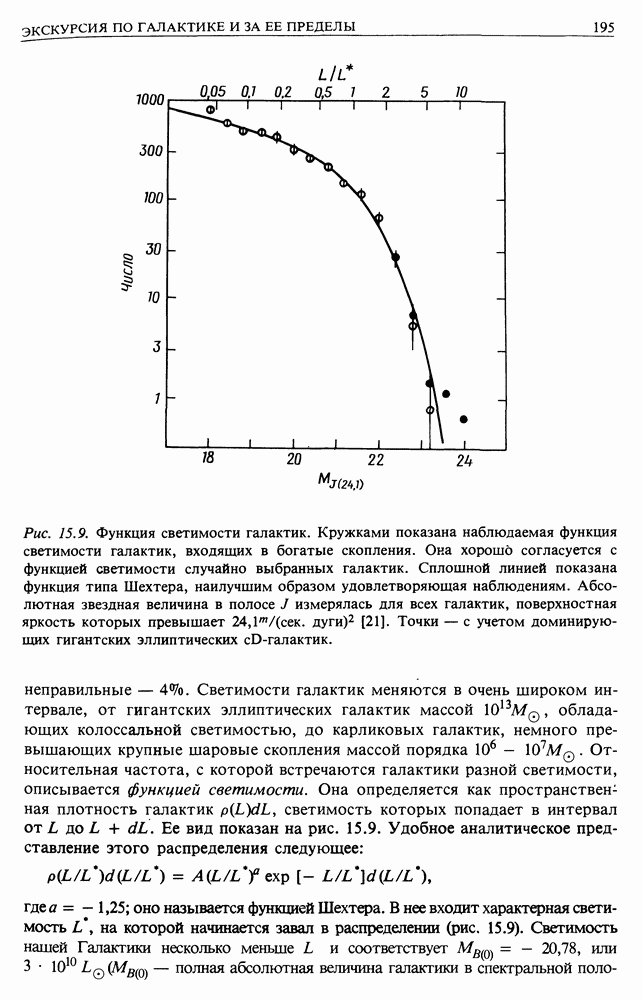
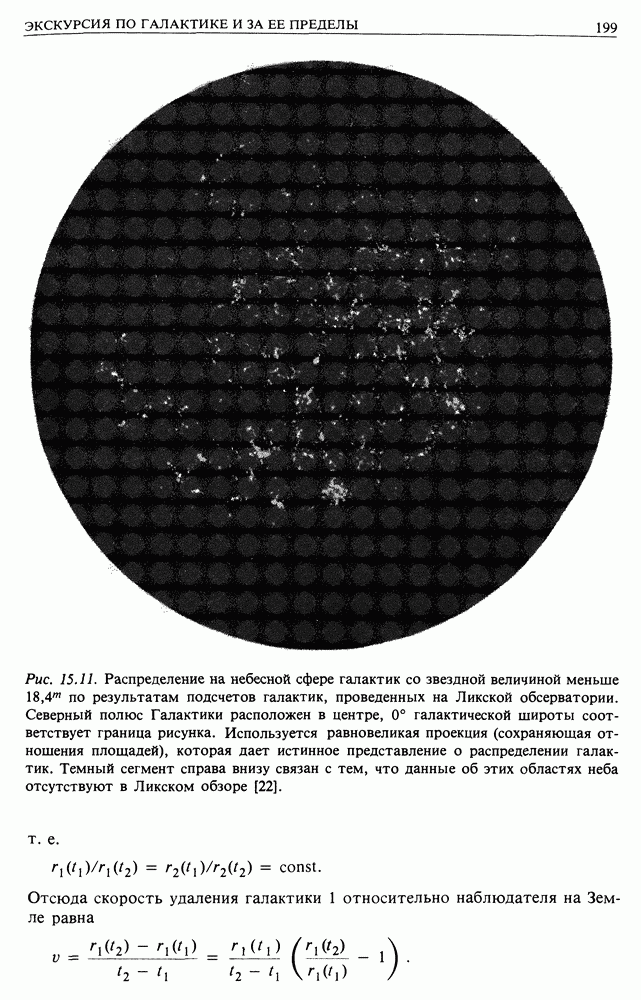
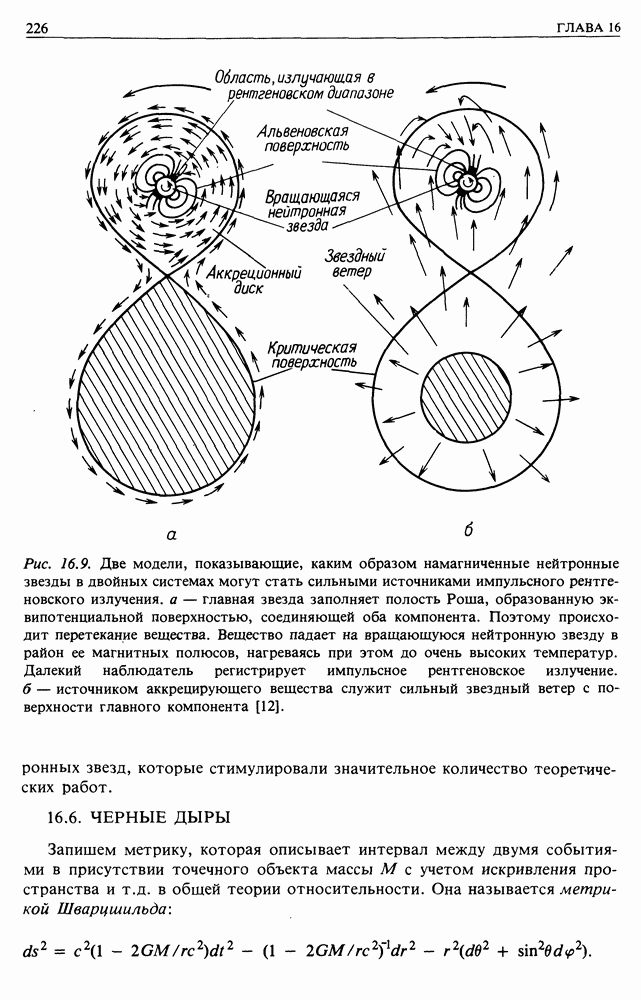
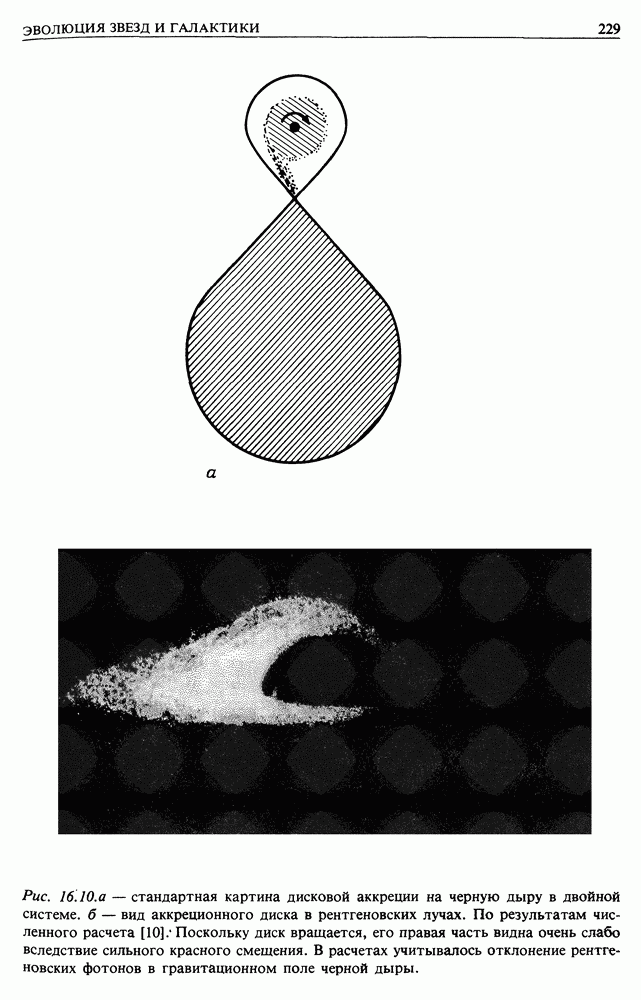
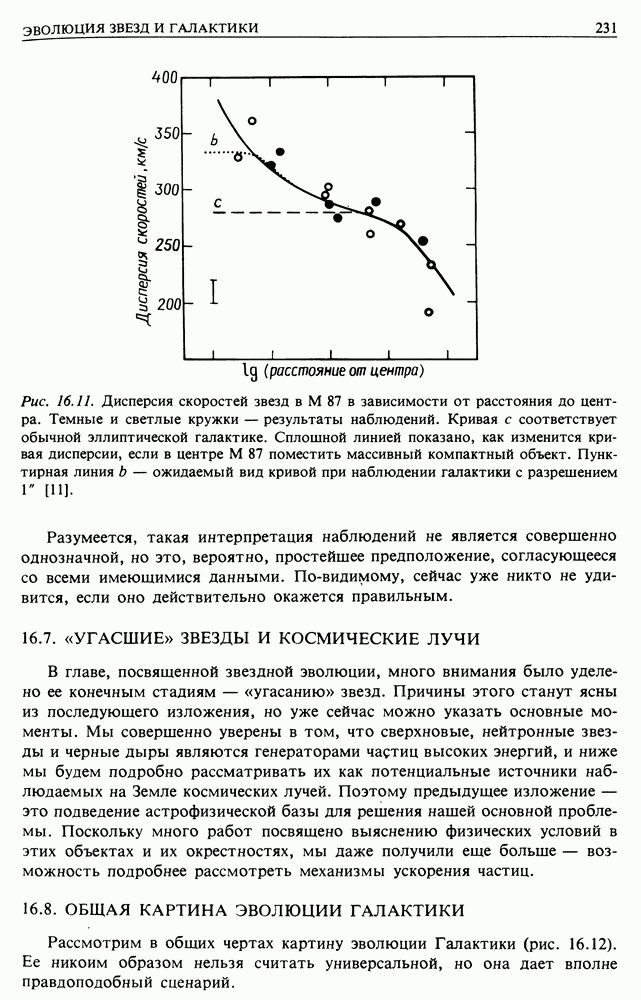
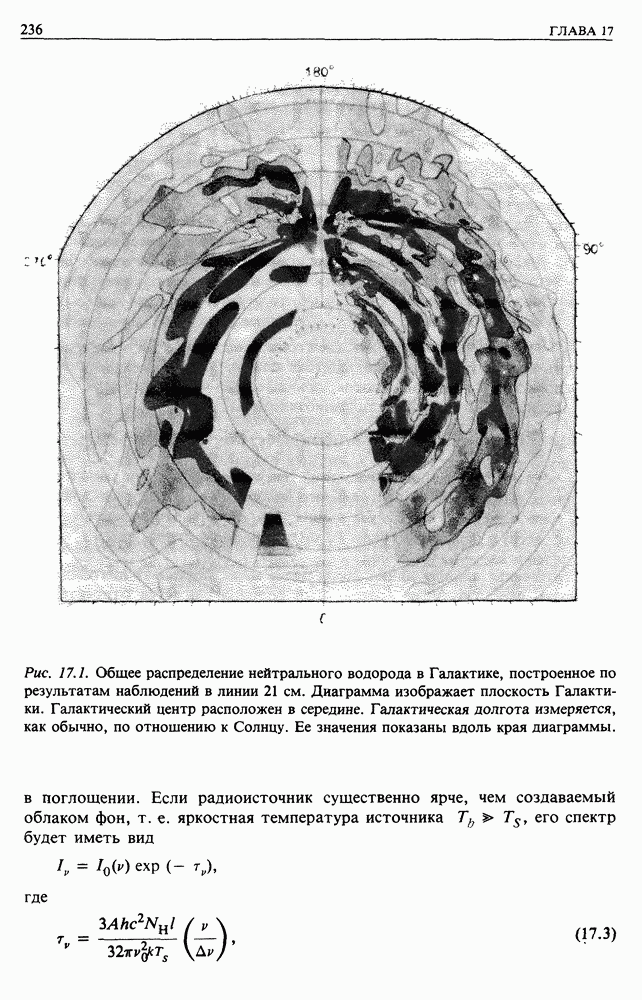
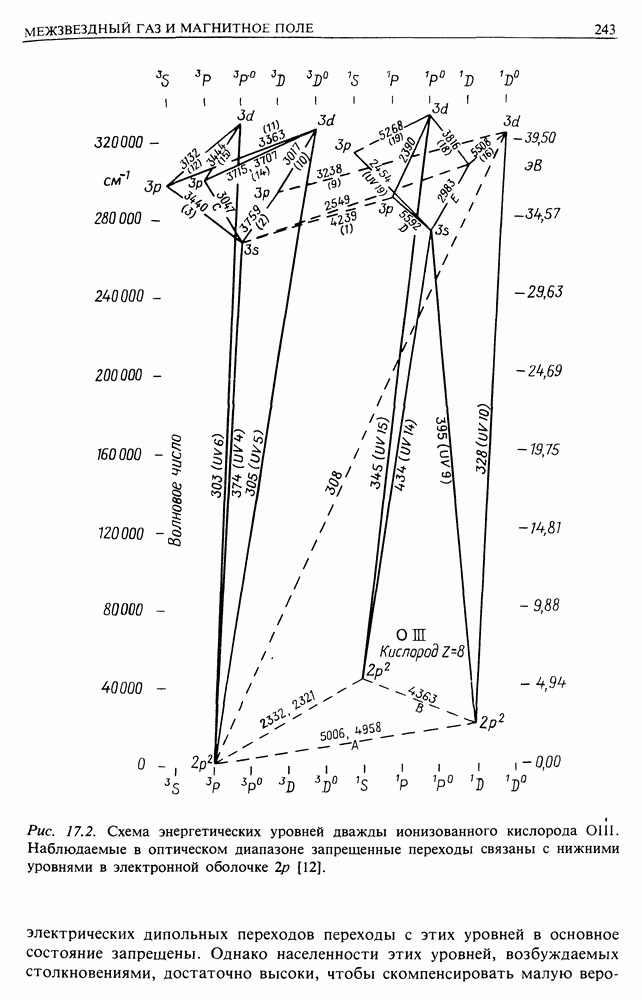
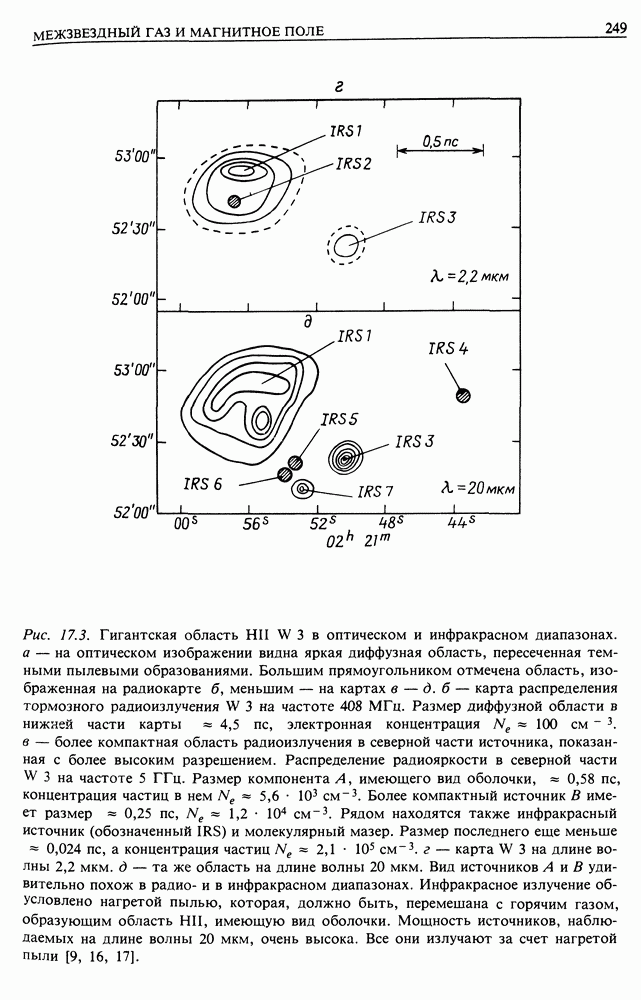
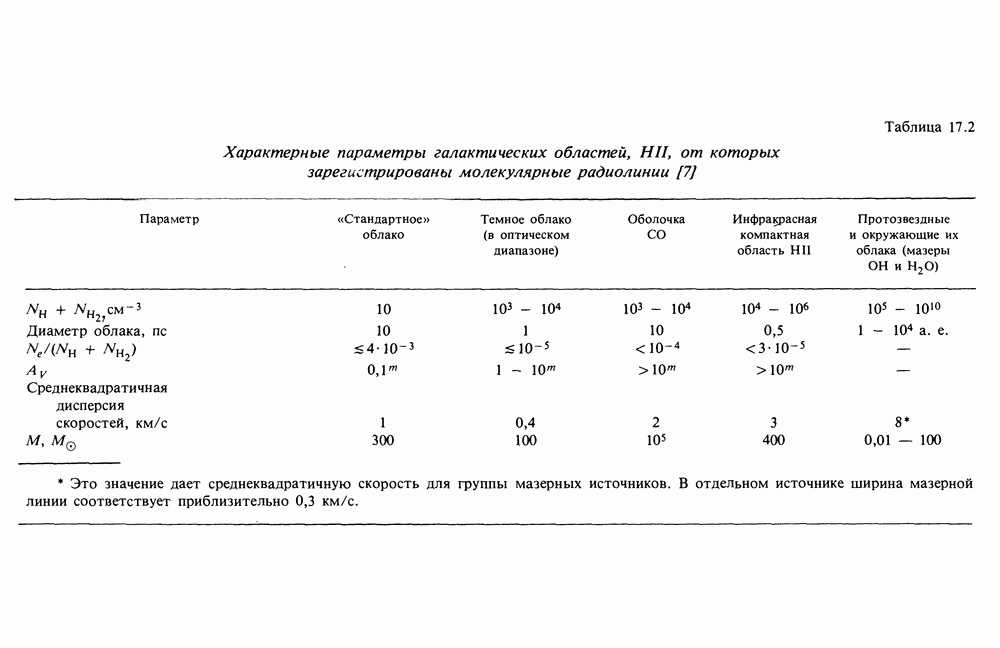
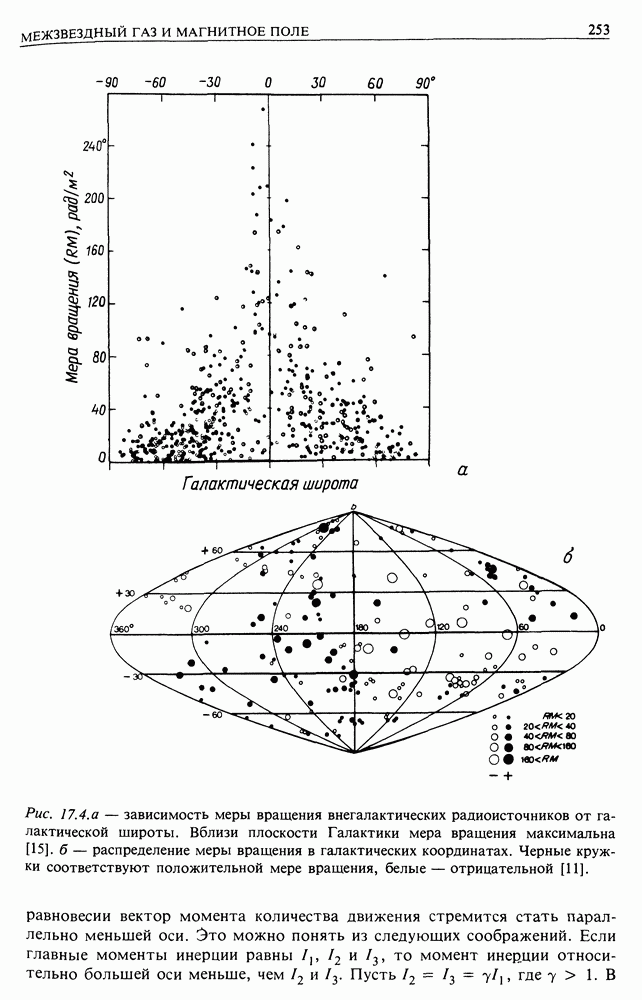
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
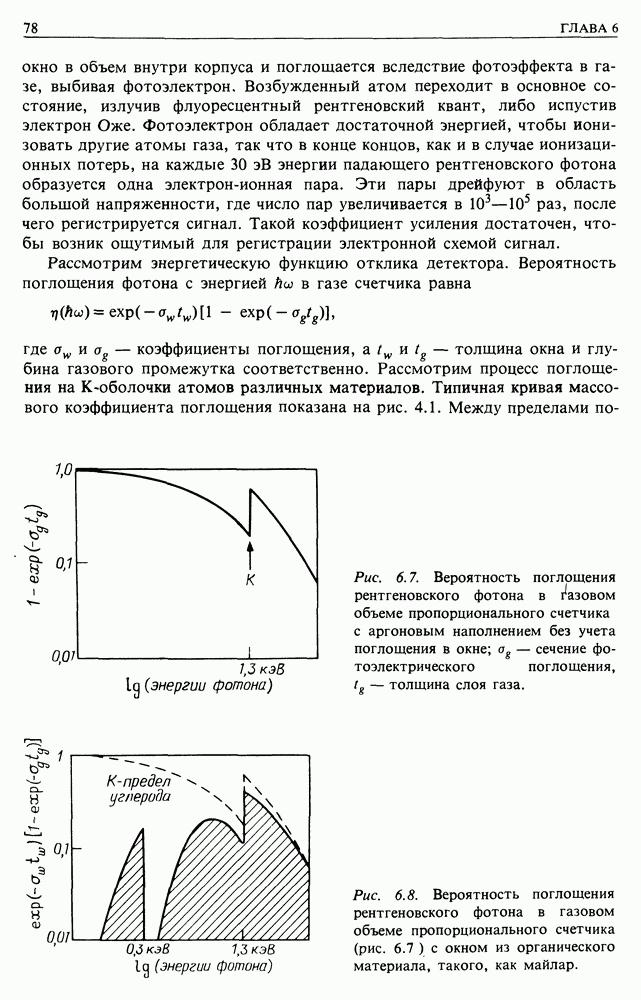
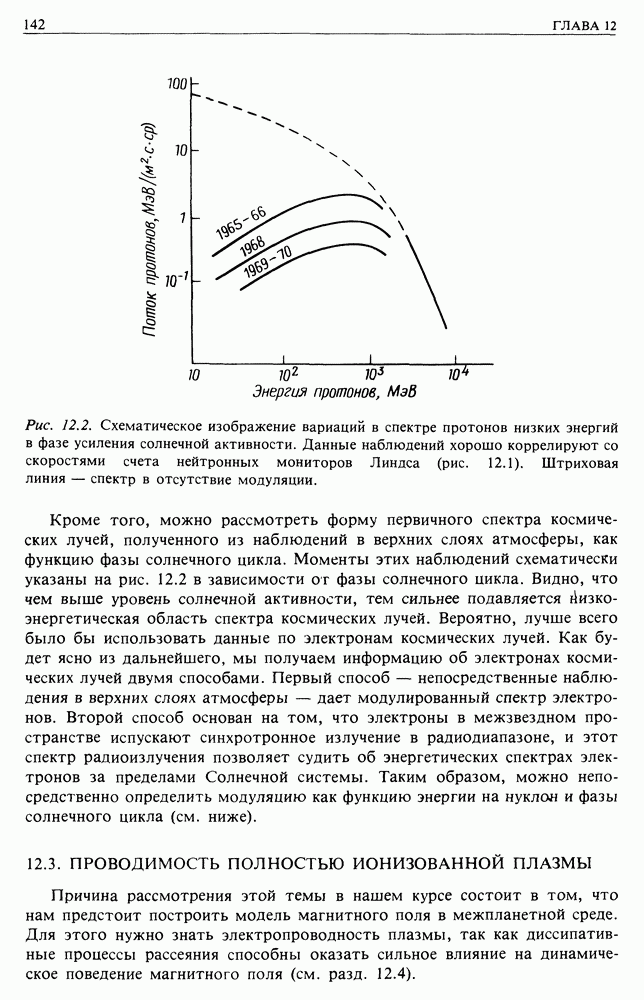
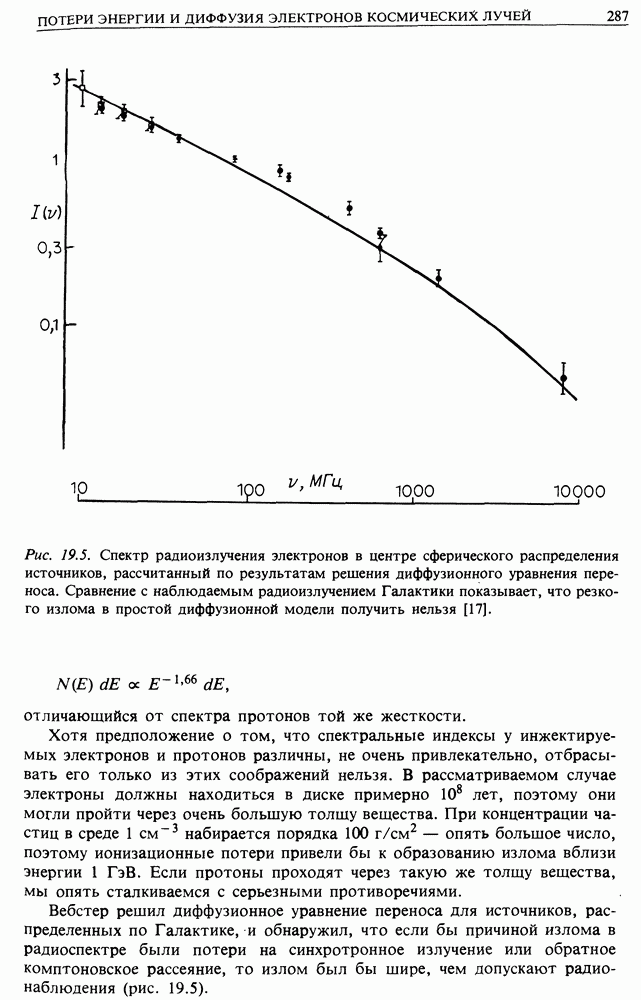
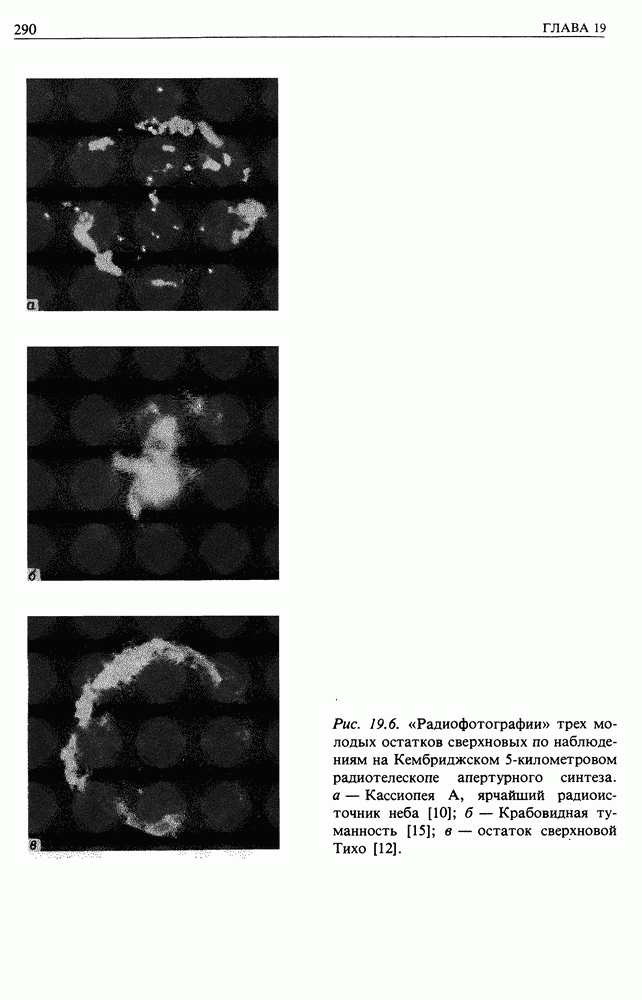
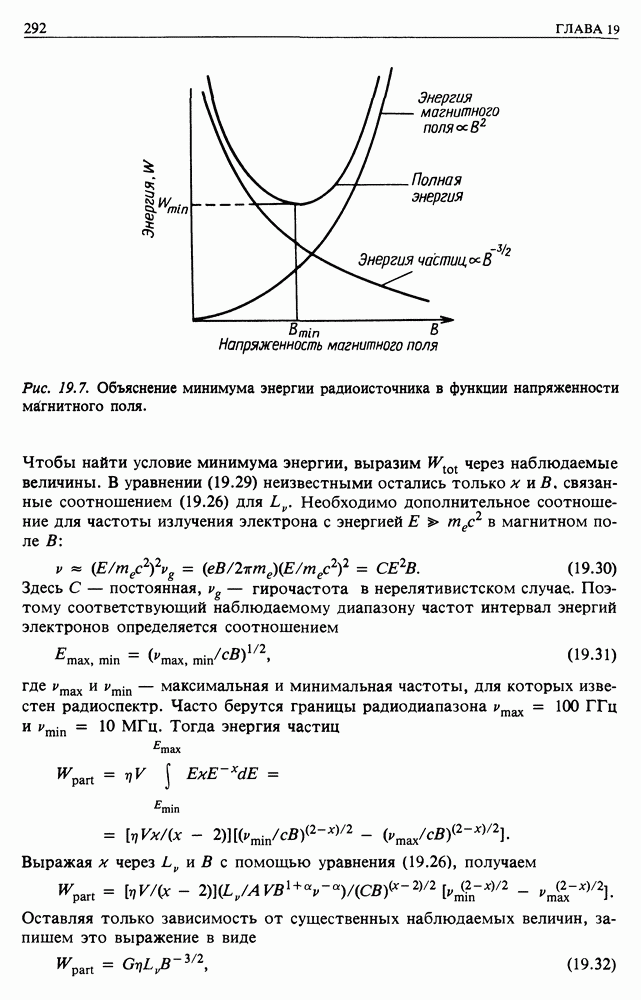
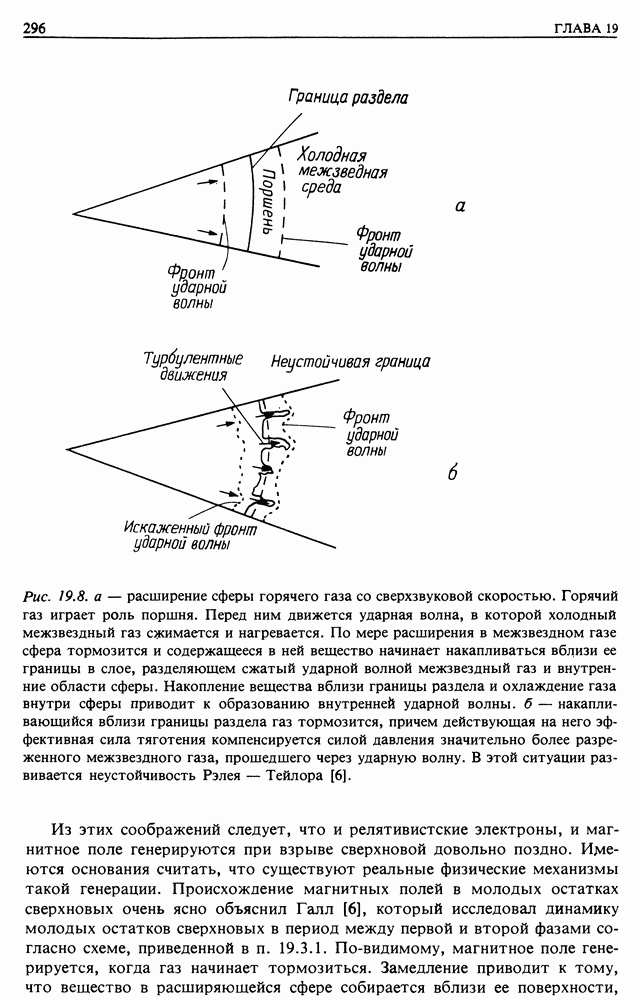
Теперь мы знаем основную конфигурацию магнитного поля, которое должны преодолеть космические лучи на пути к Земле. Они летят навстречу солнечному ветру в область усиливающегося магнитного поля. Рассмотрим динамику космических лучей, находящихся в таких магнитных полях. Это сложная задача, но мы установим лишь некоторые основные результаты, которые потребуются неоднократно в нашей дискуссии по астрофизике. Начнем с рассмотрения движения в однородном постоянном магнитном поле.
13.1.1. Однородное постоянное магнитное поле. Мы уже вывели основное уравнение, которое описывает динамику частицы с зарядом  движущейся в постоянном магнитном поле [уравнение (11.2)],
движущейся в постоянном магнитном поле [уравнение (11.2)],

Разложим  на компоненты — параллельный у у и перпендикулярный
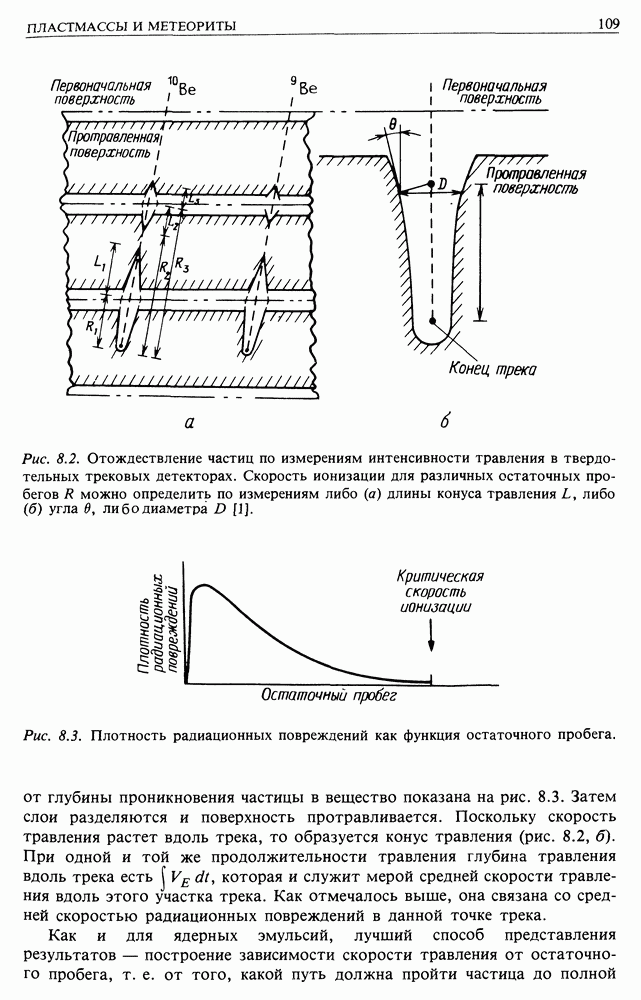
на компоненты — параллельный у у и перпендикулярный  магнитному полю, которое предполагается однородным (рис. 13.1). Питч-угол в траектории частицы задается соотношением
магнитному полю, которое предполагается однородным (рис. 13.1). Питч-угол в траектории частицы задается соотношением  это угол между векторами
это угол между векторами  Поскольку у у параллельно В, то из уравнения (13.1) следует, что у у не изменяется, т.е.
Поскольку у у параллельно В, то из уравнения (13.1) следует, что у у не изменяется, т.е.  Единственным ускорением является
Единственным ускорением является

т.е. ускорение, равное по величине  и перпендикулярное мгновенному вектору скорости
и перпендикулярное мгновенному вектору скорости  в плоскости, перпендикулярной В. Очевидно, что это постоянное ускорение, и, следовательно, оно описывает движение по окружности. Приравнивая его центробежному ускорению, имеем
в плоскости, перпендикулярной В. Очевидно, что это постоянное ускорение, и, следовательно, оно описывает движение по окружности. Приравнивая его центробежному ускорению, имеем

т. е.

Таким образом, движение заряженной частицы складывается из поступательного движения с постоянной скоростью и движения по окружности вокруг направления движения, т.е. траектория представляет винтовую линию с постоянным питч-углом  . Угловая скорость частицы по орбите равна
. Угловая скорость частицы по орбите равна  и называется циклотронной или гирочастотой частицы. В нерелятивистском случае она просто равна
и называется циклотронной или гирочастотой частицы. В нерелятивистском случае она просто равна 

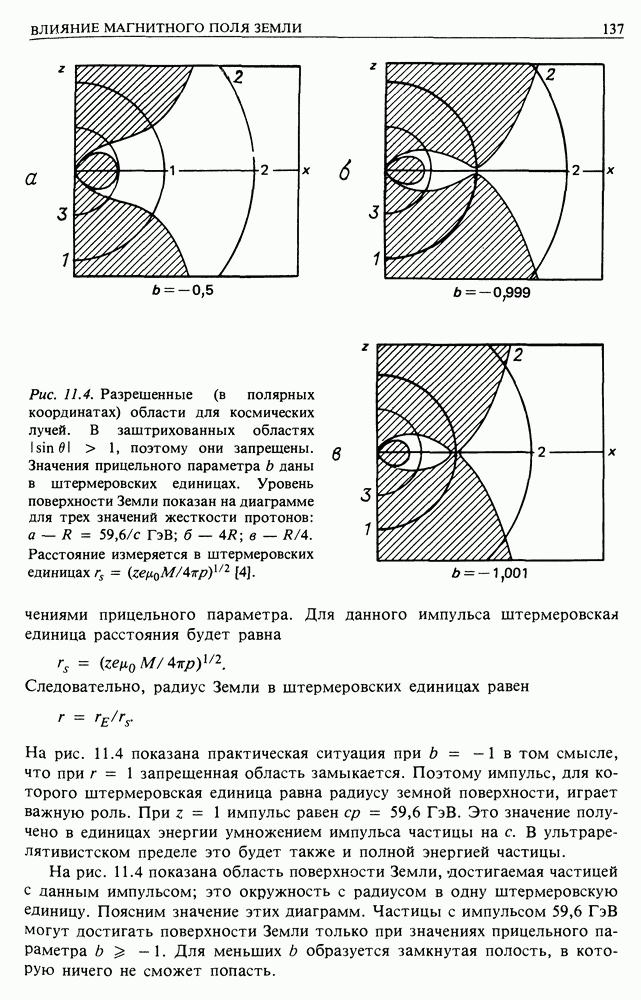
Рис. 13.1 Динамика заряженной частицы в однородном магнитном поле.
Полезно запомнить, что гирочастота электрона равна  где В измеряется в гауссах.
где В измеряется в гауссах.
В этом простом случае направление магнитного поля называется ведущим центром движения частицы, т.е. это среднее направление поступательного движения частицы, вокруг которого происходит вращение. В более сложных случаях можно постараться определить ведущий центр движения, так как он дает общий дрейф частицы в магнитном поле.
Перепишем выражение для радиуса траектории частицы в следующем виде:

Это означает, что если частицы инжектируются с одинаковым значением  в магнитное поле В при одном и том же питч-угле то их динамические параметры в магнитном поле будут совершенно одинаковы. Очевидно, что этот результат справедлив при любой конфигурации магнитного поля. Величина
в магнитное поле В при одном и том же питч-угле то их динамические параметры в магнитном поле будут совершенно одинаковы. Очевидно, что этот результат справедлив при любой конфигурации магнитного поля. Величина  называется жесткостью или магнитной жесткостью частицы. Поскольку
называется жесткостью или магнитной жесткостью частицы. Поскольку  имеет размерность энергии (к примеру, электронвольты) и
имеет размерность энергии (к примеру, электронвольты) и  размерность заряда, размерность
размерность заряда, размерность  вольты. Полезной единицей для практических целей обычно служит гигавольт
вольты. Полезной единицей для практических целей обычно служит гигавольт  Очень часто энергия частиц космических лучей описывается в единицах их жесткости, а не энергии на нуклон.
Очень часто энергия частиц космических лучей описывается в единицах их жесткости, а не энергии на нуклон.
В качестве примера рассмотрим протон и ядро углерода с  Их свойства перечислены в табл. 13.1.
Их свойства перечислены в табл. 13.1.
Таблица 13.1 (см. скан) Свойства протона и ядра углерода с 
13.1.2. Переменное во времени магнитное поле. При конфигурации поля, изображенной на рис. 13.1, частица движется по винтовой траектории с радиусом витка  Рассмотрим случай, когда напряженность магнитного поля В меняется очень медленно по сравнению с орби-тельным периодом частицы, т.е. за период
Рассмотрим случай, когда напряженность магнитного поля В меняется очень медленно по сравнению с орби-тельным периодом частицы, т.е. за период  Решим нерелятивистский случай методом, который выявит основную физику процесса. Частица, движущаяся по винтовой траектории в магнитном поле, эквивалентна контуру тока, причем ток равен
Решим нерелятивистский случай методом, который выявит основную физику процесса. Частица, движущаяся по винтовой траектории в магнитном поле, эквивалентна контуру тока, причем ток равен  площадь контура
площадь контура  Поэтому магнитный момент контура равен
Поэтому магнитный момент контура равен

 и отсюда
и отсюда

где  кинетическая энергия частицы в направлении, перпендикулярном ведущему центру.
кинетическая энергия частицы в направлении, перпендикулярном ведущему центру.
Сообщим малое приращение А В магнитному полю за время одного витка. Тогда  приведет к возникновению
приведет к возникновению  в контуре, и поэтому частица на орбите ускорится. Работа, совершенная за один виток, равна
в контуре, и поэтому частица на орбите ускорится. Работа, совершенная за один виток, равна

где  период обращения по одному витку. Поэтому изменение кинетической энергии частицы за один виток есть
период обращения по одному витку. Поэтому изменение кинетической энергии частицы за один виток есть

Чему равно изменение магнитного момента контура тока?

т.е. в нерелятивистском случае магнитный момент частицы на орбите инвариантен. Единственное условие применимости этого результата заключается в том, что поле должно медленно меняться. Рассмотрим другие способы выражения этого важного результата. Равенство  эквивалентно тому, что
эквивалентно тому, что

Поскольку  подстановка в (13.6) дает
подстановка в (13.6) дает

Этот результат объясняет явление магнитного отражения. Если частица попадает в область усиленного магнитного поля, то  возрастает, а
возрастает, а  уменьшается. В конце концов
уменьшается. В конце концов  достигнет нуля в точке, где
достигнет нуля в точке, где  (квадрату полного импульса частицы). Именно это происходит, когда захваченная в радиационйом поясе частица подходит к магнитному полю Земли, где поле сильнее.
(квадрату полного импульса частицы). Именно это происходит, когда захваченная в радиационйом поясе частица подходит к магнитному полю Земли, где поле сильнее.
И наконец, поскольку 

Рис. 13.2. Динамика заряженной частицы в медленно меняющемся магнитном поле. Диаграмма показывает, как ведущий центр движения частицы следует среднему направлению магнитного поля. Радиус кривизны траектории такой, что магнитный поток внутри витка остается постоянным.

т.е. частица следует вдоль ведущего центра таким образом, что магнитный поток внутри орбиты частицы сохраняется (рис. 13.2). Это выражение часто называют первым адиабатическим инвариантом движения частицы в магнитном поле.
Полученные формулы более точно выводятся из принципа адиабатической инвариантности, используемого в классической динамике. Он также является лучшим способом для релятивистского обобщения этих формул. В релятивистском приближении они имеют вид

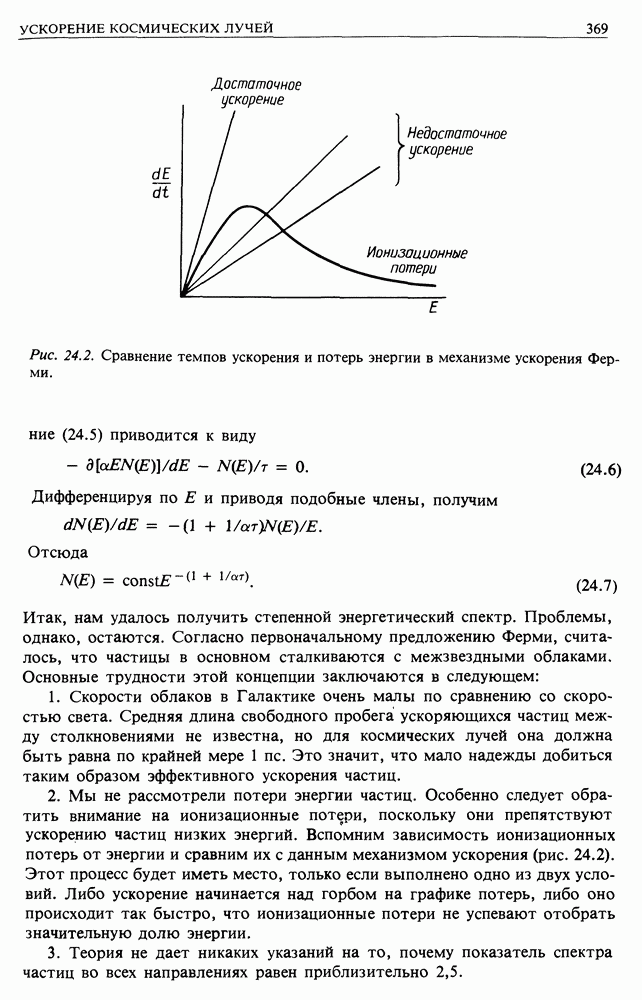
Если вы не можете вывести эти формулы самостоятельно, то прочтите следующий раздел.
13.1.3. Метод адиабатического инварианта. Этот подход требует использования лагранжева представления классической динамики. Последующий анализ заимствован из книги Джексона [2]. Джексон использует результат классической динамики, заключающийся в том, что если  обобщенные канонические координаты и импульсы, то для любой координаты, если она периодична, интеграл действия
обобщенные канонические координаты и импульсы, то для любой координаты, если она периодична, интеграл действия  постоянен для данной механической системы с заданными начальными условиями. Если свойства системы меняются медленно по сравнению с периодом осцилляций, то можно показать, что интеграл действия инвариантен. Такое изменение называется адиабатическим. Именно этот случай имеет место при исследовании динамики заряженной частицы, движущейся в магнитном поле. В частности, компоненты скорости и координаты, перпендикулярные
постоянен для данной механической системы с заданными начальными условиями. Если свойства системы меняются медленно по сравнению с периодом осцилляций, то можно показать, что интеграл действия инвариантен. Такое изменение называется адиабатическим. Именно этот случай имеет место при исследовании динамики заряженной частицы, движущейся в магнитном поле. В частности, компоненты скорости и координаты, перпендикулярные

Рис. 13.3.
направлению магнитного поля, являются периодическими. Таким образом, интеграл действия есть

где  канонический импульс частицы, перпендикулярный направлению магнитного поля, и ей — линейный элемент вдоль круговой траектории частицы. Важный результат состоит в том, что для заряженной частицы в магнитном поле канонический импульс, перпендикулярный направлению поля, равен
канонический импульс частицы, перпендикулярный направлению магнитного поля, и ей — линейный элемент вдоль круговой траектории частицы. Важный результат состоит в том, что для заряженной частицы в магнитном поле канонический импульс, перпендикулярный направлению поля, равен

где  трехмерный момент частицы,
трехмерный момент частицы,  векторный потенциал магнитного поля,
векторный потенциал магнитного поля,  Поэтому
Поэтому

где  вектор площади, связанный с интегралом по контуру С. Рассмотрим векторные соотношения между
вектор площади, связанный с интегралом по контуру С. Рассмотрим векторные соотношения между  Если поле В перпендикулярно плоскости листа бумаги,
Если поле В перпендикулярно плоскости листа бумаги,  имеет направление, указанное на рис. 13.3, то сила Лоренца
имеет направление, указанное на рис. 13.3, то сила Лоренца  для положительно заряженной частицы приводит к движению по окружности. Направление вектора
для положительно заряженной частицы приводит к движению по окружности. Направление вектора  противоположно В. Следовательно, второй член в уравнении (13.11) отрицательный. Поэтому
противоположно В. Следовательно, второй член в уравнении (13.11) отрицательный. Поэтому

Но угловая гирочастота  значит
значит

где А — площадь, охватываемая орбитой частицы. Согласно приведенному выше правилу,  для случая, когда изменение В за период движения частицы по орбите мало, т.е.
для случая, когда изменение В за период движения частицы по орбите мало, т.е. 

Именно этот результат и указан в уравнении (13.9), и другие его варианты немедленно следуют из соотношений 
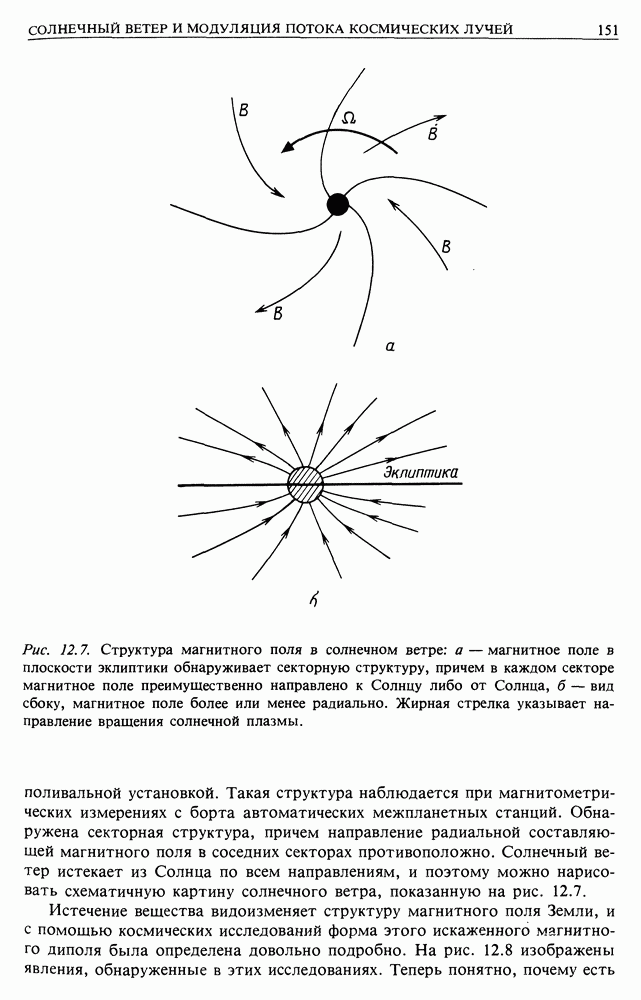
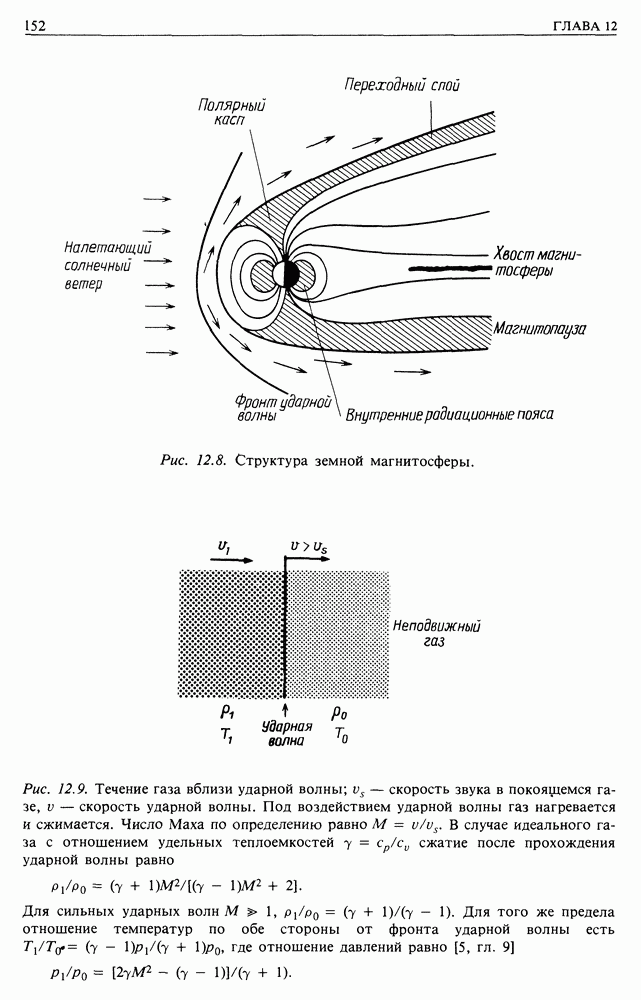
Можно рассчитать поведение частиц в более сложных случаях, например, если частицы попадут в область, где существует градиент 5, или если имеется влияние гравитационного поля. Однако должно быть ясно, что отдельные частицы привязаны к силовым линиям и требуется очень большое усилие, чтобы заставить их двигаться поперек магнитного поля. Тем, кто желает более подробно познакомиться с этим вопросом, рекомендую книгу Нортропа [3].
Результаты для отдельных частиц очень сходны с выводами для вмороженного потока. Но это разные задачи, хотя примененные при их решении методы очень похожи. Дело в том, что вмораживание потока является фундаментальным магнитогидродинамическим процессом, в котором плазма рассматривается как проводящая жидкость. Расчет для отдельных частиц является микроскопическим подходом, и, чтобы объединить эти два метода в один, надо показать, что можно выводить уравнения магнитогидродинамики из микроскопических уравнений движения. Это далеко не тривиально 
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
- 4.4. ОБРАЗОВАНИЕ ПАР
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
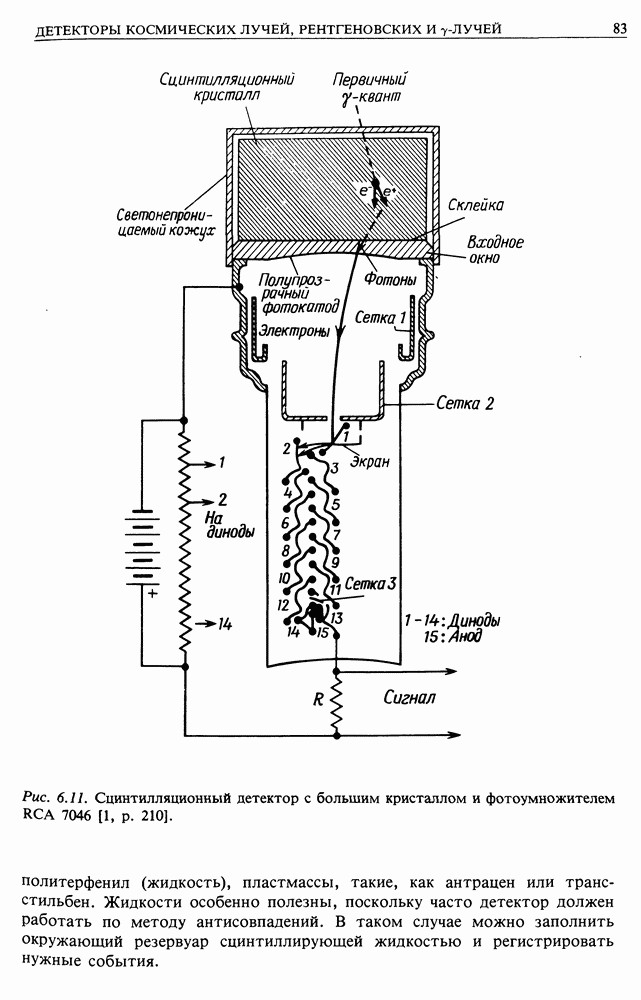
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
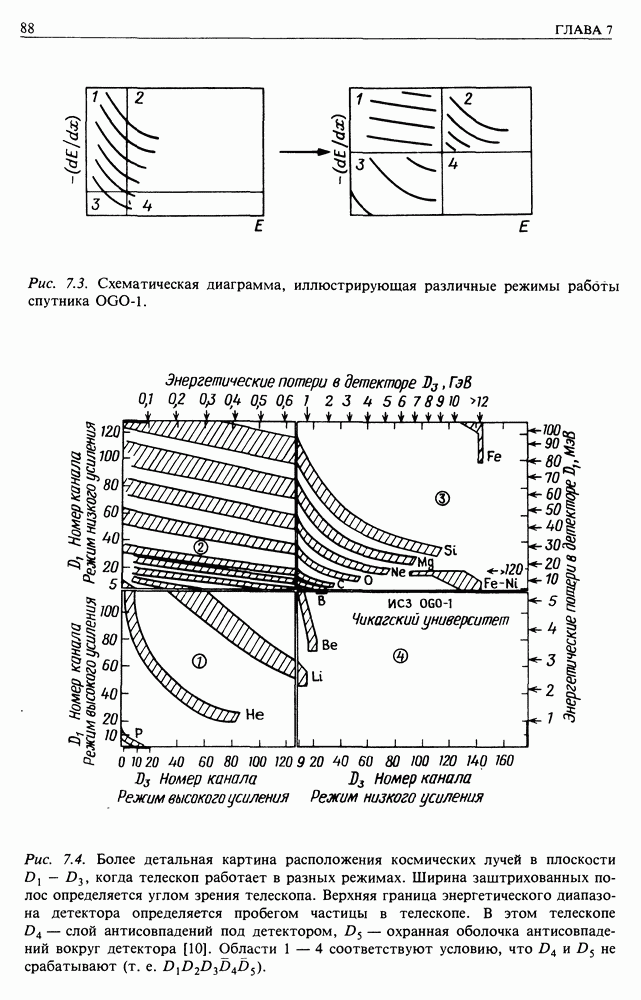
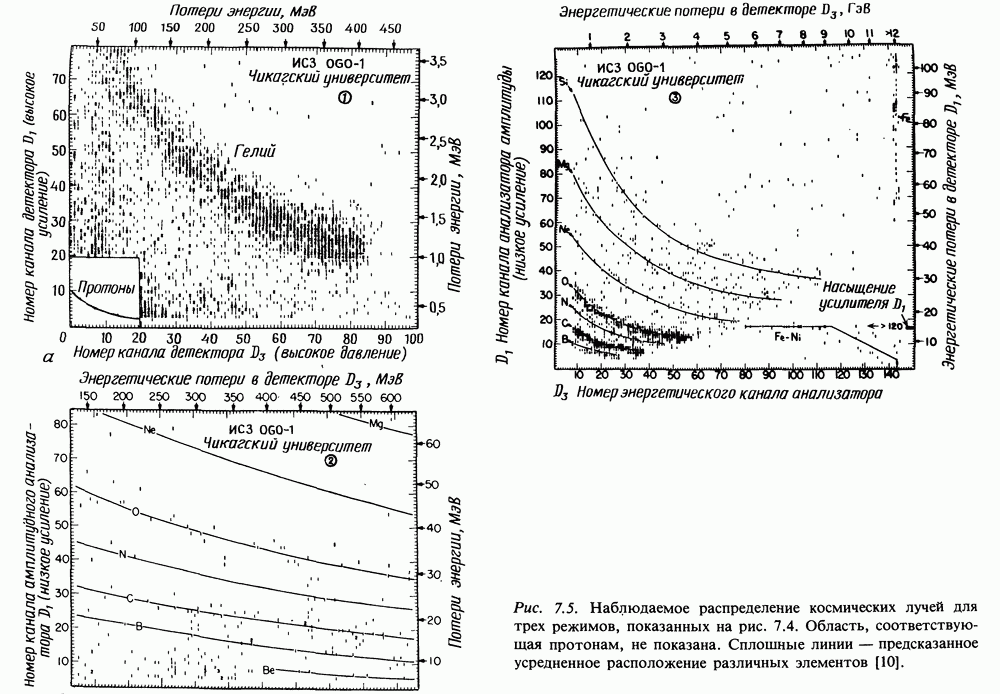
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
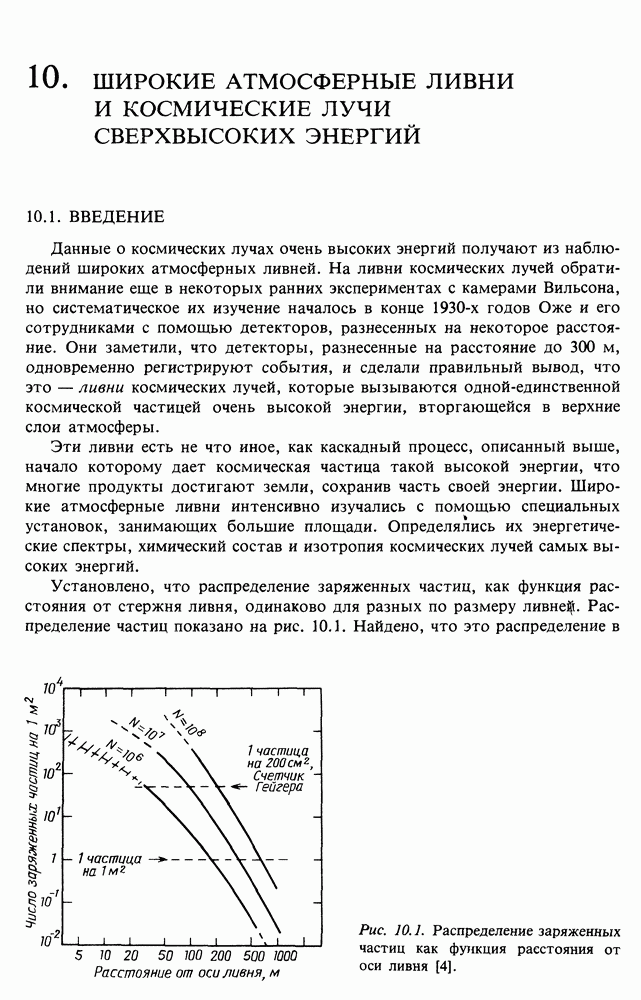
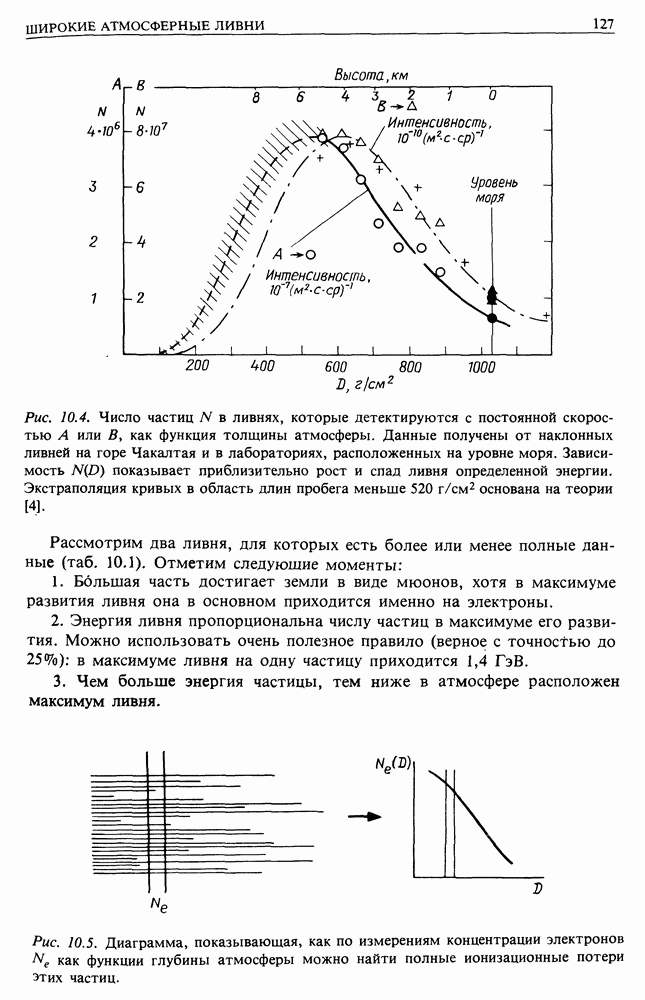
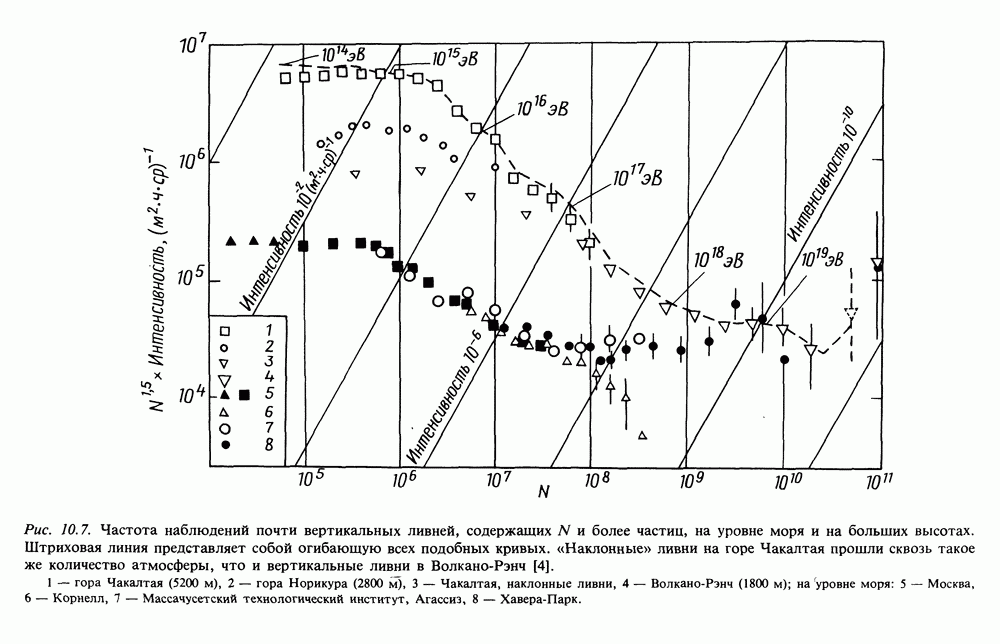
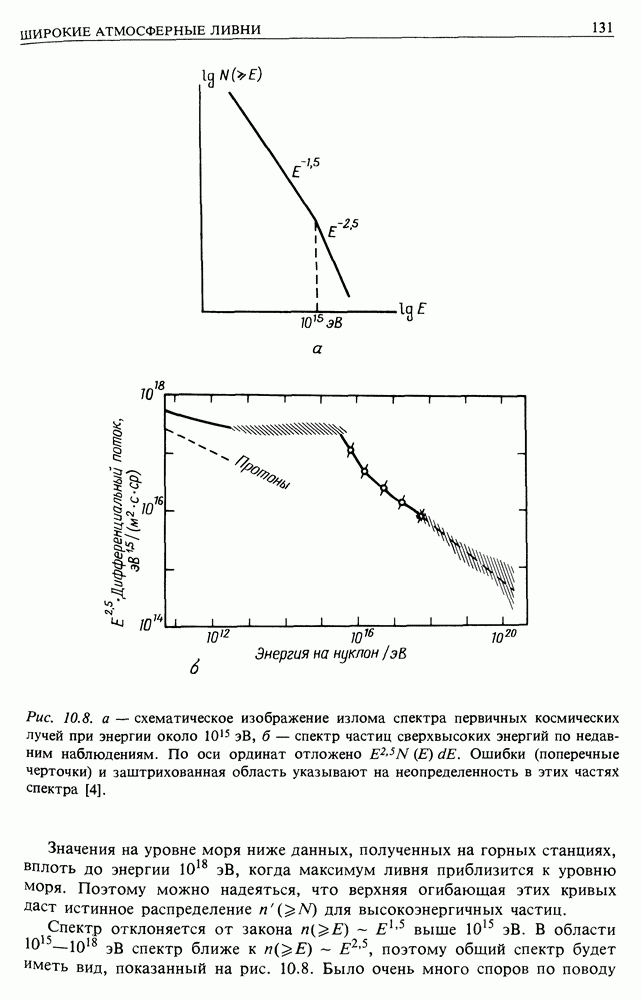
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
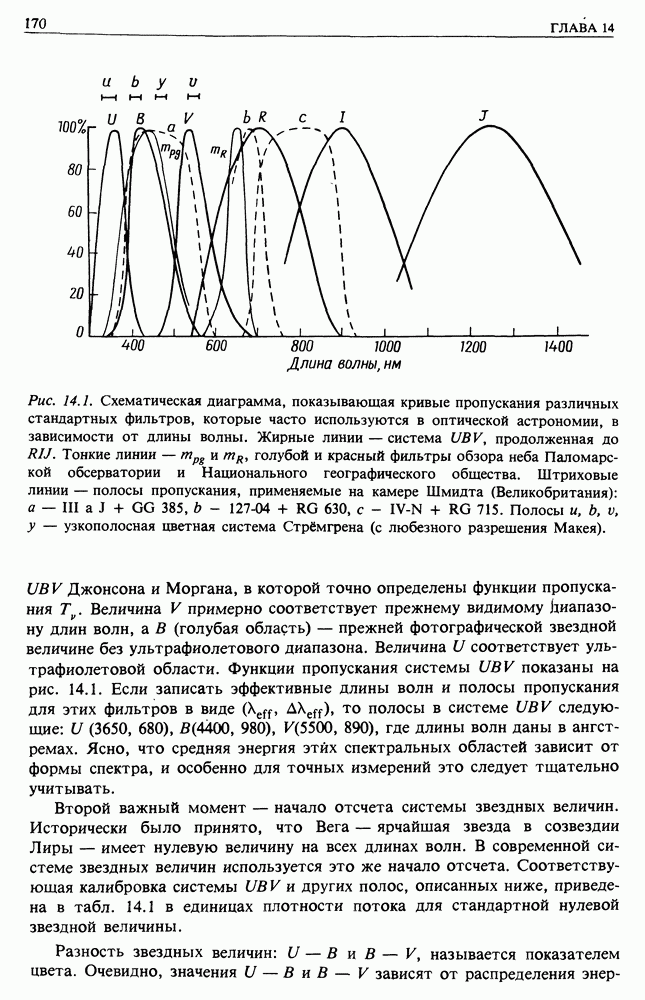
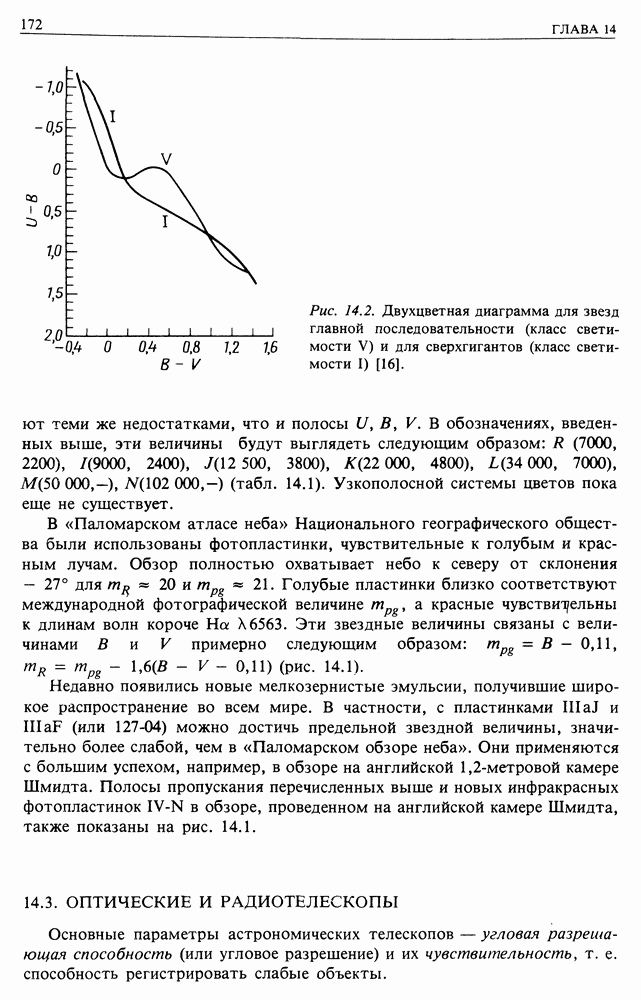
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
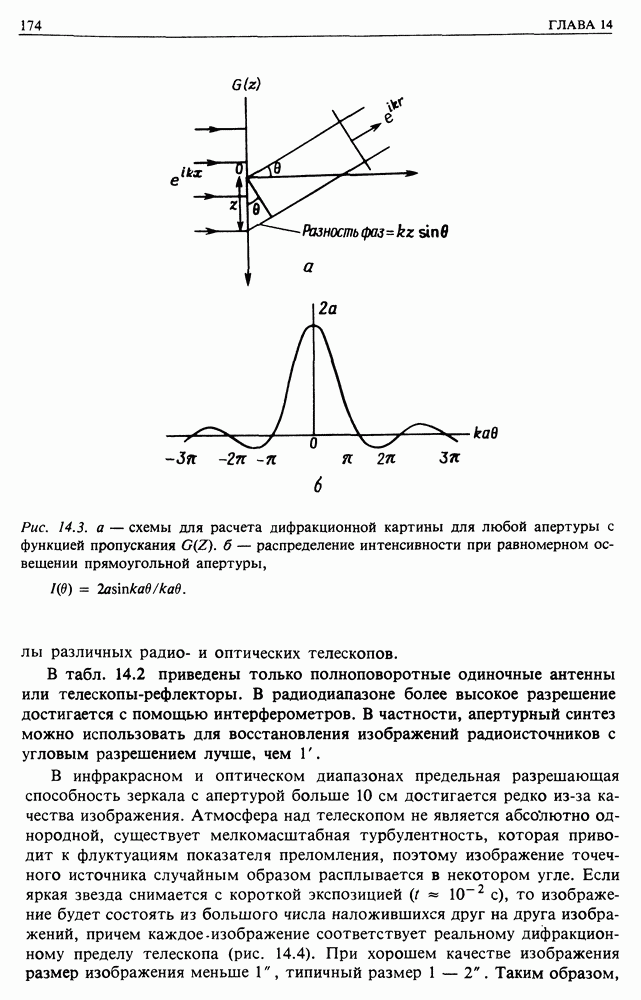
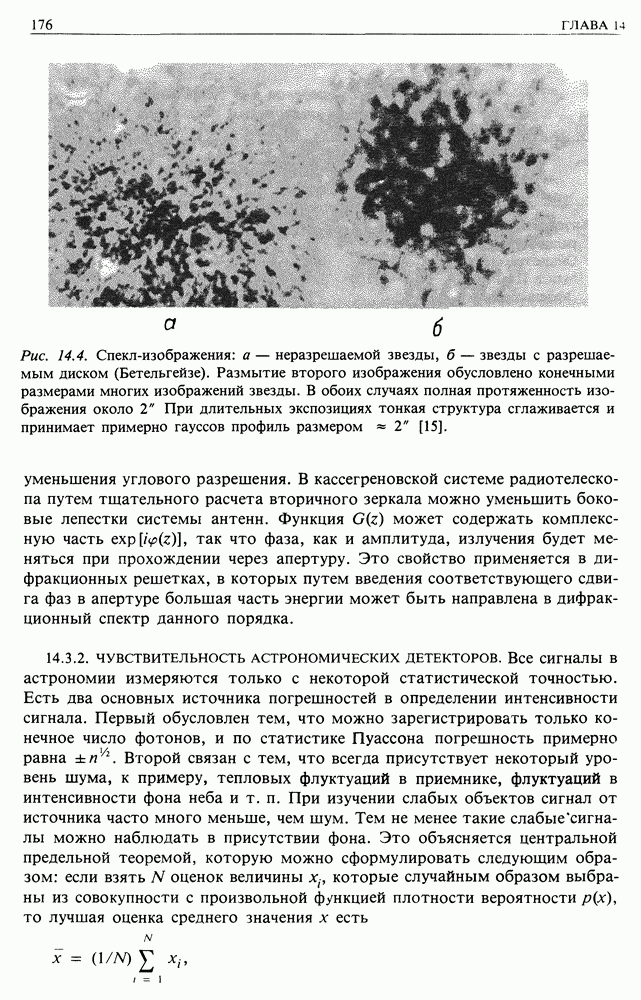
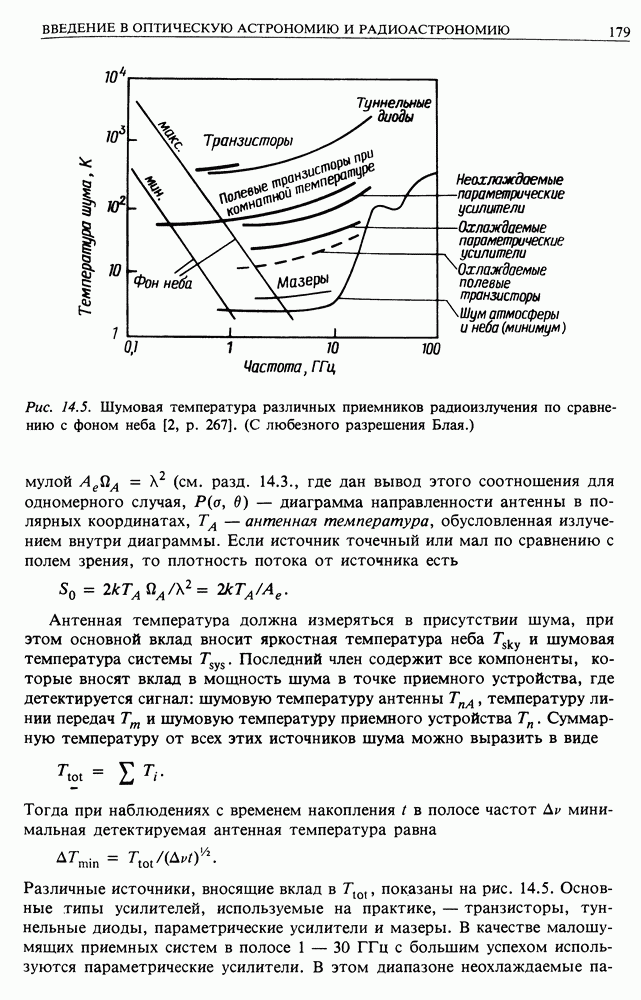
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
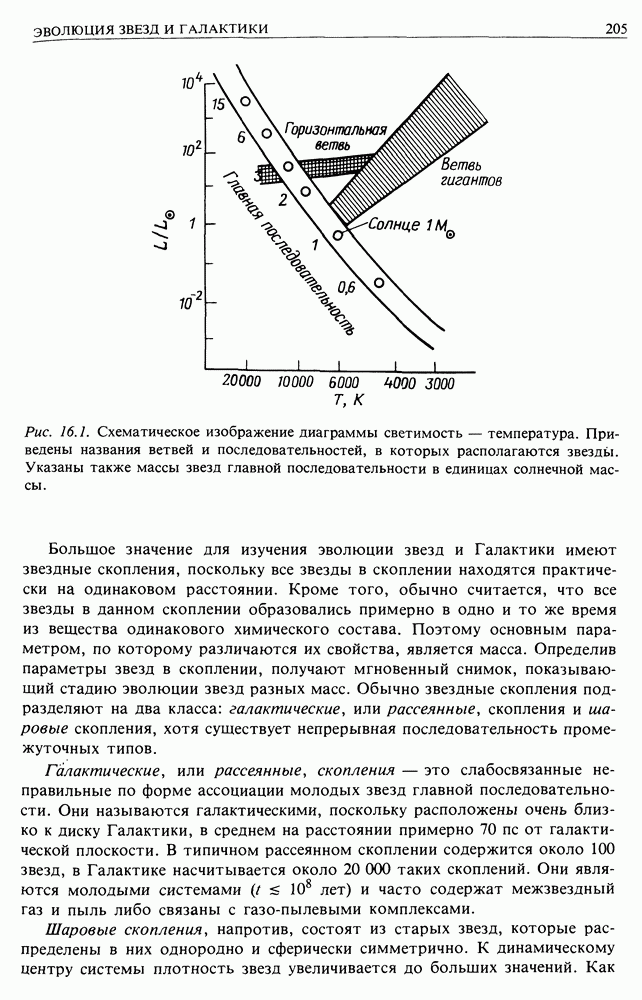
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
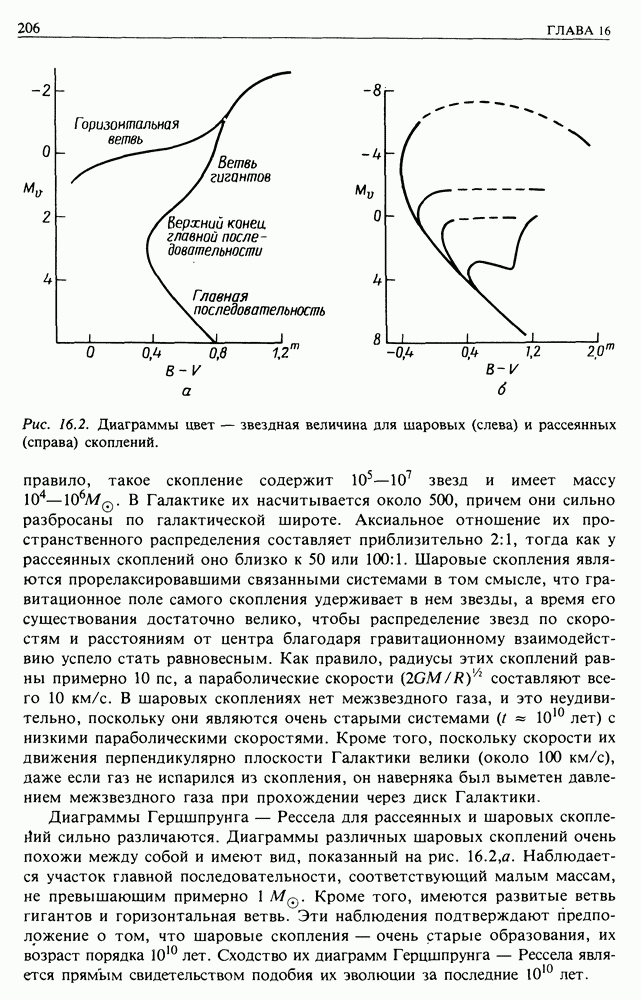
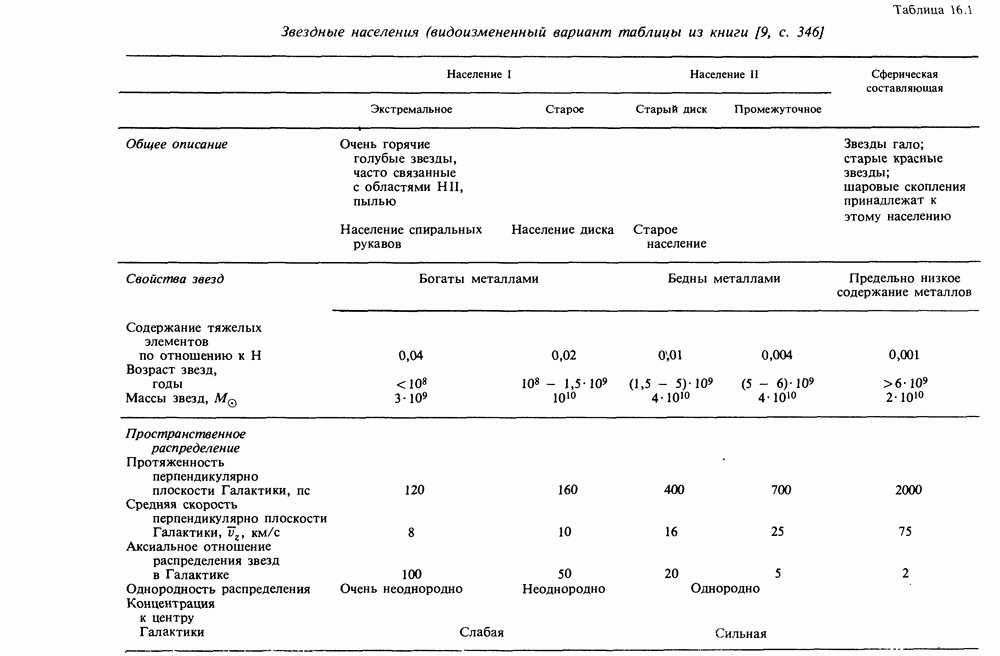
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
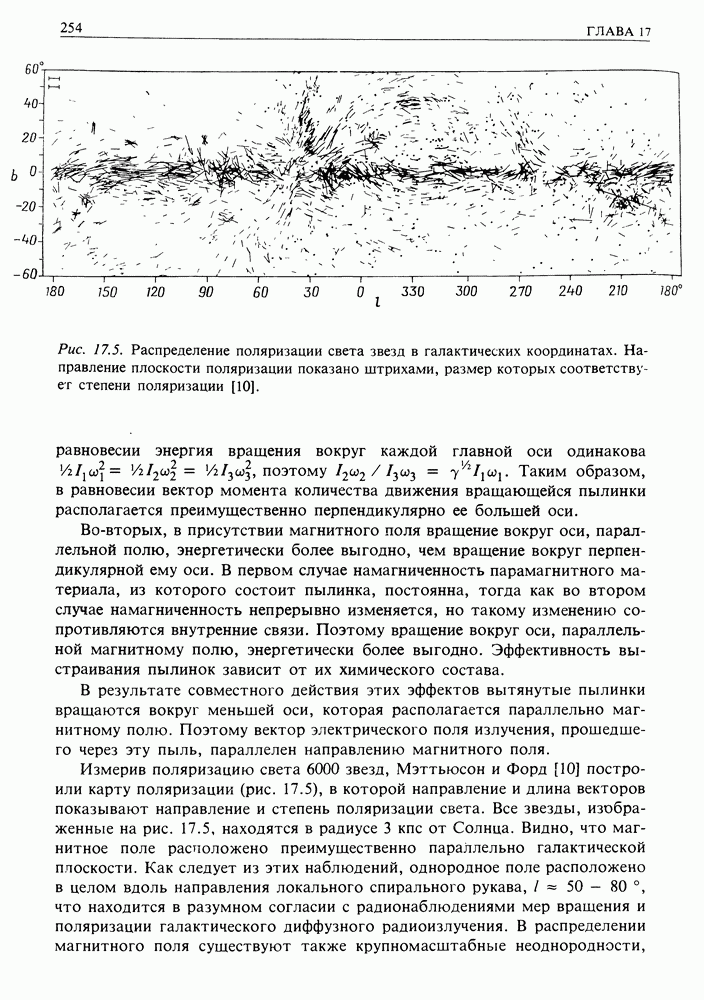
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
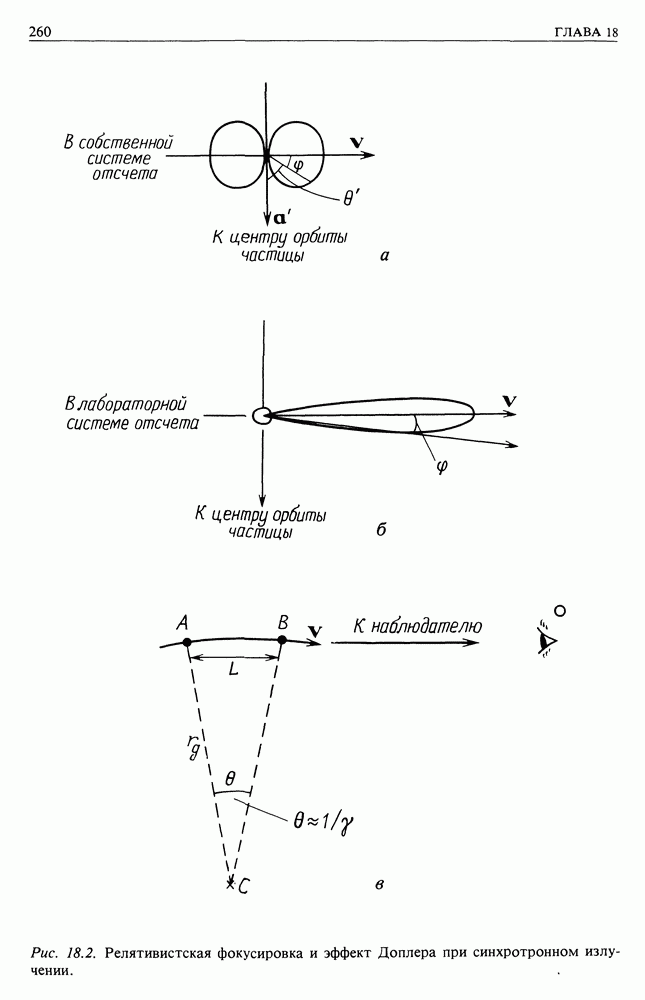
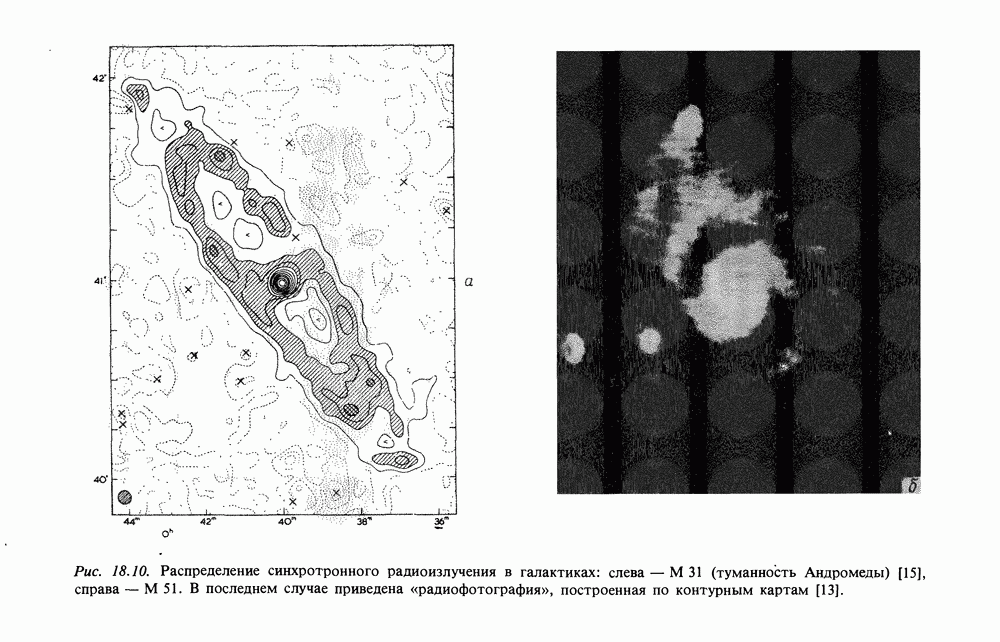
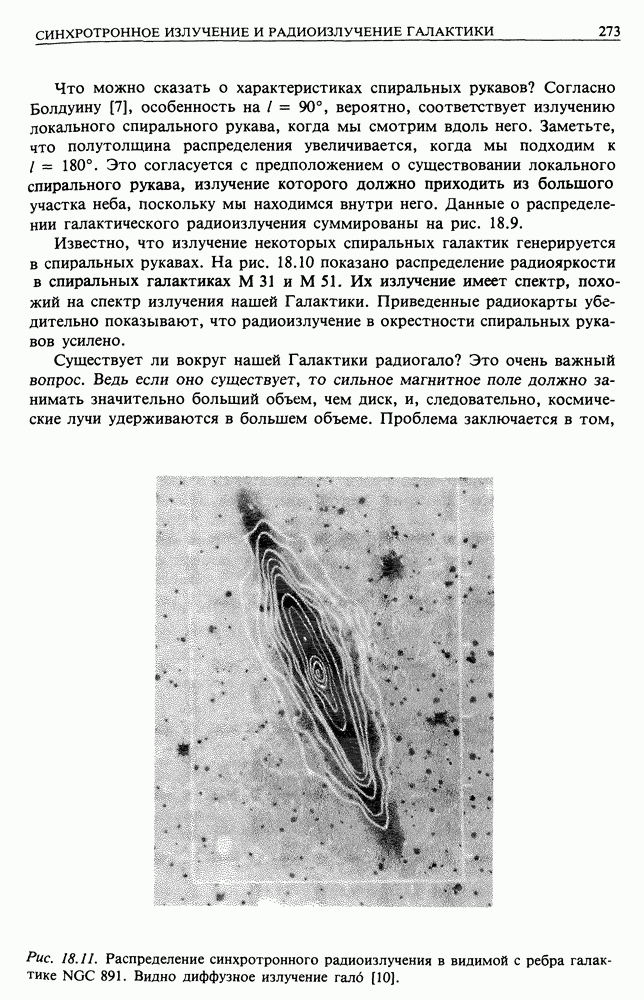
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
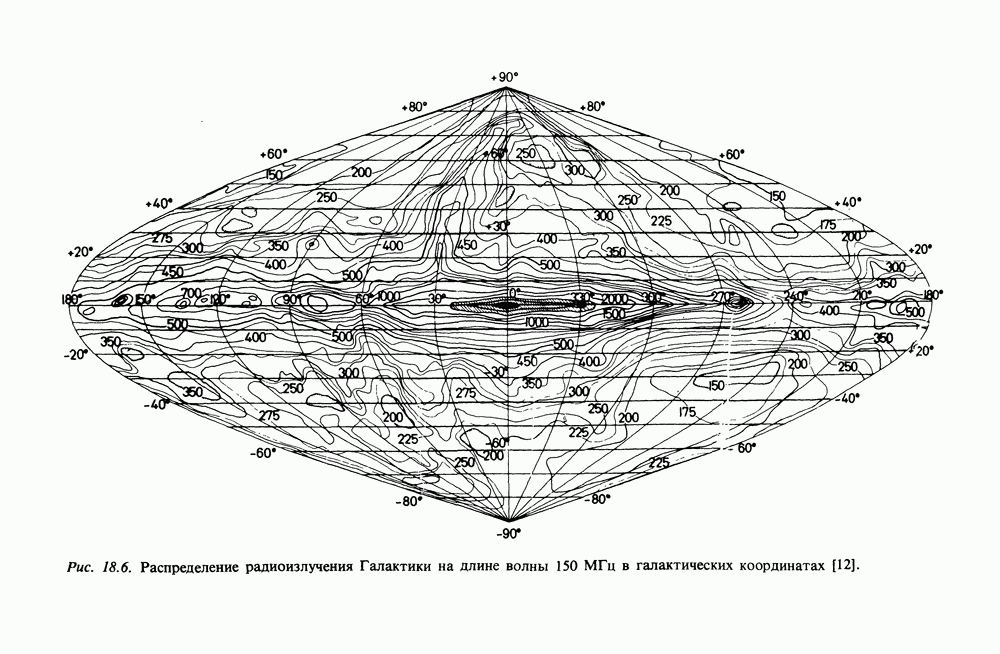
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
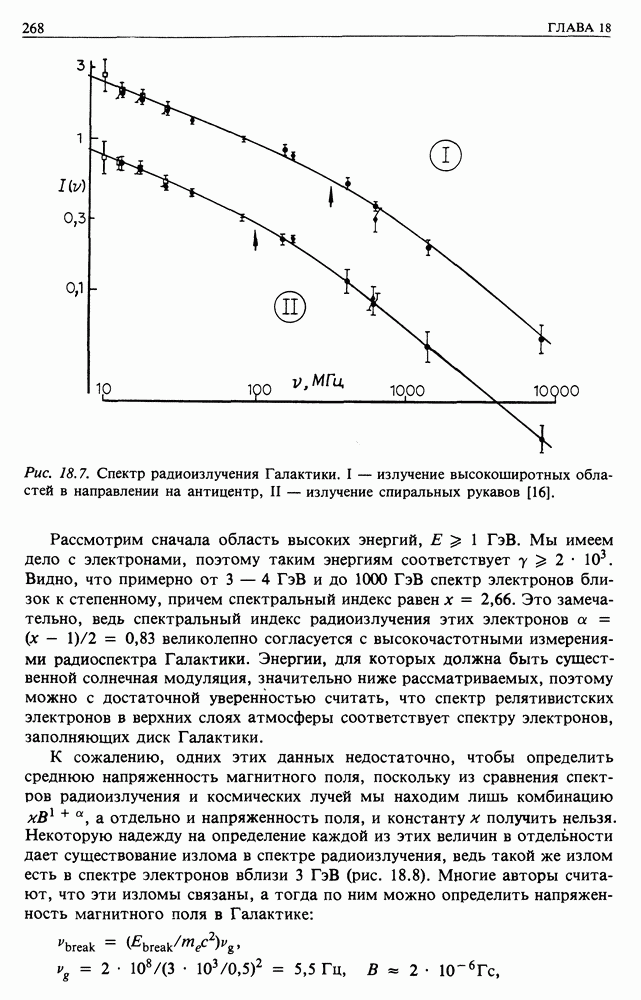
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
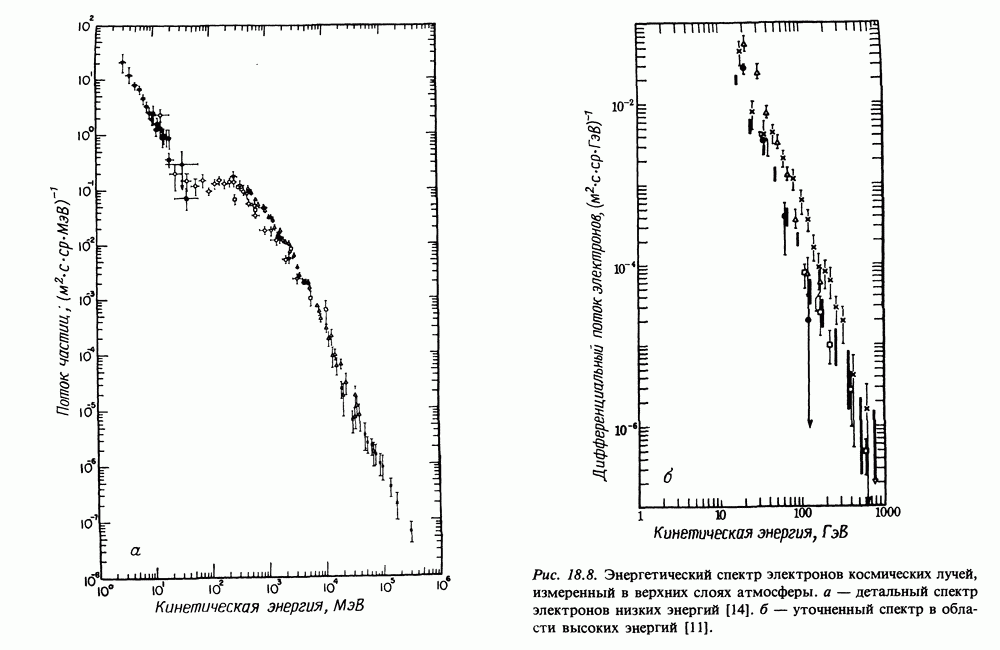
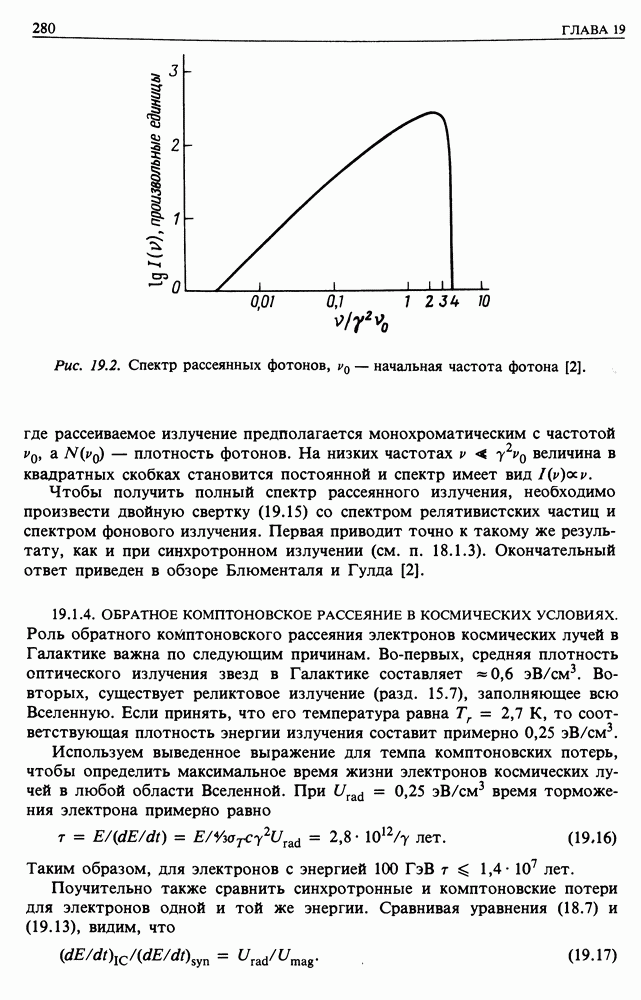
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
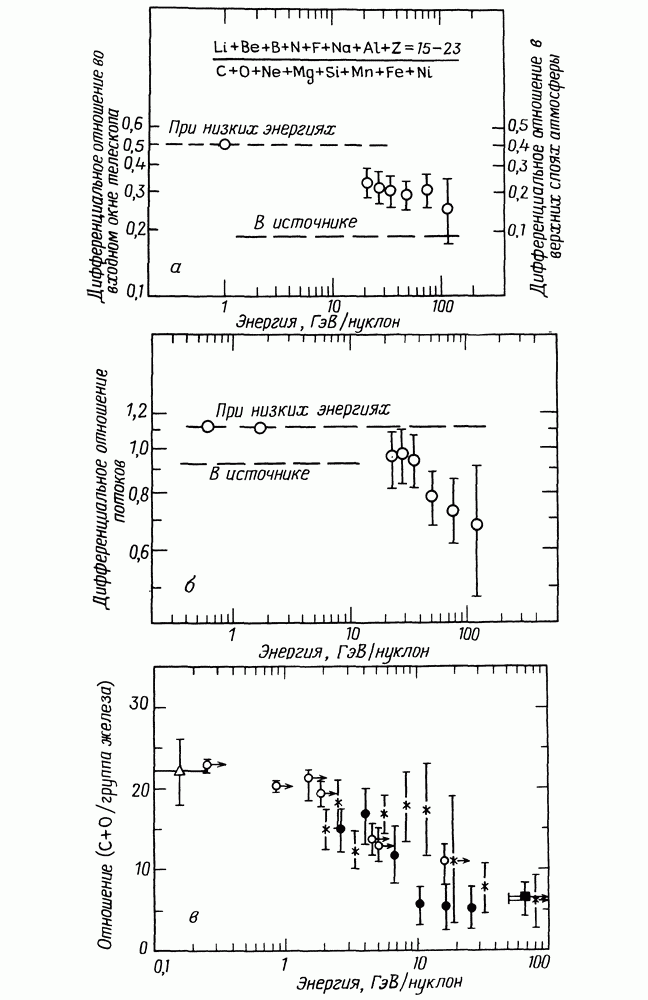
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
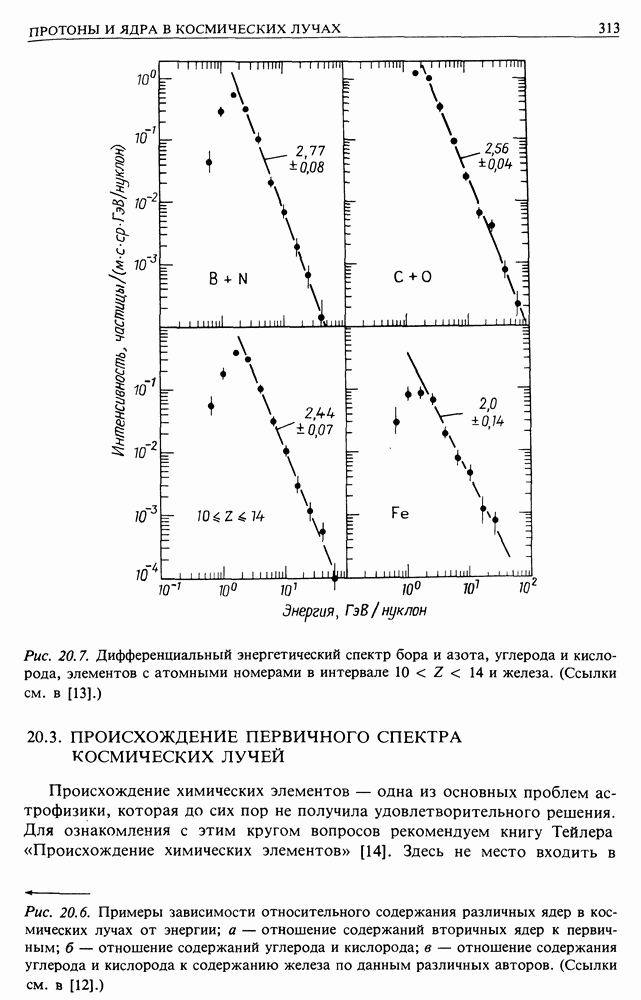
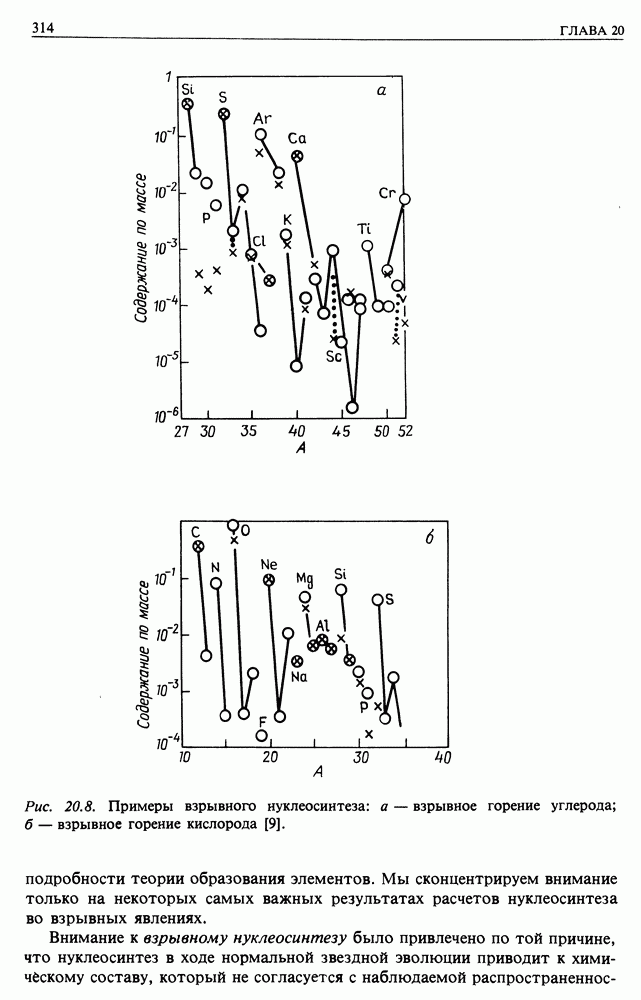
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
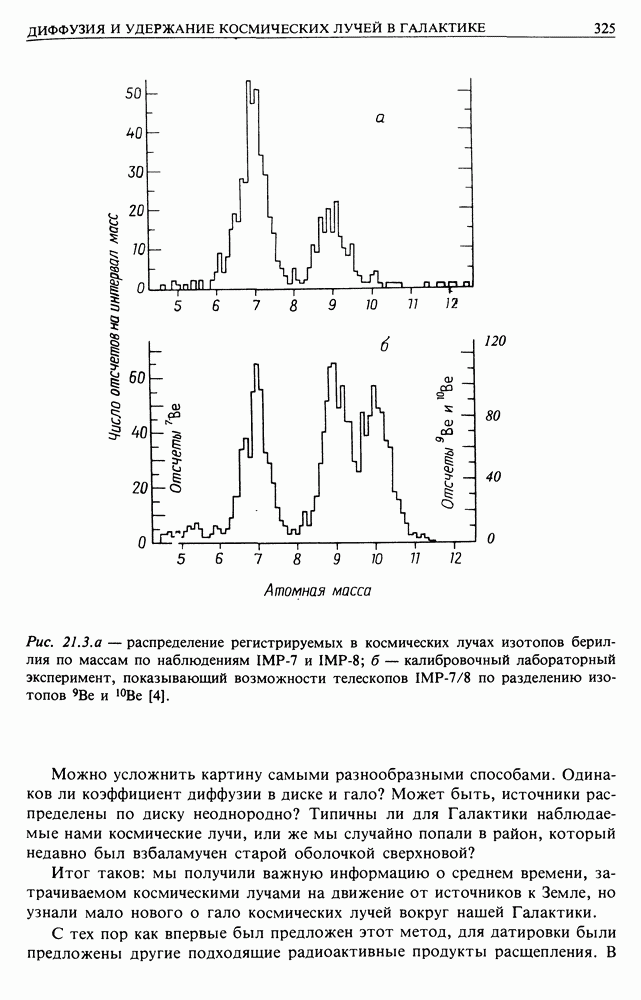
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
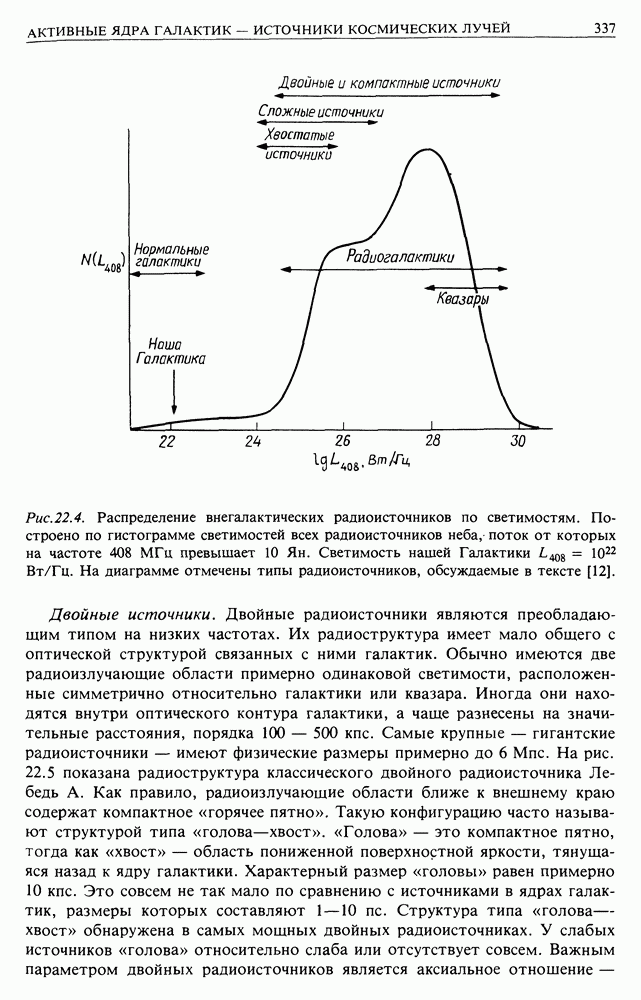
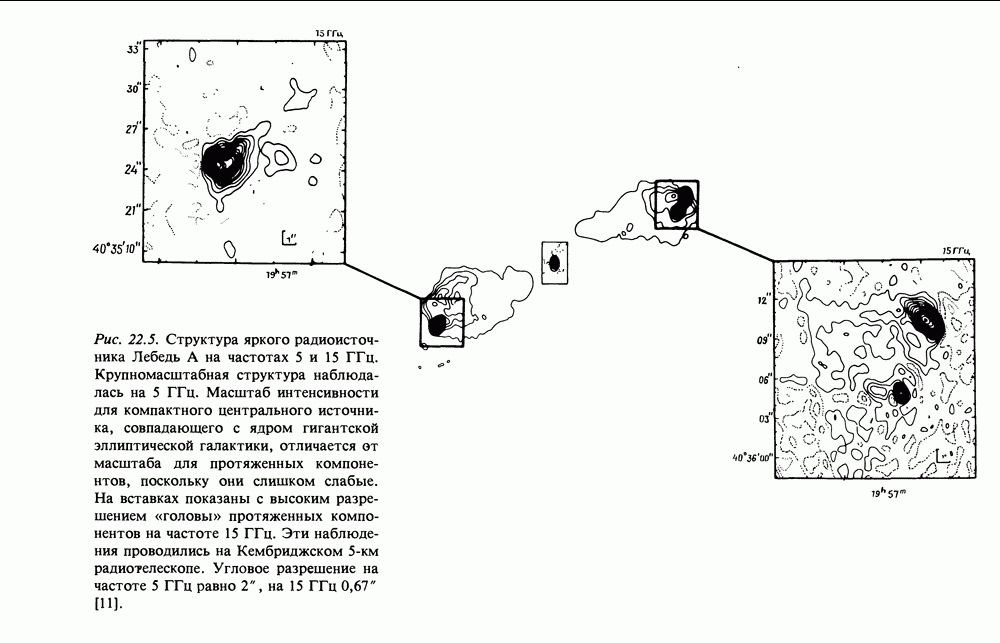
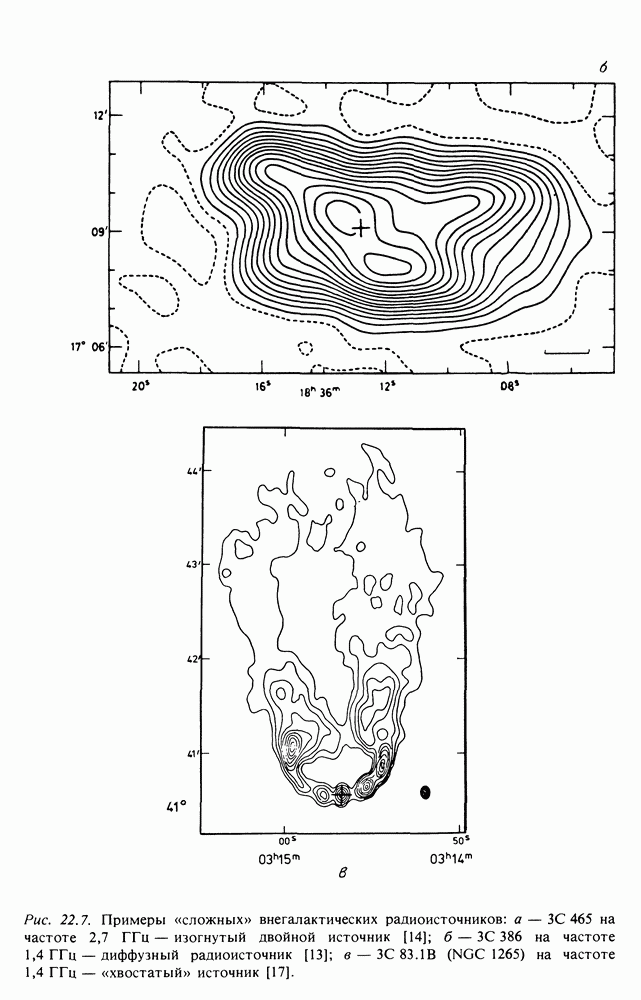
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
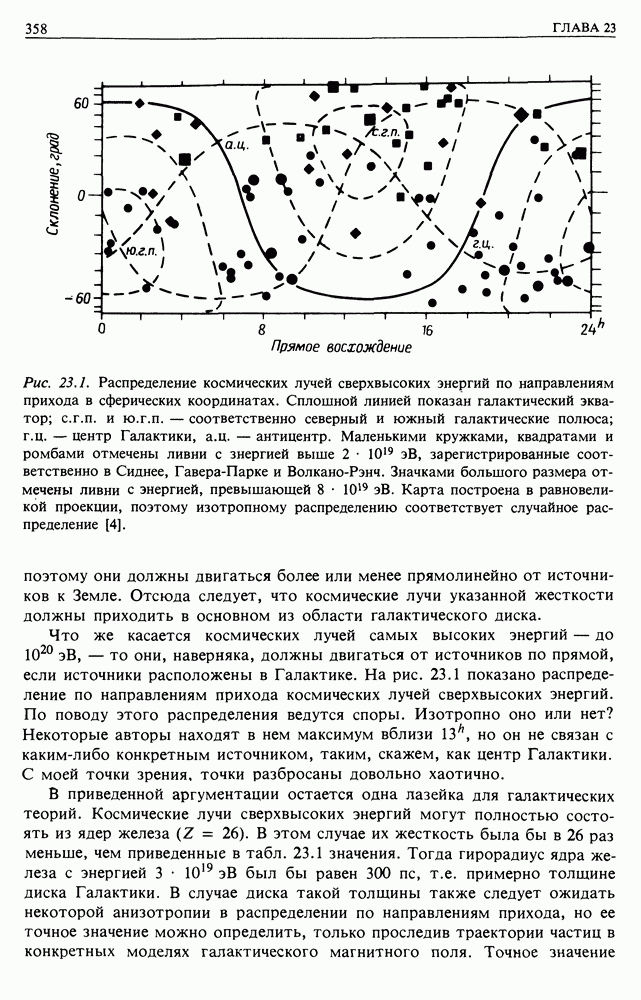
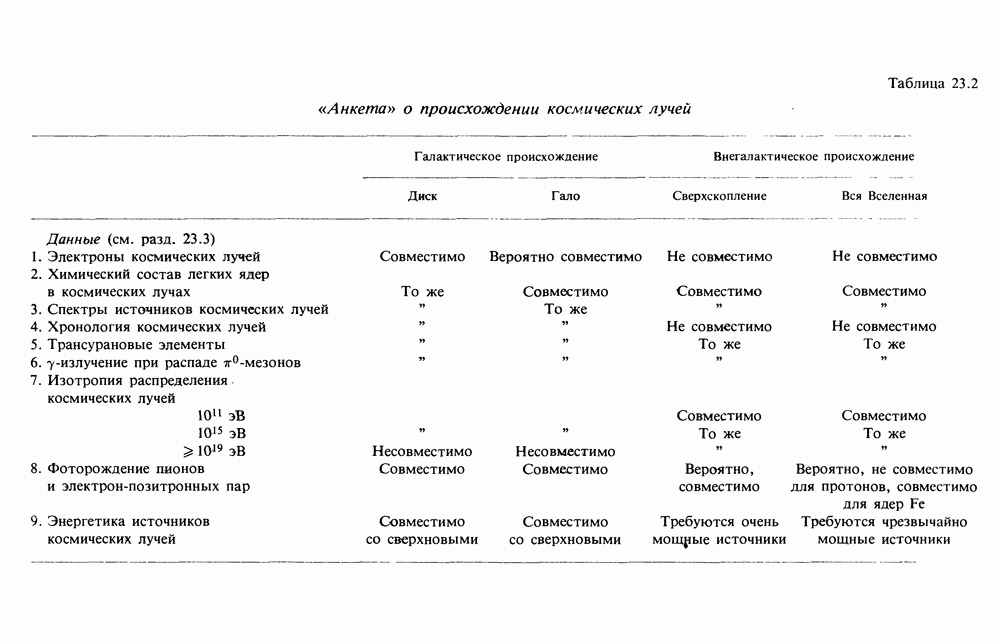
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
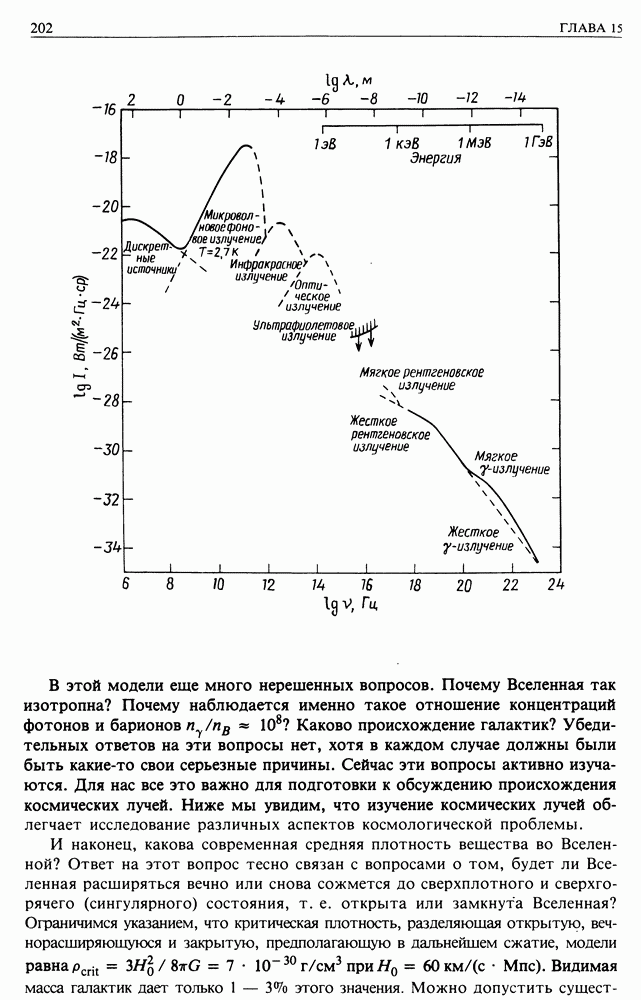
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ