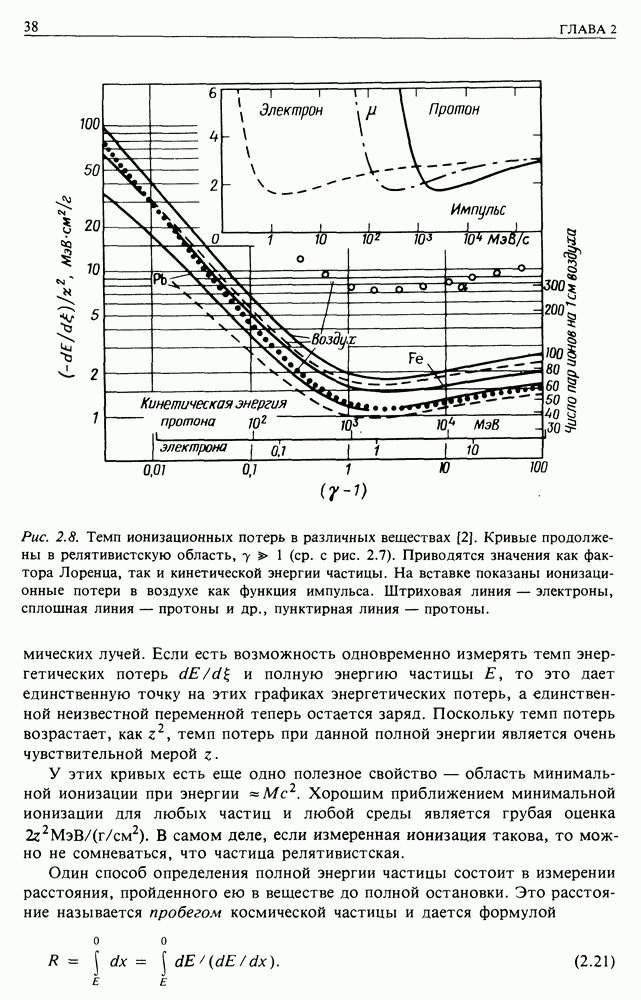
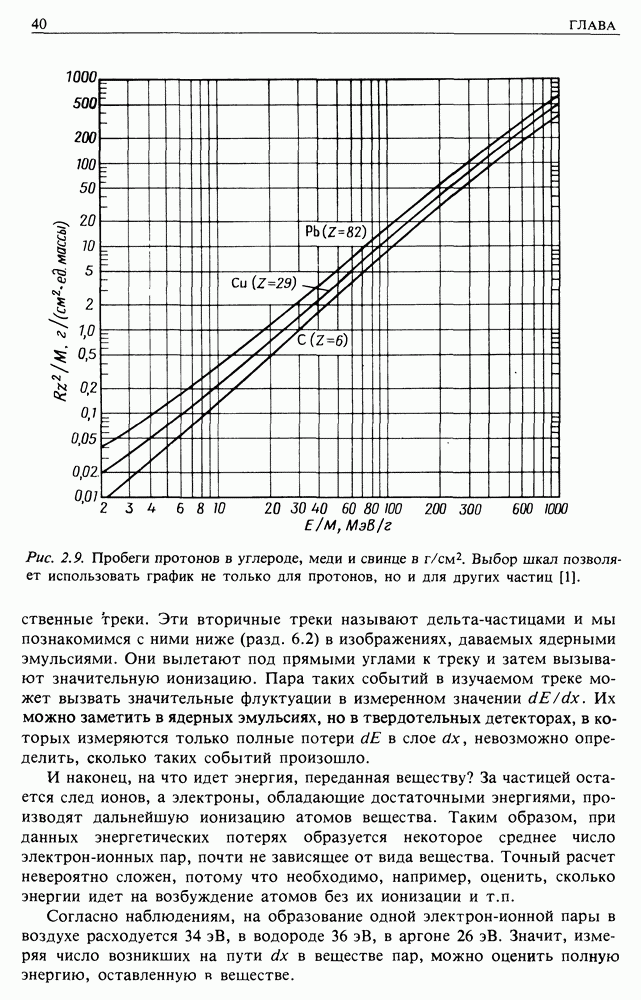
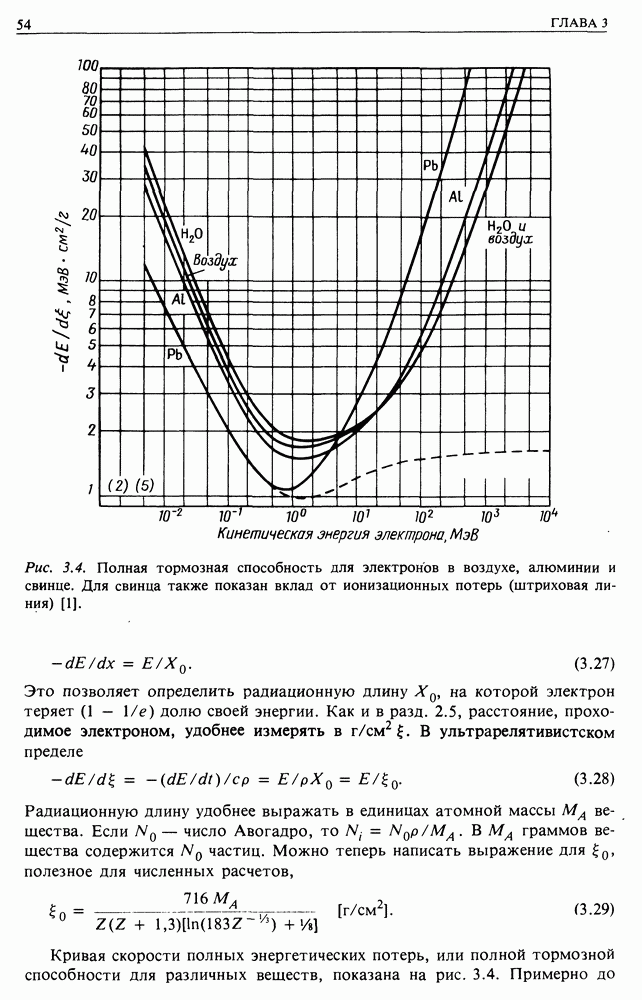
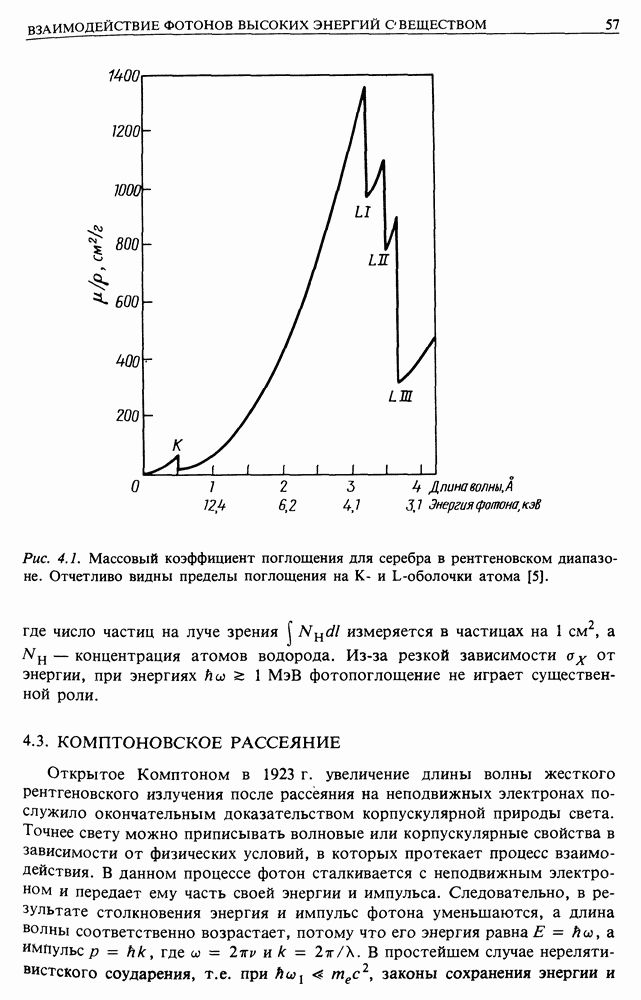
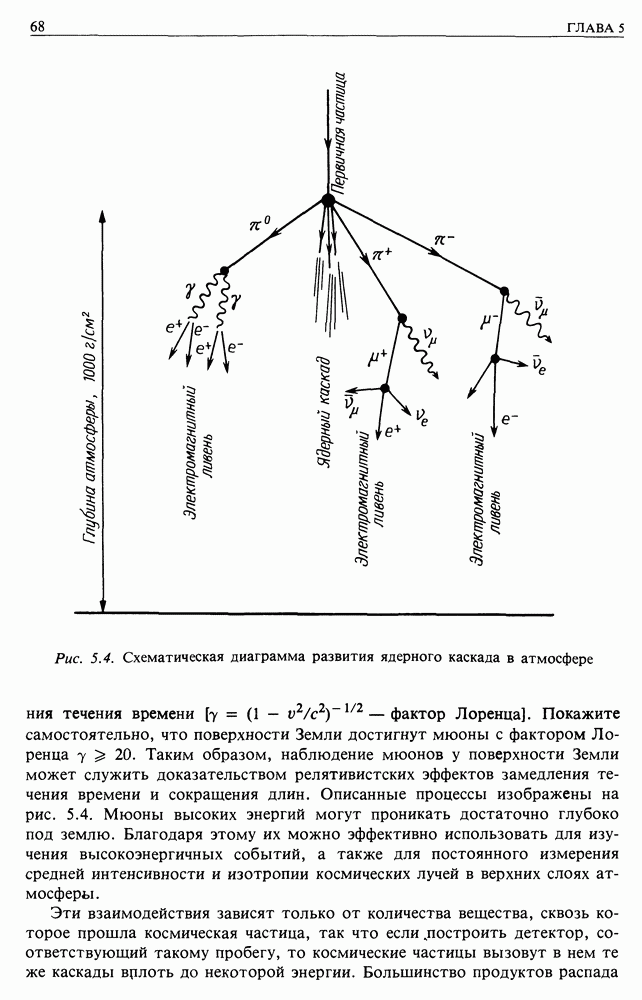
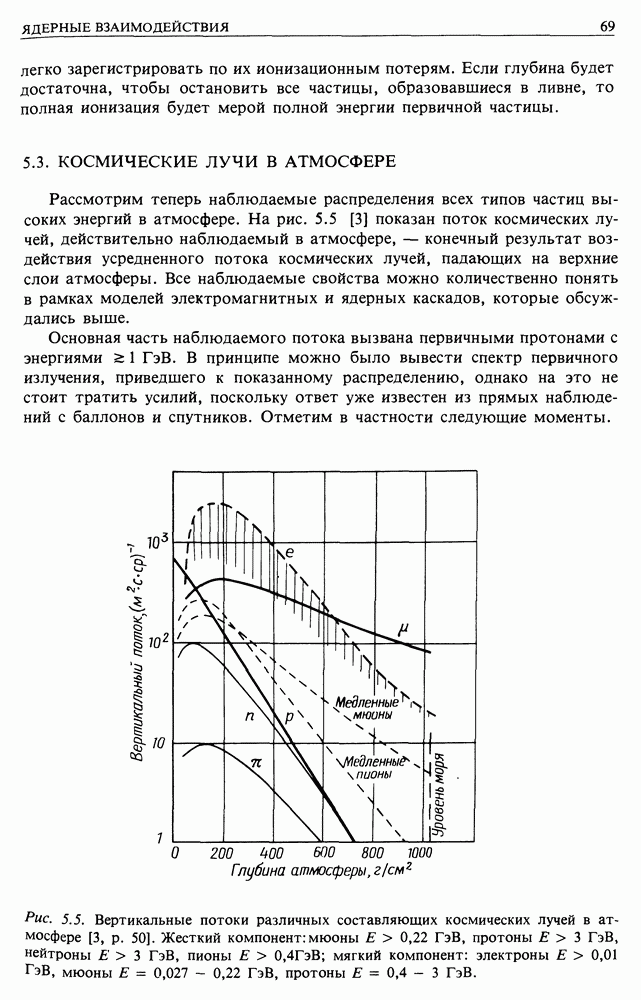
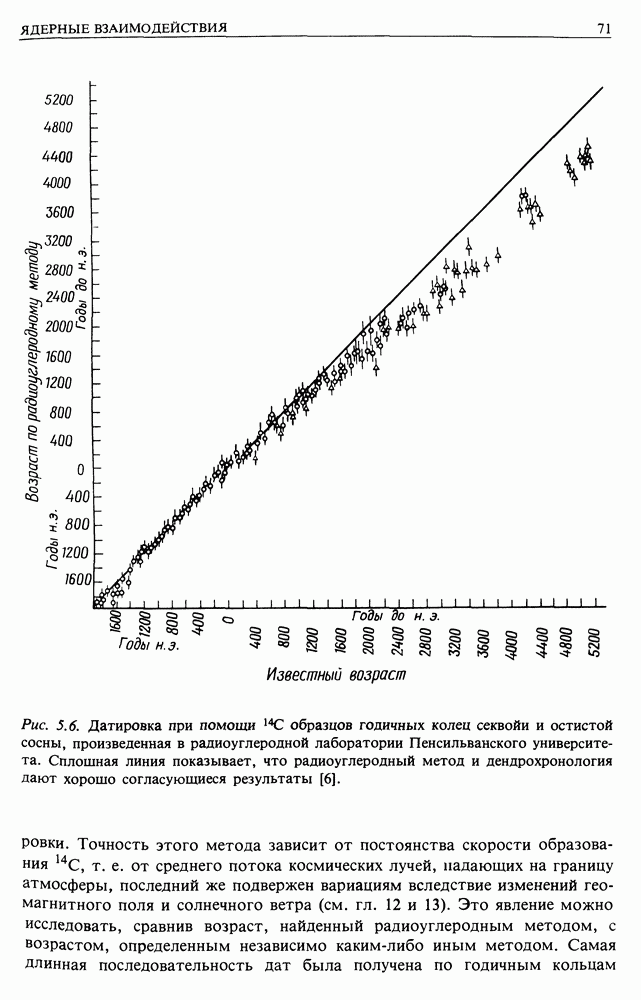
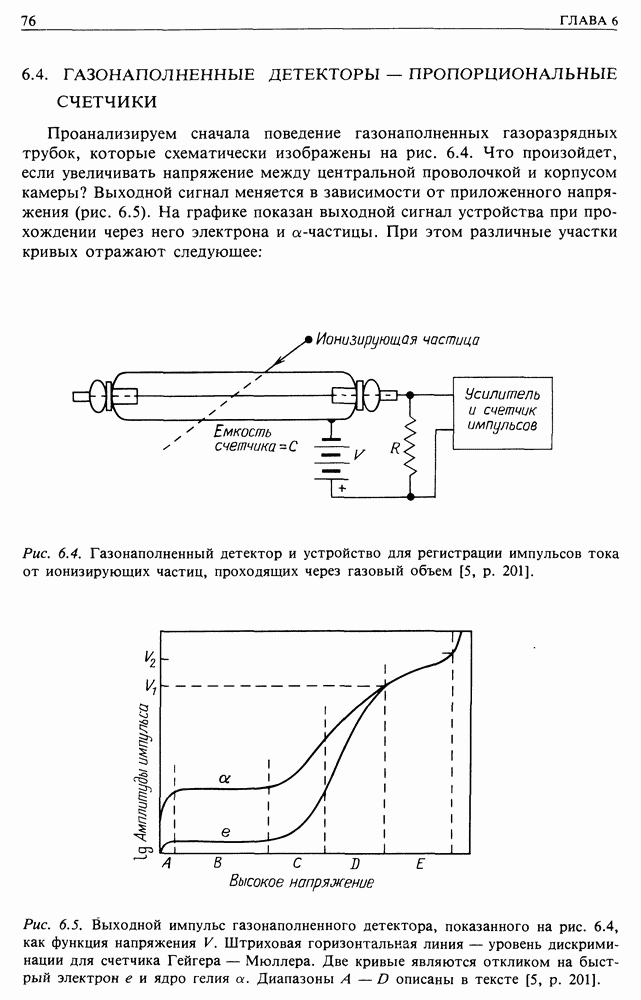
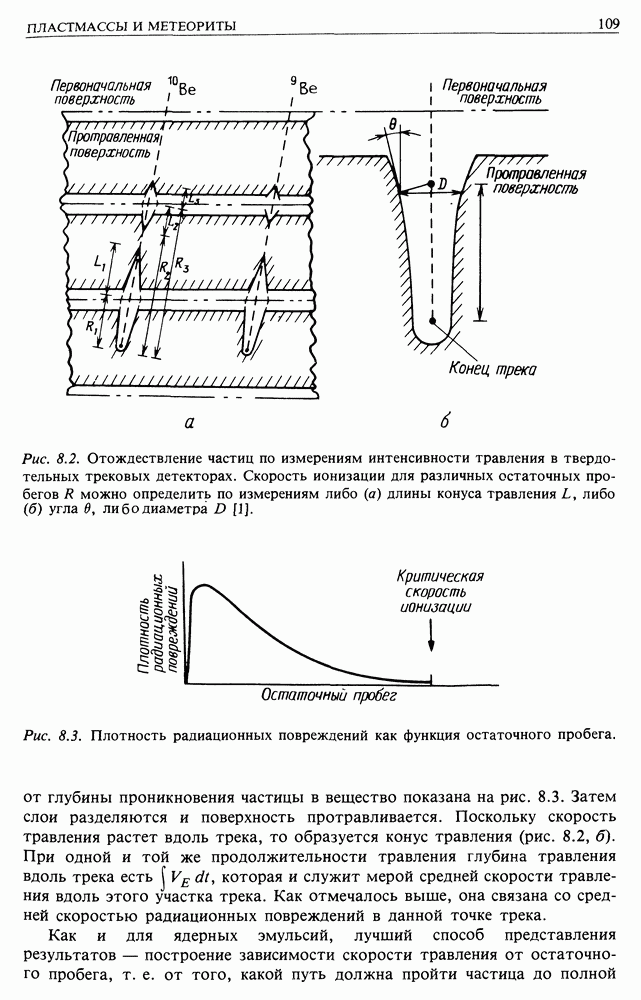
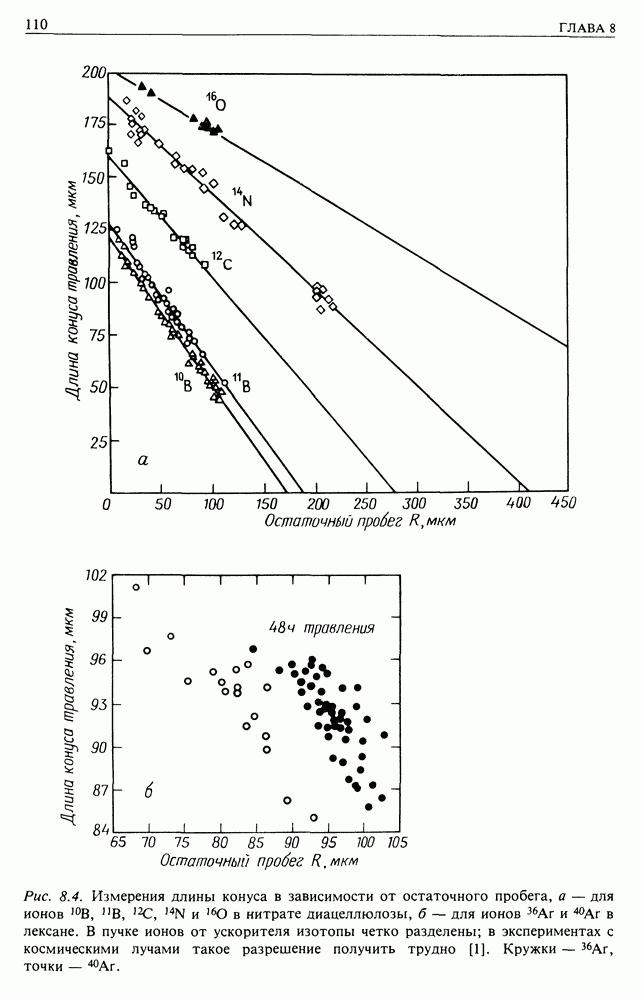
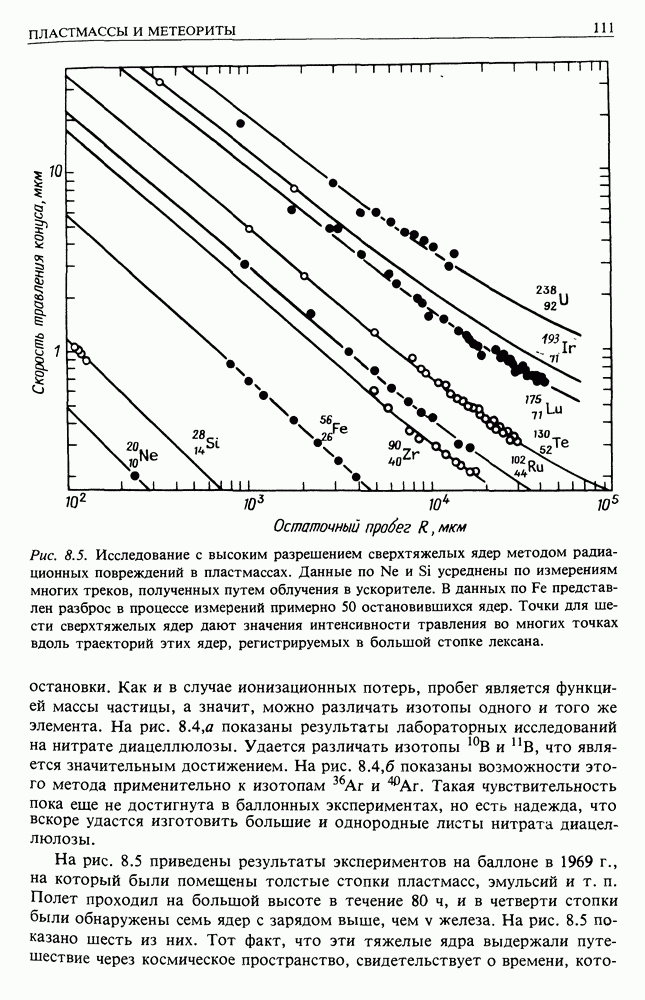
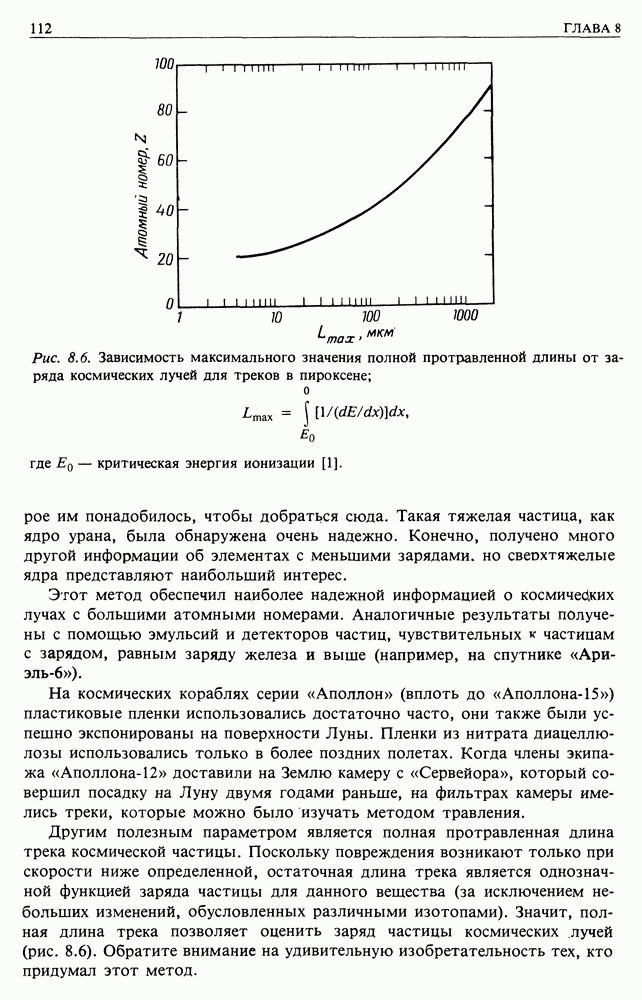
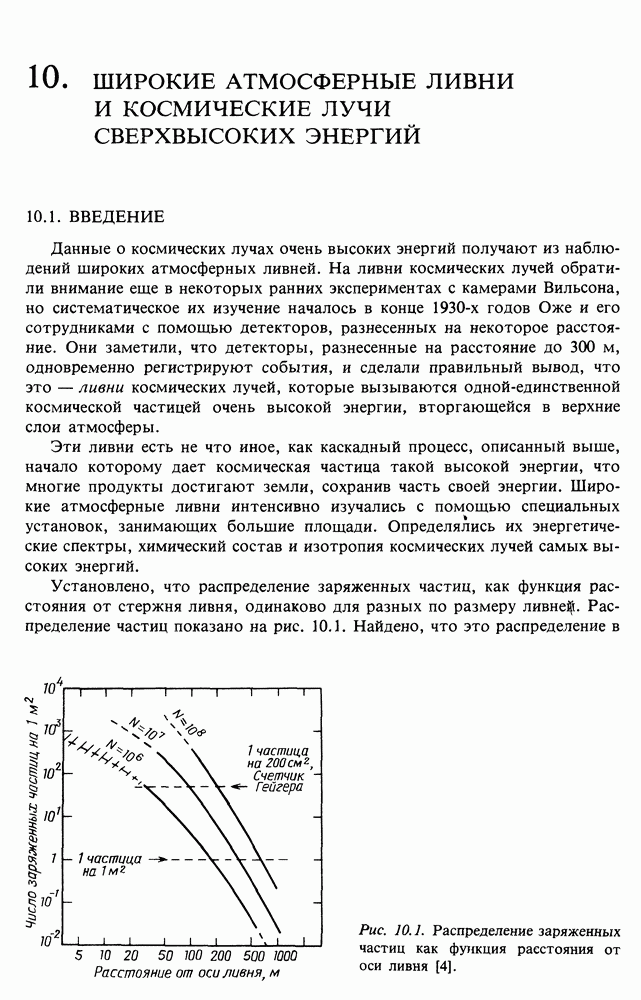
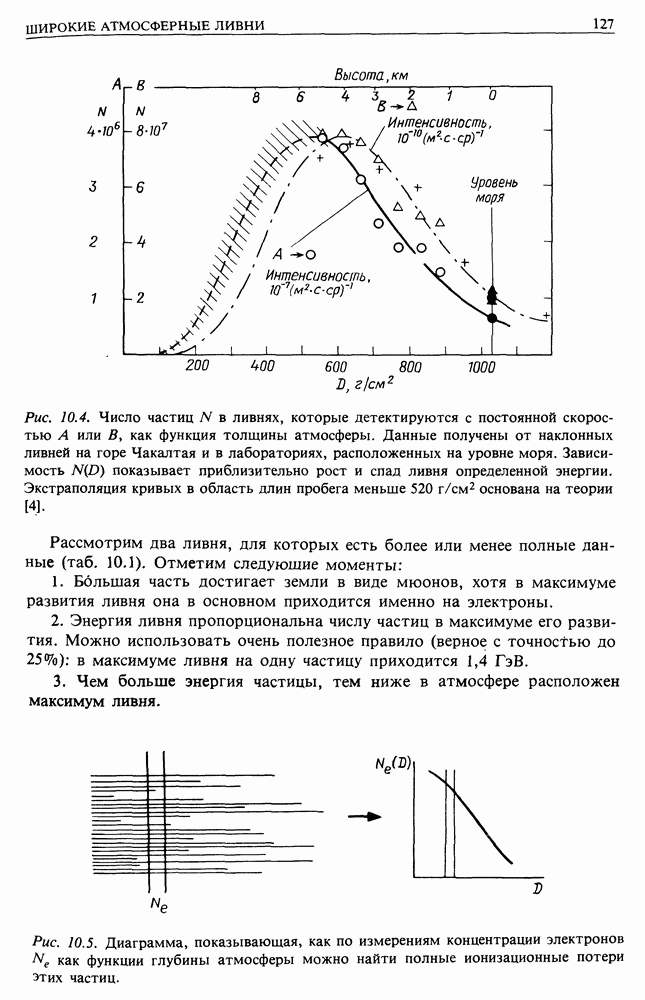
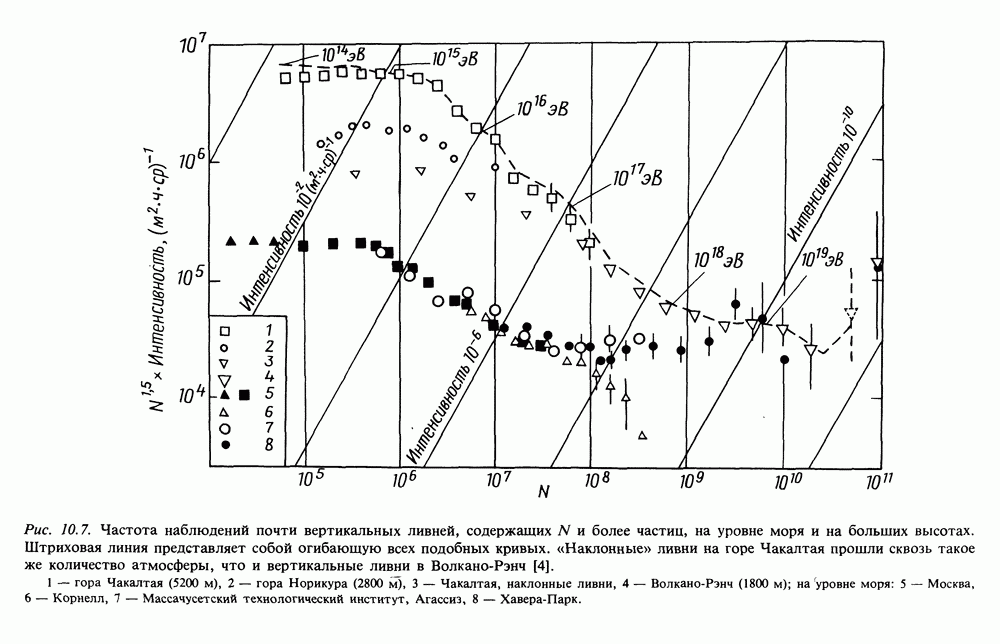
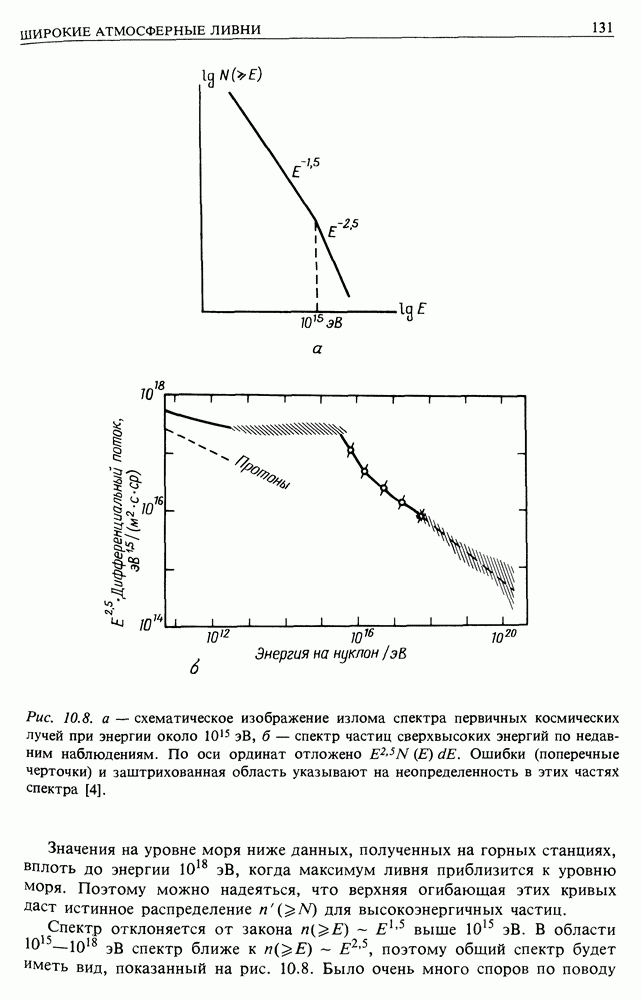
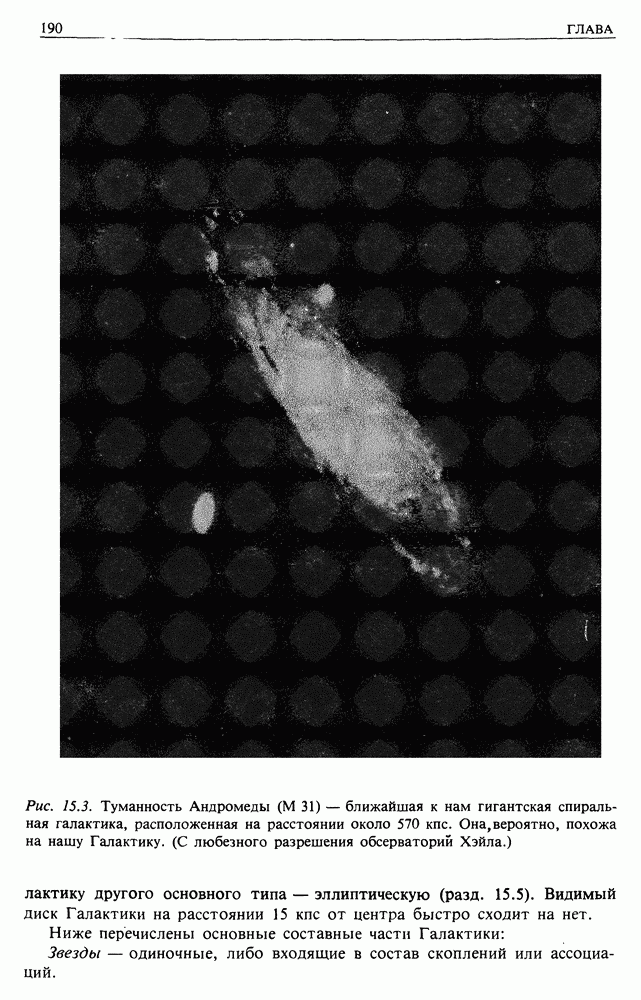
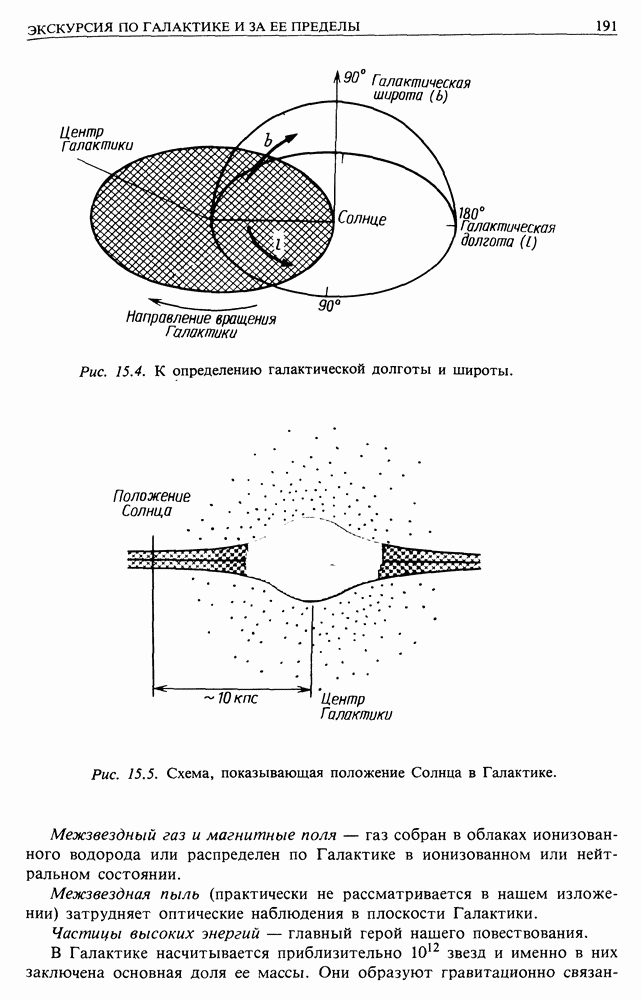
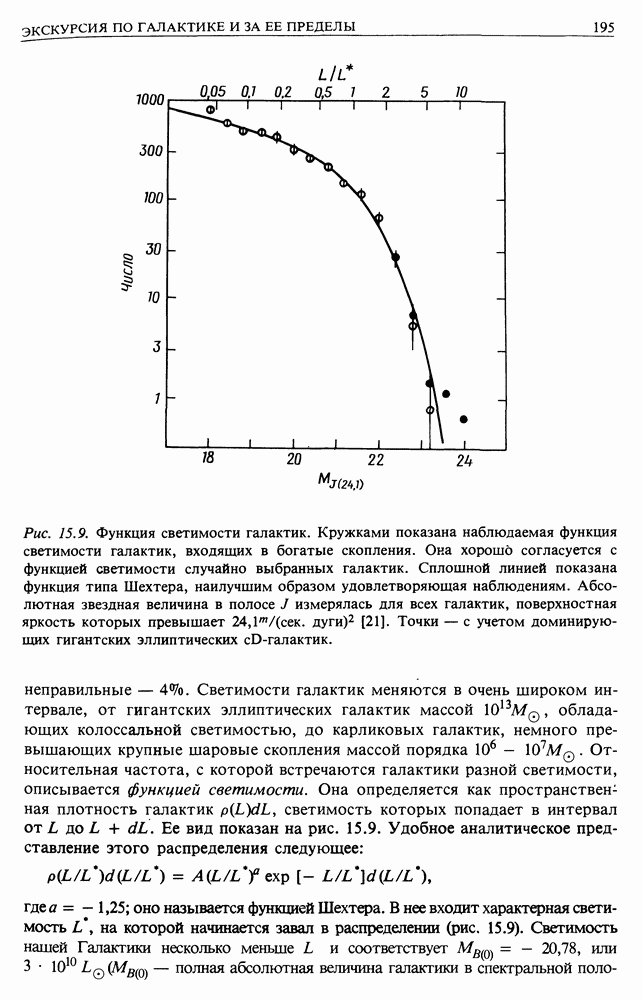
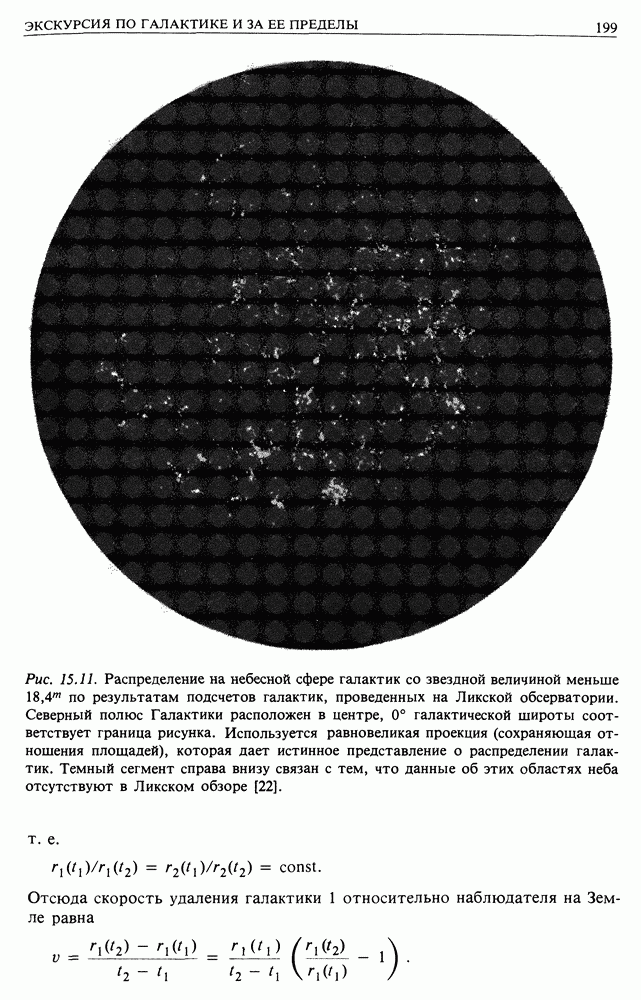
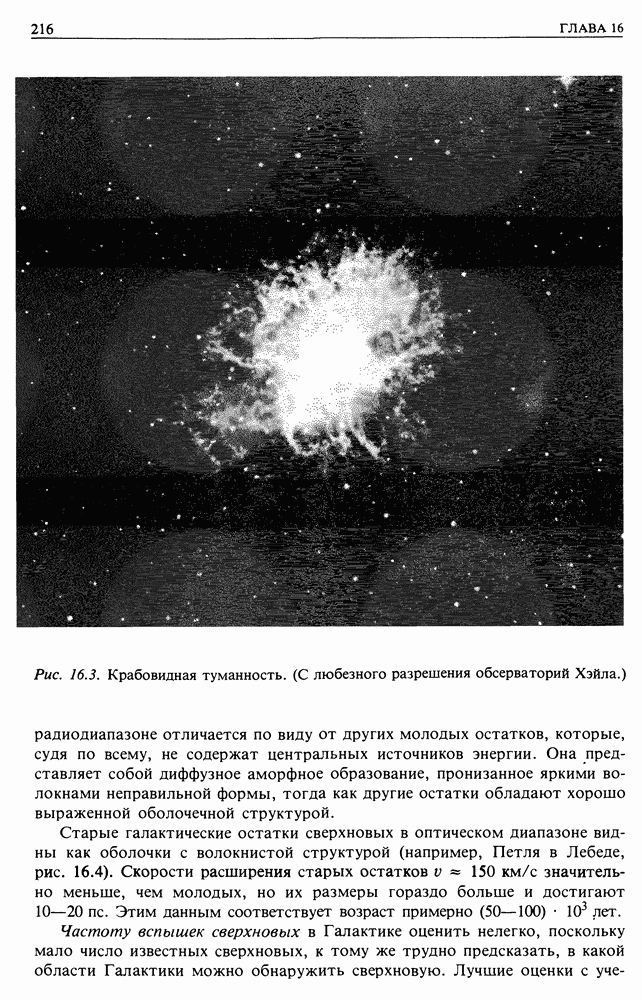
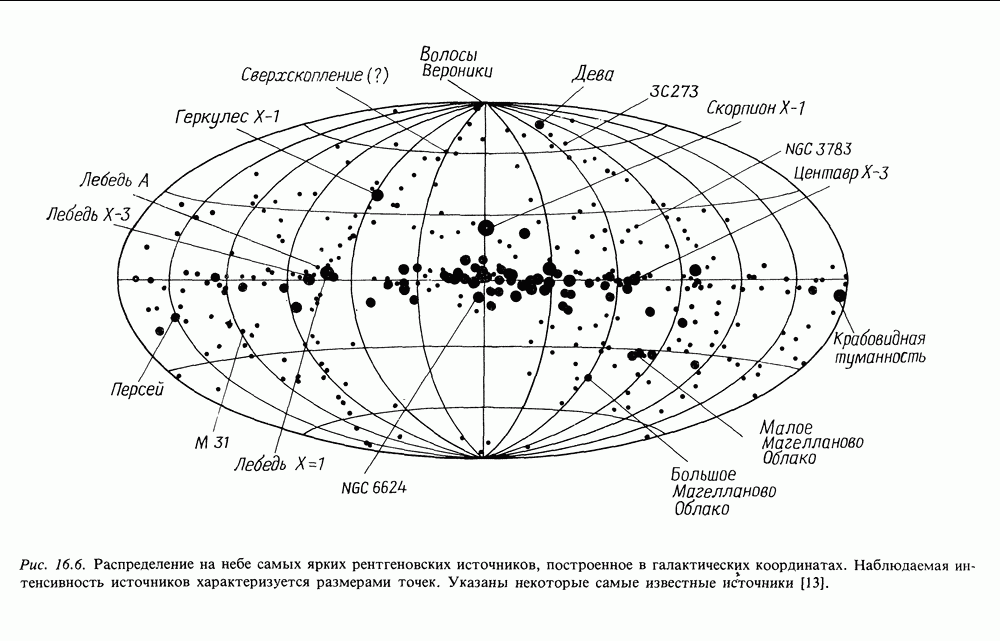
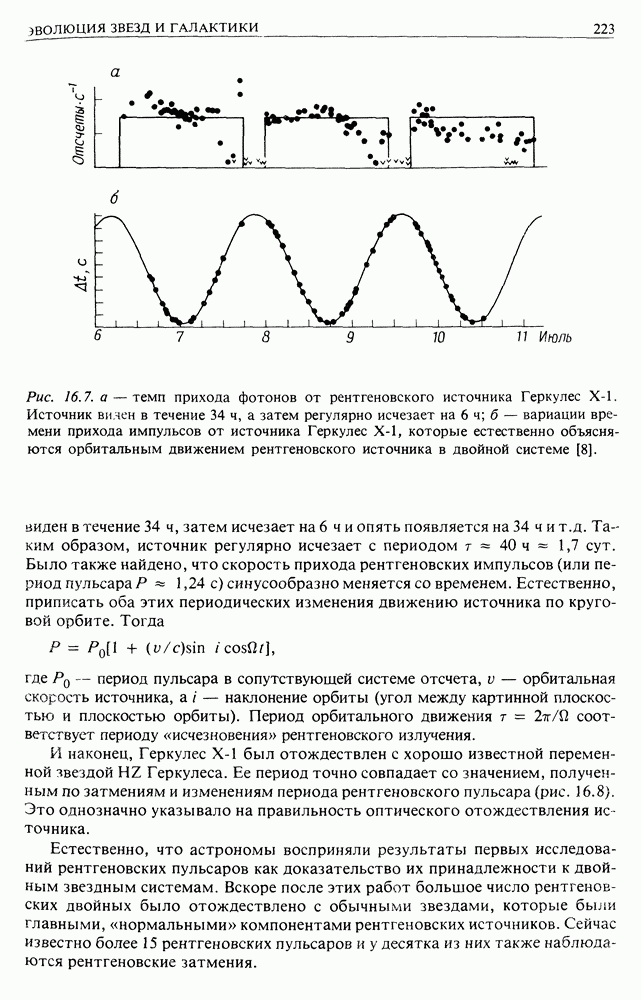
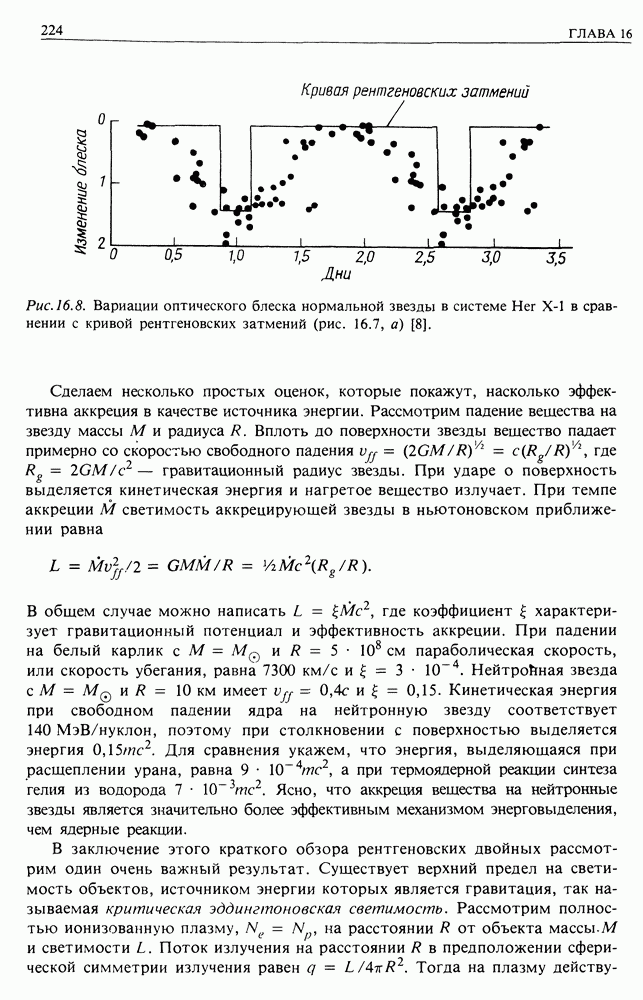
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
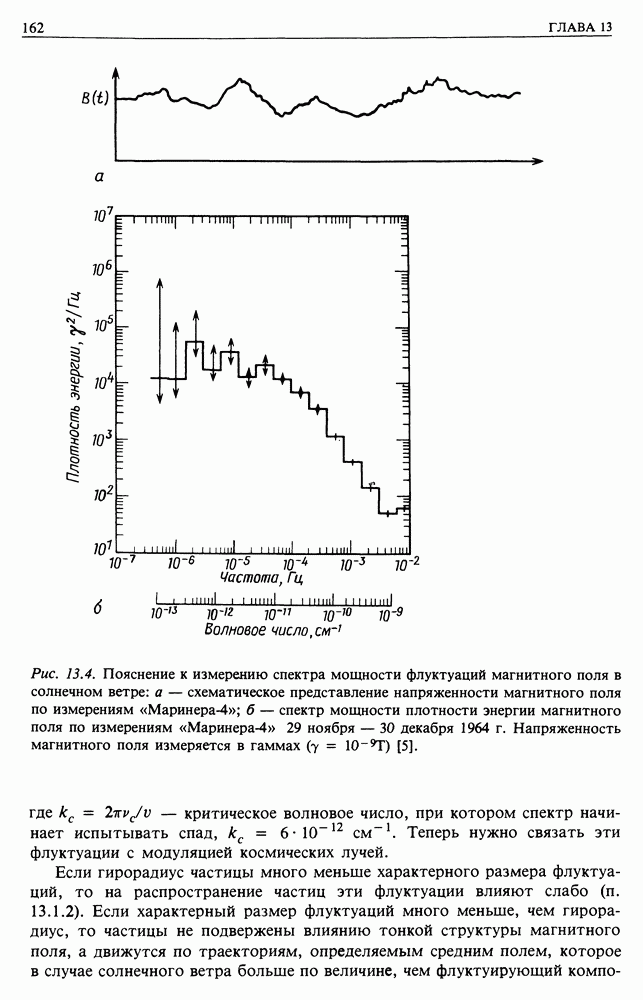
13.3.1. Спектр мощности магнитных неоднородностей. Неоднородности межпланетного магнитного поля могут непосредственно изучаться при помощи магнитометров, установленных на борту зондов, проникающих глубоко в космическое пространство. Рассмотрим результаты такого эксперимента, проведенного на борту космического зонда «Маринер-4», запущенного к Марсу. Напряженность магнитного поля измерялась непрерывно на протяжении всего полета.
Чтобы преобразовать информацию в спектр флуктуаций, используем тот же метод, что и выше (п. 3.3.2) при выводе соотношения между мгновенной интенсивностью и ее фурье-спектром, т.е. когда мы получали спектр мощности для различных фурье-компонентов, представляющих распределение интенсивности магнитного поля,

где  фурье-образ наблюдаемого распределения
фурье-образ наблюдаемого распределения  Это другое приложение теоремы Парсеваля. Этот метод показан на рис. 13.4, на котором изображен энергетический спектр неоднородностей, вызванных непрерывным истечением вещества из Солнца. Частоты относятся к системе отсчета, связанной с Солнцем, и поэтому соответствующий масштаб равен
Это другое приложение теоремы Парсеваля. Этот метод показан на рис. 13.4, на котором изображен энергетический спектр неоднородностей, вызванных непрерывным истечением вещества из Солнца. Частоты относятся к системе отсчета, связанной с Солнцем, и поэтому соответствующий масштаб равен  Спектры можно представить следующим образом:
Спектры можно представить следующим образом:

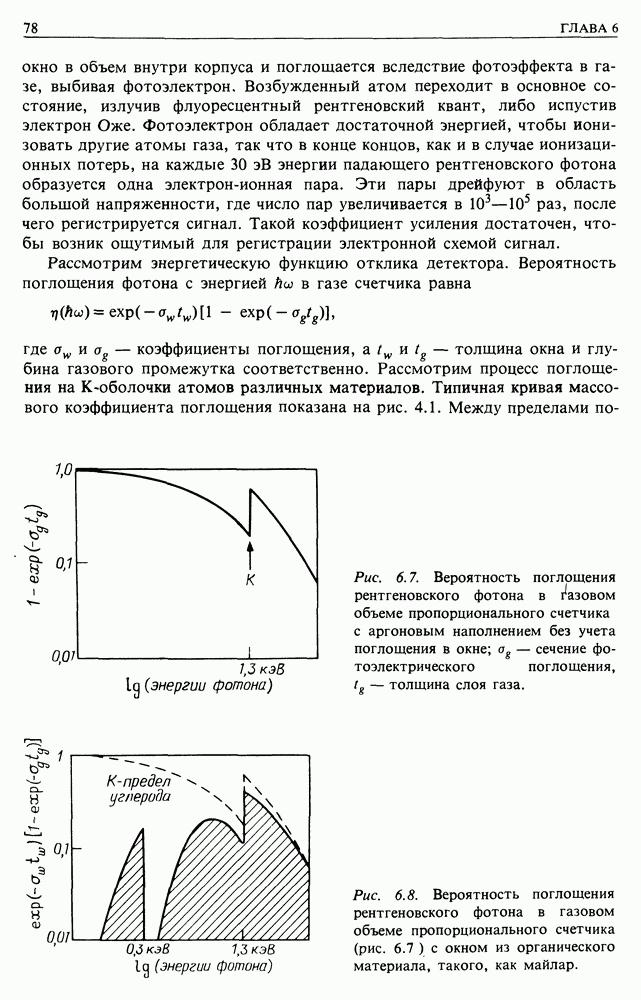
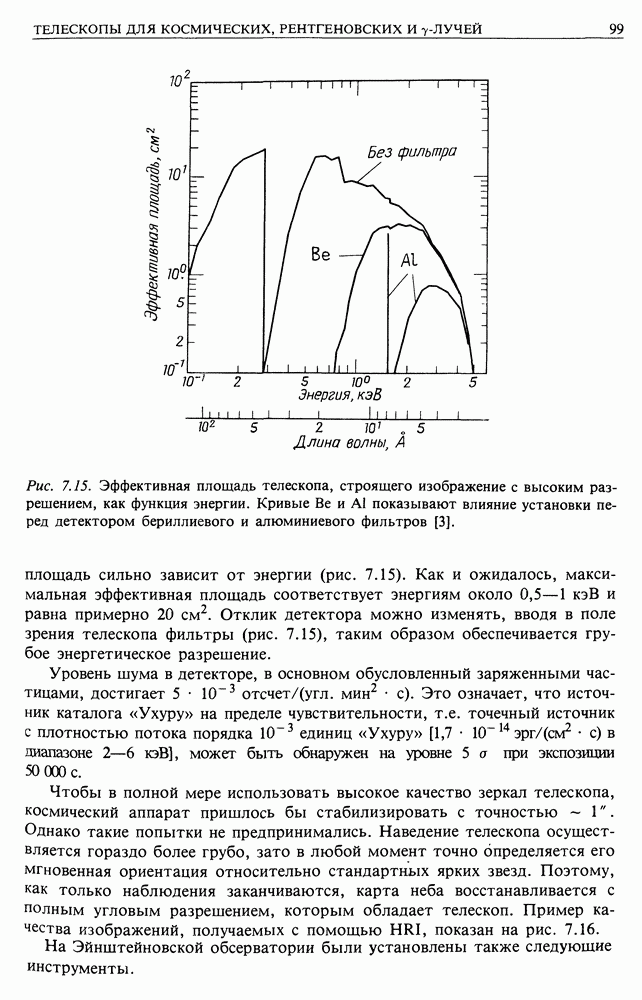
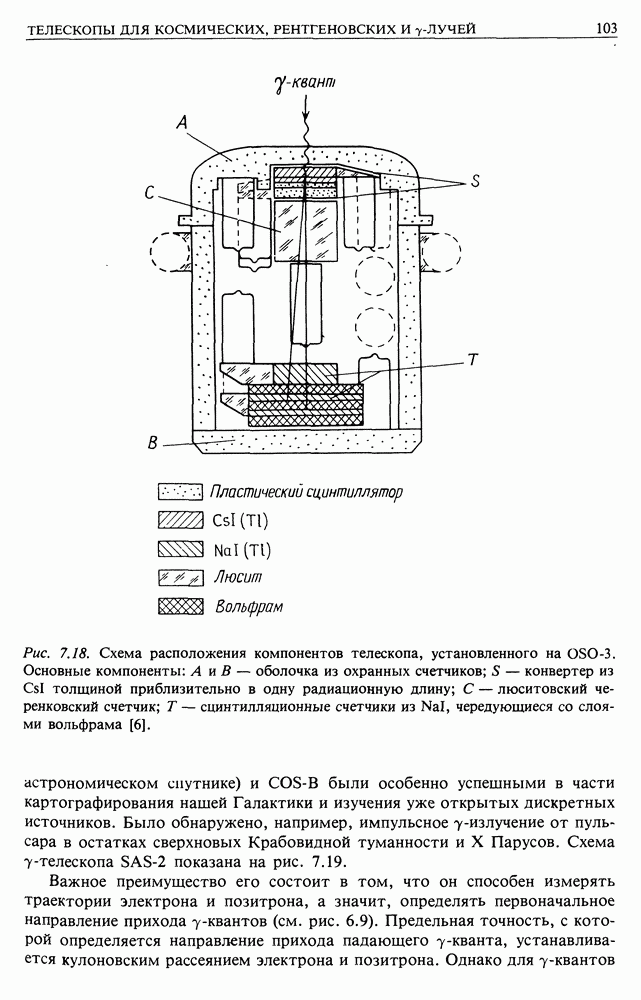
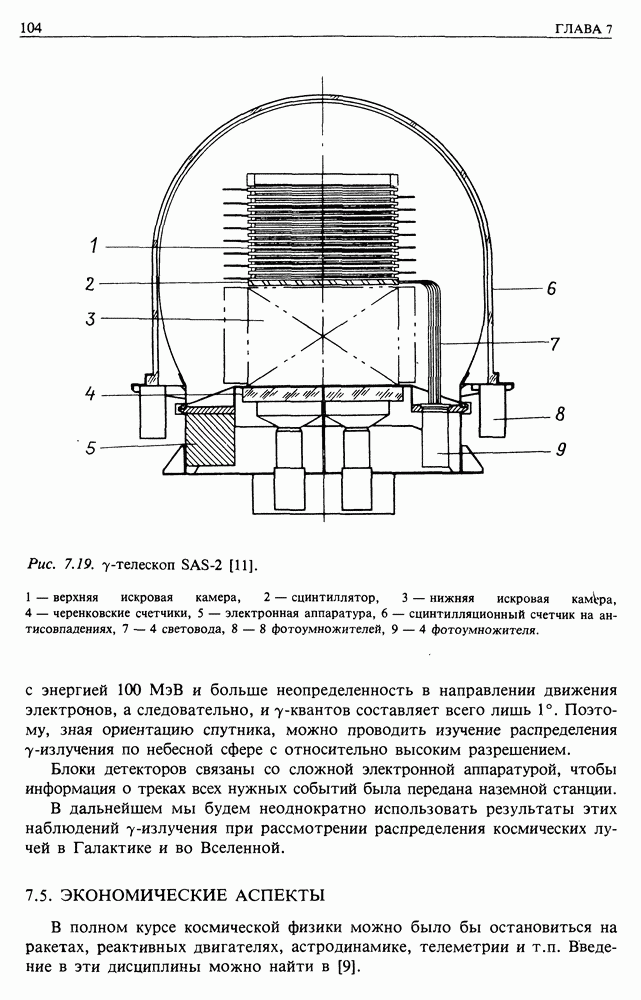
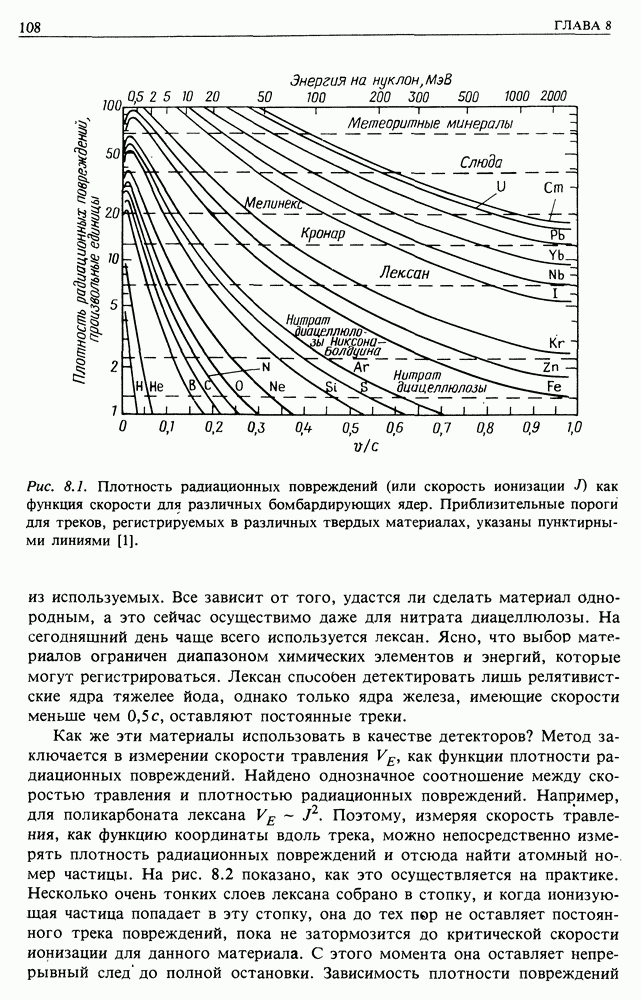
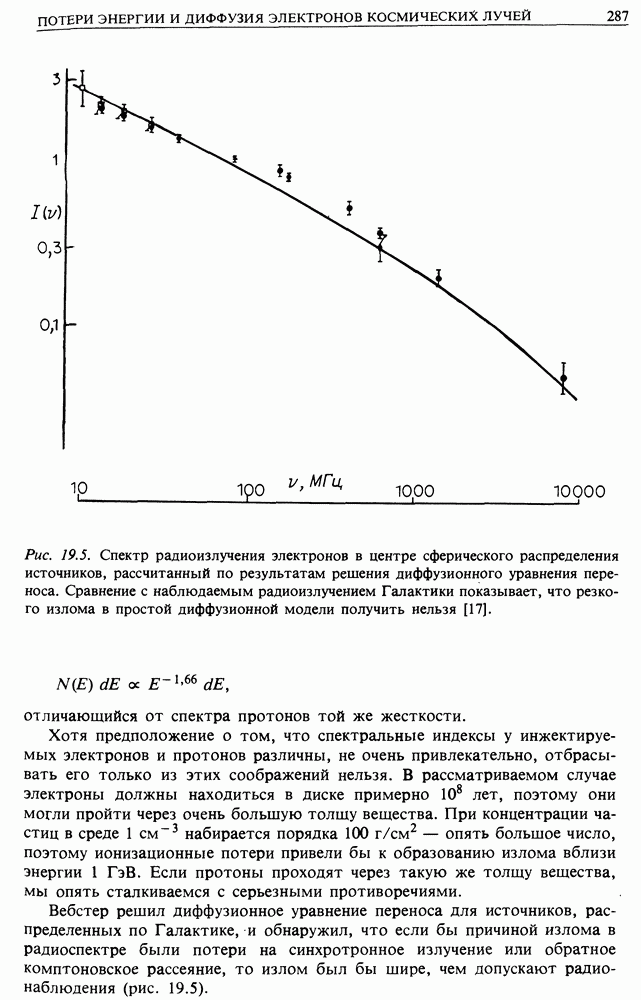
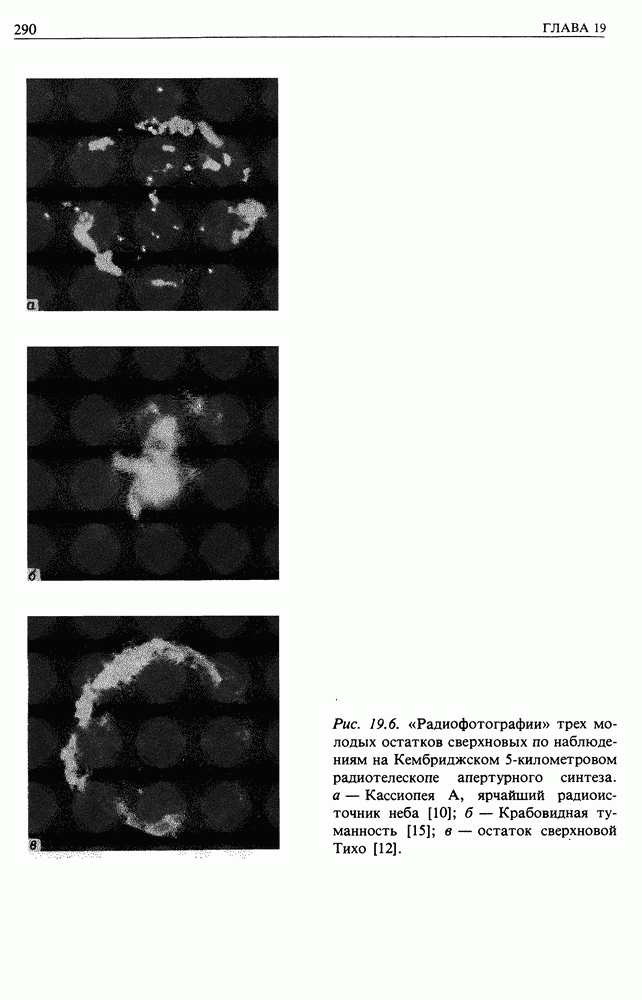
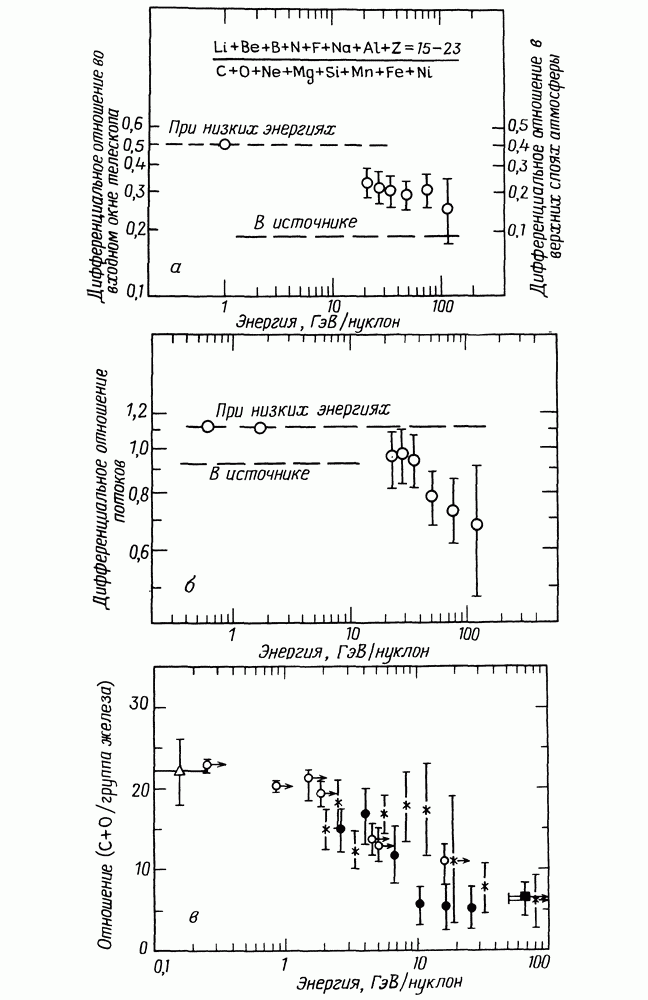
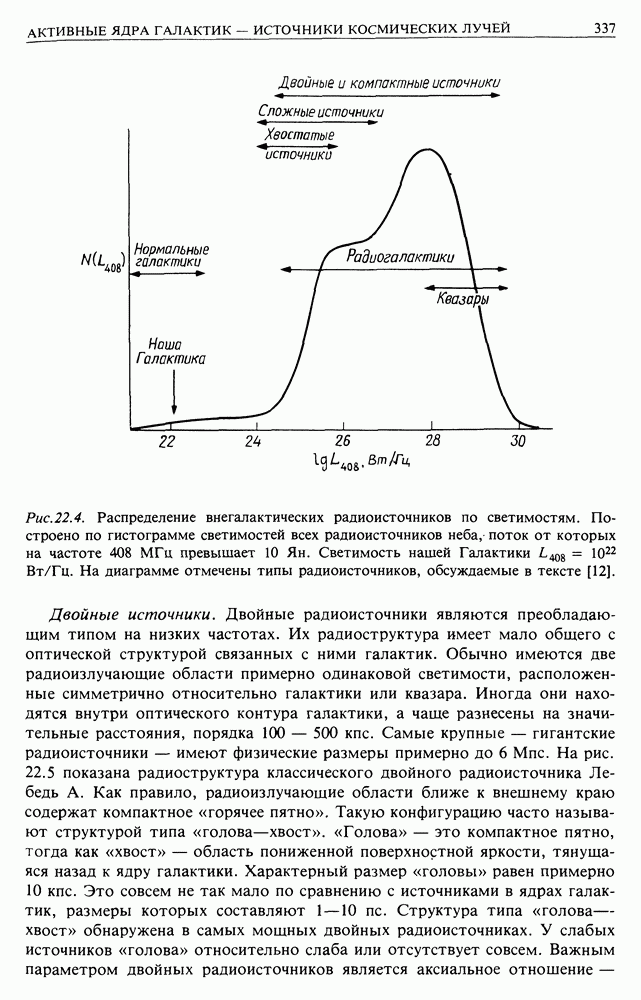
Рис. 13.4. (см. скан) Пояснение к измерению спектра мощности флуктуаций магнитного поля в солнечном ветре: а — схематическое представление напряженности магнитного поля по измерениям «Маринера-4»; б - спектр мощности плотности энергии магнитного поля по измерениям «Маринера-4» 29 ноября — 30 декабря 1964 г. Напряженность магнитного поля измеряется в гаммах 
где  критическое волновое число, при котором спектр начинает испытывать спад,
критическое волновое число, при котором спектр начинает испытывать спад,  Теперь нужно связать эти флуктуации с модуляцией космических лучей.
Теперь нужно связать эти флуктуации с модуляцией космических лучей.
Если гирорадиус частицы много меньше характерного размера флуктуаций, то на распространение частиц эти флуктуации влияют слабо  Если характерный размер флуктуаций много меньше, чем гирорадиус, то частицы не подвержены влиянию тонкой структуры магнитного поля, а движутся по траекториям, определяемым средним полем, которое в случае солнечного ветра больше по величине, чем флуктуирующий
Если характерный размер флуктуаций много меньше, чем гирорадиус, то частицы не подвержены влиянию тонкой структуры магнитного поля, а движутся по траекториям, определяемым средним полем, которое в случае солнечного ветра больше по величине, чем флуктуирующий

Рис. 13.5. Пояснение к динамике заряженной частицы, а — характерный размер неоднородностей магнитного поля мал по сравнению с гирорадиусом орбиты частицы; б - эти величины примерно одного порядка.
компонент. Только в случае, когда характерный размер флуктуаций равен гирорадиусу частиц, имеет место сильное взаимодействие (рис. 13.5).
Эти выводы были подтверждены более детальными и сложными вычислениями, поэтому можно связать энергию или жесткость частицы с любым из масштабов, присутствующих в спектре мощности на рис. 13.4. Можно ожидать наличие завала в спектре модуляции космических лучей [уравнение (13.15)], соответствующего излому в энергетическом спектре флуктуаций магнитного поля. Введем эту величину

где  гирорадиус
гирорадиус  частицы в магнитном поле с плотностью потока
частицы в магнитном поле с плотностью потока  ее жесткость. В системе СИ R измеряется в вольтах. Таким образом, беря
ее жесткость. В системе СИ R измеряется в вольтах. Таким образом, беря  находим
находим  т.е. для протонов с энергией
т.е. для протонов с энергией  или ядер с энергией
или ядер с энергией  Таким образом, по порядку величины можно связать вместе эти проявления параметров модуляции.
Таким образом, по порядку величины можно связать вместе эти проявления параметров модуляции.
Итак, можно ли получить коэффициенты диффузии? Можно, но это очень трудоемкая работа [4]. Можно также использовать следующие аргументы, которые продемонстрируют существо вопроса.
13.3.2. Вывод коэффициентов диффузии. Сущность вывода заключается в том, что магнитное поле, к которому применяется фурье-анализ, есть случайное поле. По напряженности магнитного поля можно судить об энергии, заключенной в этом фурье-компоненте, но в действительности
волны в космическом пространстве частично перекрываются случайным образом. Частица никогда не испытывает влияния отдельной волны на расстояниях, много больших длины волны, пока не встретит другую волну с другими фазой, направлением распространения и т.д. Поэтому наша модель процесса взаимодействия такова, что частица остается только в одиночной волне порядка длины волны, а затем все неоднократно повторяется.
На одной длине волны среднее наклонение магнитного поля равно

где  напряженность усредненного магнитного поля, а
напряженность усредненного магнитного поля, а  амплитуда случайного компонента. Поэтому питч-угол частицы с гирорадиусом
амплитуда случайного компонента. Поэтому питч-угол частицы с гирорадиусом  должен изменяться примерно на эту же величину на одной длине волны. Можно рассмотреть этот процесс с точки зрения изменения ведущего центра частицы на расстоянии длины волны. Ведущий центр смещается на угол
должен изменяться примерно на эту же величину на одной длине волны. Можно рассмотреть этот процесс с точки зрения изменения ведущего центра частицы на расстоянии длины волны. Ведущий центр смещается на угол  что приводит к диффузии поперек силовых линий магнитного поля, так же как и изменение питч-угла частицы. На следующей длине волны частица встретит другую волну с почти такой же плотностью энергии, но среднее изменение питч-угла будет случайным, и поэтому частицы будут рассеиваться по питч-углу случайным образом. Среднее рассеяние на длину волны есть
что приводит к диффузии поперек силовых линий магнитного поля, так же как и изменение питч-угла частицы. На следующей длине волны частица встретит другую волну с почти такой же плотностью энергии, но среднее изменение питч-угла будет случайным, и поэтому частицы будут рассеиваться по питч-углу случайным образом. Среднее рассеяние на длину волны есть  и поэтому, чтобы случайным образом получить рассеяние на один радиан, нам нужно
и поэтому, чтобы случайным образом получить рассеяние на один радиан, нам нужно  шагов, где 1 рад
шагов, где 1 рад  как при случайном блуждании. Расстояние, необходимое, чтобы произошло
как при случайном блуждании. Расстояние, необходимое, чтобы произошло  актов рассеяния, есть
актов рассеяния, есть  т.е. средняя длина свободного пробега частицы, пока она не повернет на большой угол, равна
т.е. средняя длина свободного пробега частицы, пока она не повернет на большой угол, равна  и поэтому коэффициент диффузии равен
и поэтому коэффициент диффузии равен

Представим наблюдаемый энергетический спектр неоднородностей и затем найдем теоретическую зависимость  от
от  Следует иметь в виду, что спектр мощности, получаемый из наблюдений, дает энергию на герц, а нас интересует энергия. Воспользуемся тем, что частицы могут резонировать с волнами, имеющими частоты порядка
Следует иметь в виду, что спектр мощности, получаемый из наблюдений, дает энергию на герц, а нас интересует энергия. Воспользуемся тем, что частицы могут резонировать с волнами, имеющими частоты порядка  поэтому плотность энергии магнитного поля, соответствующая данному значению
поэтому плотность энергии магнитного поля, соответствующая данному значению  есть
есть

В диапазоне низких частот 

[см. уравнение (13.17)]. В общем случае

где  Поэтому
Поэтому

Следовательно, с уменьшением частоты энергия, или жесткость частиц, с которыми волны «резонируют», т.е. рассеиваются сильно, возрастает.

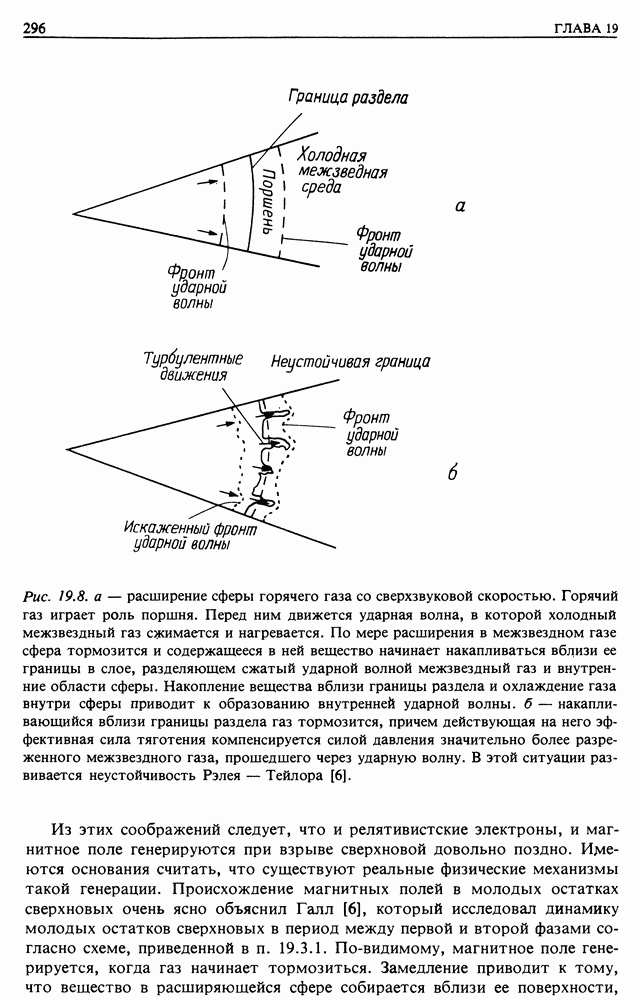
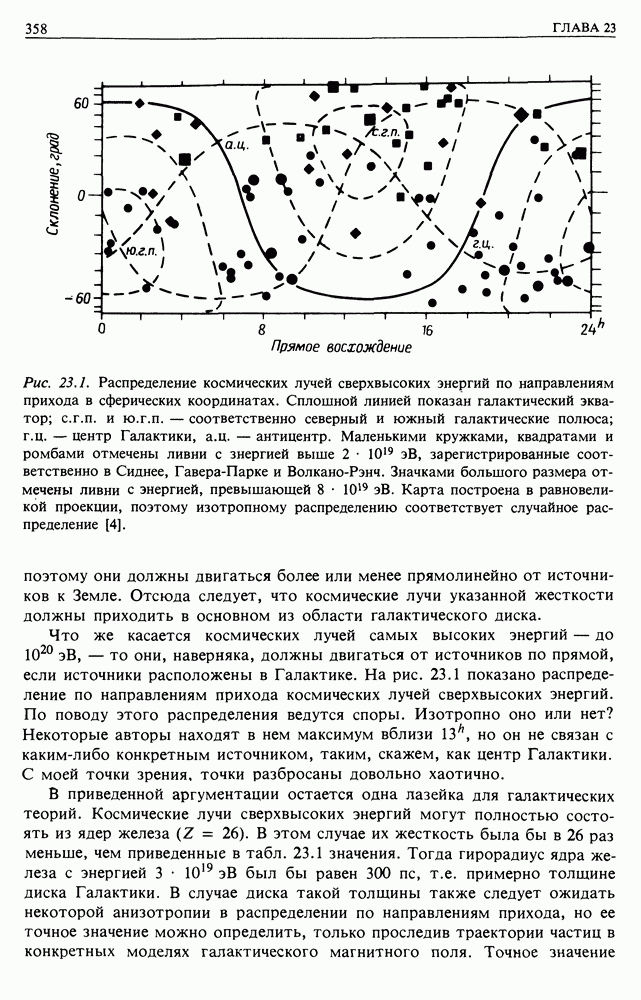
Рис. 13.6. Сравнение простой теоретической модели для коэффициентов диффузии космических лучей как функций энергии и эмпирической модели для объяснения солнечной модуляции [7].
Таким образом, для высокоэнергичных частиц с 

При высоких частотах,  тем же самым способом получаем
тем же самым способом получаем

и средняя длина свободного пробега для низкоэнергичных частиц  равна
равна

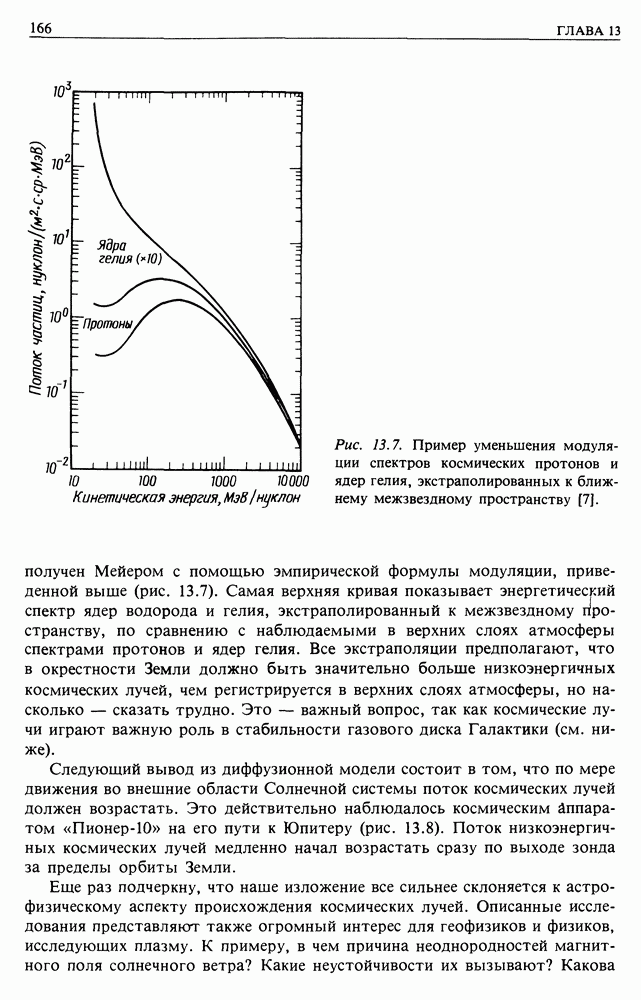
Эти результаты целиком совпадают с выводами полного спектрального анализа Джокипи [5] вплоть до численных констант. Можно сравнить эти результаты с эмпирическим анализом, описанным выше (рис. 13.6). Итак, эта модель в целом имеет верное направление, и в наблюдаемом спектре флуктуаций имеются значительные неопределенности. Надлежащий анализ должен прямо связать детали спектра со средней длиной свободного пробега.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
- 4.4. ОБРАЗОВАНИЕ ПАР
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
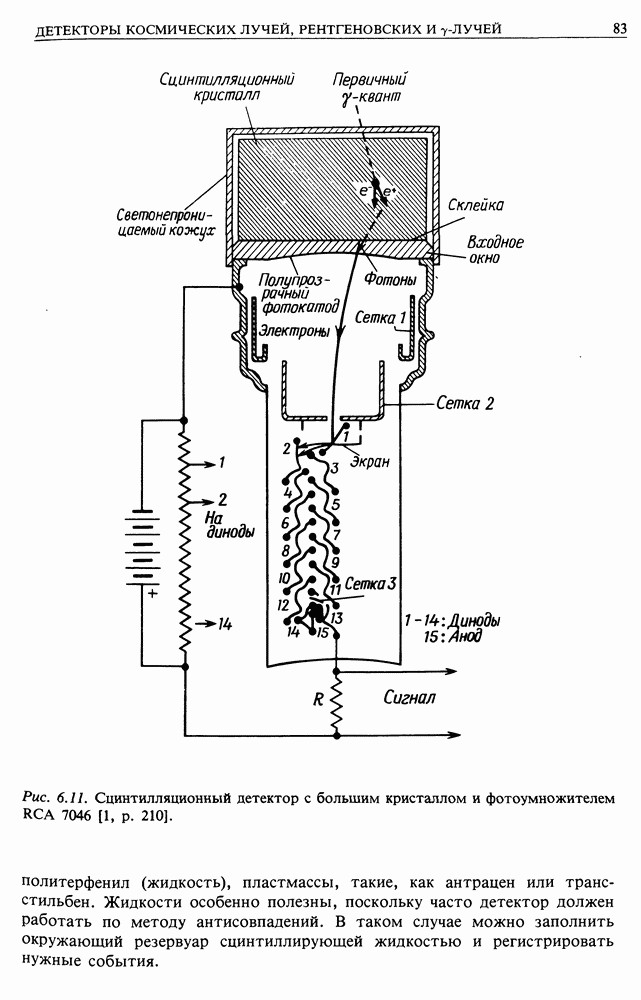
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
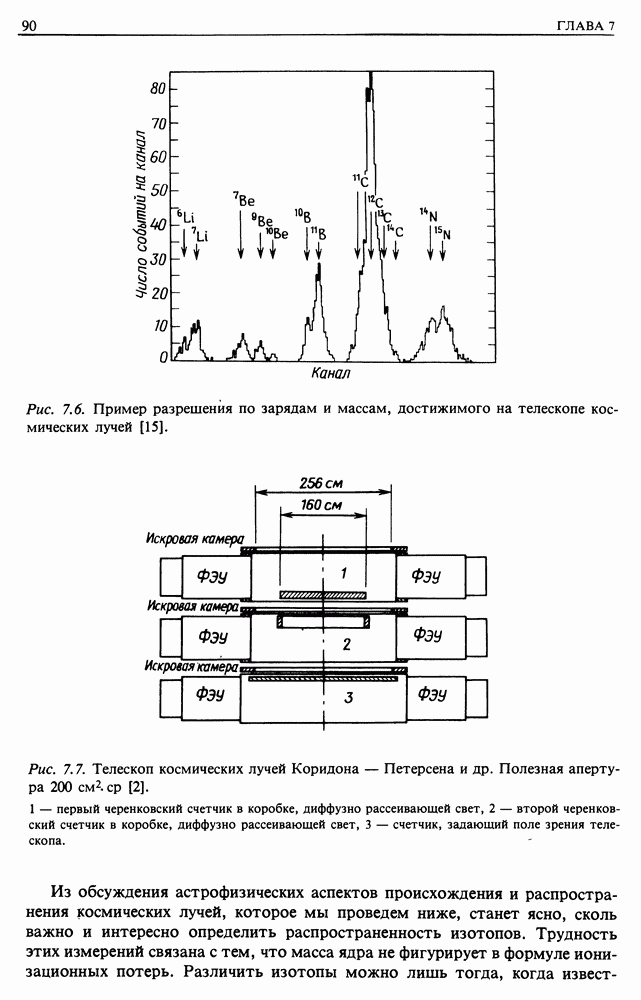
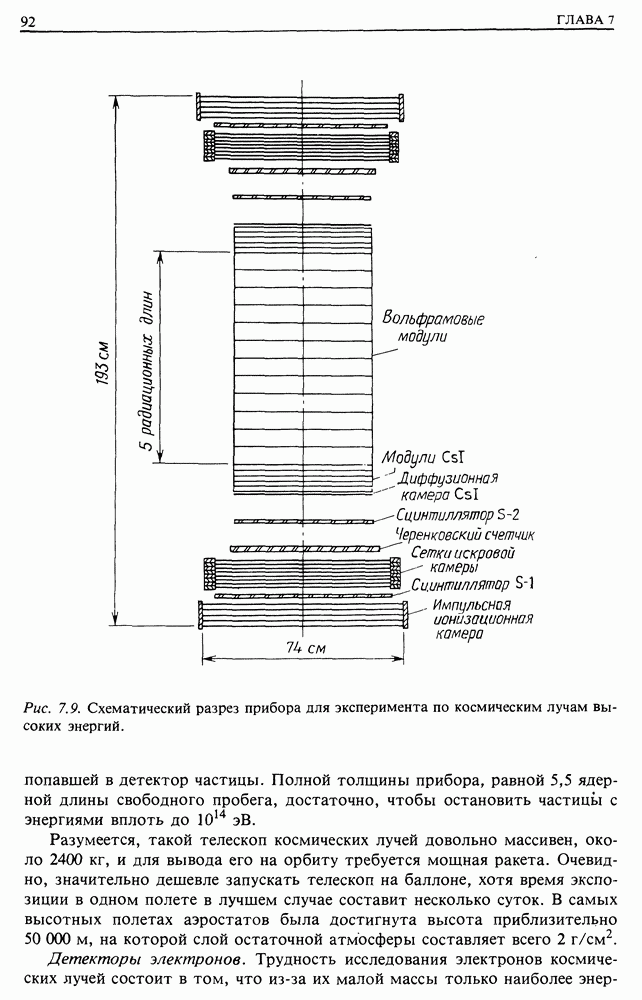
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
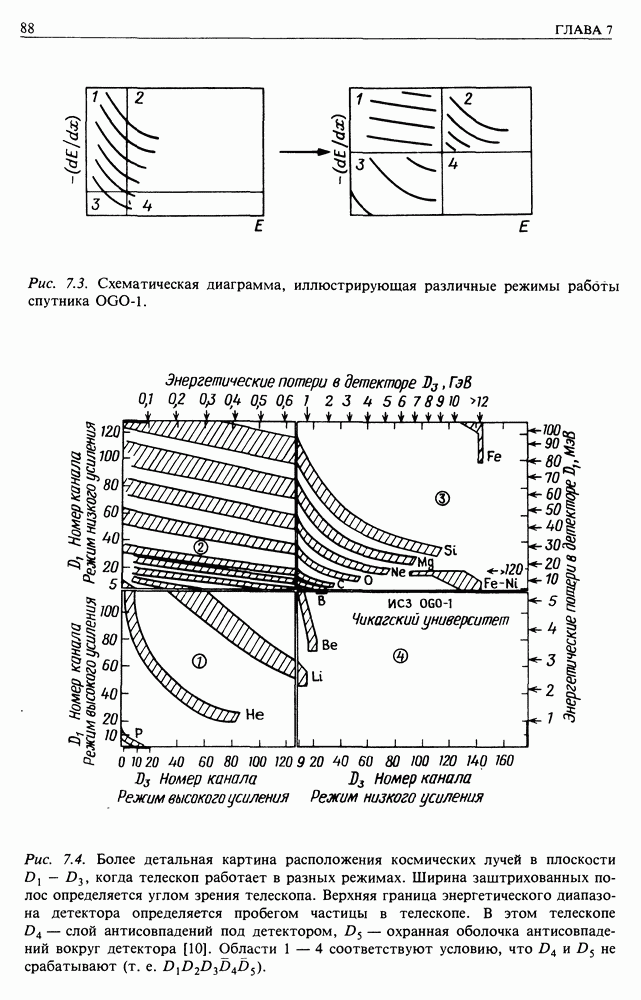
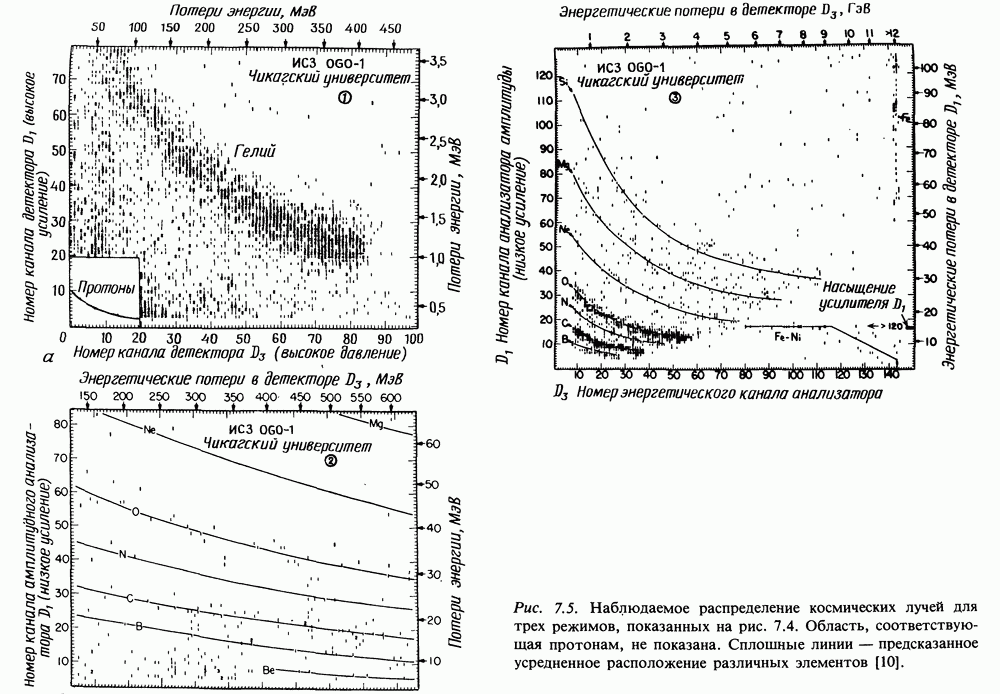
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
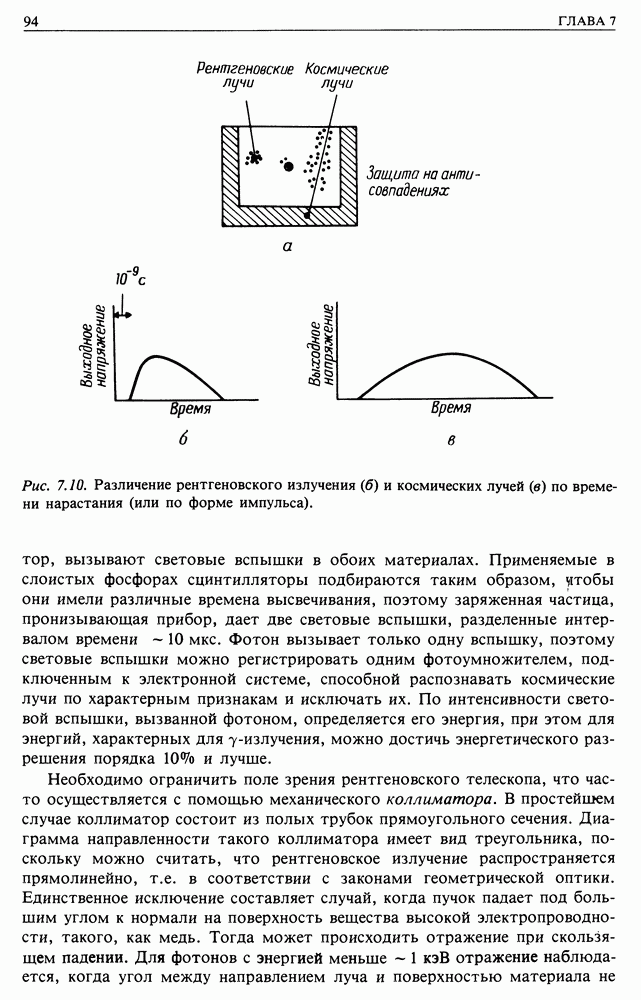
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
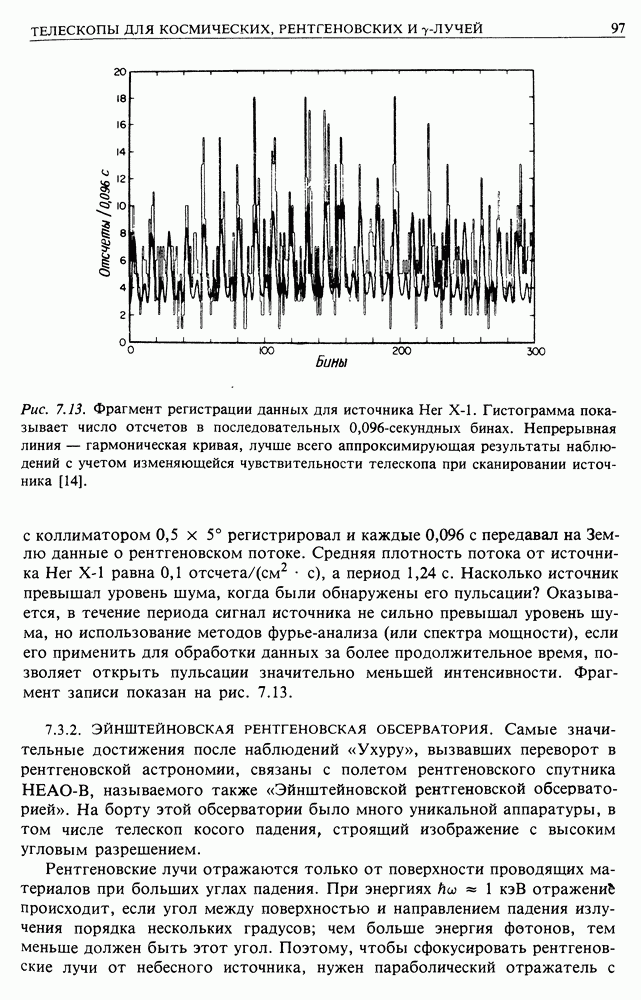
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
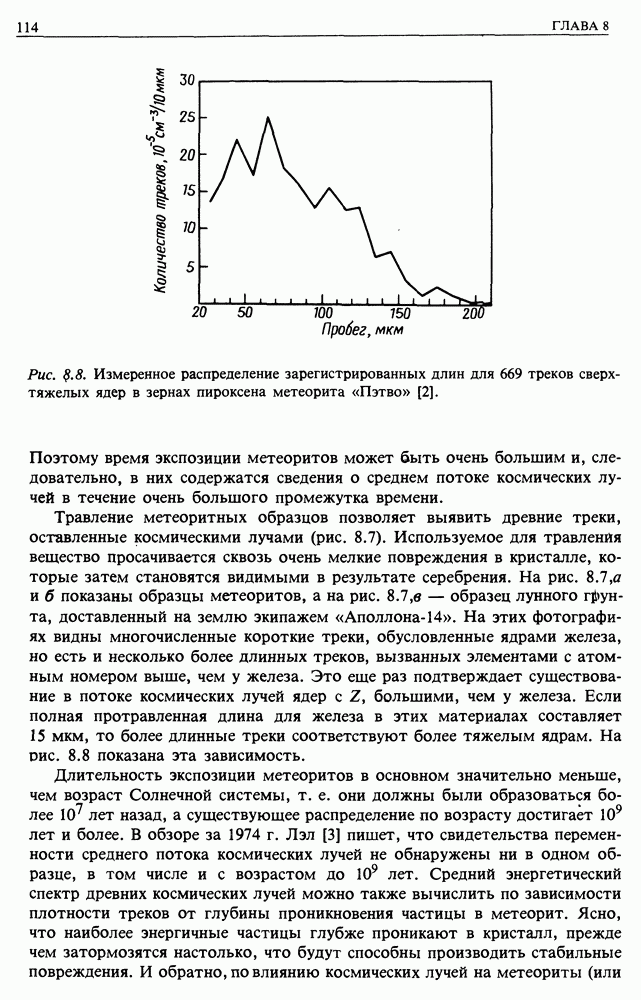
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
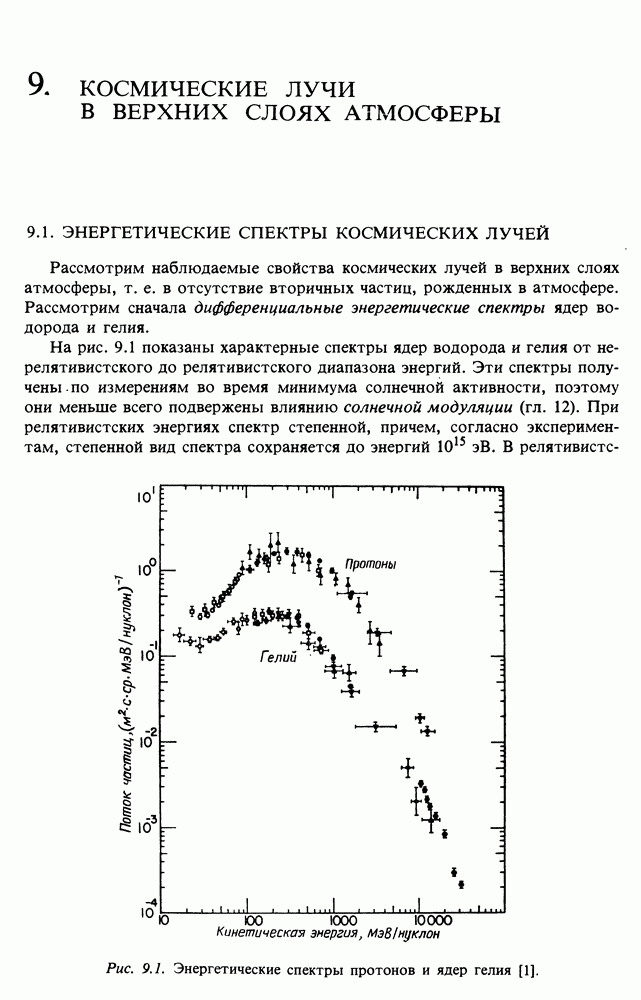
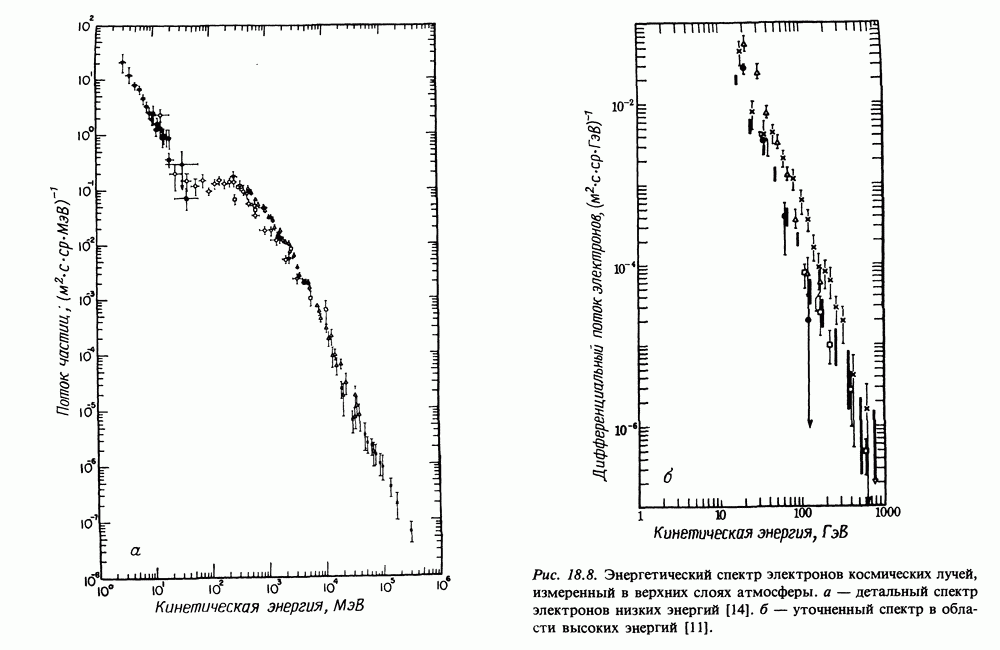
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
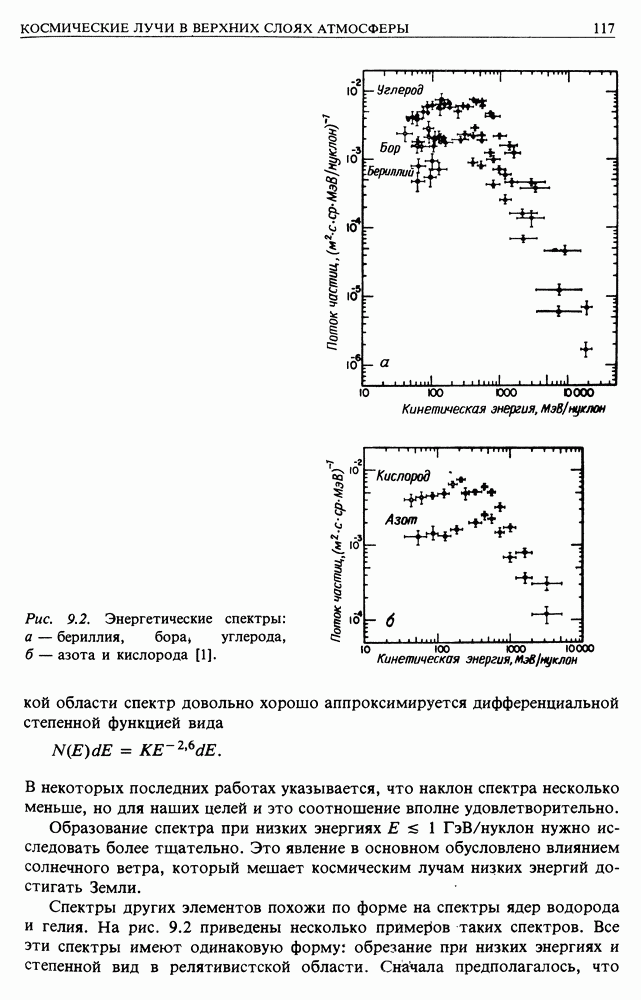
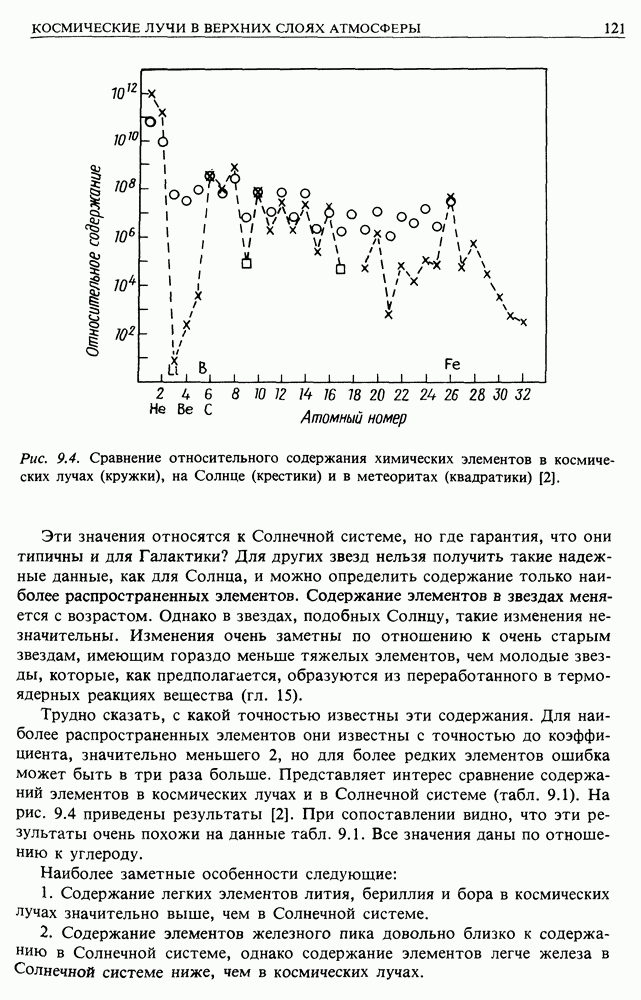
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
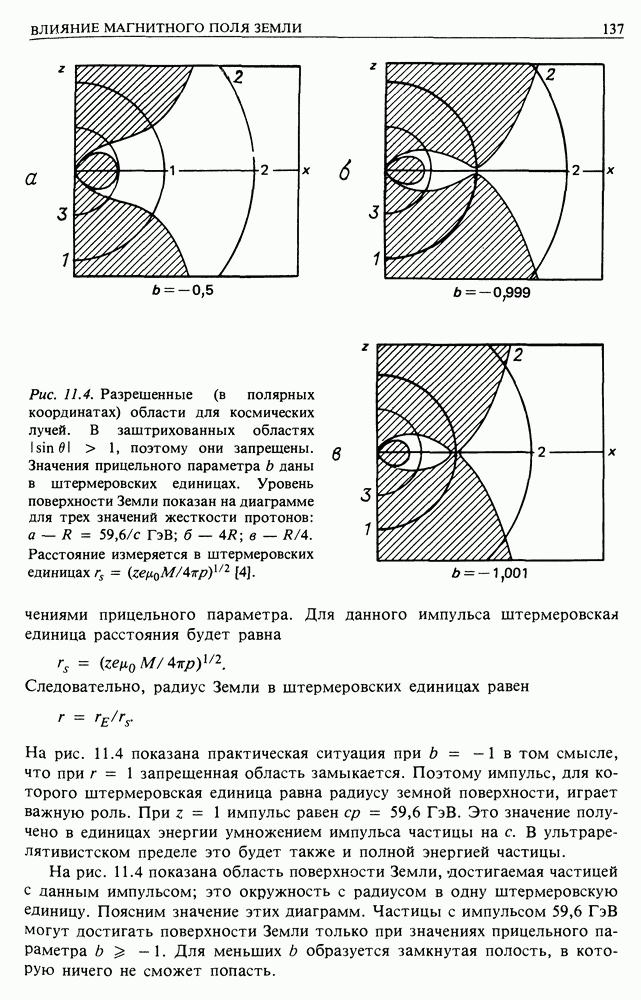
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
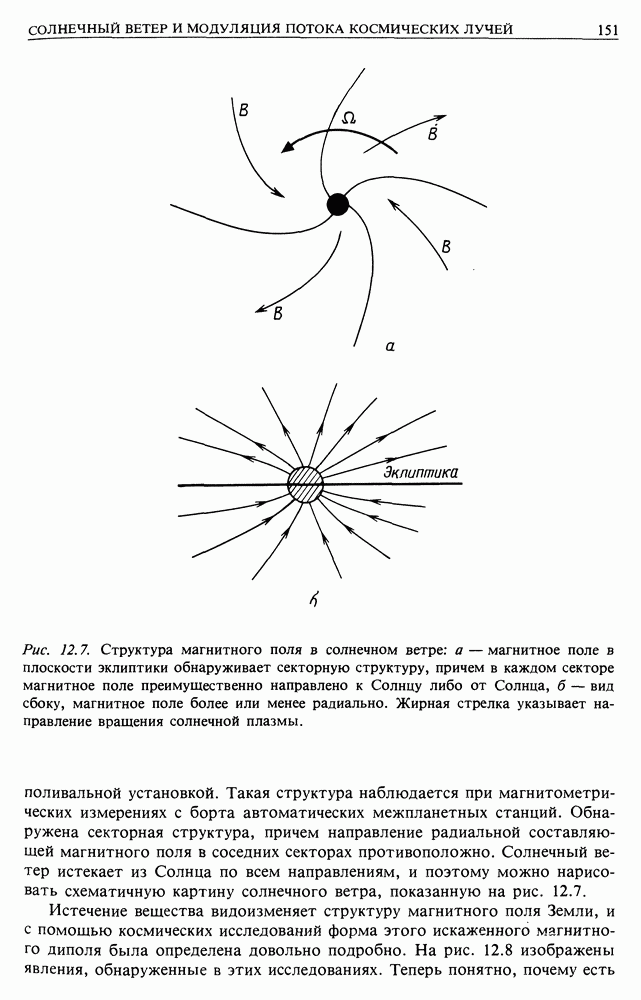
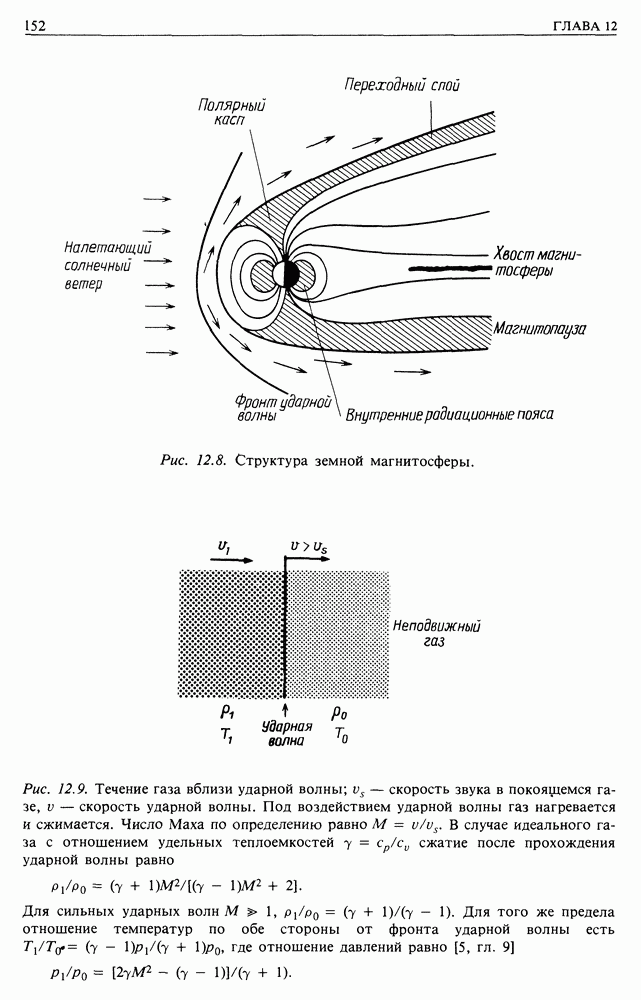
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
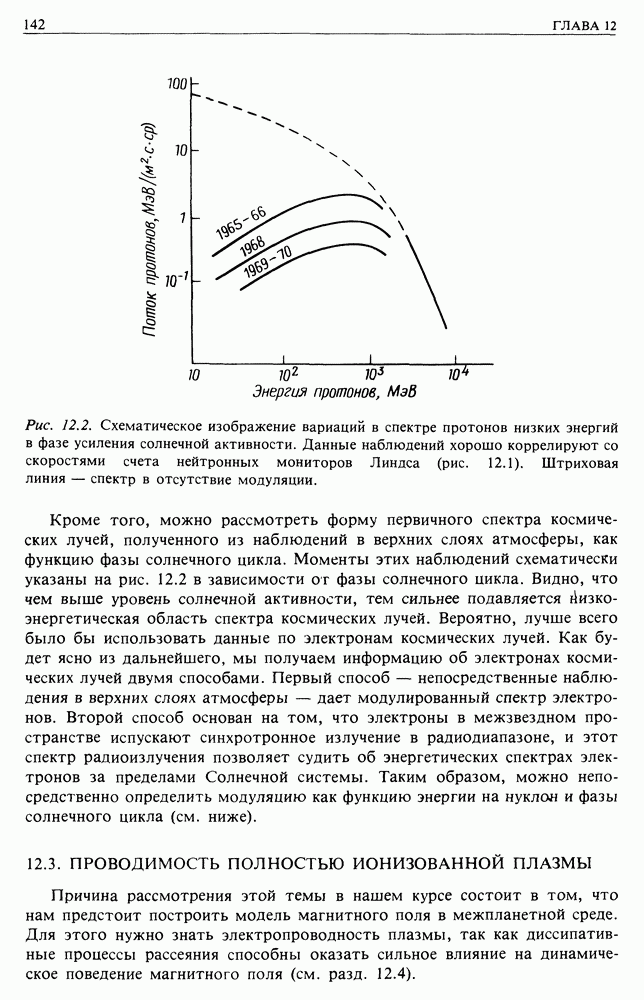
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
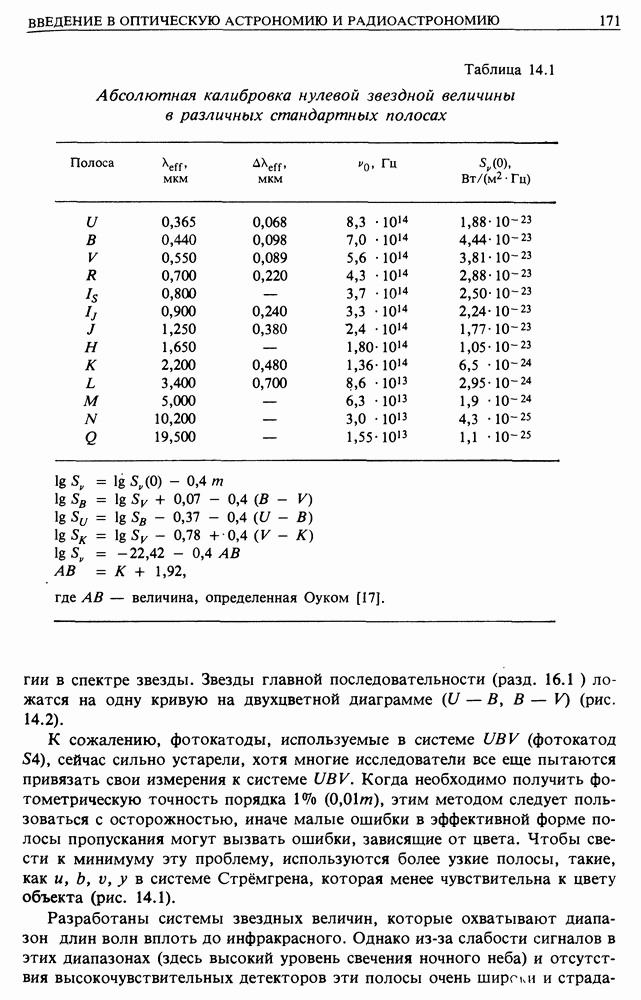
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
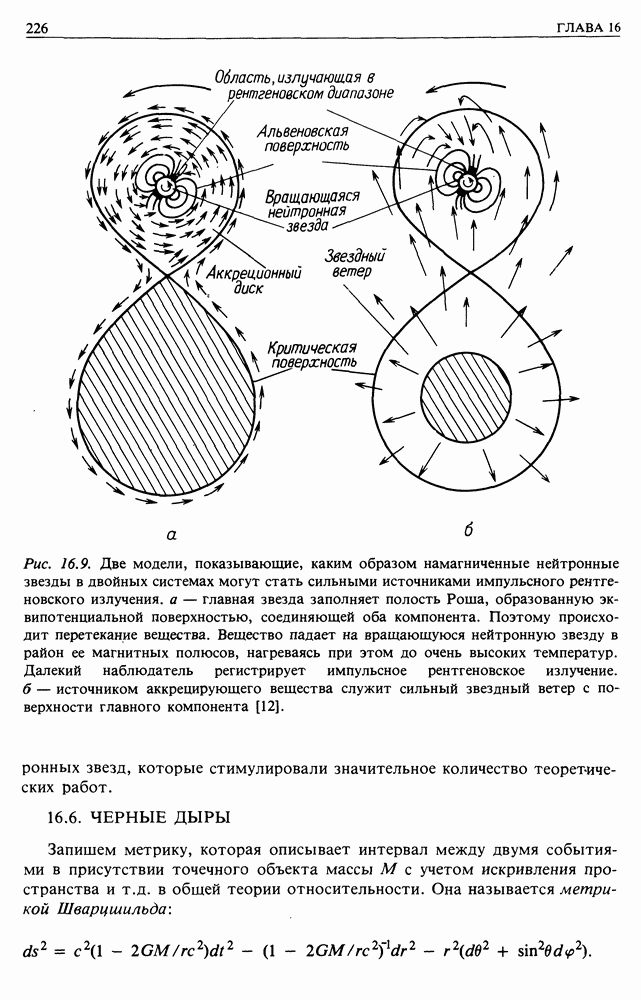
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
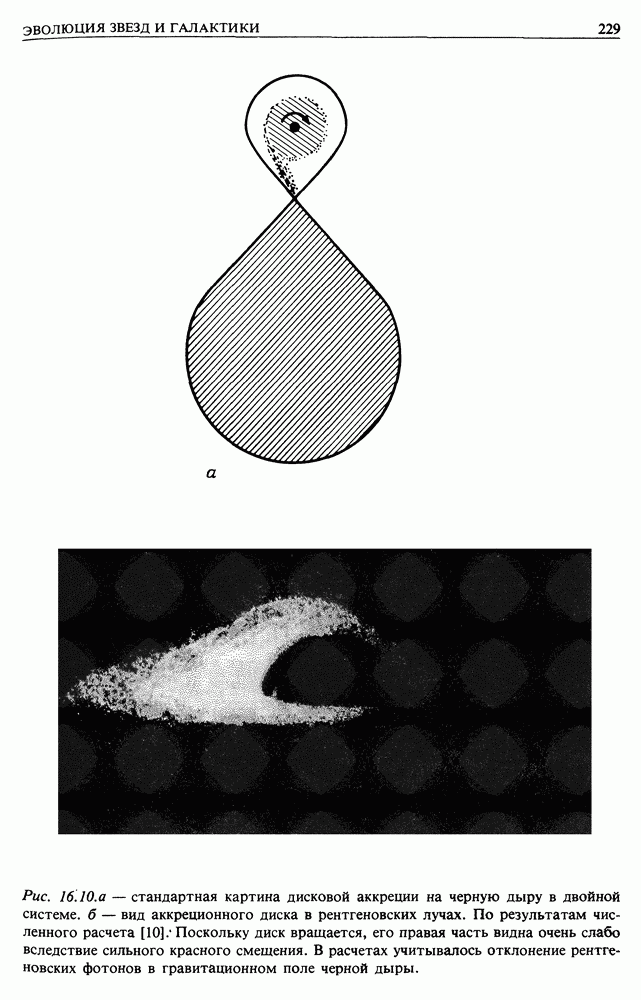
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
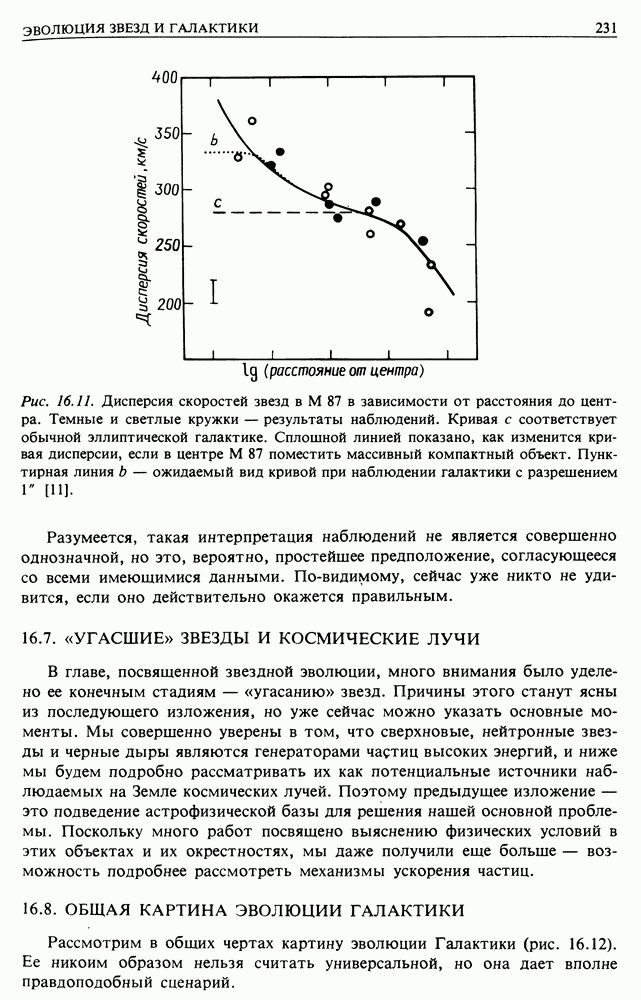
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
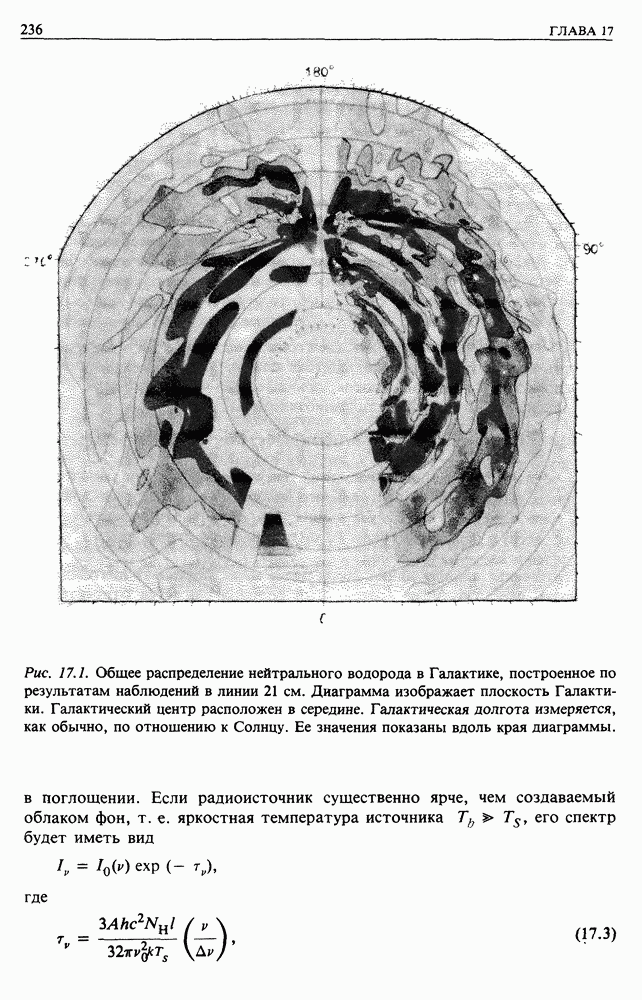
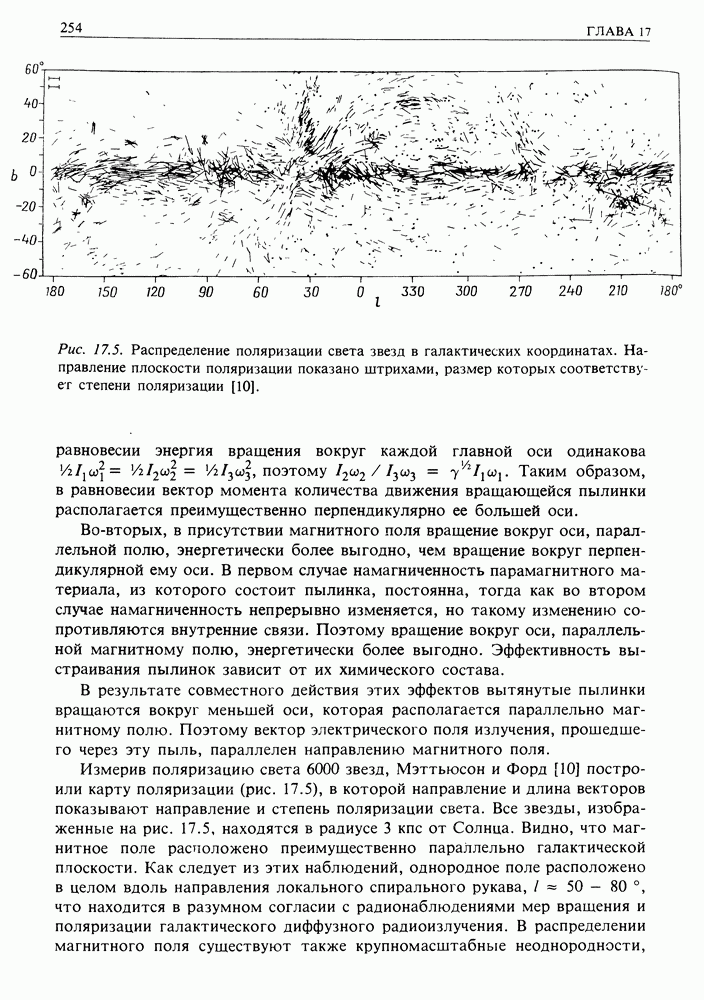
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
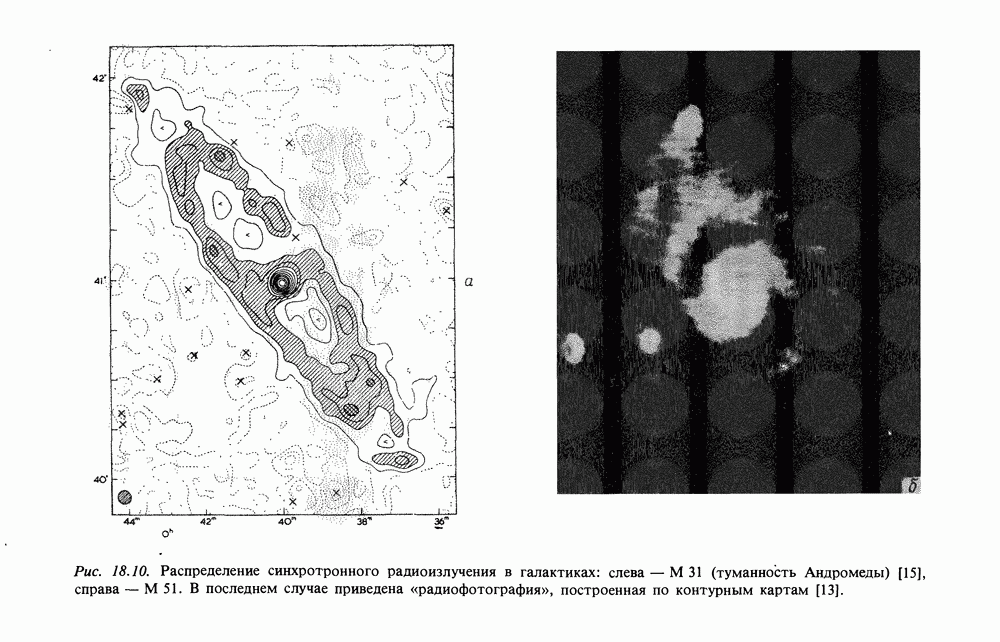
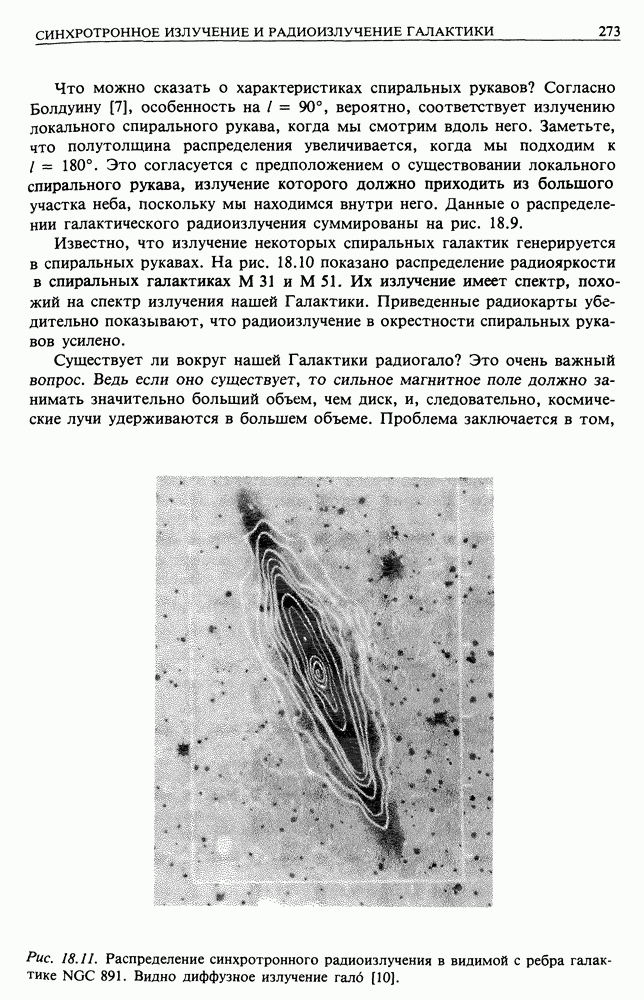
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
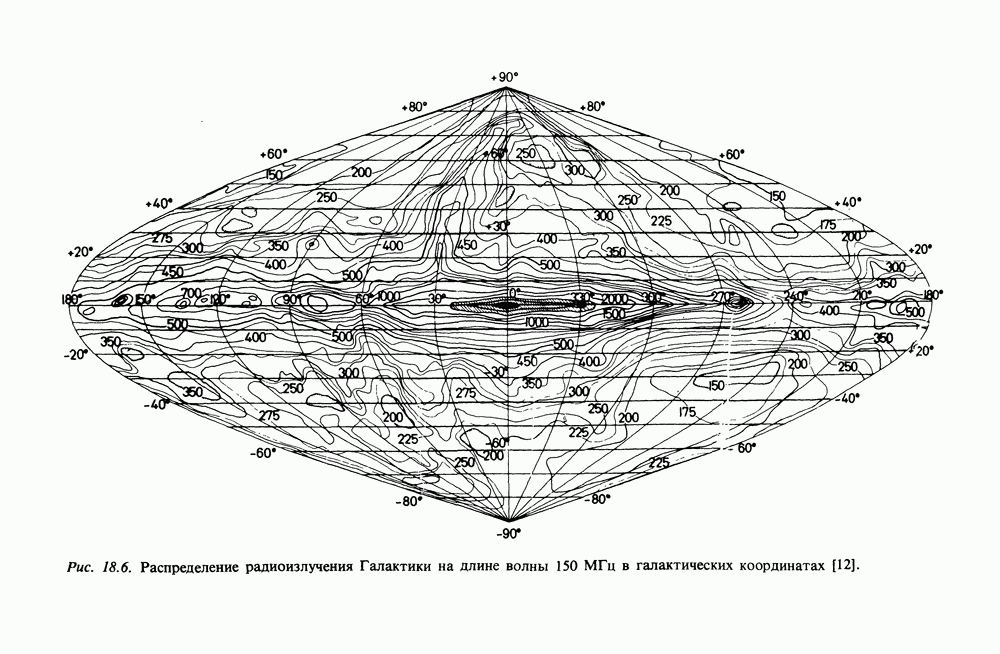
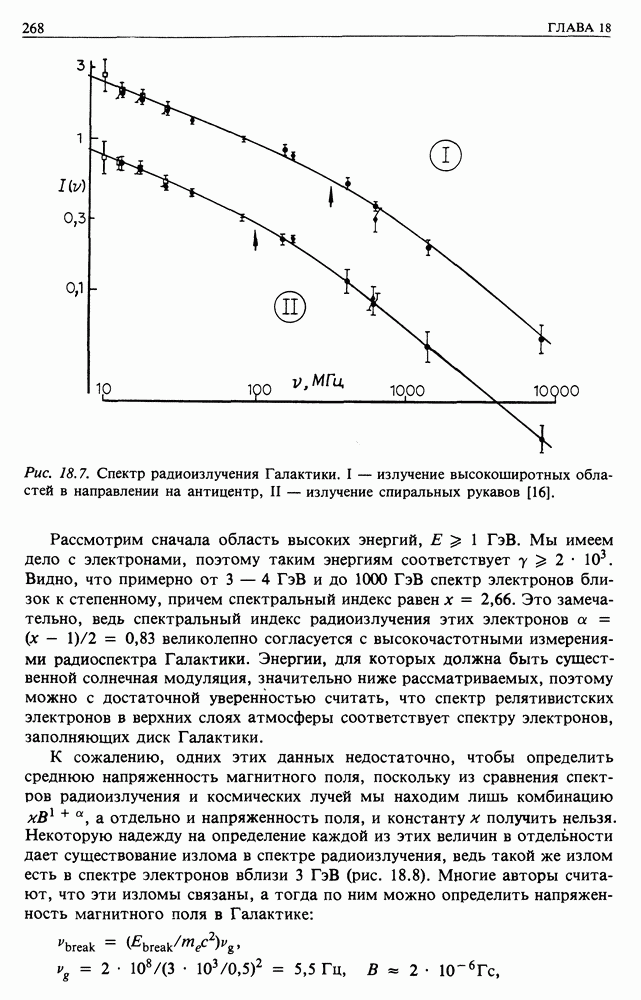
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
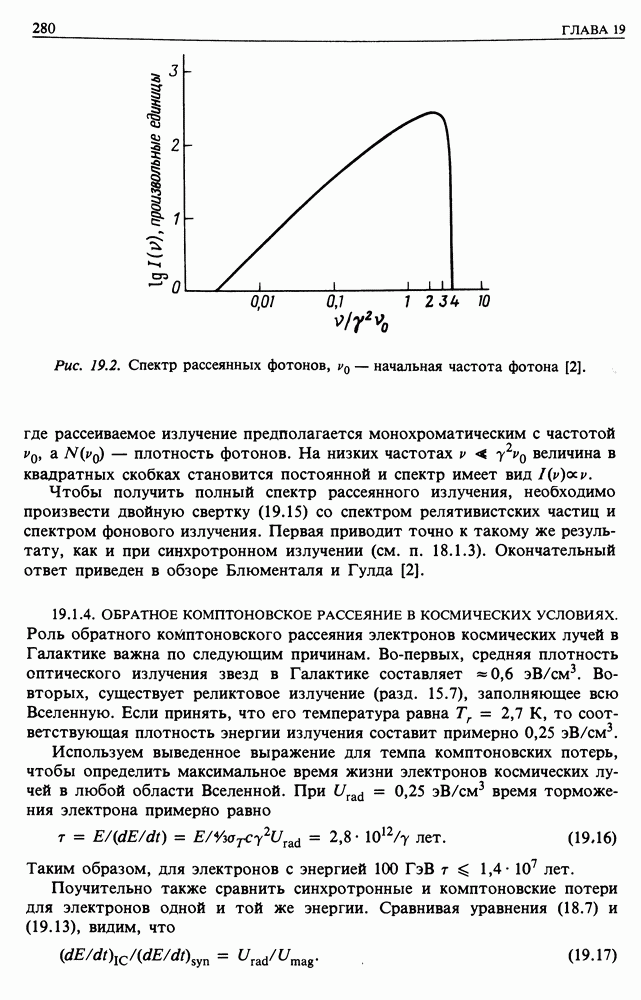
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
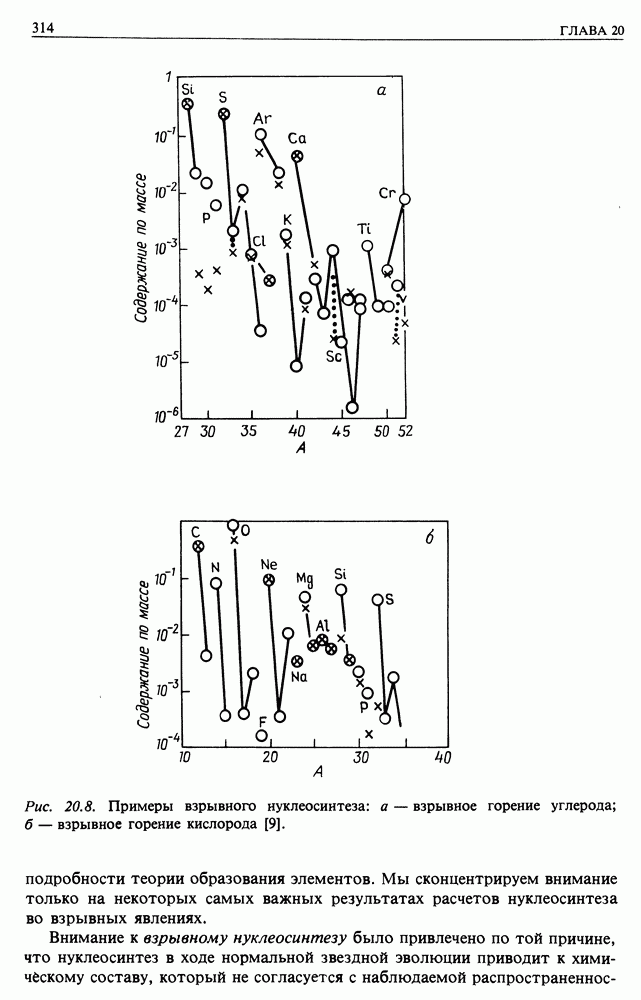
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
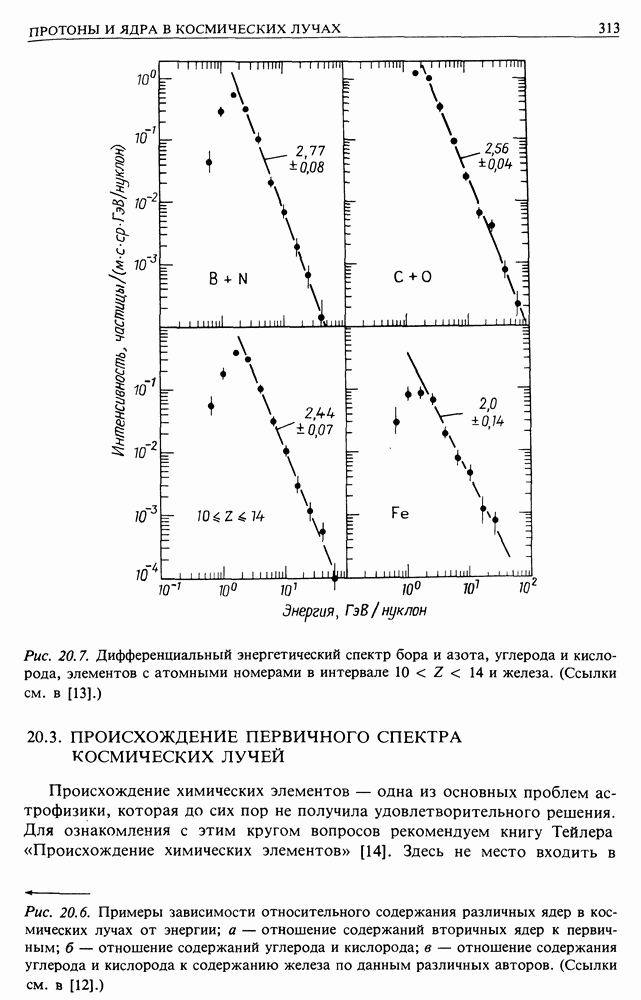
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
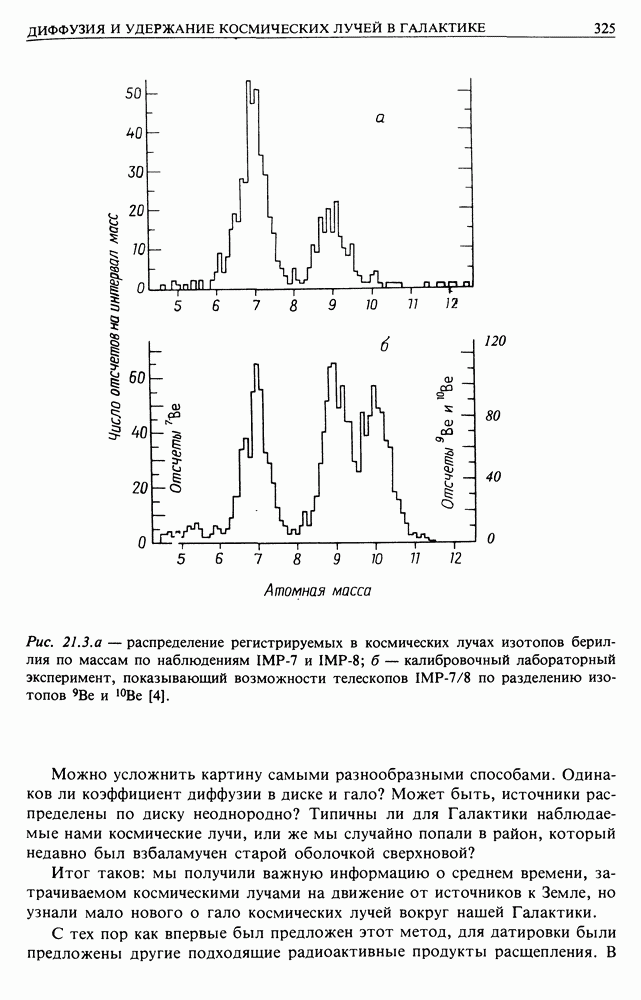
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
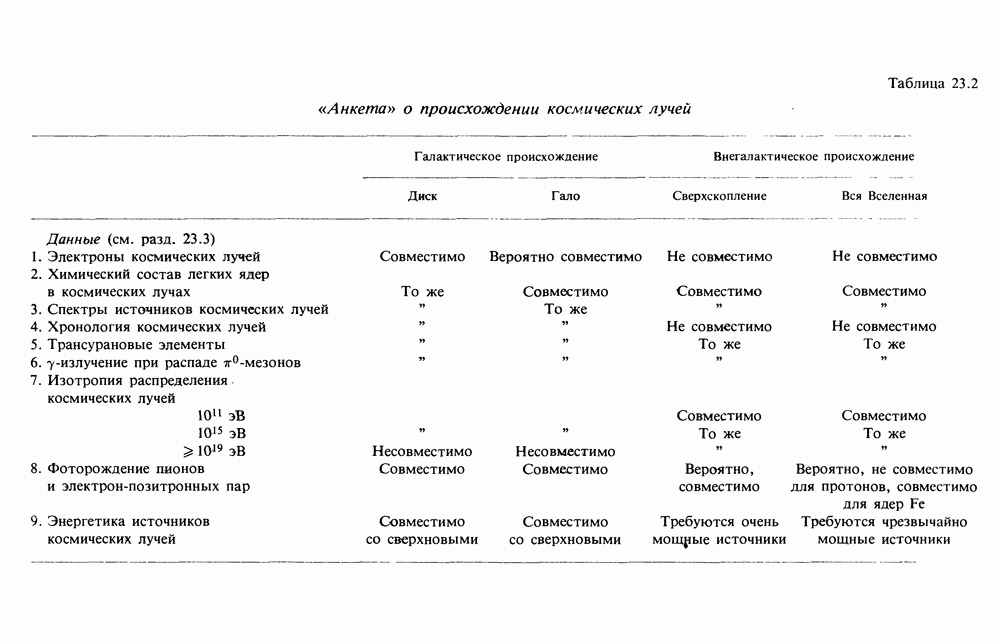
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
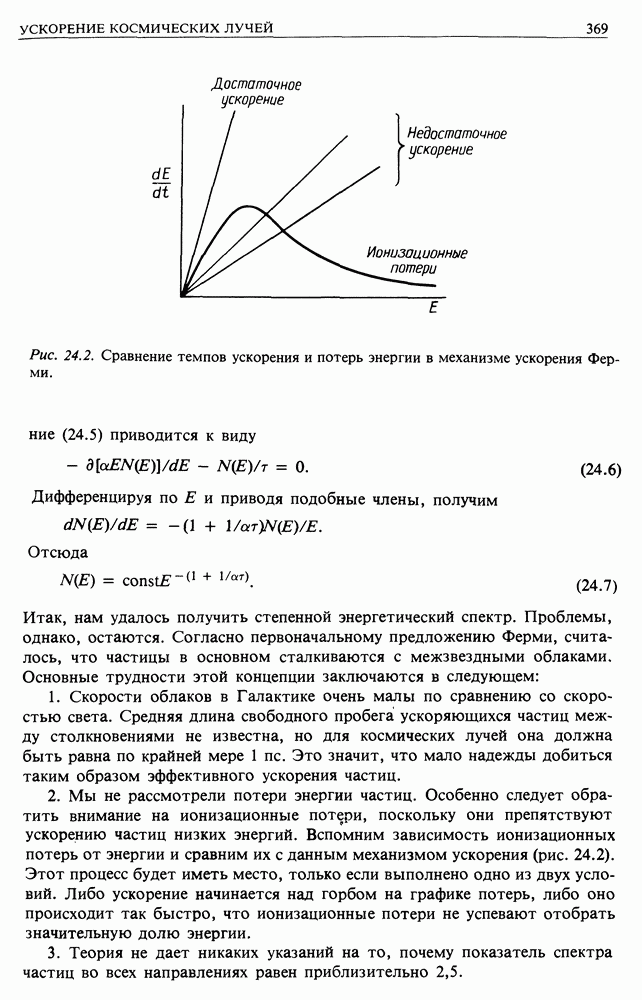
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ