| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
Придадим теперь этим результатам форму, удобную для использования. Мы уже отмечали, что в формулы для энергетических потерь не входит масса космической частицы, а только ее скорость  и заряд
и заряд  Поскольку фактор Лоренца космической частицы
Поскольку фактор Лоренца космической частицы  является единственной функцией
является единственной функцией  запишем
запишем

Мы знаем, что  где
где  число нуклонов в ядре, а
число нуклонов в ядре, а  средняя масса нуклона, которая приближенно равна массе протона
средняя масса нуклона, которая приближенно равна массе протона  т.е.
т.е.  Значит,
Значит,

т.е. если измерить  то ионизационные потери дадут меру кинетической энергии космической частицы на нуклон. Это самый удобный способ описания энергии космических лучей.
то ионизационные потери дадут меру кинетической энергии космической частицы на нуклон. Это самый удобный способ описания энергии космических лучей.
Пусть среда, в которой движется частица, имеет атомный номер  и концентрацию атомов
и концентрацию атомов  Тогда
Тогда  Поэтому можно написать
Поэтому можно написать


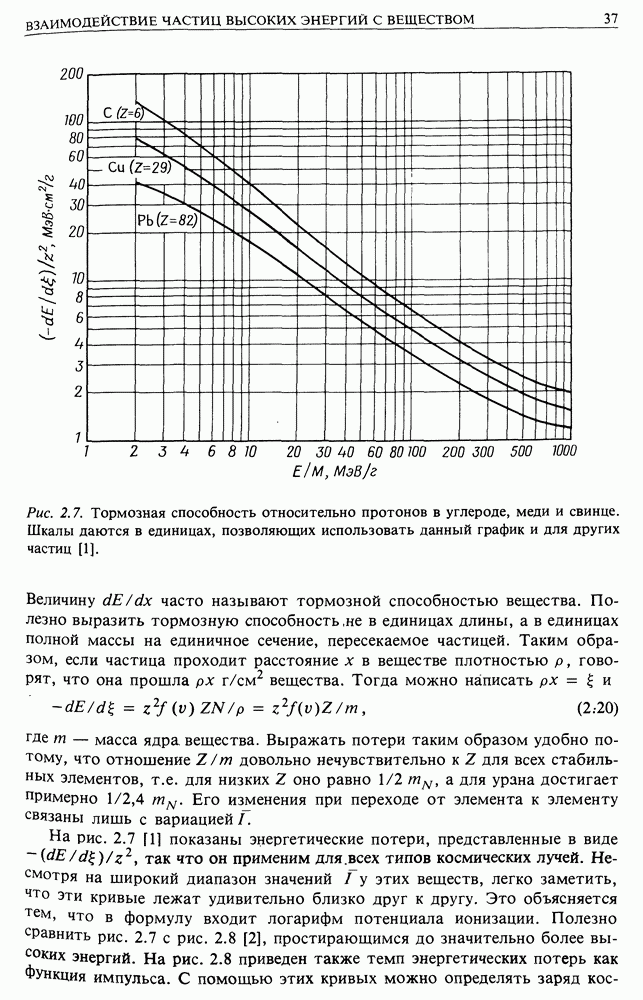
Рис. 2.7. Тормозная способность относительно протонов в углероде, меди и свинце. Шкалы даются в единицах, позволяющих использовать данный график и для других частиц [1].
Величину  часто называют тормозной способностью вещества. Полезно выразить тормозную способность, не в единицах длины, а в единицах полной массы на единичное сечение, пересекаемое частицей. Таким образом, если частица проходит расстояние х в веществе плотностью
часто называют тормозной способностью вещества. Полезно выразить тормозную способность, не в единицах длины, а в единицах полной массы на единичное сечение, пересекаемое частицей. Таким образом, если частица проходит расстояние х в веществе плотностью  говорят, что она прошла
говорят, что она прошла  вещества. Тогда можно написать
вещества. Тогда можно написать  и
и

где  масса ядра вещества. Выражать потери таким образом удобно потому, что отношение
масса ядра вещества. Выражать потери таким образом удобно потому, что отношение  довольно нечувствительно к
довольно нечувствительно к  для всех стабильных элементов, т.е. для низких
для всех стабильных элементов, т.е. для низких  оно равно
оно равно  а для урана достигает примерно
а для урана достигает примерно  Его изменения при переходе от элемента к элементу связаны лишь с вариацией
Его изменения при переходе от элемента к элементу связаны лишь с вариацией  .
.
На рис.  показаны энергетические потери, представленные в виде -
показаны энергетические потери, представленные в виде -  так что он применим для всех типов космических лучей. Несмотря на широкий диапазон значений I у этих веществ, легко заметить, что эти кривые лежат удивительно близко друг к другу. Это объясняется тем, что в формулу входит логарифм потенциала ионизации. Полезно сравнить рис. 2.7 с рис. 2.8 [2], простирающимся до значительно более высоких энергий. На рис. 2.8 приведен также темп энергетических потерь как Функция импульса. С помощью этих кривых можно определять заряд
так что он применим для всех типов космических лучей. Несмотря на широкий диапазон значений I у этих веществ, легко заметить, что эти кривые лежат удивительно близко друг к другу. Это объясняется тем, что в формулу входит логарифм потенциала ионизации. Полезно сравнить рис. 2.7 с рис. 2.8 [2], простирающимся до значительно более высоких энергий. На рис. 2.8 приведен также темп энергетических потерь как Функция импульса. С помощью этих кривых можно определять заряд

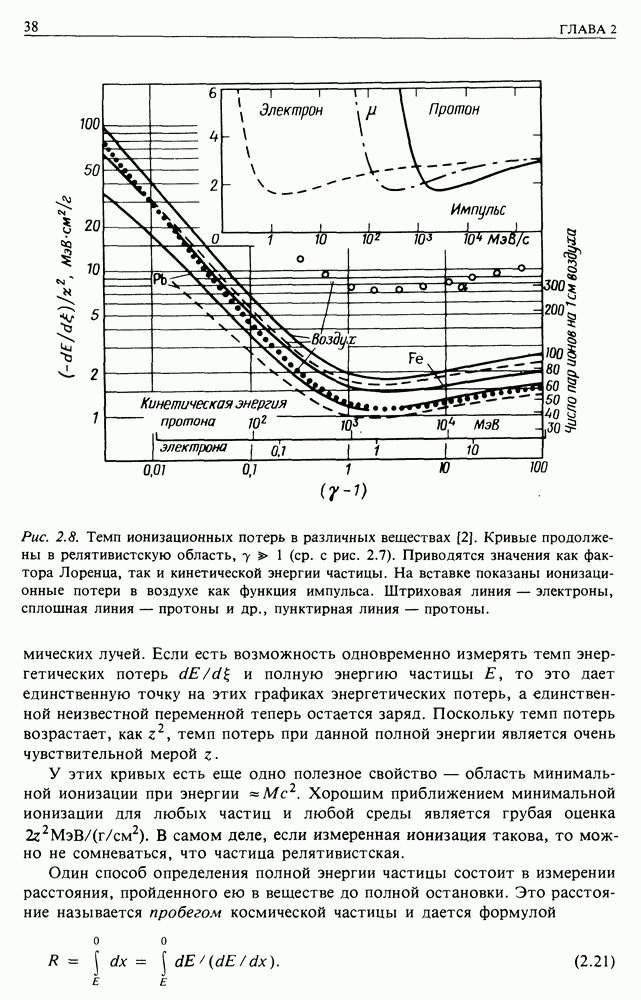
Рис. 2.8. Темп ионизационных потерь в различных веществах [2]. Кривые продолжены в релятивистскую область,  с рис. 2.7). Приводятся значения как фактора Лоренца, так и кинетической энергии частицы. На вставке показаны ионизационные потери в воздухе как функция импульса. Штриховая линия — электроны, сплошная линия — протоны и др., пунктирная линия — протоны.
с рис. 2.7). Приводятся значения как фактора Лоренца, так и кинетической энергии частицы. На вставке показаны ионизационные потери в воздухе как функция импульса. Штриховая линия — электроны, сплошная линия — протоны и др., пунктирная линия — протоны.
космических лучей. Если есть возможность одновременно измерять темп энергетических потерь  и полную энергию частицы
и полную энергию частицы  то это дает единственную точку на этих графиках энергетических потерь, а единственной неизвестной переменной теперь остается заряд. Поскольку темп потерь возрастает, как
то это дает единственную точку на этих графиках энергетических потерь, а единственной неизвестной переменной теперь остается заряд. Поскольку темп потерь возрастает, как  темп потерь при данной полной энергии является очень чувствительной мерой
темп потерь при данной полной энергии является очень чувствительной мерой 
У этих кривых есть еще одно полезное свойство — область минимальной ионизации при энергии  Хорошим приближением минимальной ионизации для любых частиц и любой среды является грубая оценка
Хорошим приближением минимальной ионизации для любых частиц и любой среды является грубая оценка  В самом деле, если измеренная ионизация такова, то можно не сомневаться, что частица релятивистская.
В самом деле, если измеренная ионизация такова, то можно не сомневаться, что частица релятивистская.
Один способ определения полной энергии частицы состоит в измерении расстояния, пройденного ею в веществе до полной остановки. Это расстояние называется пробегом космической частицы и дается формулой

Теперь мы знаем, что интегрирование обрывается при чрезвычайно малых кинетических энергиях. Однако и сама частица проходит очень малое расстояние после того, как ее энергия стала ниже порога, до которого верны наши расчеты. Строгий расчет требует, чтобы интегрирование проводилось до некоторого значения энергии  до которого наш расчет верен, затем, нужно прибавить к результату некий малый остаточный пробег.
до которого наш расчет верен, затем, нужно прибавить к результату некий малый остаточный пробег.
Покажем теперь, как по пробегу измеряется первоначальная кинетическая энергия на нуклон. Запишем

Попадая в вещество, частица имеет энергию  следовательно,
следовательно,

Поэтому

Это выражение является функцией только  или
или  т.е. функцией первоначальной кинетической энергии на нуклон. Так что если пропустить сквозь вещество космические лучи любого типа, то по пробегу можно судить о первоначальной кинетической энергии частиц на нуклон, их заряде и массе. Точное интегрирование [1] показывает, насколько малочувствительно отношение
т.е. функцией первоначальной кинетической энергии на нуклон. Так что если пропустить сквозь вещество космические лучи любого типа, то по пробегу можно судить о первоначальной кинетической энергии частиц на нуклон, их заряде и массе. Точное интегрирование [1] показывает, насколько малочувствительно отношение  к виду вещества, в которое инжектируются космические лучи (рис. 2.9).
к виду вещества, в которое инжектируются космические лучи (рис. 2.9).
Лучше всего измерять скорость энергетических потерь вдоль всего пути частицы и строить кривые, показанные на рис. 2.7 и 2.8. По оси х вместо кинетической энергии следует откладывать пробег. На практике, однако, это чаще всего очень тяжелый и трудоемкий процесс. Такие измерения можно осуществить с помощью ядерных эмульсий (разд. 6.2).
При интерпретации наблюдаемых ионизационных потерь космических лучей возникают две проблемы. Обе они связаны со статистической природой этого процесса.
Разброс. Следует помнить, что замедление космической частицы является статистическим процессом. Поэтому должен наблюдаться разброс пробегов, поскольку некоторые частицы испытывают больше столкновений, чем другие. Это налагает фундаментальные ограничения на точность измерений кинетической энергии. Конечным результатом является приблизительно гауссово распределение пробегов.
Дельта-электроны. Другое явление статистического характера, которое следует тщательно учитывать при оценке темпа потерь частицы, проявляется в том случае, если рассматриваемый трек мал, и при этом один или два близких столкновения дадут один или два электрона, энергии которых достаточно, чтобы произвести вторичную ионизацию и создать

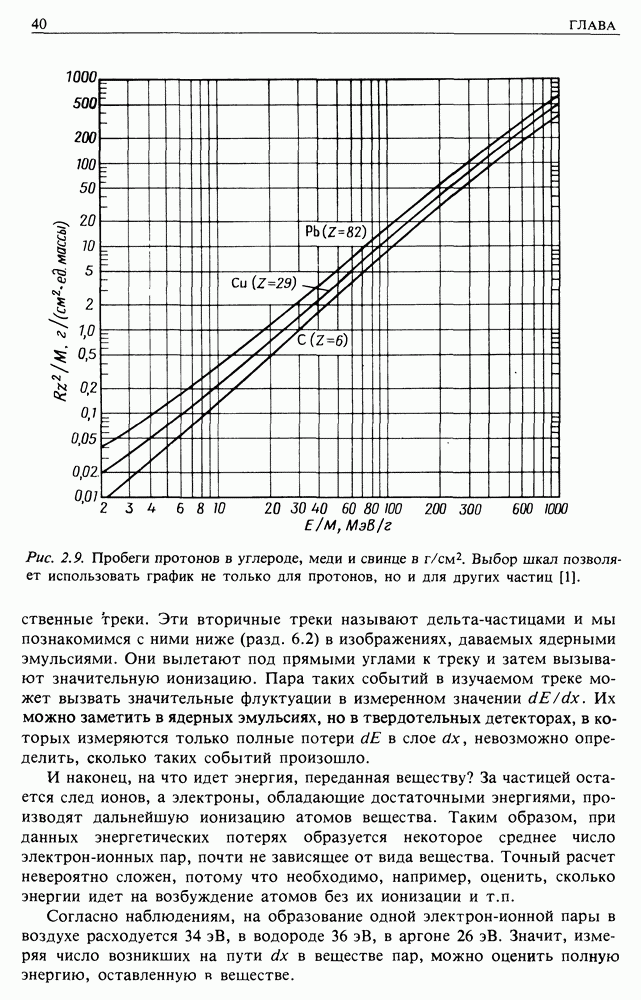
Рис. 2.9. Пробеги протонов в углероде, меди и свинце в  Выбор шкал позволяет использовать график не только для протонов, но и для других частиц [1].
Выбор шкал позволяет использовать график не только для протонов, но и для других частиц [1].
собственные треки. Эти вторичные треки называют дельта-частицами и мы познакомимся с ними ниже (разд. 6.2) в изображениях, даваемых ядерными эмульсиями. Они вылетают под прямыми углами к треку и затем вызывают значительную ионизацию. Пара таких событий в изучаемом треке может вызвать значительные флуктуации в измеренном значении  Их можно заметить в ядерных эмульсиях, но в твердотельных детекторах, в которых измеряются только полные потери
Их можно заметить в ядерных эмульсиях, но в твердотельных детекторах, в которых измеряются только полные потери  в слое
в слое  , невозможно определить, сколько таких событий произошло.
, невозможно определить, сколько таких событий произошло.
И наконец, на что идет энергия, переданная веществу? За частицей остается след ионов, а электроны, обладающие достаточными энергиями, производят дальнейшую ионизацию атомов вещества. Таким образом, при данных энергетических потерях образуется некоторое среднее число электрон-ионных пар, почти не зависящее от вида вещества. Точный расчет невероятно сложен, потому что необходимо, например, оценить, сколько энергии идет на возбуждение атомов без их ионизации и т.п.
Согласно наблюдениям, на образование одной электрон-ионной пары в воздухе расходуется  в водороде
в водороде  в аргоне
в аргоне  Значит, измеряя число возникших на пути
Значит, измеряя число возникших на пути  в веществе пар, можно оценить полную энергию, оставленную
в веществе пар, можно оценить полную энергию, оставленную  веществе.
веществе.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
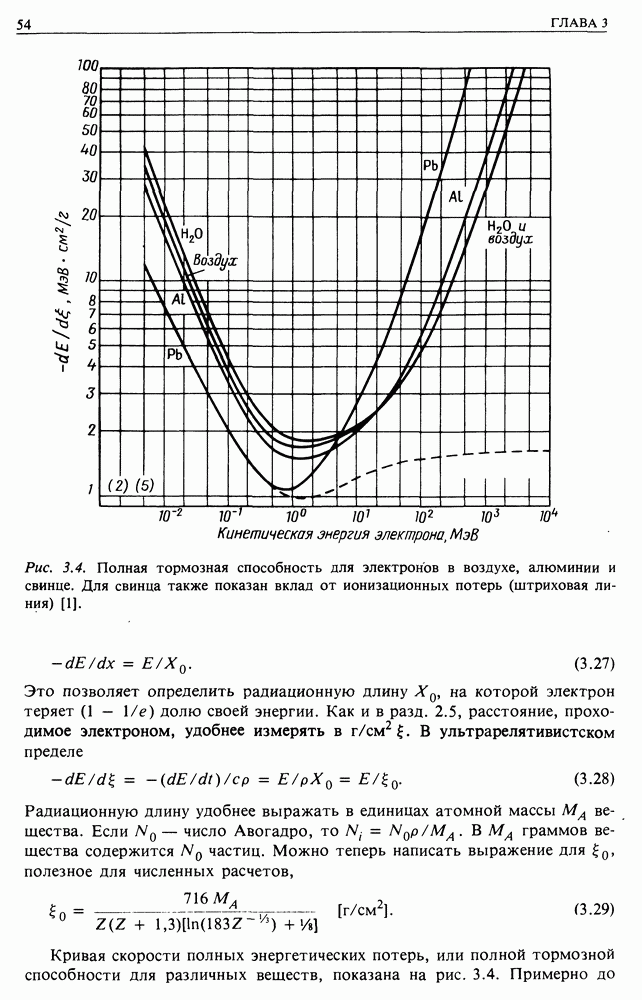
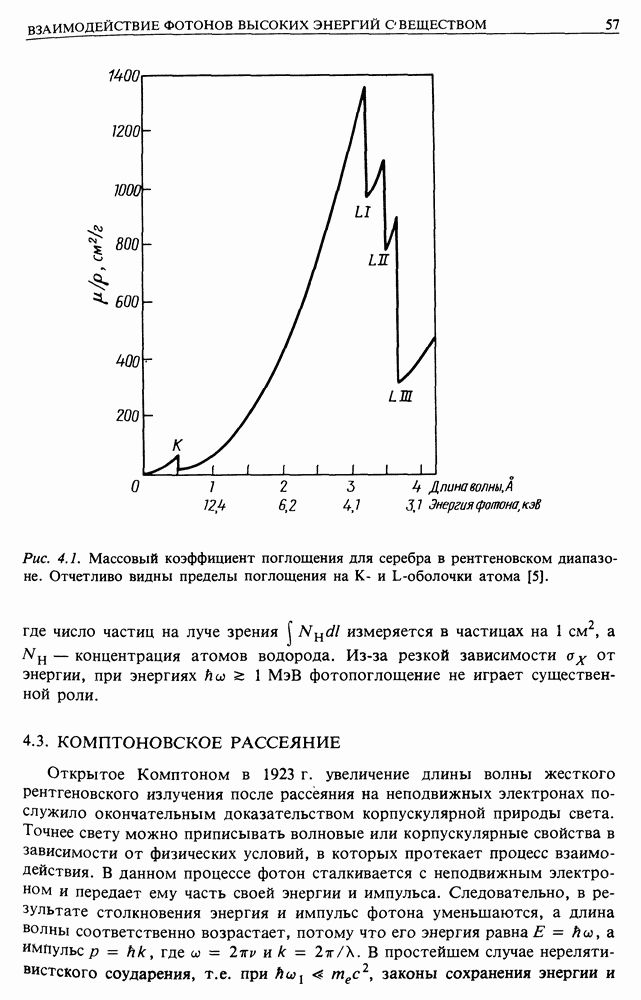
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
- 4.4. ОБРАЗОВАНИЕ ПАР
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
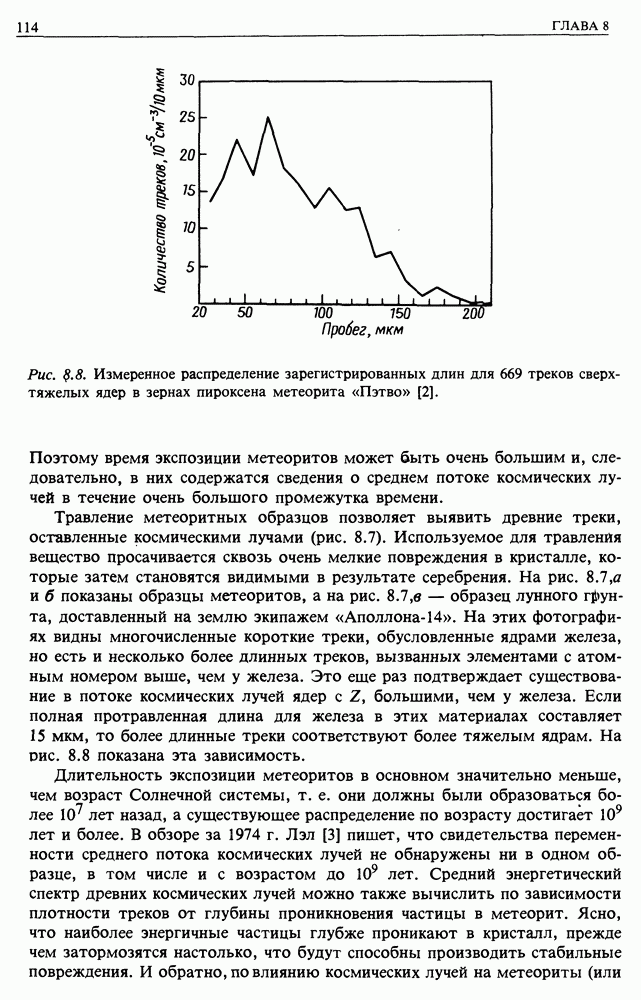
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
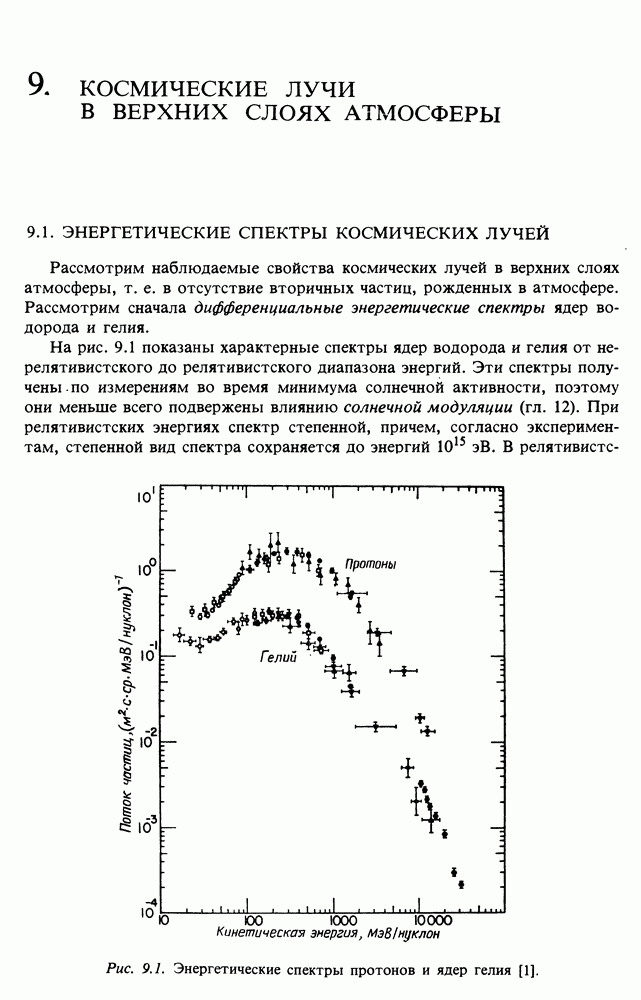
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
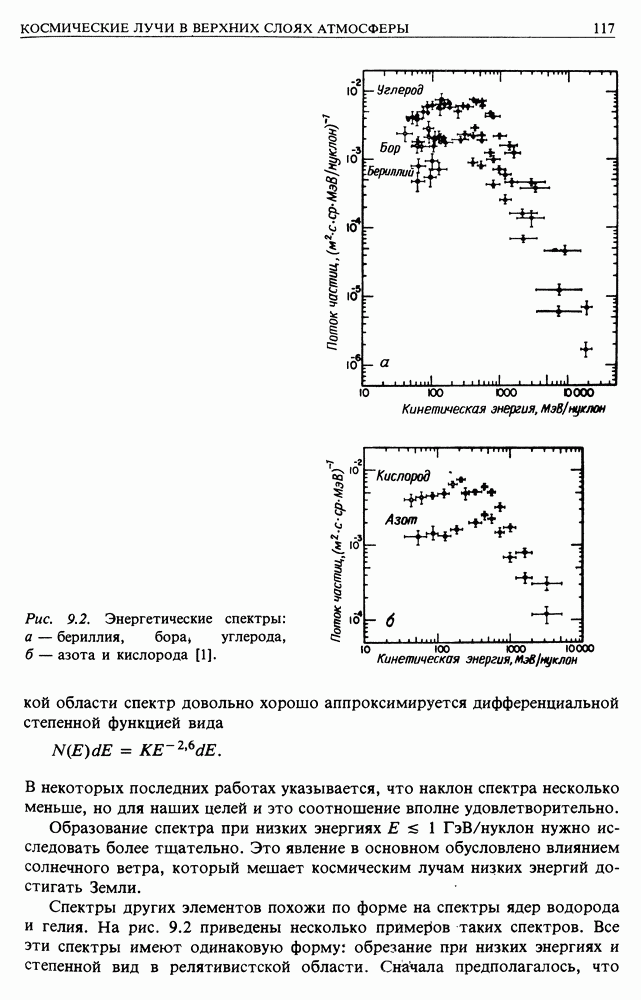
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
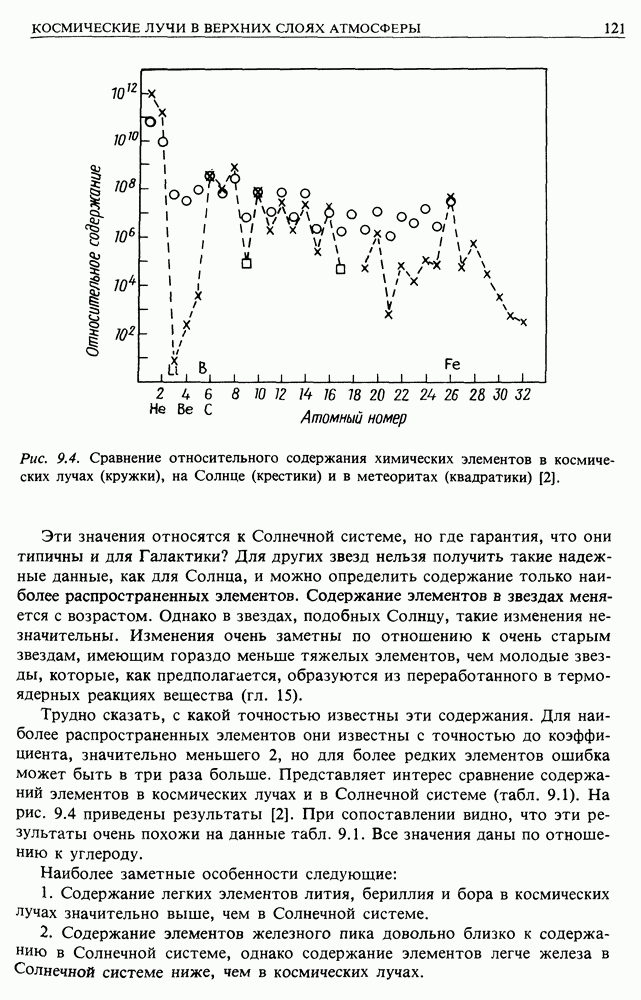
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
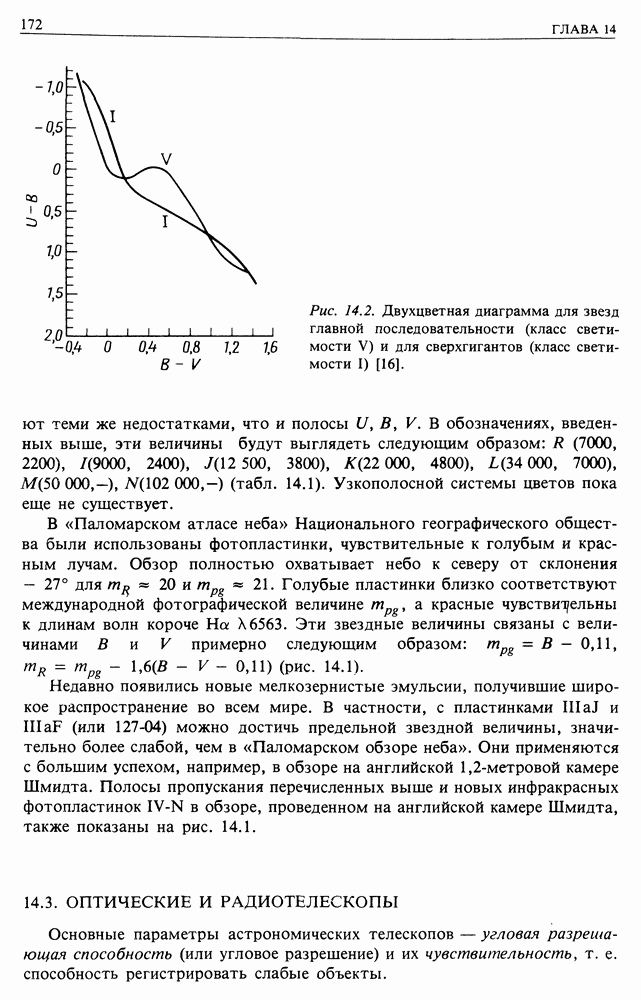
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ