| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
19.1. ПОТЕРИ ЭНЕРГИИ ЭЛЕКТРОНАМИ КОСМИЧЕСКИХ ЛУЧЕЙ
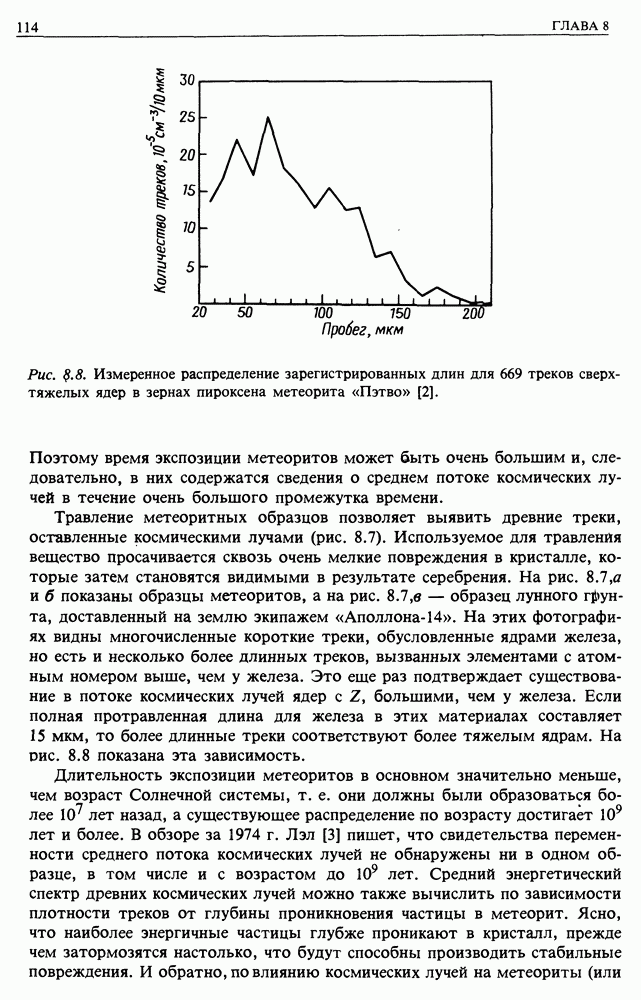
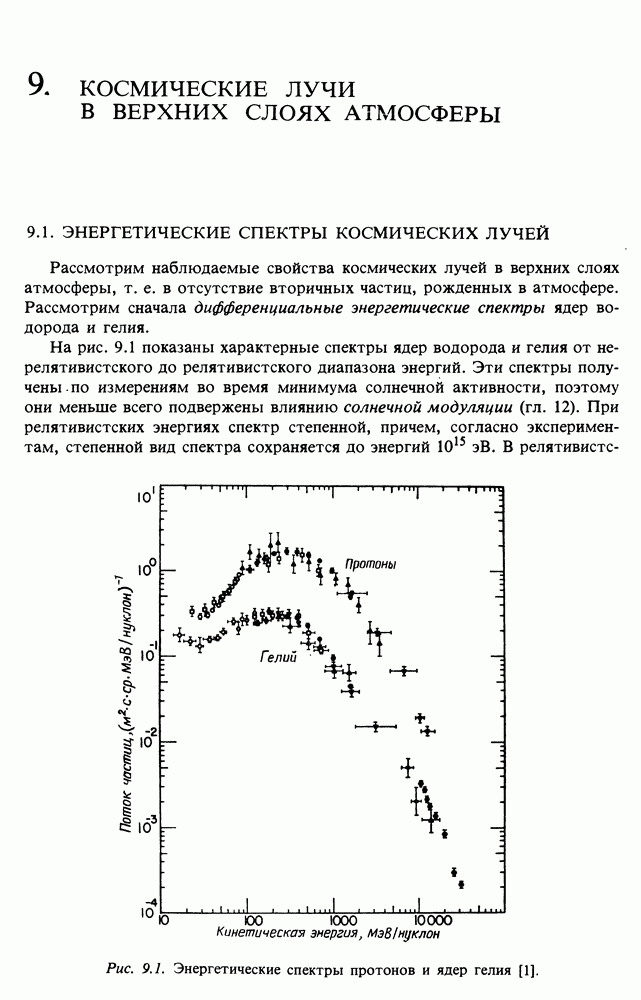
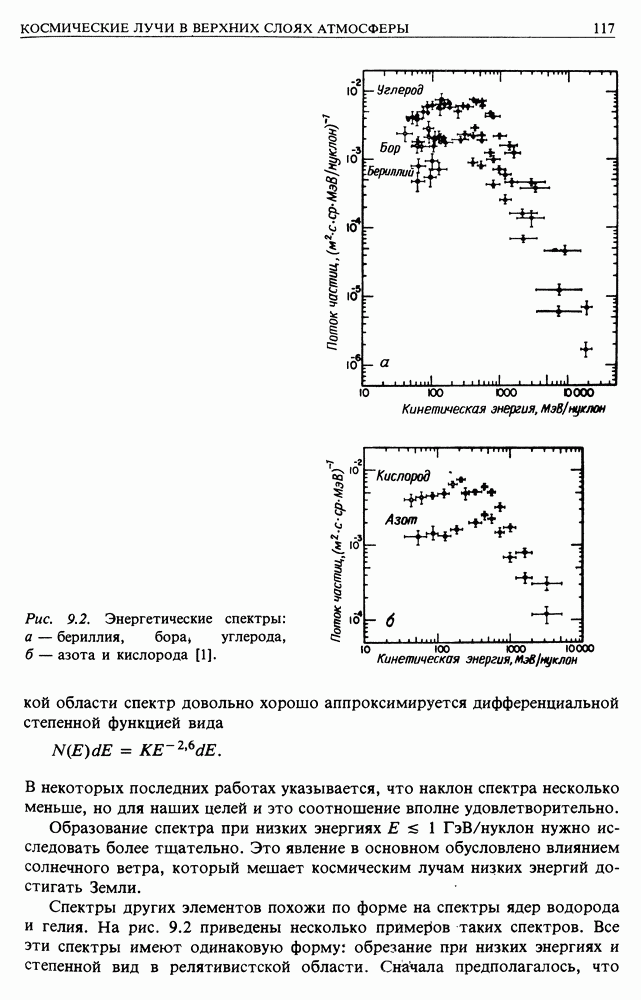
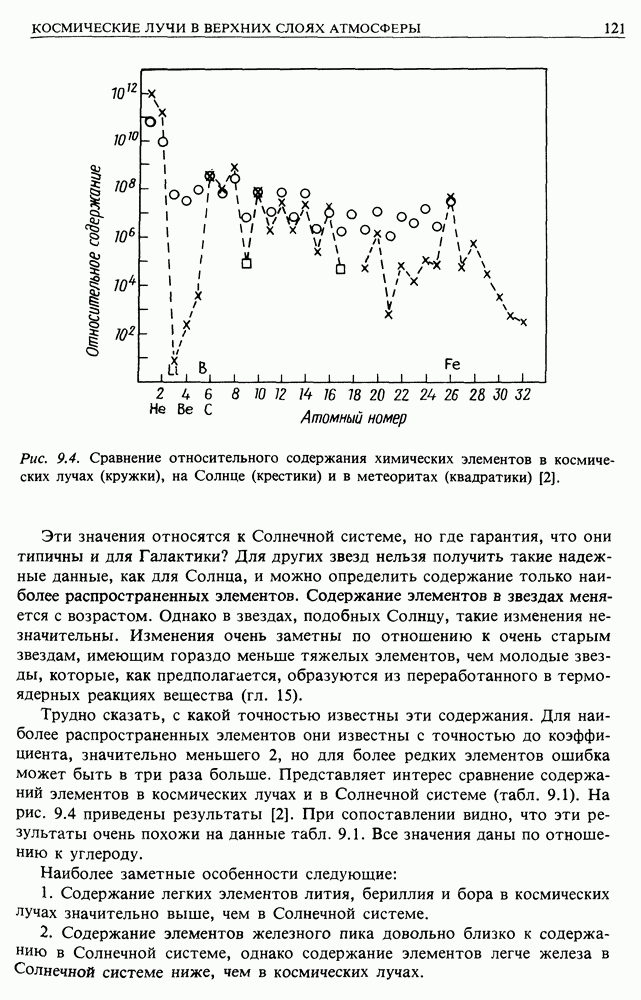
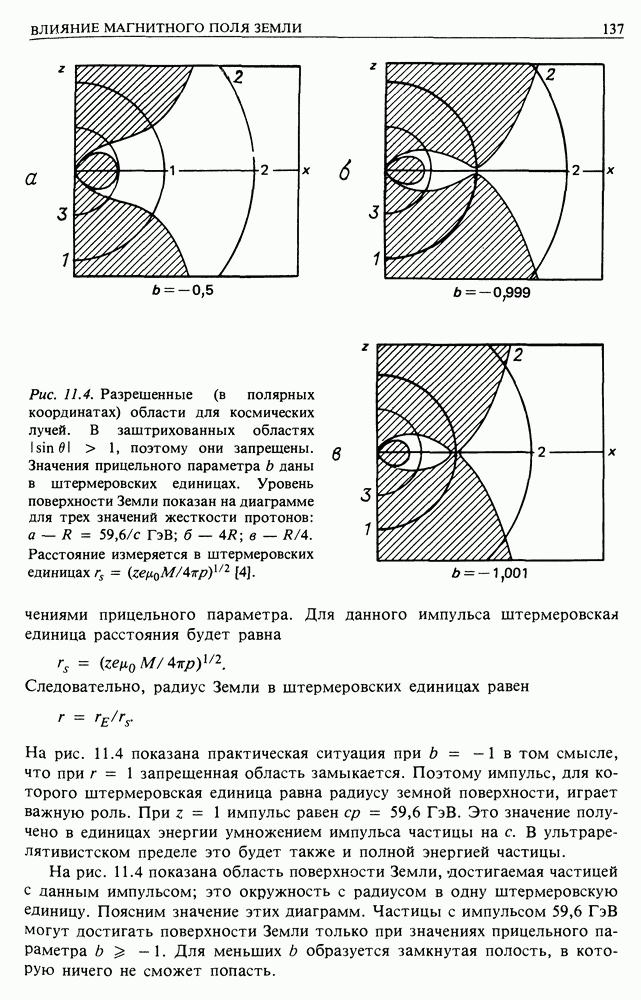
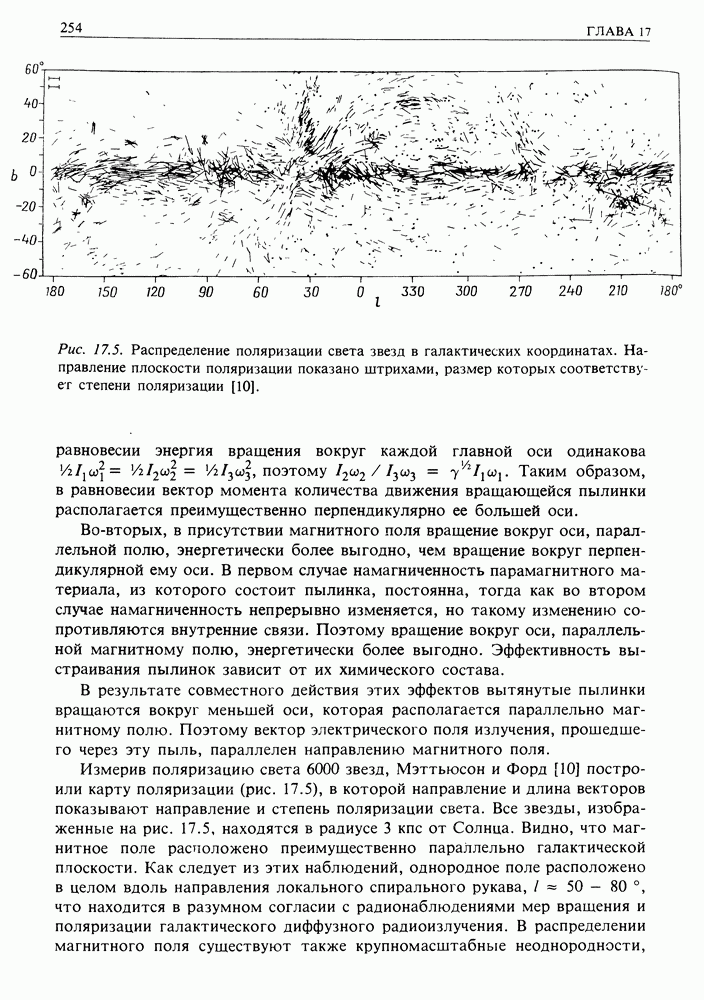
Рассмотрим распространение электронов космических лучей от источников к Земле. По дороге под действием различных механизмов электроны теряют энергию. В результате их начальный спектр изменяется, что в принципе позволяет восстановить их историю. Электроны теряют энергию при взаимодействии с веществом, магнитным полем и излучением. Прежде всего преобразуем формулы, описывающие три уже изученных нами процесса, к виду, удобному для рассмотрения распространения частиц в межзвездной среде. Затем опишем два других важных механизма: адиабатические потери и обратное комптоновское рассеяние.
19.1.1. Ионизационные потери, тормозное и синхротронное излучение. Как будет видно из дальнейшего, наибольшее значение имеет энергетическая зависимость механизмов потерь энергии, поэтому перепишем формулы так, чтобы выделить именно эту зависимость.
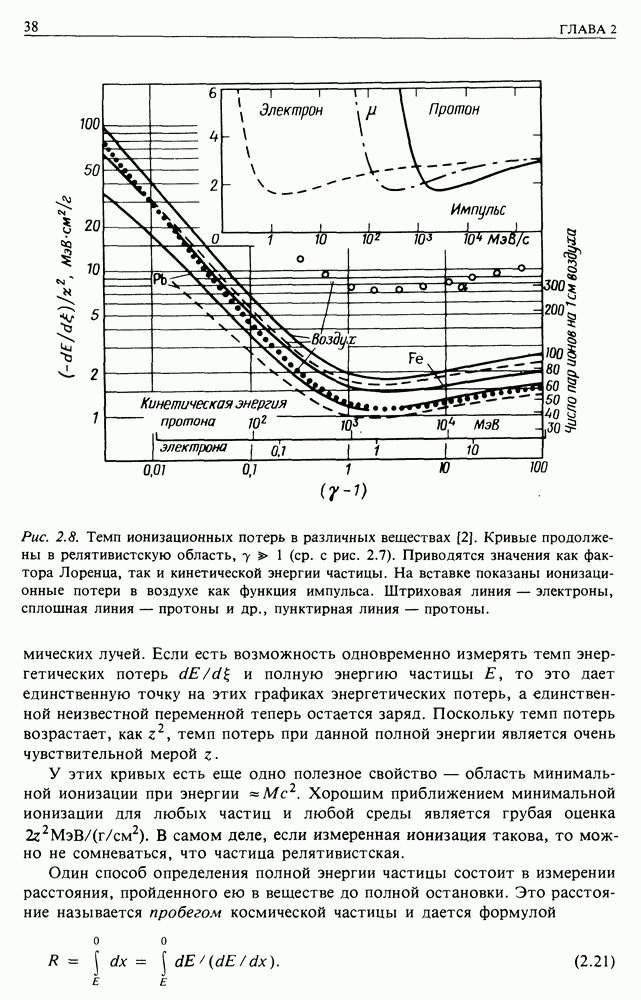
Ионизационные потери. Как правило, для электронов они не очень существенны. Если подставить численные значения в формулы, приведенные в гл. 2, то окажется, что для водорода

или

Таким образом, электрон с энергией  затормозится за
затормозится за

Поскольку зависимость от энергии только логарифмическая, всегда можно считать, что потери энергии составляют 
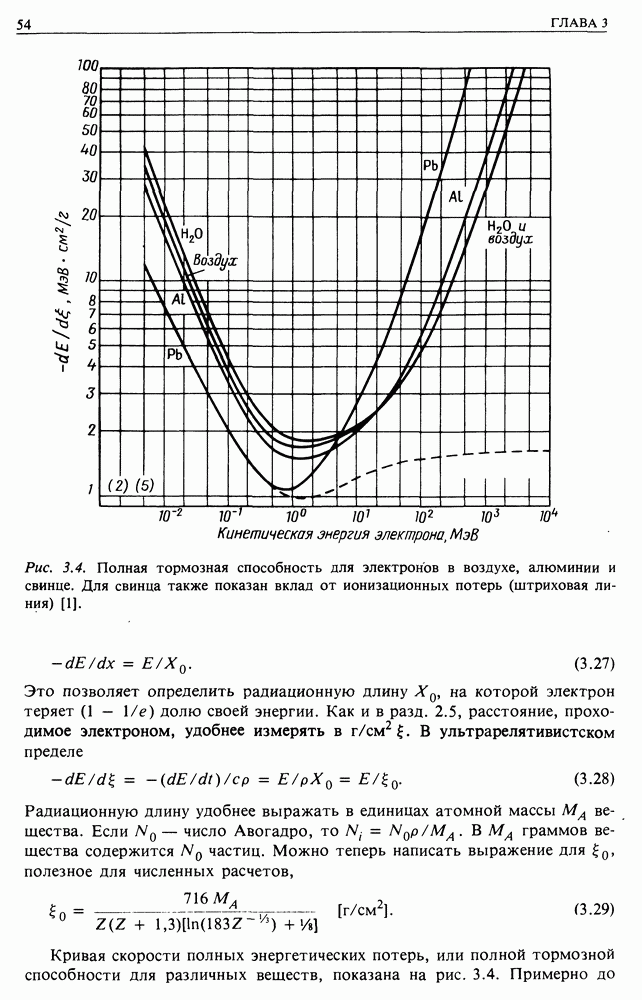
Тормозное излучение. Проделав аналогичные расчеты, получим в ультрарелятивистском пределе: в полностью ионизованном газе

в неионизованном газе (при полном экранировании)

Отметим, что в этом случае темп потерь энергии пропорционален энергии электрона.
Сынхротронное излучение. Подстановка численных значений в формулу (18.6) для полного темпа потерь энергии, которая в пределе  с имеет вид
с имеет вид

дает

где В измеряется в гауссах. Чтобы перейти к усредненному по изотропному распределению по питч-углам выражению, нужно вместо 2 перед выражением подставить  тогда
тогда

19.1.2. Адиабатические потери. Если движение релятивистских электронов ограничено областью объемом К, то оказываемое ими давление приводит к увеличению объема, при этом электроны совершают работу расширения и их энергия адиабатически уменьшается. Этот процесс играет важную роль в эволюции радиоисточников и остатков сверхновых. Энергия, отобранная у электронов, переходит в кинетическую энергию расширения излучающей области. В любом релятивистском газе показатель адиабаты (т.е. отношение удельных теплоемкостей) равен  При адиабатическом расширении
При адиабатическом расширении  где
где  внутренняя энергия,
внутренняя энергия,  Давление
Давление  релятивистского газа связано с плотностью его внутренней энергии
релятивистского газа связано с плотностью его внутренней энергии  соотношением
соотношением  Отсюда
Отсюда  Если расширение происходит во всех направлениях,
Если расширение происходит во всех направлениях,  следовательно,
следовательно,  Этот результат относится не только к энергии газа как целого, но и к энергии отдельной частицы, поскольку
Этот результат относится не только к энергии газа как целого, но и к энергии отдельной частицы, поскольку  Поэтому
Поэтому  Темп потерь энергии можно записать в виде
Темп потерь энергии можно записать в виде

или

Адиабатические потери существенны при условии, что характерное время расширения  сравнимо с временем пребывания частиц в излучающей области. Очевидно, если частицы вообще не покидают источник в ходе расширения, то адиабатические потери нужно учитывать обязательно. Обратите внимание на то, что темп потерь энергии в любой момент времени определяется мгновенной скоростью расширения
сравнимо с временем пребывания частиц в излучающей области. Очевидно, если частицы вообще не покидают источник в ходе расширения, то адиабатические потери нужно учитывать обязательно. Обратите внимание на то, что темп потерь энергии в любой момент времени определяется мгновенной скоростью расширения 
Подчеркнем, что этот механизм особенно важен для частиц, ускоряемых в остатках сверхновых. Адиабатические потери существенны всюду в межзвездной среде, где оказываемое частицами давление совершает работу.
19.1.3. Обратное комптоновское рассеяние. Релятивистские электроны при взаимодействии с фотонами теряют энергию, поскольку энергия рассеянных фотонов увеличивается. Этот процесс называется обратным комптоновским рассеянием, так как при обычном комптоновском рассеянии фотон отдает энергию первоначально покоившейся частице, т.е. теряет энергию при взаимодействии. В астрофизических условиях, как правило, встречается предельный случай, когда энергия фотона в системе центра масс много меньше энергии покоя электрона, т.е.  .
.
Наиболее часто используемые результаты можно получить из следующих простых соображений. На рис. 19.1 показан процесс столкновения фотона и релятивистского электрона в лабораторной системе  и в системе покоя электрона
и в системе покоя электрона  Если в системе
Если в системе  энергия фотона равна
энергия фотона равна  а угол падения 0, то в
а угол падения 0, то в  как следует из обычных формул для эффекта Доплера,
как следует из обычных формул для эффекта Доплера,

Угол падения в системе  связан с
связан с  формулами, описывающими аберрацию,
формулами, описывающими аберрацию,

Далее, при условии  тесг комптоновское рассеяние в системе покоя электрона
тесг комптоновское рассеяние в системе покоя электрона  сводится просто к обычному томсоновскому рассеянию, поэтому темп потерь энергии электроном совпадает со скоростью переизлучения им энергии. В соответствии с классической теорией томсоновского рассеяния
сводится просто к обычному томсоновскому рассеянию, поэтому темп потерь энергии электроном совпадает со скоростью переизлучения им энергии. В соответствии с классической теорией томсоновского рассеяния

где  плотность энергии излучения в системе покоя электрона. Неважно, изотропно излучение или нет. Свободный электрон колеблется в любом поле излучения.
плотность энергии излучения в системе покоя электрона. Неважно, изотропно излучение или нет. Свободный электрон колеблется в любом поле излучения.
Поэтому необходимо найти  в системе покоя электрона, а затем с помощью (19.9) найти
в системе покоя электрона, а затем с помощью (19.9) найти  Тогда в соответствии с результатами п. 3.3.5, мы получим и
Тогда в соответствии с результатами п. 3.3.5, мы получим и  в 5.
в 5.

Рис. 19.1. Геометрия обратного комптоновского рассеяния в системе покоя электро на  лабораторной системе
лабораторной системе 
Пусть плотность фотонов в пучке, направленном под углом  к оси х, как показано на рис. 19.1, равна
к оси х, как показано на рис. 19.1, равна  Тогда поток энергии этих фотонов в
Тогда поток энергии этих фотонов в  равен
равен 
Определим поток энергии этого пучка в системе покоя электрона  Для этого нужно знать две величины: энергию каждого фотона в
Для этого нужно знать две величины: энергию каждого фотона в  и число падающих в единицу времени фотонов. Первая дается формулой (19.7), вторую можно получить, применив обычное преобразование Лоренца к временным интервалам, измеренным в
и число падающих в единицу времени фотонов. Первая дается формулой (19.7), вторую можно получить, применив обычное преобразование Лоренца к временным интервалам, измеренным в 

Для фотона, движущегося к началу координат,  следовательно,
следовательно,

Поскольку интервал  короче, чем
короче, чем  поток фотонов в
поток фотонов в  больше в
больше в  раз, т.е. во столько же раз, во сколько увеличивается частота фотона [формула (19.7)]. Это совершенно естественно, ведь это два различных аспекта одного и того же релятивистского явления — замедления течения времени. Временной интервал между гребнями волн, который определяет частоту, и интервал между моментами прихода фотонов преобразуются при переходе в другую систему отсчета совершенно одинаково. Таким образом, в системе
раз, т.е. во столько же раз, во сколько увеличивается частота фотона [формула (19.7)]. Это совершенно естественно, ведь это два различных аспекта одного и того же релятивистского явления — замедления течения времени. Временной интервал между гребнями волн, который определяет частоту, и интервал между моментами прихода фотонов преобразуются при переходе в другую систему отсчета совершенно одинаково. Таким образом, в системе  поток энергии в луче равен
поток энергии в луче равен

или

Излучение падает в системе  под углом в, но, как мы увидим в дальнейшем, очень удобно работать с углом
под углом в, но, как мы увидим в дальнейшем, очень удобно работать с углом  Это связано с тем, что, интегрируя по 0, можно сразу найти полную плотность энергии в
Это связано с тем, что, интегрируя по 0, можно сразу найти полную плотность энергии в 

При этом предполагается, что излучение в  изотропно. Интегрируя, получим
изотропно. Интегрируя, получим

Подставляя это выражение в (19.9), получим

Поскольку  темп потерь энергии в лабораторной системе отсчета равен
темп потерь энергии в лабораторной системе отсчета равен

Это темп потерь энергии, но электрон также приобретает энергию от поля излучения. Темп набора энергии определяется формулой Томсона (19.9). Поэтому

нерелятивистском пределе  получаем
получаем

В ультрарелятивистском случае 

Это выражение в точности вплоть до коэффициента  совпадает с результатом для синхротронного излучения [формула (18.7)]. Дело в том, что в обоих случаях частица в собственной системе отсчета ускоряется электрическим полем. Для нее не важно, каково происхождение поля: испытывает ли она постоянное ускорение в однородном магнитном поле или в суммарном электрическом поле отдельных фотонов. Заметим, что в формулы для некогерентного излучения всегда входит квадрат электрического поля, поэтому складываются именно энергии. Более формально синхротронное излучение можно рассматривать как рассеяние «виртуальных фотонов» на электроне, движущемся по винтовой траектории вдоль магнитной силовой линии (см., например, [13] и гл. 15).
совпадает с результатом для синхротронного излучения [формула (18.7)]. Дело в том, что в обоих случаях частица в собственной системе отсчета ускоряется электрическим полем. Для нее не важно, каково происхождение поля: испытывает ли она постоянное ускорение в однородном магнитном поле или в суммарном электрическом поле отдельных фотонов. Заметим, что в формулы для некогерентного излучения всегда входит квадрат электрического поля, поэтому складываются именно энергии. Более формально синхротронное излучение можно рассматривать как рассеяние «виртуальных фотонов» на электроне, движущемся по винтовой траектории вдоль магнитной силовой линии (см., например, [13] и гл. 15).
Спектр рассеянного излучения можно получить, если произвести два последовательных преобразования Лоренца: сначала найти распределение падающего излучения в системе отсчета  а затем преобразовать рассеянное излучение из
а затем преобразовать рассеянное излучение из  в лабораторную систему отсчета
в лабораторную систему отсчета  Максимальная энергия передается фотону при лобовом столкновении, когда
Максимальная энергия передается фотону при лобовом столкновении, когда  и фотон рассеивается в направлении прихода. Тогда
и фотон рассеивается в направлении прихода. Тогда

Если частота изотропного поля излучения равна  то среднюю частоту
то среднюю частоту  рассеянного излучения можно найти из уравнения (19.13):
рассеянного излучения можно найти из уравнения (19.13):  Спектр рассеянного излучения
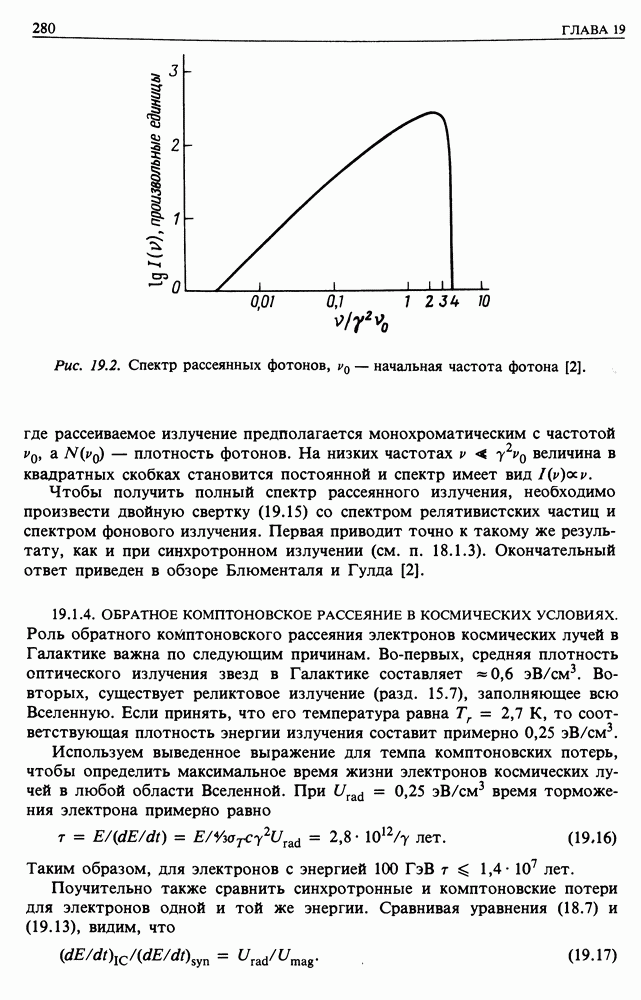
Спектр рассеянного излучения  показан на рис. 19.2. Он описывается формулой
показан на рис. 19.2. Он описывается формулой


Рис. 19.2. Спектр рассеянных фотонов,  начальная частота фотона [2].
начальная частота фотона [2].
где рассеиваемое излучение предполагается монохроматическим с частотой  плотность фотонов. На низких частотах
плотность фотонов. На низких частотах  величина в квадратных скобках становится постоянной и спектр имеет вид
величина в квадратных скобках становится постоянной и спектр имеет вид 
Чтобы получить полный спектр рассеянного излучения, необходимо произвести двойную свертку (19.15) со спектром релятивистских частиц и спектром фонового излучения. Первая приводит точно к такому же результату, как и при синхротронном излучении (см. п. 18.1.3). Окончательный ответ приведен в обзоре Блюменталя и Гулда [2].
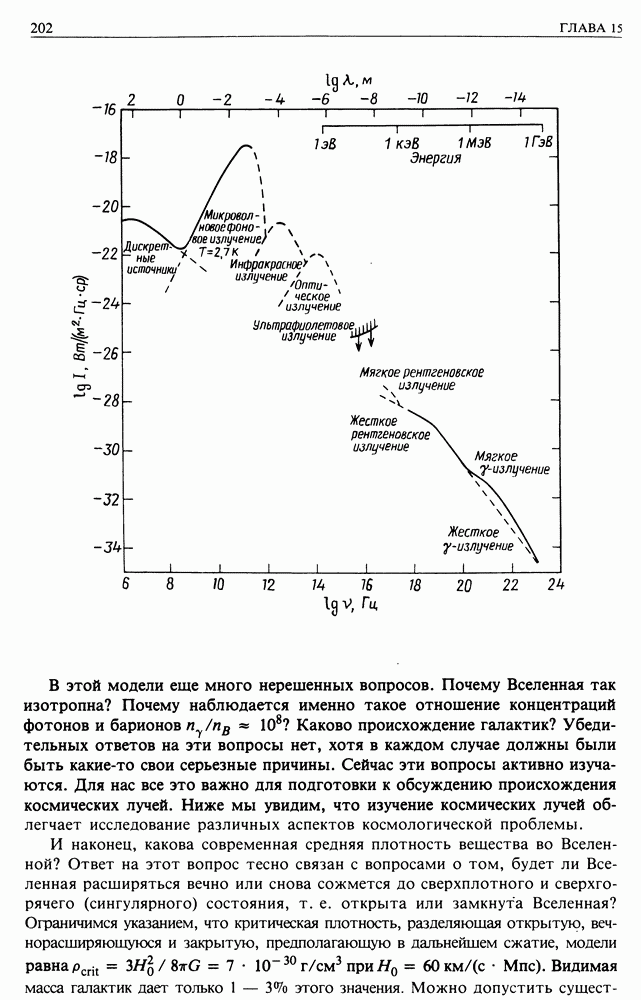
19.1.4. В БРАТНОЕ КОМПТОНОВСКОЕ РАССЕЯНИЕ В КОСМИЧЕСКИХ УСЛОВИЯХ. Роль обратного кокптоновского рассеяния электронов космических лучей в Галактике важна по следующим причинам. Во-первых, средняя плотность оптического излучения звезд в Галактике составляет  Во-вторых, существует реликтовое излучение (разд. 15.7), заполняющее всю Вселенную. Если принять, что его температура равна
Во-вторых, существует реликтовое излучение (разд. 15.7), заполняющее всю Вселенную. Если принять, что его температура равна  то соответствующая плотность энергии излучения составит примерно
то соответствующая плотность энергии излучения составит примерно 
Используем выведенное выражение для темпа комптоновских потерь, чтобы определить максимальное время жизни электронов космических лучей в любой области Вселенной. При  время торможения электрона примерно равно
время торможения электрона примерно равно

Таким образом, для электронов с энергией  лет.
лет.
Поучительно также сравнить синхротронные и комптоновские потери для электронов одной и той же энергии. Сравнивая уравнения (18.7) и (19.13), видим, что

Подставляя характерные значения  получим
получим  Таким образом, потери в результате обратного комптоновского рассеяния для электронов космических лучей должны быть существенны. Более того, предположим, что электроны должны выходить из Галактики в межгалактическое пространство. Там их потери на синхротронное излучение заведомо ничтожны, поскольку можно наложить очень низкий предел на межгалактическое магнитное поле. Но реликтовое излучение присутствует везде, поэтому электроны всюду должны терять энергию при рассеянии на реликтовых фотонах.
Таким образом, потери в результате обратного комптоновского рассеяния для электронов космических лучей должны быть существенны. Более того, предположим, что электроны должны выходить из Галактики в межгалактическое пространство. Там их потери на синхротронное излучение заведомо ничтожны, поскольку можно наложить очень низкий предел на межгалактическое магнитное поле. Но реликтовое излучение присутствует везде, поэтому электроны всюду должны терять энергию при рассеянии на реликтовых фотонах.
К чему приводит рассеяние электронов с характерным для космических лучей фактором Лоренца  Рассеяние на фотонах реликтового излучения приводит к образованию значительного числа рентгеновских фотонов с энергией
Рассеяние на фотонах реликтового излучения приводит к образованию значительного числа рентгеновских фотонов с энергией  Гц —
Гц —  а рассеяние на оптических фотонах создает поток
а рассеяние на оптических фотонах создает поток  -квантов с энергией
-квантов с энергией 
Обратное комптоновское рассеяние необходимо учитывать всегда, когда подозревается наличие релятивистских частиц и излучения высокой плотности энергии. Таким образом, в центральных областях квазаров этот механизм почти наверняка обеспечивает один из важнейших каналов отвода энергии релятивистских частиц. Особенно интересная ситуация может возникать в некоторых квазарах, в которых плотность энергии синхротронного излучения настолько велика, что обратное комптоновское рассеяние радиоизлучения на генерирующих его электронах может стать преобладающим механизмом торможения. Этот эффект называют «обратной комптоновской катастрофой».
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
- 4.4. ОБРАЗОВАНИЕ ПАР
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
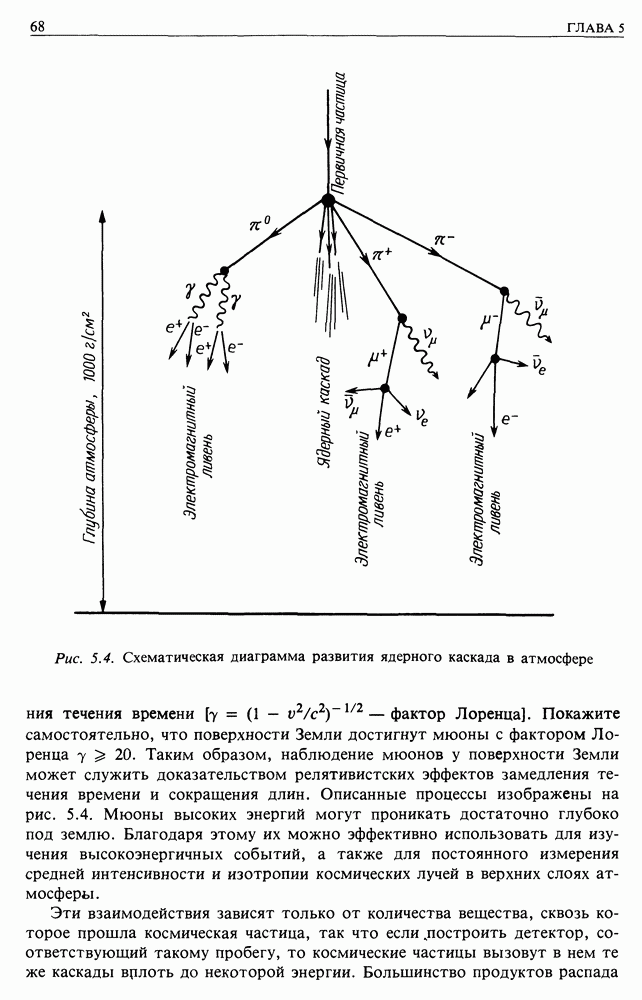
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
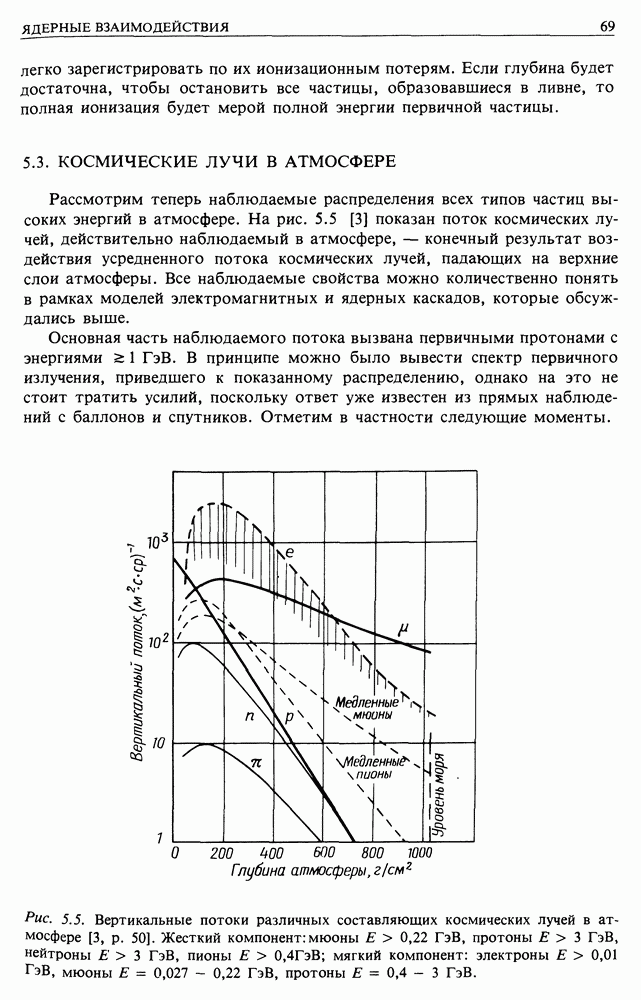
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
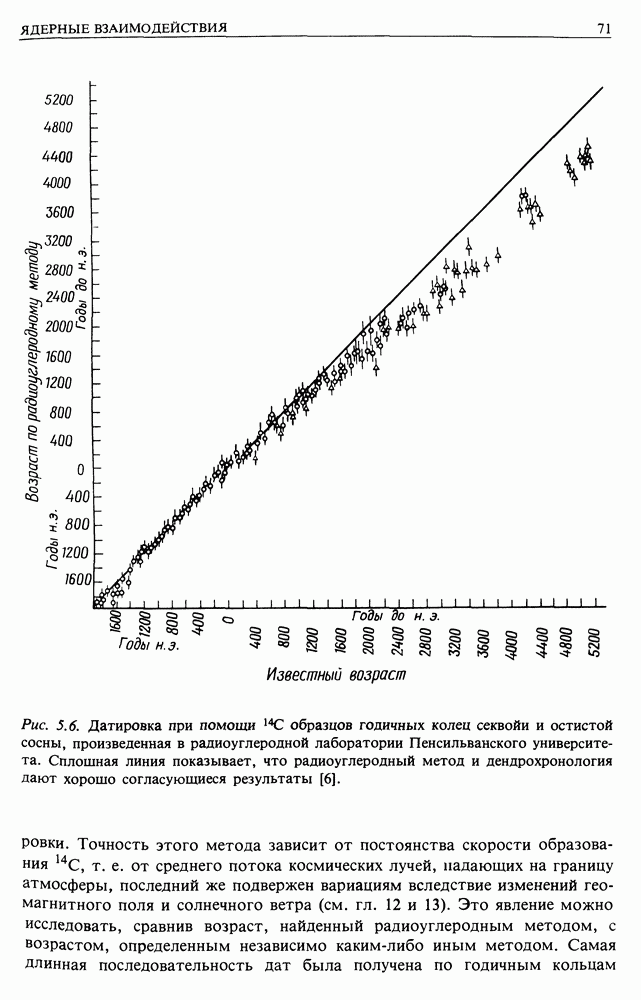
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
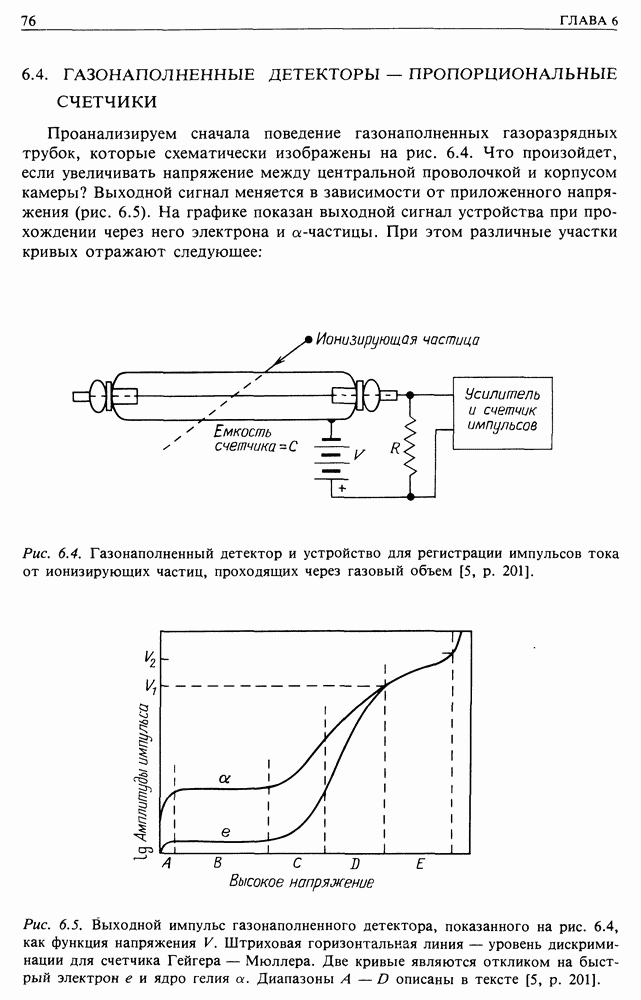
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
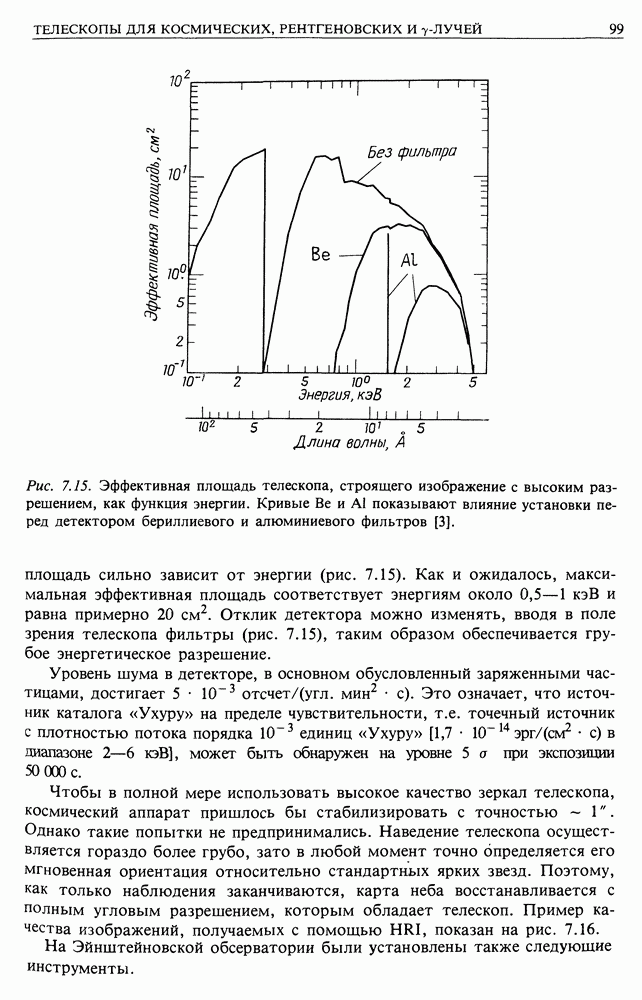
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
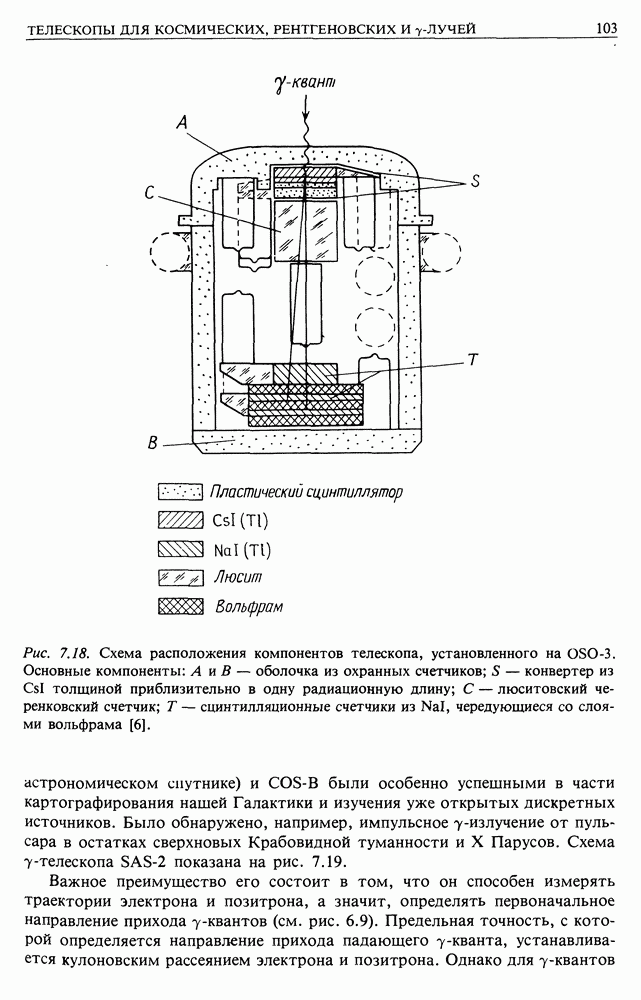
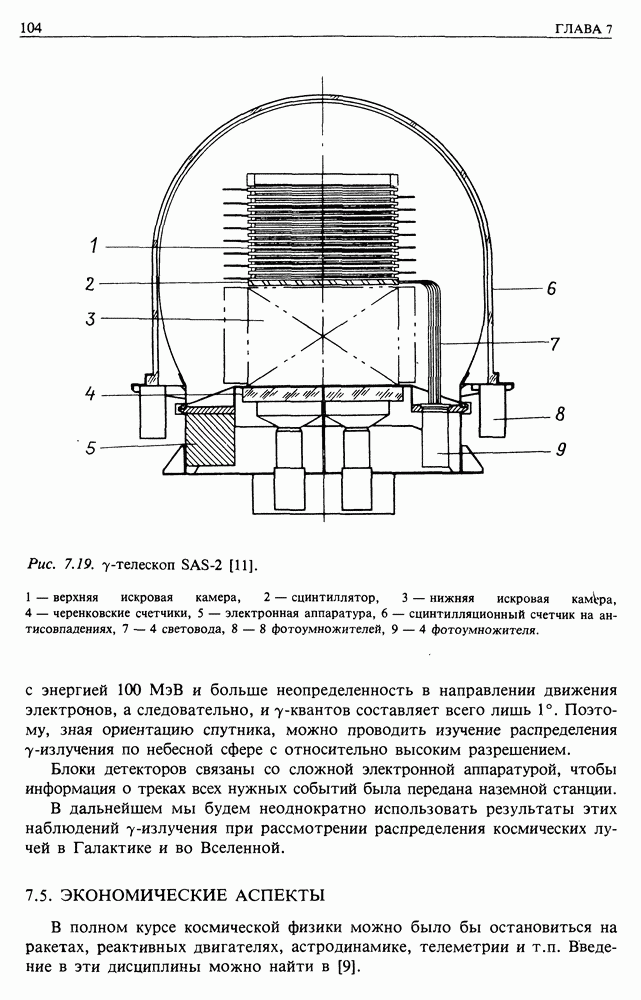
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
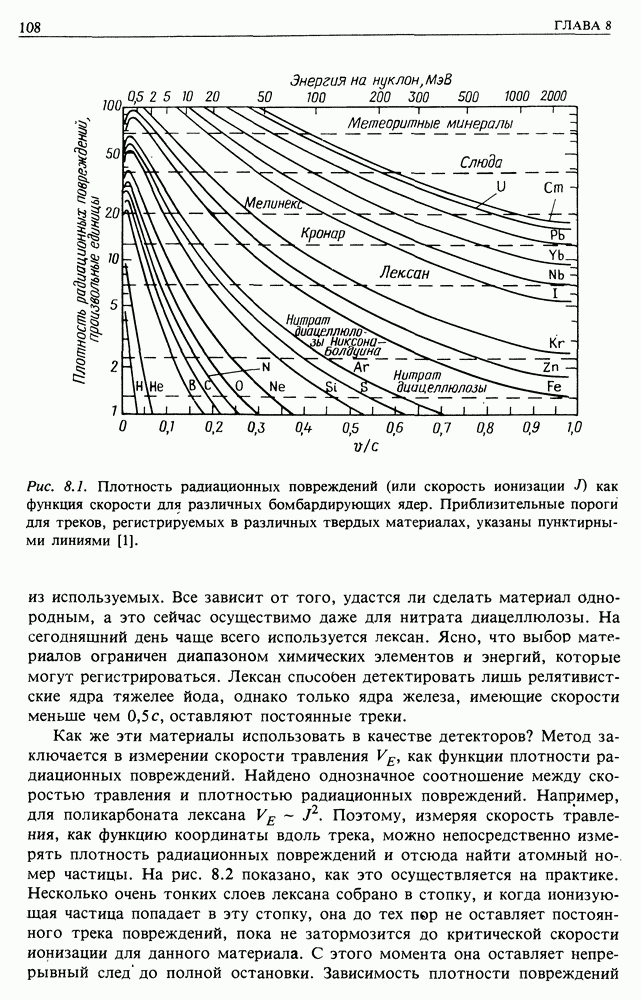
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
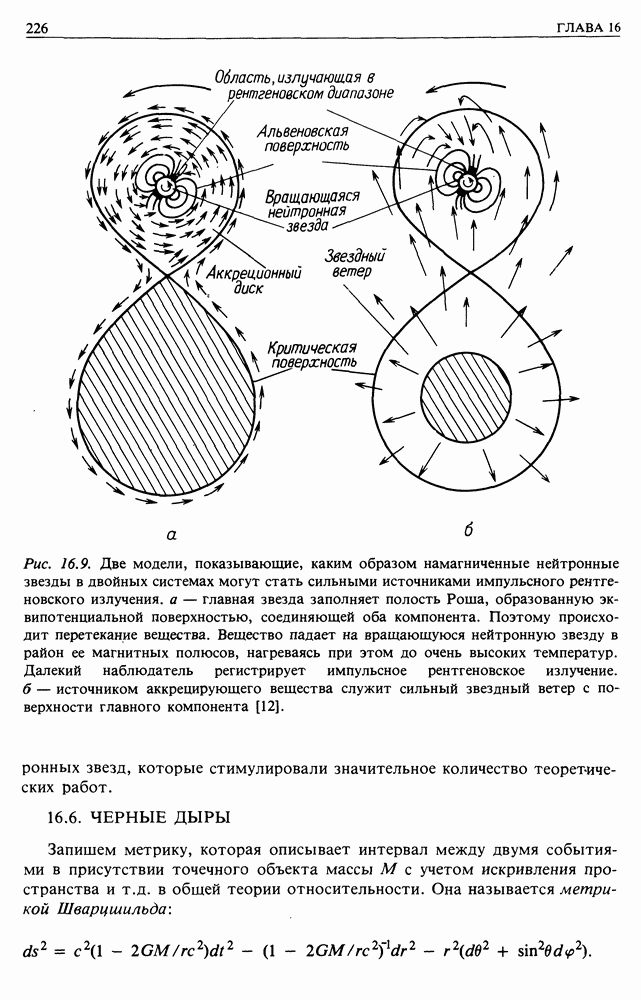
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
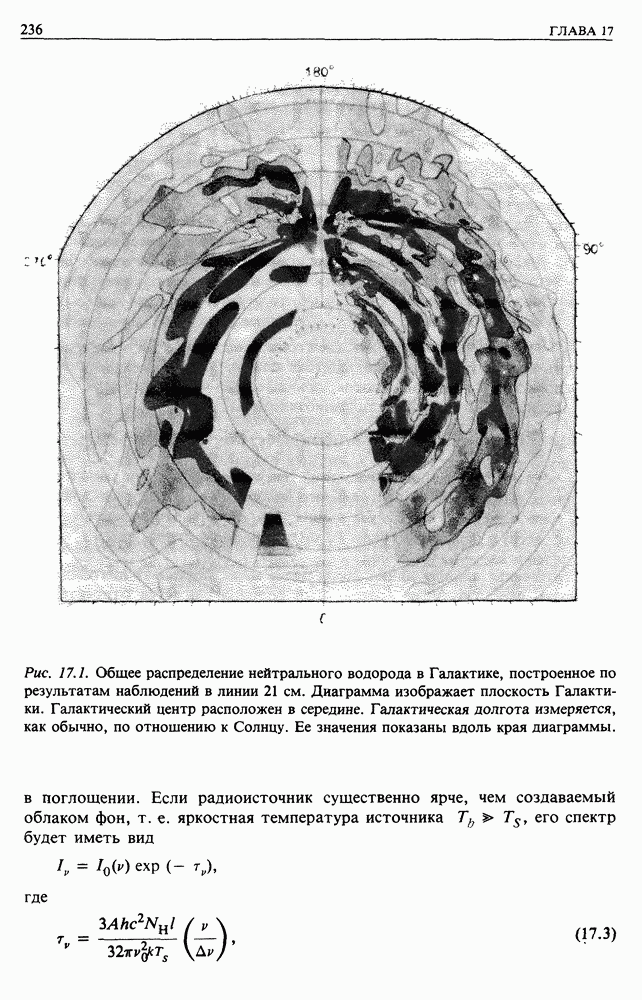
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
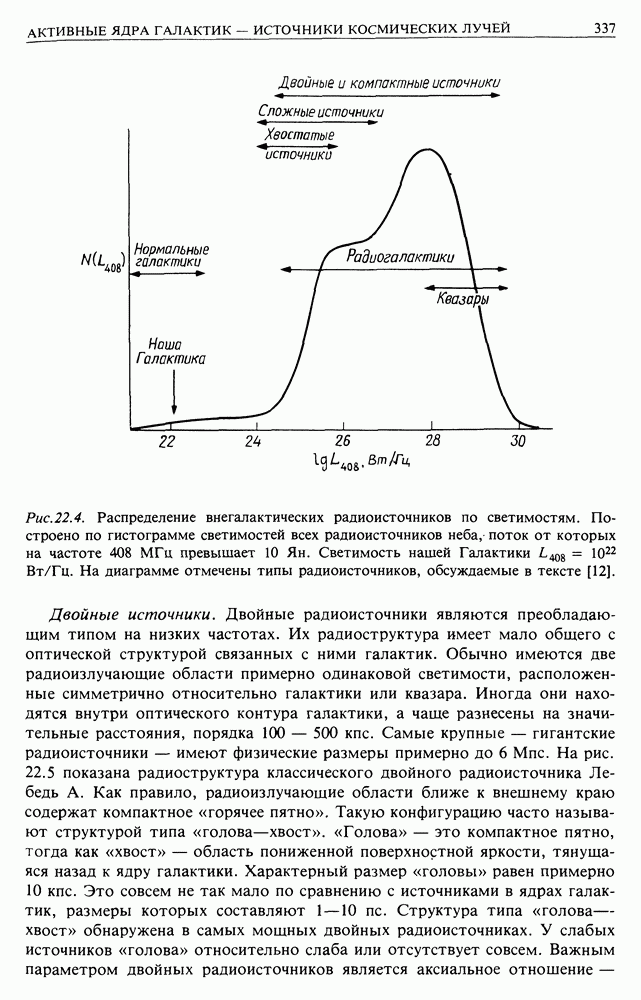
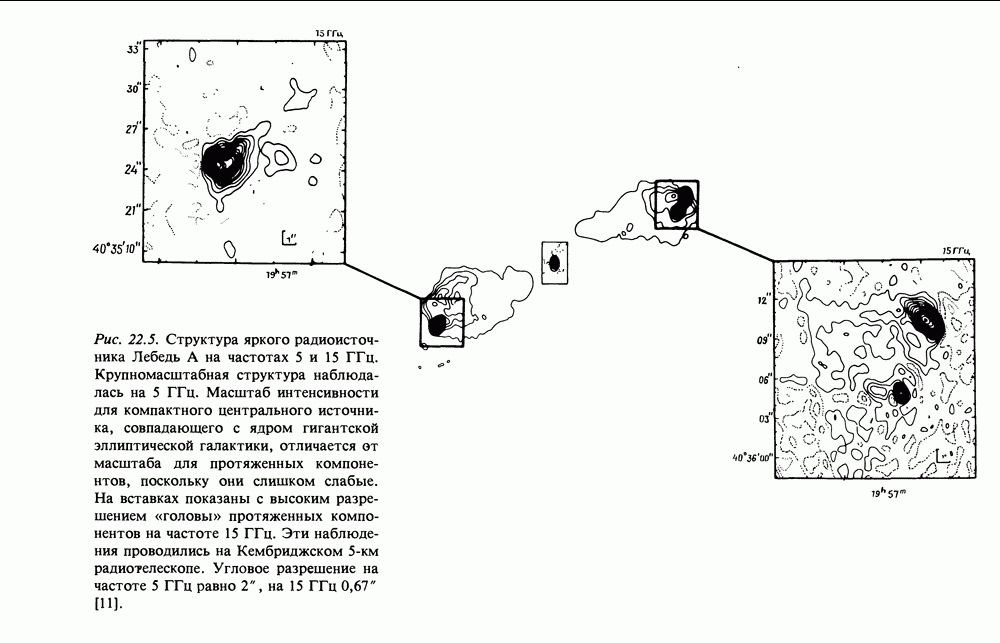
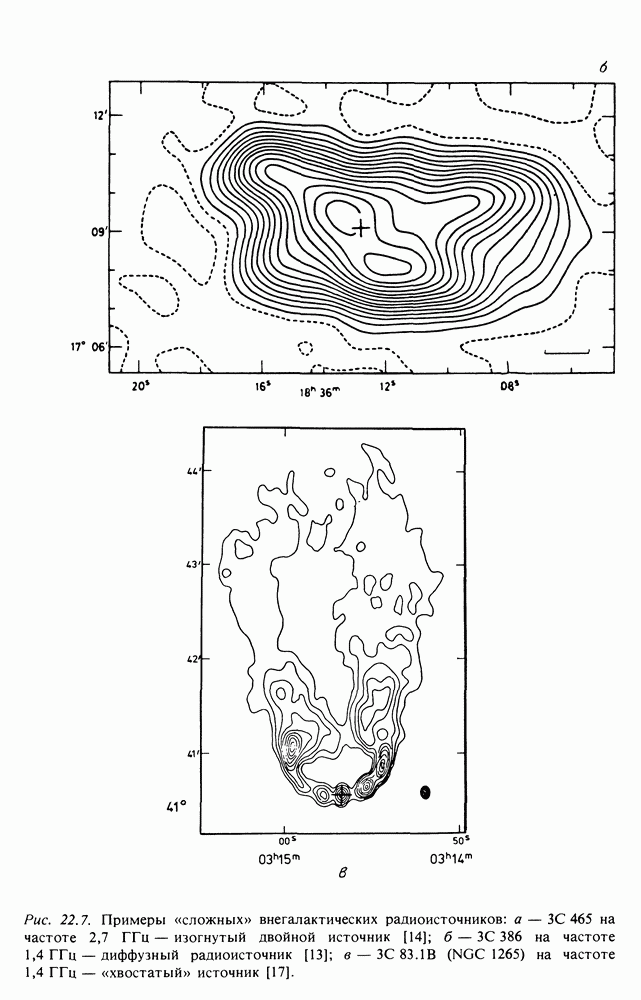
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
- 22.5. ИСТОЧНИК ЭНЕРГИИ
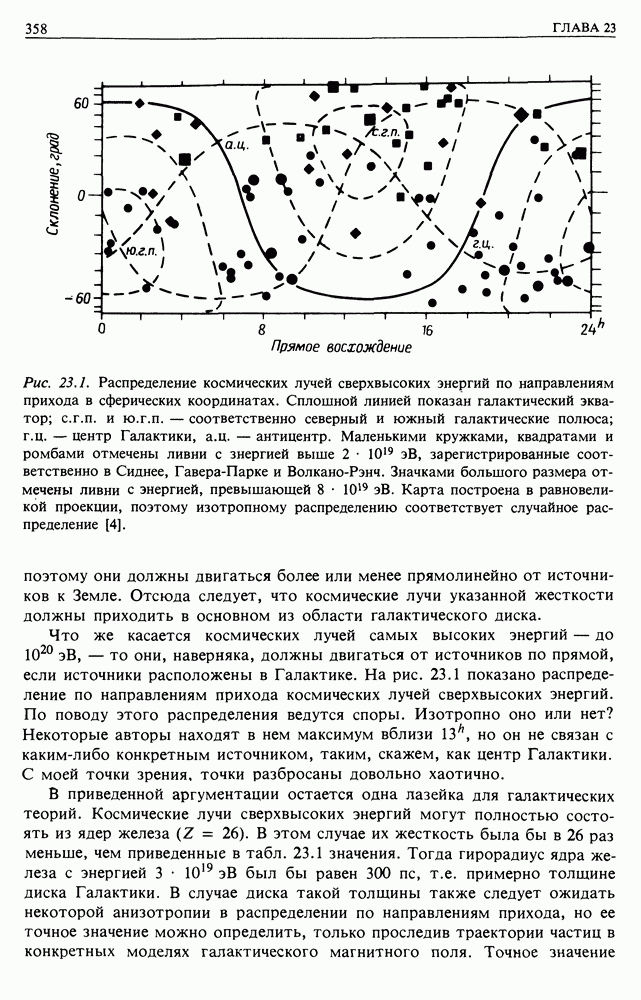
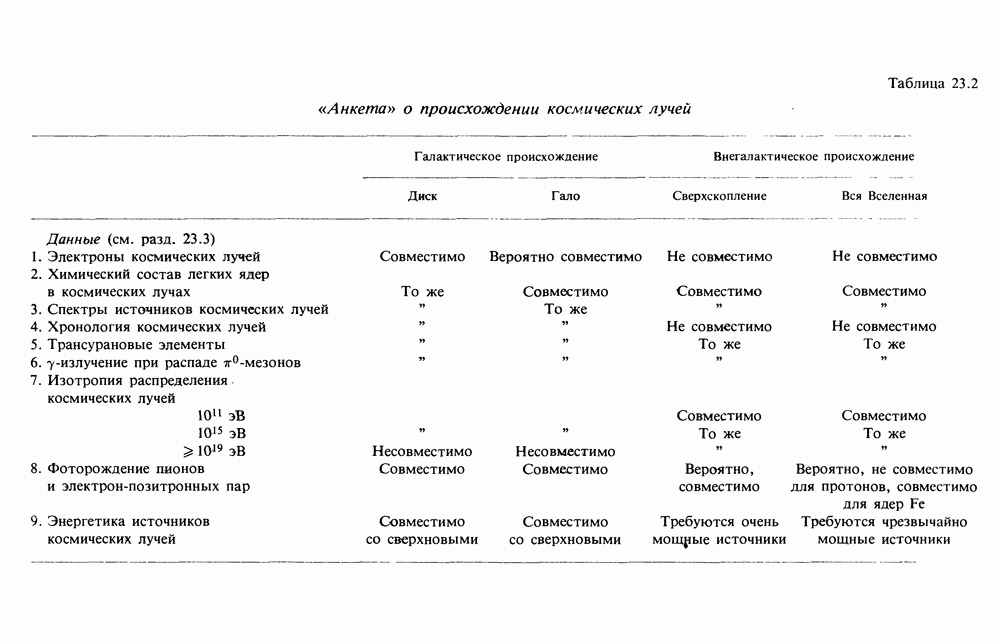
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
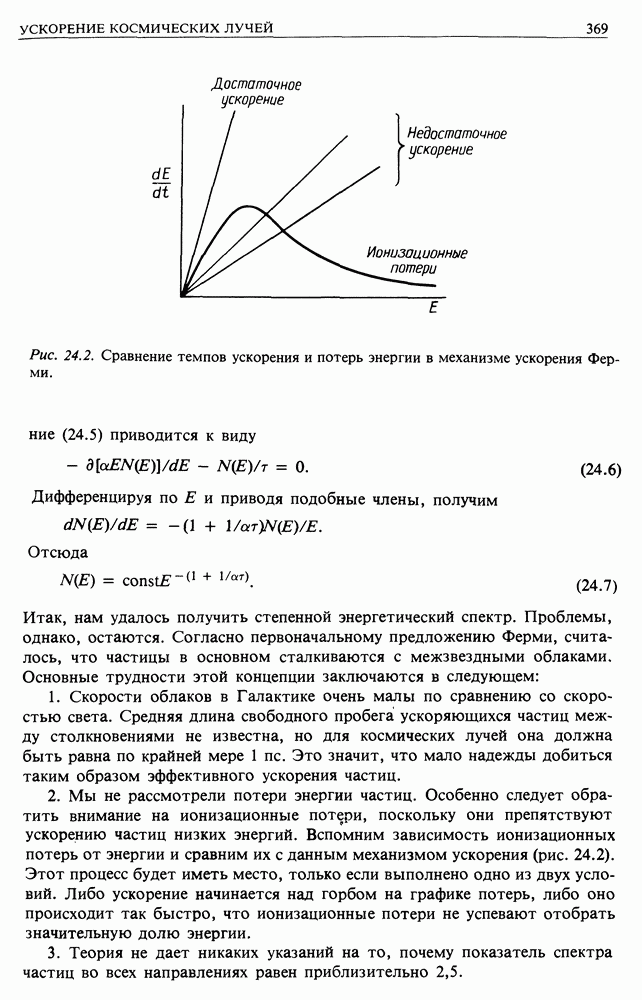
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ