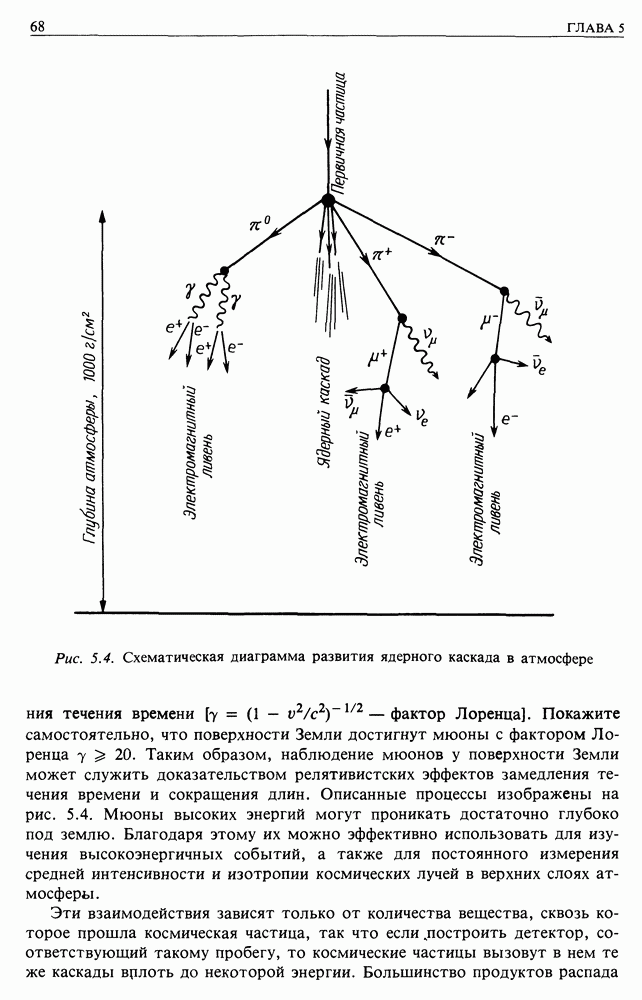
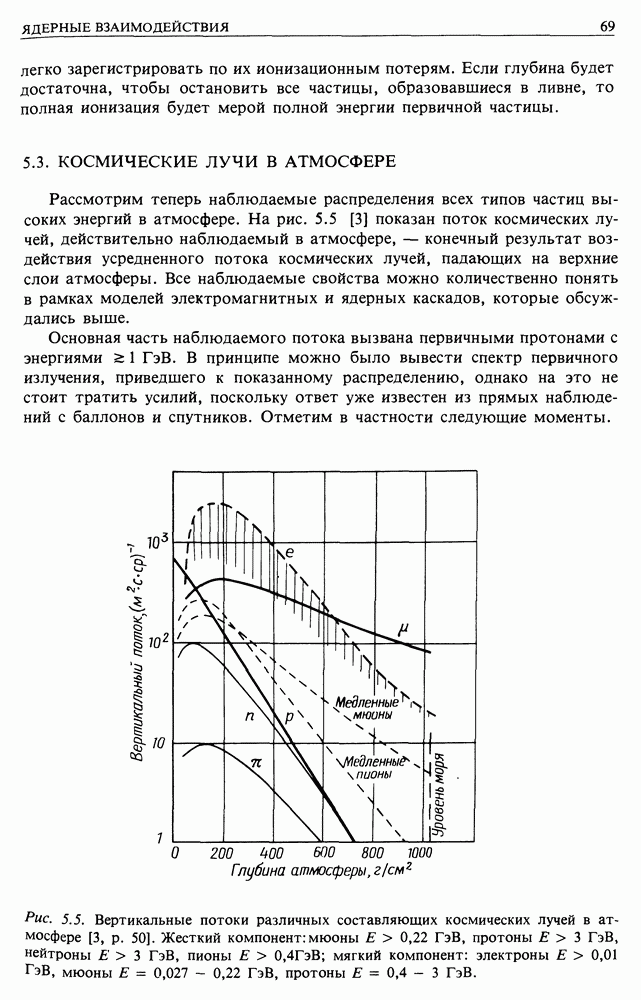
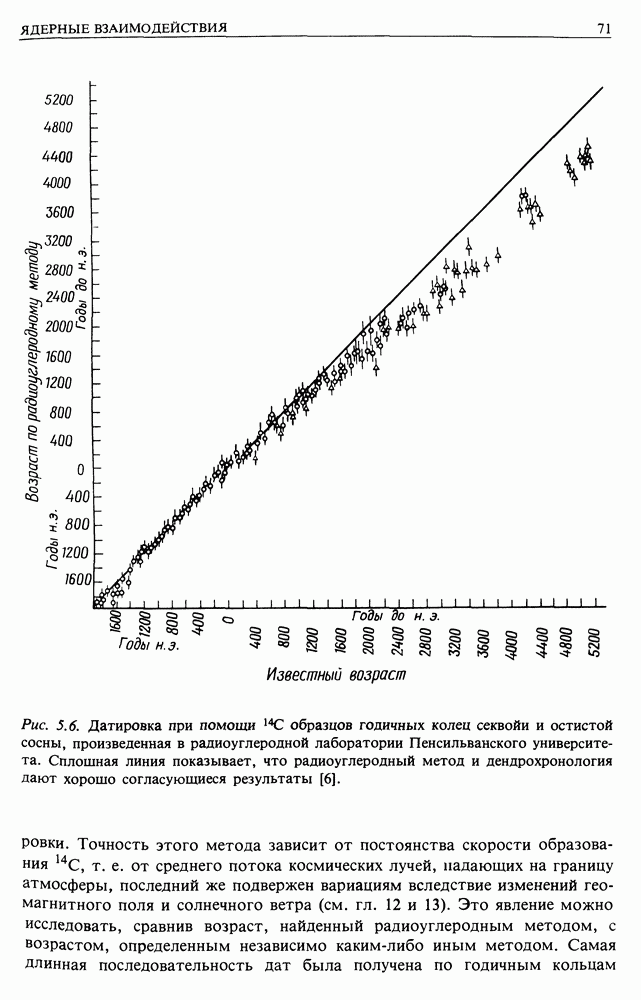
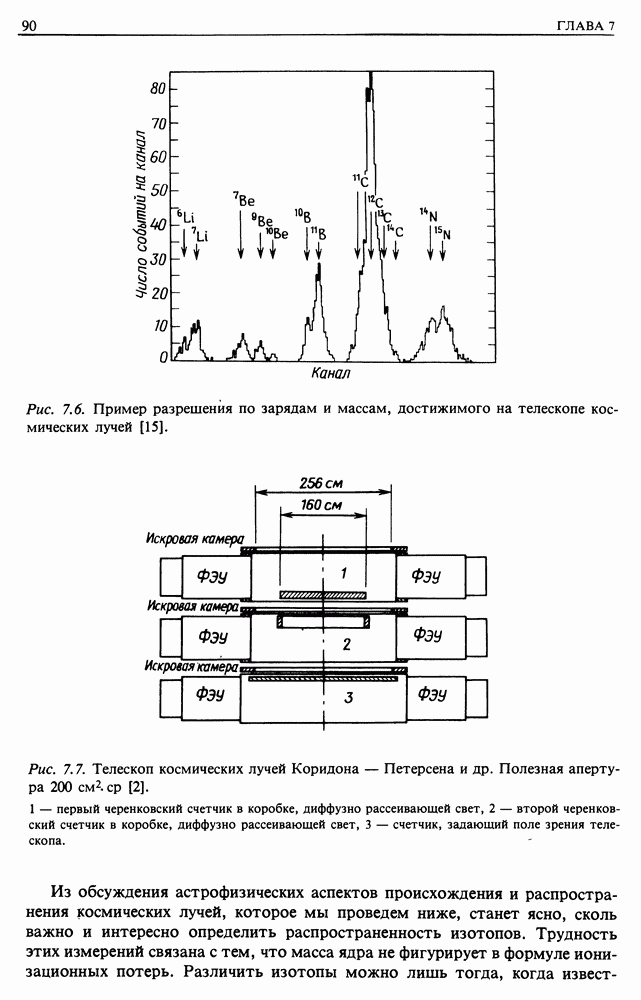
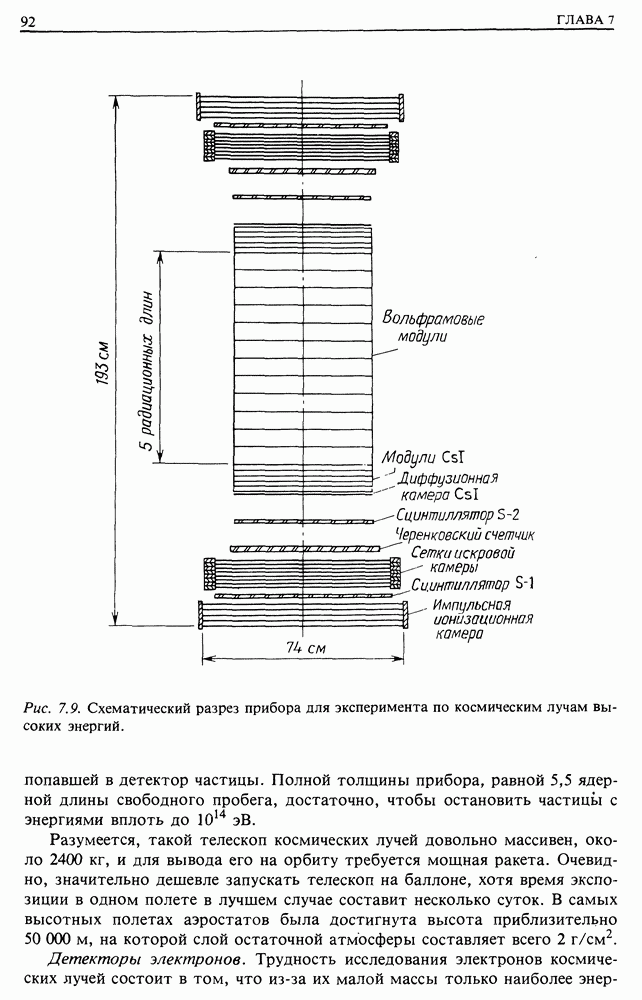
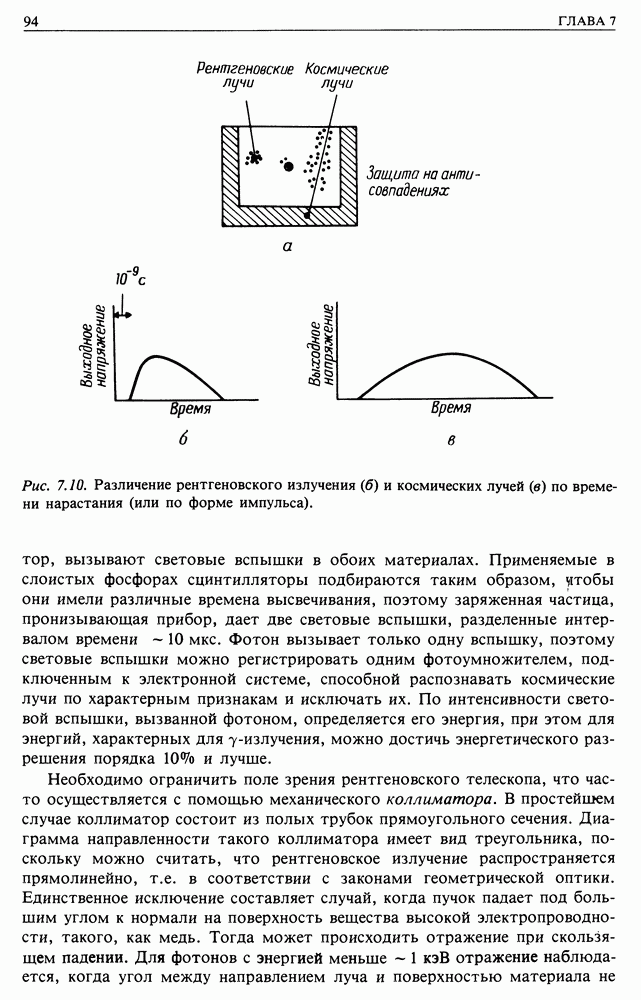
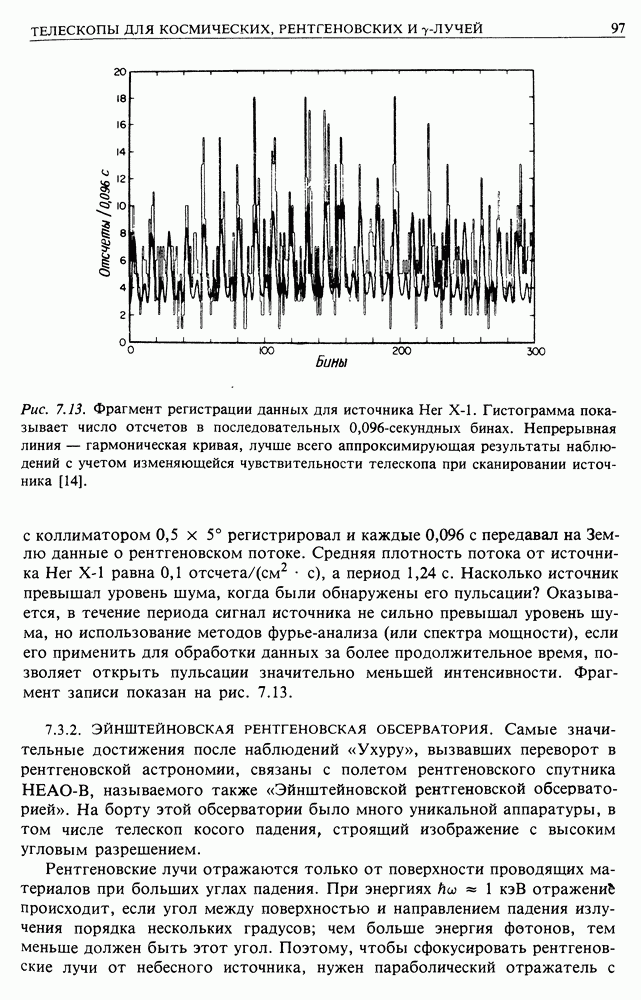
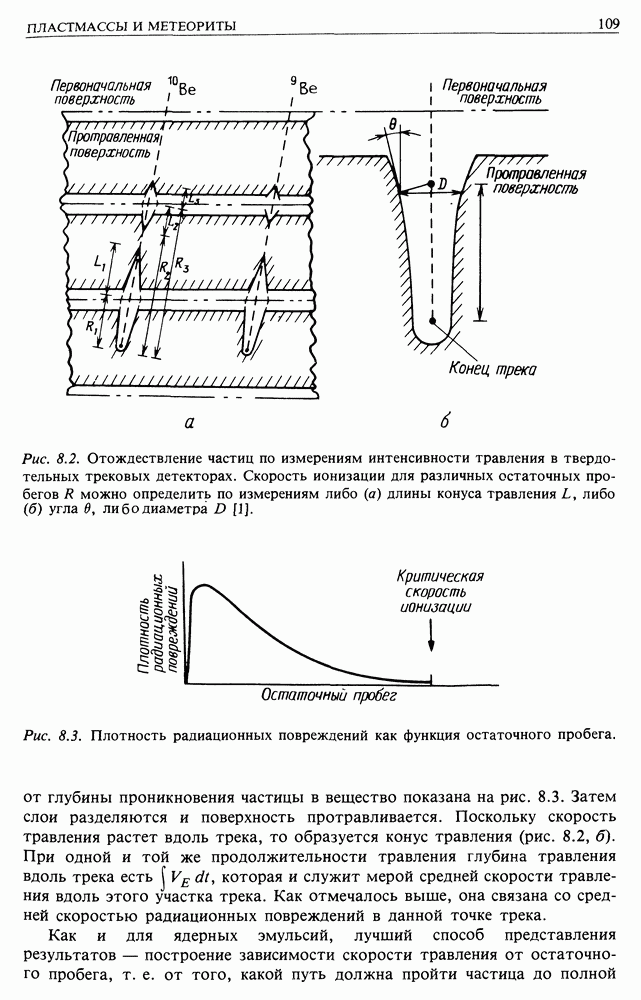
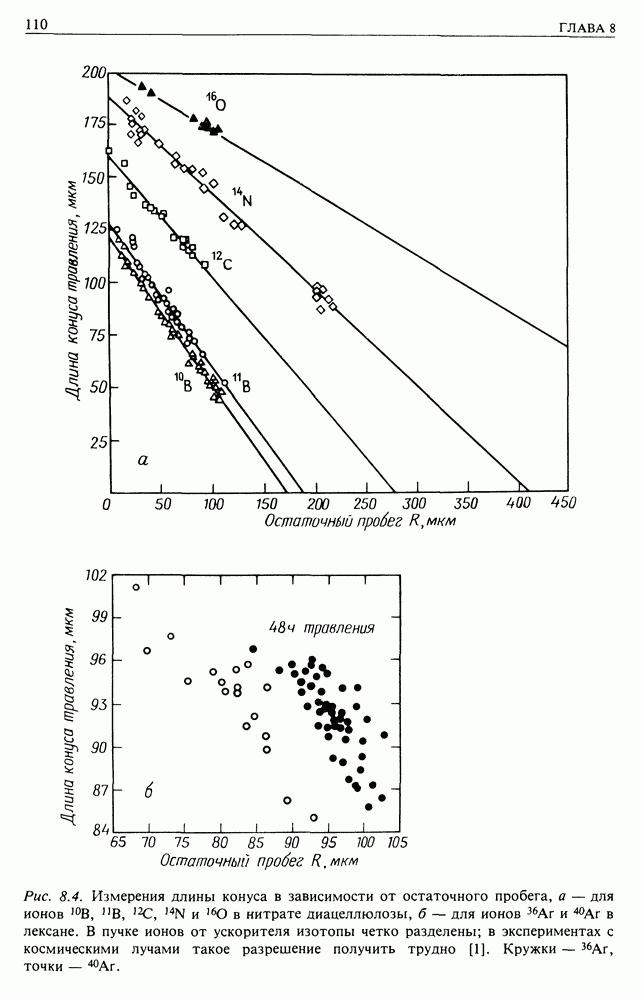
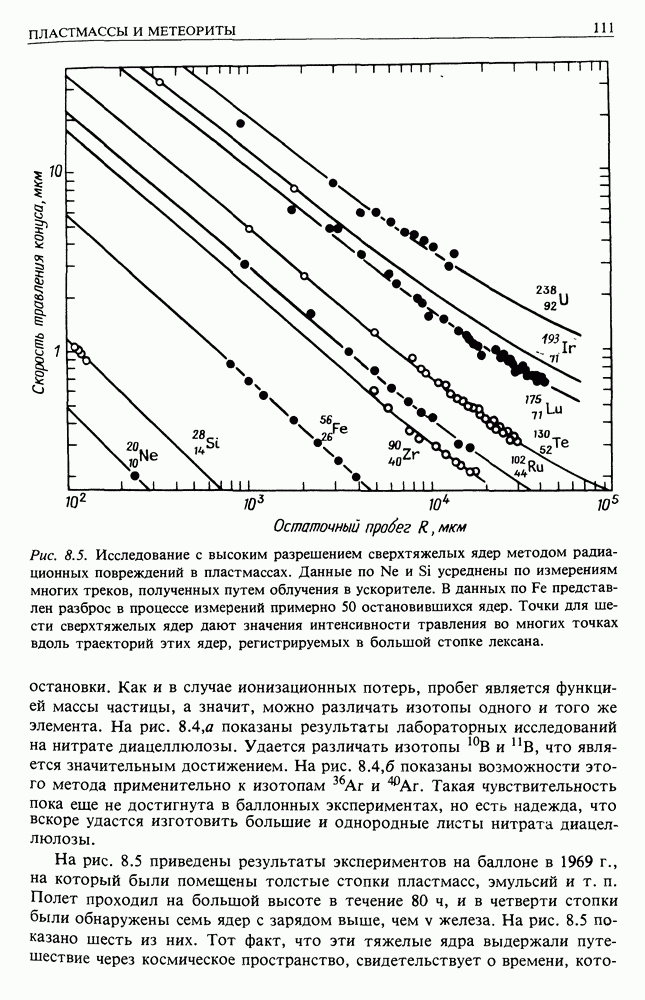
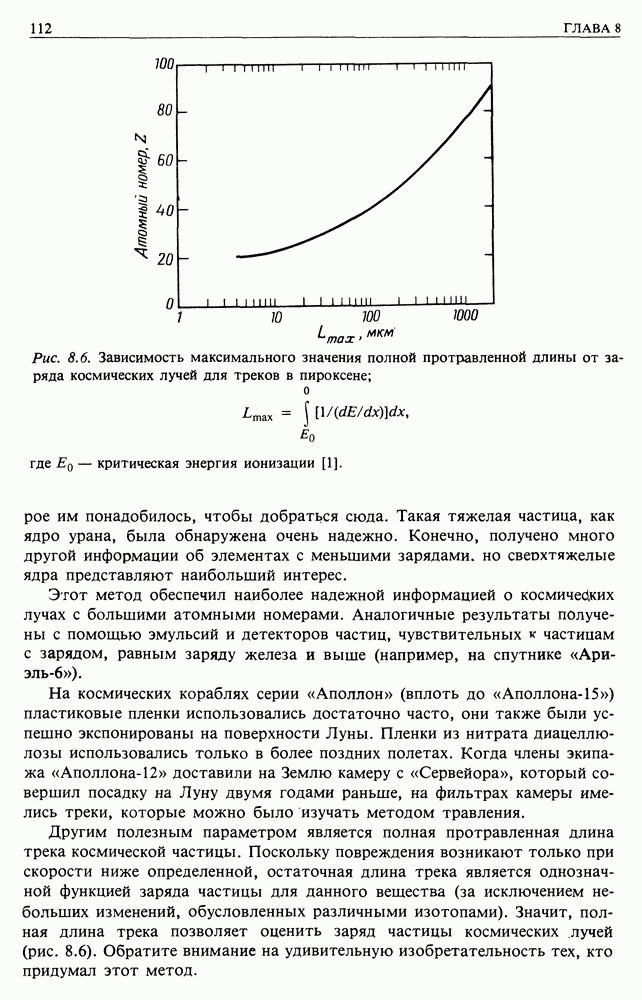
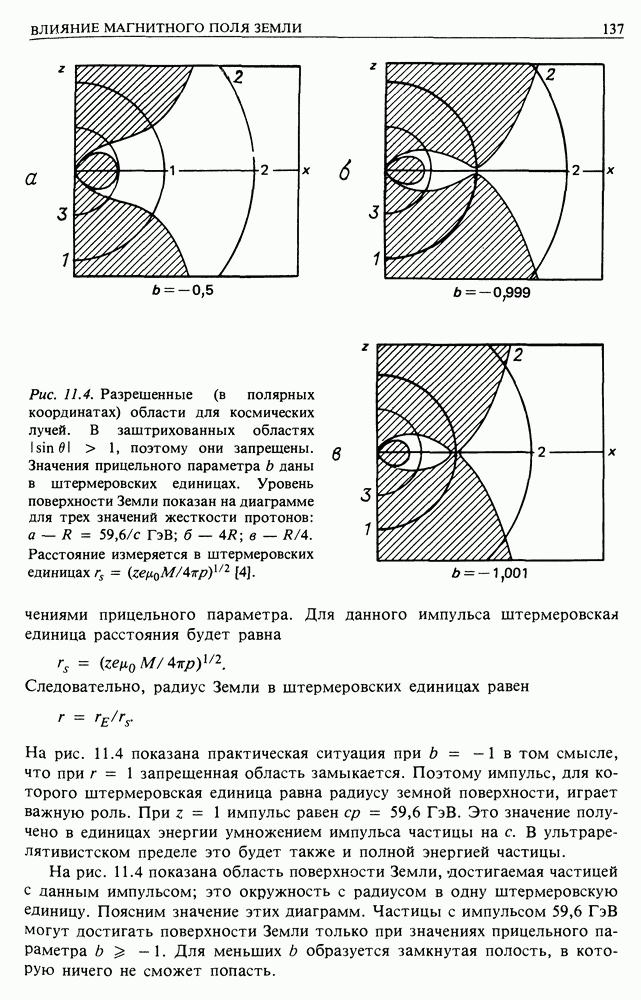
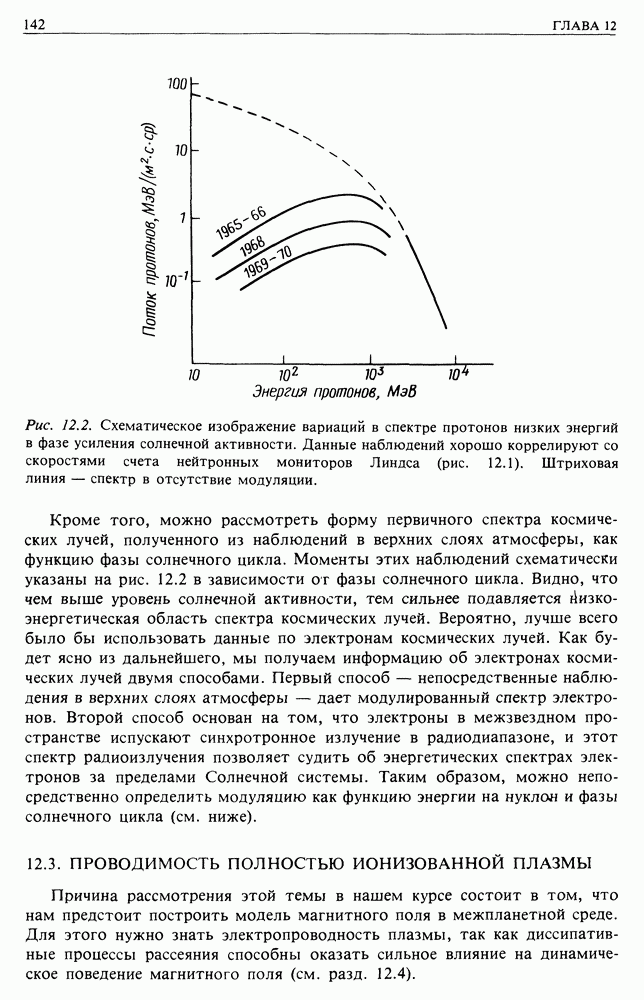
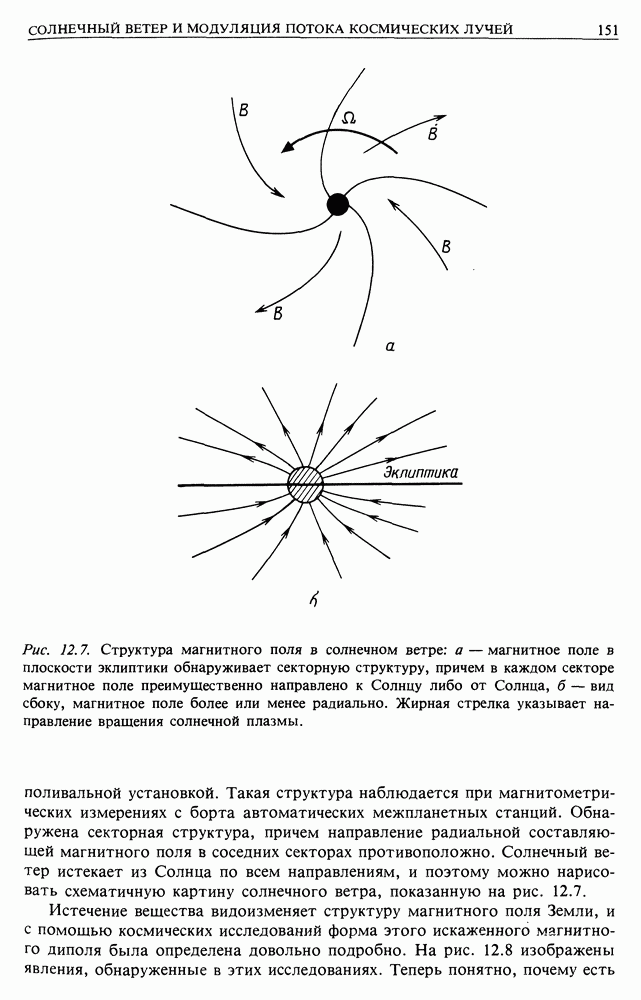
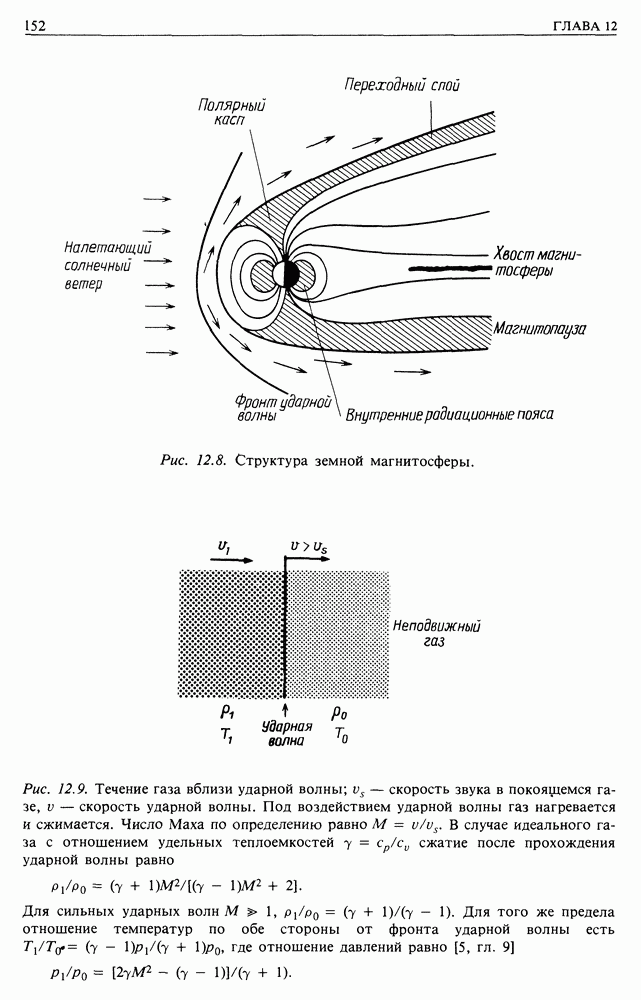
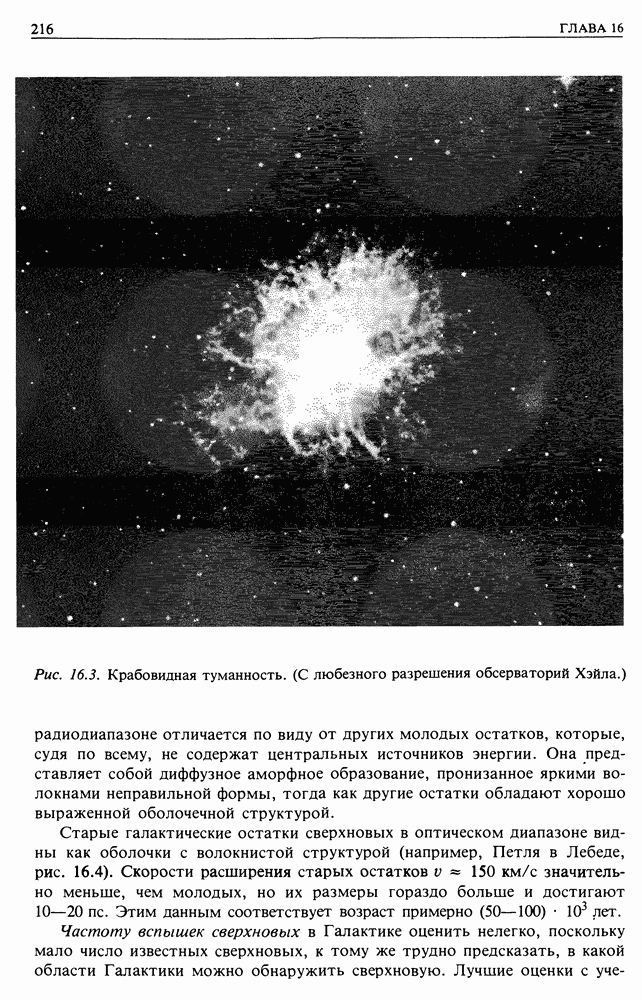
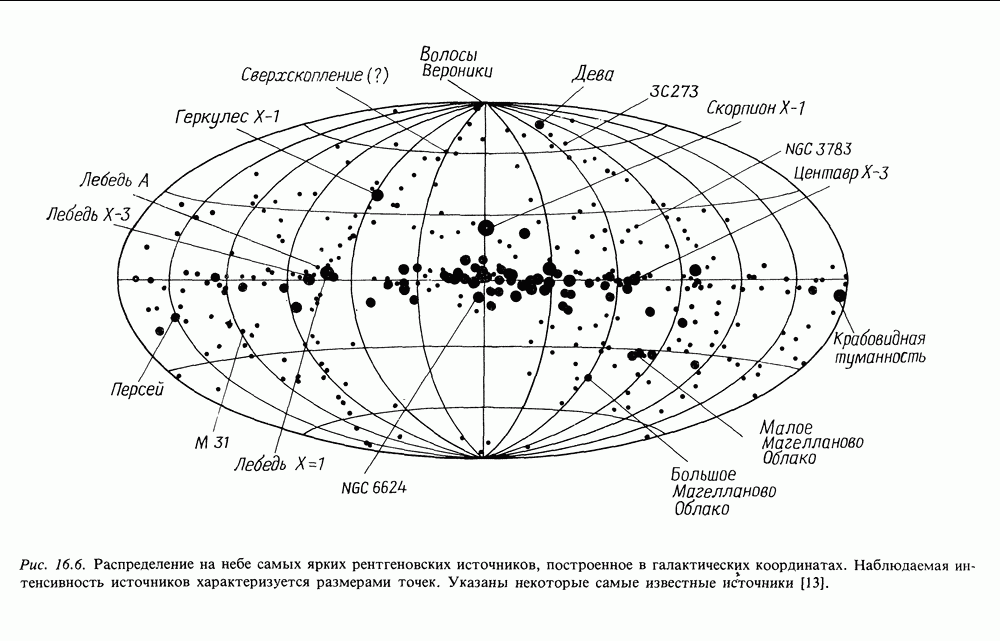
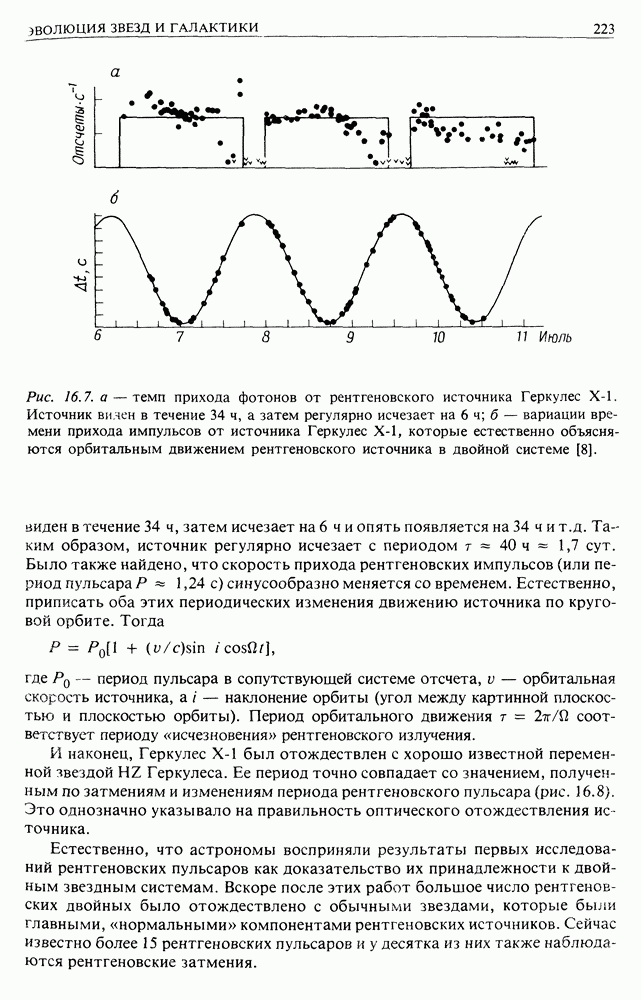
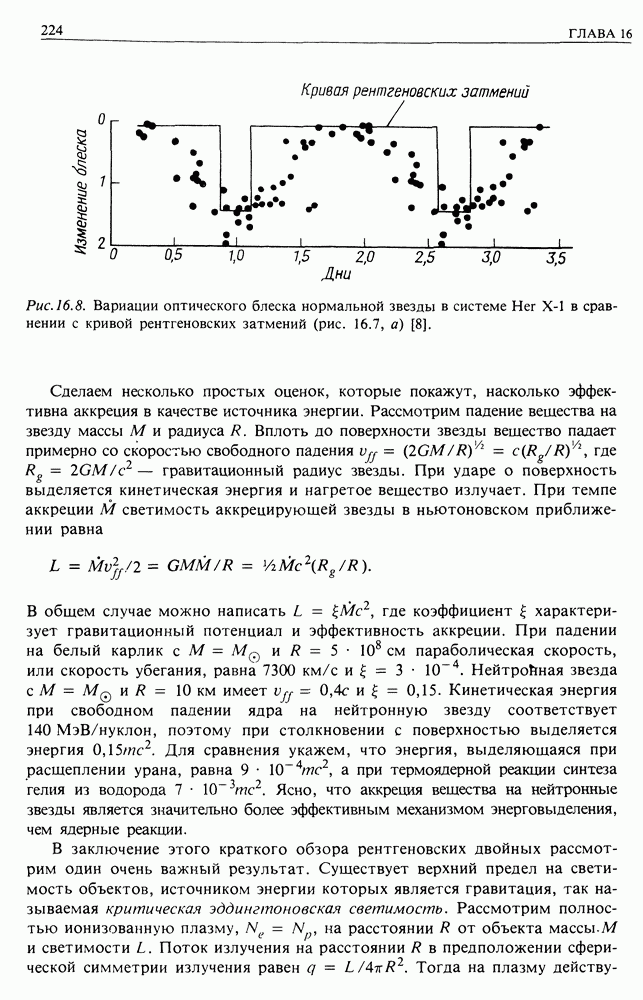
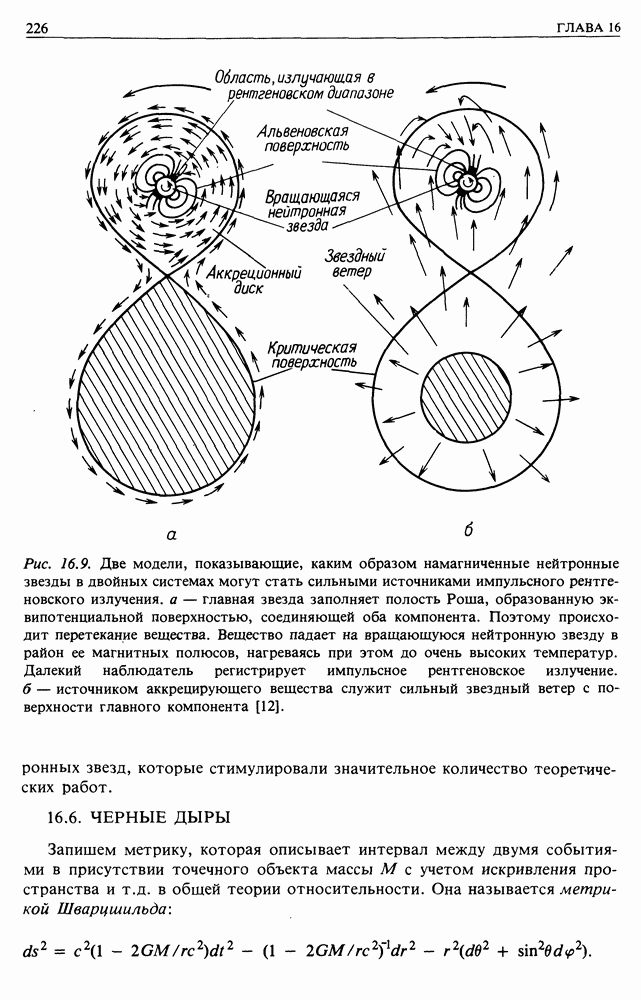
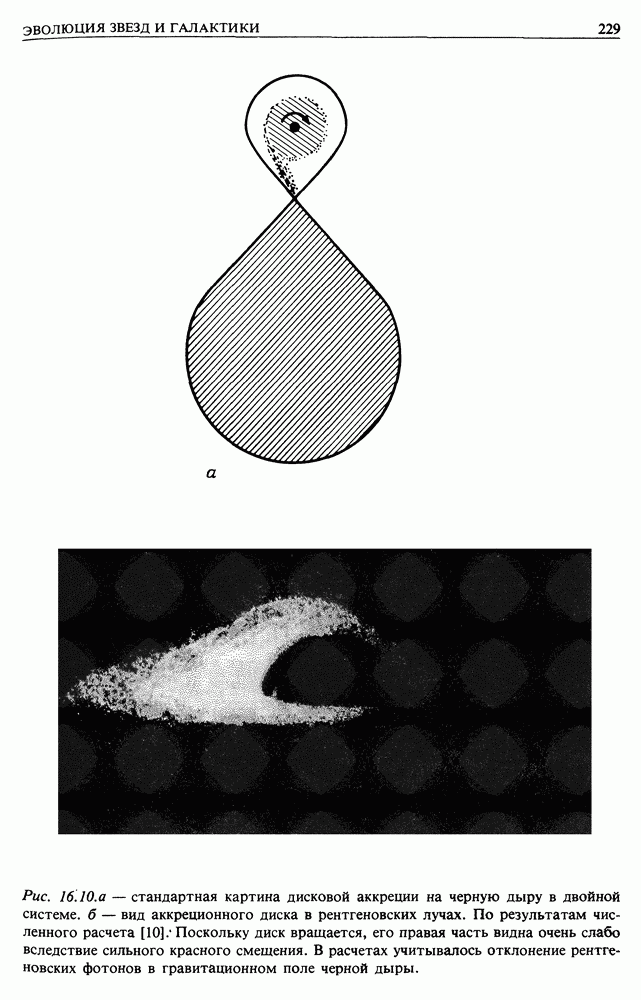
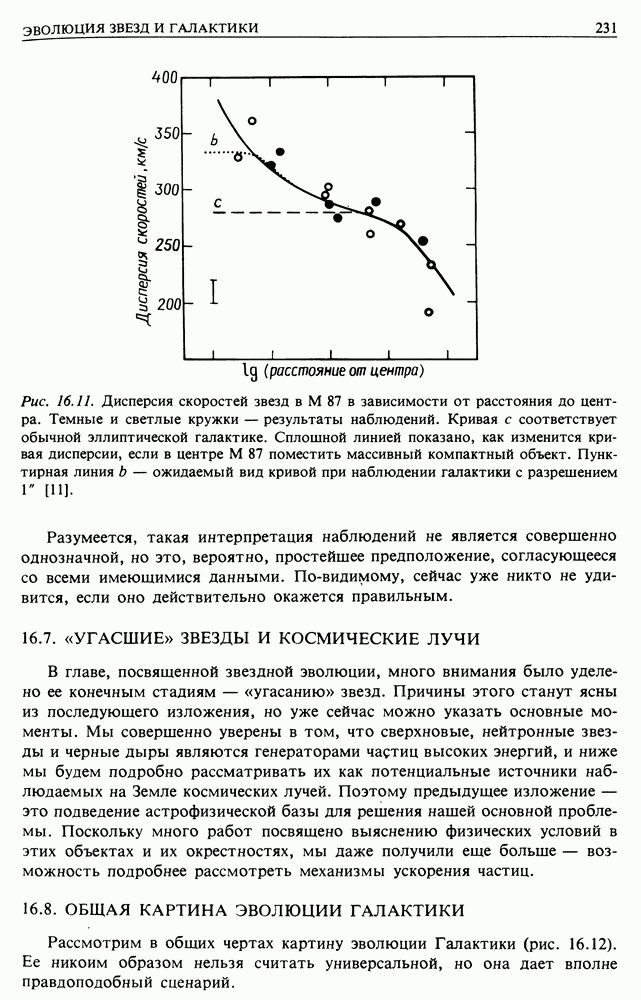
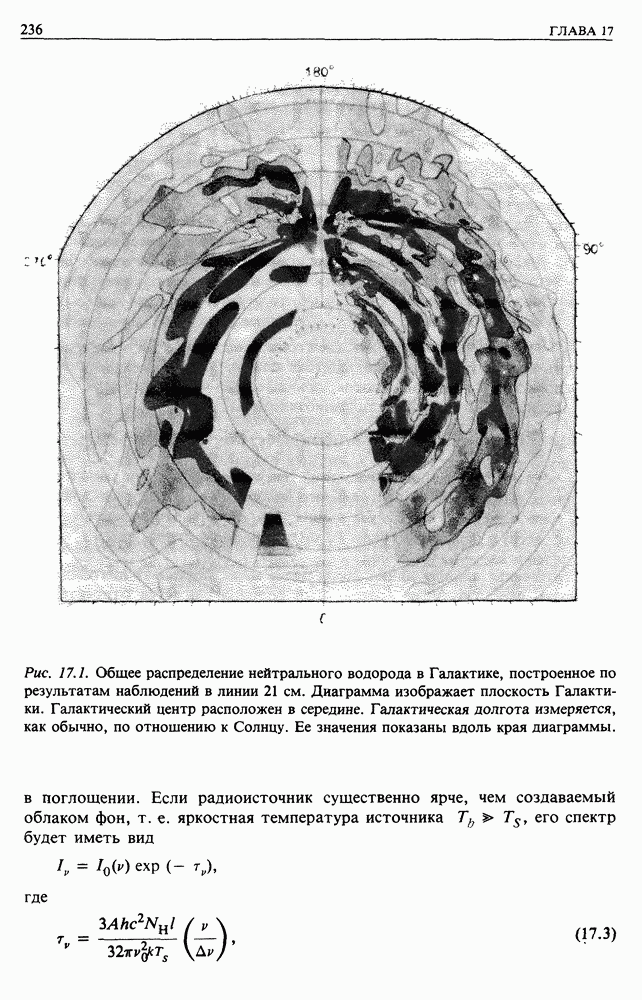
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
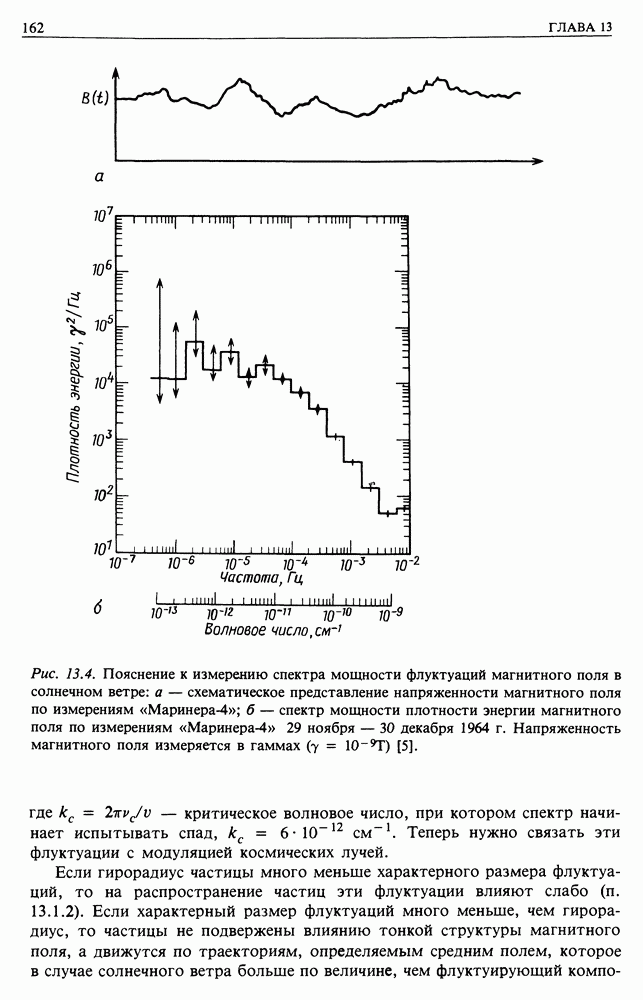
12.4. ВМОРАЖИВАНИЕ ПОТОКА
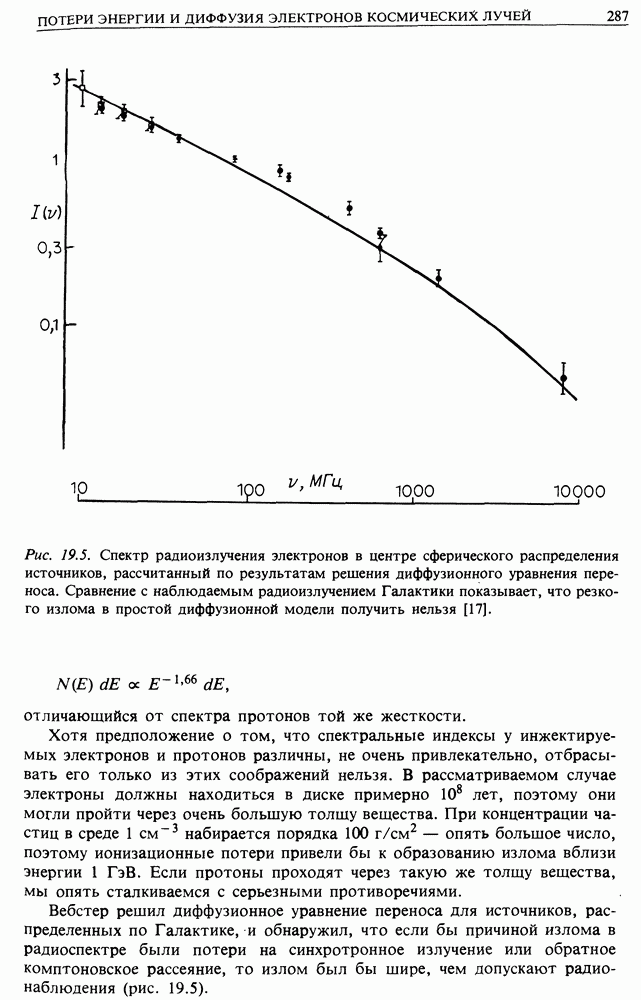
Отличительной особенностью всех видов плазмы, с которыми мы будем иметь дело в астрофизике, является очень высокая проводимость или, другими словами, частицы имеют очень большую среднюю длину свободного пробега. Значительное упрощение достигается благодаря тому, что в пределе бесконечной проводимости магнитное поле ведет себя так, как если бы его силовые линии были вморожены в плазму.
Возможны два подхода к решению задачи. Можно выписать полные магнитогидродинамические уравнения, затем перейти к пределу бесконечной проводимости и найти динамику магнитного поля и потока частиц. Это — математический подход, но он не дает непосредственно понять физический смысл. Воспользуемся другим методом и рассмотрим взаимодейсвие между потоком, связанным с данными токами, и его изменением, когда токи движутся или деформируются. Затем мы рассмотрим более математический подход.
Сформулируем теорему. Представим магнитное поле в виде силовых линий, так что число линий, проходящих через малую площадку, перпендикулярную этим силовым линиям, равно напряженн лсти поля. Тогда при движениях в плазме магнитные поля изменяются таким образом, что  иловые линии движутся и изменяют свою форму так, как если бы плазма была их носителем.
иловые линии движутся и изменяют свою форму так, как если бы плазма была их носителем.
12.4.1. Физический подход. Воспользуемся методом, изложенным в монографии Ратклиффа «Физика ионосферы и магнитосферы» [6]. Согласно

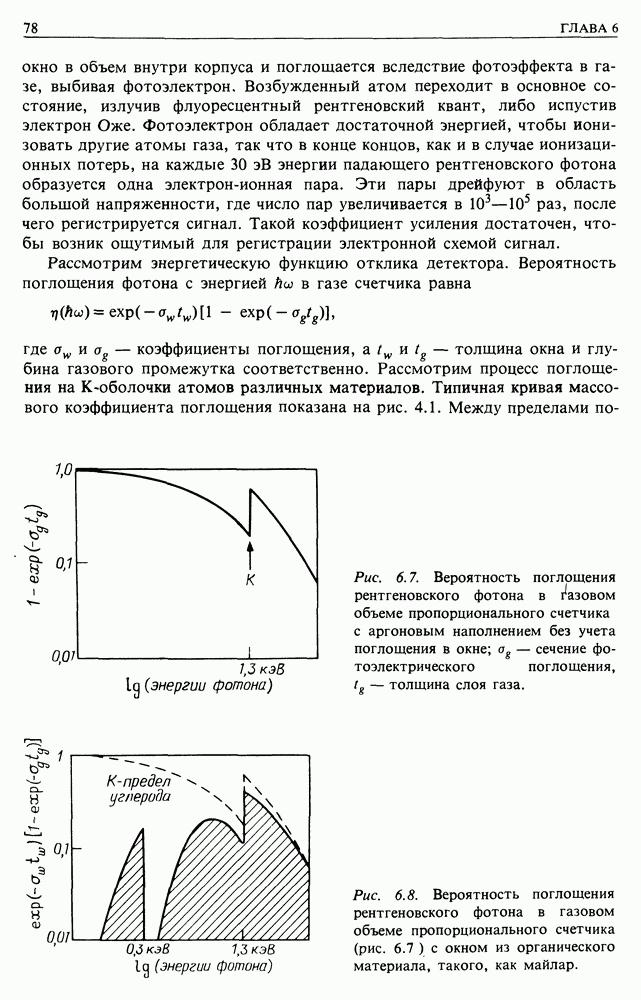
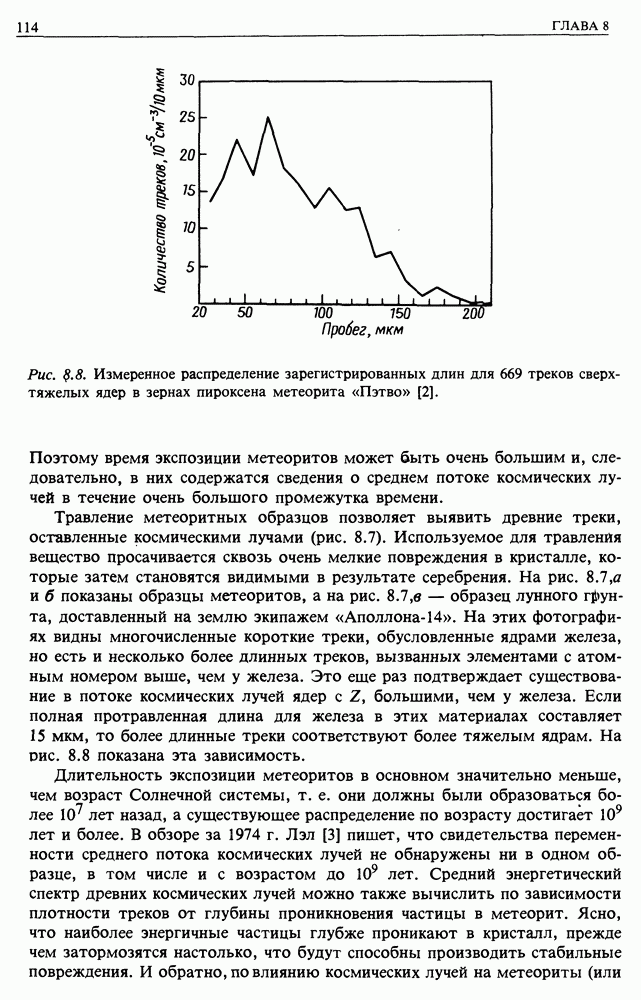
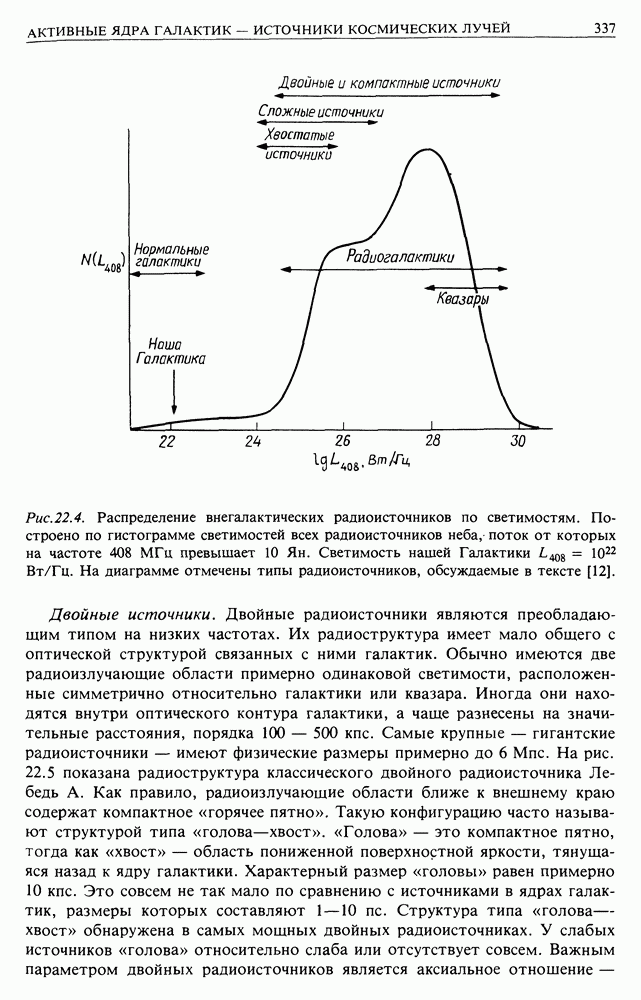
Рис. 12.4.
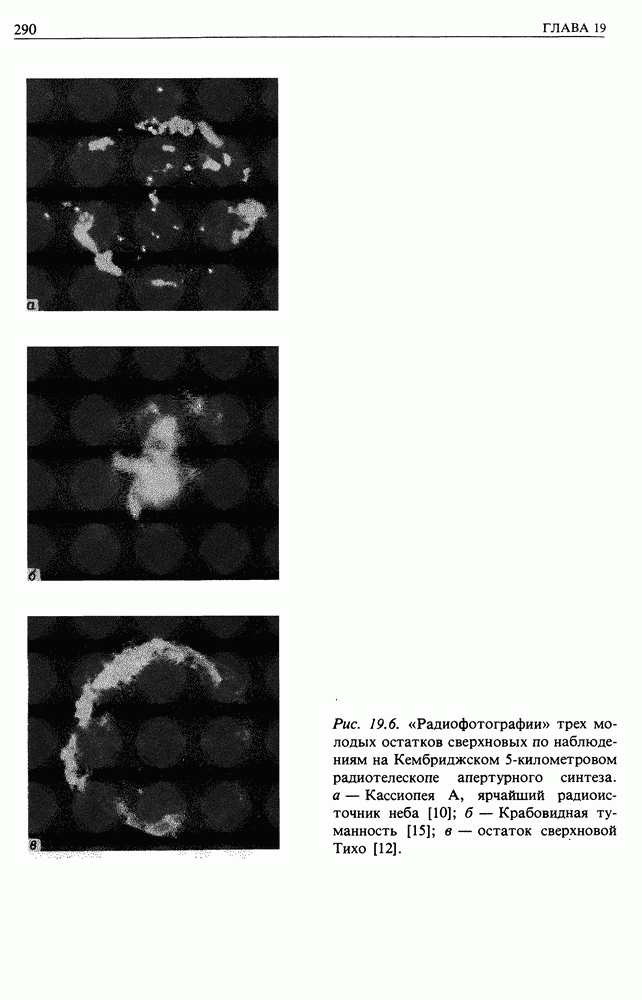
его методу, сначала изучается изменение постоянных петель тока в изменяющемся магнитном поле, а затем анализируется изменение формы этих петель.
Рассмотрим токи в плазме бесконечной проводимости. Сначала возьмем небольшой замкнутый контур в плазме — проволочное кольцо (петля) без источника тока (рис. 12.4). Тогда электродвижущая сила может быть индуцирована в этом витке только вследствие изменения потока через контур.

Поток  состоит из двух частей: первая обусловлена током в самой петле
состоит из двух частей: первая обусловлена током в самой петле  вторая — внешними токами
вторая — внешними токами  Пусть индуктивность петли равна
Пусть индуктивность петли равна  тогда по определению
тогда по определению

Если внешние токи изменяются так, что меняется  то в цепи наведется электродвижущая сила, и результирующее уравнение для наведенного тока в контуре будет иметь вид
то в цепи наведется электродвижущая сила, и результирующее уравнение для наведенного тока в контуре будет иметь вид

Предположим, что сопротивление контура равно нулю (сверхпроводящая проволока). Тогда плазма будет бесстолкновительной и

т. е.

Это означает, что хотя  может меняться, но вследствие изменений наводится ток, полностью компенсирующий уменьшение, которое может быть связано с изменениями Это свойство обусловлено тем, что контур по предположению — сверхпроводящий. Это не соответствует действительности, если
может меняться, но вследствие изменений наводится ток, полностью компенсирующий уменьшение, которое может быть связано с изменениями Это свойство обусловлено тем, что контур по предположению — сверхпроводящий. Это не соответствует действительности, если  конечная величина, но очень близко к истине, если
конечная величина, но очень близко к истине, если  чрезвычайно мало.
чрезвычайно мало.

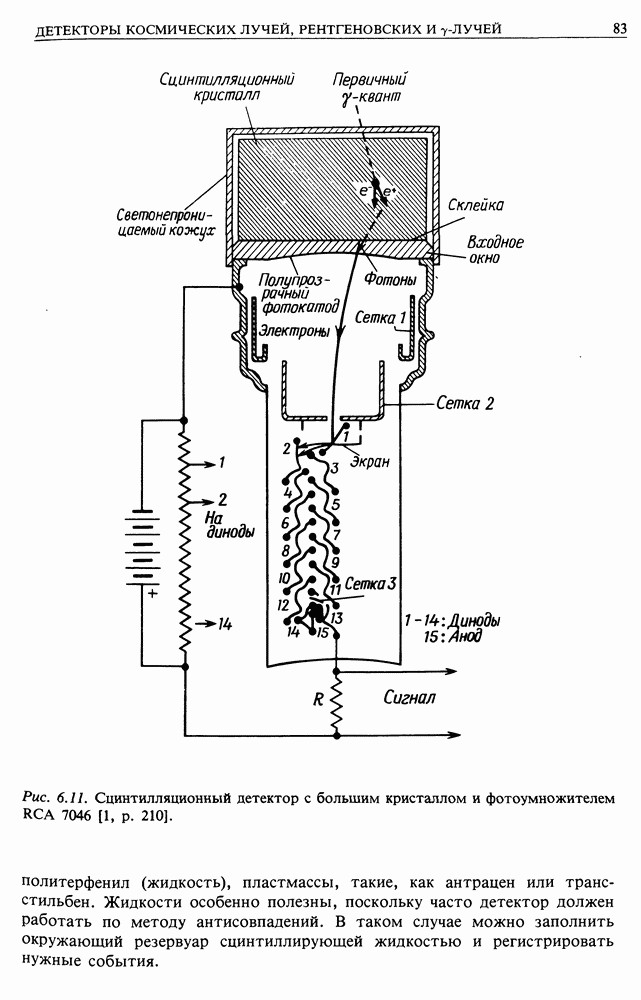
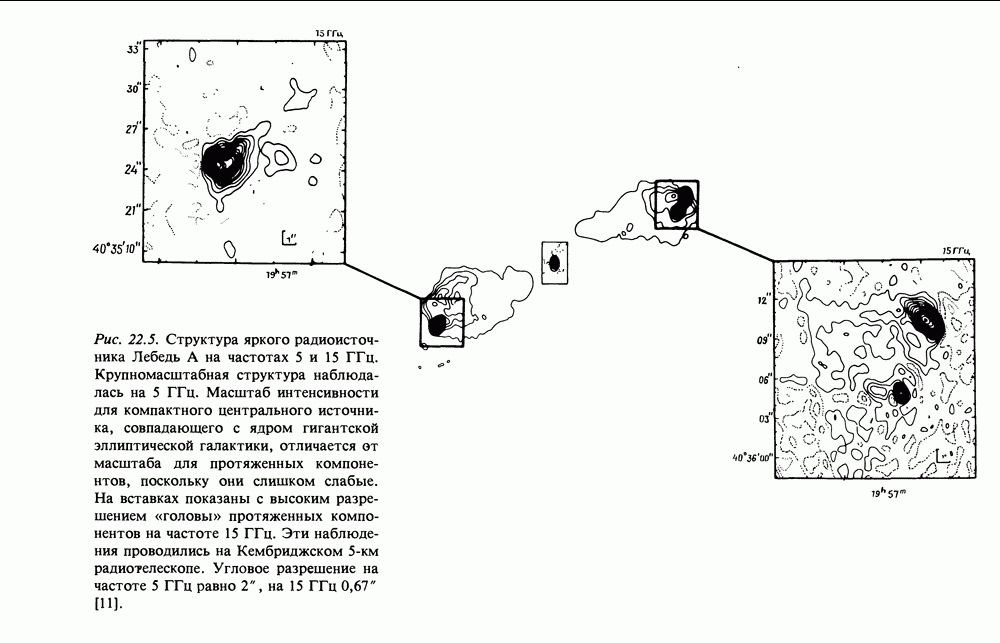
Рис. 12.5.
Предположение о существовании тока  текущего без э.д.с., вполне оправдано. Дело в том, что ток течет в проводнике с нулевым сопротивлением, поэтому он не затухает.
текущего без э.д.с., вполне оправдано. Дело в том, что ток течет в проводнике с нулевым сопротивлением, поэтому он не затухает.
Следствие состоит в том, что если контур движется, то поток будет оставаться неизменным, потому что изменяется только внешнее поле.
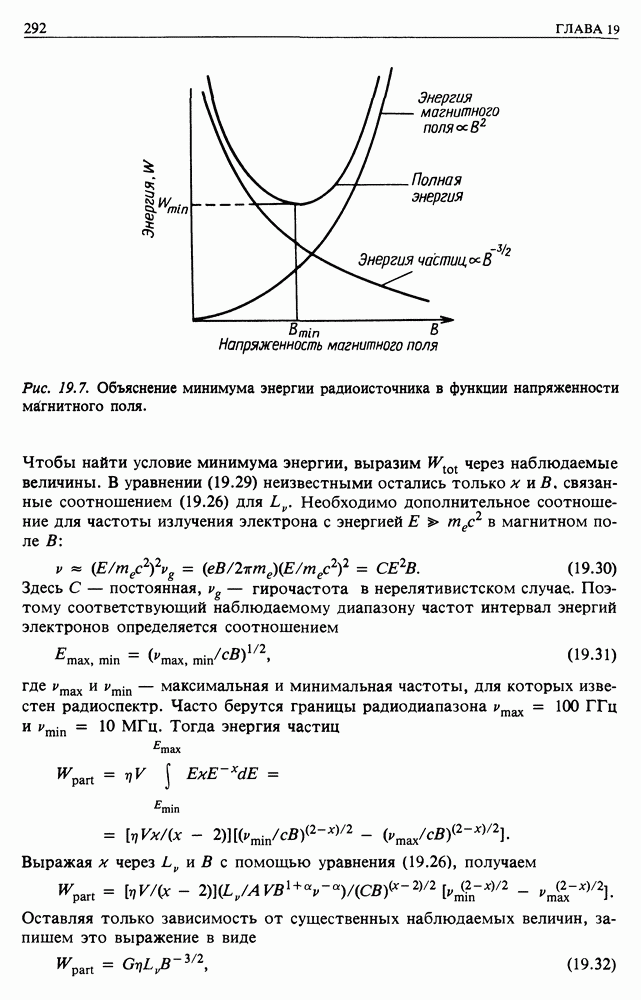
Наконец, что произойдет, если контур изменит форму? Рассмотрим цепь, показанную на рис. 12.5, состоящую из контура с параллельными проволочками, которые замыкаются проводником. Предположим, что цепь целиком изготовлена из сверхпроводящего материала и индукция поля в области, где проволочки параллельны, равна  В остальной части цепи поле может быть произвольным. Переместим цепь на расстояние
В остальной части цепи поле может быть произвольным. Переместим цепь на расстояние  со скоростью
со скоростью  Тогда напряженность наведенного электрического поля будет равна
Тогда напряженность наведенного электрического поля будет равна

(рис. 12.5). Наведенная электродвижущая сила равна

где  длина проводника, пересекающего параллельные проволочки. Но
длина проводника, пересекающего параллельные проволочки. Но  Поэтому наведенный в цепи ток равен
Поэтому наведенный в цепи ток равен

и противоположен  Вследствие увеличения площади возрастет и поток. Поскольку все изменения малы,
Вследствие увеличения площади возрастет и поток. Поскольку все изменения малы,  в том же направлении, что и
в том же направлении, что и  Следовательно, эти два эффекта полностью компенсируют Друг друга. Поэтому никаких изменений потока, проходящего через цепь, не происходит. Поток через цепь сохраняется, поэтому
Следовательно, эти два эффекта полностью компенсируют Друг друга. Поэтому никаких изменений потока, проходящего через цепь, не происходит. Поток через цепь сохраняется, поэтому  (где индексы 1 и 2 относятся к значениям
(где индексы 1 и 2 относятся к значениям  до и после деформации цепи), и здесь нет никакой ошибки, потому что изменения потока вызывают ток, который не изменяется из-за отсутствия диссипации. Поэтому электродвижущая сила вызывает большой ток, который остается, даже когда электродвижущая сила прекращает действовать. Запишем этот результат математически. Если выбрать в плазме замкнутый контур С и проследить, как меняется его форма из-за движения в плазме, то
до и после деформации цепи), и здесь нет никакой ошибки, потому что изменения потока вызывают ток, который не изменяется из-за отсутствия диссипации. Поэтому электродвижущая сила вызывает большой ток, который остается, даже когда электродвижущая сила прекращает действовать. Запишем этот результат математически. Если выбрать в плазме замкнутый контур С и проследить, как меняется его форма из-за движения в плазме, то

где  приращение площади контура,
приращение площади контура,  полная площадь контура, ограничиваемого С. Для маленького круглого проволочного кольца в равномерно расширяющейся плазме из приведенных выше результатов получим
полная площадь контура, ограничиваемого С. Для маленького круглого проволочного кольца в равномерно расширяющейся плазме из приведенных выше результатов получим

Таким образом, при равномерном расширении плотность энергии магнитного поля падает как  Покажите самостоятельно, что такой же результат получается для адиабатического расширения газа с отношением удельных теплоемкостей
Покажите самостоятельно, что такой же результат получается для адиабатического расширения газа с отношением удельных теплоемкостей  В частности, для ультрарелятивистского газа
В частности, для ультрарелятивистского газа  и это имеет глубокий смысл, поскольку такой газ ведет себя во многих отношениях как газ с безмассовыми частицами, а магнитное поле — великолепный пример безмассового газа.
и это имеет глубокий смысл, поскольку такой газ ведет себя во многих отношениях как газ с безмассовыми частицами, а магнитное поле — великолепный пример безмассового газа.
Все эти соображения непосредственно относятся к межпланетной плазме, поскольку она не обладает сопротивлением, и, следовательно, силовые линии движутся с плазмой, как если бы они были вморожены в нее. Этот результат верен практически для всех видов космической плазмы.
12.4.2. математическое описание. Выпишем уравнения магнитогидродинамики:
Уравнение неразрывности

где  плотность,
плотность,  скорость в точке среды.
скорость в точке среды.
Уравнение движения

где  давление,
давление,  плотноть тока, В — плотность магнитного потока,
плотноть тока, В — плотность магнитного потока,  силы трения и
силы трения и  гравитационное ускорение. Заметим, что
гравитационное ускорение. Заметим, что  субстанциональная производная, т.е. сила
субстанциональная производная, т.е. сила  действует на данный элемент среды в системе координат, которая движется с плазмой. Она связана с частной производной оператором
действует на данный элемент среды в системе координат, которая движется с плазмой. Она связана с частной производной оператором

Уравнения Максвелла. Нам понадобятся эти уравнения в следующем виде:

Обратите внимание, что в последнем уравнении отсутствует ток смещения  поскольку мы имеем дело с очень медленно изменяющимися явлениями,
поскольку мы имеем дело с очень медленно изменяющимися явлениями,  Поэтому в данном случае отсутствуют какие-либо эффекты, связанные с объемным зарядом, т.е. частицы плазмы всегда успевают нейтрализовать любое нарушение равновесия зарядов в масштабе движения плазмы. Наконец, закон Ома
Поэтому в данном случае отсутствуют какие-либо эффекты, связанные с объемным зарядом, т.е. частицы плазмы всегда успевают нейтрализовать любое нарушение равновесия зарядов в масштабе движения плазмы. Наконец, закон Ома

где а — электропроводность плазмы. Теперь подставим (12.11) в (12.9)

Затем подставим (12.10) в (12.12)

Поэтому

Теперь используем тождество  Поскольку
Поскольку 

Уравнения (12.6) — (12.8) и (12.14) образуют основную систему уравнений магнитогидродинамики.,
Рассмотрим два частных решения. Если плазма находится в состоянии покоя, то  и
и

Это обычное уравнение диффузии. Можно вычислить время, которое требуется, чтобы магнитное поле продиффундировало из области с помощью стандартного приема. Обозначим  где
где  характерное время диффузии, и
характерное время диффузии, и  где
где  характерный размер системы, т.е.
характерный размер системы, т.е.

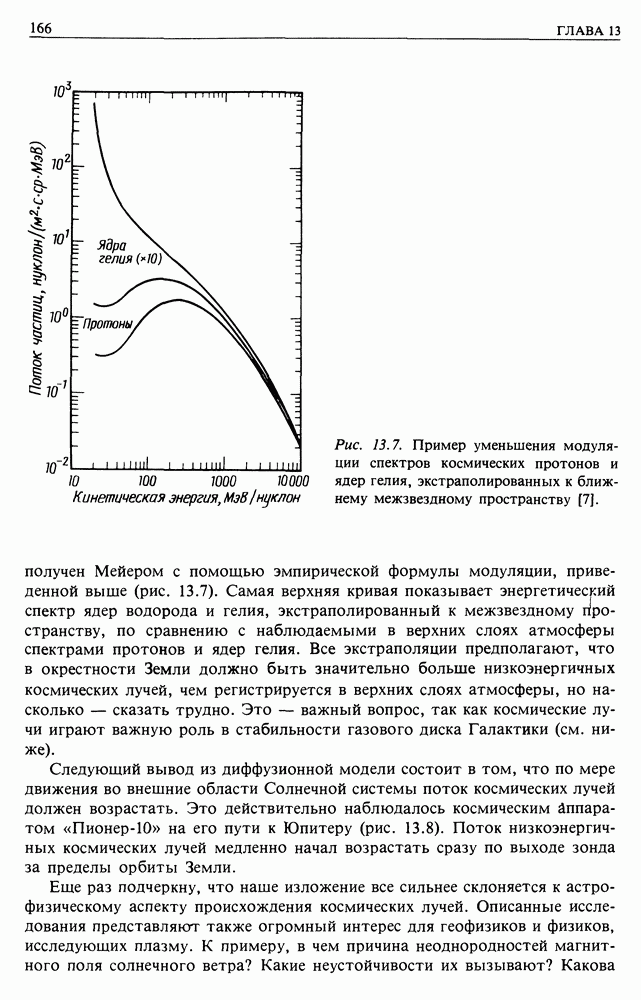
Этот прием очень хорош для оценки по порядку величины. Полученный результат важен, например, для изучения образования звезд из газового облака, пронизанного магнитным полем. Время  это время, необходимое для диффузии поля из области размером
это время, необходимое для диффузии поля из области размером 
Нас интересует случай бесконечной проводимости  когда уравнение (12.14) приобретает вид
когда уравнение (12.14) приобретает вид

В любом контуре  в плазме изменение во времени В будет состоять из двух частей. Во-первых, возможны изменения плотности магнитного потока, обусловленные внешними причинами, и, во-вторых, существует наведенный компонент, плотности потока вследствие движения контура. Первый вклад равен просто
в плазме изменение во времени В будет состоять из двух частей. Во-первых, возможны изменения плотности магнитного потока, обусловленные внешними причинами, и, во-вторых, существует наведенный компонент, плотности потока вследствие движения контура. Первый вклад равен просто

Второй вклад связан с тем, что вследствие движения контура в нем наводится электрическое поле  Тогда, поскольку
Тогда, поскольку  существует дополнительный вклад в общий поток через контур, т.е.
существует дополнительный вклад в общий поток через контур, т.е.

Поэтому, суммируя оба вклада, мы получаем

т.е. магнитный поток через контур постоянен, или «вморожен».
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- 1. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ВВЕДЕНИЕ В АСТРОФИЗИКУ ВЫСОКИХ ЭНЕРГИЙ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ
- 1.3. КРАТКАЯ ИСТОРИЯ ФИЗИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 2. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ.
- 2.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ — НЕРЕЛЯТИВИСТСКОЕ РАССМОТРЕНИЕ
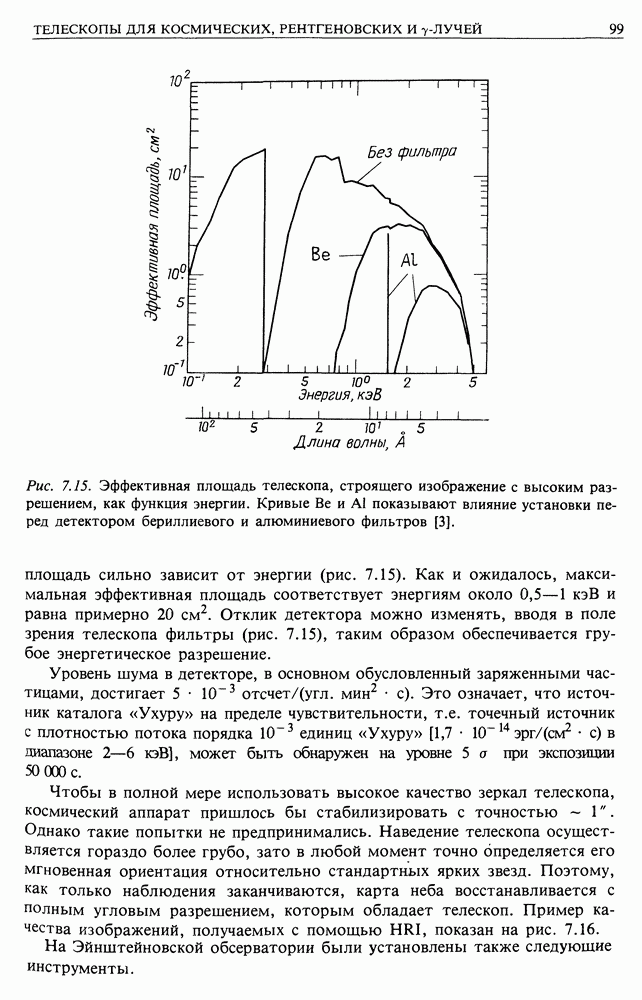
- 2.3. РЕЛЯТИВИСТСКИЙ СЛУЧАЙ
- 2.4. РЕЛЯТИВИСТСКИЕ ИОНИЗАЦИОННЫЕ ПОТЕРИ, ВСТРЕЧАЮЩИЕСЯ НА ПРАКТИКЕ
- 2.5. УДОБНЫЙ НА ПРАКТИКЕ ВИД ФОРМУЛ ДЛЯ ИОНИЗАЦИОННЫХ ПОТЕРЬ
- 2.6. ИТОГИ И КОММЕНТАРИЙ
- 3. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. 2. ИОНИЗАЦИОННЫЕ ПОТЕРИ И ТОРМОЗНОЕ ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ
- 3.2. ИОНИЗАЦИОННЫЕ ПОТЕРИ ЭЛЕКТРОНОВ
- 3.3. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
- 4. ВЗАИМОДЕЙСТВИЕ ФОТОНОВ ВЫСОКИХ ЭНЕРГИЙ С ВЕЩЕСТВОМ. И ЭЛЕКТРОН-ФОТОННЫЕ КАСКАДЫ
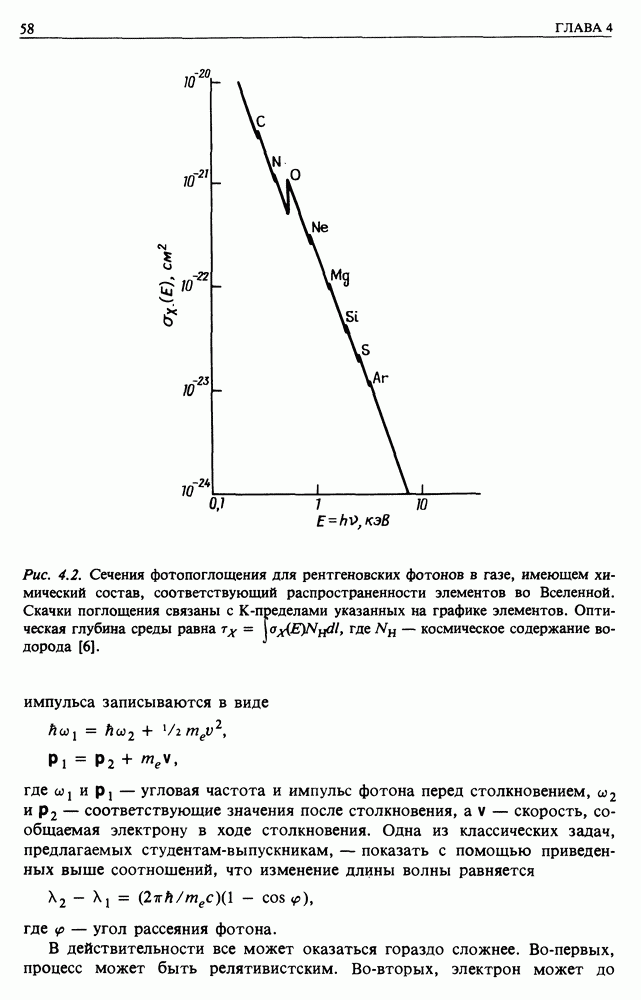
- 4.2. ФОТОПОГЛОЩЕНИЕ
- 4.3. КОМПТОНОВСКОЕ РАССЕЯНИЕ
- 4.4. ОБРАЗОВАНИЕ ПАР
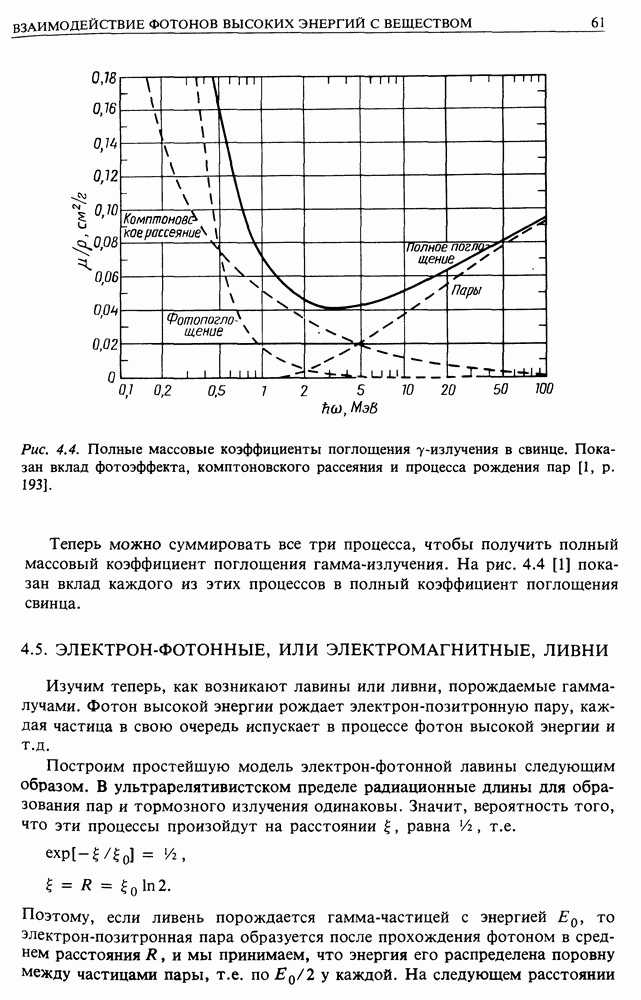
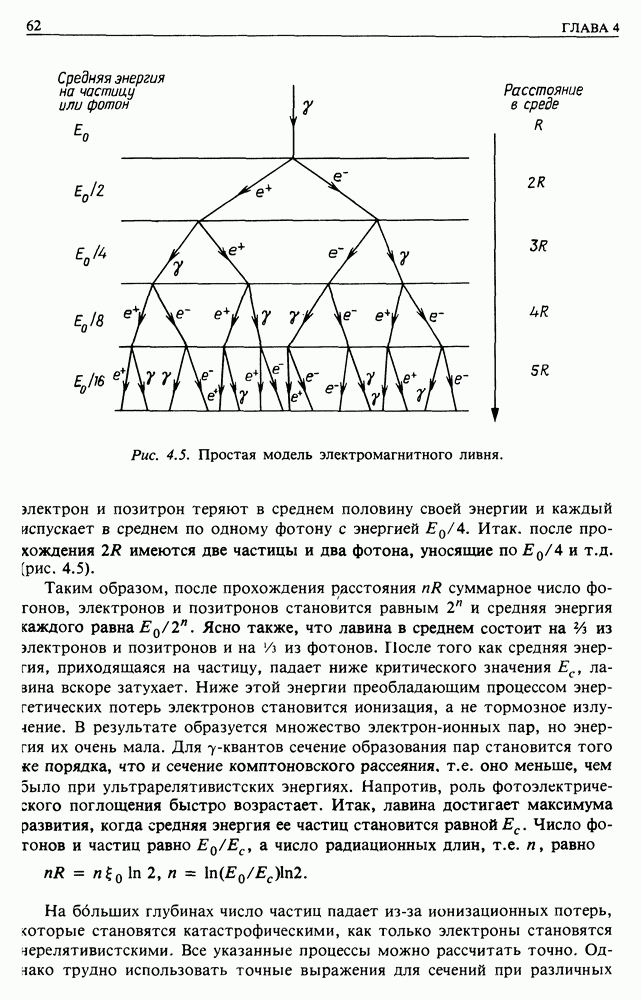
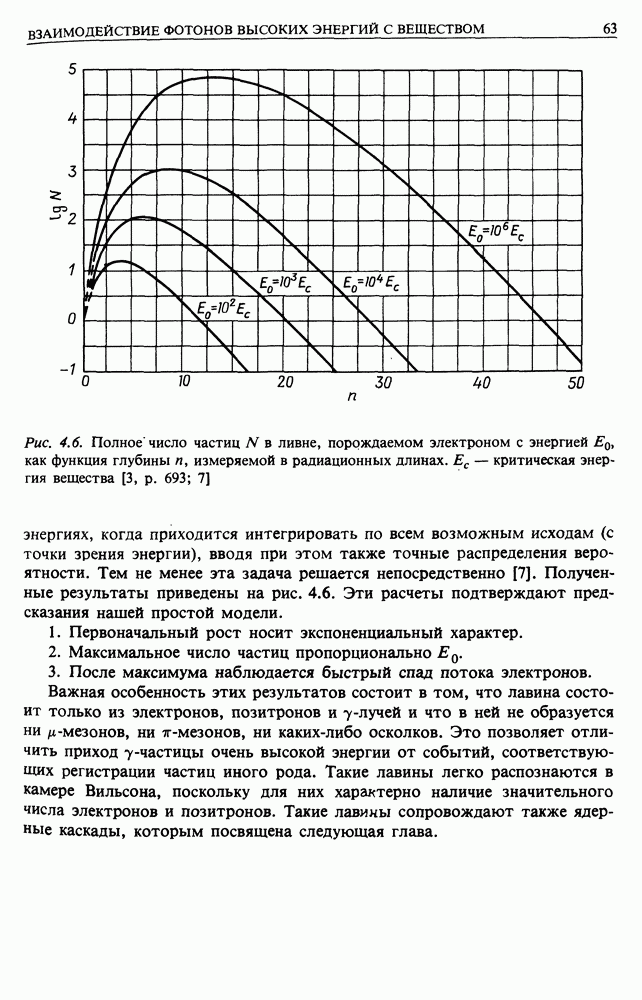
- 4.5. ЭЛЕКТРОН-ФОТОННЫЕ, ИЛИ ЭЛЕКТРОМАГНИТНЫЕ, ЛИВНИ
- 5. ЯДЕРНЫЕ ВЗАИМОДЕЙСТВИЯ
- 5.2. ИСТОРИЯ ВТОРИЧНОГО ИЗЛУЧЕНИЯ
- 5.3. КОСМИЧЕСКИЕ ЛУЧИ В АТМОСФЕРЕ
- 5.4. РАДИОАКТИВНЫЕ ЯДРА, ОБРАЗОВАННЫЕ КОСМИЧЕСКИМИ ЛУЧАМИ
- 6. ДЕТЕКТОРЫ КОСМИЧЕСКИХ ЛУЧЕЙ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 6.2. ЯДЕРНЫЕ ЭМУЛЬСИИ И ИССЛЕДОВАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 6.3. КАМЕРЫ ВИЛЬСОНА И ПУЗЫРЬКОВЫЕ КАМЕРЫ
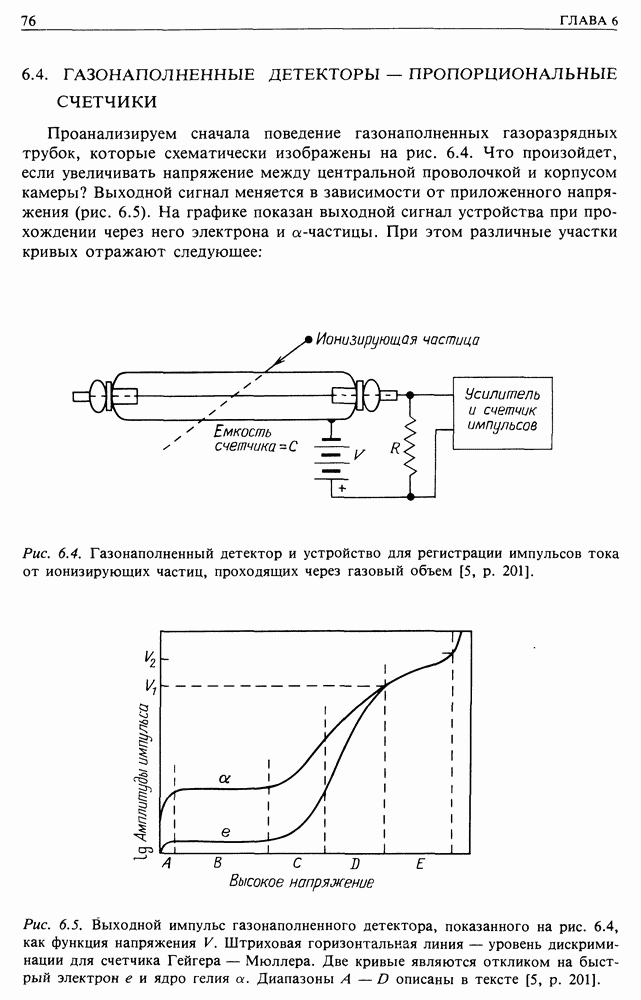
- 6.4. ГАЗОНАПОЛНЕННЫЕ ДЕТЕКТОРЫ — ПРОПОРЦИОНАЛЬНЫЕ СЧЕТЧИКИ
- 6.5. СЧЕТЧИКИ ГЕЙГЕРА И ИСКРОВЫЕ КАМЕРЫ
- 6.6. ТВЕРДОТЕЛЬНЫЕ ПОЛУПРОВОДНИКОВЫЕ ДЕТЕКТОРЫ
- 6.7. СЦИНТИЛЛЯЦИОННЫЕ СЧЕТЧИКИ
- 6.8. ЧЕРЕНКОВСКИЕ СЧЕТЧИКИ
- 7. ТЕЛЕСКОПЫ ДЛЯ КОСМИЧЕСКИХ, РЕНТГЕНОВСКИХ И ГАММА-ЛУЧЕЙ
- 7.2. МЕТОД АНТИСОВПАДЕНИЙ И ТЕЛЕСКОПЫ ДЛЯ РЕГИСТРАЦИИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 7.3. РЕНТГЕНОВСКИЕ ТЕЛЕСКОПЫ
- 7.4. ГАММА-ТЕЛЕСКОПЫ
- 7.5. ЭКОНОМИЧЕСКИЕ АСПЕКТЫ
- 8. ПЛАСТМАССЫ И МЕТЕОРИТЫ
- 8.1. РАДИАЦИОННЫЕ ПОВРЕЖДЕНИЯ В ПЛАСТМАССАХ
- 8.2. МЕТЕОРИТЫ
- 9. КОСМИЧЕСКИЕ ЛУЧИ В ВЕРХНИХ СЛОЯХ АТМОСФЕРЫ
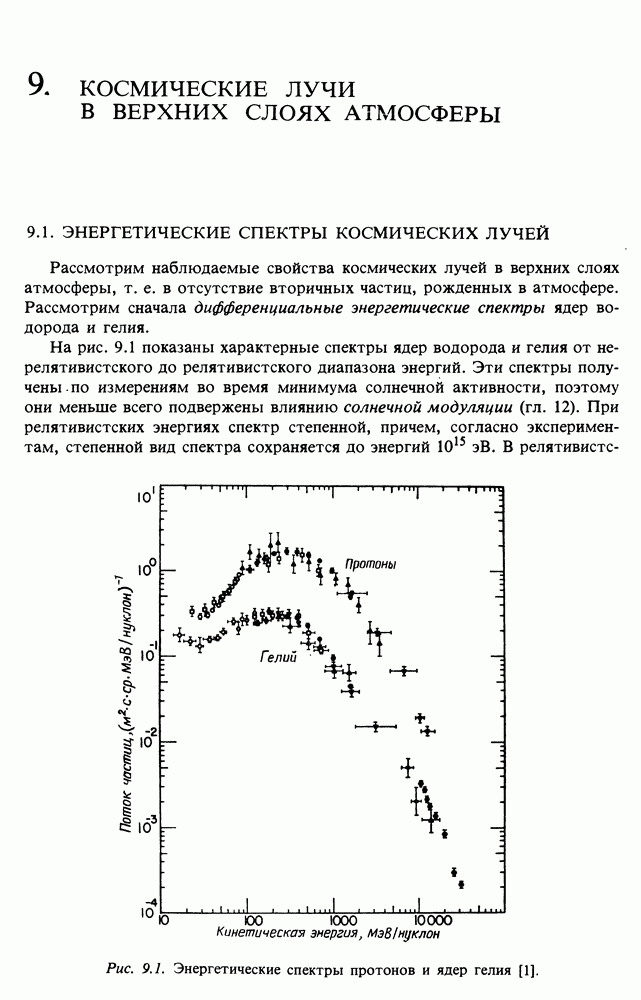
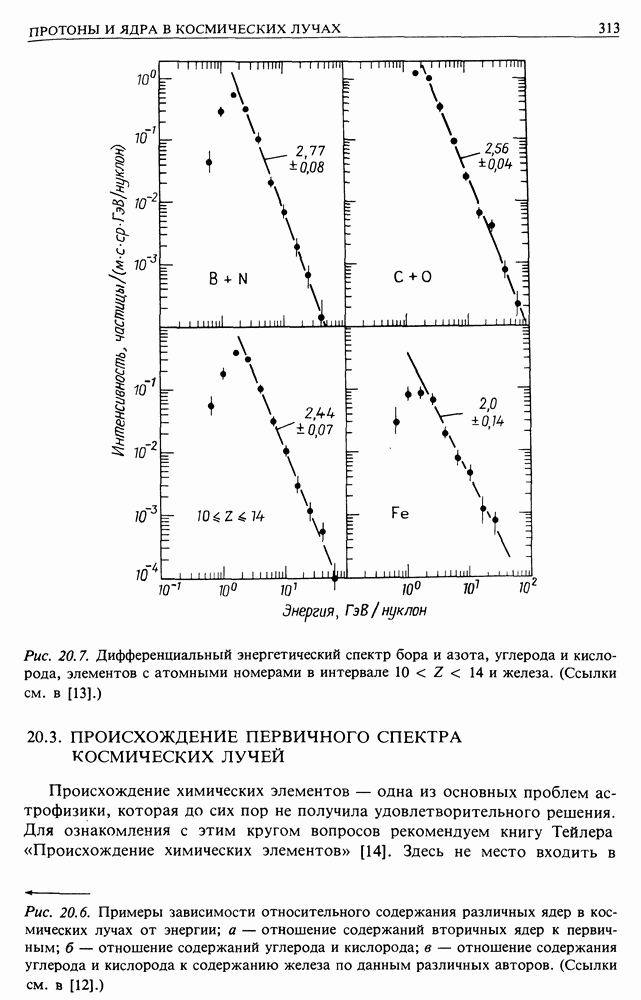
- 9.1. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ КОСМИЧЕСКИХ ЛУЧЕЙ
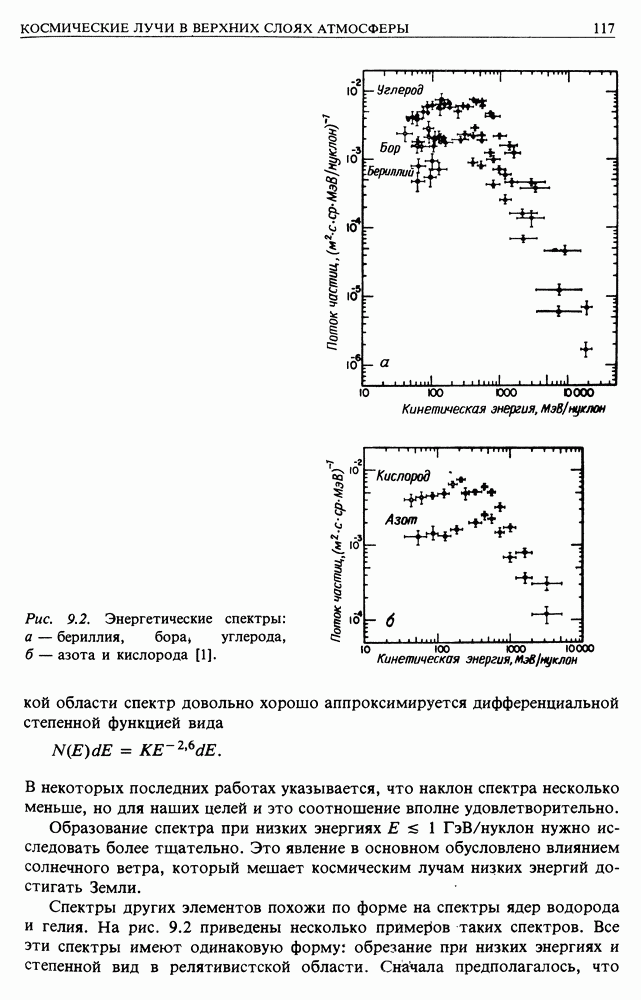
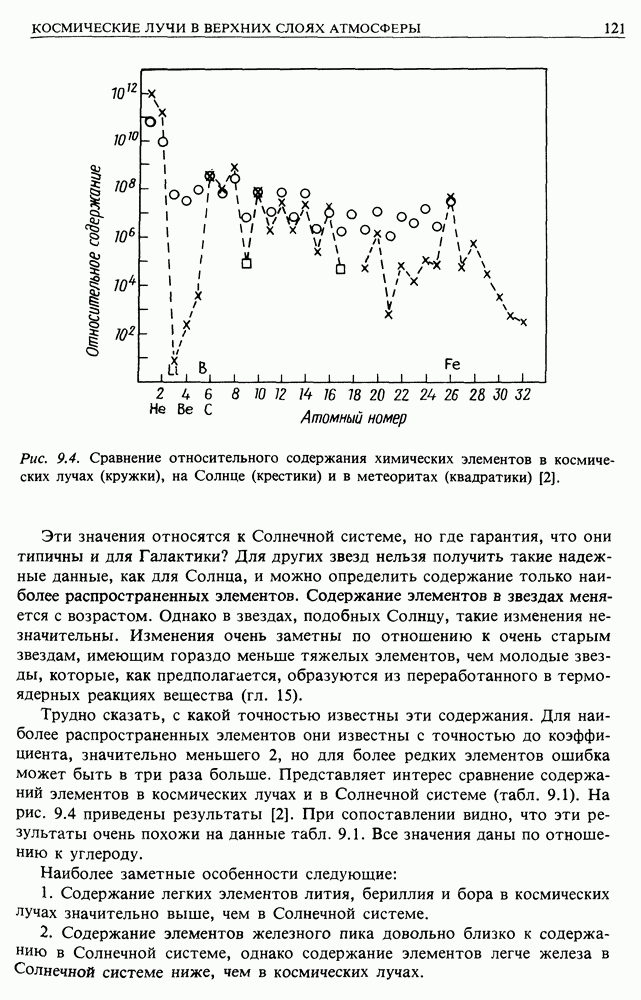
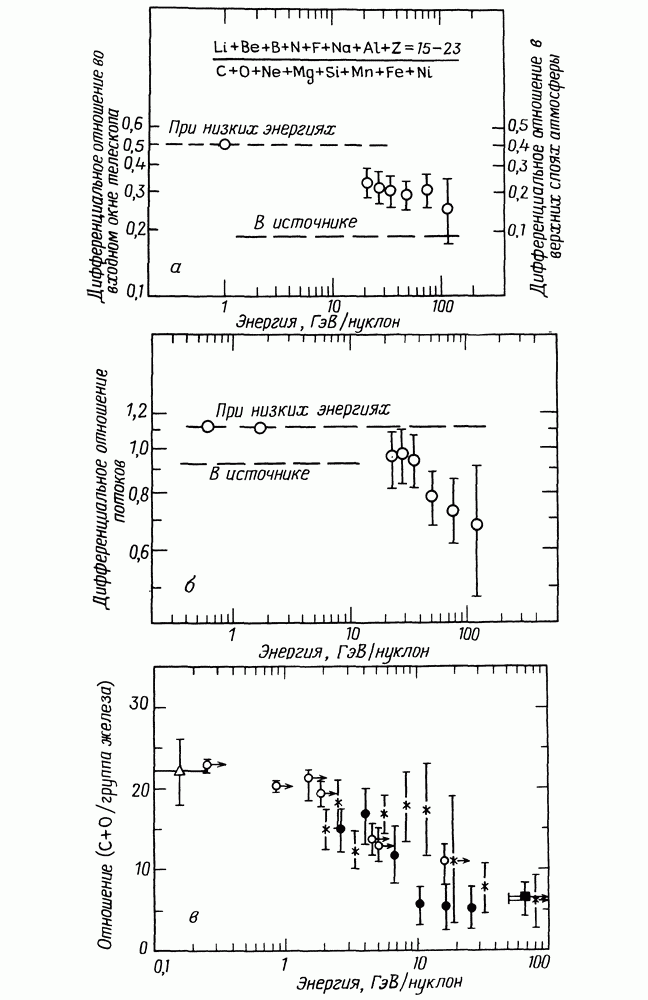
- 9.2. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В КОСМИЧЕСКИХ ЛУЧАХ
- 9.3. РАСПРОСТРАНЕННОСТЬ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ СИСТЕМЕ
- 9.4. РАСПРОСТРАНЕННОСТИ ИЗОТОПОВ
- 9.5. ИЗОТРОПИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 9.6. ЛОКАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГИИ КОСМИЧЕСКИХ ЛУЧЕЙ
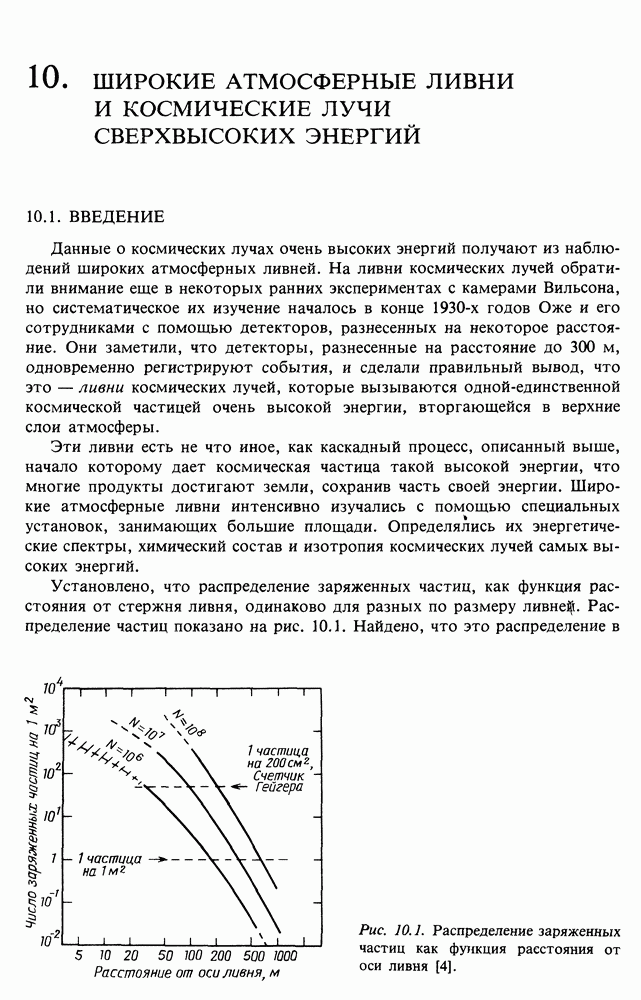
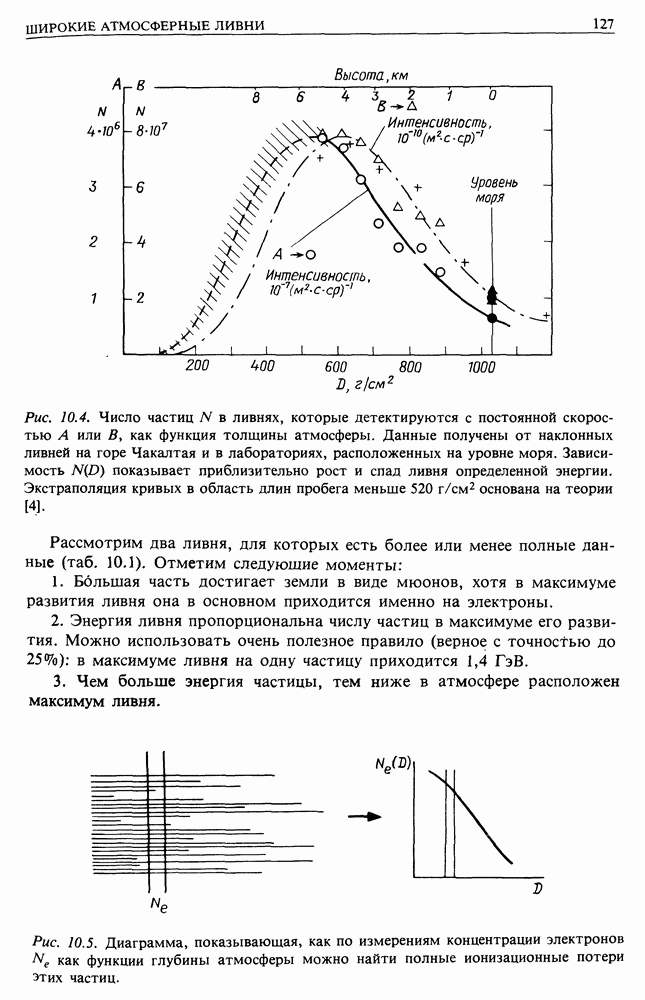
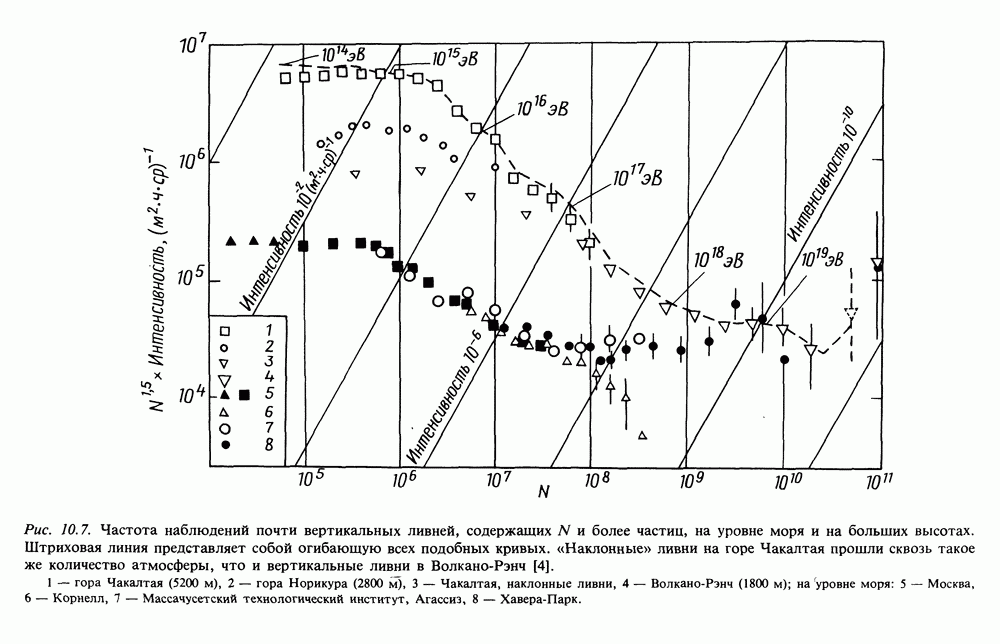
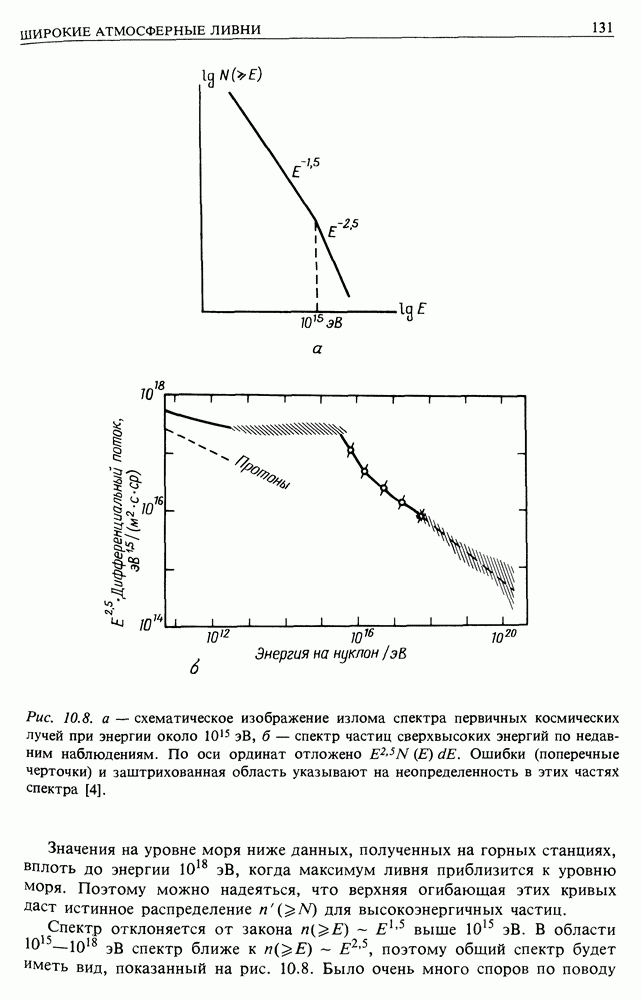
- 10. ШИРОКИЕ АТМОСФЕРНЫЕ ЛИВНИ И КОСМИЧЕСКИЕ ЛУЧИ СВЕРХВЫСОКИХ ЭНЕРГИЙ
- 10.2. РАЗВИТИЕ ШИРОКИХ АТМОСФЕРНЫХ ЛИВНЕЙ
- 10.3. НАБЛЮДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ ОЧЕНЬ ВЫСОКОЙ ЭНЕРГИИ
- 10.4. ПРОБЛЕМЫ, ТРЕБУЮЩИЕ РЕШЕНИЯ
- 11. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.2. ДИНАМИКА ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ДИПОЛЬНОМ МАГНИТНОМ ПОЛЕ
- 11.3. ДИАГНОСТИКА ЧАСТИЦ С ПОМОЩЬЮ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- 11.4. ТРУДНОСТИ, СВЯЗАННЫЕ С ПРОДЕЛАННЫМ ВЫШЕ АНАЛИЗОМ
- 12. СОЛНЕЧНЫЙ ВЕТЕР И ЕГО ВЛИЯНИЕ НА МЕСТНЫЙ ПОТОК КОСМИЧЕСКИХ ЛУЧЕЙ
- 12.1. СОЛНЕЧНЫЙ ВЕТЕР
- 12.2. СВИДЕТЕЛЬСТВА СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 12.3. ПРОВОДИМОСТЬ ПОЛНОСТЬЮ ИОНИЗОВАННОЙ ПЛАЗМЫ
- 12.4. ВМОРАЖИВАНИЕ ПОТОКА
- 12.5. ПРИЛОЖЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ К СОЛНЕЧНОМУ ВЕТРУ И МАГНИТОСФЕРЕ ЗЕМЛИ
- 13. ДИНАМИКА КОСМИЧЕСКИХ ЛУЧЕЙ В СОЛНЕЧНОМ ВЕТРЕ
- 13.1. ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНЫХ ПОЛЯХ
- 13.2. ЭМПИРИЧЕСКАЯ ДИФФУЗИОННО-КОНВЕКТИВНАЯ МОДЕЛЬ СОЛНЕЧНОЙ МОДУЛЯЦИИ
- 13.3. КОЭФФИЦИЕНТЫ ДИФФУЗИИ КОСМИЧЕСКИХ ЛУЧЕЙ ВСЛЕДСТВИЕ РАССЕЯНИЯ НА МАГНИТНЫХ НЕОДНОРОДНОСТЯХ
- 13.4. ОБСУЖДЕНИЕ
- 14. ВВЕДЕНИЕ В ОПТИЧЕСКУЮ АСТРОНОМИЮ И РАДИОАСТРОНОМИЮ
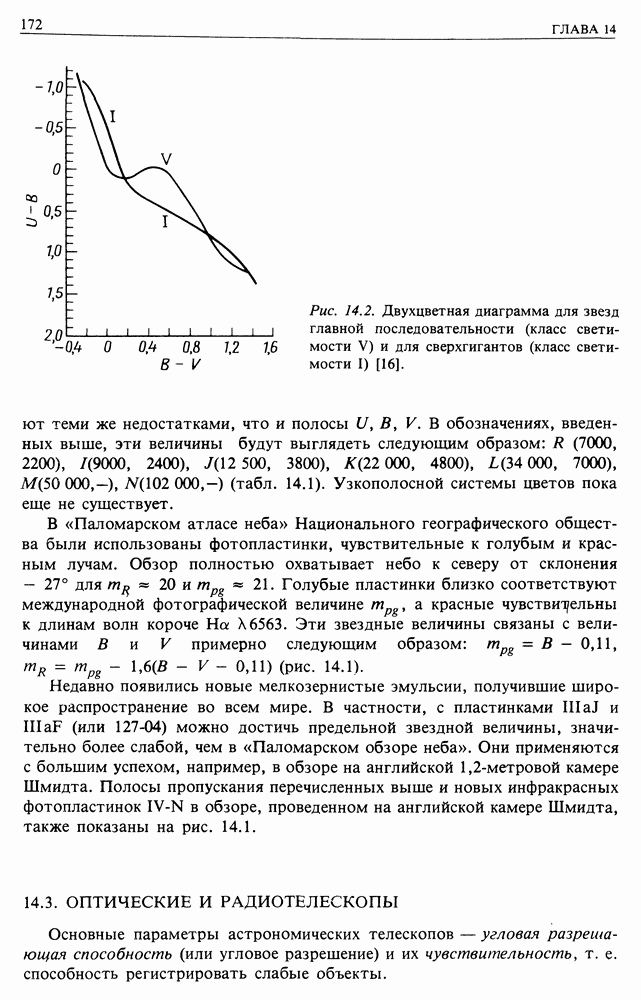
- 14.2. ИНТЕНСИВНОСТИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ
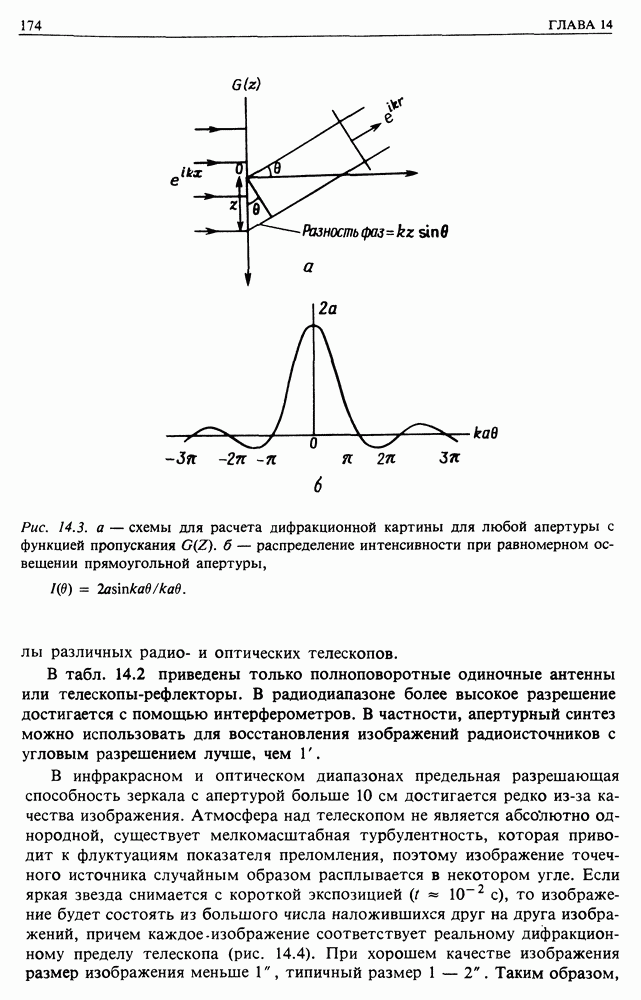
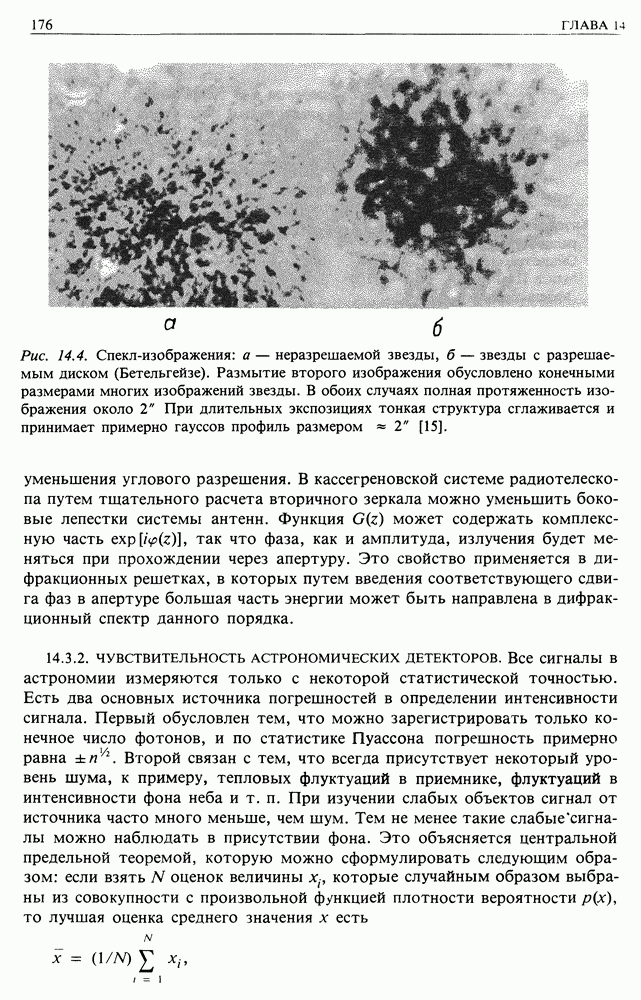
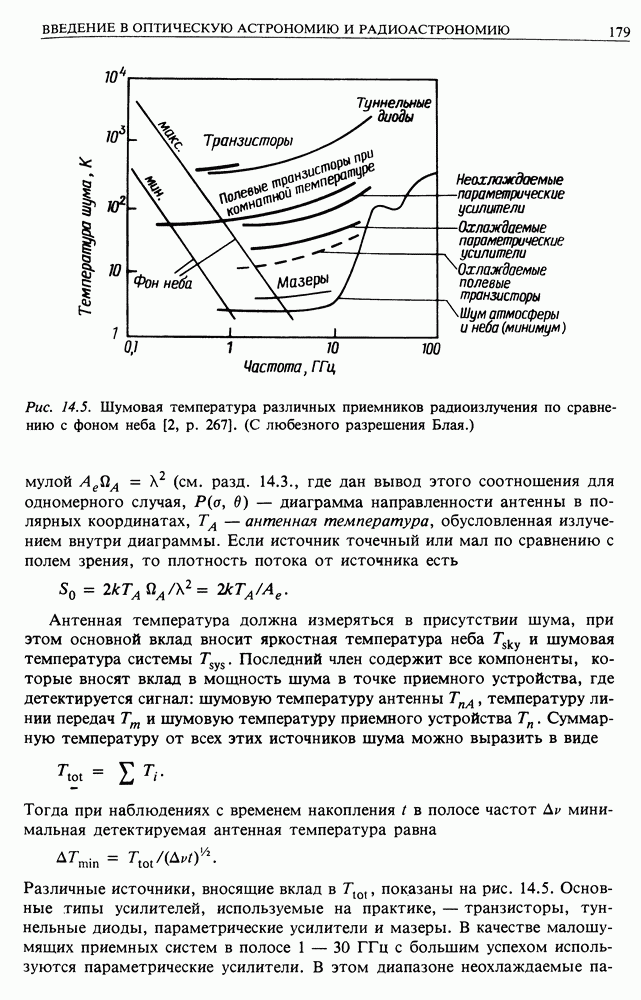
- 14.3. ОПТИЧЕСКИЕ И РАДИОТЕЛЕСКОПЫ
- 14.4. ДЕТЕКТОРЫ ДЛЯ ИНФРАКРАСНОГО, ОПТИЧЕСКОГО УЛЬТРАФИОЛЕТОВОГО И РАДИОДИАПАЗОНОВ
- 15. ЭКСКУРСИЯ ПО ГАЛАКТИКЕ И ЗА ЕЕ ПРЕДЕЛЫ
- 15.2. ИЗМЕРЕНИЕ РАССТОЯНИЙ В АСТРОНОМИИ И ОБЩАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.3. МЕТОДЫ ИЗМЕРЕНИЯ РАССТОЯНИЙ
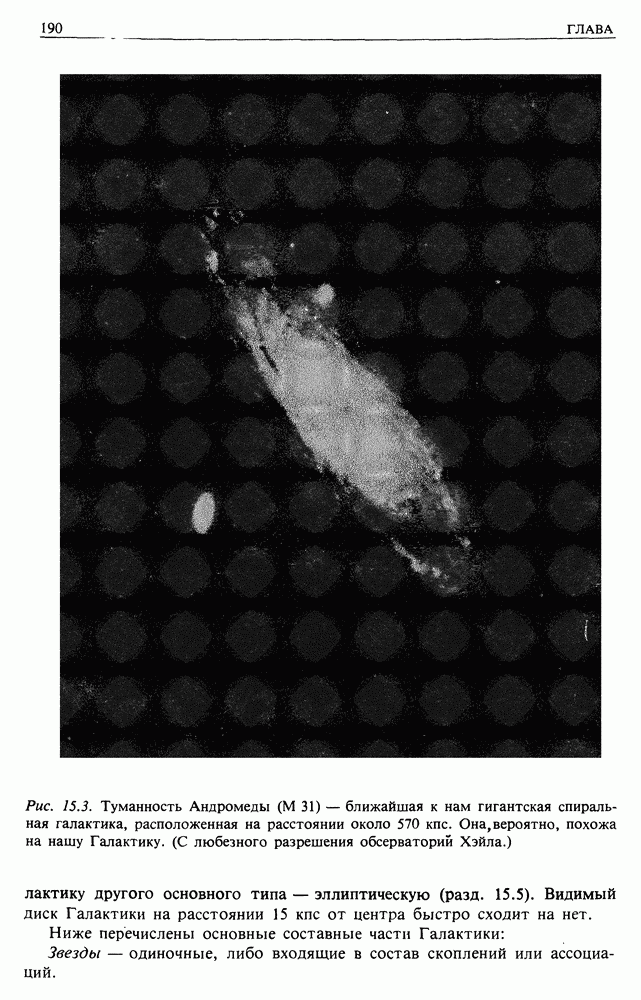
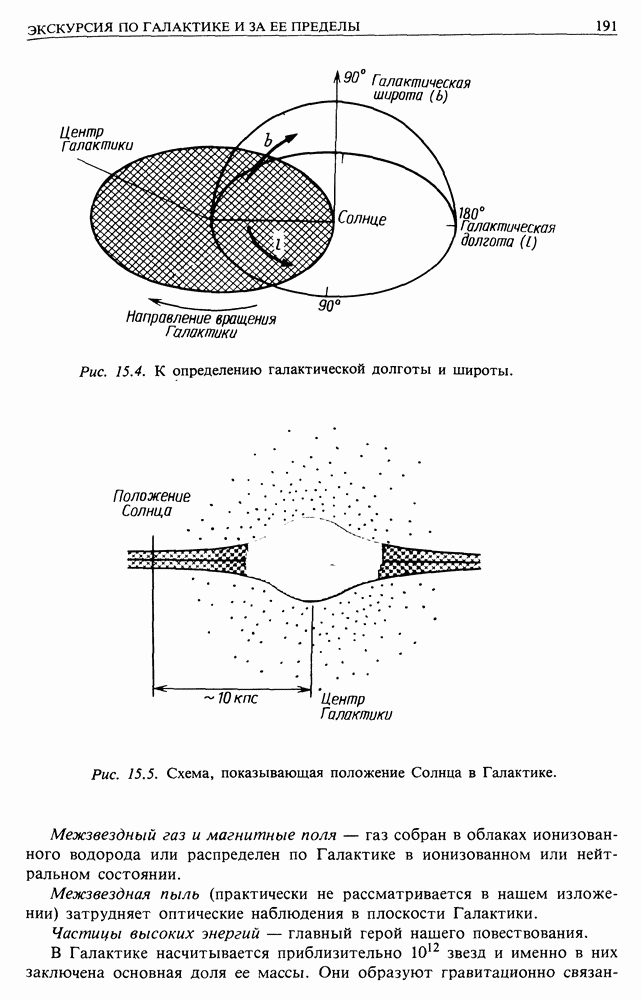
- 15.4. НАША ГАЛАКТИКА
- 15.5. КРУПНОМАСШТАБНАЯ СТРУКТУРА ВСЕЛЕННОЙ
- 15.6. РАСШИРЕНИЕ ВСЕЛЕННОЙ
- 15.7. ГОРЯЧАЯ РАСШИРЯЮЩАЯСЯ ВСЕЛЕННАЯ
- 16. ЭВОЛЮЦИЯ ЗВЕЗД И ГАЛАКТИКИ
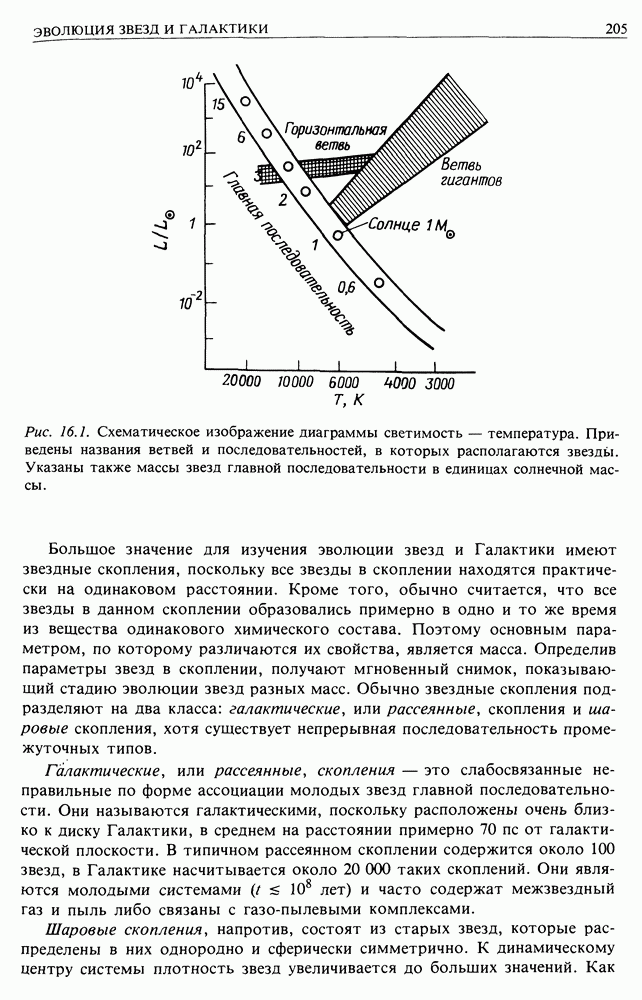
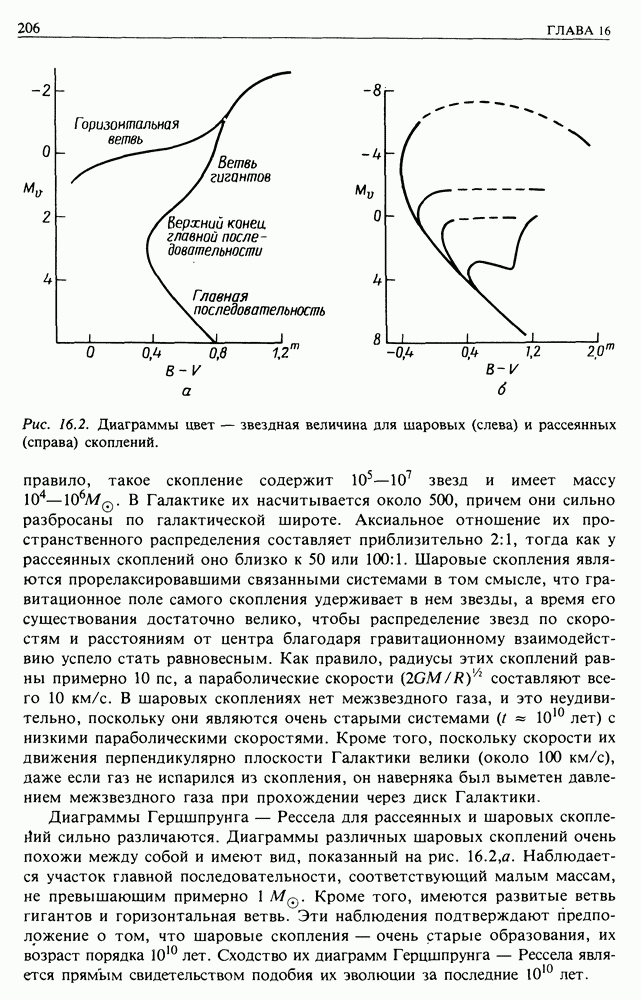
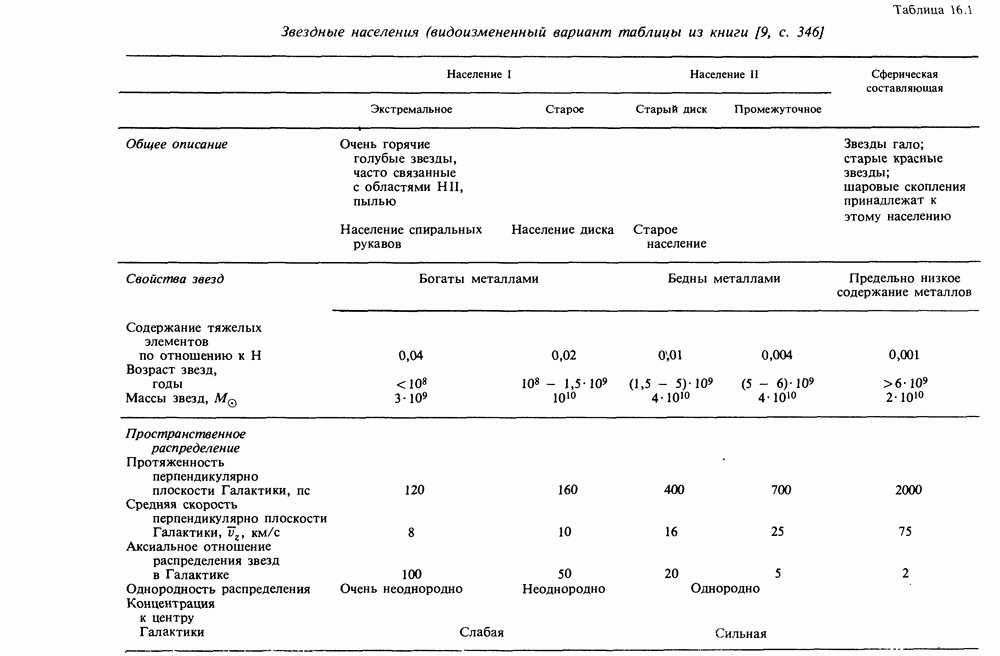
- 16.1. ДИАГРАММА ГЕРЦШПРУНГА — РЕССЕЛА И ЗВЕЗДНЫЕ НАСЕЛЕНИЯ
- 16.2. ЭВОЛЮЦИЯ ЗВЕЗД
- 16.3. ЗАКЛЮЧИТЕЛЬНЫЕ СТАДИИ ЭВОЛЮЦИИ ЗВЕЗД
- 16.4. СВЕРХНОВЫЕ
- 16.5. НЕЙТРОННЫЕ ЗВЕЗДЫ
- 16.6. ЧЕРНЫЕ ДЫРЫ
- 16.7. «УГАСШИЕ» ЗВЕЗДЫ И КОСМИЧЕСКИЕ ЛУЧИ
- 16.8. ОБЩАЯ КАРТИНА ЭВОЛЮЦИИ ГАЛАКТИКИ
- 17. МЕЖЗВЕЗДНЫЙ ГАЗ И МАГНИТНОЕ ПОЛЕ
- 17.2. НЕЙТРАЛЬНЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.3. ИОНИЗОВАННЫЙ МЕЖЗВЕЗДНЫЙ ГАЗ
- 17.4. СОВРЕМЕННОЕ СОСТОЯНИЕ МЕЖЗВЕЗДНОГО ГАЗА
- 17.5. МАГНИТНОЕ ПОЛЕ ГАЛАКТИКИ
- 18. СИНХРОТРОННОЕ ИЗЛУЧЕНИЕ И РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.2. РАДИОИЗЛУЧЕНИЕ ГАЛАКТИКИ
- 18.3. КРУПНОМАСШТАБНОЕ РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 19. ПОТЕРИ ЭНЕРГИИ И ДИФФУЗИЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ — ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 19.2. ДИФФУЗИОННОЕ УРАВНЕНИЕ ПЕРЕНОСА ДЛЯ ЭЛЕКТРОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ
- 19.3. СВЕРХНОВЫЕ КАК ИСТОЧНИКИ УЛЬТРАРЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 20. ПРОТОНЫ И ЯДРА В КОСМИЧЕСКИХ ЛУЧАХ — РАСПРЕДЕЛЕНИЕ В ГАЛАКТИКЕ И ПРОИСХОЖДЕНИЕ ЛЕГКИХ ЭЛЕМЕНТОВ
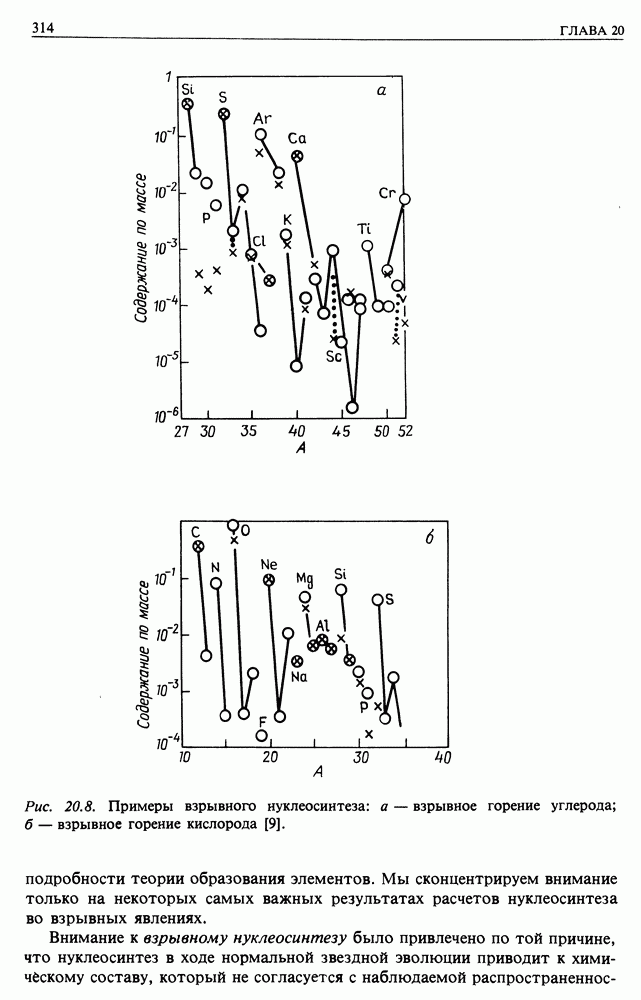
- 20.2. ПРОИСХОЖДЕНИЕ ЛЕГКИХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
- 20.3. ПРОИСХОЖДЕНИЕ ПЕРВИЧНОГО СПЕКТРА КОСМИЧЕСКИХ ЛУЧЕЙ
- 21. ДИФФУЗИЯ И УДЕРЖАНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ В ГАЛАКТИКЕ
- 21.2. ГАЛО ГАЛАКТИКИ — ОБЛАСТЬ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ?
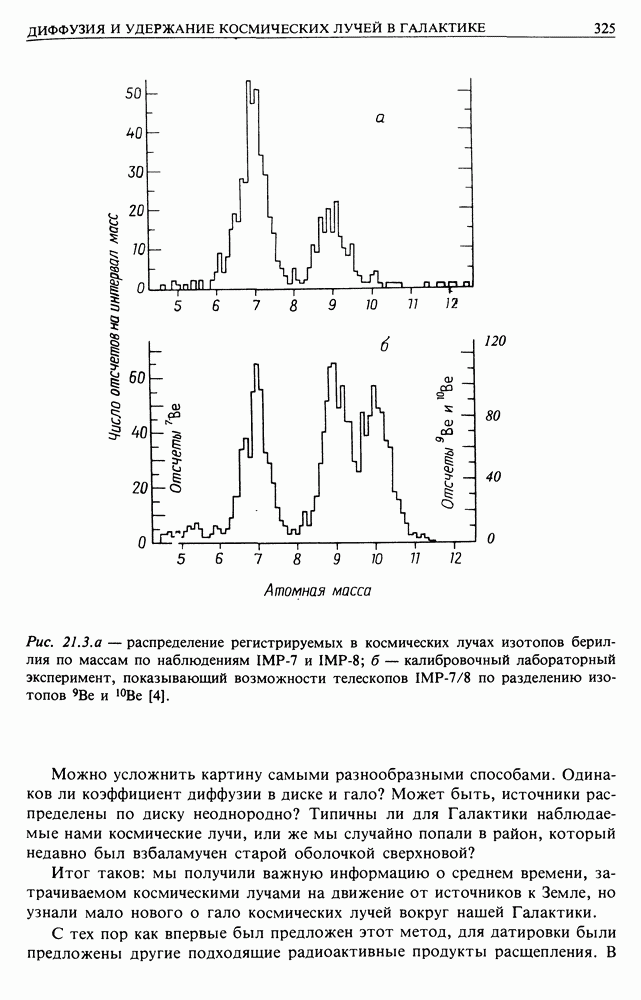
- 21.3. ХРОНОЛОГИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 21.4. РАССЕЯНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ НА АЛЬВЕНОВСКИХ И МАГНИТОЗВУКОВЫХ ВОЛНАХ
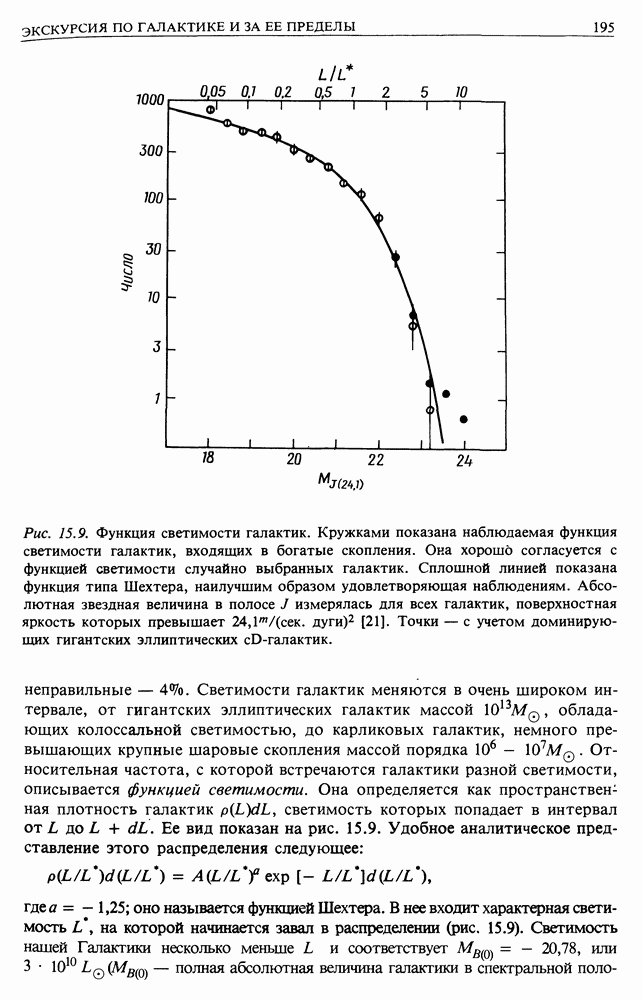
- 22, АКТИВНЫЕ ЯДРА ГАЛАКТИК — ВНЕГАЛАКТИЧЕСКИЕ ИСТОЧНИКИ КОСМИЧЕСКИХ ЛУЧЕЙ
- 22.2. ГАЛАКТИКИ С АКТИВНЫМИ ЯДРАМИ
- 22.3. ОСНОВНАЯ МОДЕЛЬ АКТИВНЫХ ЯДЕР ГАЛАКТИК
- 22.4. ВНЕГАЛАКТИЧЕСКИЕ РАДИОИСТОЧНИКИ
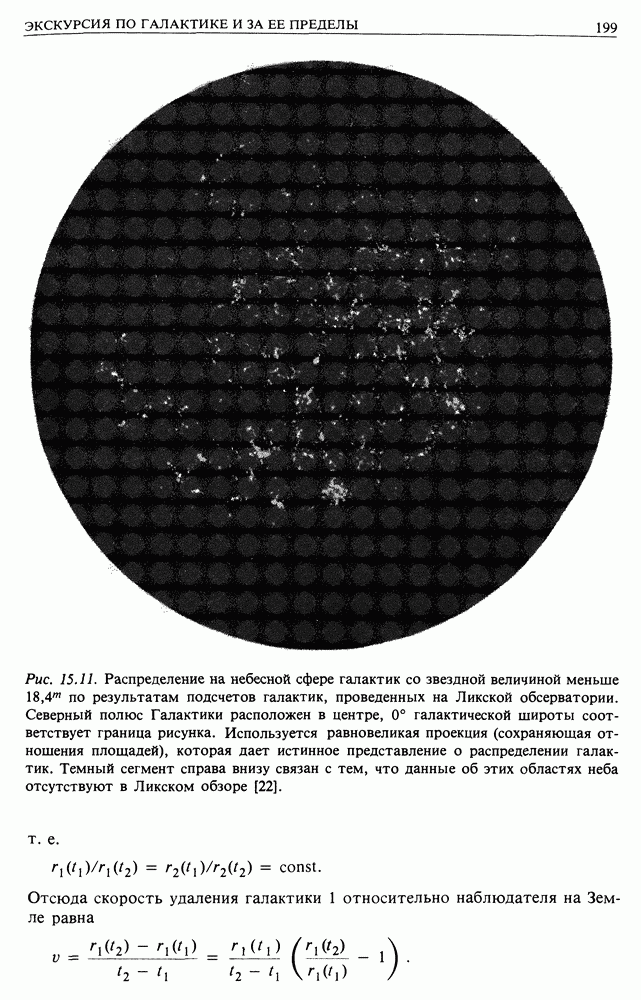
- 22.5. ИСТОЧНИК ЭНЕРГИИ
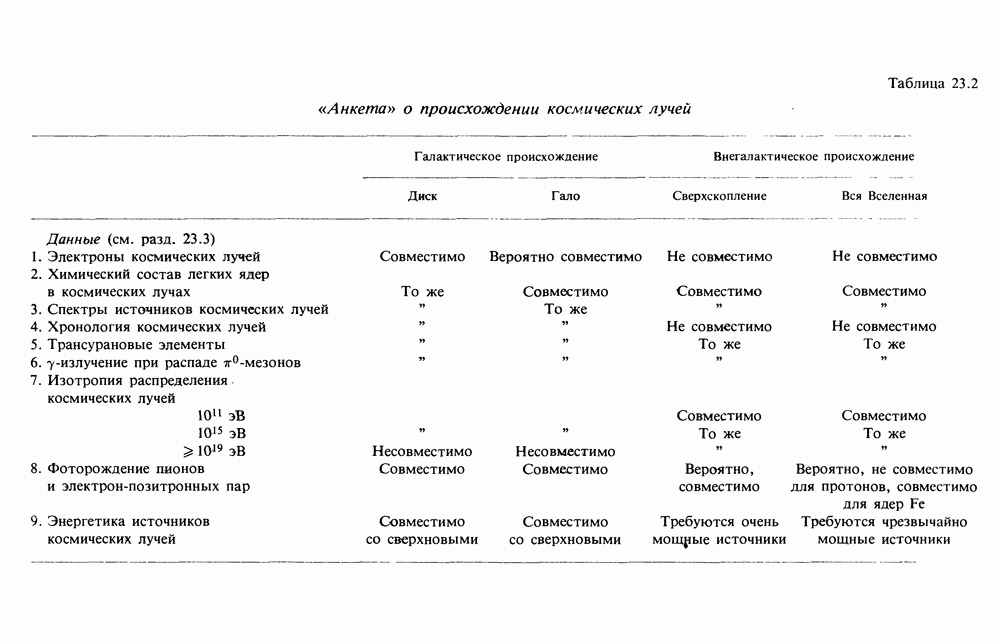
- 23. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ — ГАЛАКТИЧЕСКОЕ ИЛИ ВНЕГАЛАКТИЧЕСКОЕ?
- 23.2. ПСИХОЛОГИЯ АСТРОНОМОВ И АСТРОФИЗИКОВ
- 23.3. ДАННЫЕ ОБ ОБЛАСТИ УДЕРЖАНИЯ КОСМИЧЕСКИХ ЛУЧЕЙ
- 23.4. СВОДКА ДАННЫХ ОБ ОБЛАСТИ ЗАХВАТА КОСМИЧЕСКИХ ЛУЧЕЙ
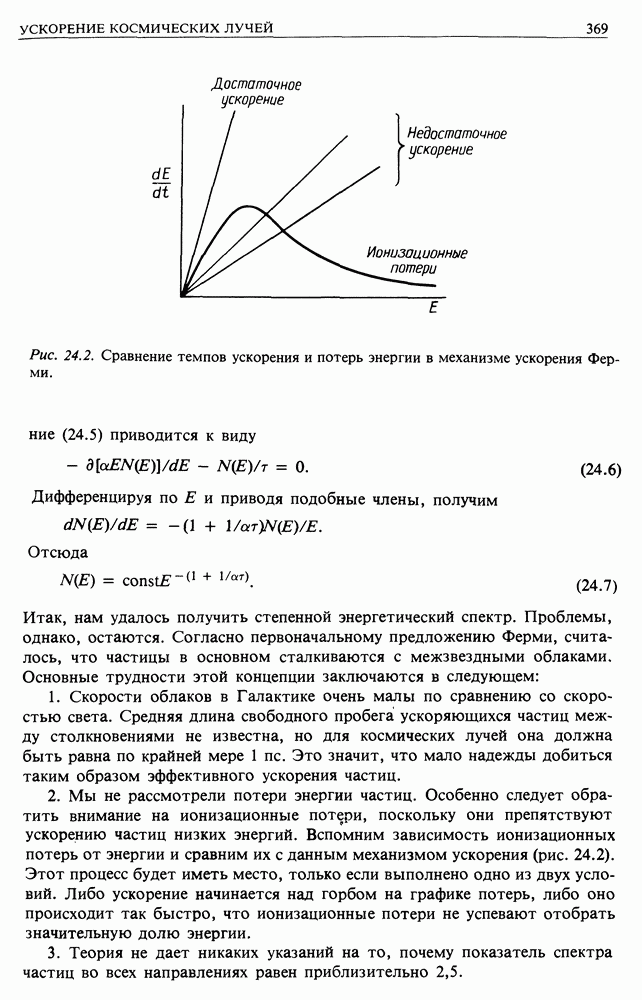
- 24. УСКОРЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- 24.2. ОБЩИЕ ПРИНЦИПЫ УСКОРЕНИЯ
- 24.3. МЕХАНИЗМ ФЕРМИ: ПЕРВЫЙ ВАРИАНТ
- 24.4. МЕХАНИЗМ ФЕРМИ. ВАРИАНТ ВТОРОЙ — УСКОРЕНИЕ ЧАСТИЦ В СИЛЬНЫХ УДАРНЫХ ВОЛНАХ
- 24.5. УДАРНЫЕ ВОЛНЫ В МОЛОДЫХ ОСТАТКАХ СВЕРХНОВЫХ
- 24.6. МЕХАНИЗМ СЫРОВАТСКОГО
- 24.7. «ПЛАЗМЕННЫЙ ТУРБУЛЕНТНЫЙ РЕАКТОР»
- 24.8. МАГНИТОСФЕРЫ ПУЛЬСАРОВ
- 24.9. ВЫВОДЫ
- 25. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ