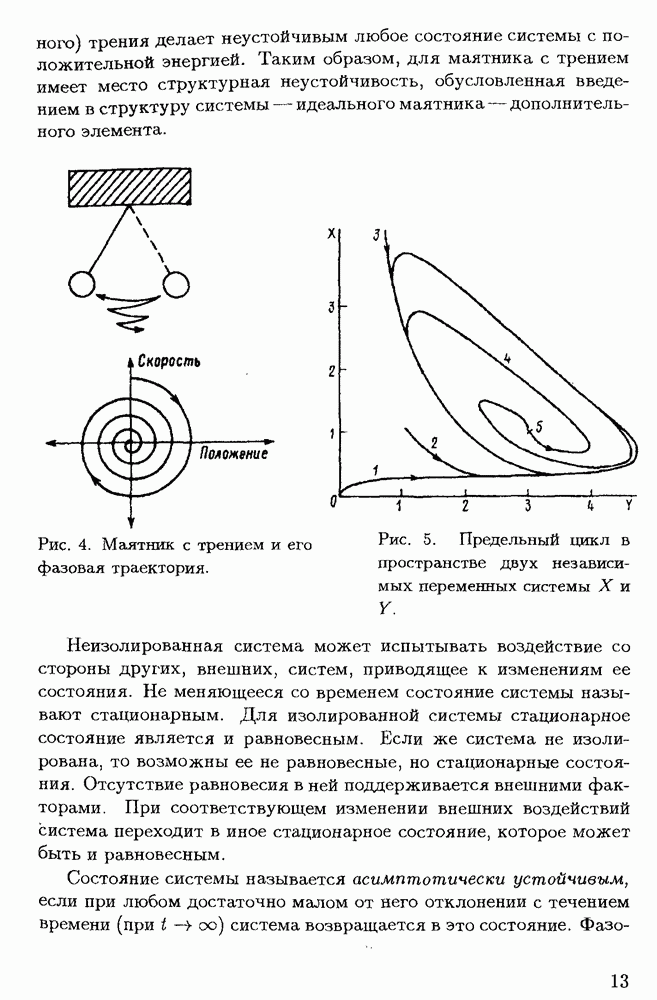
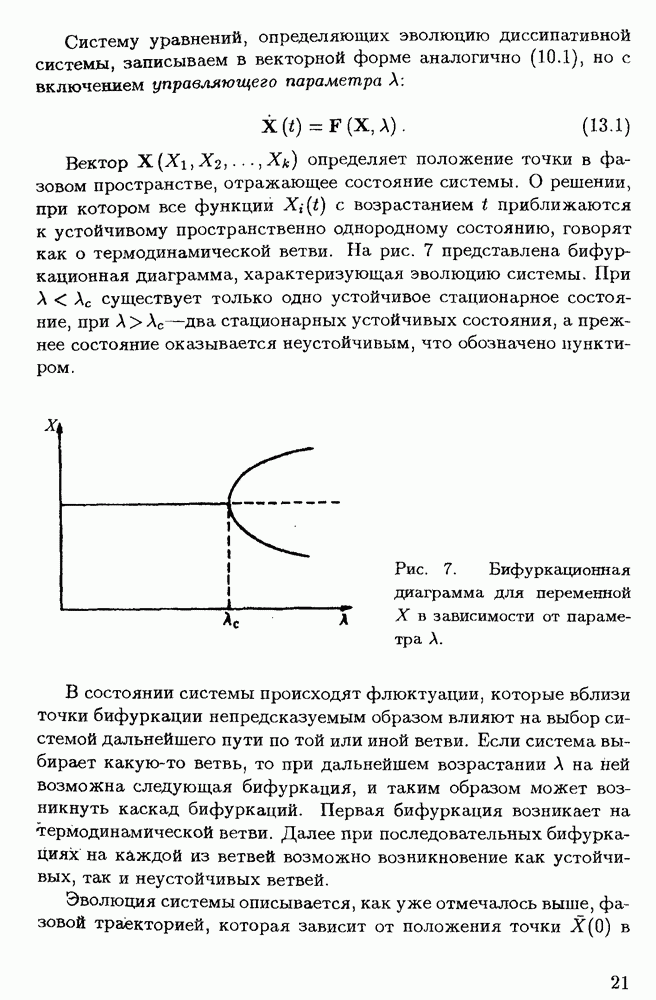
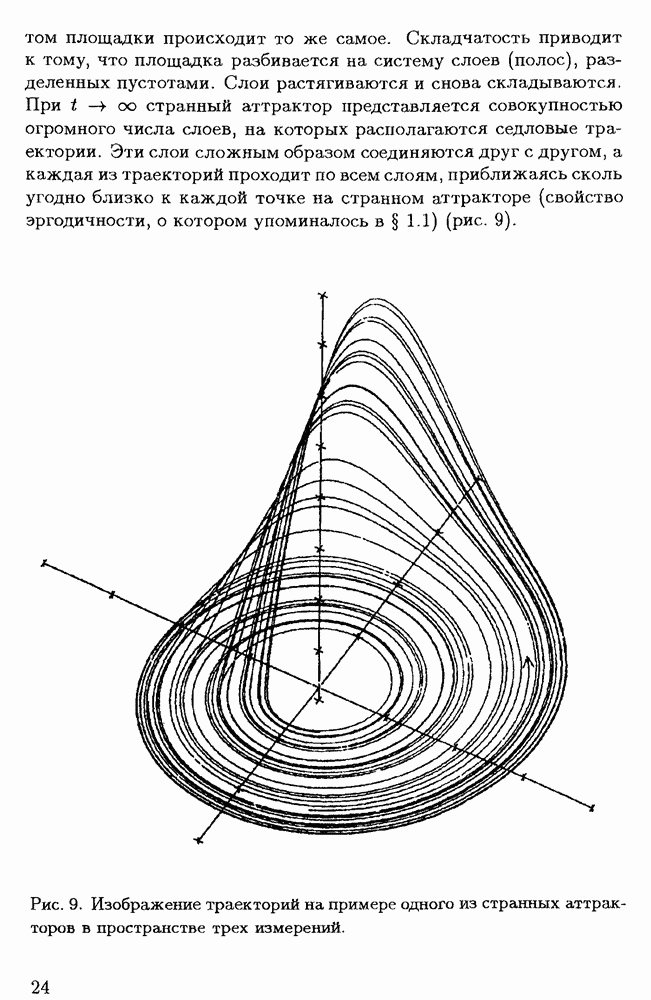
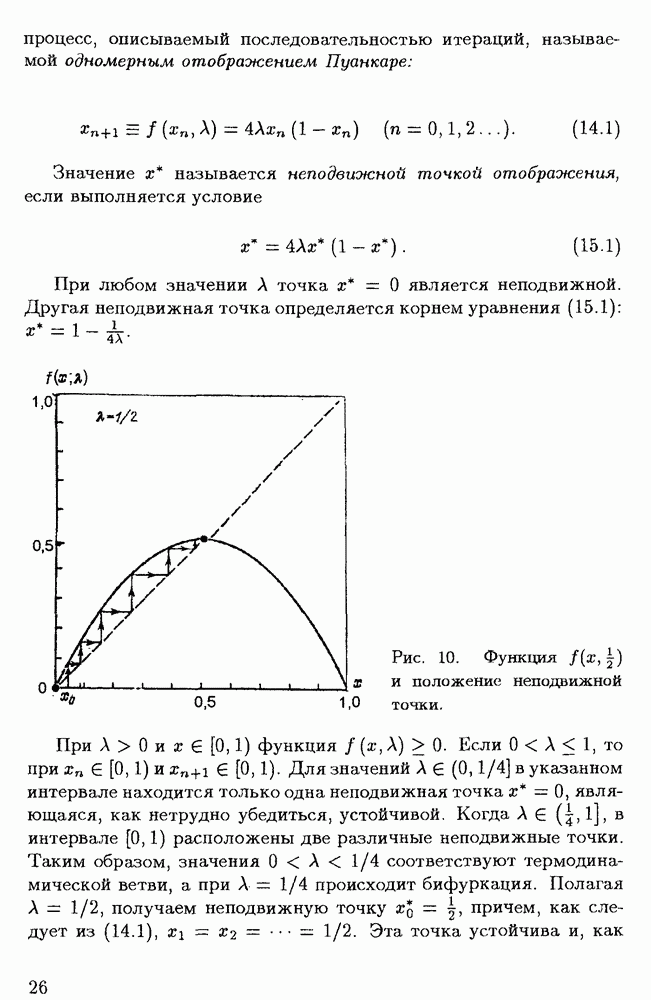
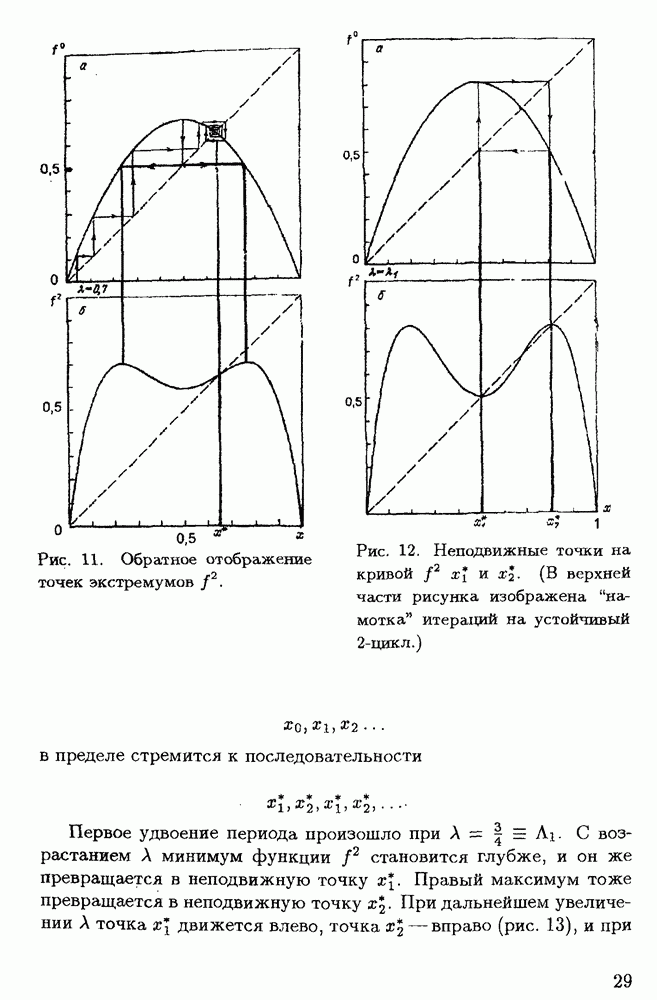
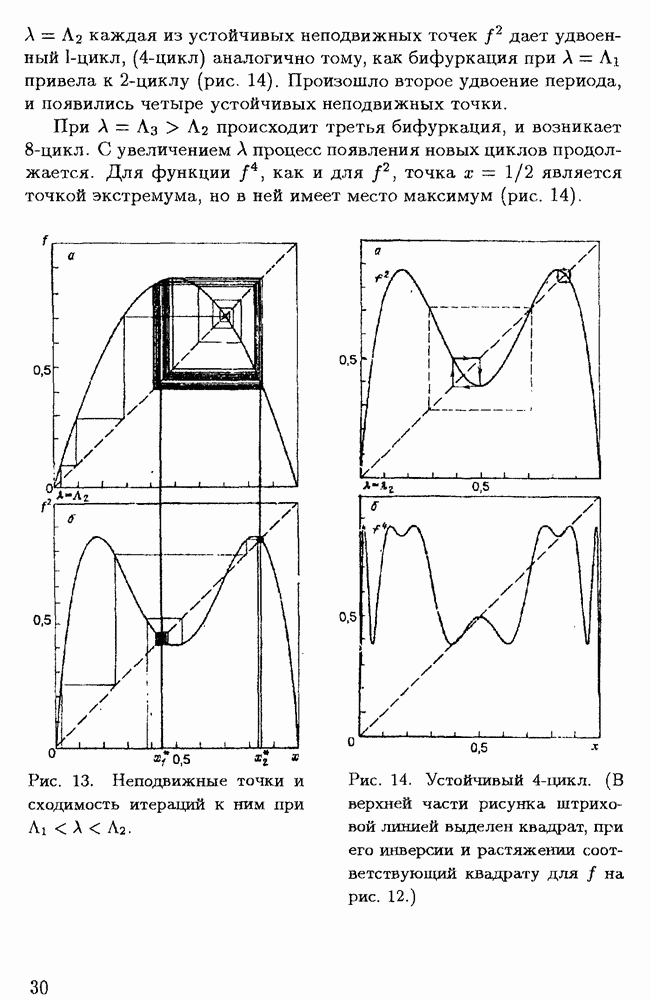
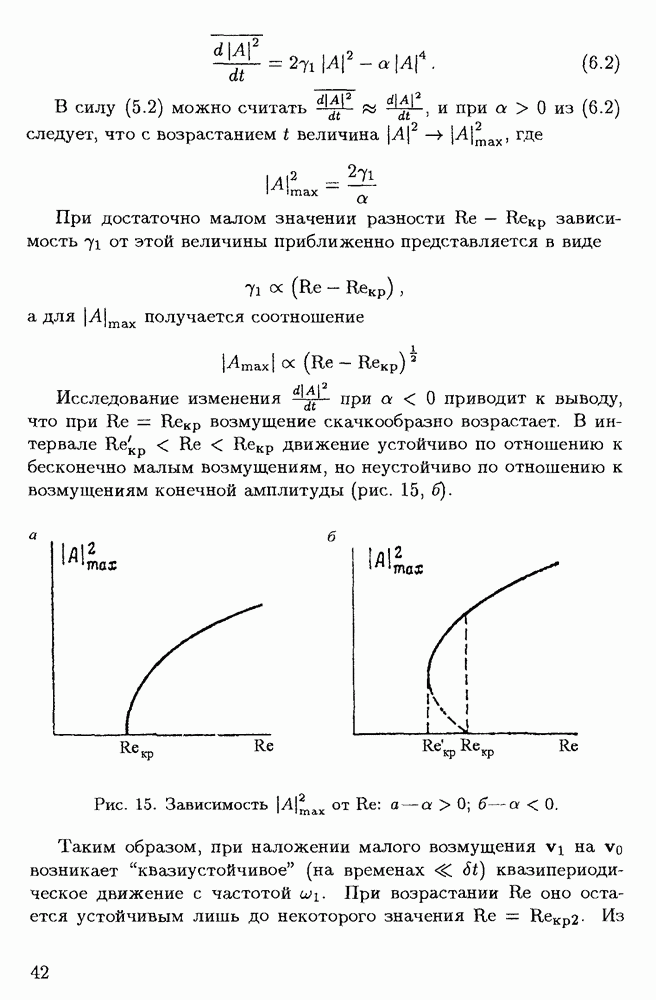
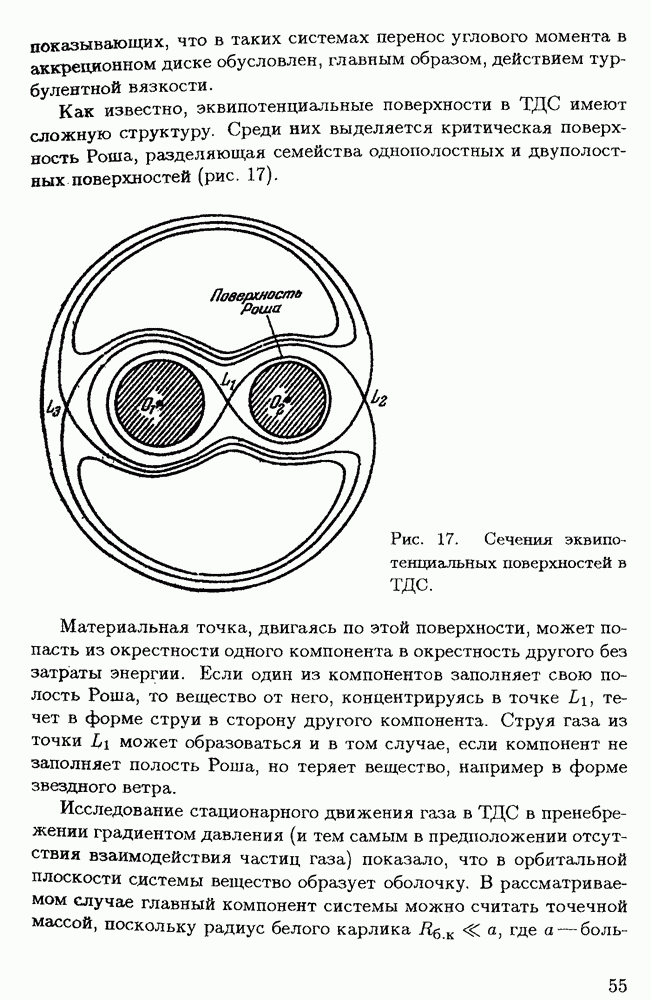
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
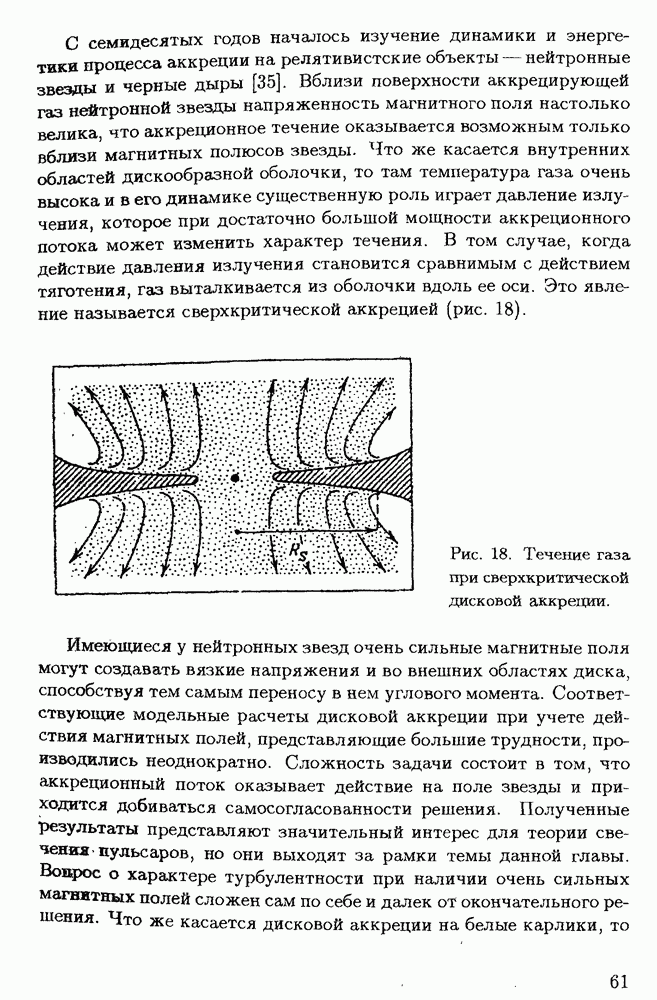
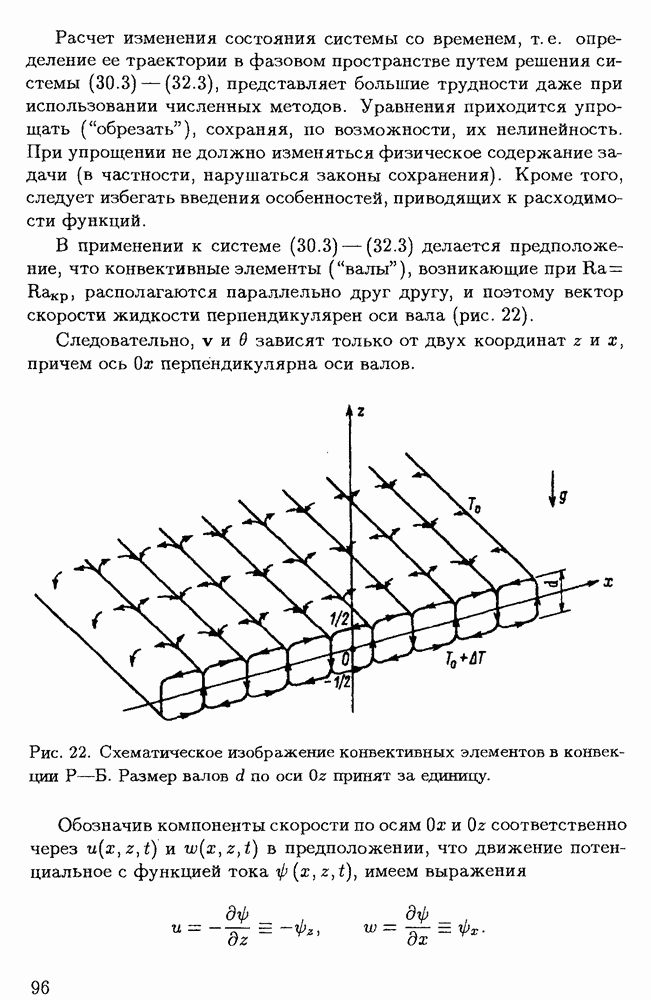
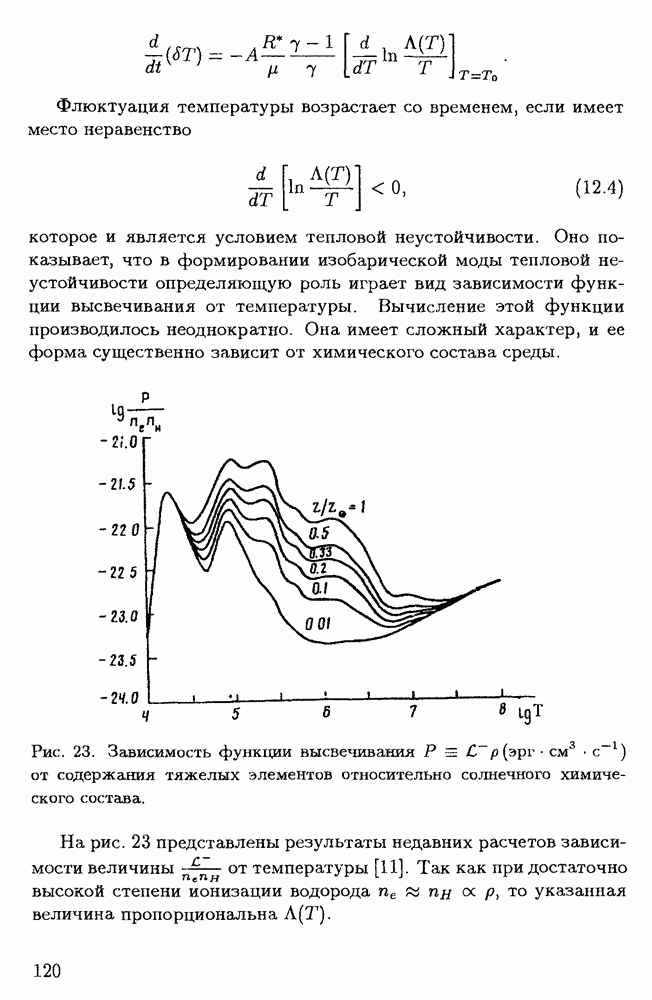
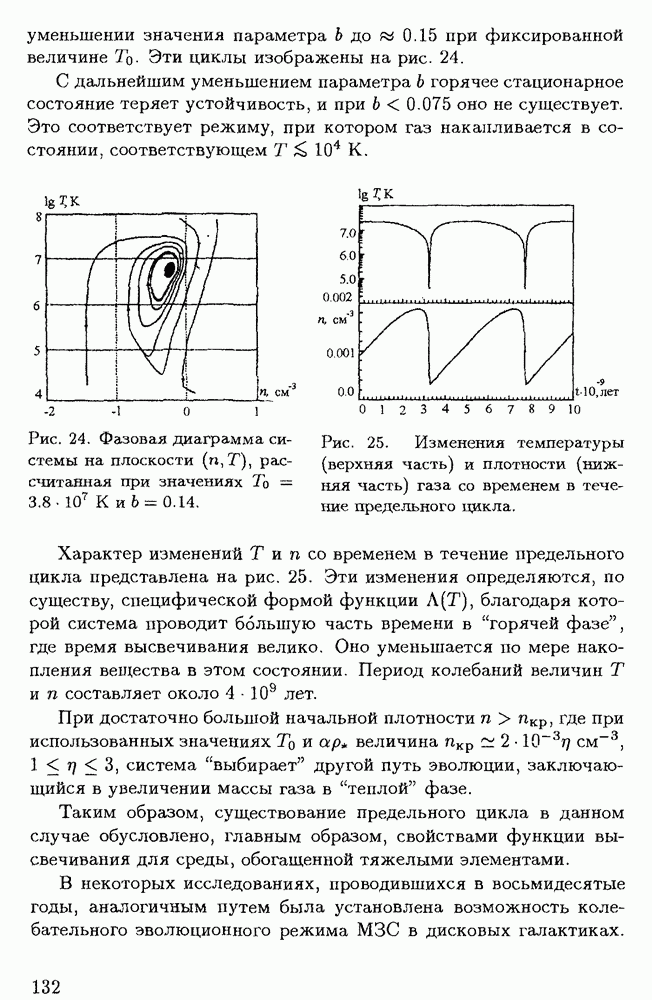
§ 2.4. Перенос углового момента в звездах турбулентной вязкостью
Среди тех  которых хотя бы один из компонентов относится к позднему спектральному классу
которых хотя бы один из компонентов относится к позднему спектральному классу  имеются системы, характеризующиеся асинхронностъю осевого вращения и орбитального обращения. Это означает, что частота вращения звезды
имеются системы, характеризующиеся асинхронностъю осевого вращения и орбитального обращения. Это означает, что частота вращения звезды  превосходит частоту орбитального движения
превосходит частоту орбитального движения  Вместе с тем многократно производившиеся оценки времени синхронизации в
Вместе с тем многократно производившиеся оценки времени синхронизации в  под действием динамических приливов показали, что синхронизация должна происходить очень быстро — синхр
под действием динамических приливов показали, что синхронизация должна происходить очень быстро — синхр  лет. За это время угловая скорость
лет. За это время угловая скорость  первоначально превосходившая
первоначально превосходившая  уменьшаясь, становится равной ей. Наблюдаемая асинхронность вращения и обращения в системах, для которых время эволюции значительно превосходит время
уменьшаясь, становится равной ей. Наблюдаемая асинхронность вращения и обращения в системах, для которых время эволюции значительно превосходит время  рассчитанное для систем с "нормальными" компонентами, служат основанием для предположения о наличии внутри звезды (компонента ТДС) источника углового момента — быстро вращающегося "ядра".
рассчитанное для систем с "нормальными" компонентами, служат основанием для предположения о наличии внутри звезды (компонента ТДС) источника углового момента — быстро вращающегося "ядра".
Во внешней конвективной зоне, существующей у звезд поздних классов, вязкость газа настолько велика, что динамические приливы должны были бы очень быстро устанавливать ее синхронное вращение. Асинхронность же — если принять указанное предположение — вызывается наличием крутящего момента на внутренней границе конвективной зоны со стороны более глубоких слоев звезды. Это означает, что происходит перенос углового момента от быстро вращающегося ядра к тормозящейся динамическими приливами конвективной оболочке.
Между ядром и конвективной оболочкой находится зона лучистого равновесия. В обычных условиях вязкость плазмы там слишком мала для того, чтобы обеспечить достаточно быстрый перенос углового момента от ядра наружу. Поэтому в зоне лучистого равновесия должен существовать иной, более эффективный, механизм переноса углового момента.
В зоне лучистого равновесия, где число Рейнольдса очень велико  при дифференциальном вращении, т. е. при изменении
при дифференциальном вращении, т. е. при изменении  с расстоянием
с расстоянием  до центра звезды, можно предполагать наличие развитой турбулентности. Действие турбулентной вязкости, превосходящей вязкость в нетурбулизованной плазме на несколько порядков, способно обеспечить быструю передачу углового момента из центральной области звезды наружу.
до центра звезды, можно предполагать наличие развитой турбулентности. Действие турбулентной вязкости, превосходящей вязкость в нетурбулизованной плазме на несколько порядков, способно обеспечить быструю передачу углового момента из центральной области звезды наружу.
Для решения задачи о скорости переноса углового момента в звезде турбулентной вязкостью и соответственно о вычислении времени, требующегося для синхронизации вращения и обращения в системе, компонент которой содержит быстро вращающееся ядро, предварительно найдем распределение угловой скорости в звезде в предположении о стационарности процесса переноса [6].
Большая доля углового момента звезды содержится в ее экваториальной зоне. Там образуются "приливные выступы", действие тяготения на которые и приводит к синхронизации. Поэтому для упрощения расчетов рассматривается перенос момента в цилиндрической газовой конфигурации. Внутренняя область цилиндра — ядро, имеющее радиус  содержит преобладающую долю массы и вращается однородно с угловой скоростью
содержит преобладающую долю массы и вращается однородно с угловой скоростью  Тонкий периферийный слой у внешней границы цилиндра — радиус его равен
Тонкий периферийный слой у внешней границы цилиндра — радиус его равен  имеет скорость вращения
имеет скорость вращения  . В области
. В области  преобладает лучистый перенос энергии, но существует и развитая турбулентность. При
преобладает лучистый перенос энергии, но существует и развитая турбулентность. При  происходит сток углового момента.
происходит сток углового момента.
Распределение угловой скорости в области лучистого переноса находится путем решения уравнения Навье-Стокса. В предположении стационарности движения это уравнение, записанное в полярных координатах, имеет следующий вид:

где  скорость вращения и
скорость вращения и  динамический коэффициент турбулентной вязкости.
динамический коэффициент турбулентной вязкости.
Примем, что величина  изменяется в зоне лучистого равновесия согласно соотношению
изменяется в зоне лучистого равновесия согласно соотношению

где  температура и
температура и  параметр, значение которого будет определено ниже. Следует заметить, что аналогичная (37.2) зависимость вязкости от
параметр, значение которого будет определено ниже. Следует заметить, что аналогичная (37.2) зависимость вязкости от  существует в высокотемпературной плазме.
существует в высокотемпературной плазме.
При обозначениях

где То — значение температуры при  из уравнения (36.2) при учете соотношения (37.2) получается уравнение
из уравнения (36.2) при учете соотношения (37.2) получается уравнение

На поверхности ядра выполняются условия

а на внешней границе зоны лучистого равновесия при 

Уравнение (38.2) имеет первый интеграл в следующей форме:

При посредстве этого интеграла находится величина 

Функция  представляется отношением
представляется отношением

Выражения (39.2) и (40.2) показывают, что действие вязкости не является локальным. На величине угловой скорости в точке  сказываются значения коэффициента вязкости во всех точках интервала
сказываются значения коэффициента вязкости во всех точках интервала 
Распределение угловой скорости в оболочке зависит от распределения температуры, которое определяется условиями механического равновесия и лучистого равновесия.
В предположении, что высота цилиндра мала по сравнению с  и пренебрегая величиной градиента турбулентного давления, уравнение механического равновесия можно записать в виде
и пренебрегая величиной градиента турбулентного давления, уравнение механического равновесия можно записать в виде

Если зависимость между давлением и плотностью газа политропная:

то при обычном уравнении состояния идеального газа из (41.2) получается следующее уравнение, определяющее изменение температуры:

где

 величина угловой скорости кругового кеплеровского движения при
величина угловой скорости кругового кеплеровского движения при  молекулярный вес. Система уравнений (39.2), (40.2) и (42.2) решает задачу о распределении скорости и температуры в области
молекулярный вес. Система уравнений (39.2), (40.2) и (42.2) решает задачу о распределении скорости и температуры в области  но остается вопрос о том, удовлетворяет ли решение условию лучистого равновесия. Для сферической конфигурации это условие имеет вид
но остается вопрос о том, удовлетворяет ли решение условию лучистого равновесия. Для сферической конфигурации это условие имеет вид

где  поток излучения и
поток излучения и  коэффициент непрозрачности. При
коэффициент непрозрачности. При  определяемым формулой Крамерса
определяемым формулой Крамерса

для  получается выражение
получается выражение

Если  то уравнения (42.2) и (43.2) совместимы. Влияние вращения звезды сводится к формальному уменьшению массы ядра на множитель
то уравнения (42.2) и (43.2) совместимы. Влияние вращения звезды сводится к формальному уменьшению массы ядра на множитель  по сравнению со случаем, когда
по сравнению со случаем, когда  величина То при тех же значениях
величина То при тех же значениях  отличается множителем
отличается множителем  от соответствующего значения для невращающейся конфигурации. При К 2 это различие составляет менее 4%.
от соответствующего значения для невращающейся конфигурации. При К 2 это различие составляет менее 4%.
Как показали расчеты, при  изменение
изменение  близко следует соотношению
близко следует соотношению  Выло установлено также, что при значениях
Выло установлено также, что при значениях  величина
величина  слабо зависит от
слабо зависит от 
Таким образом, решение задачи о распределении угловой скорости внутри звезды, обладающей быстро вращающимся ядром, можно считать приближено самосогласованным — по крайней мере для политропной звезды с показателем 
Для оценки характерного времени динамического процесса необходимо получить конкретные данные о величине коэффициента турбулентной вязкости  в дифференциально вращающейся зоне звезды. Эту величину можно оценить из соотношений, связывающих характеристики турбулентности.
в дифференциально вращающейся зоне звезды. Эту величину можно оценить из соотношений, связывающих характеристики турбулентности.
Пусть, как и выше, I означает пространственный масштаб вихря, а  соответствующую ему скорость турбулентного движения. Приняв за характерную длину расстояние от данной точки до центра звезды, из соображений размерности имеем соотношение
соответствующую ему скорость турбулентного движения. Приняв за характерную длину расстояние от данной точки до центра звезды, из соображений размерности имеем соотношение

совпадающее с указанным в § 2.3 условием того, что вихри не размываются дифференциальным вращением. Такую же зависимость между  можно получить иным путем, рассматривая диссипацию энергии турбулентного движения вследствие турбулентной вязкости. В единице объема за единицу времени диссипирует энергия
можно получить иным путем, рассматривая диссипацию энергии турбулентного движения вследствие турбулентной вязкости. В единице объема за единицу времени диссипирует энергия  определяемая равенством
определяемая равенством

Поскольку

то (45.2) записывается в виде

Учитывая, что

находим, что (46.2) совпадает с (44.2) и, следовательно, выводы о характере диссипации энергии вращения в зоне лучистого равновесия являются самосогласованными.
Здесь необходимо отметить различие между процессами диссипации энергии вследствие турбулентной вязкости и диссипацией под действием молекулярной вязкости, описанной в § 2.2. Прежде всего при дифференциальном вращении среды турбулентность не вызывается непосредственным действием источника на всю систему. В каждом из достаточно тонких слоев газа турбулентность создается действием соседнего слоя, т.е. каждый слой представляет собой систему с собственным источником турбулентной энергии. Аналогичная ситуация имеет место и для аккреционного диска, где, как следует из соотношения (30.2), энергия от "внешнего" источника (потенциальная) превращается в энергию турбулентных движений. При взаимодействии вихрей больших масштабов, обусловливающем турбулентную вязкость, происходит передача их энергии в меньшие масштабы, где она в конечном счете превращается в тепловую энергию. Однако происходящее в малых вихрях не сказывается на величине турбулентной вязкости. Поэтому при рассмотрении процесса переноса углового момента через дифференциально вращающуюся турбулентную среду следует употреблять так называемое турбулентное число Рейнолъдса

Из данных экспериментов, проводившихся, в основном, для несжимаемых жидкостей, следует, что  и поэтому
и поэтому

где величина А порядка  Как было показано выше, в большей части зоны лучистого равновесия, через которую происходит перенос углового момента от быстро вращающегося ядра,
Как было показано выше, в большей части зоны лучистого равновесия, через которую происходит перенос углового момента от быстро вращающегося ядра,  и, следовательно, зависимость
и, следовательно, зависимость  от
от  слабая. Кроме того, в физике звезд показано, что в области лучистого равновесия
слабая. Кроме того, в физике звезд показано, что в области лучистого равновесия

и поэтому для значения параметра  введенного соотношением (37.2), имеем
введенного соотношением (37.2), имеем 
Между твердотельно вращающимся ядром и той областью зоны лучистого равновесия, где имеет место равенство (47.2), существует переходный слой. Толщина этого слоя должна быть относительно малой — порядка нескольких процентов радиуса ядра. В том случае, когда ядро по своим размерам и плотности близко к белому карлику, вместо  в (47.2) следует использовать величину, соответствующую толщине пограничного слоя
в (47.2) следует использовать величину, соответствующую толщине пограничного слоя  Тогда для значения вязкости
Тогда для значения вязкости  границы ядра получается соотношение
границы ядра получается соотношение

где  Воспользуемся этим выражением для оценки характерного времени потери ядром своего углового момента, соответствующего
Воспользуемся этим выражением для оценки характерного времени потери ядром своего углового момента, соответствующего  . В "цилиндрической модели" угловая скорость вращения ядра
. В "цилиндрической модели" угловая скорость вращения ядра  изменяется согласно уравнению
изменяется согласно уравнению

получающемуся из выражения крутящего момента со стороны ядра

Величина

может быть определена на основе известного распределения угловой скорости  в зоне переноса углового момента. Через
в зоне переноса углового момента. Через  обозначен момент инерции для однородного шара с плотностью
обозначен момент инерции для однородного шара с плотностью  имеющий величину
имеющий величину

При указанных значениях величин из уравнения (48.2) находим

Уравнение, аналогичное (48.2), получается, если рассматривать скорость потери ядром энергии вращения в результате ее диссипации в зоне лучистого равновесия. Из соотношения

где V — объем зоны, в которой происходит обусловленная вязкостью диссипация энергии, получается уравнение

Здесь

Вычисление величин  при
при  дало
дало  Значение
Значение  по (50.2) практически совпадает с тем, что найдено из уравнения (48.2). Для нескольких систем оценки продолжительности времени торможения ядра, т. е. синхронизации, по (49.2) дают величину
по (50.2) практически совпадает с тем, что найдено из уравнения (48.2). Для нескольких систем оценки продолжительности времени торможения ядра, т. е. синхронизации, по (49.2) дают величину  лет. Такая величина сравнима с временем жизни систем, определяемым по статистическим данным об их численности и по теории звездной эволюции.
лет. Такая величина сравнима с временем жизни систем, определяемым по статистическим данным об их численности и по теории звездной эволюции.
Таким образом, предположение существования быстро вращающихся ядер в компонентах некоторых  не противоречит наблюдательным данным. Возможность образования подобных ядер подтверждается результатами расчетов эволюции звезд [25]. Происходящая как следствие этого турбулизация зоны лучистого равновесия звезды должна приводить к перемешиванию вещества в
не противоречит наблюдательным данным. Возможность образования подобных ядер подтверждается результатами расчетов эволюции звезд [25]. Происходящая как следствие этого турбулизация зоны лучистого равновесия звезды должна приводить к перемешиванию вещества в
звезде, т. е. к переносу продуктов ядерных реакций наружу. Имеющиеся наблюдательные данные о химическом составе внешних слоев звезд указывают на то, что перемешивание в некоторых случаях действительно имеет место. О процессе турбулентного перемешивания подробнее говорится в следующем параграфе.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
- § 1.4. Бифуркация удвоения периода
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
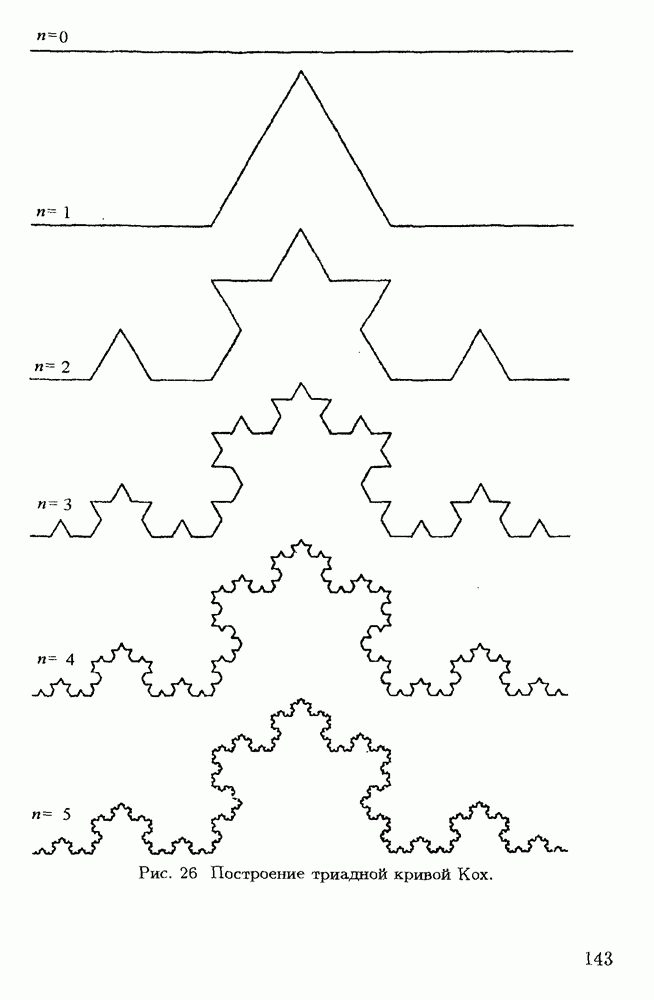
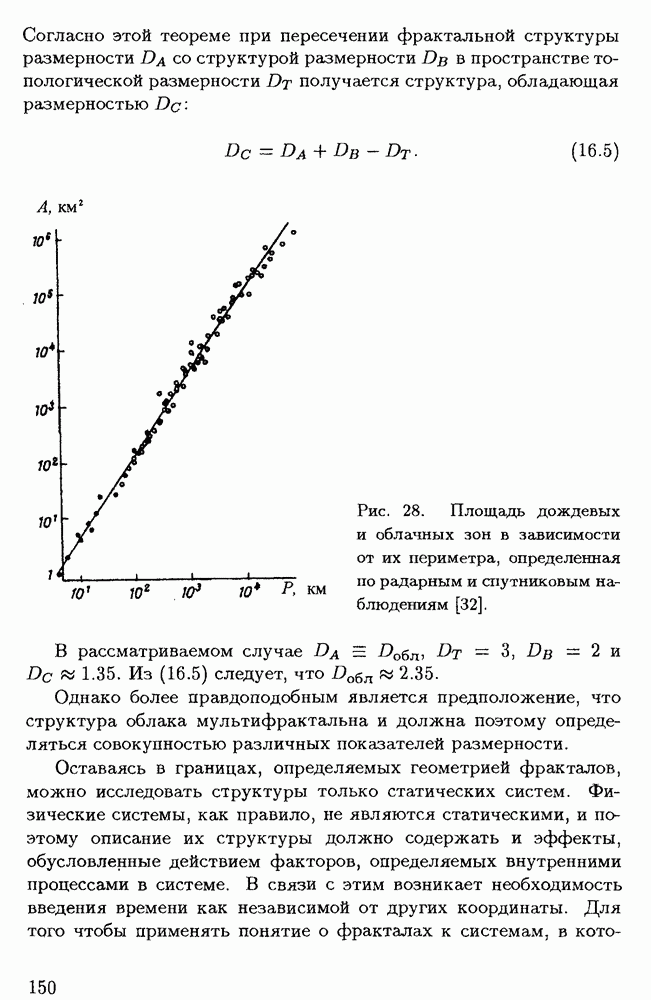
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение