| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 1. Основные понятия теории устойчивости физических систем
§ 1.1. Эволюция динамических систем
Среди изучаемых классической механикой объектов важнейшее место занимают динамические системы, содержащие конечное число  взаимодействующих друг с другом точечных масс. Энергия такой системы слагается из потенциальной энергии
взаимодействующих друг с другом точечных масс. Энергия такой системы слагается из потенциальной энергии  , обусловленной взаимодействием масс, и кинетической
, обусловленной взаимодействием масс, и кинетической  энергии их движения. Полное описание системы включает в себя помимо выражений
энергии их движения. Полное описание системы включает в себя помимо выражений  и Екии внешние условия, которые могут сказываться на ее состоянии. Система, не взаимодействующая с какими-либо другими системами, называется изолированной. В таких системах при отсутствии диссипации энергия не меняется со временем, поэтому их относят к числу консервативных систем.
и Екии внешние условия, которые могут сказываться на ее состоянии. Система, не взаимодействующая с какими-либо другими системами, называется изолированной. В таких системах при отсутствии диссипации энергия не меняется со временем, поэтому их относят к числу консервативных систем.
Для исследования динамических систем используют хорошо разработанный математический аппарат. Состояние системы определяется значениями координат  и импульсов
и импульсов  всех ее точек
всех ее точек  Эти величины, называемые обобщенными координатами, образуют
Эти величины, называемые обобщенными координатами, образуют  пространство (фазовое пространство). Состоянию системы в каждый данный момент соответствует точка фазового пространства. При изменении состояния эта точка описывает некоторую траекторию.
пространство (фазовое пространство). Состоянию системы в каждый данный момент соответствует точка фазового пространства. При изменении состояния эта точка описывает некоторую траекторию.
В динамической системе непрерывно происходит обмен между кинетической и потенциальной энергиями. Динамическому равновесию системы соответствует замкнутая траектория в фазовом пространстве, что означает периодическое изменение состояния.
В механике при изучении эволюции систем употребляют выражение, называемое гамильтонианом  Он представляет собой сумму
Он представляет собой сумму

т. е. полную энергию системы, выраженную через обобщенные координаты. Для консервативных систем  явно от времени не зависит.
явно от времени не зависит.
Изменение состояния системы со временем в классической механике описывается каноническими уравнениями

решение которых ищется при определенных начальных условиях:

Простой пример консервативной системы представляет гармонический осциллятор, состоящий из точечной массы  и упругой связи — "пружины", действие которой зависит от расстояния до положения равновесия. Потенциальная энергия определяется положением точки, и если сила действия пружины пропорциональна ее удлинению
и упругой связи — "пружины", действие которой зависит от расстояния до положения равновесия. Потенциальная энергия определяется положением точки, и если сила действия пружины пропорциональна ее удлинению  то гамильтониан системы имеет вид
то гамильтониан системы имеет вид

а движение точки представляет собой синусоидальные колебания относительно положения  с циклической частотой
с циклической частотой 
Другим примером простой динамической системы является математический маятник (точечной массы  качающийся в плоскости при постоянном ускорении силы тяжести
качающийся в плоскости при постоянном ускорении силы тяжести  Соответствующее фазовое пространство двухмерно — одна из координат
Соответствующее фазовое пространство двухмерно — одна из координат  а за другую можно принять величину, определяющую положение маятника относительно точки равновесия (рис. 1).
а за другую можно принять величину, определяющую положение маятника относительно точки равновесия (рис. 1).
При условии, что полная энергия Еишш  фазовая траектория представляет собой окружность, причем радиус окружности тем меньше, чем меньше Еполн. Точка в начале координат соответствует положению статического равновесия.
фазовая траектория представляет собой окружность, причем радиус окружности тем меньше, чем меньше Еполн. Точка в начале координат соответствует положению статического равновесия.
Более сложное движение с двумя степенями свободы получается, если на гармонический осциллятор, колеблющийся с частотой  накладывается некоторое периодическое возмущение с частотой
накладывается некоторое периодическое возмущение с частотой  . В фазовом пространстве траектория движения точки изображается намоткой на торе (рис. 2). Фазы обоих периодических движений произвольны, и поэтому движение точки обладает двумя степенями свободы.
. В фазовом пространстве траектория движения точки изображается намоткой на торе (рис. 2). Фазы обоих периодических движений произвольны, и поэтому движение точки обладает двумя степенями свободы.
Если отношение  не равно рациональному числу, то движущаяся по траектории точка, отражающая состояние системы,
не равно рациональному числу, то движущаяся по траектории точка, отражающая состояние системы,

Рис. 1. Идеальный маятник (без трения) и его фазовая траектория.

Рис. 2. Фазовая траектория в виде намотки на торе.
никогда не попадет в начальное положение — траектория не замкнута. С течением времени движущаяся точка проходит через сколь угодно малую окрестность любой точки на поверхности тора. Это свойство фазовой траектории называют эргодичностью, а системы, обладающие таким свойством, — эргодическими. Движение же при указанном отношении  является квазипериодическим. Поскольку в рассмотренном случае невозможно прогнозировать приход системы в данную точку фазового пространства, понятие о траектории размывается. Она оказывается не столь удобным объектом для исследования движений, как долгое время принималось в классической механике.
является квазипериодическим. Поскольку в рассмотренном случае невозможно прогнозировать приход системы в данную точку фазового пространства, понятие о траектории размывается. Она оказывается не столь удобным объектом для исследования движений, как долгое время принималось в классической механике.
Особый интерес представляют те случаи, когда частоты  соизмеримы, т. е. отношение
соизмеримы, т. е. отношение  равно рациональному числу. При этом фазовая траектория оказывается замкнутой, а состояние системы изменяется периодически. Однако взаимодействие двух движений с соизмеримыми частотами может привести к резонансу, при котором будет происходить передача энергии от одного периодического движения к другому. Результат такого
равно рациональному числу. При этом фазовая траектория оказывается замкнутой, а состояние системы изменяется периодически. Однако взаимодействие двух движений с соизмеримыми частотами может привести к резонансу, при котором будет происходить передача энергии от одного периодического движения к другому. Результат такого
взаимодействия непредсказуем — траектория становится стохастической. Это было продемонстрировано численными экспериментами.

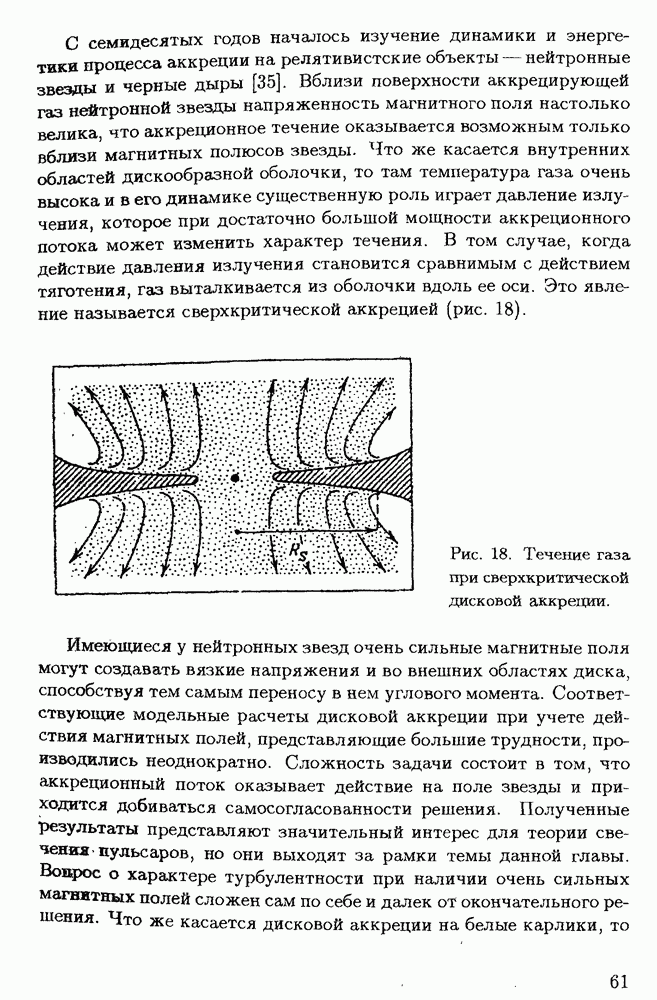
Рис. 3. Сечение Пуанкаре для различных видов траекторий: а) периодическая; б) условно-периодическая; в) стохастическая.
Различие между движениями по периодическим, квазипериодическим и стохастическим траекториям иллюстрируется так называемым сечением Пуанкаре. Для динамической системы, состоящей из двух материальных точек, фазовое пространство четырехмерное с координатами  Если система консервативна, т.е. ее энергия
Если система консервативна, т.е. ее энергия  постоянна, то одна из переменных, например
постоянна, то одна из переменных, например  выражается через остальные и фазовая траектория представляет собой кривую в трехмерном пространстве
выражается через остальные и фазовая траектория представляет собой кривую в трехмерном пространстве  -Пересечение этой кривой с плоскостью
-Пересечение этой кривой с плоскостью  и является сечением Пуанкаре, которое изображено на рис. 3. Это сечение для периодического движения является точкой, для квазипериодического движения оно представляет собой множество дискретных точек на замкнутой кривой, а для стохастического движения точки располагаются случайным образом в некоторой области плоскости
и является сечением Пуанкаре, которое изображено на рис. 3. Это сечение для периодического движения является точкой, для квазипериодического движения оно представляет собой множество дискретных точек на замкнутой кривой, а для стохастического движения точки располагаются случайным образом в некоторой области плоскости 
Возможность появления стохастических траекторий, не следующая непосредственно из уравнений (2.1), обусловлена принципиальным различием между двумя типами динамических систем.
Для некоторых динамических систем выражение гамильтониана (1.1) можно привести к виду

путем так называемого канонического преобразования. Величины  называются переменными действия. Для простой системы — гармонического осциллятора — преобразование
называются переменными действия. Для простой системы — гармонического осциллятора — преобразование  имеет вид
имеет вид

где а — угловая переменная. При подстановке (5.1) в (3.1) получается

В общем случае для системы  точек выражением гамильтониана (4.1) аналогично (6.1) определяется
точек выражением гамильтониана (4.1) аналогично (6.1) определяется  частотам
частотам  соотношениями
соотношениями

Таким образом, вместо обобщенных координат  введены координаты
введены координаты  Канонические уравнения (2.1) в новых координатах принимают вид
Канонические уравнения (2.1) в новых координатах принимают вид

Из второй формулы (8.1) следует, что переменные действия являются интегралами движения, а величины  как следует из (7.1), — линейными функциями времени.
как следует из (7.1), — линейными функциями времени.
Системы, для которых возможно преобразование гамильтониана к виду (4.1), называются интегрируемыми. По существу, каноническое преобразование позволяет не учитывать в явном виде взаимодействие между материальными точками системы, т. е. "исключить" потенциальную энергию.
Рассмотренная выше система двух тел, у которой фазовая траектория представляет собой намотку на тор, является неинтегрируемой, так как возникающее в ней резонансное взаимодействие исключить невозможно. В данном случае резонансные случаи
встречаются очень редко по сравнению с нерезонансными, поскольку мера множества рациональных чисел нулевая по сравнению с мерой множества иррациональных чисел. Однако важен сам факт неизбежности появления стохастических траекторий наряду с квазипериодическими. Это обстоятельство позволило сделать решающий шаг в развитии последований динамических систем, заключающийся в создании теории КАМ (Колмогорова — Арнольда-Мозера).
Стохастических траекторий нет только у интегрируемых систем — наименее сложных. Поскольку появление стохастических траекторий связано с взаимодействием между телами, входящими в систему, при увеличении числа тел возможность резонансов становится больше и соответственно возрастает число стохастических траекторий. В предельном случае "Больших систем Пуанкаре" (БСП) резонансы играют главную роль, преобладают стохастические траектории и движения в системе становятся хаотическими.
Само понятие траектории в этих случаях теряет свой прежний смысл. Для того чтобы фазовая траектория была адекватной формой представления об эволюции системы, она должна быть и оставаться очень мало меняющейся при малом изменении начальных условий. У неинтегрируемых систем некоторые из траекторий этим свойством не обладают, а для хаотических систем возможность точных предсказаний хода эволюции полностью отсутствует.
До сих пор здесь рассматривались только изолированные системы. Возможность диссипации механической энергии, т. е. перехода ее в другую форму, например в тепловую энергию, меняет характер эволюции системы и, в частности, влияет на устойчивость ее состояний.
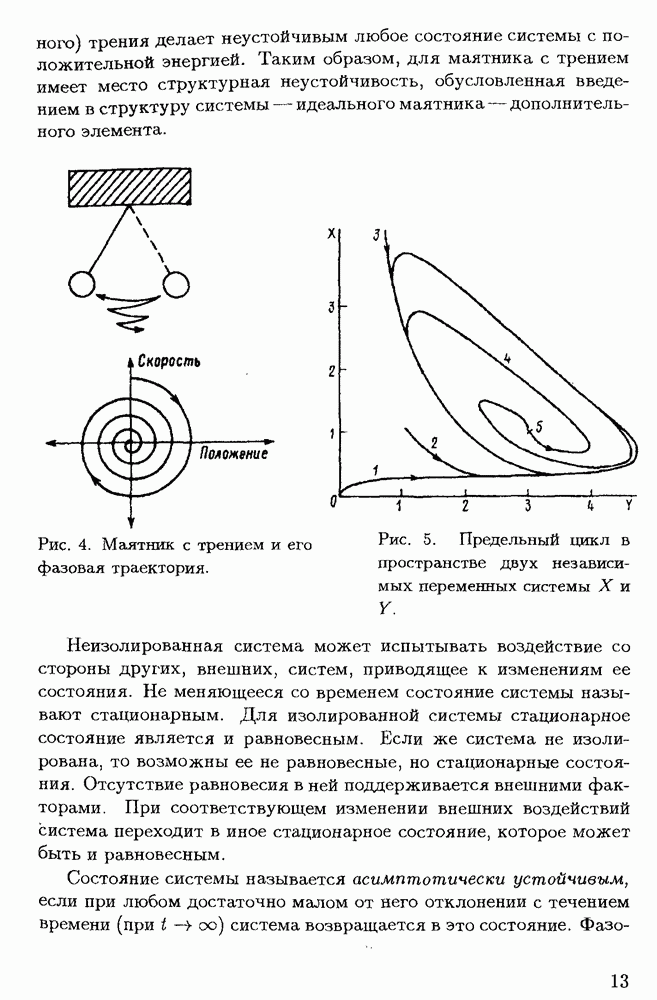
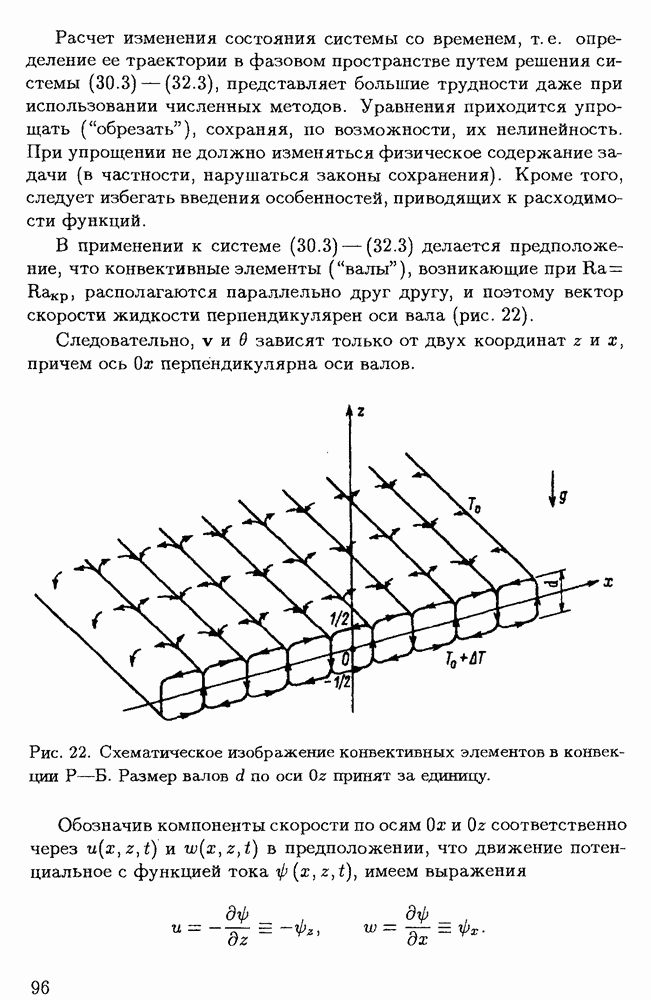
Понятие устойчивости состояния системы проиллюстрируем на примере математического маятника при учете трения. По своему поведению эта система принципиально отличается от идеального маятника, так как его механическая энергия со временем уменьшается, превращаясь в тепловую. Фазовая траектория представляет собой спираль, сходящуюся в точку, соответствующую статическому равновесию (рис. 4).
При любом исходном состоянии в процессе своей эволюции система будет стремиться к статическому равновесию. Поэтому указанную точку называют аттрактором (от слова "attraction", означающего притяжение). Введение сколь угодно слабого (но конечного)
трения делает неустойчивым любое состояние системы с положительной энергией. Таким образом, для маятника с трением имеет место структурная неустойчивость, обусловленная введением в структуру системы — идеального маятника — дополнительного элемента.

Рис. 4. Маятник с трением и его фазовая траектория.

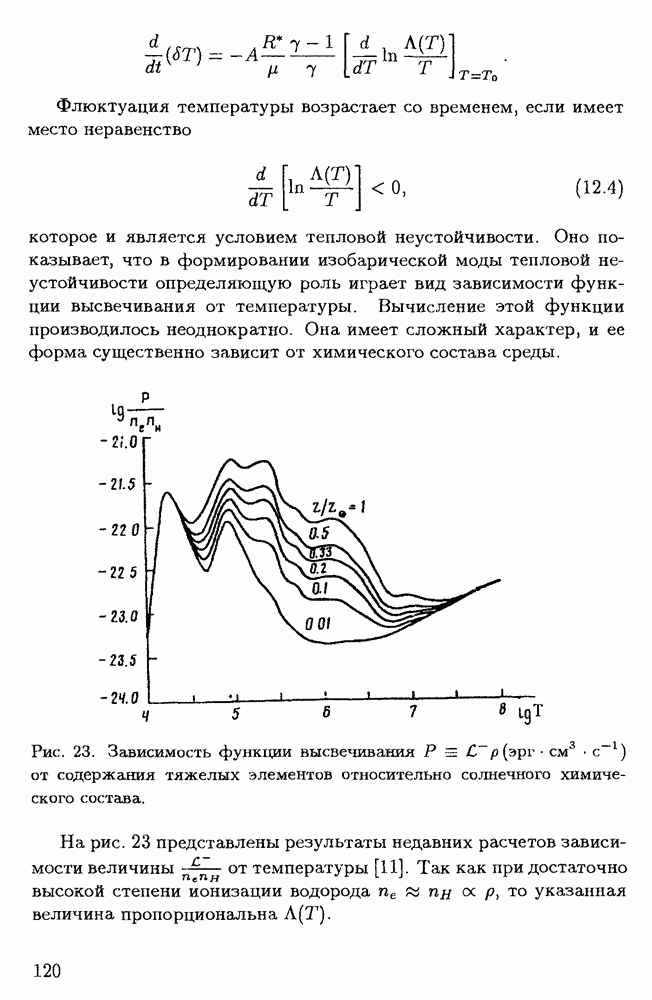
Рис. 5. Предельный цикл в пространстве двух независимых переменных системы 
Неизолированная система может испытывать воздействие со стороны других, внешних, систем, приводящее к изменениям ее состояния. Не меняющееся со временем состояние системы называют стационарным. Для изолированной системы стационарное состояние является и равновесным. Если же система не изолирована, то возможны ее не равновесные, но стационарные состояния. Отсутствие равновесия в ней поддерживается внешними факторами. При соответствующем изменении внешних воздействий система переходит в иное стационарное состояние, которое может быть и равновесным.
Состояние системы называется асимптотически устойчивым, если при любом достаточно малом от него отклонении с течением времени (при  система возвращается в это состояние.
система возвращается в это состояние.
Фазовая траектория сходится в соответствующую устойчивому состоянию точку из любой достаточно близкой к ней точки фазового пространства. При невыполнении этого условия состояние является неустойчивым. В случае неидеального маятника состояние, соответствующее минимуму энергии  оказывается асимптотически устойчивым.
оказывается асимптотически устойчивым.
Для многих систем устойчивым является не выделенное состояние, которому соответствует точка фазового пространства, а некоторый периодический режим. В таком случае в фазовом пространстве существует замкнутая кривая, к которой сходятся все кривые, исходящие из достаточно близких к ней точек. Эта кривая является для системы аттрактором, называемым предельным циклом. Пример такого аттрактора в пространстве двух переменных представлен на рис. 5.
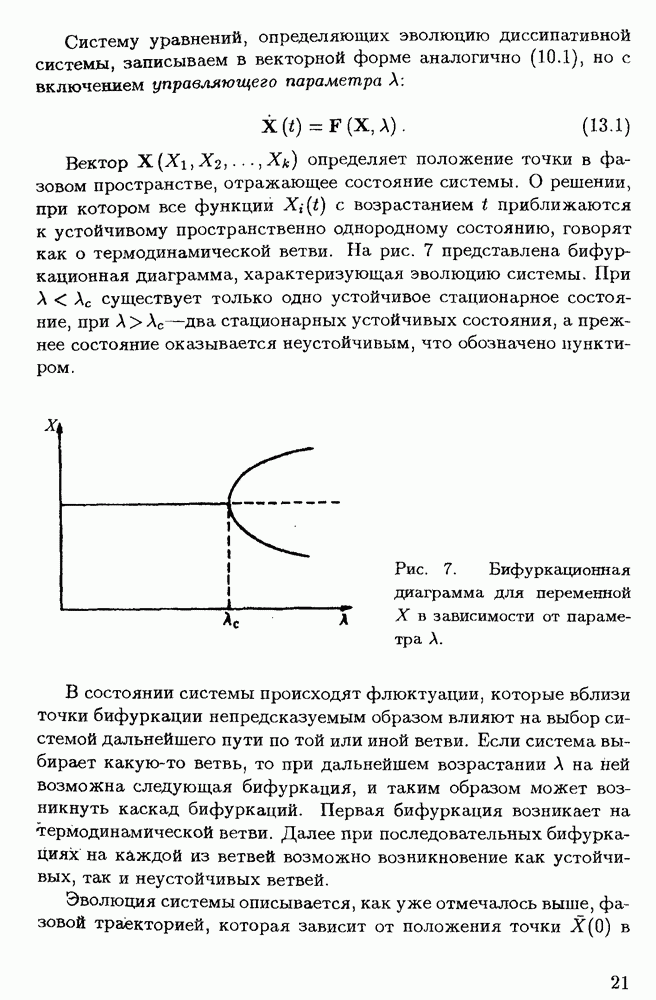
В следующем параграфе рассматривается вопрос об эволюции более сложных систем, в частности газовых, для изучения которых необходим иной подход.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
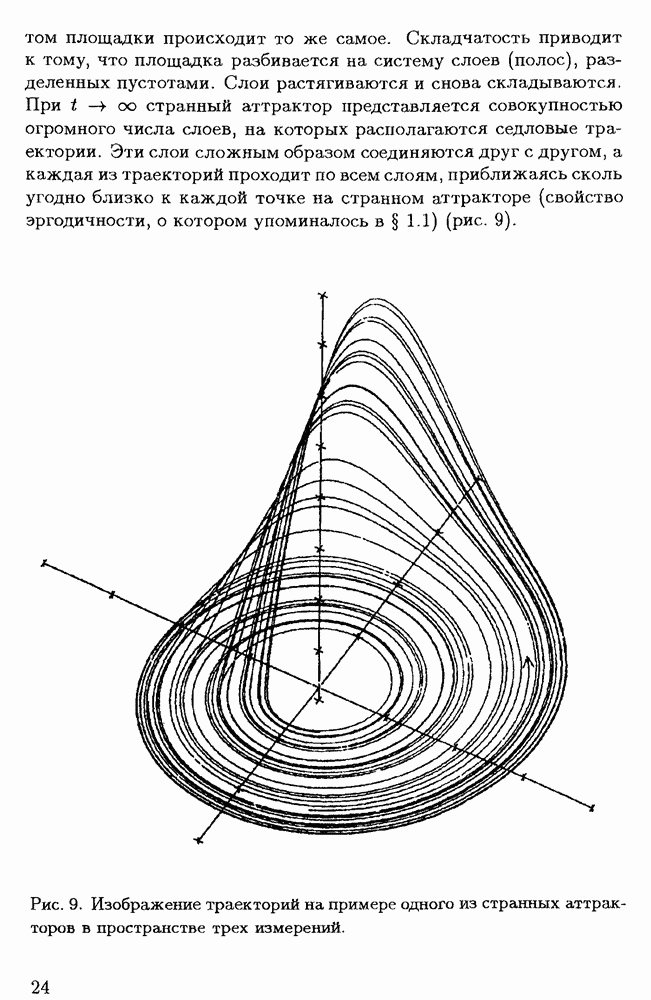
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
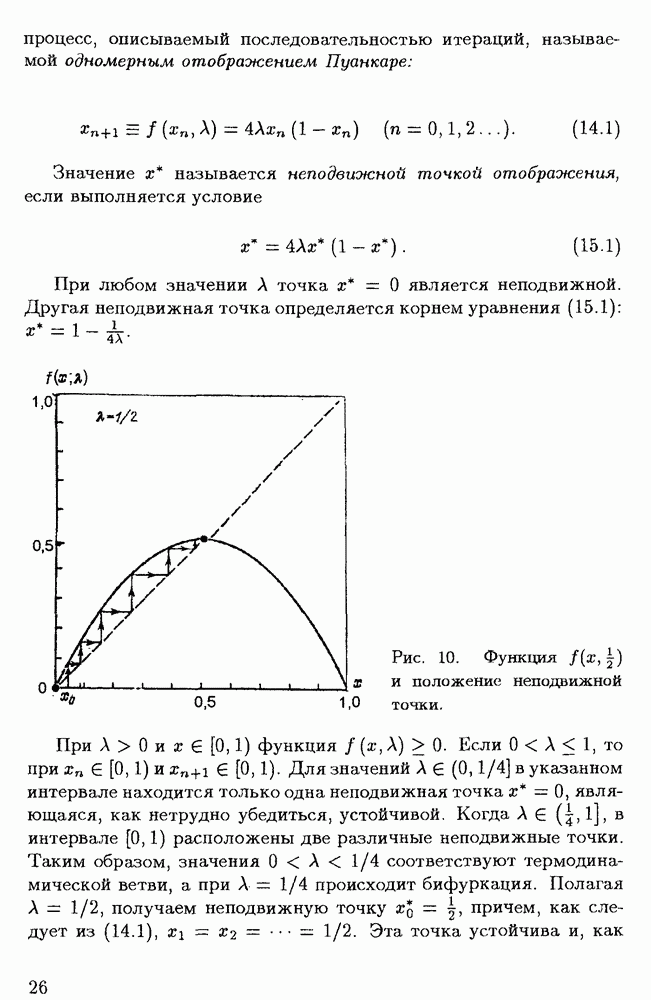
- § 1.4. Бифуркация удвоения периода
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение