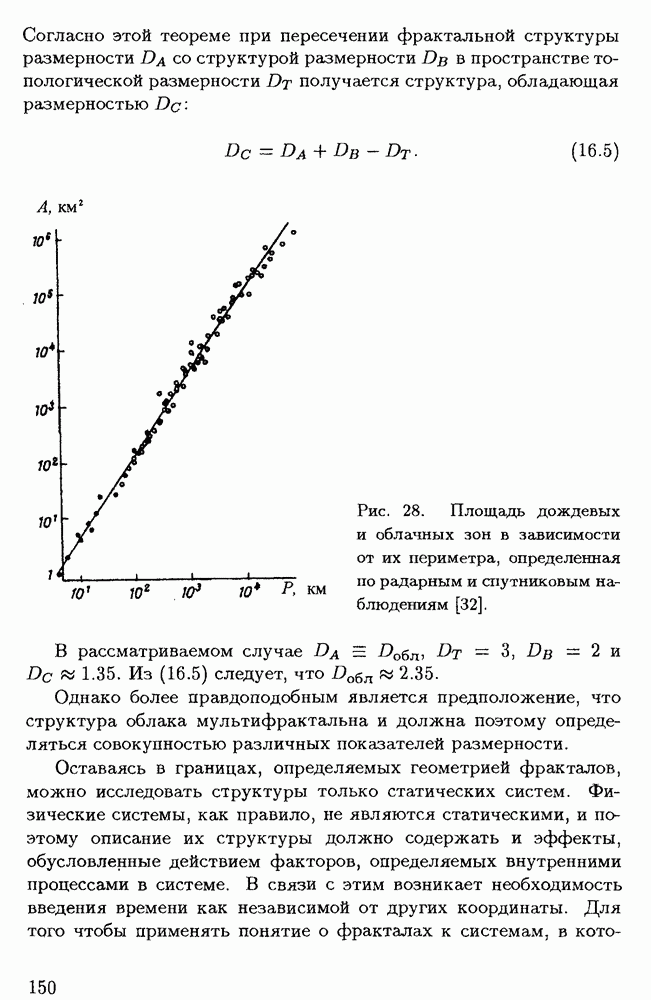
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
Эволюция физических систем, как правило, описывается нелинейными дифференциальными уравнениями. Эти уравнения содержат параметры, от значений которых может зависеть характер решений, а значит, и определяемый ими ход эволюции системы. В качестве примера приведем гидродинамическую систему. Движение вязкой жидкости описывается уравнениями Навье-Стокса, содержащими безразмерный параметр  (число Рейнольдса). При возрастании
(число Рейнольдса). При возрастании  от значений порядка единицы до
от значений порядка единицы до  характер течения кардинальным образом изменяется — происходит переход от гладкого (ламинарного) течения с одной степенью свободы к запутанному (турбулентному) течению с очень большим числом степеней свободы. Этот переход происходит постепенно, при монотонном возрастании
характер течения кардинальным образом изменяется — происходит переход от гладкого (ламинарного) течения с одной степенью свободы к запутанному (турбулентному) течению с очень большим числом степеней свободы. Этот переход происходит постепенно, при монотонном возрастании  Вначале при
Вначале при  в системе возникает режим с двумя степенями свободы — как говорят, произошла бифуркация (ветвление).
в системе возникает режим с двумя степенями свободы — как говорят, произошла бифуркация (ветвление).
Бифуркацией в общем случае называется изменение числа решений задачи — возникновение новых (дополнительных) решений при определенном значении управляющего параметра. Соответственно появляется иной, в частности по отношению к устойчивости, возможный режим поведения системы.
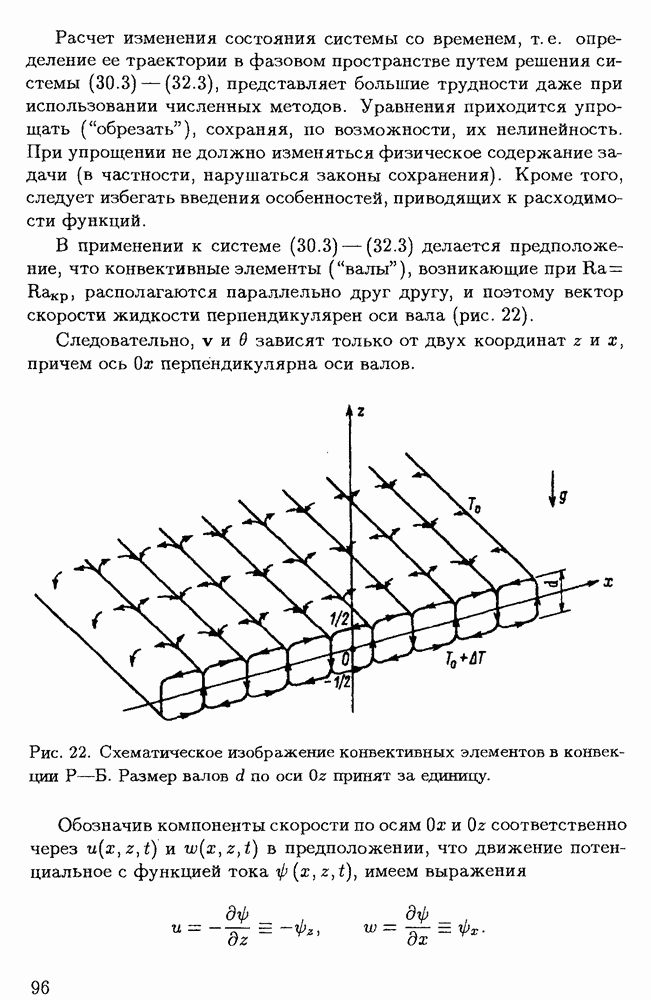
Систему уравнений, определяющих эволюцию диссипативной системы, записываем в векторной форме аналогично (10.1), но с включением управляющего параметра А:

Вектор  определяет положение точки в фазовом пространстве, отражающее состояние системы. О решении, при котором все функции
определяет положение точки в фазовом пространстве, отражающее состояние системы. О решении, при котором все функции  с возрастанием
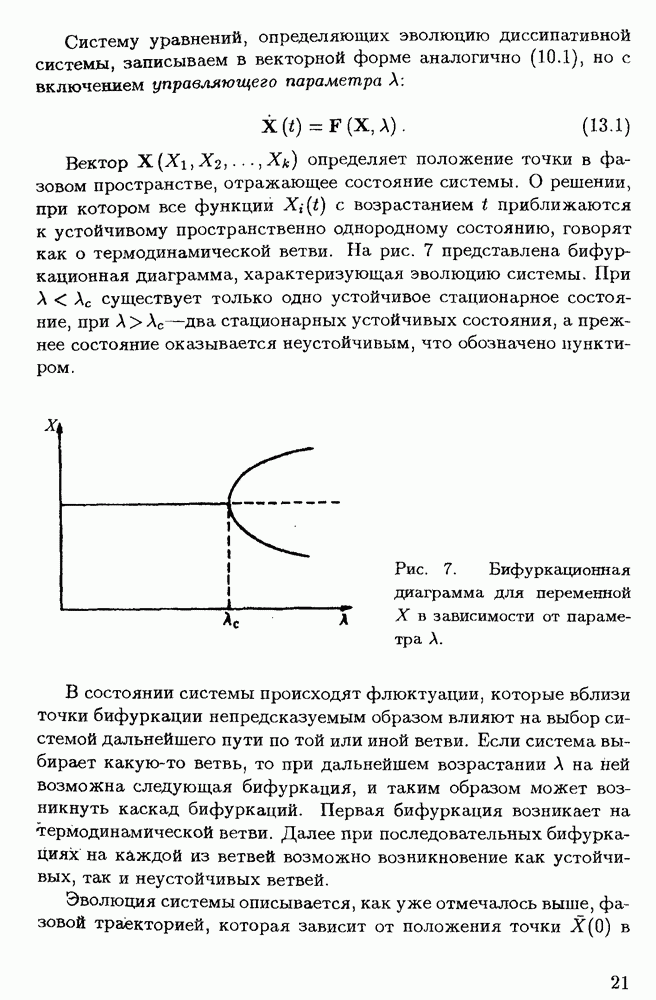
с возрастанием  приближаются к устойчивому пространственно однородному состоянию, говорят как о термодинамической ветви. На рис. 7 представлена бифуркационная диаграмма, характеризующая эволюцию системы. При
приближаются к устойчивому пространственно однородному состоянию, говорят как о термодинамической ветви. На рис. 7 представлена бифуркационная диаграмма, характеризующая эволюцию системы. При  существует только одно устойчивое стационарное состояние, при
существует только одно устойчивое стационарное состояние, при  — два стационарных устойчивых состояния, а прежнее состояние оказывается неустойчивым, что обозначено пунктиром.
— два стационарных устойчивых состояния, а прежнее состояние оказывается неустойчивым, что обозначено пунктиром.

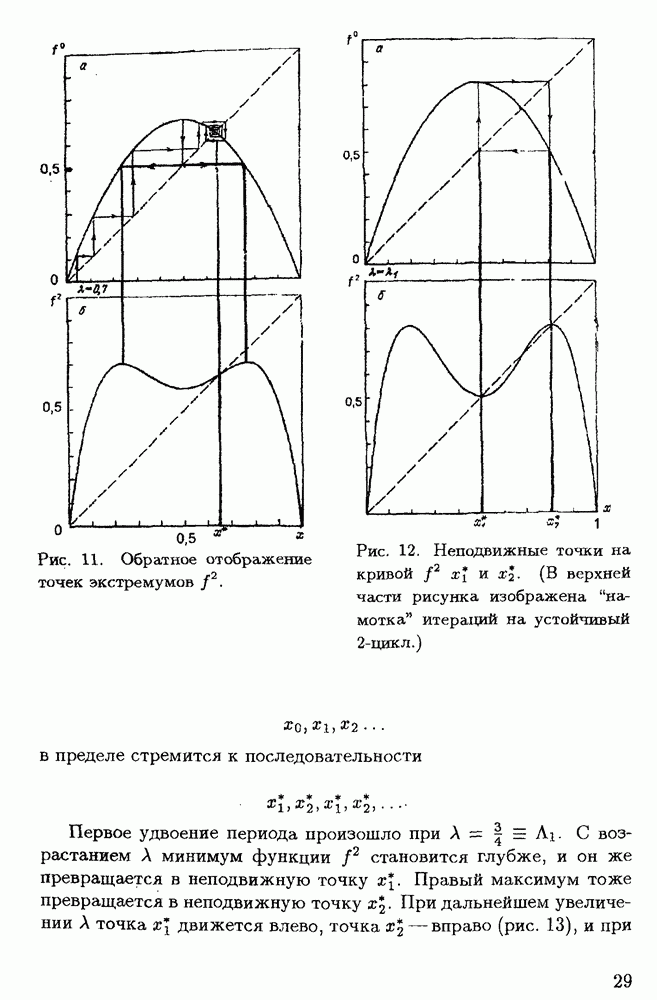
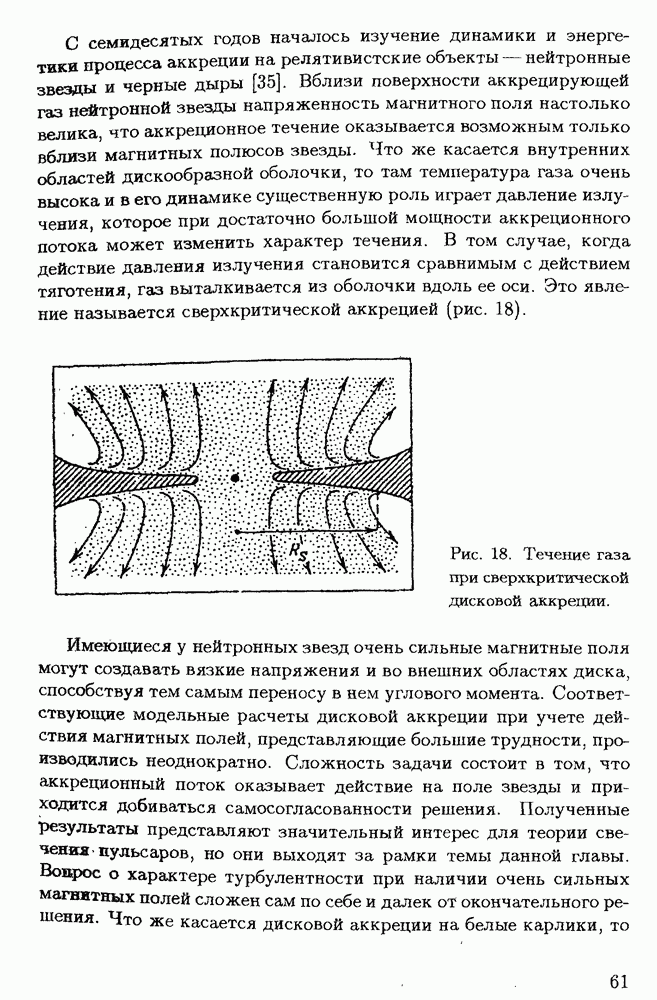
Рис. 7. Бифуркационная диаграмма для переменной X в зависимости от параметра А.
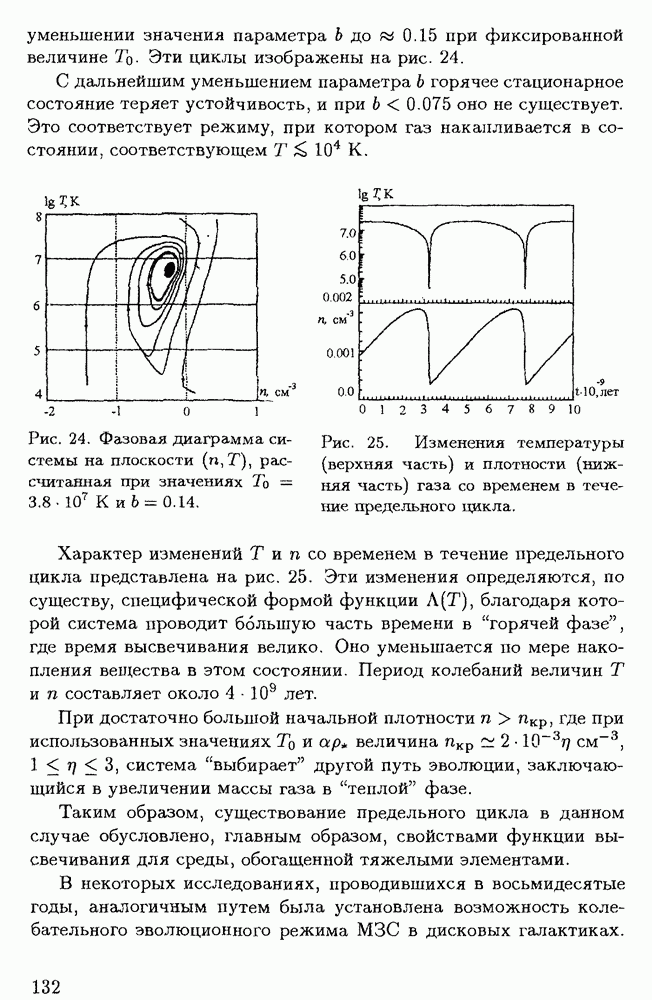
В состоянии системы происходят флюктуации, которые вблизи точки бифуркации непредсказуемым образом влияют на выбор системой дальнейшего пути по той или иной ветви. Если система выбирает какую-то ветвь, то при дальнейшем возрастании А на ней возможна следующая бифуркация, и таким образом может возникнуть каскад бифуркаций. Первая бифуркация возникает на термодинамической ветви. Далее при последовательных бифуркациях на каждой из ветвей возможно возникновение как устойчивых, так и неустойчивых ветвей.
Эволюция системы описывается, как уже отмечалось выше, фазовой траекторией, которая зависит от положения точки  в
в
начальный момент. Неустойчивость системы в точке  означает, что траектории исходящие из точек, сколь угодно близких к данной, в дальнейшем расходятся, причем сколь угодно далеко. Таким образом, эволюция системы является чувствительной к малым изменениям в начальных условиях. При очень малом различии в них происходит быстрое разбегание соответствующих решениям системы (13.1) фазовых траекторий.
означает, что траектории исходящие из точек, сколь угодно близких к данной, в дальнейшем расходятся, причем сколь угодно далеко. Таким образом, эволюция системы является чувствительной к малым изменениям в начальных условиях. При очень малом различии в них происходит быстрое разбегание соответствующих решениям системы (13.1) фазовых траекторий.
Изменение со временем расстояния между траекториями описывают экспоненциальной функцией где  характерное время разбегания ("время Ляпунова"). Для получения более точной характеристики скорости разбегания на выбранной траектории в момент
характерное время разбегания ("время Ляпунова"). Для получения более точной характеристики скорости разбегания на выбранной траектории в момент  произвольно задаваемая точка окружается сферой радиусом
произвольно задаваемая точка окружается сферой радиусом  малым по сравнению с масштабом области фазового пространства. В объеме, охватываемом сферой, находятся и соседние с данной, пересекающие ее траектории. С течением времени при движении центра сферы по траектории она деформируется, превращаясь в эллипсоид. Как направления, так и длины его осей все время изменяются. Если длина по направлению с номером
малым по сравнению с масштабом области фазового пространства. В объеме, охватываемом сферой, находятся и соседние с данной, пересекающие ее траектории. С течением времени при движении центра сферы по траектории она деформируется, превращаясь в эллипсоид. Как направления, так и длины его осей все время изменяются. Если длина по направлению с номером  равна
равна  имеем
имеем

где величина  называемая показателем Ляпунова, определяется выражением
называемая показателем Ляпунова, определяется выражением

Расходятся со временем не только траектории, но и соседние точки на одной и той же траектории — за исключением той из них, по которой эволюционирует система.
Число показателей Ляпунова равно размерности фазового пространства. Для направления, которое соответствует движению системы, этот показатель равен нулю.
Режим, при котором расстояние между двумя любыми сколь угодно близкими точками (не лежащими на траектории, по которой происходит эволюция) экспоненциально возрастает, называется хаотическим.
Поскольку объем области фазового пространства ограничен, все траектории при  не могут быть разбегающимися. В
не могут быть разбегающимися. В
 -мерном фазовом пространстве существует так называемая седловая траектория, по которой движется точка, изображающая состояние системы (рис. 8). Среди других траекторий, соседних с данной, должны иметься как приближающиеся к седловой — устойчивые, так и удаляющиеся от нее — неустойчивые.
-мерном фазовом пространстве существует так называемая седловая траектория, по которой движется точка, изображающая состояние системы (рис. 8). Среди других траекторий, соседних с данной, должны иметься как приближающиеся к седловой — устойчивые, так и удаляющиеся от нее — неустойчивые.

Рис. 8. Седловая траектория и близкие к ней.
Разбегание траекторий сколь угодно далеко невозможно вследствие ограниченности размеров области фазового пространства, в которой допустима эволюция системы. Поэтому траектории со временем изгибаются, и общая картина их оказывается сильно запутанной. Продолжительность времени, в течение которого поведение системы при заданных начальных условиях полностью предсказуемо, очень мала. По истечении времени порядка  начальные условия системой "забываются", и состояние системы оказывается не вполне определяемым. Практически
начальные условия системой "забываются", и состояние системы оказывается не вполне определяемым. Практически  очень мало и даже при возрастании точности задания начальных условий в
очень мало и даже при возрастании точности задания начальных условий в  раз
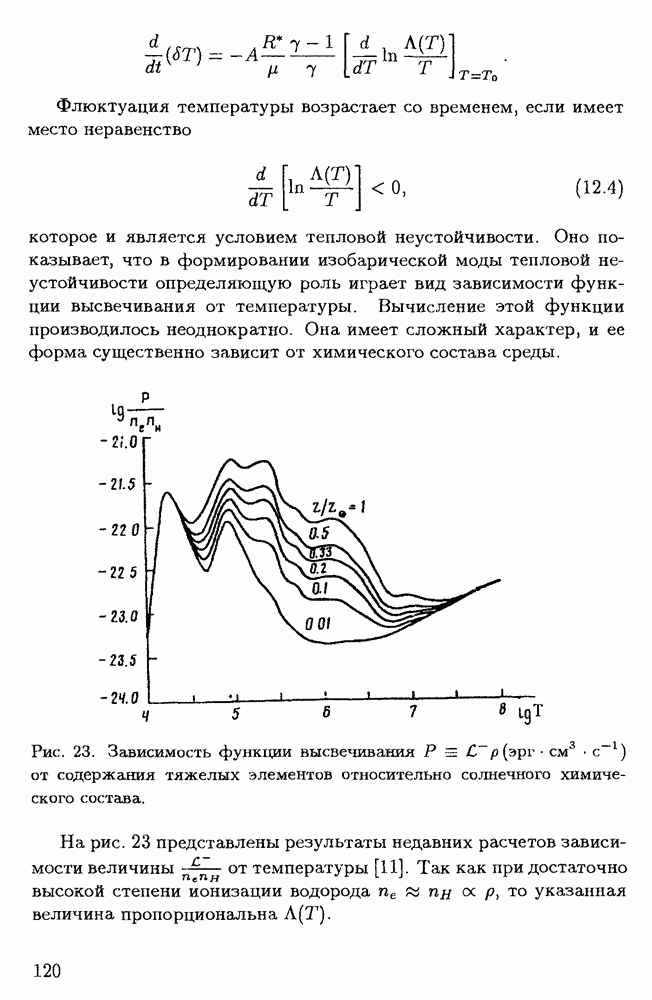
раз  увеличивается лишь на один порядок. Вследствие неопределенности эволюции для диссипативной системы даже при малом отклонении ее от равновесного состояния нельзя указать аттрактор как конкретное состояние (точка или предельный цикл), к которому она приближается с течением времени. В таком случае вводится понятие "странного аттрактора", под которым понимается притягивающее множество траекторий в фазовом пространстве [30].
увеличивается лишь на один порядок. Вследствие неопределенности эволюции для диссипативной системы даже при малом отклонении ее от равновесного состояния нельзя указать аттрактор как конкретное состояние (точка или предельный цикл), к которому она приближается с течением времени. В таком случае вводится понятие "странного аттрактора", под которым понимается притягивающее множество траекторий в фазовом пространстве [30].
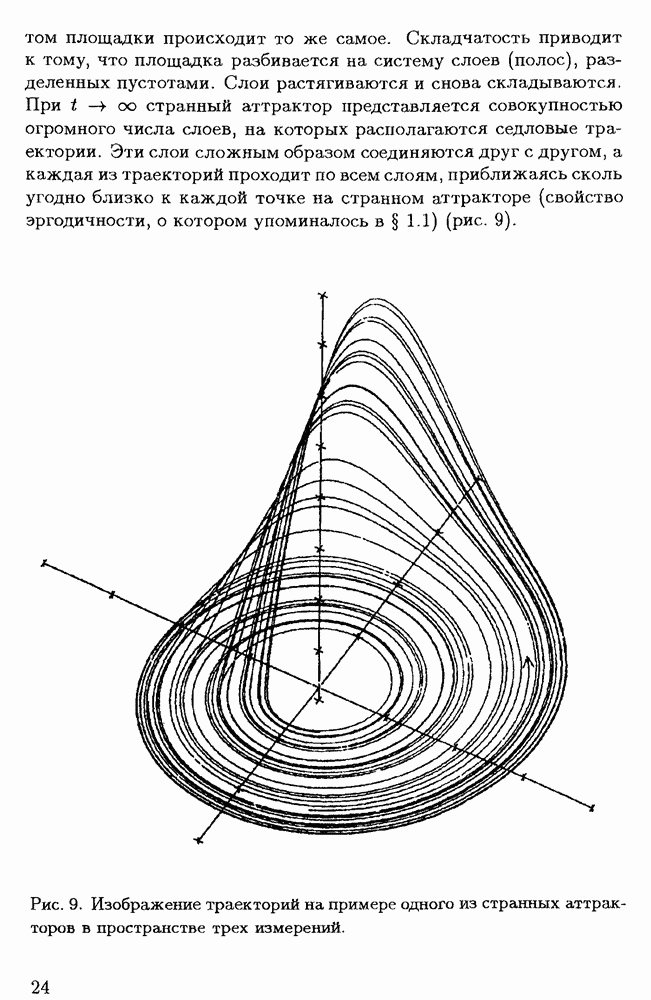
Структура странного аттрактора является очень сложной. Происхождение усложнений можно проиллюстрировать следующим образом. Пусть в переходном режиме существует пучок траекторий в  -мерном фазовом пространстве. Сечение пучка — площадка в пространстве
-мерном фазовом пространстве. Сечение пучка — площадка в пространстве  измерений. Вследствие того, что система диссипативная, эта площадка со временем уменьшается и одновременно сплющивается и изгибается. С каждым
измерений. Вследствие того, что система диссипативная, эта площадка со временем уменьшается и одновременно сплющивается и изгибается. С каждым
элементом площадки происходит то же самое. Складчатость приводит к тому, что площадка разбивается на систему слоев (полос), разделенных пустотами. Слои растягиваются и снова складываются. При  странный аттрактор представляется совокупностью огромного числа слоев, на которых располагаются седловые траектории. Эти слои сложным образом соединяются друг с другом, а каждая из траекторий проходит по всем слоям, приближаясь сколь угодно близко к каждой точке на странном аттракторе (свойство эргодичности, о котором упоминалось в § 1.1) (рис. 9).
странный аттрактор представляется совокупностью огромного числа слоев, на которых располагаются седловые траектории. Эти слои сложным образом соединяются друг с другом, а каждая из траекторий проходит по всем слоям, приближаясь сколь угодно близко к каждой точке на странном аттракторе (свойство эргодичности, о котором упоминалось в § 1.1) (рис. 9).

Рис. 9. Изображение траекторий на примере одного из странных аттракторов в пространстве трех измерений.
На двухмерной поверхности (например, при намотке фазовой траектории на поверхность тора в трехмерном пространстве) странного аттрактора быть не может, так как нельзя избежать точек, в которых траектория пересекается сама с собой. Следовательно, появление странного аттрактора возможно не ранее чем на третьей бифуркации после разрушения двухчастотного квазипериодического режима и возникновения трехчастотного движения, фазовая траектория для которого будет располагаться на трехмерной поверхности тора в четырехмерном пространстве.
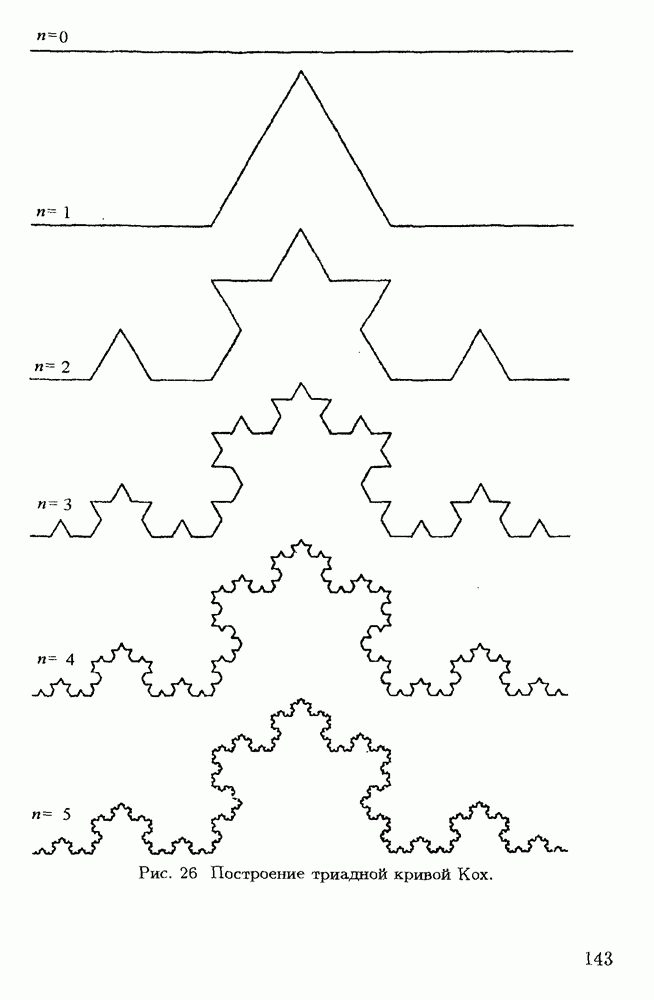
Важной особенностью структуры странного аттрактора является самоподобие. Это означает, что любая сколь угодно малая его часть по своему строению подобна целому. Кроме того, в фазовом пространстве системы, имеющем  измерений, объем странного аттрактора равен нулю, и, следовательно, этот объект обладает топологической размерностью меньше
измерений, объем странного аттрактора равен нулю, и, следовательно, этот объект обладает топологической размерностью меньше  Обычно размерность оказывается дробной. Из сказанного вытекает, что странные аттракторы являются фракталами. Определение понятия фрактал и описание его свойств приведено в § 5.1.
Обычно размерность оказывается дробной. Из сказанного вытекает, что странные аттракторы являются фракталами. Определение понятия фрактал и описание его свойств приведено в § 5.1.
В заключение этого параграфа заметим, что хаос, возникающий в результате эволюции неравновесных диссипативных систем (и называемый диссипативным хаосом), в принципиальном отношении не отличается от хаоса в динамических системах. В обоих случаях имеет место разбегание фазовых траекторий и вытекающая из этого непредсказуемость поведения системы.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
- § 1.4. Бифуркация удвоения периода
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение