| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2.3. Турбулентная вязкость в аккреционном диске
Аккрецией на звезду в астрофизике называют процесс выпадения вещества из околозвездного пространства на поверхность звезды. Здесь будет идти речь только о выпадении на звезду столкновительного газа, и использоваться описание аккреции как газодинамического процесса.
В том случае, когда звезда неподвижна относительно окружающего вещества, аккреционное течение газа к ее поверхности является сферически-симметричным. При наличии же у падающего газа углового момента относительно звезды аккреция имеет совершенно иной характер. Текущий под действием тяготения звезды к ее поверхности газ образует вокруг звезды диск, и поэтому аккреция в данном случае названа дисковой. В процессе дисковой аккреции важную, а часто и определяющую роль играет турбулентная вязкость. Об этом в данном параграфе будет сказано подробно, но предварительно кратко опишем сферически-симметричную аккрецию.
Для стационарного сферически-симметричного течения в поле тяготения звезды в предположении его изэнтропичности существует интеграл энергии (уравнение Бернулли), записываемый в виде

Здесь  — скорость газа и адиабатическая скорость звука соответственно,
— скорость газа и адиабатическая скорость звука соответственно,  расстояние точки от центра звезды и у — показатель адиабаты. При
расстояние точки от центра звезды и у — показатель адиабаты. При  скорость звука с
скорость звука с  и плотность газа
и плотность газа  Уравнение неразрывности для принятых условий имеет вид
Уравнение неразрывности для принятых условий имеет вид

Значение параметра А определяется мощностью аккреционного потока  Из соотношений (20.2) и (21.2) следует, что при условии
Из соотношений (20.2) и (21.2) следует, что при условии  значения
значения  соответствующего определенной мощности потока — сферически-симметричная аккреция реализуется, причем характер течения зависит от величины давления газа
соответствующего определенной мощности потока — сферически-симметричная аккреция реализуется, причем характер течения зависит от величины давления газа  » У поверхности звёзды.
» У поверхности звёзды.
Наличие у падающего газа углового момента мешает ему непосредственно "выпасть" на звезду. Для того чтобы попасть на поверхность звезды, газ должен передать ей свой угловой момент, но это оказывается возможным только в том случае, когда вокруг звезды существует дискообразная оболочка, в которой происходит перенос углового момента. Газ, попадая на периферию оболочки, вращается вместе с ней и благодаря вязкости передает ей свой угловой момент, постепенно приближаясь при этом к поверхности звезды (рис. 16).

Рис. 16. Схематичное представление дисковой аккреции.
Возможность передачи углового момента через диск вначале была установлена при исследовании перетекания газа от одной компоненты тесной двойной системы  на другую [4]. Этот механизм передачи углового момента ("дисковая аккреция") оказался очень важным также для объяснения природы галактических источников рентгеновского излучения, представляющих собой
на другую [4]. Этот механизм передачи углового момента ("дисковая аккреция") оказался очень важным также для объяснения природы галактических источников рентгеновского излучения, представляющих собой  один из компонентов которой является нейтронной звездой. В активных ядрах галактик
один из компонентов которой является нейтронной звездой. В активных ядрах галактик  наиболее мощных из известных источников энергии во Вселенной — процесс освобождения энергии обусловлен дисковой аккрецией газа на сверхмассивный компактный объект.
наиболее мощных из известных источников энергии во Вселенной — процесс освобождения энергии обусловлен дисковой аккрецией газа на сверхмассивный компактный объект.
Несмотря на то, что теории дисковой аккреции и ее применениям в астрофизических исследованиях посвящены сотни статей, обзоры и монографии, остаются невыясненными многие стороны этого процесса для конкретных объектов, в частности относительная роль факторов, обеспечивающих вязкость аккрецируемого газа. Здесь будет рассмотрен один из наиболее простых случаев  -дисковая аккреция на белый карлик, входящий в состав
-дисковая аккреция на белый карлик, входящий в состав  газа, теряемого другим компонентом системы. Этот процесс в конечном итоге приводит к вспышке новой звезды. Есть много данных,
газа, теряемого другим компонентом системы. Этот процесс в конечном итоге приводит к вспышке новой звезды. Есть много данных,
показывающих, что в таких системах перенос углового момента в аккреционном диске обусловлен, главным образом, действием турбулентной вязкости.
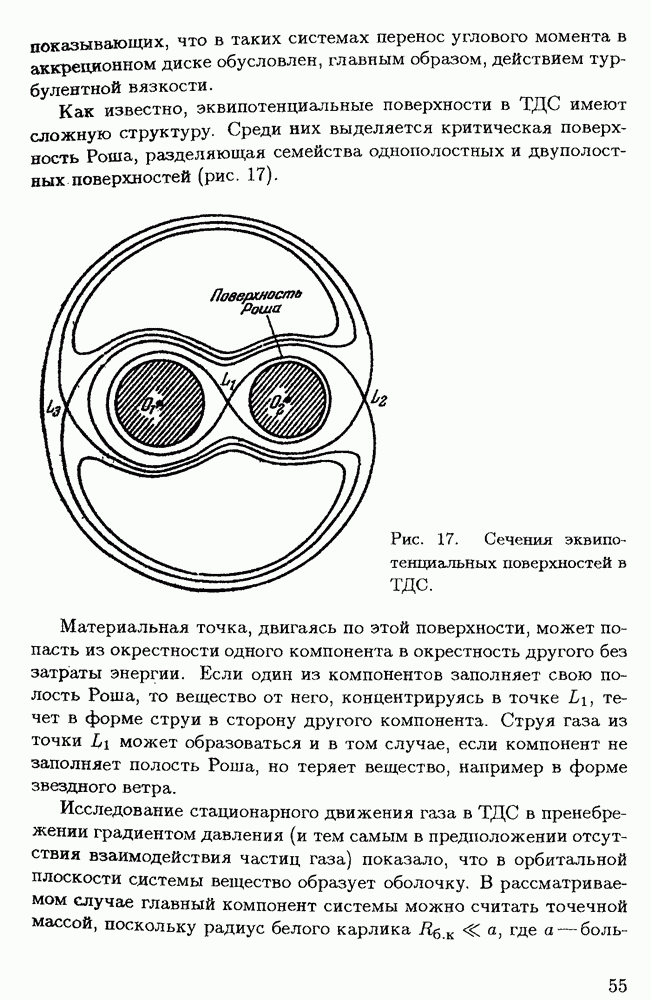
Как известно, эквипотенциальные поверхности в  имеют сложную структуру. Среди них выделяется критическая поверхность Роша, разделяющая семейства однополостных и двуполостных поверхностей (рис. 17).
имеют сложную структуру. Среди них выделяется критическая поверхность Роша, разделяющая семейства однополостных и двуполостных поверхностей (рис. 17).

Рис. 17. Сечения эквипотенциальных поверхностей в 
Материальная точка, двигаясь по этой поверхности, может попасть из окрестности одного компонента в окрестность другого без затраты энергии. Если один из компонентов заполняет свою полость Роша, то вещество от него, концентрируясь в точке  течет в форме струи в сторону другого компонента. Струя газа из точки
течет в форме струи в сторону другого компонента. Струя газа из точки  может образоваться и в том случае, если компонент не заполняет полость Роша, но теряет вещество, например в форме звездного ветра.
может образоваться и в том случае, если компонент не заполняет полость Роша, но теряет вещество, например в форме звездного ветра.
Исследование стационарного движения газа в  в пренебрежении градиентом давления (и тем самым в предположении отсутствия взаимодействия частиц газа) показало, что в орбитальной плоскости системы вещество образует оболочку. В рассматриваемом случае главный компонент системы можно считать точечной массой, поскольку радиус белого карлика
в пренебрежении градиентом давления (и тем самым в предположении отсутствия взаимодействия частиц газа) показало, что в орбитальной плоскости системы вещество образует оболочку. В рассматриваемом случае главный компонент системы можно считать точечной массой, поскольку радиус белого карлика  где а - большая
где а - большая
полуось орбиты. Вблизи этой звезды движение частиц почти круговое кеплеровское, т. е. азимутальная составляющая скорости движения 

Здесь  расстояние от центра белого карлика. Радиальная составляющая скорости
расстояние от центра белого карлика. Радиальная составляющая скорости  . Таким образом, в орбитальной плоскости системы вещество образует дискообразную осесимметричную оболочку. Струя газа, текущая из точки
. Таким образом, в орбитальной плоскости системы вещество образует дискообразную осесимметричную оболочку. Струя газа, текущая из точки  встречается с оболочкой в области, называемой горячим пятном. Там газ струи присоединяется к оболочке, внося в нее массу и угловой момент. Тем самым создается источник углового момента на краю оболочки. Если оболочка стационарна — существует в течение достаточно долгого времени, — то у поверхности звезды должен происходить сток массы и углового момента.
встречается с оболочкой в области, называемой горячим пятном. Там газ струи присоединяется к оболочке, внося в нее массу и угловой момент. Тем самым создается источник углового момента на краю оболочки. Если оболочка стационарна — существует в течение достаточно долгого времени, — то у поверхности звезды должен происходить сток массы и углового момента.
При кеплеровском движении в оболочке существует градиент угловой скорости, который делает газ неустойчивым и при большом значении числа Рейнольдса  может привести к его турбулизации. По-видимому, вязкость турбулизованного газа и является основным фактором, способствующим переносу углового момента в оболочке. Исследование этого процесса производится на основе осредненных по турбулентным пульсациям уравнений газодинамики в цилиндрических координатах. Такие уравнения были использованы ранее при моделировании эволюции догалактической среды [38].
может привести к его турбулизации. По-видимому, вязкость турбулизованного газа и является основным фактором, способствующим переносу углового момента в оболочке. Исследование этого процесса производится на основе осредненных по турбулентным пульсациям уравнений газодинамики в цилиндрических координатах. Такие уравнения были использованы ранее при моделировании эволюции догалактической среды [38].
Движение в оболочке предполагается осесимметричным, т.е. тяготение спутника в достаточной близости к главной звезде не учитывается. Оболочка считается тонкой (т. е. ее толщина мала по сравнению с радиусом). На основе этих предположений можно записать следующие соотношения:


Для стационарного газового диска уравнения Навье-Стокса, осредненные по турбулентным пульсациям и проинтегрированные по толщине диска, принимают следующую форму:

а уравнение неразрывности имеет вид

В этих уравнениях введены обозначения

 -динамический коэффициент турбулентной вязкости. Интегрирование в (26.2) производится по всей толщине оболочки
-динамический коэффициент турбулентной вязкости. Интегрирование в (26.2) производится по всей толщине оболочки  Гравитационный потенциал записывается в виде
Гравитационный потенциал записывается в виде

где  и
и  -массы компонентов
-массы компонентов  выражено в единицах большой оси системы, за единицу времени принят орбитальный период, а за единицу массы
выражено в единицах большой оси системы, за единицу времени принят орбитальный период, а за единицу массы 
Член, соответствующий градиенту давления, в (23.2) опущен, так как предполагается, что

Решение системы  ищется при условии
ищется при условии  которое, как будет показано далее, соответствует самосогласованному решению. Обозначив удельный угловой момент
которое, как будет показано далее, соответствует самосогласованному решению. Обозначив удельный угловой момент  вместо (23.2) получаем уравнение, дающее распределение
вместо (23.2) получаем уравнение, дающее распределение  в дискообразной оболочке:
в дискообразной оболочке:

Общее решение уравнения (27.2) позволяет получить  в виде
в виде

где  произвольные постоянные. Постановкой задачи предусматривается близость скорости движения к скорости, вычисляемой по соотношению (22.2). Этим определяются значения
произвольные постоянные. Постановкой задачи предусматривается близость скорости движения к скорости, вычисляемой по соотношению (22.2). Этим определяются значения  и С:
и С:

Поскольку  то
то  и из (29.2) следует, что
и из (29.2) следует, что  Таким образом, существует поток газа, направленный к звезде, т. е. происходит аккреция газа на поверхность звезды.
Таким образом, существует поток газа, направленный к звезде, т. е. происходит аккреция газа на поверхность звезды.
С приближением содержащегося в оболочке газа к звезде его потенциальная энергия частично превращается в энергию турбулентных пульсаций, а за счет остающейся части увеличивается кинетическая энергия газа. Баланс удельной энергии в расчете на единицу времени выражается соотношением

Так как движение частицы газа близко к круговому кеплеровскому,  и поэтому
и поэтому

а из (30.2) с помощью соотношений (25.2), (28.2) и (29.2) получается

В предположении, что турбулентность близка к стационарной,  можно приравнять величине диссипирующей энергии турбулентности:
можно приравнять величине диссипирующей энергии турбулентности:

Здесь  -скорость вихрей большого масштаба. Взаимодействием таких же вихрей создается турбулентная вязкость, и поэтому для коэффициента
-скорость вихрей большого масштаба. Взаимодействием таких же вихрей создается турбулентная вязкость, и поэтому для коэффициента  можно принять соотношение
можно принять соотношение

Из соотношений (31.2) и (32.2) следует, что

Другое соотношение, связывающее  находится из условия, что за время своей жизни
находится из условия, что за время своей жизни  вихрь не должен существенно размываться дифференциальным вращением. Это условие записывается в виде
вихрь не должен существенно размываться дифференциальным вращением. Это условие записывается в виде

откуда следует

Сопоставляя равенства (33.2) и (34.2), имеем приближенное равенство

т.е. то же условие, что и (29.2). Отсюда следует вывод о самосогласованности приведенного решения задачи о дисковой аккреции. Приближенно кеплеровское движение в оболочке обеспечивается
постоянством величины 77, а это постоянство, в свою очередь, является результатом определения турбулентной вязкости именно для кеплеровского диска.
Сущность механизма дисковой аккреции заключается в том, что попавший на периферию дискообразной оболочки газ приближается к звезде, двигаясь по спирали с большим числом витков (малым шагом), и при этом передает свой угловой момент внутренним слоям оболочки. Как показывает решение уравнения (24.2), скорость радиального движения остается малой по сравнению со скоростью вращения. Из уравнения (24.2) при  получается
получается

и вследствие неравенства (29.2) имеем

Соотношения (25.2), (32.2) и (33.2) дают выражения

а из (25.2) при учете (35.2) получается зависимость поверхностной плотности 

С приближением к поверхности звезды значения  увеличиваются. На достаточно большой глубине в оболочке температура газа также становится очень высокой, и соответственно его давление настолько возрастает, что движение газа там приходится описывать более сложными уравнениями, учитывая давление как газа, так и излучения и другие факторы, например действие магнитного поля. Для систем, содержащих в качестве главной звезды белый карлик, это относится к области
увеличиваются. На достаточно большой глубине в оболочке температура газа также становится очень высокой, и соответственно его давление настолько возрастает, что движение газа там приходится описывать более сложными уравнениями, учитывая давление как газа, так и излучения и другие факторы, например действие магнитного поля. Для систем, содержащих в качестве главной звезды белый карлик, это относится к области  Преобладающая доля потенциальной энергии переходит в тепловую энергию и затем в излучение именно во внутренних частях дискообразной оболочки, непрозрачных для излучения.
Преобладающая доля потенциальной энергии переходит в тепловую энергию и затем в излучение именно во внутренних частях дискообразной оболочки, непрозрачных для излучения.
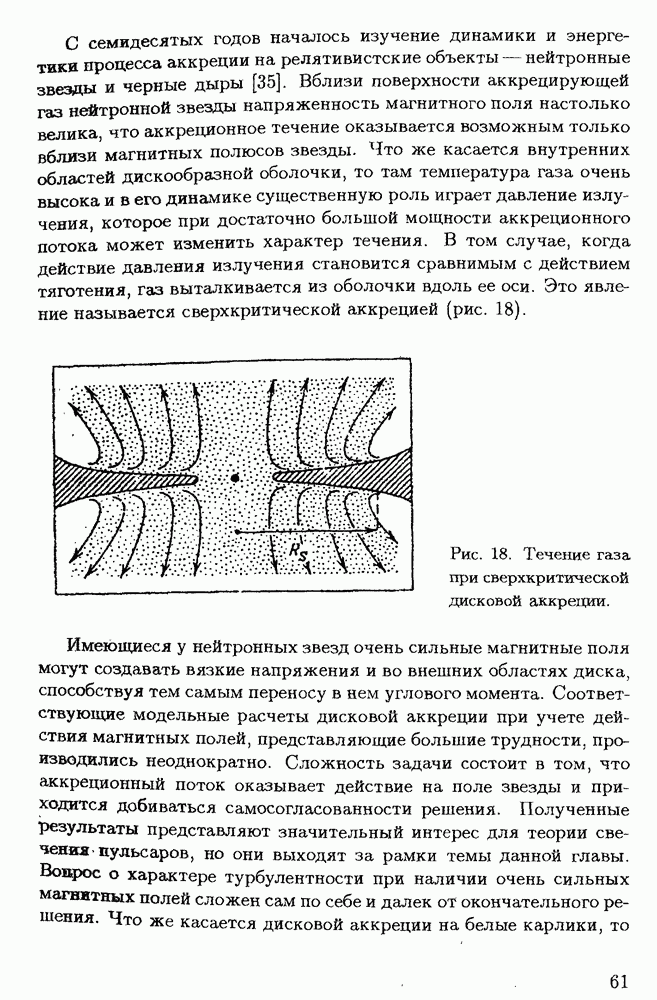
С семидесятых годов началось изучение динамики и энергетики процесса аккреции на релятивистские объекты — нейтронные звезды и черные дыры [35]. Вблизи поверхности аккрецирующей газ нейтронной звезды напряженность магнитного поля настолько велика что аккреционное течение оказывается возможным только вблизи магнитных полюсов звезды. Что же касается внутренних областей дискообразной оболочки, то там температура газа очень высока и в его динамике существенную роль играет давление излучения, которое при достаточно большой мощности аккреционного потока может изменить характер течения. В том случае, когда действие давления излучения становится сравнимым с действием тяготения, газ выталкивается из оболочки вдоль ее оси. Это явление называется сверхкритической аккрецией (рис. 18).

Рис. 18. Течение газа при сверхкритической дисковой аккреции.
Имеющиеся у нейтронных звезд очень сильные магнитные поля могут создавать вязкие напряжения и во внешних областях диска, способствуя тем самым переносу в нем углового момента. Соответствующие модельные расчеты дисковой аккреции при учете действия магнитных полей, представляющие большие трудности, производились неоднократно. Сложность задачи состоит в том, что аккреционный поток оказывает действие на поле звезды и приходится добиваться самосогласованности решения. Полученные результаты представляют значительный интерес для теории свечения пульсаров, но они выходят за рамки темы данной главы. Вопрос о характере турбулентности при наличии очень сильных магнитных полей сложен сам по себе и далек от окончательного решения. Что же касается дисковой аккреции на белые карлики, то
по крайней мере для внешних областей дискообразной оболочки, в которых определяющая роль в переносе углового момента должна принадлежать турбулентной вязкости, магнитные поля не могут сильно изменить установленный выше характер течения газа.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
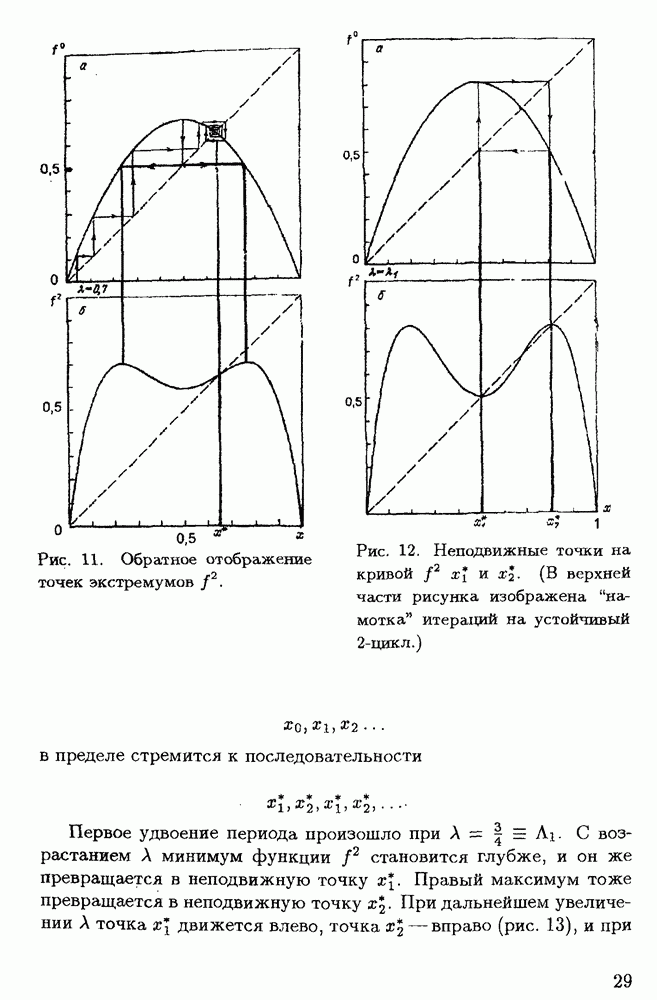
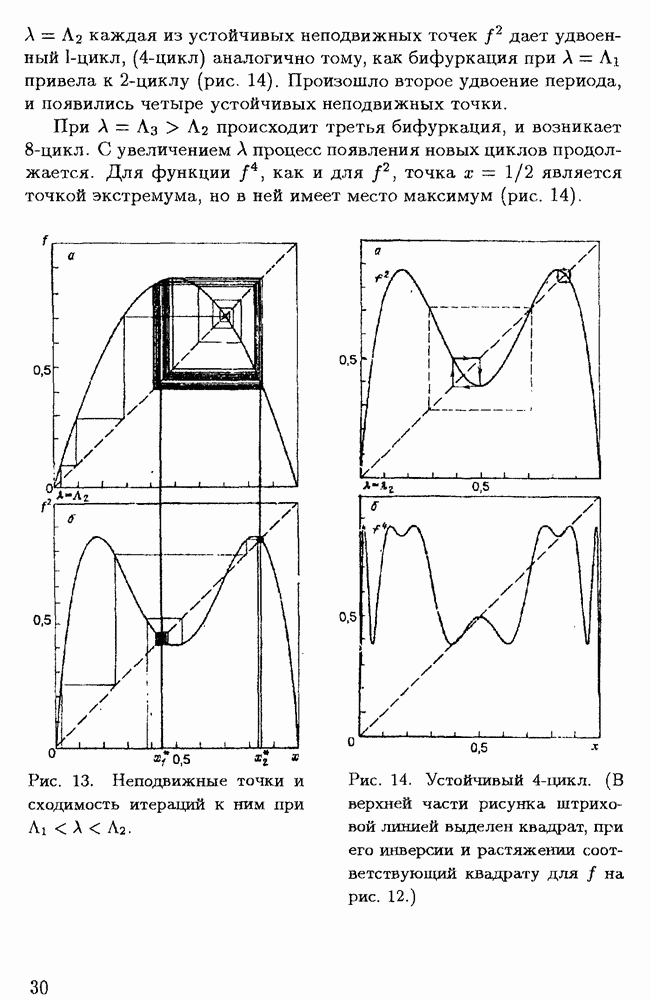
- § 1.4. Бифуркация удвоения периода
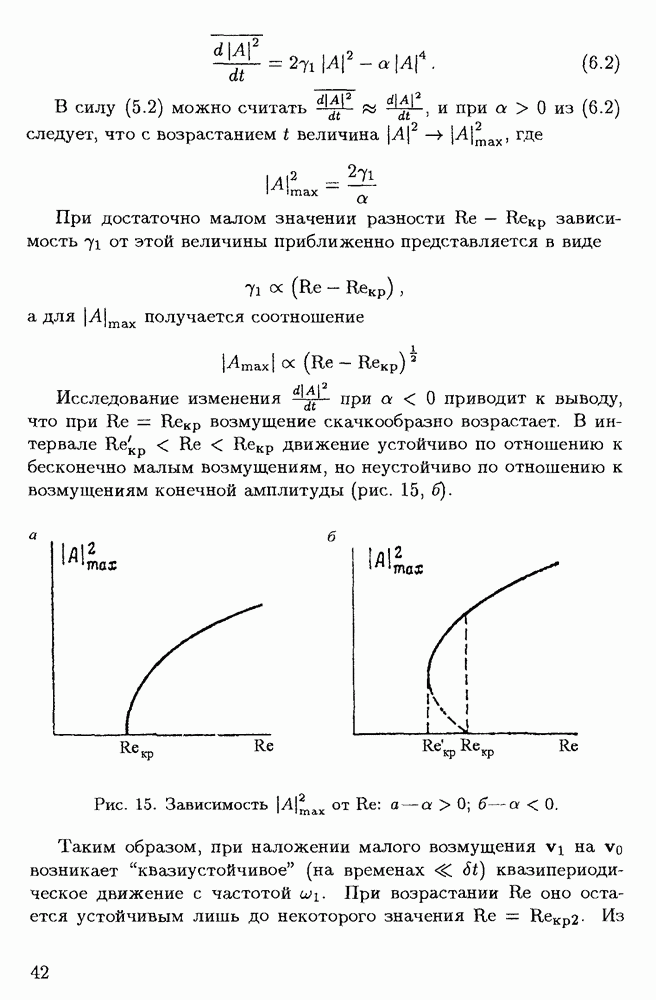
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
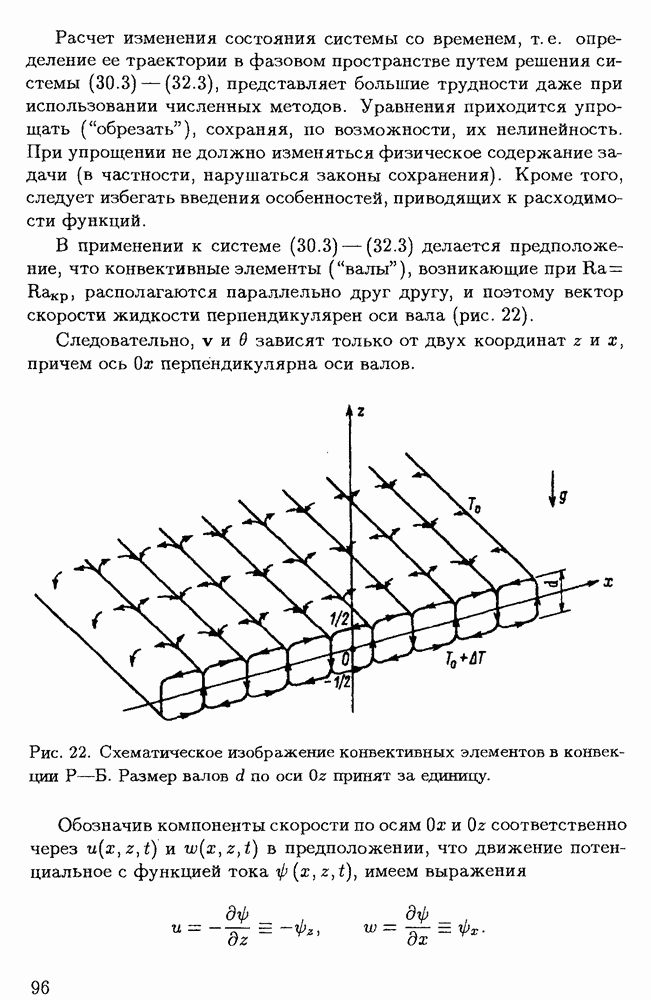
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
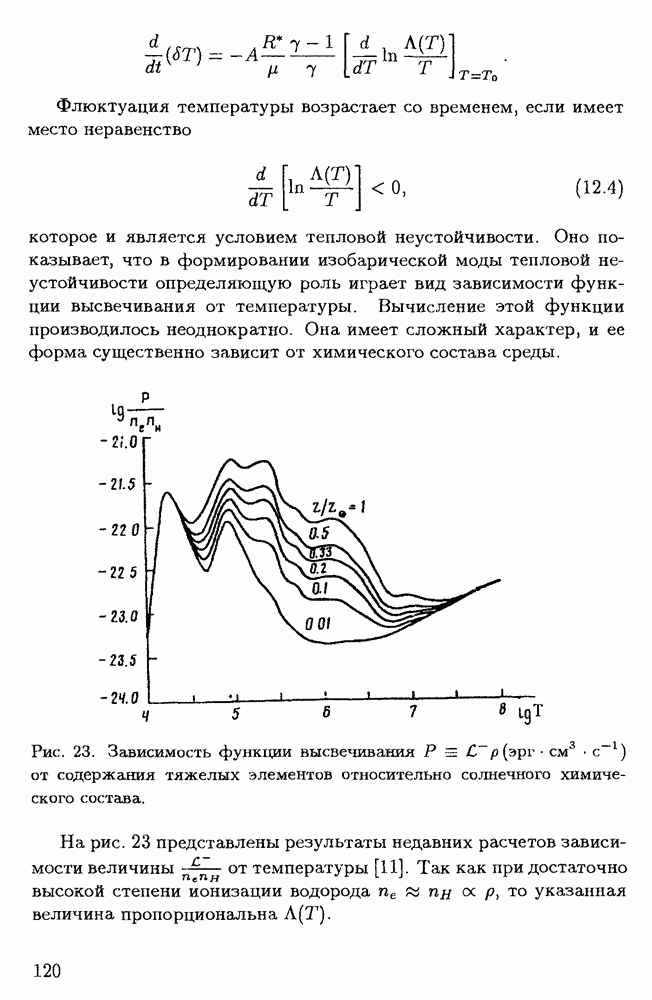
- § 4.1. Локальный критерий тепловой неустойчивости
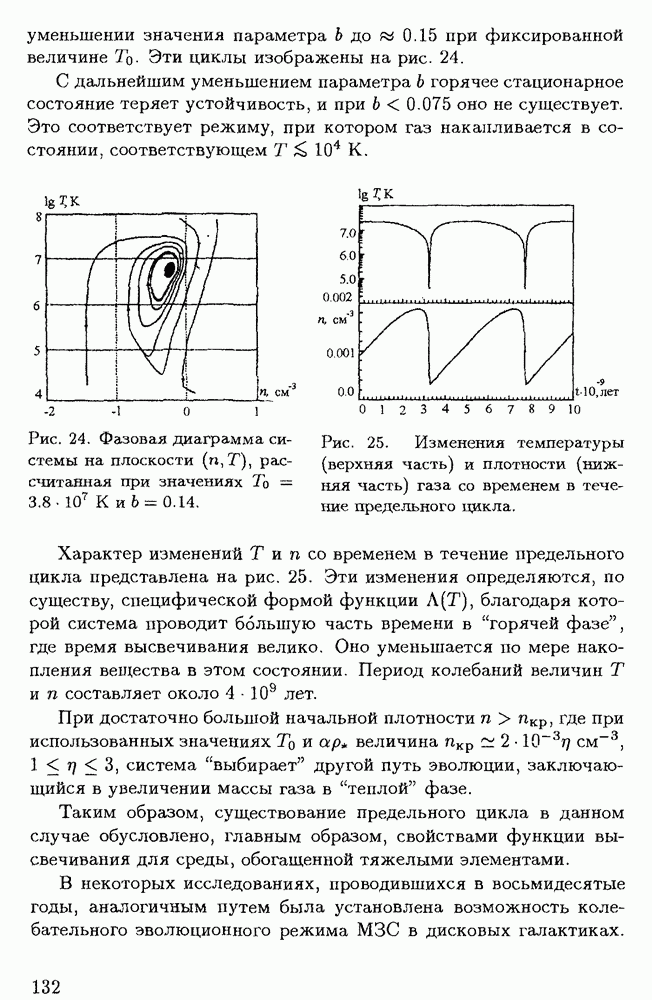
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение