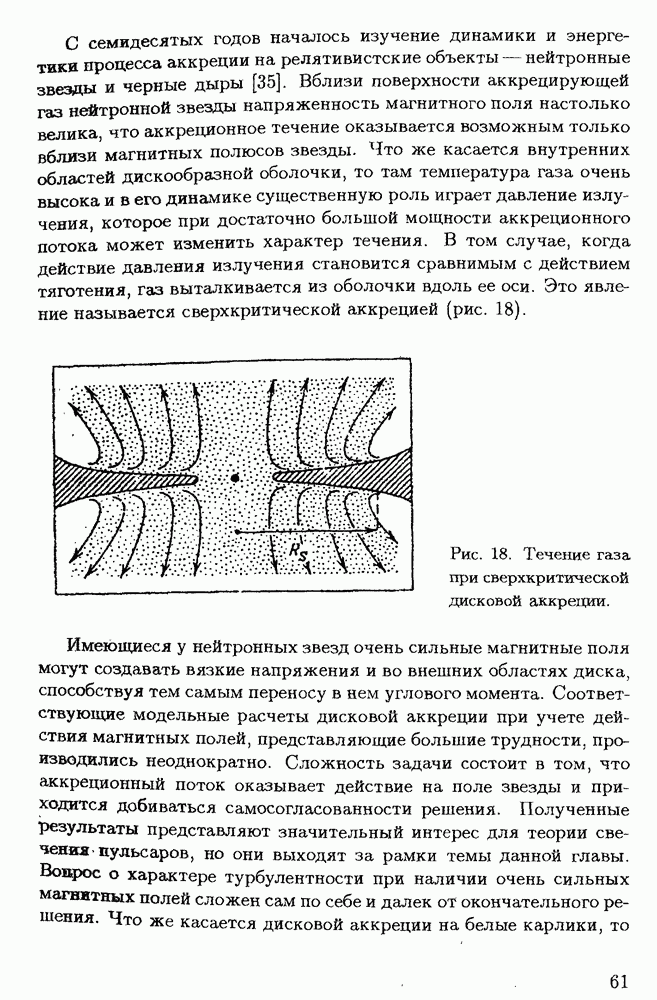
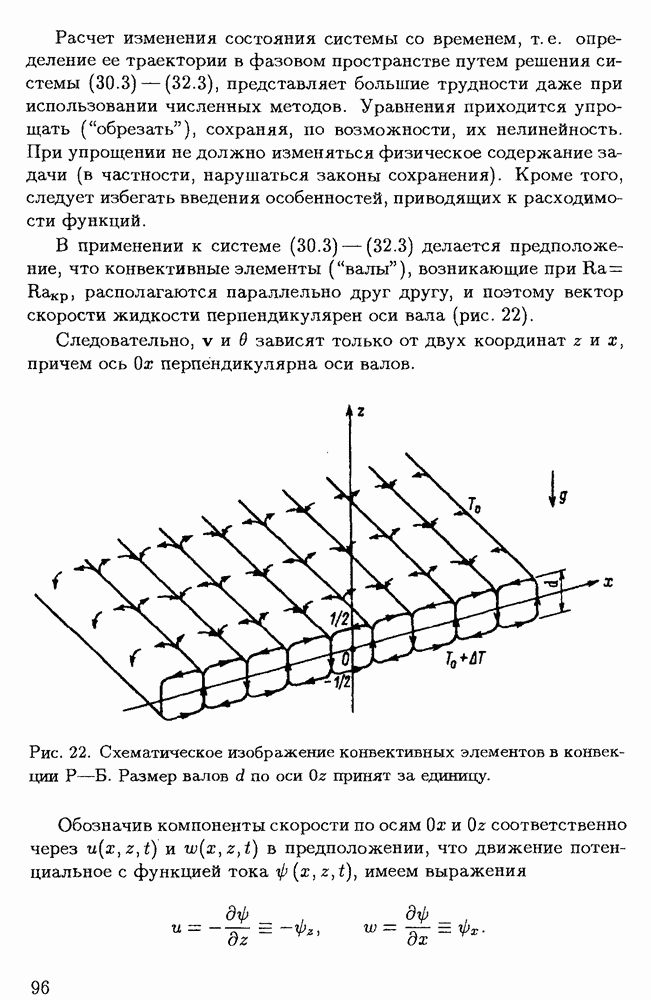
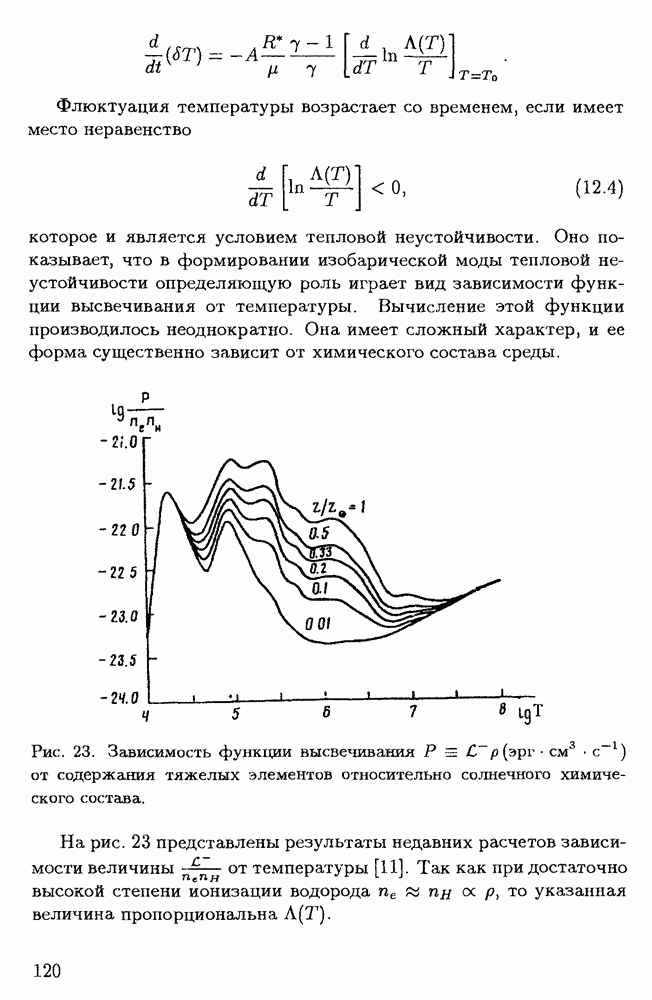
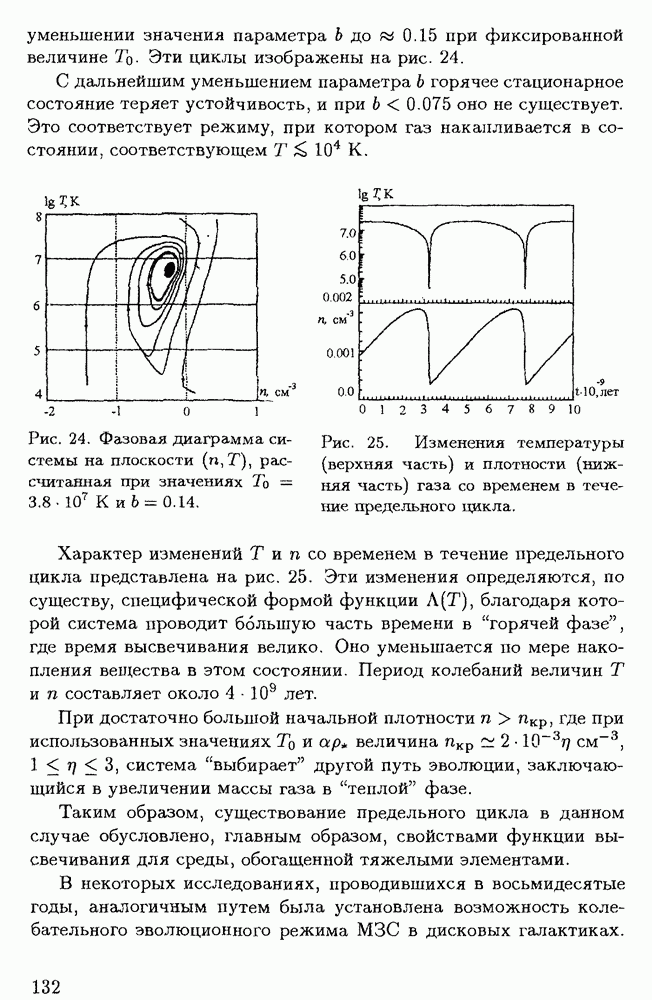
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. Турбулентность и ее проявления в астрофизических объектах
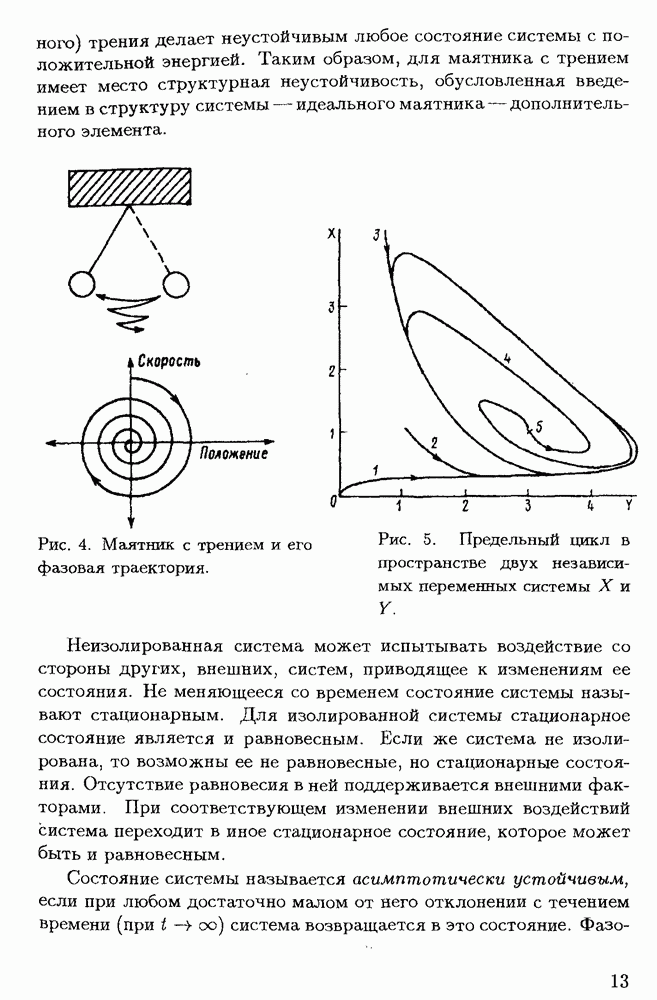
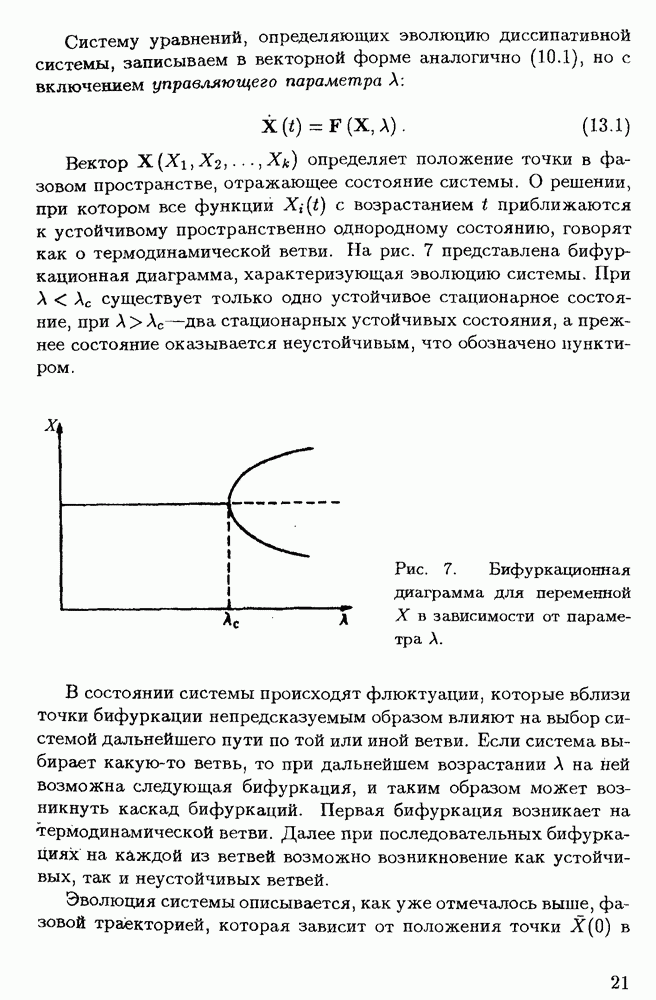
§ 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
В этом и следующем параграфах рассматриваются, главным образом, процессы, приводящие к возникновению турбулентности в несжимаемой жидкости. Хотя в астрофизических исследованиях обычно приходится иметь дело с течениями газа, выводы, относящиеся к неустойчивости жидкости, во многих случаях могут быть использованы и для газовой среды, поскольку сжимаемость газа не сказывается существенно на дозвуковых течениях. Что же касается сверхзвуковых течений, то решение проблем, связанных с их устойчивостью, гораздо сложнее. В таких течениях возникают разрывы, прежде всего ударные волны, сильно влияющие на состояние газа. Вопросы, связанные со сверхзвуковой турбулентностью, пока остаются далекими от полного их решения.
Движение вязкой несжимаемой жидкости при отсутствии внешних полей описывается системой уравнений Навье-Стокса с добавлением условия несжимаемости:

Здесь  оператор Гамильтона,
оператор Гамильтона,  -скорость течения, р — плотность,
-скорость течения, р — плотность,  давление и
давление и  кинематическая вязкость. Величины
кинематическая вязкость. Величины  характеризуют свойства жидкости. Внешние условия определяют пространственный масштаб течения I и характерную скорость — например,
характеризуют свойства жидкости. Внешние условия определяют пространственный масштаб течения I и характерную скорость — например,  Уравнения (1.2) и (2.2) можно записать в безразмерной форме. При этом в уравнении движения будет содержаться всего один параметр — число Рейнольдса
Уравнения (1.2) и (2.2) можно записать в безразмерной форме. При этом в уравнении движения будет содержаться всего один параметр — число Рейнольдса 

являющийся безразмерным, так как единицами величин  являются
являются

Свойства течения, определяемые решением системы, т. е. величины  зависят от величины
зависят от величины  Это подтверждается многочисленными экспериментами. Моделирование течений при различных значениях
Это подтверждается многочисленными экспериментами. Моделирование течений при различных значениях  показало, что при
показало, что при  движение спокойное, макроскопически детерминированное, обладающее одной степенью свободы (его называют ламинарным). Что же касается течения при
движение спокойное, макроскопически детерминированное, обладающее одной степенью свободы (его называют ламинарным). Что же касается течения при  то оно является, как уже отмечалось в § 1.3, хаотическим.
то оно является, как уже отмечалось в § 1.3, хаотическим.
Физический смысл параметра  заключается в том, что он выражает относительную роль двух факторов — вязкости, стремящейся выравнивать различие скорости в близких объемах жидкости, и инерции, содействующей сохранению скорости движения элемента. При достаточно малых значениях
заключается в том, что он выражает относительную роль двух факторов — вязкости, стремящейся выравнивать различие скорости в близких объемах жидкости, и инерции, содействующей сохранению скорости движения элемента. При достаточно малых значениях  вязкость преобладает, препятствуя развитию малых возмущений скорости жидкости. С возрастанием скорости движения сглаживающая роль вязкости снижается.
вязкость преобладает, препятствуя развитию малых возмущений скорости жидкости. С возрастанием скорости движения сглаживающая роль вязкости снижается.
Устойчивость стационарного движения жидкости по отношению к бесконечно малым возмущениям исследуется на основе линеаризованного уравнения, получающегося из (1.2). На движение, в котором распределение скорости дано функцией  налагается возмущение
налагается возмущение  т.е. движение происходит со скоростью
т.е. движение происходит со скоростью

Величина  удовлетворяет уравнению (1.2). Поэтому, пренебрегая членами второго порядка малости по
удовлетворяет уравнению (1.2). Поэтому, пренебрегая членами второго порядка малости по  получаем уравнения
получаем уравнения

Общее решение этих линейных уравнений находится как сумма членов вида  Если среди частот
Если среди частот  нет ни одной с положительной мнимой частью, то возмущение
нет ни одной с положительной мнимой частью, то возмущение  со временем
со временем
стремится к нулю, т. е. течение устойчиво. Так как оно при  устойчиво, а для
устойчиво, а для  неустойчиво, то должно существовать такое значение
неустойчиво, то должно существовать такое значение  что при
что при  устойчивость нарушается. Величина.
устойчивость нарушается. Величина.  зависит от внешних обстоятельств, при которых происходит течение, например от наличия тел, препятствующих движению жидкости и обтекаемых ею. Неустойчивость означает возрастание возмущения со временем. Следовательно, среди частот при
зависит от внешних обстоятельств, при которых происходит течение, например от наличия тел, препятствующих движению жидкости и обтекаемых ею. Неустойчивость означает возрастание возмущения со временем. Следовательно, среди частот при  имеется такая:
имеется такая:

причем  вещественно, а
вещественно, а  Можно полагать, что при достаточно малой разности
Можно полагать, что при достаточно малой разности  выполняется неравенство
выполняется неравенство  поскольку при
поскольку при  появлению одной частоты
появлению одной частоты  предшествует значение
предшествует значение  а для остальных частот
а для остальных частот  Тогда соответствующая
Тогда соответствующая  величина
величина  имеет вид
имеет вид

Так как множитель  быстро возрастает со временем, то предположение о малости
быстро возрастает со временем, то предположение о малости  через некоторое время нарушается и непосредственное использование (4.2) становится неоправданным. Однако в течение короткого времени
через некоторое время нарушается и непосредственное использование (4.2) становится неоправданным. Однако в течение короткого времени  движение жидкости, а значит, и изменение
движение жидкости, а значит, и изменение  можно считать периодическим с периодом
можно считать периодическим с периодом 
Амплитуда такого периодического движения — вещественная часть комплексной величины 

которая при возрастании  стремится к некоторому конечному пределу. Это следует из усреднения по промежутку времени
стремится к некоторому конечному пределу. Это следует из усреднения по промежутку времени  где
где

разложения величины по  с точностью до членов четвертого порядка включительно. После усреднения нечетные члены, содержащие периодический множитель, не будут входить в разложение, которое принимает вид
с точностью до членов четвертого порядка включительно. После усреднения нечетные члены, содержащие периодический множитель, не будут входить в разложение, которое принимает вид

В силу (5.2) можно считать  и при
и при  из (6.2) следует, что с возрастанием
из (6.2) следует, что с возрастанием  величина
величина  где
где

При достаточно малом значении разности  зависимость
зависимость  от этой величины приближенно представляется в виде
от этой величины приближенно представляется в виде

а для  получается соотношение
получается соотношение

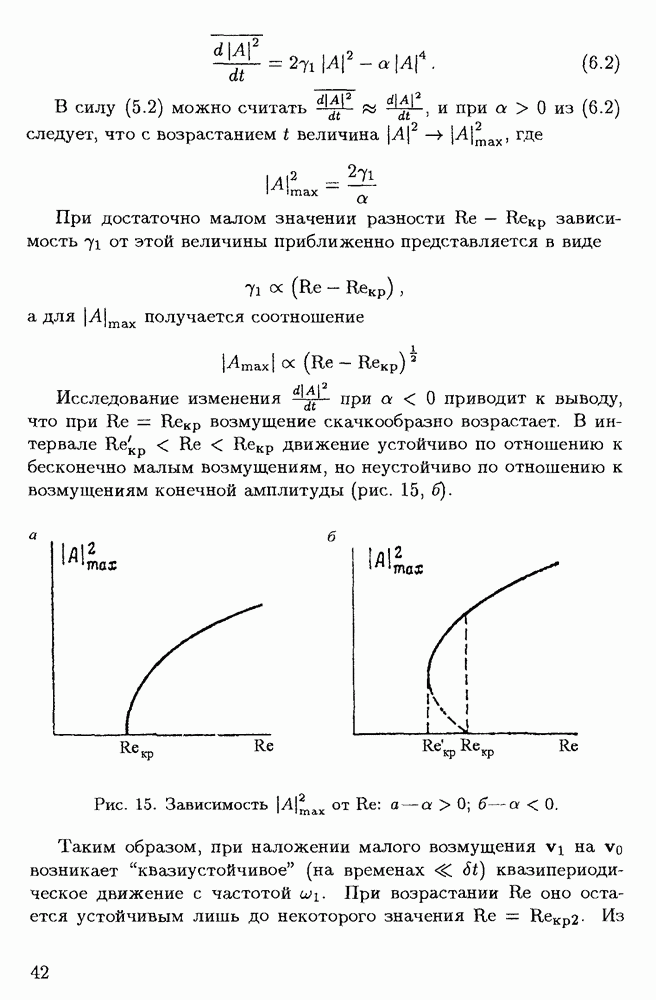
Исследование изменения  при
при  приводит к выводу, что при
приводит к выводу, что при  возмущение скачкообразно возрастает. В интервале
возмущение скачкообразно возрастает. В интервале  движение устойчиво по отношению к бесконечно малым возмущениям, но неустойчиво по отношению к возмущениям конечной амплитуды (рис. 15, б).
движение устойчиво по отношению к бесконечно малым возмущениям, но неустойчиво по отношению к возмущениям конечной амплитуды (рис. 15, б).

Рис. 15. Зависимость от 
Таким образом, при наложении малого возмущения  на
на  возникает "квазиустойчивое" (на временах
возникает "квазиустойчивое" (на временах  квазипериодическое движение с частотой
квазипериодическое движение с частотой  При возрастании
При возрастании  оно остается устойчивым лишь до некоторого значения
оно остается устойчивым лишь до некоторого значения  . Из
. Из
уравнений (аналогичных) (3.2) с заменой  на
на  на
на  следует появление еще одного периода, равного После бифуркации в точке
следует появление еще одного периода, равного После бифуркации в точке  Для малых значений
Для малых значений  если
если  иррациональное число, имеет место квазипериодическое движение, описываемое как намотка незамкнутой траектории на двухмерный тор (см. § 1.3). Если частоты
иррациональное число, имеет место квазипериодическое движение, описываемое как намотка незамкнутой траектории на двухмерный тор (см. § 1.3). Если частоты  и соизмеримы, то движение периодическое, но приводящее к резонансным явлениям.
и соизмеримы, то движение периодическое, но приводящее к резонансным явлениям.
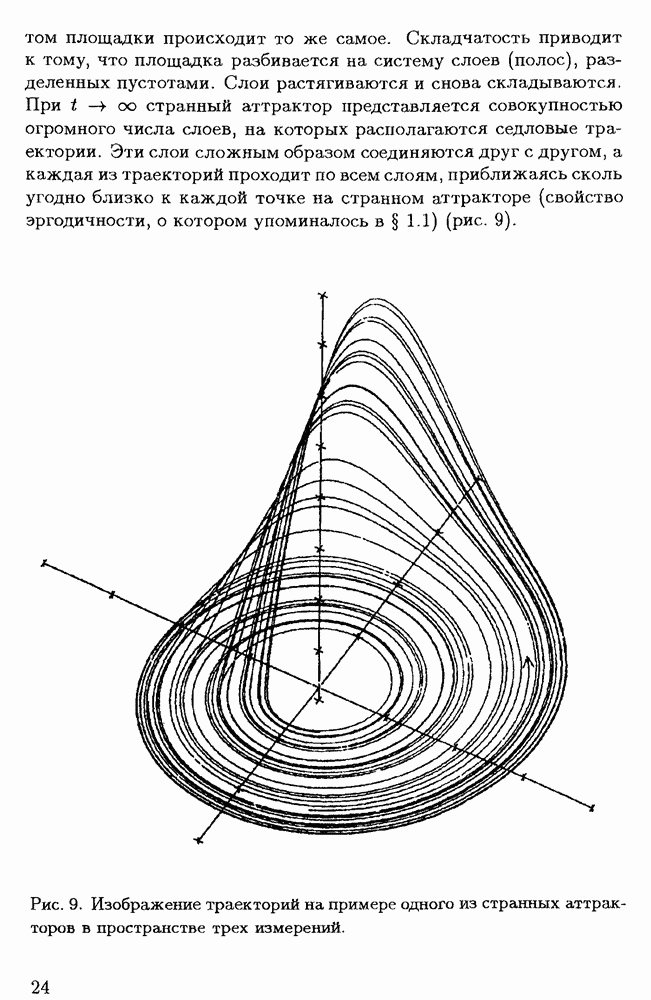
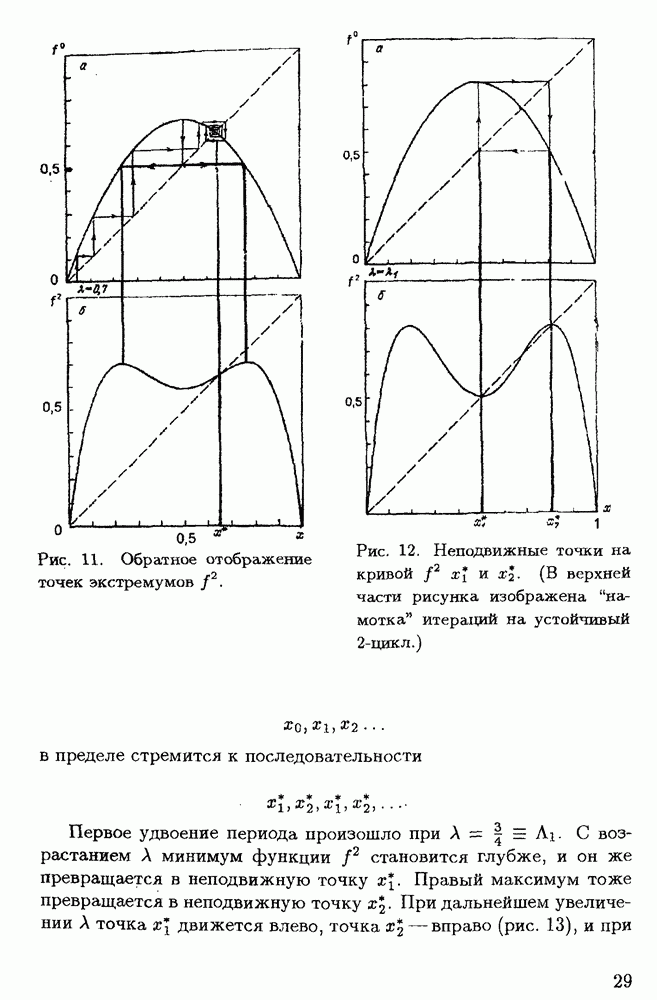
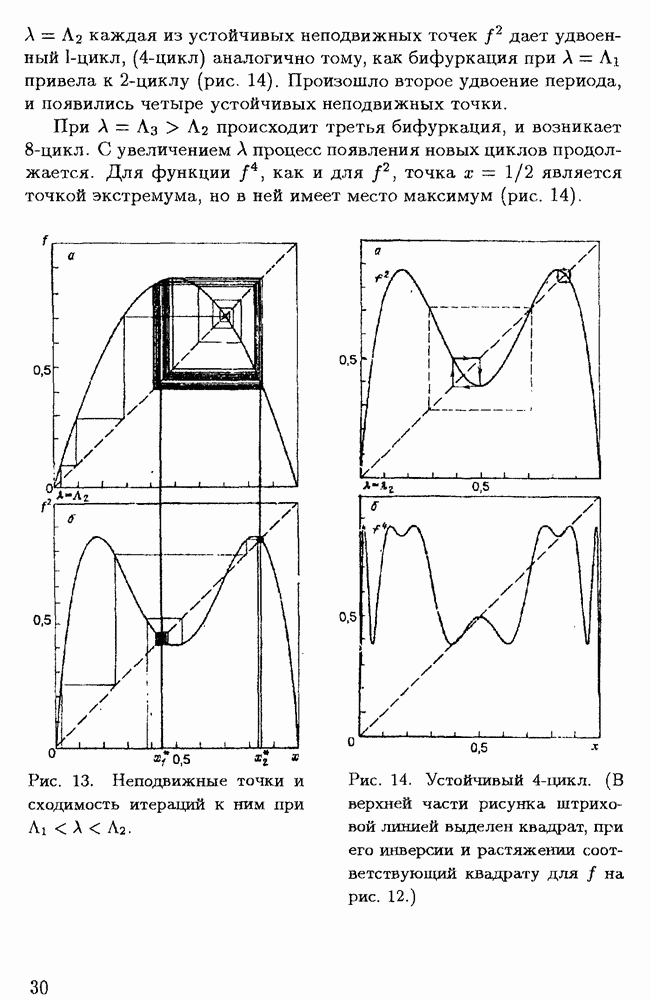
В результате последующих бифуркаций в потоке жидкости может возникнуть хаотическое состояние. Как один из возможных путей перехода ламинарного течения в турбулентное предполагается рассмотренный выше процесс удвоения периода для одномерного отображения Пуанкаре.
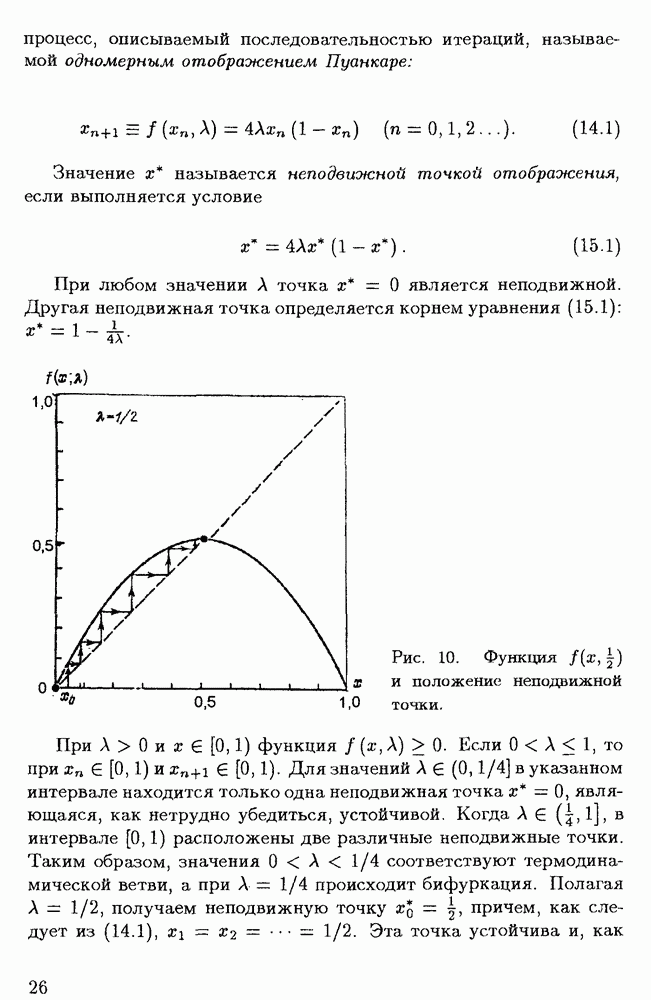
В качестве одномерного отображения Пуанкаре, описывающего процесс последовательного удвоения периода при возрастании числа Рейнольдса, удобно использовать следующее:

Отображение (7.2) имеет неподвижную точку при  и в этом соотношении правая часть представляет, по существу, разложение в окрестности указанной точки.
и в этом соотношении правая часть представляет, по существу, разложение в окрестности указанной точки.
Когда  то
то

и точка  устойчива. Если же
устойчива. Если же  то
то

и точка  является неустойчивой. Следовательно, при
является неустойчивой. Следовательно, при  происходит бифуркация.
происходит бифуркация.
Если считать, что  и
и  достаточно малы, то для второй итерации получается выражение:
достаточно малы, то для второй итерации получается выражение:

Точка  при
при  является неподвижной для (8.2) и устойчивой, но для
является неподвижной для (8.2) и устойчивой, но для  она оказывается неустойчивой. Вместе с тем в момент бифуркации появляются две устойчивые неподвижные точки, симметричные относительно точки
она оказывается неустойчивой. Вместе с тем в момент бифуркации появляются две устойчивые неподвижные точки, симметричные относительно точки 

Эти точки соответствуют движению с удвоенным периодом, названному прежде (§ 1.4)  -циклом. Отображение (7.2) переводит каждую из указанных точек в другую, а (8.2) оставляет эти точки на своем месте. Цикл с единичным периодом при бифуркации не исчез, но стал неустойчивым. Повторение бифуркаций при возрастании значений
-циклом. Отображение (7.2) переводит каждую из указанных точек в другую, а (8.2) оставляет эти точки на своем месте. Цикл с единичным периодом при бифуркации не исчез, но стал неустойчивым. Повторение бифуркаций при возрастании значений  образующих сходящуюся к
образующих сходящуюся к  последовательность
последовательность

в пределе приводит к появлению странного аттрактора.
Эксперименты пока не дают данных для вывода о том, что описанный возможный путь возникновения турбулентности является единственным. Указывались и другие способы перехода ламинарного движения жидкости в турбулентное. Один из них — "переход через перемежаемость" — описан в книге [14].
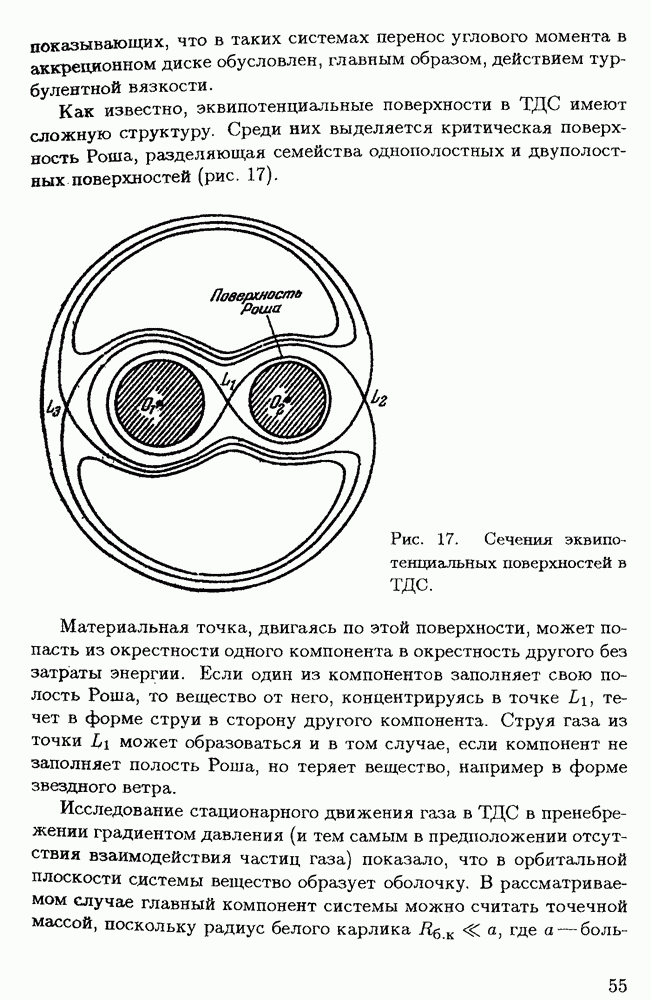
Неустойчивость движения жидкости приводит к турбулизации потока, если в нем возникают большие градиенты скорости. Это может произойти при обтекании жидкостью твердого тела, так как скорость частиц, прилегающих к его поверхности, равна нулю. Вопрос же о том, всегда ли неустойчивость ведет к турбулизации, пока остается открытым — по крайней мере, для газа, находящегося в астрофизических условиях, где скорости движения часто сверхзвуковые. Число Рейнольдса в течениях, наблюдающихся в астрофизике, очень велико не только вследствие малой вязкости, но и благодаря большим пространственным масштабам системы.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
- § 1.4. Бифуркация удвоения периода
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
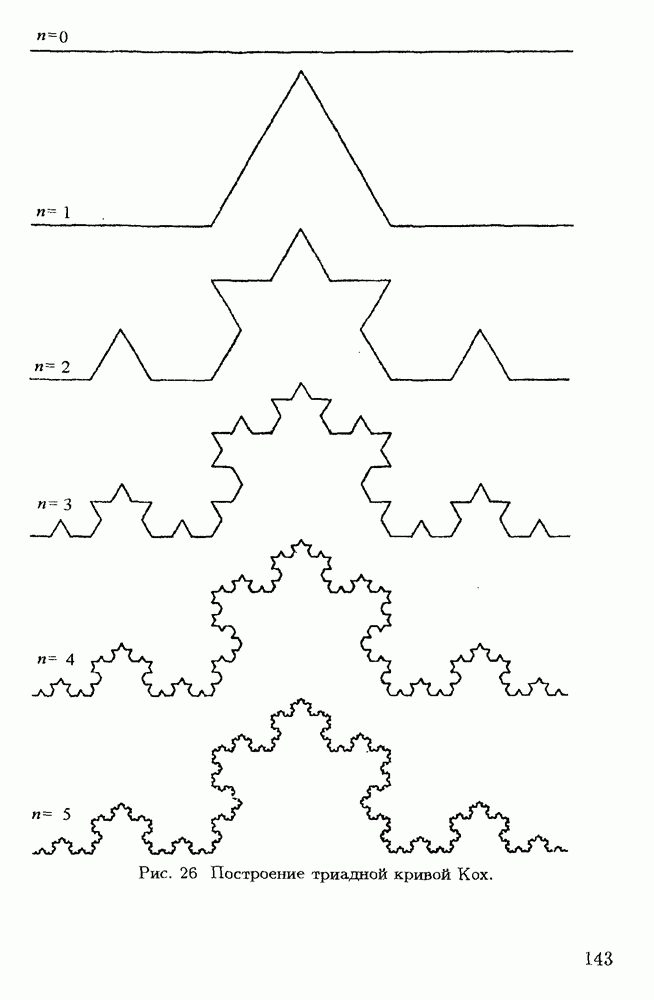
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
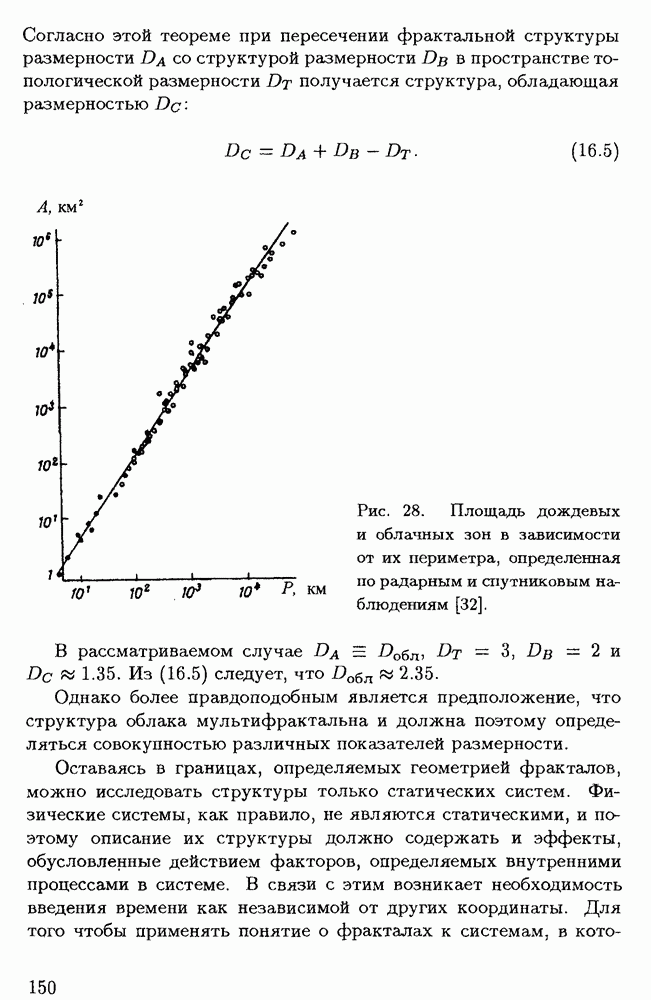
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение