| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2.2. Развитая турбулентность
В любой точке турбулентной среды характеризующие ее состояния величины — скорость, плотность, давление, температура — все время изменяются. Это явление называют турбулентными пульсациями. Расстояние между соседними точками, на котором при цульсациях значение скорости остается приблизительно одинаковым, определяет масштаб пульсаций А. В системе, характерный
размер которой  наибольший масштаб пульсаций ("основной") сравним с
наибольший масштаб пульсаций ("основной") сравним с  может быть и в несколько раз меньше
может быть и в несколько раз меньше  . В процессе перехода от ламинарного течения к турбулентному возникают в первую очередь крупномасштабные пульсации. По мере возрастания
. В процессе перехода от ламинарного течения к турбулентному возникают в первую очередь крупномасштабные пульсации. По мере возрастания  появляются все более мелкомасштабные пульсации.
появляются все более мелкомасштабные пульсации.
Каждому масштабу А при развитой турбулентности соответствует "свое" число Рейнольдса. Так как величина и одна и та же для всей среды, то с уменьшением А становится меньше и  При некотором значении
При некотором значении  величина
величина  . В этом и меньших масштабах турбулентность не развивается, так как инерционное движение практически полностью подавляется действием вязкости.
. В этом и меньших масштабах турбулентность не развивается, так как инерционное движение практически полностью подавляется действием вязкости.
Энергия, обусловливающая турбулентные движения, может поступать или от внешних по отношению к среде источников, или за счет кинетической энергии течения. Эта энергия передается пульсациям основного масштаба. Энергия турбулентных пульсаций переходит в тепловую ("вязкая диссипация") в пульсациях наименьшего масштаба  Если поступление энергии в турбулентную среду полностью уравновешивается ее диссипацией, то состояние среды стационарное — характеристики турбулентности не зависят от времени.
Если поступление энергии в турбулентную среду полностью уравновешивается ее диссипацией, то состояние среды стационарное — характеристики турбулентности не зависят от времени.
Турбулентные пульсации рассматриваются как случайный процесс, но в различных точках они не являются статистически независимыми. Пульсации взаимодействуют друг с другом, и это приводит к явлениям переноса вещества (турбулентная диффузия), количества движения (турбулентная вязкость) и тепла (турбулентная теплопроводность). Когда главную роль в явлениях переноса играют пульсации скорости, то говорят о вихревой турбулентности, а если преимущественное значение имеют пульсации Давления, то турбулентность называется акустической. Для астрофизических объектов наиболее важны явления, обусловленные вихревой турбулентностью, о которой и говорится в дальнейшем.
Уравнения, определяющие движение несжимаемой жидкости при наличии в ней развитой турбулентности, получаются путем усреднения уравнений  При этом используются обычные правила усреднения случайных коррелированных величин:
При этом используются обычные правила усреднения случайных коррелированных величин:

Компонента скорости вдоль оси  определяемая пульсациями, обозначается
определяемая пульсациями, обозначается 

Из уравнений

при  и учете условия несжимаемости
и учете условия несжимаемости

получаются уравнения, определяющие изменение компонент средней скорости (и,-):

Как следует из (9.2), величина  (обозначаемая
(обозначаемая  обеспечивает дополнительный перенос импульса в среде. Тензор потока импульса теперь выражается в виде
обеспечивает дополнительный перенос импульса в среде. Тензор потока импульса теперь выражается в виде

где  -тензор напряжений, создаваемых взаимодействием между частицами — атомами или молекулами — жидкости. Напряжения вследствие взаимодействия турбулентных пульсаций создал
-тензор напряжений, создаваемых взаимодействием между частицами — атомами или молекулами — жидкости. Напряжения вследствие взаимодействия турбулентных пульсаций создал  так называемую турбулентную вязкость, для которой коэффициент
так называемую турбулентную вязкость, для которой коэффициент  определяется следующим образом:
определяется следующим образом:

Величины  являются новыми неизвестными в системе (9.2), которая поэтому оказывается незамкнутой. При учете (10.2) она может быть переписана в виде
являются новыми неизвестными в системе (9.2), которая поэтому оказывается незамкнутой. При учете (10.2) она может быть переписана в виде

Во многих случаях величина  может быть оценена на основе полуэмпирических теорий турбулентности. Так как отношение
может быть оценена на основе полуэмпирических теорий турбулентности. Так как отношение

то при исследовании движений турбулизованной жидкости с помощью системы (11.2) действием молекулярной вязкости обычно пренебрегают.
Для описания явлений, связанных с вихревой турбулентностью, используется феноменологическая модель, согласно которой среда представляется состоящей из множества элементов, называемых также турбулентными вихрями. Каждый из элементов, проходя путь I, теряет свою индивидуальность, перемешиваясь с другими элементами и передавая им количество движения и энергию. Величину I называют длиной перемешивания и уподобляют ее длине свободного пробега молекул. Модель, основанная на понятии длины перемешивания, оказывается особенно удобной при изучении турбулентной газовой среды.
Каждому элементу масштаба А сопоставляется волновое число  Обычно предполагается, что длина свободного пробега вихря приблизительно равна его масштабу, т.е.
Обычно предполагается, что длина свободного пробега вихря приблизительно равна его масштабу, т.е.  Для наибольших из вихрей масштаб — порядка
Для наибольших из вихрей масштаб — порядка  а для наименьших он близок к
а для наименьших он близок к  Между вихрями этих масштабов существует иерархия вихрей промежуточных масштабов.
Между вихрями этих масштабов существует иерархия вихрей промежуточных масштабов.
В стационарной турбулентной среде энергия, поступающая от источника турбулизации, передается через иерархию вихрей к меньшим масштабам, вплоть до элементов с размерами порядка 10. При этом в области значений 

поток энергии не должен зависеть ни от способа поступления энергии извне, ни от диссипации, обусловленной молекулярной вязкостью. Поэтому рассчитанный на единицу массы поток энергии  через иерархию вихрей с масштабами, удовлетворяющими (12.2), зависит только от I и скорости этого вихря и. Так как размерность величины
через иерархию вихрей с масштабами, удовлетворяющими (12.2), зависит только от I и скорости этого вихря и. Так как размерность величины  выражаемой в единицах
выражаемой в единицах

совпадает с размерностью отношения  то эти величины могут различаться только множителем порядка 1. Из постоянства величины
то эти величины могут различаться только множителем порядка 1. Из постоянства величины  в стационарной среде следует соотношение
в стационарной среде следует соотношение

называемое законом Колмогорова. Зависимость между скоростью вихря и его размером может иметь иной вид, если учитывать сжимаемость среды, так как в этом случае в масштабах  могут существовать иные способы диссипации энергии — например, путем образования ударных волн.
могут существовать иные способы диссипации энергии — например, путем образования ударных волн.
Что касается внутреннего масштаба турбулентности  то он по своему физическому смыслу должен определяться величинами гмол и
то он по своему физическому смыслу должен определяться величинами гмол и  Учитывая размерности этих величин, получаем
Учитывая размерности этих величин, получаем

Из соотношения (14.2) следует, что  Поскольку максимальное число
Поскольку максимальное число  для системы соответствует масштабам вихрей, сравнимым с
для системы соответствует масштабам вихрей, сравнимым с  то количество вихрей наименьшего масштаба в системе
то количество вихрей наименьшего масштаба в системе

Вихри масштаба  вследствие отсутствия в них турбулентных движений можно считать точечными массами. Поэтому турбулентная система является по существу системой с очень большим — при
вследствие отсутствия в них турбулентных движений можно считать точечными массами. Поэтому турбулентная система является по существу системой с очень большим — при  числом степеней свободы.
числом степеней свободы.
Скорости турбулентного движения в соседних точках  потока жидкости в данный момент не являются независимыми Их разность по закону (13.2)
потока жидкости в данный момент не являются независимыми Их разность по закону (13.2)

Изменение средней скорости на расстоянии  мало по сравнению с
мало по сравнению с 
Корреляция существует не только между скоростями движения в различных точках, но и между компонентами скорости в одной и той же точке. Связь компонентов скорости в данной точке  в различные моменты
в различные моменты  характеризуется корреляционной функцией
характеризуется корреляционной функцией 

При стационарной турбулентности

Корреляционная функция пульсаций скорости в стационарном процессе определяется выражением:

где  средние значения компонент скорости
средние значения компонент скорости
Связь между значениями турбулентной скорости в двух различных точках  в различные моменты
в различные моменты  определяется тензором двухточечных моментов второго порядка, получаемым усреднением посредством функции распределения вероятностей значений
определяется тензором двухточечных моментов второго порядка, получаемым усреднением посредством функции распределения вероятностей значений  в точках
в точках 

Структурный тензор ггъг) определяет корреляционные связи между значениями скорости в разных точках в меньших масштабах, чем В. Он имеет вид

Для стационарной турбулентности компоненты обоих тензоров зависят лишь от разности 
В том случае, когда

турбулентность называют однородной, а если к тому же

она является и изотропной. Если аналогичные условия выполняются для компонент тензора  то турбулентность называют соответственно локально-однородной и локально-изотропной.
то турбулентность называют соответственно локально-однородной и локально-изотропной.
Для того чтобы выполнялись условия однородности и изотропности для  необходимо равномерное распределение источников турбулизации по всему объему системы, что осуществляется в экспериментах, но вряд ли может иметь место в астрофизических системах. Условия для существования локально-однородной изотропной турбулентности менее жесткие.
необходимо равномерное распределение источников турбулизации по всему объему системы, что осуществляется в экспериментах, но вряд ли может иметь место в астрофизических системах. Условия для существования локально-однородной изотропной турбулентности менее жесткие.
Путем усреднения уравнений движения жидкости получаются уравнения для корреляционных тензоров второго и более высоких рангов. Выводимая таким образом система всегда оказывается незамкнутой и для ее замыкания предлагались различные способы, основанные на физических соображениях.
Указанный метод изучения развитой турбулентности применим лишь при условии несжимаемости среды, и, значит, при скоростях движения газа меньше звуковой. Другой метод — спектральный — является более общим.
Спектром турбулентности задается распределение энергии движения в зависимости от волнового числа  вихрей. В пространстве волновых векторов к вводится случайная функция
вихрей. В пространстве волновых векторов к вводится случайная функция  Произвольная случайная функция координат
Произвольная случайная функция координат  представляется в виде
представляется в виде

(интеграл берется по всему пространству волновых векторов). Корреляционная функция

где  комплексно-сопряженная
комплексно-сопряженная  величина, с учетом (15.2) выражается интегралом Фурье от спектральной плотности
величина, с учетом (15.2) выражается интегралом Фурье от спектральной плотности  определенной равенством
определенной равенством

Функция  представляет собой среднюю энергию турбулентных движений, приходящуюся на единичный объем пространства
представляет собой среднюю энергию турбулентных движений, приходящуюся на единичный объем пространства  Выражение
Выражение

получающееся из формул (16.2) и (17.2) путем обратного преобразования Фурье, дает функцию

Если проинтегрировать  по сфере
по сфере 

то получается функция  представляющая собой энергию, приходящуюся на единичный интервал волновых чисел. Полная энергия турбулентных движений
представляющая собой энергию, приходящуюся на единичный интервал волновых чисел. Полная энергия турбулентных движений  находится интегрированием
находится интегрированием  по всем значениям к:
по всем значениям к:

Изменение  со временем можно определить в случае однородной и изотропной турбулентности посредством уравнения Навье-Стокса. В этом случае
со временем можно определить в случае однородной и изотропной турбулентности посредством уравнения Навье-Стокса. В этом случае

и для  получается уравнение
получается уравнение

где  -функция, описывающая взаимодействие турбулентных вихрей разных масштабов и удовлетворяющая условию
-функция, описывающая взаимодействие турбулентных вихрей разных масштабов и удовлетворяющая условию

Равенство (19.2) означает, что потеря энергии большими вихрями компенсируется приобретением от них энергии малыми вихрями. Вторым слагаемым в (18.2) учитывается диссипация энергии вследствие вязкости. Если турбулентность стационарная, то в уравнение (18.2) должен быть добавлен член, описывающий действие источников энергии.
В уравнении (18.2) содержатся две неизвестные функции, что является следствием нелинейности уравнения  Для получения замкнутой системы предлагались различные гипотезы относительно формы функции
Для получения замкнутой системы предлагались различные гипотезы относительно формы функции  Однако для интервала масштабов, определяемого по формуле (12.2), все они приводят в случае стационарной турбулентности к выражению
Однако для интервала масштабов, определяемого по формуле (12.2), все они приводят в случае стационарной турбулентности к выражению

которое следует и из соображений размерности, так как  в указанном интервале зависит лишь от величины
в указанном интервале зависит лишь от величины  являющейся постоянной.
являющейся постоянной.
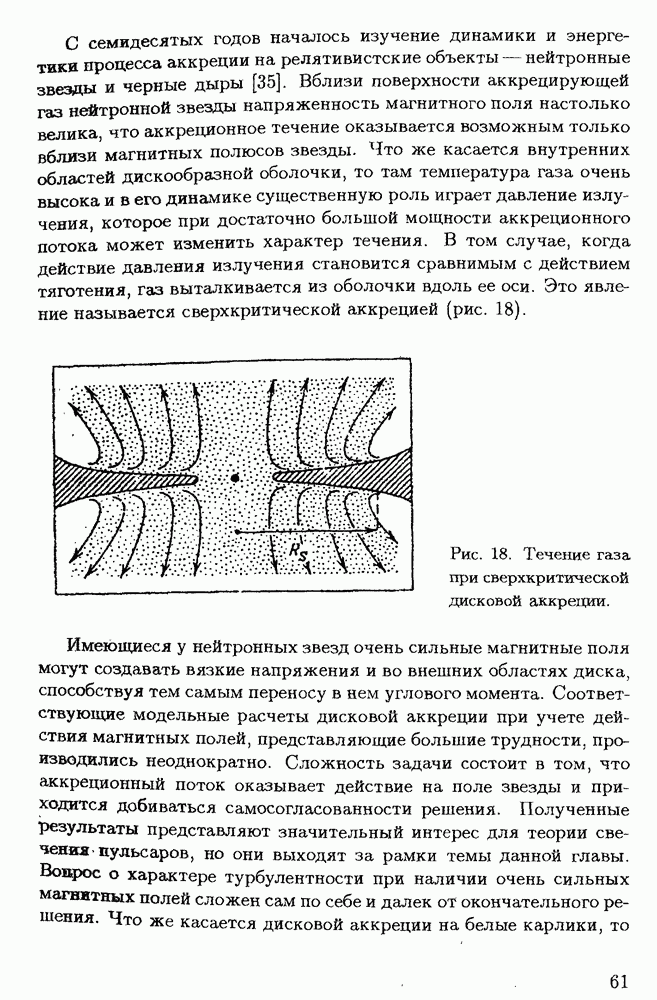
Среди обусловленных турбулентностью явлений важнейшую роль в динамике космического газа играет турбулентная вязкость. В следующих двух параграфах описывается действие турбулентной вязкости при переносе углового момента в дискообразных звездных оболочках и во внутренних областях звезд.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
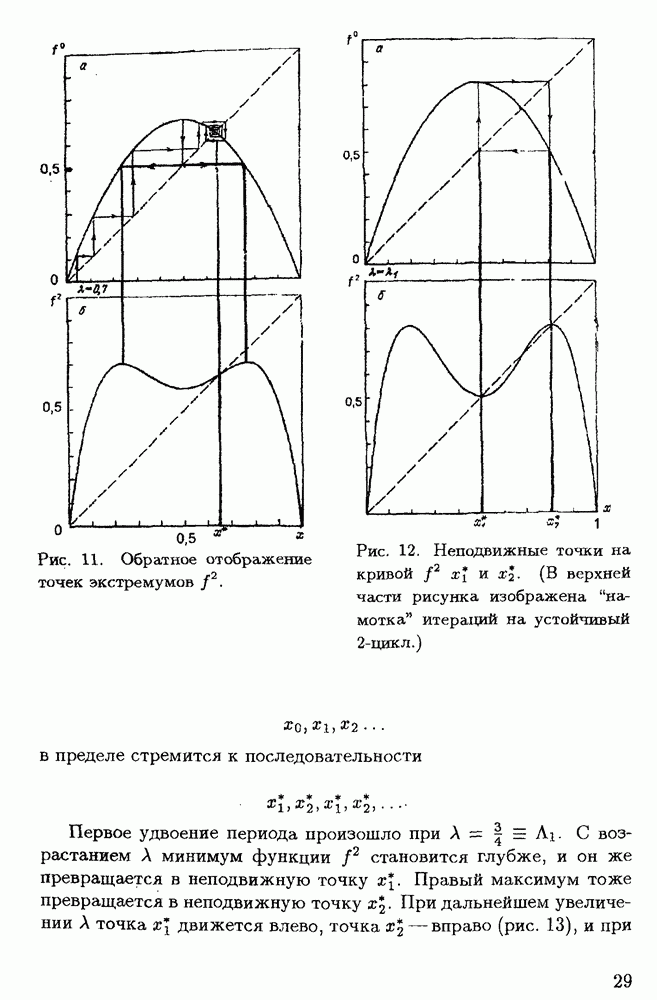
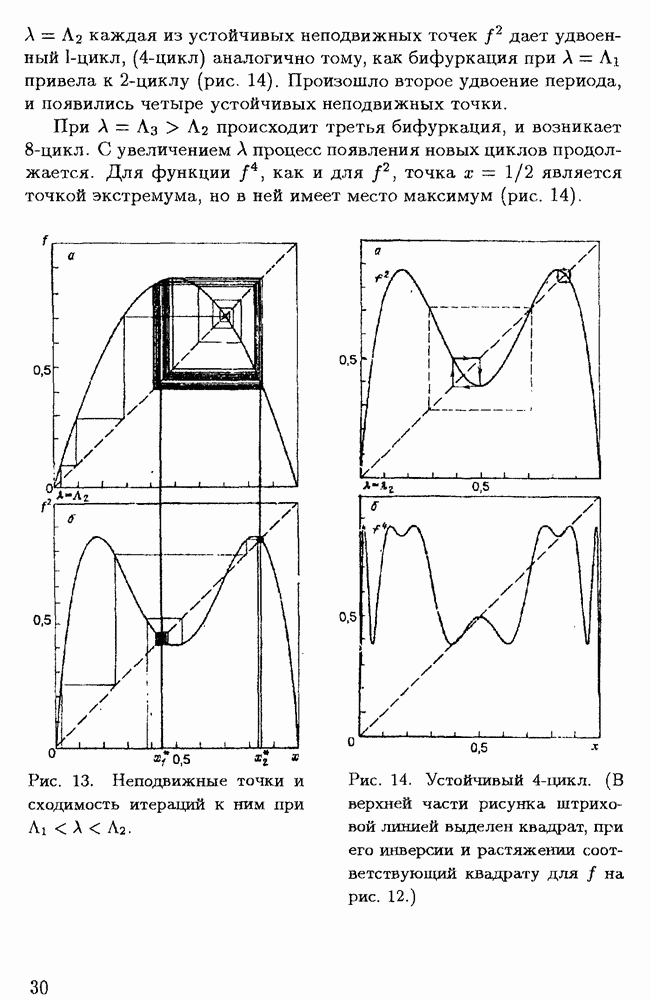
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
- § 1.4. Бифуркация удвоения периода
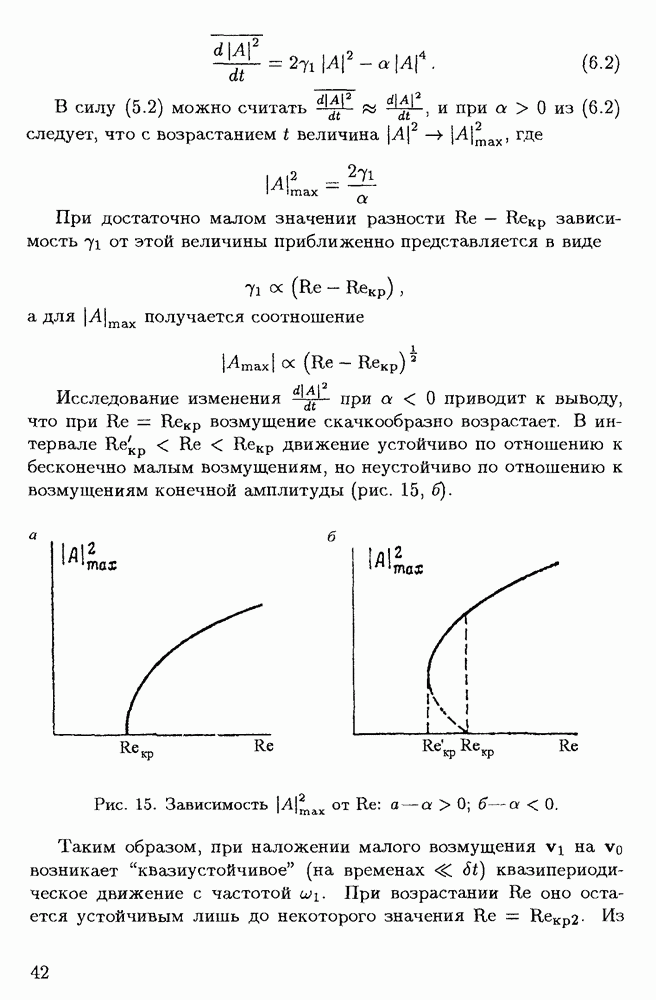
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
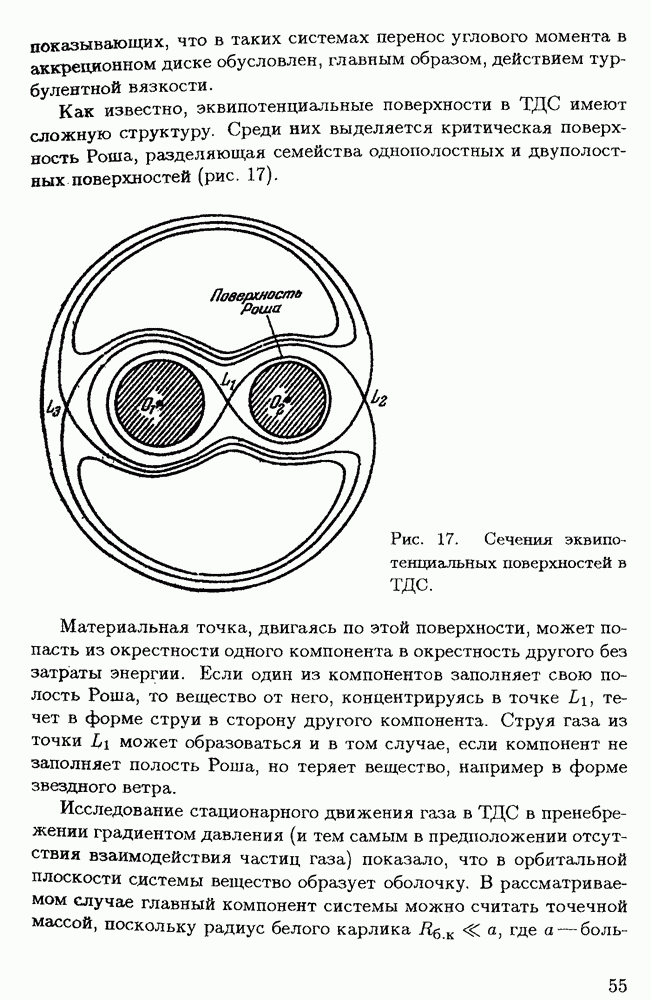
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
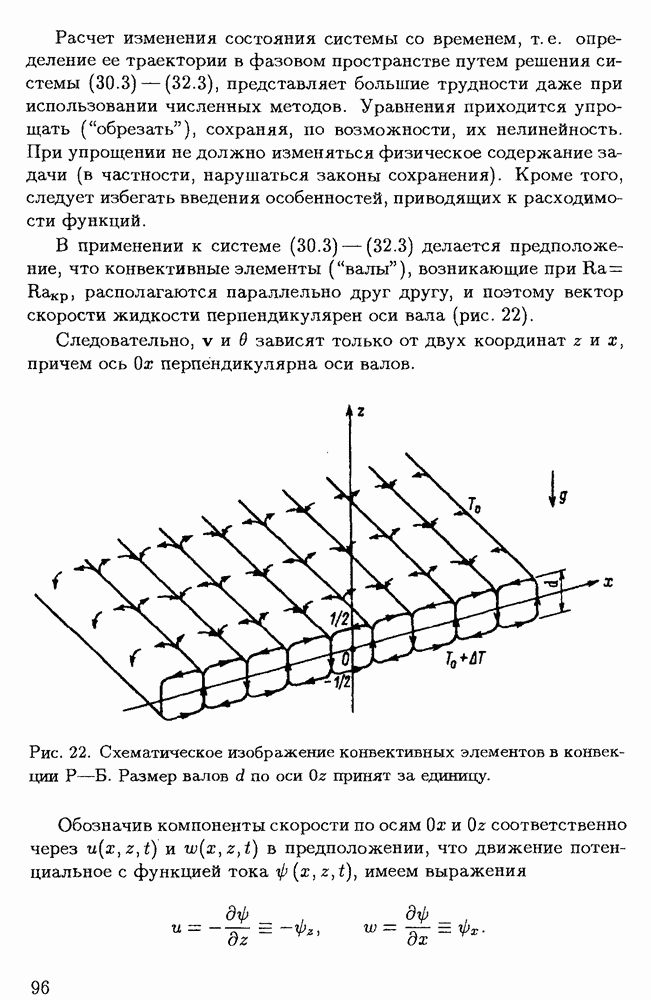
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
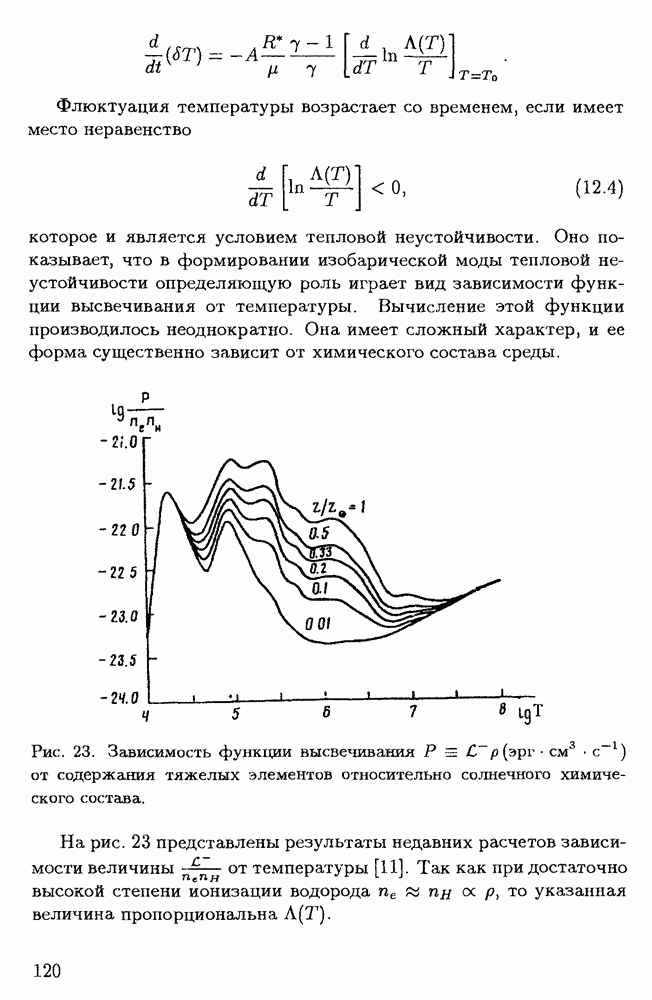
- § 4.1. Локальный критерий тепловой неустойчивости
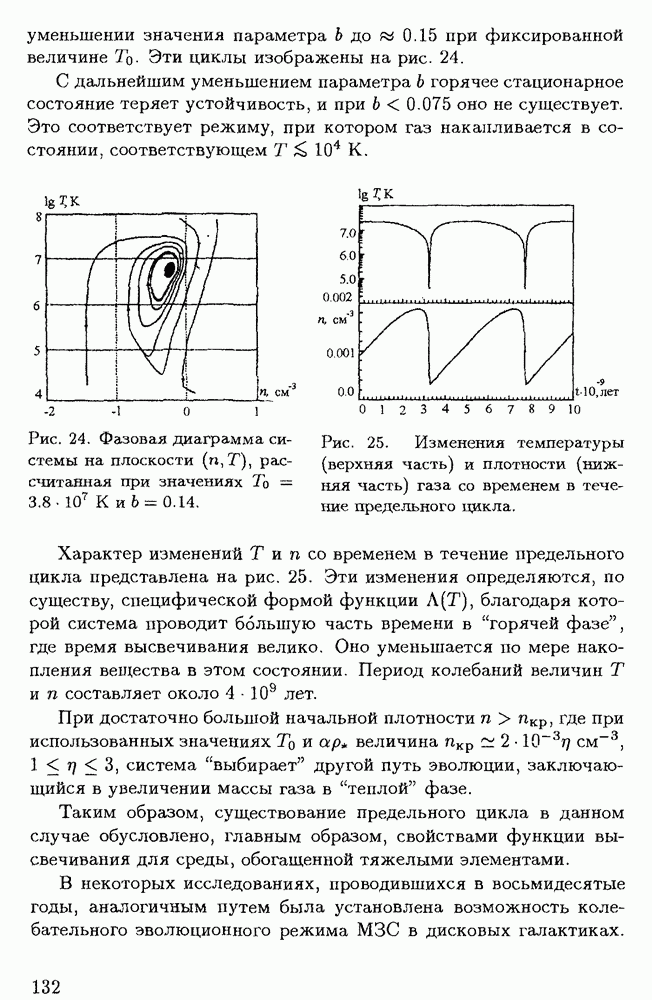
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
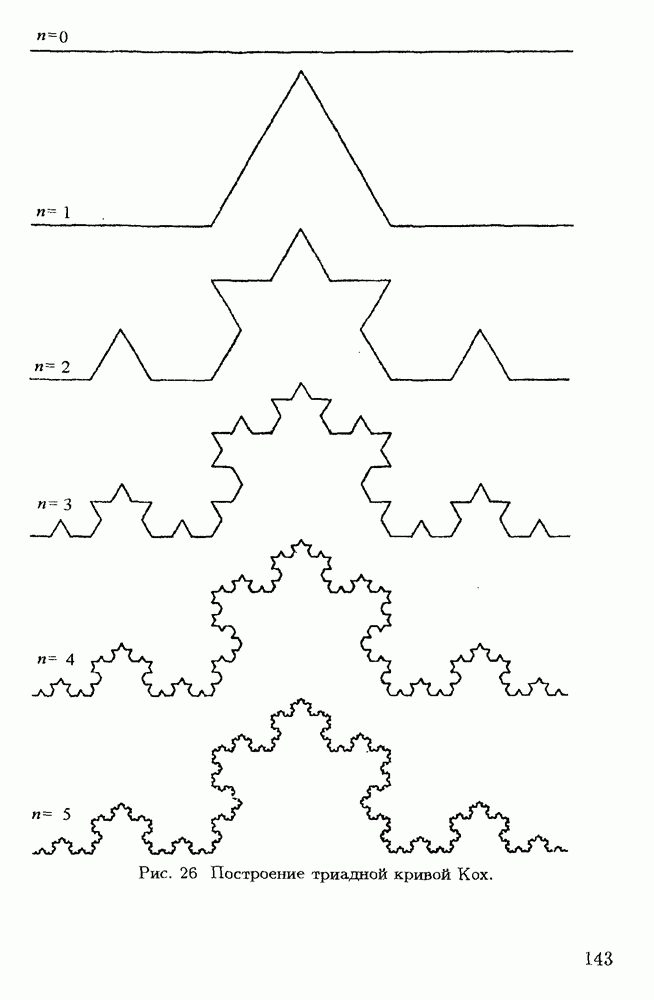
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
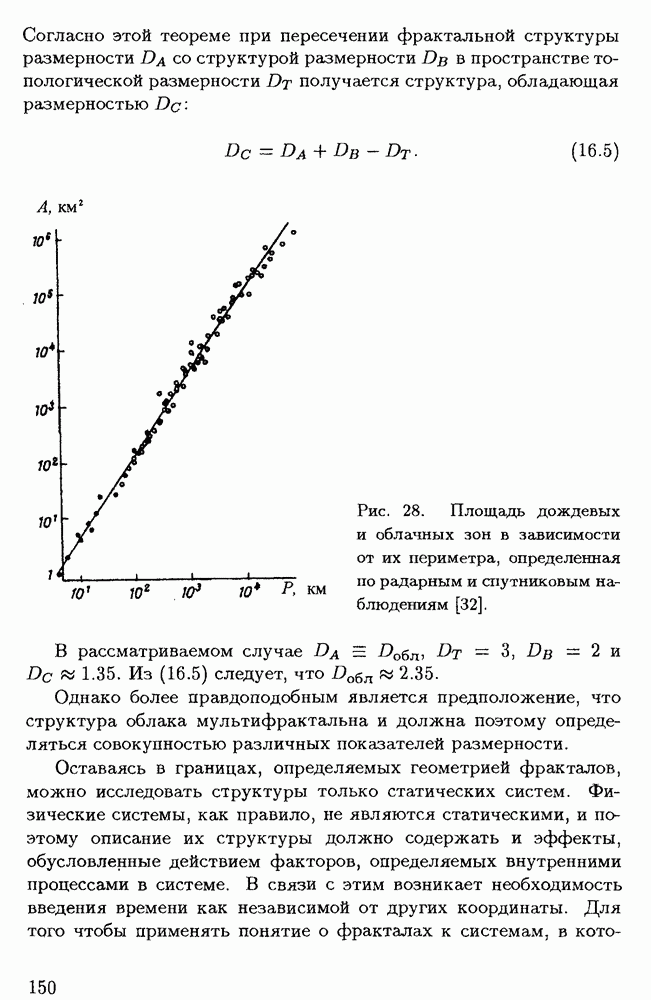
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение