§ 1.2. Термодинамические системы

Методы классической механики в их обычной форме не пригодны при исследовании поведения систем, состоящих из очень большого количества (порядка где более) взаимодействующих между собой частиц. Дело не только в технических сложностях. Как показали многочисленные эксперименты, специфичность подобных систем сказывается также в явлениях, которые совершенно не имеют аналогов в механических системах. К ним относится, например, турбулентность, о которой подробно говорится в главе 2. Однако некоторые из понятий, введенных в классической механике, в частности понятие фазового пространства, соответствующим образом модифицированное, успешно применяется при исследованиях систем, состоящих из очень большого числа частиц.

Систему рассматривают как совокупность малых ее частей — подсистем, также состоящих из очень большого числа частиц. Подсистемы можно считать замкнутыми, т. е. для каждой из них предполагается возможность обмена энергией с внешней средой, но исключается обмен веществом. Хотя в каждой из подсистем

непрерывно происходят изменения состояния, они мало зависят от того, что делается в других подсистемах. Поэтому допустимо, рассматривая подсистемы как материальные точки, вводить фазовое пространство для системы, состоящей из этих точек. Тем самым устанавливается связь между классической механикой и физикой систем, состоящих из газа. Для определенной указанным образом динамической системы можно составить гамильтониан и при заданных начальных условиях изучать ее эволюцию.

Описание состояний системы в последовательные моменты времени можно заменить рассмотрением множества одинаковых по природе систем, отличающихся конфигурацией и скоростями содержащихся в них объектов (подсистем), но соответствующих одному и тому же гамильтониану. Такое множество представляет собой статистический ансамбль. Очевидно, что изучение эволюции системы указанным методом правомерно лишь в тех временных интервалах, в которых подсистемы допустимо считать замкнутыми.

При заданных начальных условиях соответствующие ансамблю точки фазового пространства системы сосредоточены в ограниченной области ("облако точек"). С возрастанием числа подсистем это облако приближается по структуре к сплошной среде. Вводится понятие нормированной плотности этой среды в фазовом пространстве

где число подсистем, определяющей вероятность нахождения точки, соответствующей состоянию системы, в момент в объеме

Воспользовавшись уравнениями (2.1), можно показать, что

Из равенства (9.1) следует, что плотность вероятности постоянна вдоль фазовых траекторий (теорема Лиувилля). Таким образом поток в фазовом пространстве "несжимаем", что означает сохранение соответствующего системе объема фазового пространства. Однако форма этого объема со временем может меняться.

При известном распределении в системе (подсистемах) можно рассчитать средние значения физических величин для всей системы (подсистем). Все функции распределения вероятности физических величин в замкнутых статистических системах имеют очень резкий максимум при средних значениях этих величин. Поэтому наблюдаемые за достаточно большой промежуток времени физические величины в равновесном состоянии системы можно считать постоянными. В состоянии термодинамического равновесия для любой части системы физические величины с большой точностью равны средним значениям.

Состояние системы характеризуется ее энергией которая является аддитивной функцией плотности и температуры в каждой из малых подсистем. В то время как для системы, находящейся в состоянии термодинамического равновесия, значения и одни и те же всюду (во всех подсистемах), в состоянии локального термодинамического равновесия характеризуют подсистему, и значения этих величин могут меняться от точки к точке.

В отсутствие в изолированной системе макроскопических движений Если движения наличествуют, то где через обозначена их скорость. Величины могут быть приняты за обобщенные координаты. При состоянию системы, находящейся в термодинамическом равновесий, соответствует точка в двумерном фазовом пространстве. В рамках равновесной термодинамики при изучении эволюции системы предполагается, что в каждый отдельный момент в ней существует термодинамическое равновесие, т.е. переход из одного состояния в другое представляется прохождением последовательности равновесных состояний. Такое предположение выполняется далеко не всегда, и в связи с этим была развита неравновесная термодинамика, где допускается, что в процессе эволюции система оказывается в состояниях, отличных от термодинамического равновесия. Однако для того чтобы сохранить понятие температуры среды, предполагается, что имеет место

Следует отметить, что равновесное состояние системы характеризуется малой длиной корреляции, т. е. отсутствием связи между далекими друг от друга объектами. В неравновесных же системах длина корреляции бывает на много порядков больше, в чем можно будет убедиться при рассмотрении конкретных процессов в

следующих разделах. Таким образом неравновесные состояния оказываются "сильно нелинейными". В описывающих эволюцию таких состояний уравнениях нелинейность не может быть устранена.

Величины Тиру системы, находящейся в термодинамическом равновесии, могут изменяться лишь при изменении внешних условий. Поэтому для изолированной системы такое состояние является устойчивым — происходящие внутри нее флюктуации, не изменяющие энергию не способны вывести систему из равновесия. Указанное положение соответствует второму закону термодинамики, т.е. энтропия изолированной равновесной системы не изменяется со временем.

При исследовании эволюции систем, и в частности выяснении вопроса об устойчивости состояний, используется известная теорема Ляпунова [15]. Рассмотрим систему, эволюция которой описывается совокупностью дифференциальных уравнений

где вектор определяет положение точки в фазовом пространстве. Если при , то точка является точкой равновесия. Теорема Ляпунова позволяет установить является ли точка равновесия аттрактором. Заметим, что понятие аттрактора, введенное в § 1.1 для механических систем, применимо и к термодинамическим системам.

Пусть имеется функционал положительный во всей области допустимых значений аргументов:

и при этом в точке

Производная по времени выражается посредством (10.1) следующим образом:

Теорема Ляпунова. Состояние равновесия является аттрактором, если величина в окрестности этой точки имеет знак, противоположный знаку

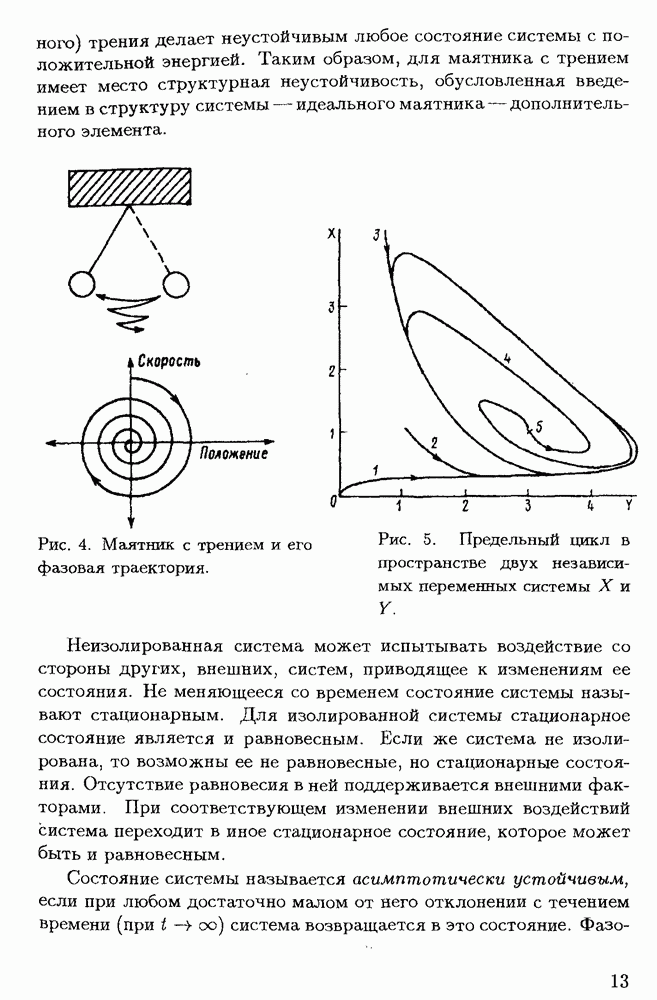
Рис. 6. Устойчивость состояния равновесия, изображаемого точкой 0.

Смысл теоремы можно пояснить рис. 6. Система из состояния располагающегося на кривой стремится перейти в состояние 0.

В случае изолированной системы состояние термодинамического равновесия, являющееся, как было отмечено выше, устойчивым, служит аттрактором для неравновесных состояний.

Система под действием внешних возмущений становится неравновесной, если состояние ее равновесия неустойчивое.

Важнейшая роль в образовании различных структур в физике и астрофизике принадлежит так называемым диссипативным системам. Диссипативная система теряет энергию и поэтому является не изолированной, но замкнутой. Вследствие процессов, приводящих к диссипации энергии, энтропия системы со временем возрастает.

Используя понятие статистического ансамбля для диссипативной системы, можно показать, что соответствующий ей фазовый объем со временем уменьшается, т. е. состояние системы является нестационарным. Однако при том условии, что диссипация энергии компенсируется поступающей в систему энергией, ее состояние может оказаться стационарным. Вопросы о механизме такой компенсации и об устойчивости возникающего стационарного состояния нуждаются в специальном исследовании для конкретных систем.

В отличие от изолированной системы, в которой при необратимых

процессах изменение энтропии для замкнутой системы возможно стационарное состояние, когда Состояние оказывается стационарным, если существует поток отрицательной энтропии извне, а производство внутренней энтропии и выполняется равенство

Устойчивость такого состояния может быть обеспечена, в частности, поддержанием в диссипативной системе постоянной температуры путем поступления в нее тепловой энергии. Разность между изменением энергии системы и величиной поступающей тепловой энергии при изотермическом процессе выражается в следующем виде:

Функция

называемая свободной энергией (Гельмгольца), для системы с постоянной температурой должна убывать с уменьшением энергии. Это положение аналогично закону возрастания энтропии для изолированных систем. При малой энергии и невысоком значении энтропия 5 мала, и близко к минимальному значению. Поскольку 5 является "мерой беспорядка", то малая величина соответствует упорядоченным структурам. Указанное обстоятельство делает возможным существование систем в высокой степени упорядоченных — кристаллические вещества, которые при достаточном повышении температур могут перейти в газообразную форму. Свободная энергия является термодинамическим потенциалом по отношению к переменным в силу равенств

В дальнейшем будет использовано еще одно часто употребляемое в термодинамике понятие химического потенциала. Энергия тела зависит от числа содержащихся в нем частиц Предполагая возможность изменения и обобщая при учете свойства аддитивности энергии известное термодинамическое тождество

можно записать следующее соотношение для

Входящая в (12.1) величина

и называется химическим потенциалом.