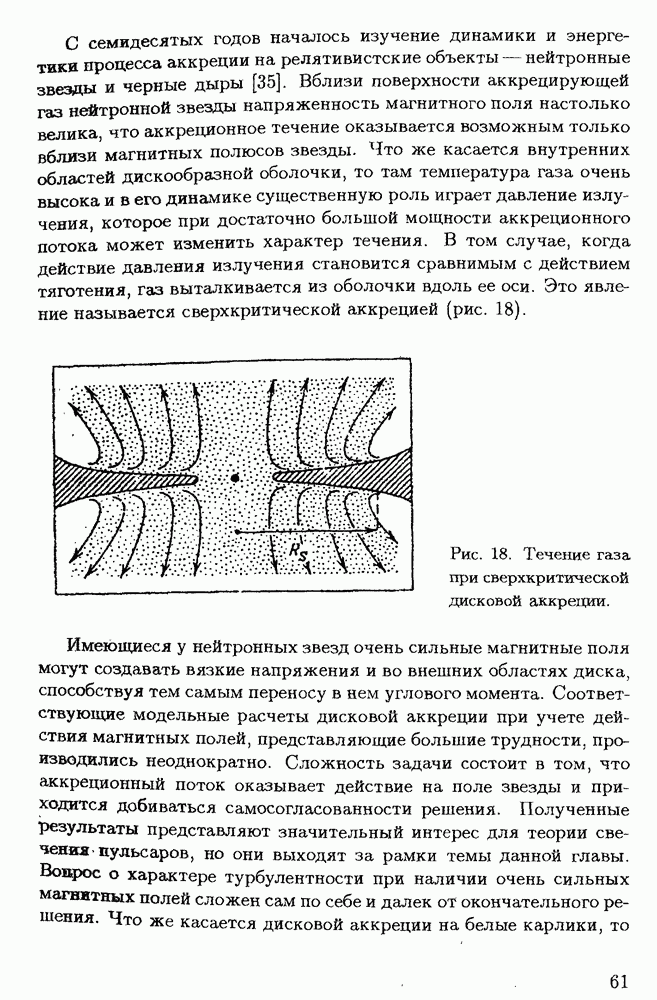
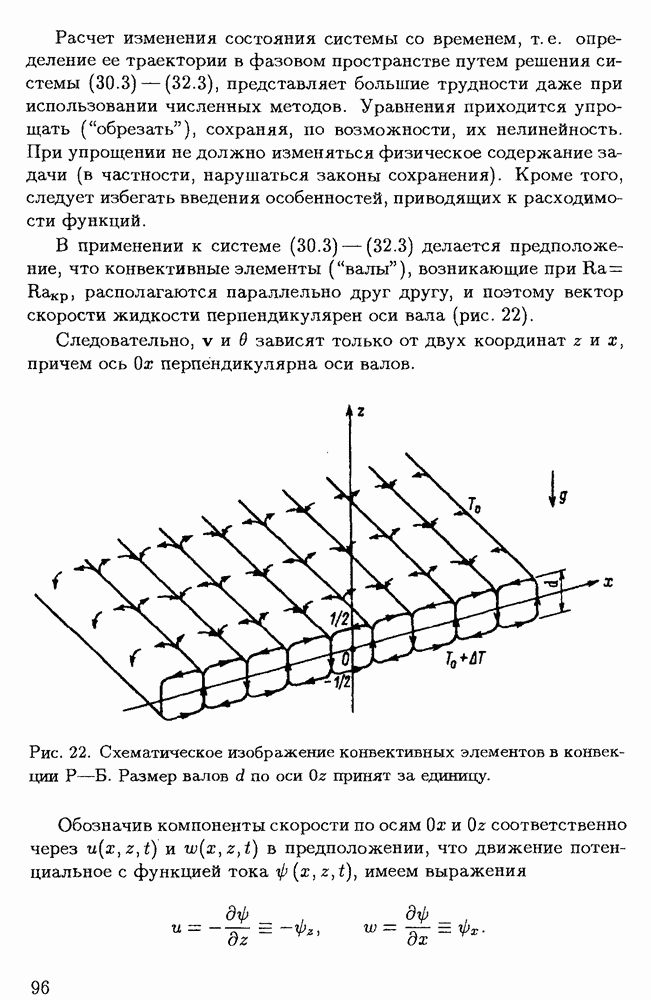
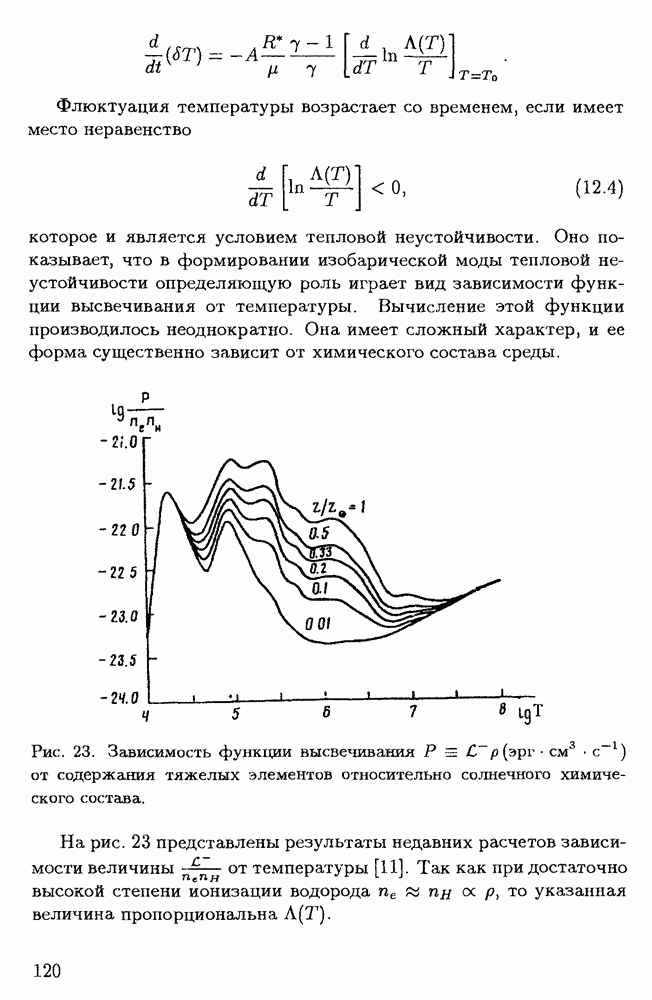
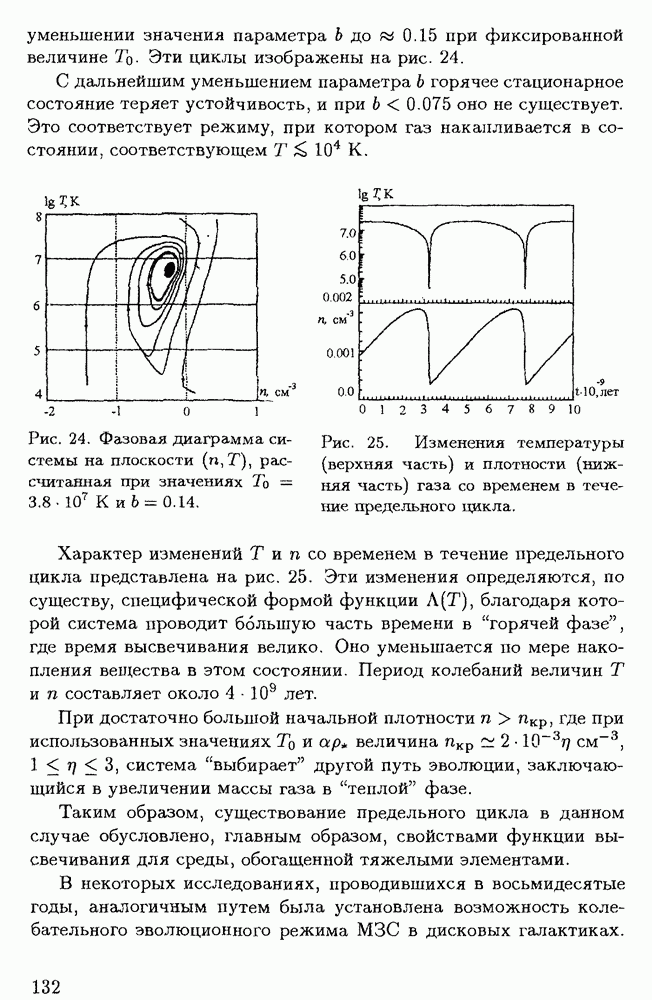
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 5. Фрактальность в астрофизических системах
§ 5.1. Фрактальные множества
Понятие фрактала как множества вложенных в пространство точек сформировалось в математике в семидесятые годы. Вскоре выяснилось, что во многих физических явлениях возникают структуры с особенностями, характерными для фрактальных множеств. Число работ, посвященных изучению фрактальных структур, стало быстро увеличиваться и к настоящему времени их многие сотни. В последние годы эти вопросы стали также привлекать внимание астрофизиков.
Фрактальные структуры в физических и астрофизических объектах будут рассматриваться в следующих параграфах. Здесь фракталы описываются как геометрическое понятие, приводятся примеры фракталов и указываются возможности обобщения этого понятия.
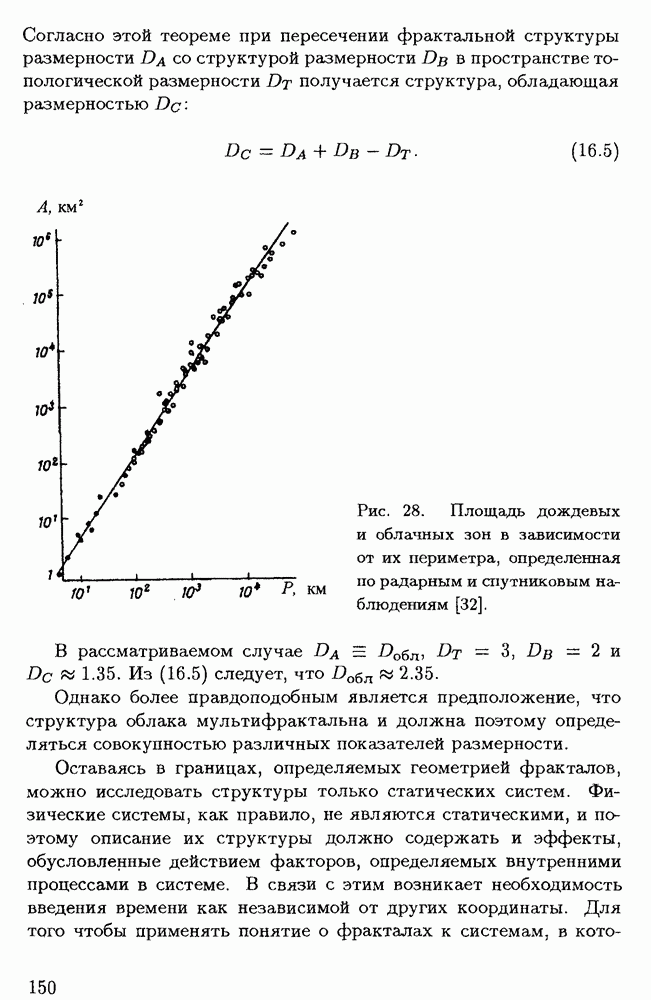
Согласно определению, данному Б.Б. Мандельбротом [32], фракталом называется множество, размерность Хаусдорфа-Безиковича для которого строго больше его топологической размерности.
Топологическая размерность  обусловлена размерностью пространства, в котором рассматривается данное множество, и всегда представляет собой целое число. Что же касается размерности Хаусдорфа-Безиковича
обусловлена размерностью пространства, в котором рассматривается данное множество, и всегда представляет собой целое число. Что же касается размерности Хаусдорфа-Безиковича  , то она может быть найдена следующим образом. Пространство, содержащее множество
, то она может быть найдена следующим образом. Пространство, содержащее множество  делится на одинаковые части. В пространстве
делится на одинаковые части. В пространстве  это можно сделать, выбирая в качестве элементов кубы с ребром
это можно сделать, выбирая в качестве элементов кубы с ребром  (или сферы того же радиуса). Число элементов, необходимых для покрытия ими множества
(или сферы того же радиуса). Число элементов, необходимых для покрытия ими множества  обозначим
обозначим  Занимаемый ими объем
Занимаемый ими объем

Если множество  представляет собой тело с определенным обычным способом объемом
представляет собой тело с определенным обычным способом объемом  то для него
то для него

Однако если  множество точек, образующих поверхность в пространстве
множество точек, образующих поверхность в пространстве  то поскольку
то поскольку

где  площадь поверхности, из (1.5) получается
площадь поверхности, из (1.5) получается

т. е. "объем поверхности" равен нулю.
При условии, что для множества  существует такое число
существует такое число  что
что

Величина  называется размерностью Хаусдорфа-Безиковича для этого множества ("клеточная" размерность). Если
называется размерностью Хаусдорфа-Безиковича для этого множества ("клеточная" размерность). Если  то множество
то множество  согласно определению является фракталом. Указанное определение нетрудно распространить на фракталы в пространстве
согласно определению является фракталом. Указанное определение нетрудно распространить на фракталы в пространстве 
В ряде случаев величину  можно находить просто путем подсчета числа клеток
можно находить просто путем подсчета числа клеток  необходимых для покрытия множества при различной величине
необходимых для покрытия множества при различной величине  Для очень малых значений
Для очень малых значений 

Определение величины  приведенное выше, не отражает всех особенностей, встречающихся в "физических фракталах". Поэтому тем же автором было дано следующее нестрогое определение.
приведенное выше, не отражает всех особенностей, встречающихся в "физических фракталах". Поэтому тем же автором было дано следующее нестрогое определение.
Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Это определение даже при его неполноте соответствует наблюдаемой в экспериментах и получаемой при расчетах тождественности структуры фрактала в целом и для любой его области.
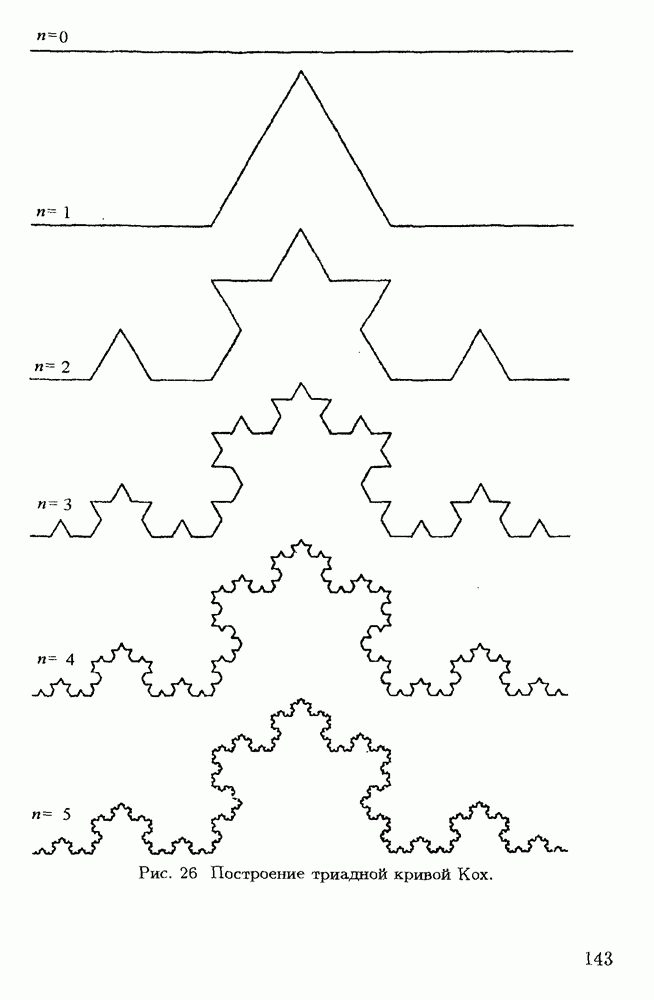
Простой пример фрактального множества представляет триадная кривая  Исходным для ее построения служит отрезок, длина которого принимается за единицу. Он делится на три равные части, средняя часть вынимается и вместо нее вкладывается двухзвенная ломаная, длина которой равна
Исходным для ее построения служит отрезок, длина которого принимается за единицу. Он делится на три равные части, средняя часть вынимается и вместо нее вкладывается двухзвенная ломаная, длина которой равна  Таким образом, на первом шаге построения
Таким образом, на первом шаге построения  вместо линии с длиной, равной 1,
вместо линии с длиной, равной 1,

(кликните для просмотра скана)
получается четырехзвенная линия с длиной, равной Для каждого из звеньев указанная процедура повторяется (рис. 26).
В  поколении длина каждого звена
поколении длина каждого звена  а количество звеньев
а количество звеньев  Предел произведения
Предел произведения  при
при 

Согласно определению фрактальная размерность триадной кривой  Так как на каждом этапе построения ломаная может быть растянута в прямую, для которой
Так как на каждом этапе построения ломаная может быть растянута в прямую, для которой  то оно в пределе приводит к фрактальному множеству.
то оно в пределе приводит к фрактальному множеству.
Другим примером фрактальной структуры является триадное канторовское множество. Оно образуется путем деления единичного отрезка на три равные части, вынимания средней части и повторения этой процедуры с остающимися двумя отрезками (рис. 27).

Рис. 27. Построение триадного канторовского множества.
При бесконечном повторении процесса деления на длине единичного отрезка остается бесконечное множество, для которого размерность  определяется из того условия, что число отрезков
определяется из того условия, что число отрезков  а длина каждого из них
а длина каждого из них  . При
. При  предел произведения
предел произведения 

Таким образом, фрактальная размерность полученного множества  а топологическая
а топологическая  (так как множество "отдельных" точек не может составить конечную длину). Следовательно, это множество представляет собой фрактал.
(так как множество "отдельных" точек не может составить конечную длину). Следовательно, это множество представляет собой фрактал.
В приложениях теории фракталов к физическим проблемам важную роль играет представление о самоподобии фракталов. Множество  называется самоподобным, если получающееся из него при изменении длин в
называется самоподобным, если получающееся из него при изменении длин в  раз множество
раз множество  покрывает без пересечений исходное множество
покрывает без пересечений исходное множество  Величина
Величина  в этом случае называется коэффициентом подобия. В простых случаях самоподобие очевидно. Например, для любого целого
в этом случае называется коэффициентом подобия. В простых случаях самоподобие очевидно. Например, для любого целого  можно выбрать
можно выбрать  такое, чтобы прямоугольник на плоскости покрывался подобными ему прямоугольниками. В этом случае
такое, чтобы прямоугольник на плоскости покрывался подобными ему прямоугольниками. В этом случае  случае прямоугольного параллелепипеда коэффициент подобия
случае прямоугольного параллелепипеда коэффициент подобия  Для фрактальных множеств коэффициент подобия
Для фрактальных множеств коэффициент подобия  записывается в виде
записывается в виде

где через  обозначена так называемая "размерность подобия". Если множество самоподобно, то
обозначена так называемая "размерность подобия". Если множество самоподобно, то  Самоподобные фракталы обладают свойством скейлинга
Самоподобные фракталы обладают свойством скейлинга  означающего масштабную инвариантность и инвариантность относительно параллельного переноса.
означающего масштабную инвариантность и инвариантность относительно параллельного переноса.
Фракталу можно сопоставить некоторую функцию. Так, например, фрактальной кривой, рассматриваемой как геометрическое место точек с координатами  может быть сопоставлена функция
может быть сопоставлена функция

Эта функция не является аналитической — она не дифференцируема и не интегрируема. Для самоподобных фракталов  является однородной, т. е. удовлетворяющей скейлинговому соотношению
является однородной, т. е. удовлетворяющей скейлинговому соотношению

с соответствующим масштабным множителем.
Самоподобные фракталы представляют собой сравнительно простой вид множеств. Более сложными являются, например, самоаффинные фракталы с неодинаковыми коэффициентами подобия по различным переменным. В математике аффинным называют преобразование, переводящее точку  в другую
в другую
точку  с координатами
с координатами  причем не все коэффициенты
причем не все коэффициенты  одинаковы. Множество
одинаковы. Множество  называется самоаффинным по отношению к вектору подобия
называется самоаффинным по отношению к вектору подобия  если
если

Здесь каждое из подмножеств  путем параллельного переноса и/или поворота приводится к совпадению со множеством
путем параллельного переноса и/или поворота приводится к совпадению со множеством  получаемым из
получаемым из  при посредстве аффинного преобразования, определяемого
при посредстве аффинного преобразования, определяемого 
В связи с различными применениями фракталов в физике и других дисциплинах было введено понятие мультифрактальности. Это означает, что множество  может состоять из взаимно связанных подмножеств
может состоять из взаимно связанных подмножеств  которые в свою очередь имеют фрактальную структуру:
которые в свою очередь имеют фрактальную структуру:

Каждому из этих подмножеств соответствует свой показатель фрактальности. Они образуют множество фрактальных размерностей, характеризующее систему. Важным свойством мультифракталов является возможность различия масштабных свойств в разных областях системы. Структура системы (множества  детерминирована создающим ее алгоритмом. Подробно понятие мультифрактала и свойства этих объектов описаны в книге [18].
детерминирована создающим ее алгоритмом. Подробно понятие мультифрактала и свойства этих объектов описаны в книге [18].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
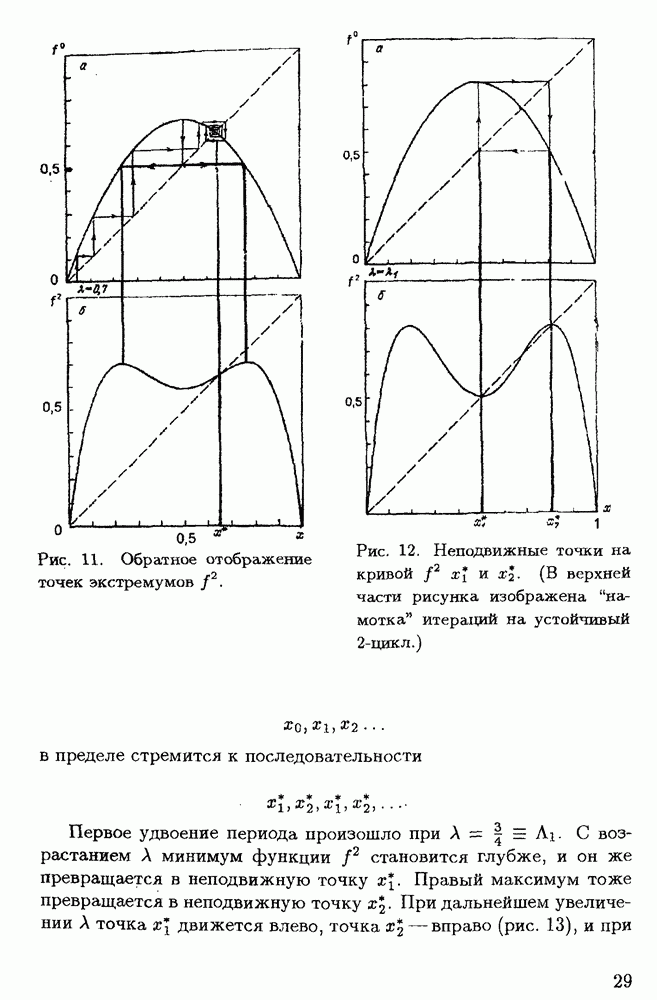
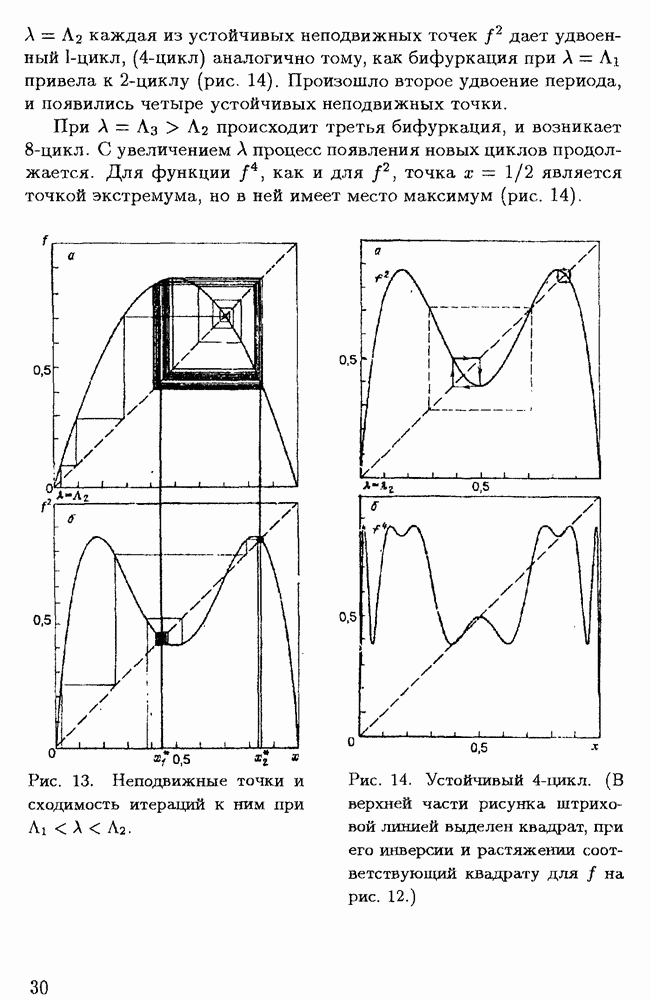
- § 1.4. Бифуркация удвоения периода
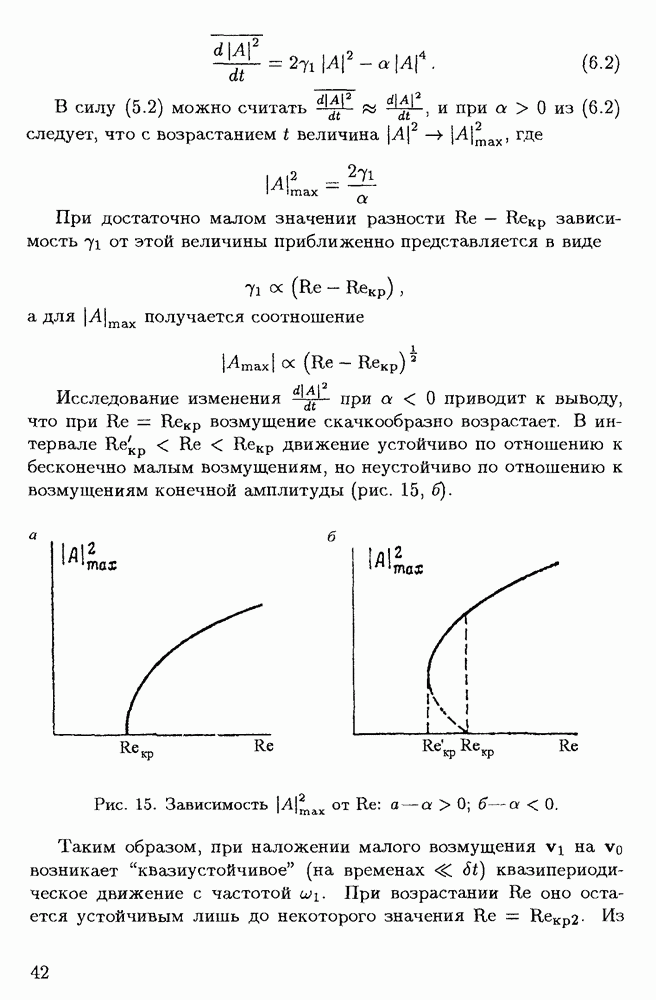
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
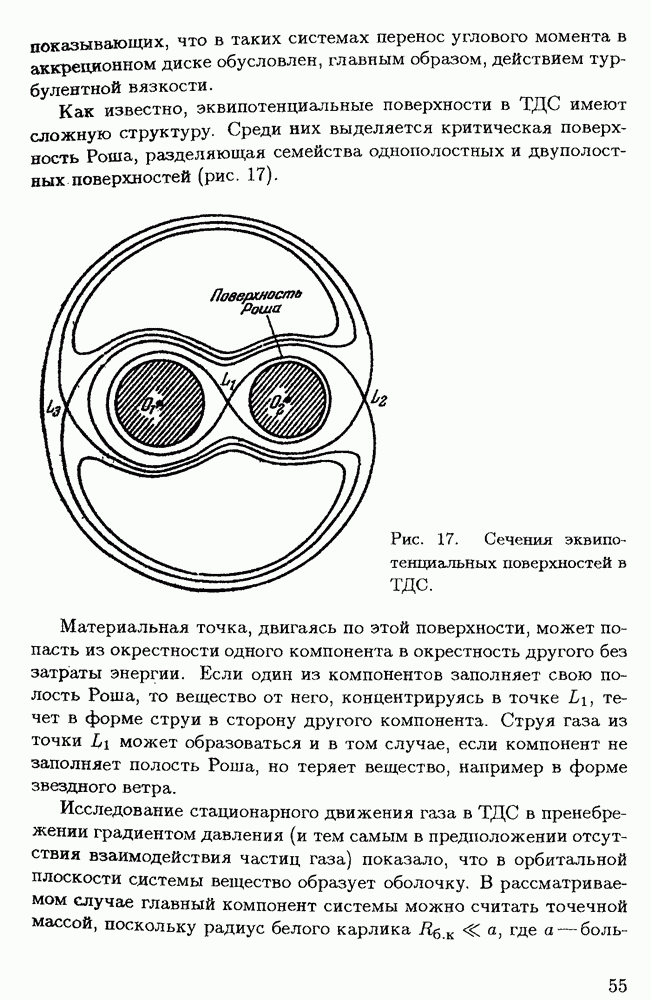
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение