| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 3. Конвекция и вызываемые ею явления в звездах
§ 3.1. Устойчивость равновесия газа в присутствии внешнего поля
При наличии внешнего поля на возможные состояния системы накладываются дополнительные ограничения, и условия устойчивости равновесных состояний зависят от наложенных связей. Простым примером такой связи является внешнее гравитационное поле с постоянным в пространстве ускорением силы тяжести  Равновесное состояние несжимаемой жидкости в этом поле определяется уравнением
Равновесное состояние несжимаемой жидкости в этом поле определяется уравнением

При выборе системы координат так, чтобы направление оси  совпадало с направлением
совпадало с направлением  имеем
имеем  Для величины давления в этом случае из (1.3) получается равенство
Для величины давления в этом случае из (1.3) получается равенство

Если плоскость  соответствует свободной поверхности жидкости, то
соответствует свободной поверхности жидкости, то

Жидкость с такой зависимостью  находится в механическом равновесии.
находится в механическом равновесии.
При исследовании равновесного состояния газа в гравитационном поле следует учитывать его сжимаемость. Плотность газа, а значит, и его давление зависят от температуры, распределение которой должно быть известно.
При условии теплового равновесия газа, т. е. его однородности по температуре, механическое равновесие имеет место при выполнении равенства

где  свободная энергия. При однородном гравитационном поле
свободная энергия. При однородном гравитационном поле  в использованной выше системе координат уравнение (3.3) приводит к условию механического равновесия в виде
в использованной выше системе координат уравнение (3.3) приводит к условию механического равновесия в виде

Зависимость  от
от  выражаемая формулой (4.3), определяет и условие термодинамического равновесия системы, находящейся в гравитационном поле.
выражаемая формулой (4.3), определяет и условие термодинамического равновесия системы, находящейся в гравитационном поле.
В тех случаях, когда температура среды в различных точках плоскости  не одинакова, механическое равновесие в гравитационном поле невозможно. В среде происходят движения, ведущие к установлению равновесия, хотя статическое состояние может реализоваться не всегда. Механическое равновесие в отсутствие теплового равновесия при определенных условиях оказывается возможным, если температура в среде зависит только от координаты
не одинакова, механическое равновесие в гравитационном поле невозможно. В среде происходят движения, ведущие к установлению равновесия, хотя статическое состояние может реализоваться не всегда. Механическое равновесие в отсутствие теплового равновесия при определенных условиях оказывается возможным, если температура в среде зависит только от координаты  т.е. "глубины", отсчитываемой от верхней свободной границы.
т.е. "глубины", отсчитываемой от верхней свободной границы.
Рассмотрим газ, находящийся в однородном гравитационном поле  при наличии в нем градиента температуры
при наличии в нем градиента температуры  имеющего то же направление, что и
имеющего то же направление, что и  Чтобы получить условие равновесия, предположим, что элемент газа с глубины
Чтобы получить условие равновесия, предположим, что элемент газа с глубины  сместился в сторону верхней границы на малую величину
сместился в сторону верхней границы на малую величину  Первоначально давление в этом элементе больше, чем на уровне
Первоначально давление в этом элементе больше, чем на уровне  следовательно, температура в нем
следовательно, температура в нем  превосходит температуру окружающей среды
превосходит температуру окружающей среды  Соответственно плотность в этом элементе меньше, чем в окружающей среде, т.е. он "легче". Если бы состояние элемента не менялось, он бы "всплывал", т.е. двигался в сторону уменьшения
Соответственно плотность в этом элементе меньше, чем в окружающей среде, т.е. он "легче". Если бы состояние элемента не менялось, он бы "всплывал", т.е. двигался в сторону уменьшения  под действием силы плавучести
под действием силы плавучести  . В расчете на единицу объема на элемент с плотностью
. В расчете на единицу объема на элемент с плотностью  действует сила
действует сила

где  — плотность окружающей среды, находящейся по предположению в состоянии механического равновесия. Так как
— плотность окружающей среды, находящейся по предположению в состоянии механического равновесия. Так как  с приближением к верхней границе увеличивается, то при постоянной величине
с приближением к верхней границе увеличивается, то при постоянной величине  сила
сила  должна была бы возрастать и соответственно должно увеличиваться со временем начальное смещение
должна была бы возрастать и соответственно должно увеличиваться со временем начальное смещение
элемента. Аналогично становилось бы со временем больше и смещение  элемент должен был бы "тонуть". Однако для реальных жидкостей величина
элемент должен был бы "тонуть". Однако для реальных жидкостей величина  не является абсолютно постоянной. При изменении температуры меняется плотность среды. Температура в элементе, попавшем в среду с меньшим давлением
не является абсолютно постоянной. При изменении температуры меняется плотность среды. Температура в элементе, попавшем в среду с меньшим давлением  падает вследствие его расширения до тех пор, пока давление в нем не сравняется с внешним. Здесь для простоты рассмотрим только тот случай, когда среда представляет собой идеальный газ. Если считать расширение происходящим адиабатически, т. е. зависимость между
падает вследствие его расширения до тех пор, пока давление в нем не сравняется с внешним. Здесь для простоты рассмотрим только тот случай, когда среда представляет собой идеальный газ. Если считать расширение происходящим адиабатически, т. е. зависимость между  и
и  принять в виде
принять в виде

то изменение давления в элементе связано с изменением температуры следующим образом:

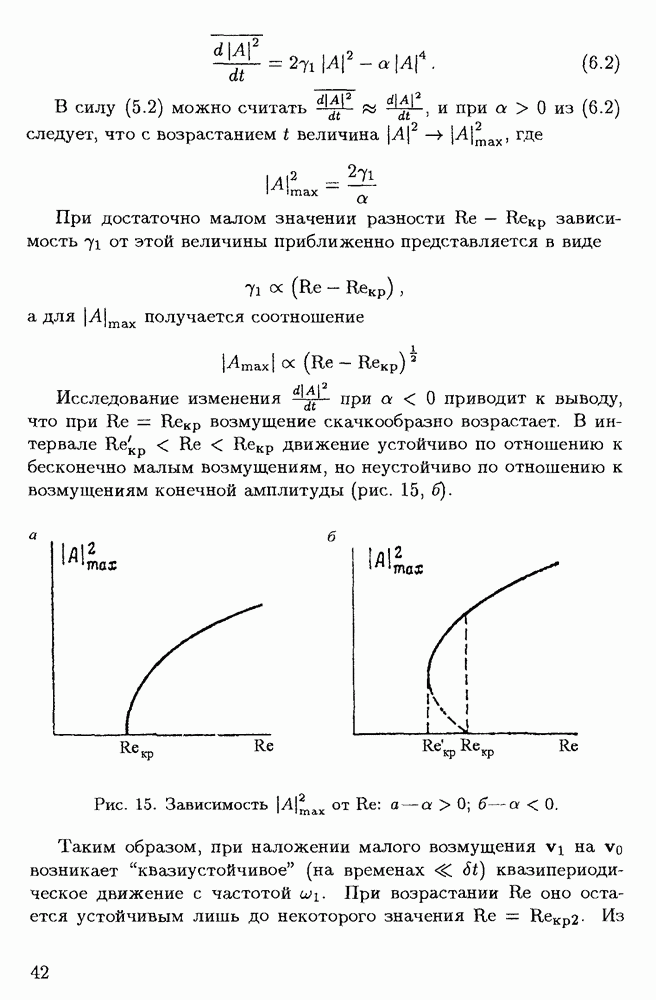
Смещающийся вверх элемент охлаждается, его плотность возрастает — он "тяжелеет", и соответственно действующая на него сила плавучести уменьшается. Если скорость адиабатического охлаждения меньше, чем скорость падения температуры в окружающей среде с приближением к поверхности, что выражается неравенством

то начальные возмущения продолжают увеличиваться под действием силы плавучести. Неустойчивость такого вида называют конвективной. Критерий наступления неустойчивости (7.3) был установлен К.Шварцшильдом (1906 г.). При выполнении неравенства, противоположного (7,3), газ находится в состоянии механического равновесия. Величина

называется сверхадиабатическим градиентом. Если  то среда устойчива в отношении конвекции. Из выражения (6.3) получается, что
то среда устойчива в отношении конвекции. Из выражения (6.3) получается, что

и критерий (7.3) принимает форму

При использовании уравнения состояния идеального газа неравенство (8.3) может быть записано в виде

В конвективно неустойчивой жидкости происходят движения, обусловливающие перераспределение температуры по объему жидкости. На этих движениях сказывается действие вязкости, препятствующей перемещениям элементов. Кроме того, расширение (или сжатие) элементов может отличаться от адиабатического — в процессе их движения происходит обмен тепловой энергией между элементами и окружающей средой. Указанные факторы самым существенным образом влияют на процесс развития конвективной неустойчивости, который будет рассмотрен в следующих разделах.
Выше для получения критерия устойчивости был использован метод, основанный на сравнении эффективности двух факторов, действующих на возмущенный элемент — силы плавучести и силы тяжести. Аналогичным методом исследуется устойчивость стационарного движения жидкости в пространстве между двумя вращающимися коаксиальными цилиндрами (течение Куэтта). В этом случае элементы жидкости движутся по круговой траектории, на которой действие центробежной силы уравновешивается градиентом давления. Если сместить данный элемент с его траектории, то равновесие нарушается и поведение элемента определяется возможностью восстановления баланса указанных сил.
Течение Куэтта создается вращением двух бесконечных цилиндров — внутреннего с радиусом  и угловой скоростью
и угловой скоростью  и внешнего с радиусом
и внешнего с радиусом  и угловой скоростью
и угловой скоростью  Принимается цилиндрическая система координат с осью
Принимается цилиндрическая система координат с осью  совпадающей с осью цилиндров. Из симметрии течения следует, что
совпадающей с осью цилиндров. Из симметрии течения следует, что

Уравнение Навье-Стокса при учете (9.3) приводится к следующим двум уравнениям:

Общее решение уравнения (11.3) имеет вид

Скорость жидкости на твердой поверхности совпадает со скоростью этой поверхности. Поэтому

При таких граничных условиях выражение для  записывается как
записывается как

В стационарном состоянии центробежная сила, действующая на находящийся на расстоянии  от оси элемент жидкости массой
от оси элемент жидкости массой  равна
равна  Она уравновешивается величиной
Она уравновешивается величиной  Здесь
Здесь  -угловой момент элемента. Если этот элемент смещен на расстояние
-угловой момент элемента. Если этот элемент смещен на расстояние  то поскольку угловой момент сохраняется, он останется равным
то поскольку угловой момент сохраняется, он останется равным  но центробежная сила окажется иной — она равна
но центробежная сила окажется иной — она равна  Равновесное же значение центробежной силы на расстоянии
Равновесное же значение центробежной силы на расстоянии  от оси равно
от оси равно  . Поэтому для возвращения элемента на первоначальную траекторию необходимо выполнение условия
. Поэтому для возвращения элемента на первоначальную траекторию необходимо выполнение условия

При  это условие можно переписать в виде
это условие можно переписать в виде

Учитывая, что  и используя выражение для
и используя выражение для  вместо (13.3) получаем
вместо (13.3) получаем

Из (14.3) следует, что при противоположных направлениях вращения цилиндров течение неустойчиво, так как  должно менять знак в промежутке
должно менять знак в промежутке  Если же цилиндры вращаются в одну сторону, то, считая положительным, находим условие устойчивости в форме
Если же цилиндры вращаются в одну сторону, то, считая положительным, находим условие устойчивости в форме

Следует иметь в виду, что при решении задачи об устойчивости не учитывалось влияние вязкости, поскольку в системе (10.3)-(11.3) коэффициент  не содержится. Однако градиент давления может существовать лишь при наличии вязкости. Поэтому указанный вывод условия устойчивости пригоден только при малых значениях и. За число Рейнольдса в течении Куэтта можно принять величину
не содержится. Однако градиент давления может существовать лишь при наличии вязкости. Поэтому указанный вывод условия устойчивости пригоден только при малых значениях и. За число Рейнольдса в течении Куэтта можно принять величину  или
или  . При малом
. При малом  значение
значение  может оказаться достаточно большим, что скажется на характере течения.
может оказаться достаточно большим, что скажется на характере течения.
В следующем параграфе будет произведен анализ конвективной неустойчивости и устойчивости течения Куэтта в линейном приближении.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
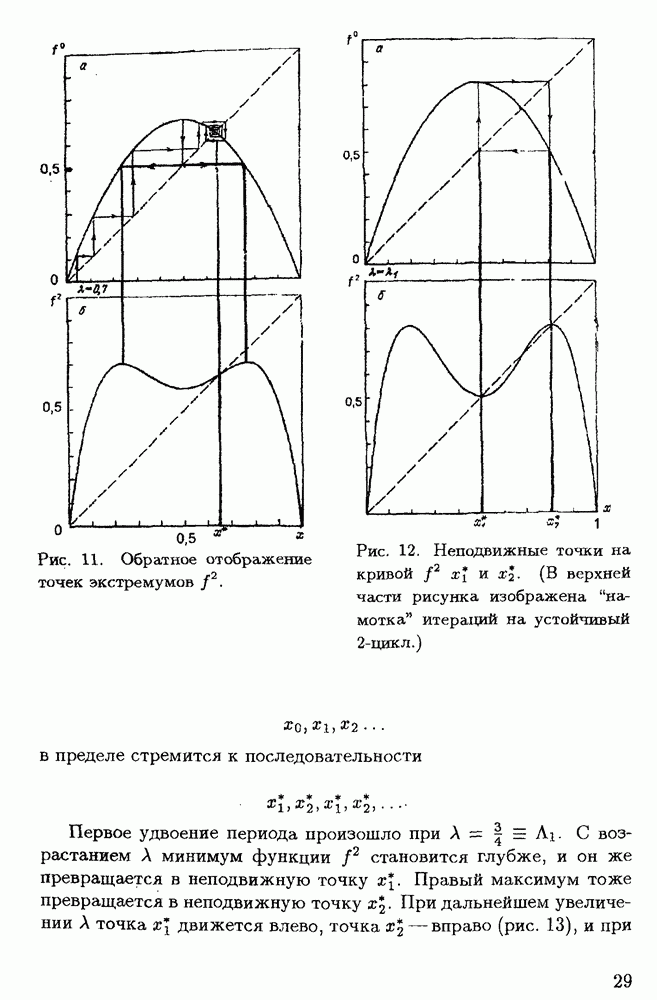
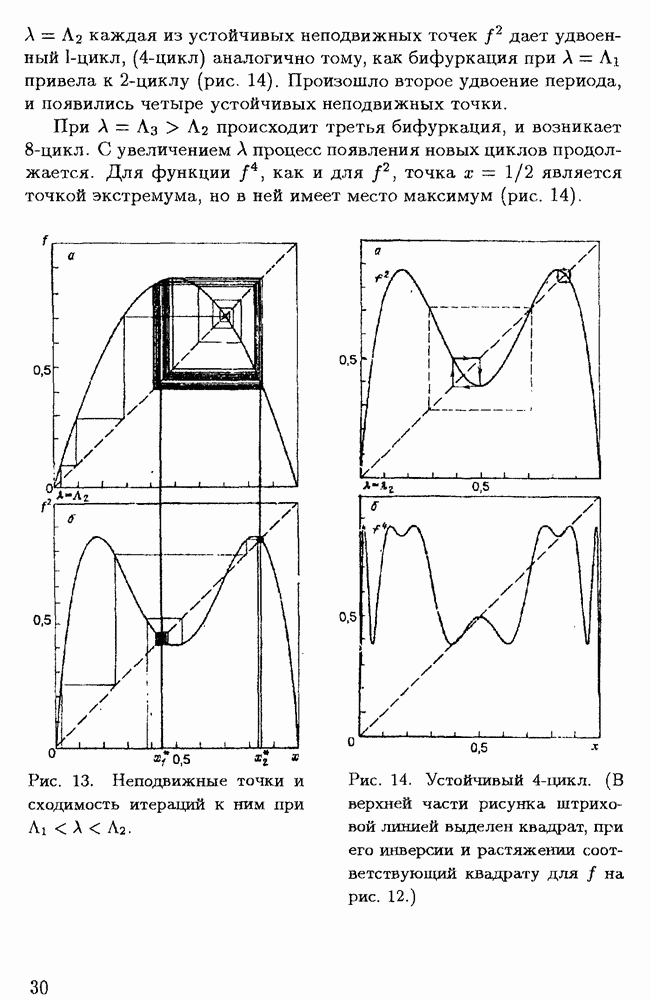
- § 1.4. Бифуркация удвоения периода
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
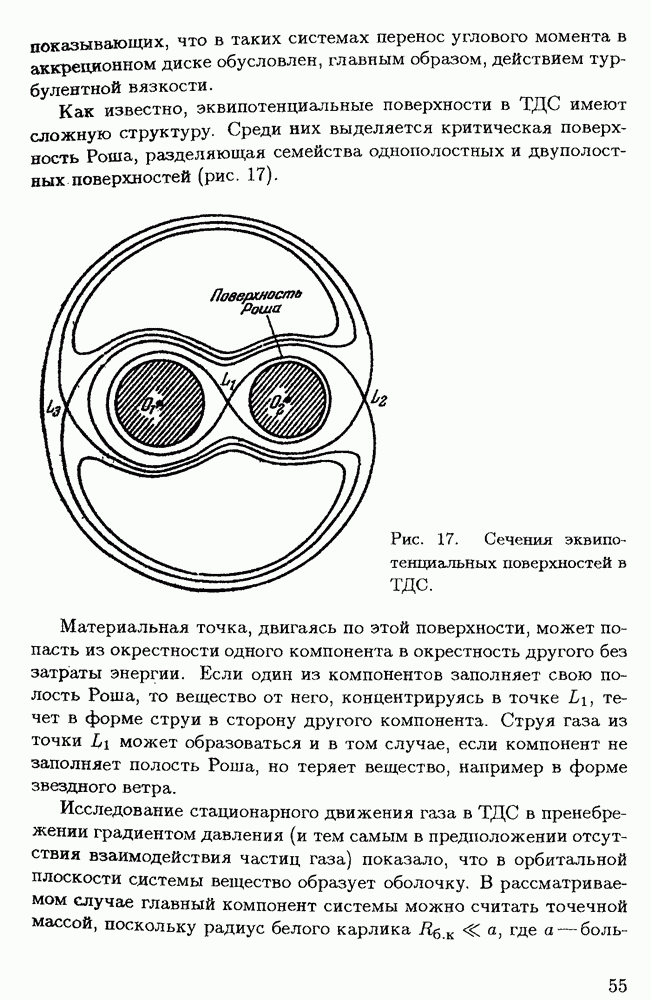
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
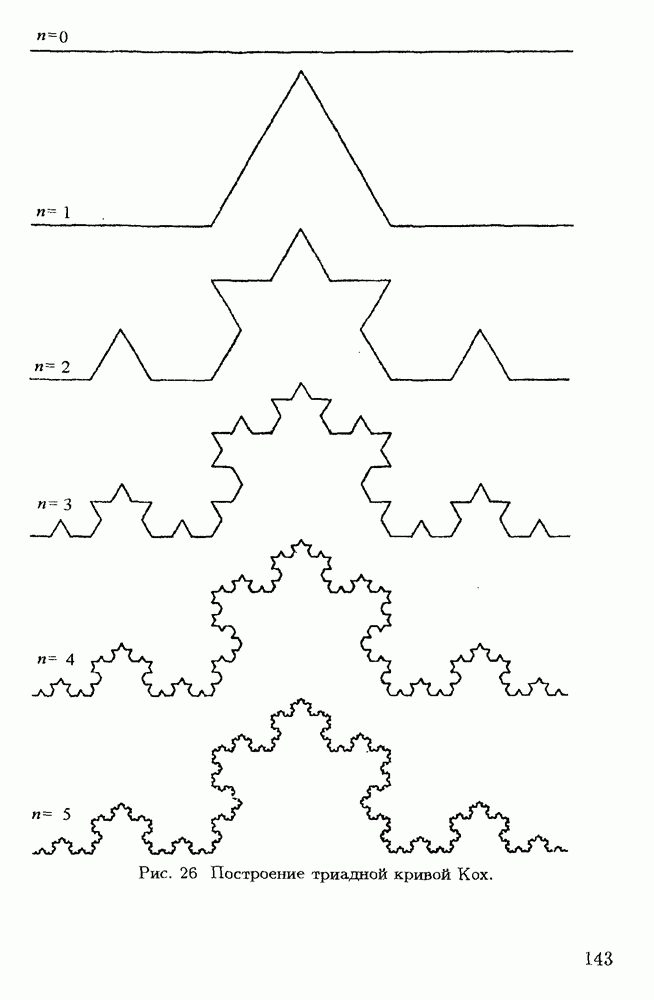
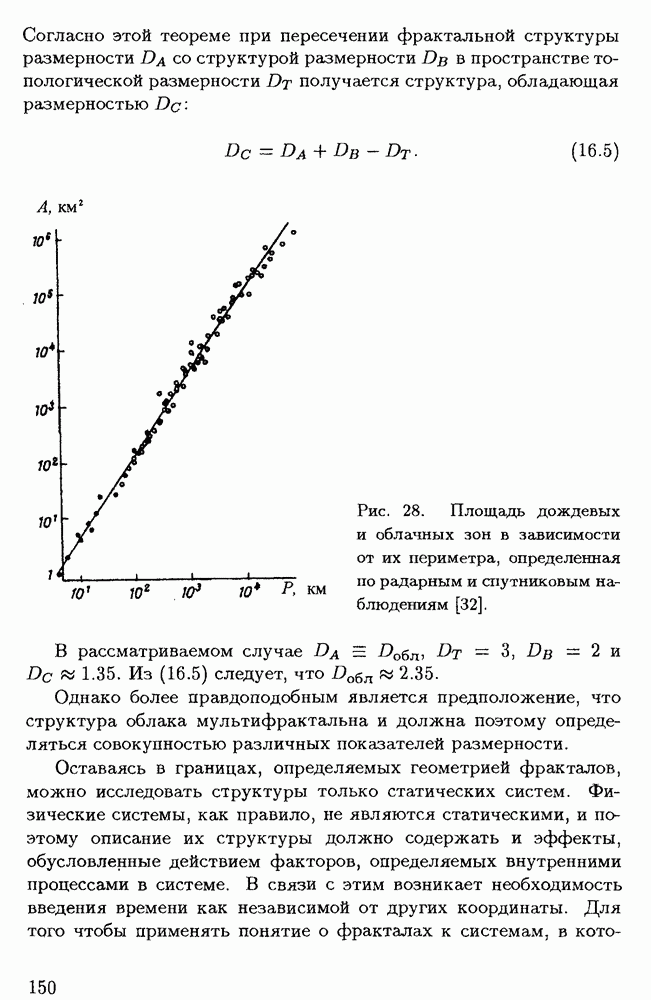
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение