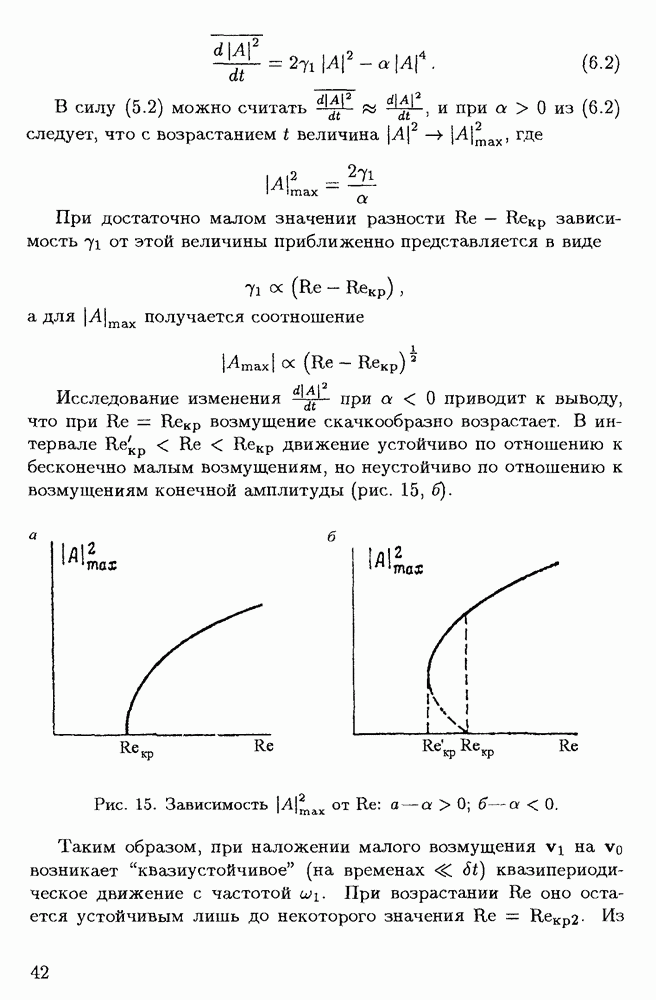
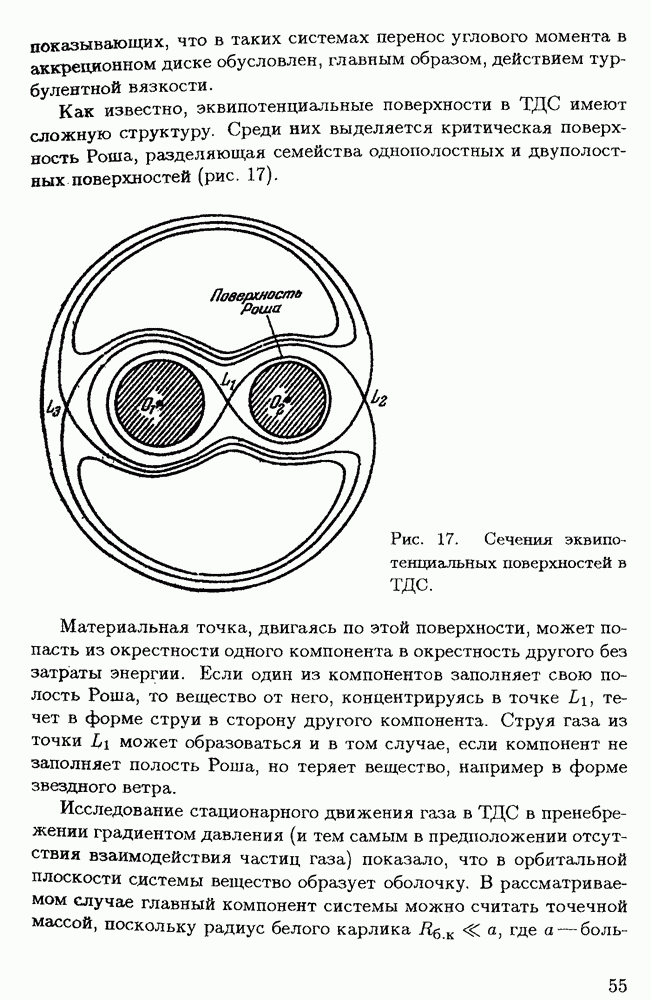
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1.4. Бифуркация удвоения периода
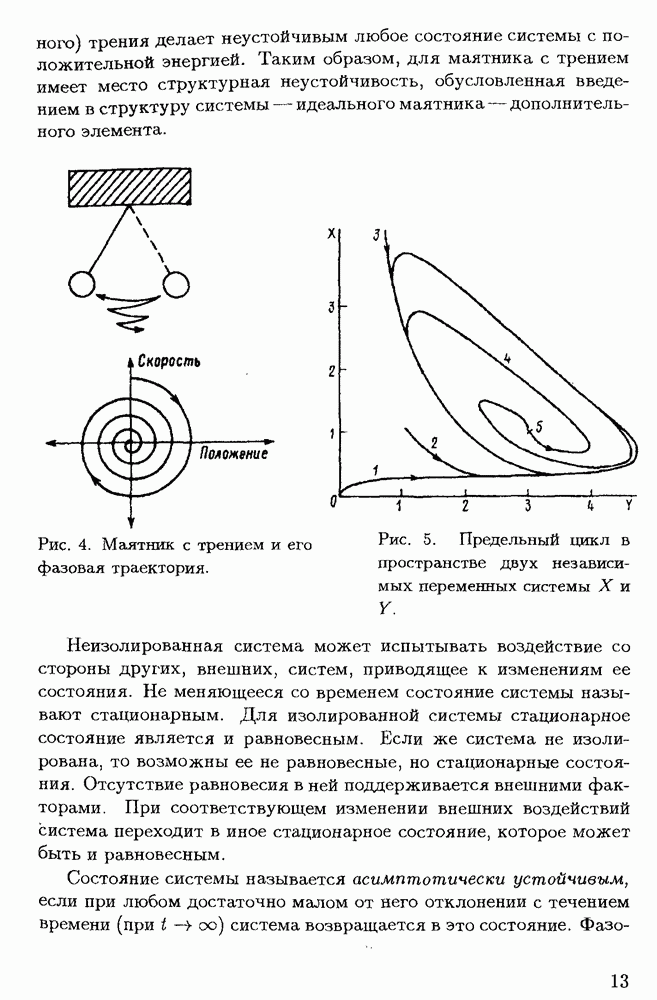
Одним из путей перехода нелинейной системы к состоянию хаоса является последовательное удвоение периода при достижении управляющим параметром соответствующего критического значения. Этот процесс, оказавшийся в значительной степени универсальным, может объяснить, в частности, возникновение турбулентности. Здесь исследование свойств бифуркации удвоения периода производится на примере простой нелинейной функции

где А управляющий параметр. Вместо изменения непрерывной функции  рассматривается соответствующий ей дискретный
рассматривается соответствующий ей дискретный
процесс, описываемый последовательностью итераций, называемой одномерным отображением Пуанкаре:

Значение  называется неподвижной тонкой отображения, если выполняется условие
называется неподвижной тонкой отображения, если выполняется условие

При любом значении А точка  является неподвижной. Другая неподвижная точка определяется корнем уравнения (15.1):
является неподвижной. Другая неподвижная точка определяется корнем уравнения (15.1): 

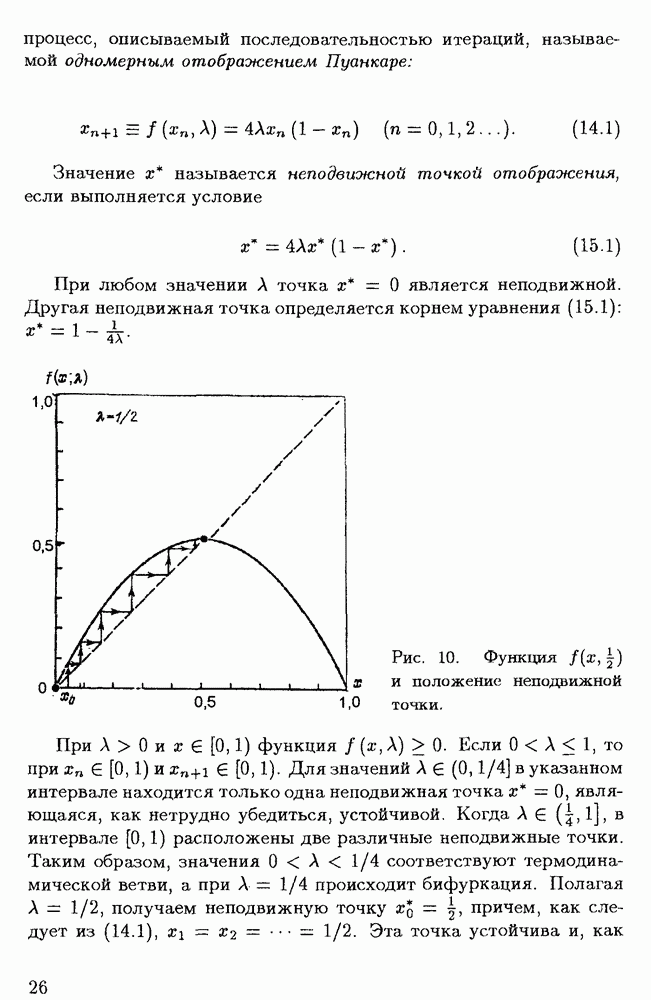
Рис. 10. Функция  и положение неподвижной точки.
и положение неподвижной точки.
При  функция
функция  Если
Если  то при
то при  . Для значений
. Для значений  в указанном интервале находится только одна неподвижная точка
в указанном интервале находится только одна неподвижная точка  являющаяся, как нетрудно убедиться, устойчивой. Когда
являющаяся, как нетрудно убедиться, устойчивой. Когда  в интервале [0,1) расположены две различные неподвижные точки. Таким образом, значения
в интервале [0,1) расположены две различные неподвижные точки. Таким образом, значения  соответствуют термодинамической ветви, а при
соответствуют термодинамической ветви, а при  происходит бифуркация. Полагая
происходит бифуркация. Полагая  получаем неподвижную точку
получаем неподвижную точку  причем, как следует из (14.1),
причем, как следует из (14.1),  Эта точка устойчива и, как
Эта точка устойчива и, как
иллюстрируется рис. 10, является аттрактором. Итерации от любой точки  приводят к точке
приводят к точке  тем самым демонстрируя ее устойчивость.
тем самым демонстрируя ее устойчивость.
Заметим, что функция  имеет единственный максимум, причем в точке
имеет единственный максимум, причем в точке 
Для устойчивой неподвижной точки итерационное поведение статично и может рассматриваться как периодическое с периодом 1.
Условие устойчивости в неподвижной точке в аналитической форме имеет вид

а неустойчивой точка получается, если

Из условий (16.1) и (17.1) видно, что точка  является неустойчивой, а точка
является неустойчивой, а точка  устойчивой.
устойчивой.
Обобщая (16.1), при любом А для условия устойчивости точки  имеем
имеем

а согласно условию (17.1) в случае, когда

точка неустойчива.
Если  точка
точка  является неустойчивой. Другая точка
является неустойчивой. Другая точка  остается устойчивой, однако по (19.1) при
остается устойчивой, однако по (19.1) при  и она становится неустойчивой. Таким образом, значение
и она становится неустойчивой. Таким образом, значение  оказывается критическим. Покажем, что при
оказывается критическим. Покажем, что при  вместо устойчивого цикла с периодом 1 присутствует устойчивый цикл
вместо устойчивого цикла с периодом 1 присутствует устойчивый цикл  периодом 2, поскольку возникли две устойчивые неподвижные точки.
периодом 2, поскольку возникли две устойчивые неподвижные точки.
Из соотношения (14.1) следует, что

Все неподвижные точки для  являются также неподвижными точками для
являются также неподвижными точками для  Кроме того,
Кроме того,  так же как и
так же как и  симметрична относительно
симметрична относительно 
Пусть

Для производных имеет место соотношение

Если 

При  абсолютная величина производной
абсолютная величина производной  и поэтому
и поэтому  Так как
Так как  то при
то при  производная
производная  имеет экстремум (минимум). В двух симметричных относительно минимума точках
имеет экстремум (минимум). В двух симметричных относительно минимума точках  отображающихся в
отображающихся в  функция
функция  имеет максимум (поскольку при
имеет максимум (поскольку при  величины
величины  то и
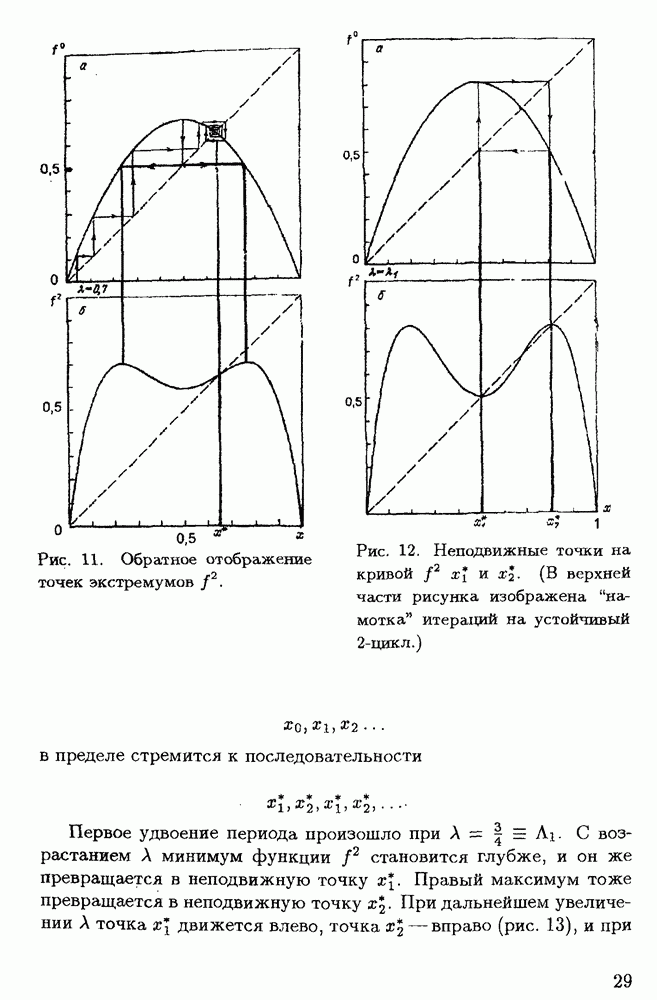
то и  Обратное отображение представлено на рис. 11. Положение точек экстремумов
Обратное отображение представлено на рис. 11. Положение точек экстремумов  определено путем обратного отображения их в точку
определено путем обратного отображения их в точку  на кривой
на кривой  (Отображение представлено жирными линиями при противоположном направлении стрелок.).
(Отображение представлено жирными линиями при противоположном направлении стрелок.).
Двузначность обратного отображения является следствием наличия максимума у функции 
Когда  то вместо неподвижной (при
то вместо неподвижной (при  точки
точки  существуют две новые неподвижные точки
существуют две новые неподвижные точки  на кривой
на кривой  (рис. 12), но они не являются неподвижными точками для
(рис. 12), но они не являются неподвижными точками для 
Неподвижная точка  теперь не является таковой ни для
теперь не является таковой ни для  ни для
ни для  так как
так как 
Поскольку имеют место соотношения

то возникает двойной цикл. В этих точках  т. е. они устойчивы, причем величина производной
т. е. они устойчивы, причем величина производной  в точках
в точках  одинакова. Таким путем образовался аттрактор — устойчивый цикл с периодом 2. Любая последовательность итераций
одинакова. Таким путем образовался аттрактор — устойчивый цикл с периодом 2. Любая последовательность итераций

Рис. 11. Обратное отображение точек экстремумов 

Рис. 12. Неподвижные точки на кривой  . (В верхней части рисунка изображена "намотка" итераций на устойчивый
. (В верхней части рисунка изображена "намотка" итераций на устойчивый  -цикл.)
-цикл.)

в пределе стремится к последовательности

Первое удвоение периода произошло при  . С возрастанием
. С возрастанием  минимум функции
минимум функции  становится глубже, и он же превращается в неподвижную точку
становится глубже, и он же превращается в неподвижную точку  Правый максимум тоже превращается в неподвижную точку
Правый максимум тоже превращается в неподвижную точку  При дальнейшем увеличении А точка
При дальнейшем увеличении А точка  движется влево, точка
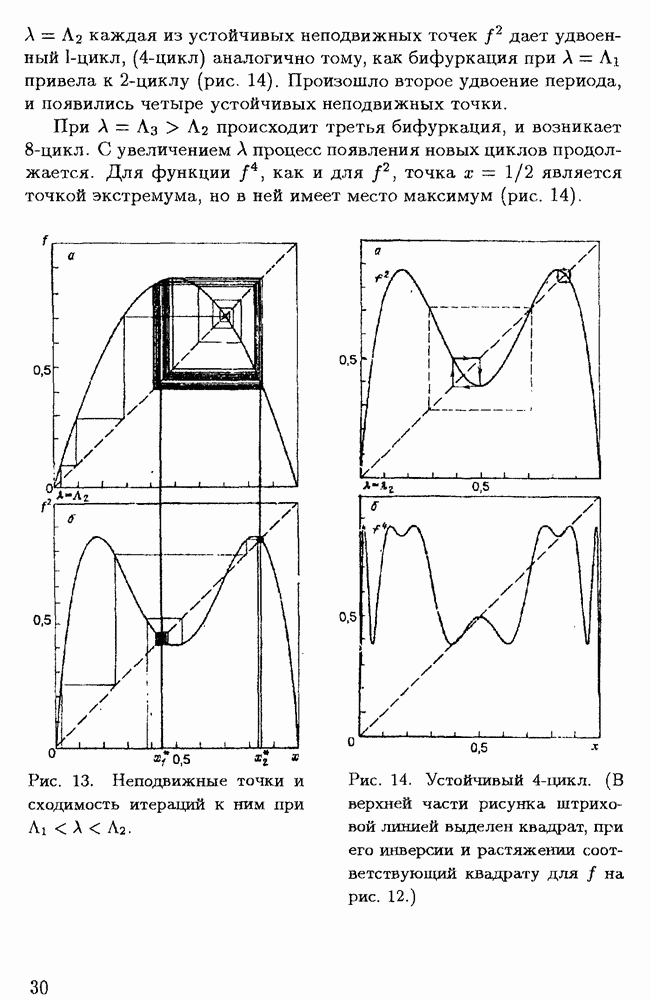
движется влево, точка  — вправо (рис. 13), и при
— вправо (рис. 13), и при
 каждая из устойчивых неподвижных точек
каждая из устойчивых неподвижных точек  дает удвоенный
дает удвоенный  -цикл,
-цикл,  -цикл) аналогично тому, как бифуркация при
-цикл) аналогично тому, как бифуркация при  привела к
привела к  -циклу (рис. 14). Произошло второе удвоение периода, и появились четыре устойчивых неподвижных точки.
-циклу (рис. 14). Произошло второе удвоение периода, и появились четыре устойчивых неподвижных точки.
При  происходит третья бифуркация, и возникает
происходит третья бифуркация, и возникает  -цикл. С увеличением А процесс появления новых циклов продолжается. Для функции
-цикл. С увеличением А процесс появления новых циклов продолжается. Для функции  как и для
как и для  точка
точка  является точкой экстремума, но в ней имеет место максимум (рис. 14).
является точкой экстремума, но в ней имеет место максимум (рис. 14).

Рис. 13. Неподвижные точки и сходимость итераций к ним при 

Рис. 14. Устойчивый  -цикл. (В верхней части рисунка штриховой линией выделен квадрат, при его инверсии и растяжении соответствующий квадрату для
-цикл. (В верхней части рисунка штриховой линией выделен квадрат, при его инверсии и растяжении соответствующий квадрату для  на рис. 12.)
на рис. 12.)
Операция последовательного удвоения периода при  обозначается следующим образом:
обозначается следующим образом:

т. е. результат ее действия на  при
при  заключается в появлении функции
заключается в появлении функции  для значений
для значений  лежащих в интервале
лежащих в интервале 
Функция  входящая в (20.1), рассматривается лишь в интервале, включающем ближайшую к
входящая в (20.1), рассматривается лишь в интервале, включающем ближайшую к  неподвижную точку, и ширина этого интервала уменьшается с возрастанием А. Часть
неподвижную точку, и ширина этого интервала уменьшается с возрастанием А. Часть  образующая эту область, постепенно сжимается в малую область вблизи
образующая эту область, постепенно сжимается в малую область вблизи  (рис. 14). Поведение
(рис. 14). Поведение  вдали от
вдали от  (точки максимума) не сказывается на свойствах итерации, приводящих к удвоению периода, и поэтому при больших значениях
(точки максимума) не сказывается на свойствах итерации, приводящих к удвоению периода, и поэтому при больших значениях  итерации для всех гладких функций с квадратичным максимумом
итерации для всех гладких функций с квадратичным максимумом  одинаковы.
одинаковы.
Действующая на функции операция имеет устойчивую неподвижную точку в пространстве функций.
Сжатие масштаба при переходе от  -цикла к
-цикла к  -циклу таково, что в пределе при больших
-циклу таково, что в пределе при больших  расстояние
расстояние  от точки
от точки  до ближайшей к ней неподвижной точки при удвоении периода становится меньше приблизительно в
до ближайшей к ней неподвижной точки при удвоении периода становится меньше приблизительно в  раз:
раз:

Путем численного интегрирования было установлено, что  для любой функции, испытывающей удвоение периода. Поскольку при каждом удвоении ближайшая к
для любой функции, испытывающей удвоение периода. Поскольку при каждом удвоении ближайшая к  неподвижная точка (элемент аттрактора) перемещается с одной стороны точки
неподвижная точка (элемент аттрактора) перемещается с одной стороны точки  на другую, то
на другую, то 
Для отображений с бесконечным удвоением периода есть еще одно универсальное соотношение. Если  — значения А, соответствующие последовательным бифуркациям удвоения периода, и
— значения А, соответствующие последовательным бифуркациям удвоения периода, и

то

Величина а задает масштаб преобразования ("скейлинг"). Пусть функция  определенная на промежутке [0,1), имеет квадратичный максимум, равный 1 при
определенная на промежутке [0,1), имеет квадратичный максимум, равный 1 при  и симметрична относительно этой точки. Смещая координаты так, что
и симметрична относительно этой точки. Смещая координаты так, что  переходит в
переходит в  и изменяя масштаб в а раз, получаем функциональное уравнение, определяющее а вместе с
и изменяя масштаб в а раз, получаем функциональное уравнение, определяющее а вместе с 

Считая  получаем, что
получаем, что  уравнения (21.1) существует единственное гладкое решение [19], соответствующее указанному выше значению а. [19]. Приведенные значения
уравнения (21.1) существует единственное гладкое решение [19], соответствующее указанному выше значению а. [19]. Приведенные значения  носят название "числа Фейгенбаума".
носят название "числа Фейгенбаума".
Из вида уравнения (21.1) следует, что операция удвоения периода состоит в композиции функций с последующим растяжением в пространстве состояний. Отображение (14.1) соответствует одномерному пространству состояний.
Усложнение аттрактора, возникающего при последовательном удвоении периода, продолжается с возрастанием  Он состоит из все увеличивающегося число неподвижных точек, однако остающегося даже при
Он состоит из все увеличивающегося число неподвижных точек, однако остающегося даже при  счетным множеством. При
счетным множеством. При  где
где  поведение системы предсказуемо. Однако когда
поведение системы предсказуемо. Однако когда  - движение непериодическое, аттрактор является странным и имеет место хаос (в определенном выше смысле).
- движение непериодическое, аттрактор является странным и имеет место хаос (в определенном выше смысле).
Итерации и процесс бесконечного удвоения периода возможны также в  -мерном пространстве. Соответственно уравнение (21.1) должно быть модифицировано и будет содержать композицию функций, зависящих от
-мерном пространстве. Соответственно уравнение (21.1) должно быть модифицировано и будет содержать композицию функций, зависящих от  переменных. Отображение для диссипативного процесса является сжимающим, но по одному из направлений в пространстве сжатие более медленное, чем по другим. Процесс становится близким к одномерному, и поэтому решение уравнения (21.1) представляет неподвижную точку
переменных. Отображение для диссипативного процесса является сжимающим, но по одному из направлений в пространстве сжатие более медленное, чем по другим. Процесс становится близким к одномерному, и поэтому решение уравнения (21.1) представляет неподвижную точку  -мерного уравнения.
-мерного уравнения.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
- § 1.4. Бифуркация удвоения периода
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение