| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
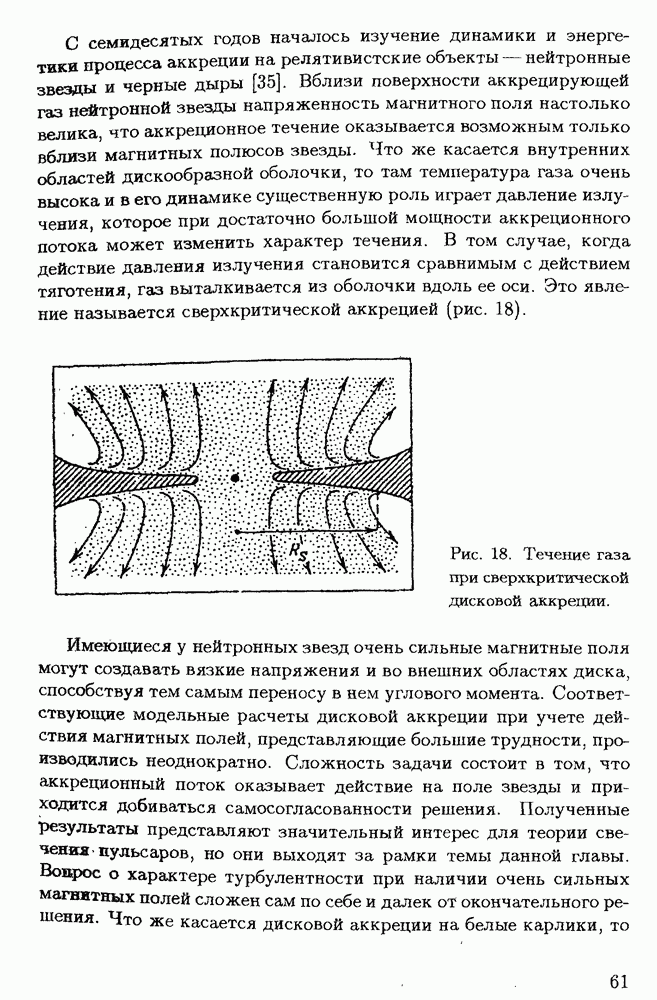
§ 3.3. Нелинейная модель конвекции Рэлея-Бенара
Условие наступления конвекции  было получено в предыдущем параграфе. Здесь на основе уже приведенных результатов рассматривается приближенная модель конвекции, в которой учитывается нелинейность уравнений, описывающих процесс, принадлежащая Лоренцу [30]. Поскольку для такого исследования необходимо применение численных методов, то используются уравнения гидродинамики в безразмерном виде.
было получено в предыдущем параграфе. Здесь на основе уже приведенных результатов рассматривается приближенная модель конвекции, в которой учитывается нелинейность уравнений, описывающих процесс, принадлежащая Лоренцу [30]. Поскольку для такого исследования необходимо применение численных методов, то используются уравнения гидродинамики в безразмерном виде.
Примем в качестве масштаба длины толщину слоя жидкости  за масштаб времени —
за масштаб времени —  Соответственно масштабом скорости служит величина
Соответственно масштабом скорости служит величина  и масштабом давления — величина
и масштабом давления — величина  . В качестве масштаба температуры принято произведение
. В качестве масштаба температуры принято произведение  где А определено согласно формуле (18.3). Система безразмерных уравнений при таком выборе масштабов имеет вид
где А определено согласно формуле (18.3). Система безразмерных уравнений при таком выборе масштабов имеет вид

где 
В приведенной системе через 9 обозначено значение избытка температуры по отношению к значению температуры в данной точке, соответствующему стационарной конвекции, т. е. в — в обозначениях предыдущего параграфа. Как скорость  так и в являются функциями времени:
так и в являются функциями времени:

Расчет изменения состояния системы со временем, т.е. определение ее траектории в фазовом пространстве путем решения системы (30.3) — (32.3), представляет большие трудности даже при использовании численных методов. Уравнения приходится упрощать ("обрезать"), сохраняя, по возможности, их нелинейность. При упрощении не должно изменяться физическое содержание задачи (в частности, нарушаться законы сохранения). Кроме того, следует избегать введения особенностей, приводящих к расходимости функций.
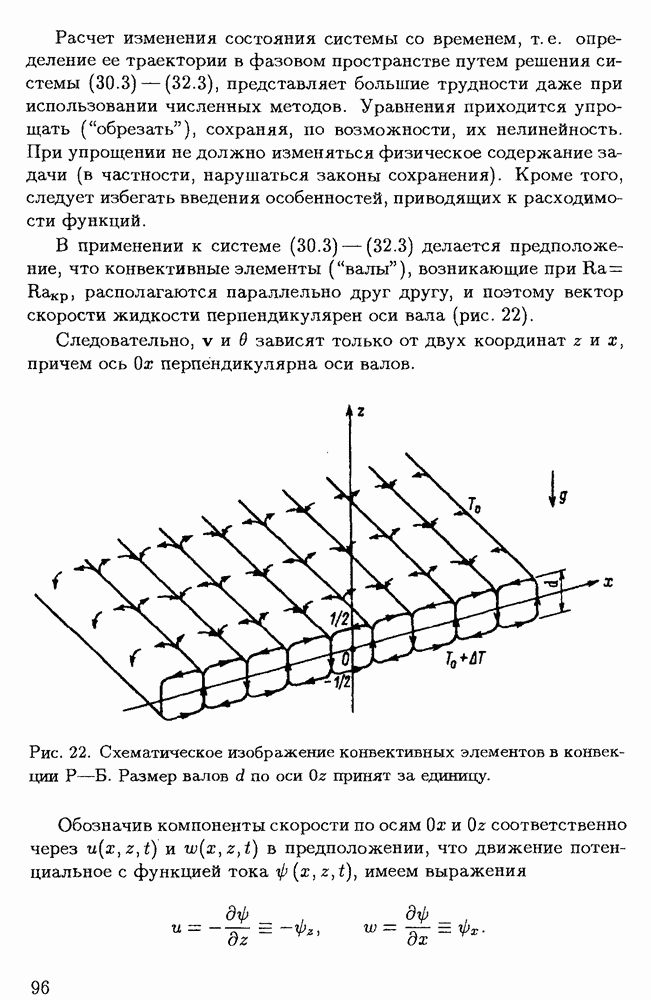
В применении к системе (30.3) — (32.3) делается предположение, что конвективные элементы ("валы"), возникающие при  располагаются параллельно друг другу, и поэтому вектор скорости жидкости перпендикулярен оси вала (рис. 22).
располагаются параллельно друг другу, и поэтому вектор скорости жидкости перпендикулярен оси вала (рис. 22).
Следовательно,  и в зависят только от двух координат
и в зависят только от двух координат  их, причем ось
их, причем ось  перпендикулярна оси валов.
перпендикулярна оси валов.

Рис. 22. Схематическое изображение конвективных элементов в конвекции  Размер валов
Размер валов  по оси
по оси  принят за единицу.
принят за единицу.
Обозначив компоненты скорости по осям  соответственно через
соответственно через  в предположении, что движение потенциальное с функцией тока
в предположении, что движение потенциальное с функцией тока  имеем выражения
имеем выражения

Одно из условий, налагаемых на поле скоростей, состоит в том, что поток жидкости через границы  равен нулю. Это условие выражается соотношениями
равен нулю. Это условие выражается соотношениями

Другим условием является отсутствие сдвиговых напряжений на границах (считаемых свободными). Так как это напряжение пропорционально градиенту скорости, то указанное условие записывается в следующем виде:

Оба условия выполняются, если имеют место равенства

Соотношения (33.3) и (34.3) выполняются, в частности, для функции  имеющей вид
имеющей вид

Множитель  обеспечивает воспроизведение системы валов вдоль оси
обеспечивает воспроизведение системы валов вдоль оси  (периодичность по
(периодичность по  . В модели Лоренца функция (35.3) используется для представления поля скоростей. Величины
. В модели Лоренца функция (35.3) используется для представления поля скоростей. Величины  определяются при этом соотношениями
определяются при этом соотношениями

Записывая векторное уравнение (30.3) в компонентах, имеем

Вычисление величины — при учете равенства

приводит к следующему уравнению:

При выборе модельного выражения для функции в следует иметь в виду, что изменение в связано с изменениями скорости и поэтому периодичность в по  предполагается такой же, как для скорости
предполагается такой же, как для скорости  Кроме того, отклонение температуры на граничных поверхностях предполагается равным нулю, что выражается равенствами
Кроме того, отклонение температуры на граничных поверхностях предполагается равным нулю, что выражается равенствами

Из указанных соображений функция  принимается в таком виде:
принимается в таком виде:

Введение второго слагаемого в правую часть (39.3) оказывается необходимым для сохранения нелинейности в уравнении (32.3).
Подстановка в уравнение (38.3) выражений  и (39.3) превращает его в следующее линейное уравнение для функции
и (39.3) превращает его в следующее линейное уравнение для функции 

Нелинейность в уравнении (30.3) исчезла благодаря специфической форме выбранных для  и в выражений. Однако нелинейность уравнения (32.3) сохраняется. Соответствующий нелинейный член
и в выражений. Однако нелинейность уравнения (32.3) сохраняется. Соответствующий нелинейный член  в записывается в виде
в записывается в виде

Используя в уравнении (32.3) выражение (41.3) и пренебрегая членом, содержащим  имеем
имеем

Поскольку функции  линейно независимы, равенство (42.3) удовлетворяется при условии, что оба выражения, содержащиеся в фигурных скобках, равны нулю. Отсюда получаются уравнения
линейно независимы, равенство (42.3) удовлетворяется при условии, что оба выражения, содержащиеся в фигурных скобках, равны нулю. Отсюда получаются уравнения

Таким путем выведена система трех дифференциальных уравнений (40.3), (43.3) и (44.3), определяющих функции  Система преобразуется в более компактную путем замены переменных
Система преобразуется в более компактную путем замены переменных

и введения параметров

Получаемая таким способом система уравнений, описывающих эволюцию модели Лоренца, имеет следующий вид:

Управляющим параметром является  Можно показать, что ни одно из решений системы (45.3) не обращается в бесконечность. Кроме того, занимаемый системой объем в фазовом пространстве (
Можно показать, что ни одно из решений системы (45.3) не обращается в бесконечность. Кроме того, занимаемый системой объем в фазовом пространстве ( со временем сокращается. Это следует из соотношения, получаемого непосредственно из (45.3):
со временем сокращается. Это следует из соотношения, получаемого непосредственно из (45.3):

которое определяет зависимость объема  занимаемого системой, от времени:
занимаемого системой, от времени:

Волновое число валов  определяется путем линеаризации системы уравнений, так как валы возникают в результате потери устойчивости слоем жидкости, находившимся в механическом равновесии, в котором передача тепловой энергии происходила лишь путем теплопроводности. В таком состоянии
определяется путем линеаризации системы уравнений, так как валы возникают в результате потери устойчивости слоем жидкости, находившимся в механическом равновесии, в котором передача тепловой энергии происходила лишь путем теплопроводности. В таком состоянии

Линеаризованная система при этих условиях имеет вид

Величина  затухающая, так как
затухающая, так как  Дисперсионное соотношение, позволяющее найти значение параметра
Дисперсионное соотношение, позволяющее найти значение параметра  при котором наступает неустойчивость, получается из первых двух уравнений системы (46.3), где принято
при котором наступает неустойчивость, получается из первых двух уравнений системы (46.3), где принято

Это соотношение имеет следующую форму:

При  один из корней уравнения (47.3) является положительным, что свидетельствует о возрастании возмущений
один из корней уравнения (47.3) является положительным, что свидетельствует о возрастании возмущений  и
и  со временем. Поэтому неустойчивость имеет место при значениях числа Рэлея, удовлетворяющих неравенству
со временем. Поэтому неустойчивость имеет место при значениях числа Рэлея, удовлетворяющих неравенству

Правая часть этого неравенства минимальна, когда  Соответственно значение
Соответственно значение  равно
равно  что совпадает с результатом линейного анализа (§ 3.2). При этом значении
что совпадает с результатом линейного анализа (§ 3.2). При этом значении  параметр
параметр 
Возможны два разных направления движения жидкости внутри конвективного элемента (вала). Поэтому можно говорить о происходящей при  бифуркации. Вместо одного устойчивого состояния, в котором скорость движения жидкости равна нулю, появляются два устойчивых состояния с отличными от нуля и противоположными по направлению скоростями. Модель Лоренца демонстрирует наличие двух состояний, поскольку при
бифуркации. Вместо одного устойчивого состояния, в котором скорость движения жидкости равна нулю, появляются два устойчивых состояния с отличными от нуля и противоположными по направлению скоростями. Модель Лоренца демонстрирует наличие двух состояний, поскольку при 

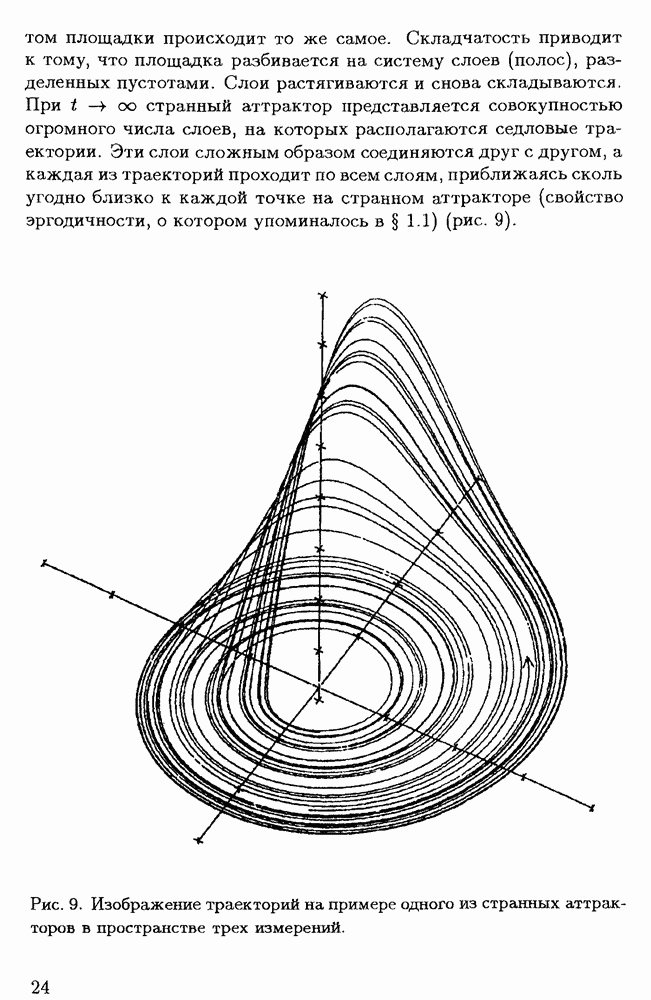
Дальнейшее исследование зависимости решения от управляющего параметра  производится численными методами. Именно таким путем Лоренц впервые в 1963 г. обнаружил существование аттракторов особого вида, впоследствии получивших название "странных" [30]. Решение системы производилось при значениях
производится численными методами. Именно таким путем Лоренц впервые в 1963 г. обнаружил существование аттракторов особого вида, впоследствии получивших название "странных" [30]. Решение системы производилось при значениях  Странный аттрактор появляется, когда
Странный аттрактор появляется, когда  возрастает до значения
возрастает до значения  и существует до того момента, когда
и существует до того момента, когда  . В интервале значений
. В интервале значений  происходит чередование хаотических и периодических решений (существуют "окна периодичности").
происходит чередование хаотических и периодических решений (существуют "окна периодичности").
Конвекция Рэлея-Бенара не только служит примером образования структур в первоначально равновесной в механическом отношении жидкости. Она выделяется и тем, что в образовании структур не принимают участия внешние механические факторы, что имеет место, например, в течении Куэтта. Таким образом, при конвекции  происходит самоорганизация системы.
происходит самоорганизация системы.
Корреляционная длина при конвективном движении порядка размеров конвективного элемента, тогда как в отсутствие конвекции  корреляционная длина того же порядка, что и межмолекулярные расстояния. Естественно поставить вопрос о том, что понимать под упорядоченностью. Неустойчивость может привести в некотором смысле к упорядоченности движения.
корреляционная длина того же порядка, что и межмолекулярные расстояния. Естественно поставить вопрос о том, что понимать под упорядоченностью. Неустойчивость может привести в некотором смысле к упорядоченности движения.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
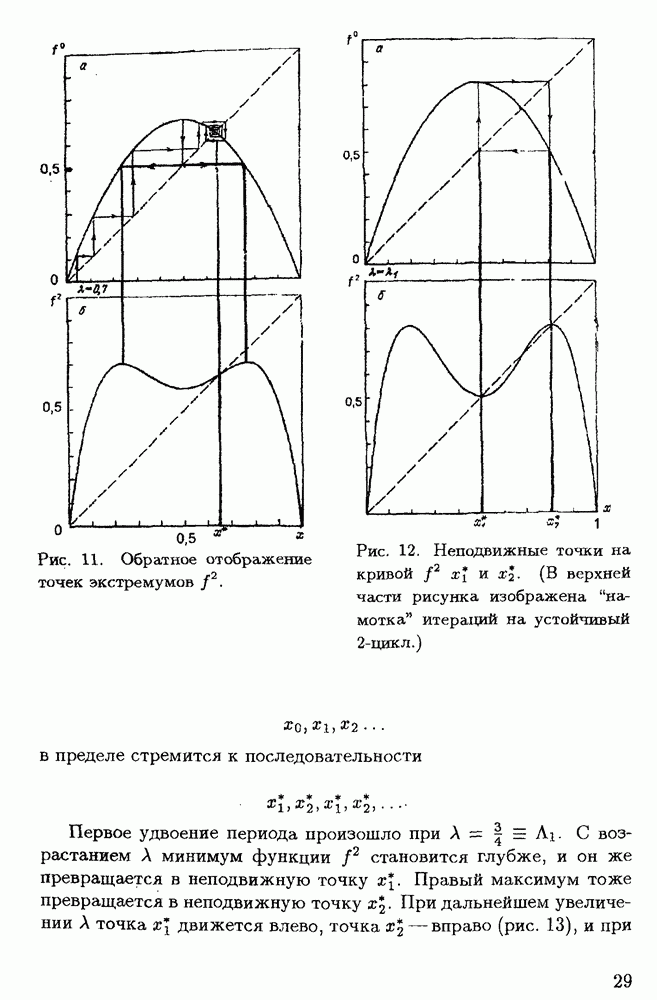
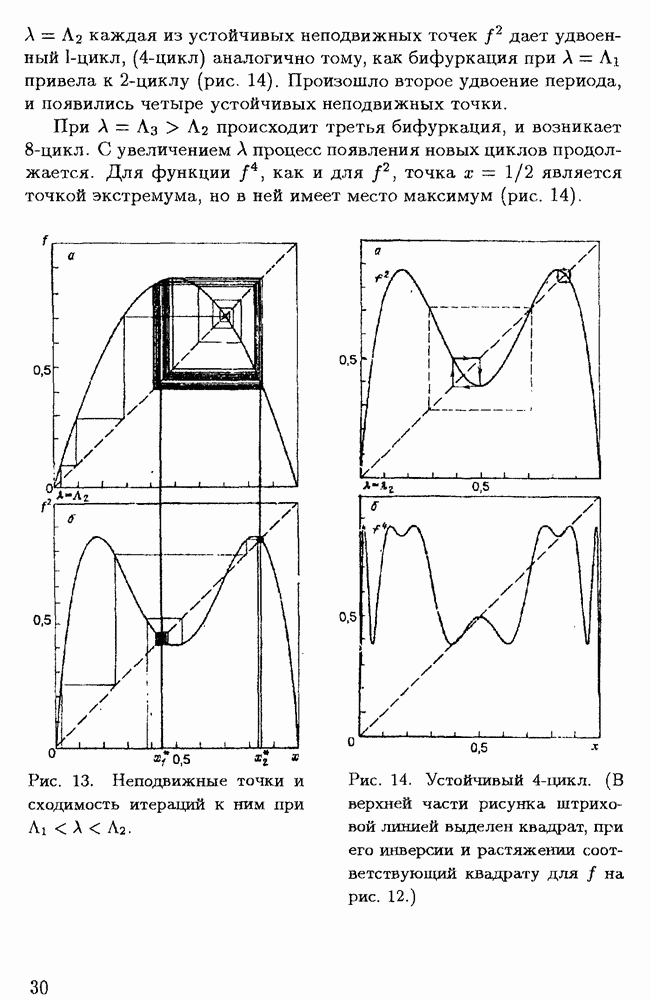
- § 1.4. Бифуркация удвоения периода
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение