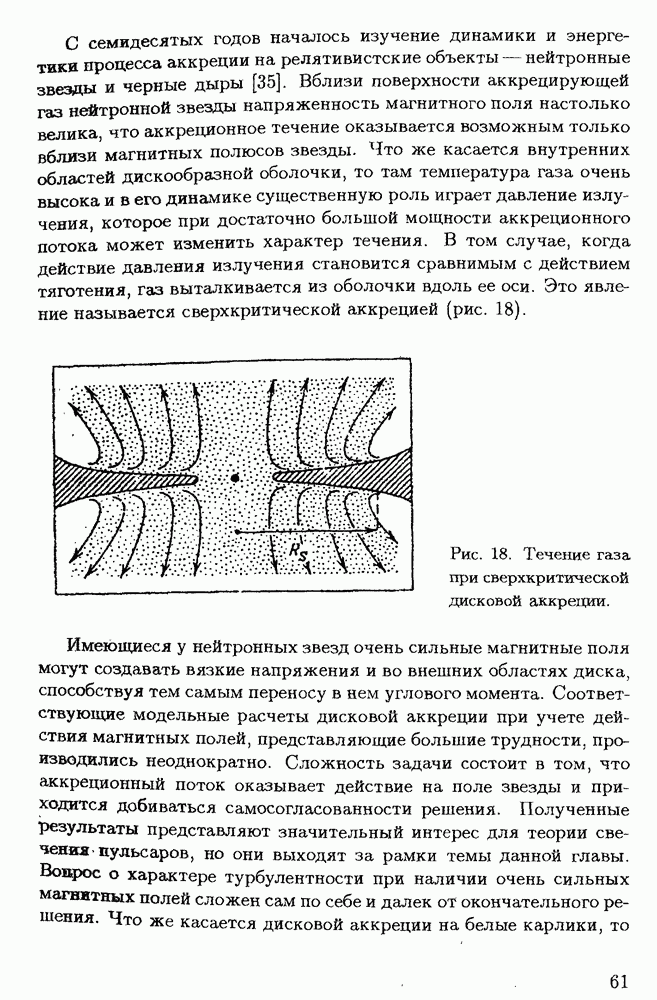
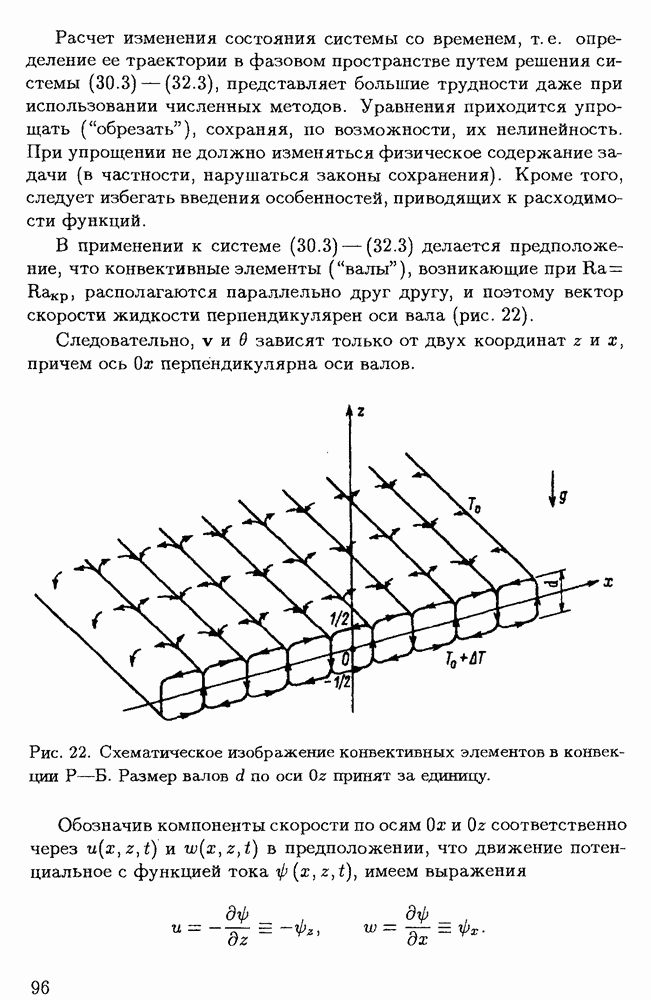
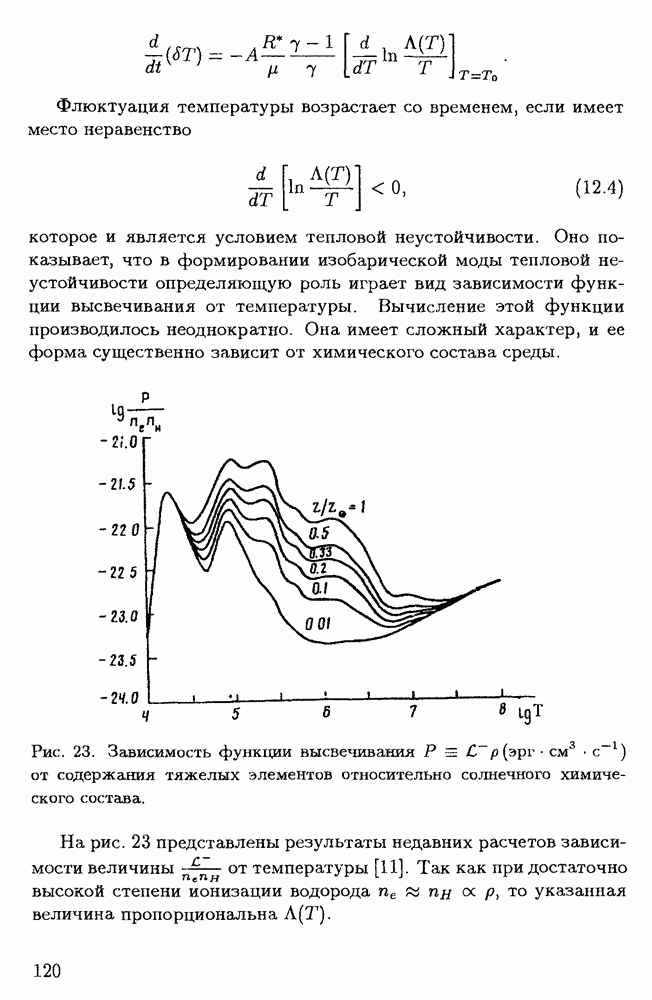
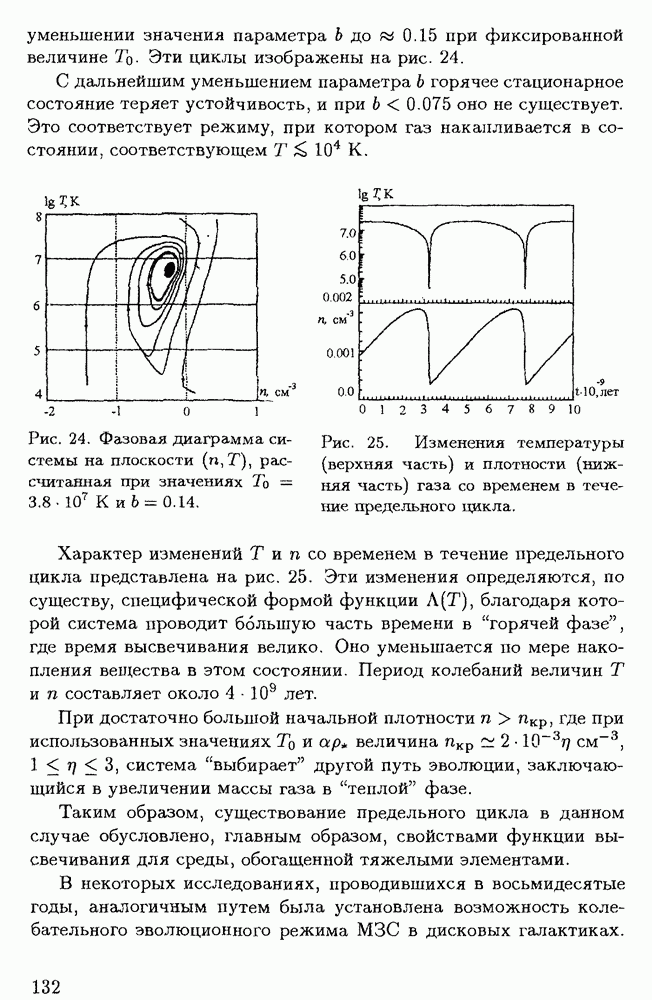
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4.2. Тепловая неустойчивость неравновесных систем
Локальный критерий тепловой неустойчивости, выведенный в § 4.1, имеет ограниченную область применимости. Многие из реально существующих газовых систем неоднородны и находятся в нестационарном состоянии. Для исследования тепловой устойчивости таких систем и получения соответствующего критерия в работе [12] был использован метод Ляпунова (§ 1.3). В качестве функции Ляпунова в соответствии с монографией [3] принималась величина производства энтропии, определяемая для однородной среды выражением (36.1). В [12] этот подход применялся для изучения устойчивости систем, в которых имеются объемные источники и стоки энергии. Для того чтобы можно было пользоваться термодинамическим описанием системы, она предполагается находящейся в состоянии локального термодинамического равновесия 
Энтропия системы выражается следующим образом:

Величина представляет собой приток тепловой энергии через границу системы и поэтому зависит от условий на границе. В случае, когда система изолирована,  Выделение энергии в системе в результате необратимых процессов учтено величиной Присутствие объемных источников энергии определяется слагаемым
Выделение энергии в системе в результате необратимых процессов учтено величиной Присутствие объемных источников энергии определяется слагаемым 
Изменение энтропии выражается равенством

где  энтропии через границу системы, а остальные два слагаемых обусловлены величинами
энтропии через границу системы, а остальные два слагаемых обусловлены величинами 
Поскольку система предполагается неоднородной, сначала вводится удельная энтропия  зависящая от условий в элементарном объеме. Величину второго дифференциала
зависящая от условий в элементарном объеме. Величину второго дифференциала  можно выразить формулой, аналогичной (36.1):
можно выразить формулой, аналогичной (36.1):

При  правая часть выражения (14.4) является, как и в (36.1), отрицательно определенной квадратичной формой величин
правая часть выражения (14.4) является, как и в (36.1), отрицательно определенной квадратичной формой величин  и 8 Считая ее коэффициенты фиксированными при
и 8 Считая ее коэффициенты фиксированными при  имеем равенство
имеем равенство

где  удельная внутренняя энергия, а значения
удельная внутренняя энергия, а значения  принимаются при
принимаются при  По теореме Ляпунова локальное достаточное условие устойчивости системы относительно малых флюктуаций
По теореме Ляпунова локальное достаточное условие устойчивости системы относительно малых флюктуаций  имеет вид
имеет вид

Соответствующее условие для всей системы в целом получается следующим образом [12]:

где  определено путем интегрирования
определено путем интегрирования  по объему системы:
по объему системы:

В производную по времени от  входит величина производства избыточной энтропии за единицу времени в результате необратимых процессов.
входит величина производства избыточной энтропии за единицу времени в результате необратимых процессов.
Посредством выражения (15.4) исследовалась тепловая неустойчивость межзвездной среды в нестационарных условиях. Предполагается, что она состоит из идеального газа и ее температура позволяет пренебречь эффектами, связанными с ионизацией атомов. Рассматриваются однородные по температуре и плотности состояния при отсутствии крупномасштабных движений.
В данном случае изменение энергии в элементе определяется притоком ее от источников и высвечиванием. Совокупное действие этих факторов описывается функцией  На изменение энергии газа влияет также и теплопроводность.
На изменение энергии газа влияет также и теплопроводность.
Используя выражение для потока энергии, обусловленного теплопроводностью

получаем для слагаемых, входящих в (13.4), выражения

где  объем системы и
объем системы и  поверхность, ее ограничивающая.
поверхность, ее ограничивающая.
Рассматривая малые изобарические возмущения и учитывая (10.4), из (14.4) имеем соотношение

Для производной от  по времени используется соотношение, следующее из (13.4) и (10.4):
по времени используется соотношение, следующее из (13.4) и (10.4):

При отсутствии возмущений температуры на границе системы (это означает, что  и при учете выражения
и при учете выражения

находится величина  и соответствующее (15.4) условие устойчивости
и соответствующее (15.4) условие устойчивости

В случае малых адиабатических возмущений, когда

при отличной от нуля скорости и, что соответствует наличию конвекции, а также  в работе [12] найдено условие устойчивости
в работе [12] найдено условие устойчивости

Для равновесных систем  и по условиям неравенств (16.4) и (17.4) получаются те же критерии неустойчивости, которые находятся методом малых возмущений, но для более общего случая — с учетом потока энергии через границу. По отношению к изобарическим возмущениям система неустойчива, если
и по условиям неравенств (16.4) и (17.4) получаются те же критерии неустойчивости, которые находятся методом малых возмущений, но для более общего случая — с учетом потока энергии через границу. По отношению к изобарическим возмущениям система неустойчива, если

а по отношению к адиабатическим — при условии

Длина волны изобарических неустойчивых возмущений находится в пределах

где  величины, определенные выше (§ 4.1).
величины, определенные выше (§ 4.1).
Внешнее гравитационное поле существенно влияет на характер тепловой неустойчивости. В этом случае стационарная среда не может быть однородной по плотности и температуре — она стратифицирована, так как тяготение должно уравновешиваться градиентом давления. Для стационарности среды необходимо одновременное выполнение условий гидростатического и теплового равновесия. Тепловая неустойчивость в слое газа, находящемся в однородном поле тяготения, приводит к возникновению конвекции. Это было показано в работе [22] следующим образом. Рассматривается движение некоторого объема газа ("пакета"), характеризующегося
значениями  отличающимися от соответствующих термодинамических величин
отличающимися от соответствующих термодинамических величин  в окружающей среде, и находится условие неустойчивости этого движения. Уравнение энергии для пакета при выполнении условия
в окружающей среде, и находится условие неустойчивости этого движения. Уравнение энергии для пакета при выполнении условия

и малости разностей  и
и  имеет вид
имеет вид

Пакет движется в поле тяготения с ускорением  под действием силы плавучести в вертикальном направлении со скоростью
под действием силы плавучести в вертикальном направлении со скоростью  Уравнение его движения записывается следующим образом:
Уравнение его движения записывается следующим образом:

Так как имеют место соотношения

то из (20.4) при учете уравнения состояния газа и при использовании соотношений (19.4) и (21.4) выводится уравнение

Полагая в  для величины
для величины  имеем выражение
имеем выражение

где

При  из (23.4) получается критерий тепловой неустойчивости (18.4). Если же
из (23.4) получается критерий тепловой неустойчивости (18.4). Если же  то монотонный рост
то монотонный рост  со временем происходит при условии
со временем происходит при условии

совпадающем с критерием, конвективной неустойчивости (7.3). Когда  и имеет место неравенство, противоположное (24.4), то происходят колебания пакета. При
и имеет место неравенство, противоположное (24.4), то происходят колебания пакета. При  величина
величина  монотонно возрастает, если выполняется неравенство
монотонно возрастает, если выполняется неравенство

Таким образом, условия конвективной неустойчивости и тепловой неустойчивости оказываются связанными между собой.
В работе [12] аналогичные выводы о характере неустойчивости газа в поле тяготения сделаны посредством найденного там же интегрального соотношения, дающего критерий тепловой неустойчивости при скорости движения  Решение задачи об эволюции малых возмущений производилось в приближении Буссинеска, т. е. сжимаемость газа в уравнении неразрывности не учитывалась. Полученные термодинамическое и гидродинамическое условия неустойчивости имеют вид
Решение задачи об эволюции малых возмущений производилось в приближении Буссинеска, т. е. сжимаемость газа в уравнении неразрывности не учитывалась. Полученные термодинамическое и гидродинамическое условия неустойчивости имеют вид

Здесь  -толщина слоя, и усреднение производится по горизонтальной плоскости
-толщина слоя, и усреднение производится по горизонтальной плоскости  -среднее по шкале высот
-среднее по шкале высот
значение плотности среды,  - соответствующее значение теплопроводности и
- соответствующее значение теплопроводности и  - компонента скорости в направлении, перпендикулярном слою. Из соотношений (26.4) видно, что неустойчивость развивается в форме конвекции, которая связана с одновременным уменьшением избыточной энтропии в системе, следующим из неравенства (25.4).
- компонента скорости в направлении, перпендикулярном слою. Из соотношений (26.4) видно, что неустойчивость развивается в форме конвекции, которая связана с одновременным уменьшением избыточной энтропии в системе, следующим из неравенства (25.4).
При учете диссипативных процессов в газе критерий его тепловой неустойчивости изменяется. Вязкость, как и теплопроводность, оказывает стабилизирующее воздействие на газ, делая его более устойчивым относительно коротковолновых возмущений
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
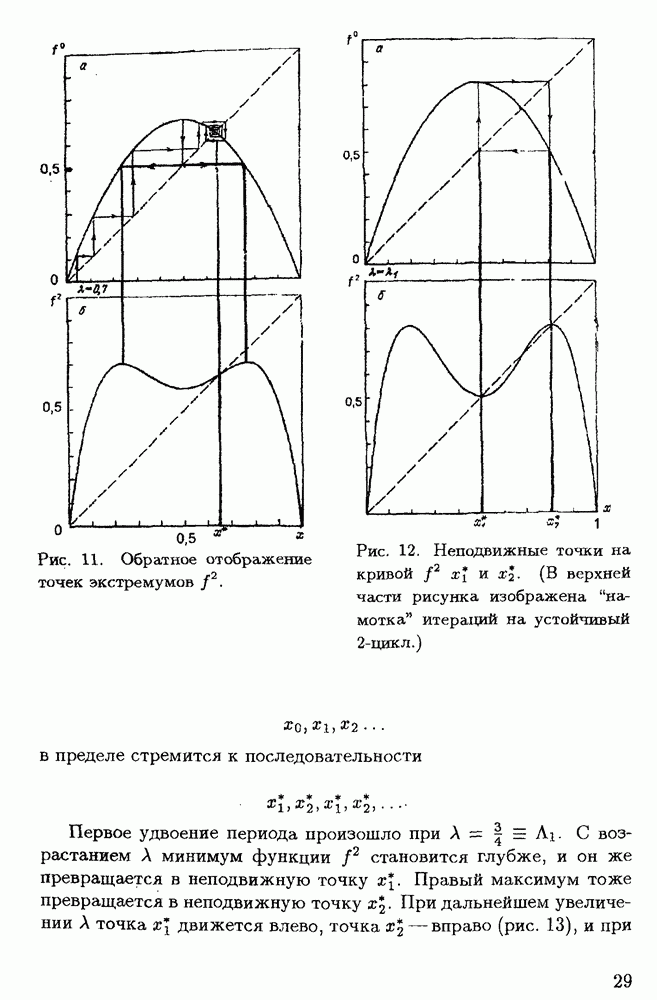
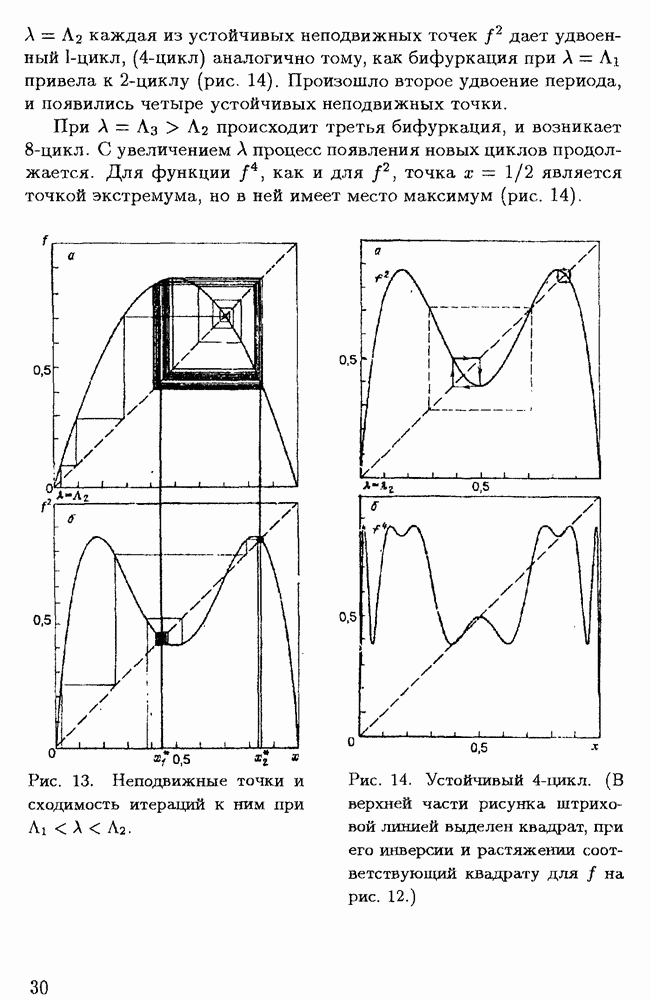
- § 1.4. Бифуркация удвоения периода
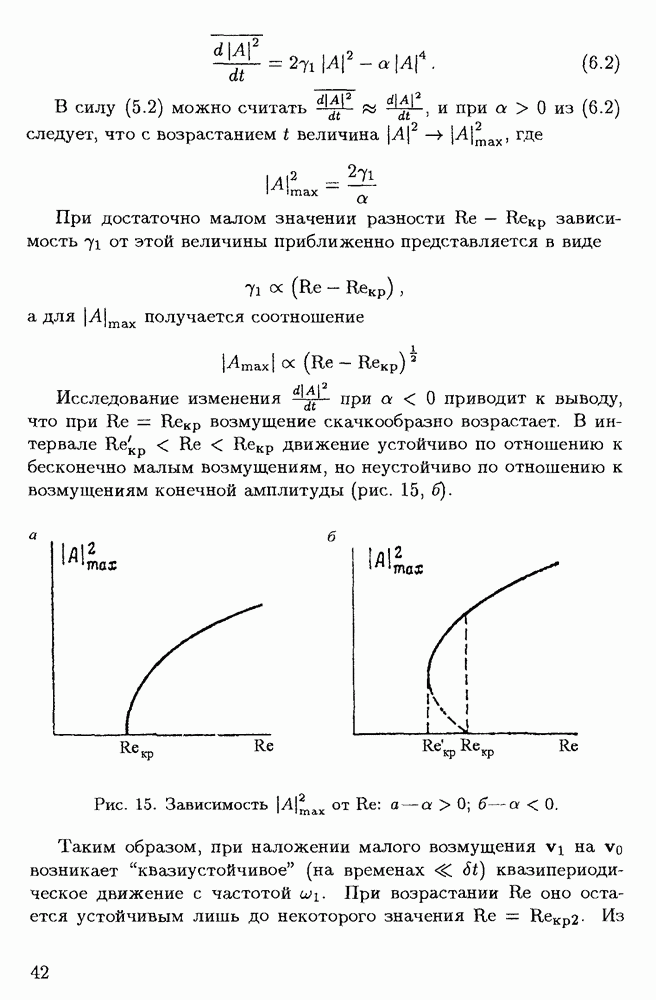
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
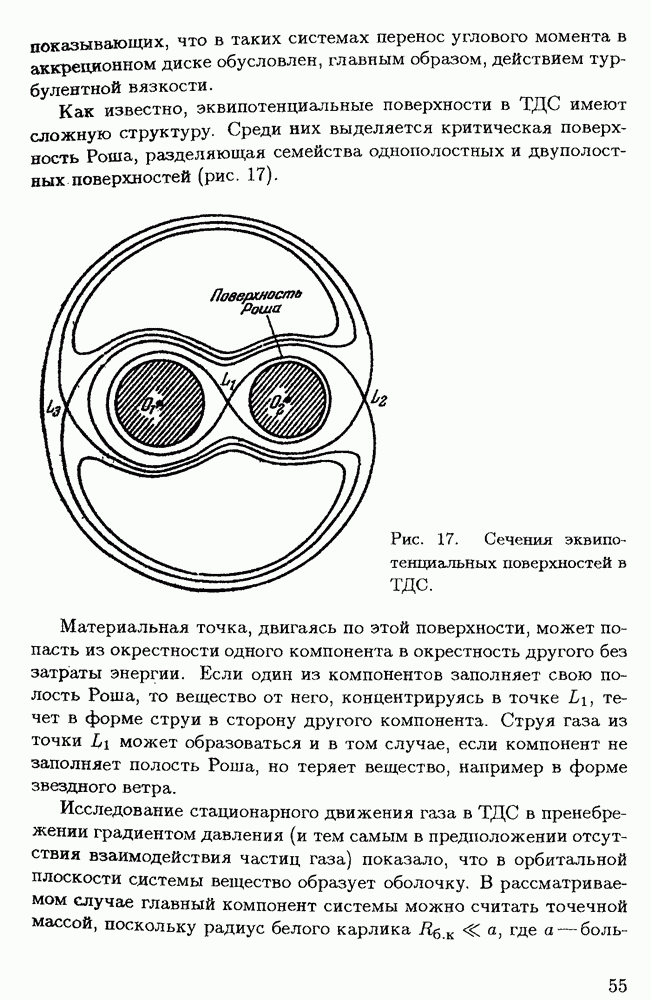
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
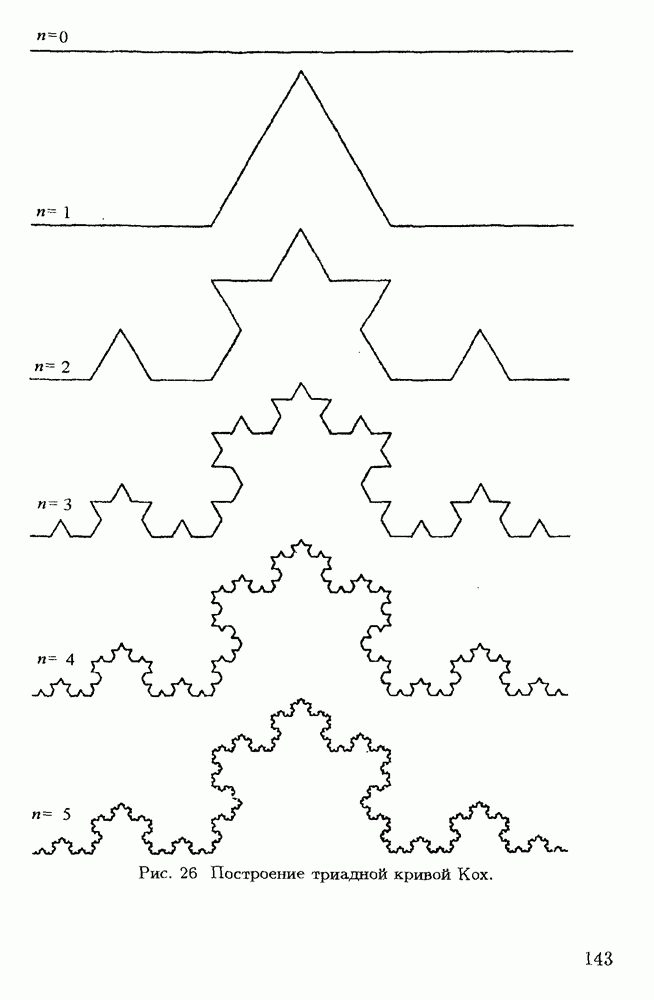
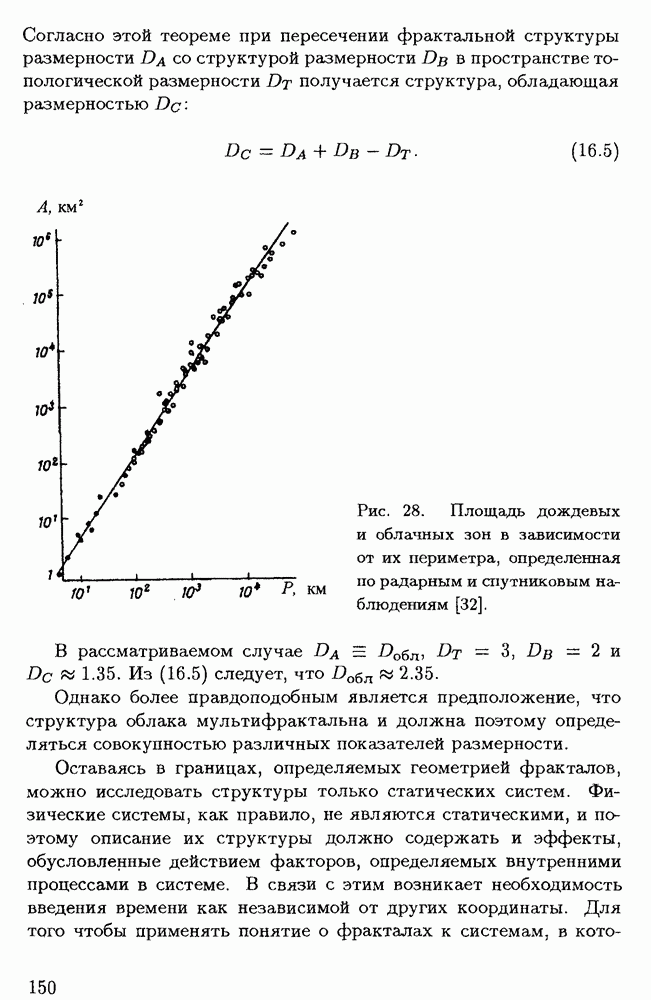
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение