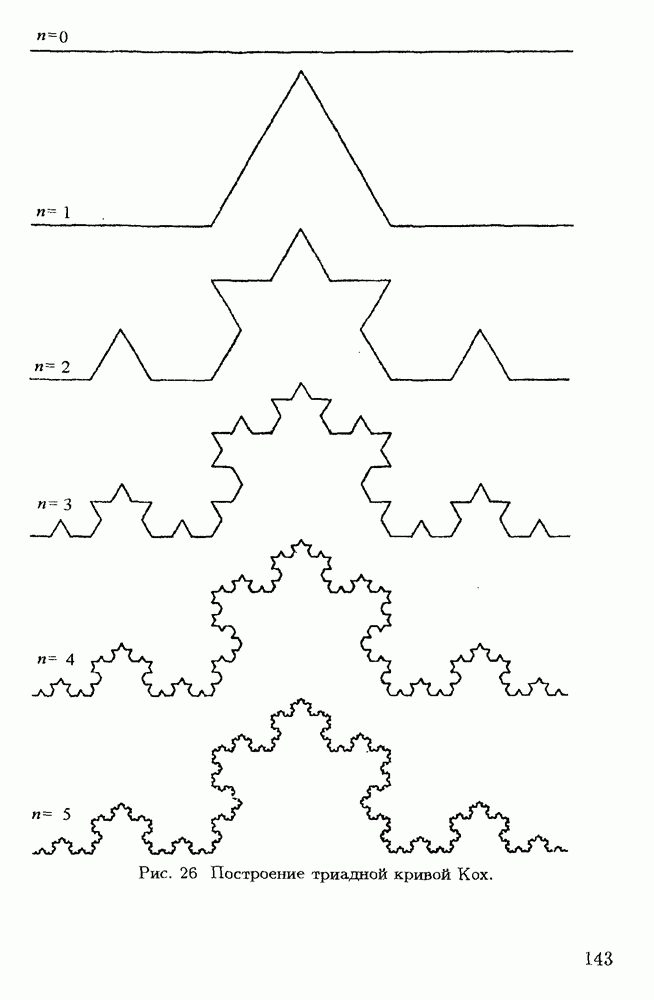
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5.2. Фрактальность физических структур
Математическое определение фрактала предусматривает для самоподобных фракталов условия, не выполняющиеся в реальных физических объектах:
1. В множестве нет наименьшего элемента — размер "клеток" 
2. Совершается предельный переход — число клеток 
В любой физической структуре должен существовать конечный наименьший масштаб. Кроме того, такая структура всегда
ограничена в занимаемом ею пространстве. Это приводит к нарушению самоподобия вблизи границы. Достаточно малая область, содержащая границу множества, отличается в отношении самоподобия от области того же размера, не включающей границу. В связи с этим обстоятельством можно говорить о самоподобии структуры только в определенном смысле. Если внутренний масштаб определяется размером наименьшего из элементов  внешний — размером системы
внешний — размером системы  то описание структуры как самоподобного фрактала возможно лишь при
то описание структуры как самоподобного фрактала возможно лишь при  и для значений
и для значений  . В таких случаях предпочтительнее говорить о квазифракталъности структуры.
. В таких случаях предпочтительнее говорить о квазифракталъности структуры.
Для выяснения возможности описания структуры какого-либо физического объекта в рамках фрактальной геометрии используется метод, основанный на подсчете числа элементов, содержащихся в определенном объеме. Таким путем в ряде случаев можно найти показатель  определяющий размерность фрактального множества, являющегося "носителем" объектов, содержащихся в системе.
определяющий размерность фрактального множества, являющегося "носителем" объектов, содержащихся в системе.
Пусть некоторая система обладает самоподобной фрактальной структурой, состоит из одинаковых элементов и в объемах, ограниченных концентрическими сферами радиусов  содержит соответственно
содержит соответственно  элементов. Полагаем, что
элементов. Полагаем, что

а величина  представима в виде
представима в виде

где А — некоторая постоянная и показатель степени  должен зависеть от
должен зависеть от  Из формул (11.5) и (12.5) следует равенство
Из формул (11.5) и (12.5) следует равенство

которое определяет величину  :
:

Величина  для самоподобных фракталов совпадает с определенной в § 5.1 фрактальной размерностью
для самоподобных фракталов совпадает с определенной в § 5.1 фрактальной размерностью  Для коэффициента А, называемого префактором, имеем выражение
Для коэффициента А, называемого префактором, имеем выражение

Здесь  означает наименьший из рассматриваемых масштабов и
означает наименьший из рассматриваемых масштабов и  число элементов в соответствующем объеме.
число элементов в соответствующем объеме.
Важное для применения в астрофизических исследованиях соотношение получается из равенства (12.5) для систем, в которых все элементы имеют одну и ту же массу то. Отношение масс, содержащихся в соответствующих сферических объемах, записывается в следующем виде:

и, следовательно,

В соотношении  означает расстояние от любой выбранной в пределах системы точки. При таком условии средняя плотность вещества в произвольно выбираемом сферическом объеме оказывается зависящей от размера этого объема:
означает расстояние от любой выбранной в пределах системы точки. При таком условии средняя плотность вещества в произвольно выбираемом сферическом объеме оказывается зависящей от размера этого объема:

Соотношение между средней плотностью в сферической конфигурации и радиусом этой конфигурации, сходное с зависимостью (14.5), получается, если плотность в конфигурации изменяется с расстоянием до ее центра  по закону
по закону  Однако принципиальное различие между фрактальной структурой, для которой справедлива зависимость (14.5), и сферической системой заключается в том, что величина
Однако принципиальное различие между фрактальной структурой, для которой справедлива зависимость (14.5), и сферической системой заключается в том, что величина  может отсчитываться от любой точки в системе, по предположению не имеющей центра.
может отсчитываться от любой точки в системе, по предположению не имеющей центра.
Более сложной является система, состоящая из объектов различной массы. Если структура системы фрактальна, то в этом случае множество, являющееся геометрическим "носителем" объектов, представляет собой мультифрактал.
Существуют системы, для которых фрактальную размерность приходится определять по их проекции. В частности, так поступают при анализе размерности атмосферных облаков, используя зависимость между площадью области и ее периметром. Для многоугольников, кругов и других областей, ограниченных обычными кривыми, отношение длины периметра  к величине
к величине  где
где  площадь области, является величиной, не зависящей от размера области. Однако когда область фрактальна, то фракталей и периметр. Результат измерения величины
площадь области, является величиной, не зависящей от размера области. Однако когда область фрактальна, то фракталей и периметр. Результат измерения величины  в этом случае зависит от применяемого эталона. Для фрактального периметра
в этом случае зависит от применяемого эталона. Для фрактального периметра  при
при  Площадь же области, определяемая путем наложения на нее квадратов со стороной
Площадь же области, определяемая путем наложения на нее квадратов со стороной  при
при  остается постоянной. С учетом этого обстоятельства в [32] получено соотношение
остается постоянной. С учетом этого обстоятельства в [32] получено соотношение

где  любой достаточно малый эталон длины. Величина С зависит от степени точности, желаемой при измерениях с данным эталоном. Фрактальная размерность, определяемая с помощью соотношения (15.5),
любой достаточно малый эталон длины. Величина С зависит от степени точности, желаемой при измерениях с данным эталоном. Фрактальная размерность, определяемая с помощью соотношения (15.5), 
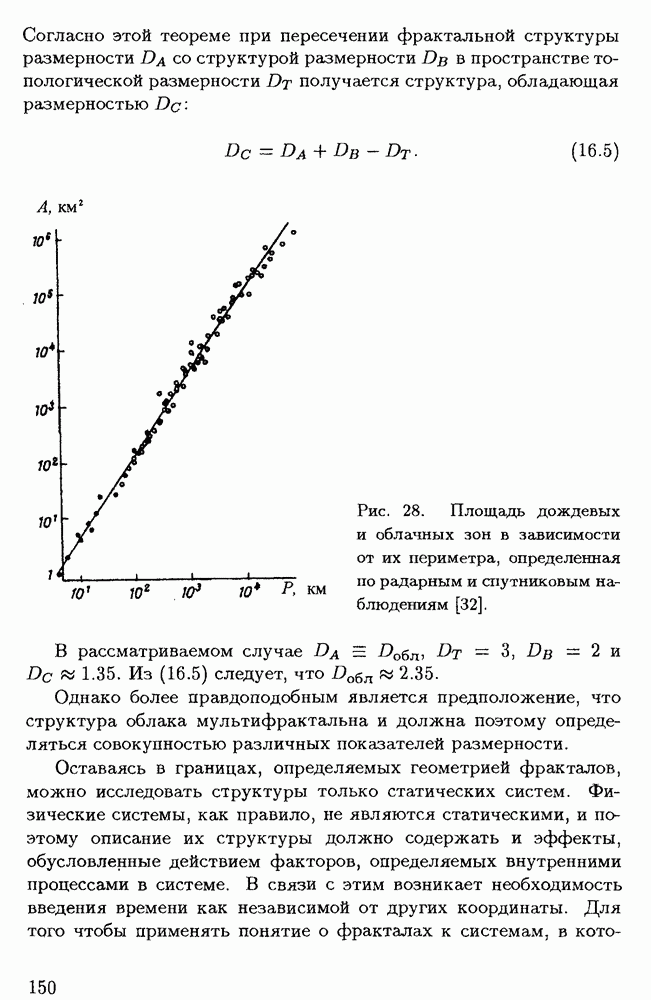
Обширные измерения площади и периметра атмосферных облаков и дождевых зон привели к установлению зависимости между  (рис. 28) [31]. Точки соответствуют значениям
(рис. 28) [31]. Точки соответствуют значениям  полученным радиолокационными методами и при наблюдениях с
полученным радиолокационными методами и при наблюдениях с  хорошо ложатся на одну прямую (при различии площадей на шесть порядков!) и по наклону прямой найдено значение
хорошо ложатся на одну прямую (при различии площадей на шесть порядков!) и по наклону прямой найдено значение  . Эта величина не зависит ни от размера облаков при
. Эта величина не зависит ни от размера облаков при  ни от физических условий в них. Таким образом, в облаках нет выделенных масштабов, принадлежащих указанному диапазону, и они представляются фракталами. Эти фракталы, по-видимому, являются самоаффинными, так как при наблюдаемой толщине облаков
ни от физических условий в них. Таким образом, в облаках нет выделенных масштабов, принадлежащих указанному диапазону, и они представляются фракталами. Эти фракталы, по-видимому, являются самоаффинными, так как при наблюдаемой толщине облаков  и соответственном различии масштабов в горизонтальном и вертикальном направлении на несколько порядков трудно ожидать в них самоподобия.
и соответственном различии масштабов в горизонтальном и вертикальном направлении на несколько порядков трудно ожидать в них самоподобия.
Полученная величина  относится к периметру облаков и непосредственно не дает информации о фрактальной размерности облаков как фрактальных образований. Поскольку граница облака представляет собой линию пересечения поверхности облака с плоскостью, то значение
относится к периметру облаков и непосредственно не дает информации о фрактальной размерности облаков как фрактальных образований. Поскольку граница облака представляет собой линию пересечения поверхности облака с плоскостью, то значение  для облака, вообще говоря, может быть оценено на основании теоремы о сложении (см., например, [32]).
для облака, вообще говоря, может быть оценено на основании теоремы о сложении (см., например, [32]).
Согласно этой теореме при пересечении фрактальной структуры размерности  со структурой размерности
со структурой размерности  в пространстве топологической размерности
в пространстве топологической размерности  получается структура, обладающая размерностью
получается структура, обладающая размерностью 


Рис. 28. Площадь дождевых и облачных зон в зависимости от их периметра, определенная по радарным и спутниковым наблюдениям [32].
В рассматриваемом случае  Из (16.5) следует, что
Из (16.5) следует, что 
Однако более правдоподобным является предположение, что структура облака мультифрактальна и должна поэтому определяться совокупностью различных показателей размерности.
Оставаясь в границах, определяемых геометрией фракталов, можно исследовать структуры только статических систем. Физические системы, как правило, не являются статическими, и поэтому описание их структуры должно содержать и эффекты, обусловленные действием факторов, определяемых внутренними процессами в системе. В связи с этим возникает необходимость введения времени как независимой от других координаты. Для того чтобы применять понятие о фракталах к системам,
в которых важную роль играет случайность, вводится понятие стохастических фракталов. Примером таких процессов является броуновское движение. Как было показано (см., напр., [18]), если время рассматривать как дополнительное измерение, то зависимость положения частицы от времени при броуновском движении оказывается самоаффинной. Там же описаны другие процессы, в которых случайность играет видную роль, например образование волн на море. Статистические свойства оказываются фрактальными.
В астрофизических объектах — таких, как звездные системы, межзвездная среда, межгалактическая среда — всегда имеет место гравитационное взаимодействие между элементами системы. По этой причине элементы движутся в пространстве, и одной фрактальной геометрии в ее обычном виде недостаточно для исследования структуры системы. Тем не менее структуры в таких системах могут обладать фрактальностью в смысле ее второго определения (см. § 5.1). Подобие "в какой-то мере" частей системы целому может существовать и при учете гравитации. Фрактальные структуры, в которых существенную роль играет гравитация, уместно называть динамическими фракталами. Подробнее о таких объектах будет сказано в следующем разделе.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основные понятия теории устойчивости физических систем
- § 1.2. Термодинамические системы
- § 1.3. Переход к хаотическому режиму в нелинейных системах; странные аттракторы
- § 1.4. Бифуркация удвоения периода
- § 1.5. Устойчивость термодинамических диссипативных систем
- Глава 2. Турбулентность и ее проявления в астрофизических объектах
- § 2.1. Потеря устойчивости течением жидкости и переход к турбулентному режиму
- § 2.2. Развитая турбулентность
- § 2.3. Турбулентная вязкость в аккреционном диске
- § 2.4. Перенос углового момента в звездах турбулентной вязкостью
- § 2.5. Турбулентная диффузия и турбулентное перемешивание
- § 2.6. Усиление магнитного поля турбулентными движениями
- § 2.7. Турбулентные струи
- Глава 3. Конвекция и вызываемые ею явления в звездах
- § 3.1. Устойчивость равновесия газа в присутствии внешнего поля
- § 3.2. Конвективная неустойчивость в несжимаемой жидкости: линейное приближение
- § 3.3. Нелинейная модель конвекции Рэлея-Бенара
- § 3.4. Особенности конвекции в астрофизических объектах
- § 3.5. Внешние конвективные зоны звезд
- § 3.6. Турбулентная конвекция
- Глава 4. Тепловая неустойчивость
- § 4.1. Локальный критерий тепловой неустойчивости
- § 4.2. Тепловая неустойчивость неравновесных систем
- § 4.3. Влияние тепловой неустойчивости на эволюцию межзвездной среды в галактиках
- § 4.4. Гидростатическая модель горячей короны эллиптической галактики
- Глава 5. Фрактальность в астрофизических системах
- § 5.2. Фрактальность физических структур
- § 5.3. Фрактальные структуры в межзвездной среде и в межгалактических облаках
- § 5.4. Проблема распределения вещества во вселенной: однородность или фрактальность?
- Заключение