| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
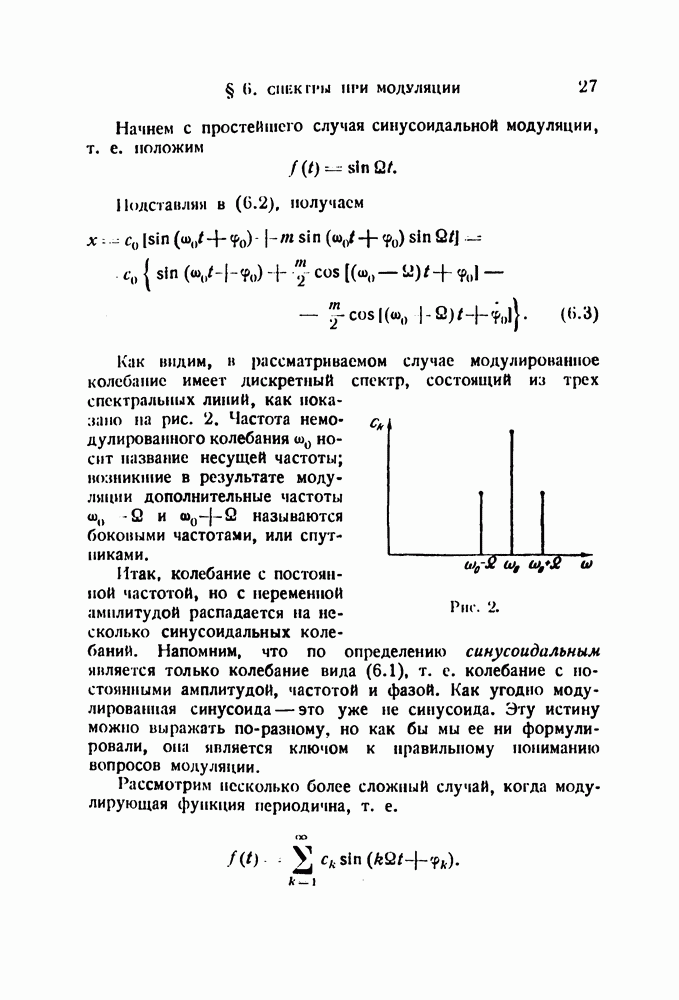
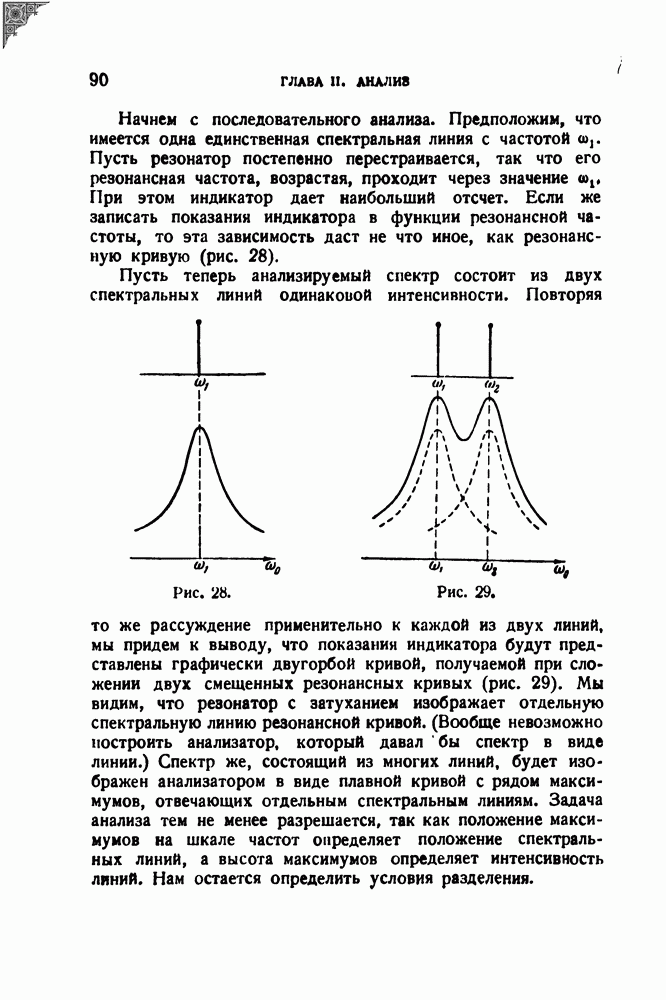
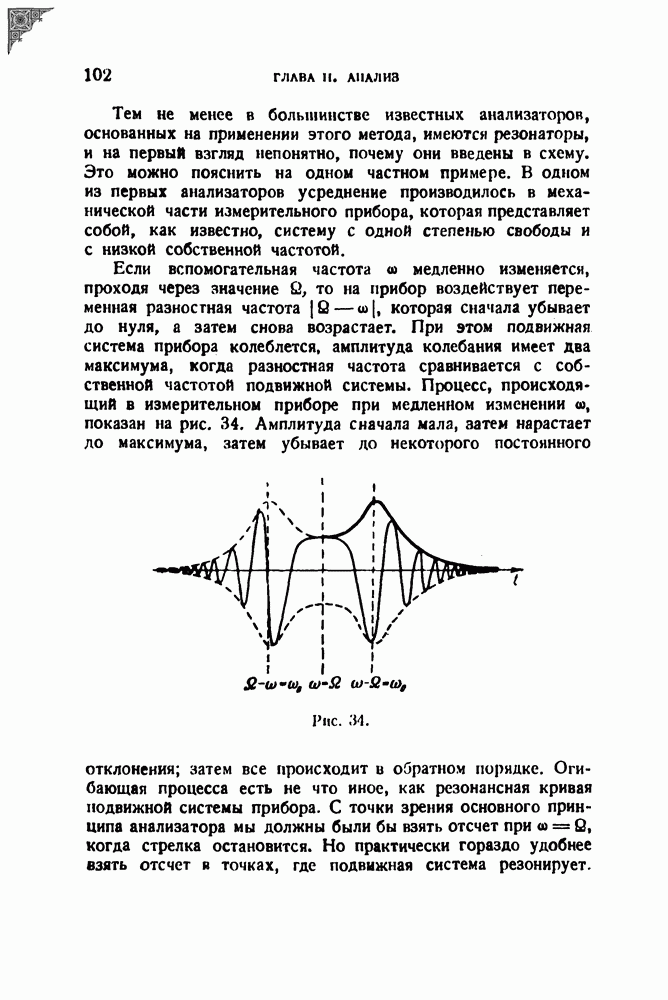
§ 9. Спектры некоторых импульсов
Вычислим сначала спектры одного специального вида разрывных функций. Эти функции образуют семейство, начальным членом которого является так называемая единичная функция, определяемая следующим образом:

Можно построить семейство функций при помощи рекуррентной формулы

Так мы получим в качестве определения функции о, следующее соотношение:

Функция о, известна под названием единичного импульса, импульсивной  -функции Дирака. Мы будем называть ее разрывной функцией первого порядка. Для того чтобы составить себе представление об ее свойствах, заметим, что функция
-функции Дирака. Мы будем называть ее разрывной функцией первого порядка. Для того чтобы составить себе представление об ее свойствах, заметим, что функция  претерпевает разрыв при
претерпевает разрыв при  в то время как функция
в то время как функция  замечательна тем, что при
замечательна тем, что при  происходит разрыв ее
происходит разрыв ее
интеграла. Мы можем принять для рекуррентной формулы (8.2) запись в виде

Этим мы разрешим применение к функциям о операций анализа, что оказывается во многих случаях оправданным, но на этом мы подробно останавливаться не будем.
Мы представляем себе функцию о, так: она равна нулю при всех  при
при  она совершает скачок в бесконечность и, возвратясь обратно, остается равной нулю при всех
она совершает скачок в бесконечность и, возвратясь обратно, остается равной нулю при всех  При этом, однако, интеграл от о, по любому интервалу, включающему в себя
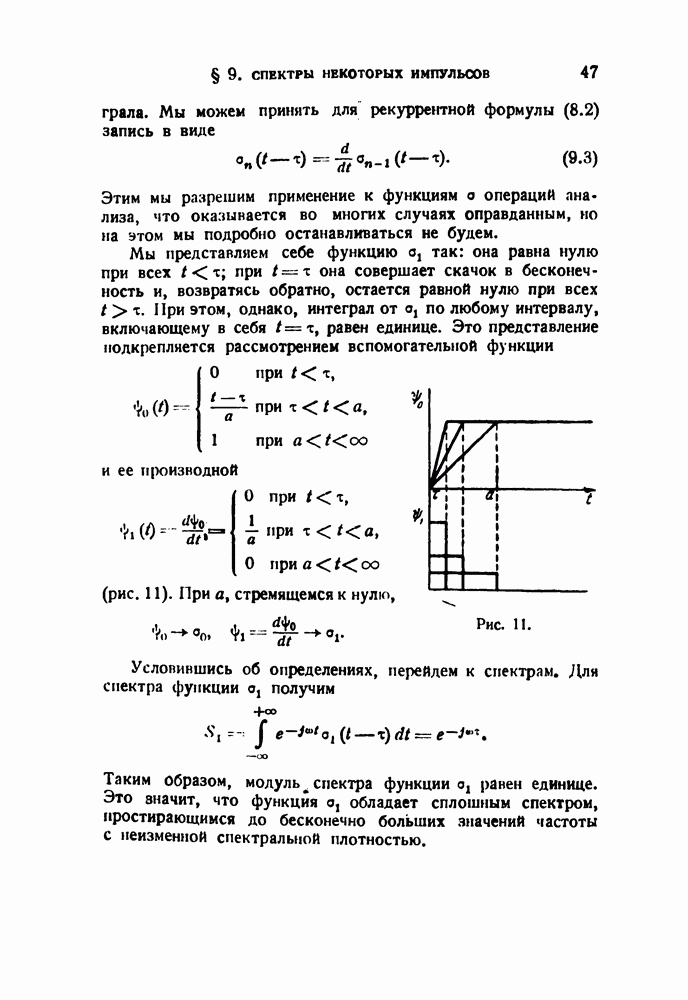
При этом, однако, интеграл от о, по любому интервалу, включающему в себя  равен единице. Это представление подкрепляется рассмотрением вспомогательной функции
равен единице. Это представление подкрепляется рассмотрением вспомогательной функции

при
1 при  и ее производной
и ее производной

О при  (рис. 11). При а, стремящемся к нулю,
(рис. 11). При а, стремящемся к нулю,

Условившись об определениях, перейдем к спектрам. Для спектра функции  получим
получим

Таким образом, модуль спектра функции  равен единице. Это эначит, что функция о, обладает сплошным спектром, простирающимся до бесконечно больших значений частоты с неизменной спектральной плотностью.
равен единице. Это эначит, что функция о, обладает сплошным спектром, простирающимся до бесконечно больших значений частоты с неизменной спектральной плотностью.

Рис. 11.
При попытке вычислить спектр функции  возникает затруднение, связанное с тем, что эта функция не абсолютно интегрируема и имеет конечное значение на бесконечности
возникает затруднение, связанное с тем, что эта функция не абсолютно интегрируема и имеет конечное значение на бесконечности  Можно обойти это затруднение, умножив функцию
Можно обойти это затруднение, умножив функцию  на
на  Тогда
Тогда

Модуль спектра функции  есть К этому же результату можно притти и другим путем. Воспользуемся известным
есть К этому же результату можно притти и другим путем. Воспользуемся известным
соотношением

Интеграл в правой части можно рассматривать как вещественную форму интеграла Фурье для функции  . В таком случае спектр этой функции ( т. е. множитель при синусе) есть
. В таком случае спектр этой функции ( т. е. множитель при синусе) есть 
Составляя выражения для спектров функций  можно путем интегрирования по частям убедиться, что спектр функции
можно путем интегрирования по частям убедиться, что спектр функции  есть
есть 
К этому выводу мы могли бы также притти, сопоставляя рекуррентную формулу (9.3) с теоремой (5.3).
Рассмотрим теперь спектр весьма короткого импульса произвольной формы. Импульс характеризуется тем, что функция, представляющая его, равна нулю вне некоторого очень малого интервала х около 
Мы можем записать для спектра такого импульса

Но если х мало, то  мало отличается от единицы, и
мало отличается от единицы, и

т. е. спектр равен постоянной величине, определяемой площадью импульса. Такое соотношение мы уже встретили,
разбирая вопрос о спектре единичного импульса  Однакб тогда речь шла о некоторой определенной функции, здесь же в интервале, в котором функция существует, она может иметь произвольный вид, т. е. импульс может иметь какую угодно форму. С другой стороны, говоря О функции
Однакб тогда речь шла о некоторой определенной функции, здесь же в интервале, в котором функция существует, она может иметь произвольный вид, т. е. импульс может иметь какую угодно форму. С другой стороны, говоря О функции  мы ссылались на ее определение, здесь же требуем кратковременности импульса.
мы ссылались на ее определение, здесь же требуем кратковременности импульса.

Рис. 12.
Этот вопрос играет здесь основную роль, и мы на нем немного задержимся. Мы требуем, чтобы х было мало. Но требование малости лишено смысла до тех пор, пока не указано, с чем та или иная величина сравнивается. В рассматриваемом случае положение определяется тем, что вследствие малости  функция
функция  мало отличается от единицы. Но это выполняется при условии
мало отличается от единицы. Но это выполняется при условии

или

где Т — период, соответствующий частоте 
Таким образом, мы приходим к простому, но очень важному как с принципиальной, так и с практической точки зрения выводу.
Одиночный импульс произвольной формы имеет сплошной спектр, который может быть приближенно выражен постоянной величиной, пропорциональной площади импульса, в пределах того интервала частот, в котором период остается большим по сравнению с длительностью импульса.
Мы будем еще неоднократно возвращаться к этому положению.
С повышением частоты, когда Т делается уже сравнимым с х, функция Л начинает убывать. Прежде чем изучать общие закономерности, мы рассмотрим ряд примеров.
Вычислим спектр прямоугольного импульса высотой  и длительностью
и длительностью  Мы получаем
Мы получаем

где площадь импульса  График
График  для этого случая изображен на рис. 12.
для этого случая изображен на рис. 12.
И качестве иллюстрации предыдущего заметим, что при

и

Для импульса в форме треугольника с основанием  и высотой
и высотой  имеем
имеем

Следовательно,

Разлагая числитель в степенной ряд, можно убедиться, что отношение стремится к единице при  стремящемся к нулю.
стремящемся к нулю.
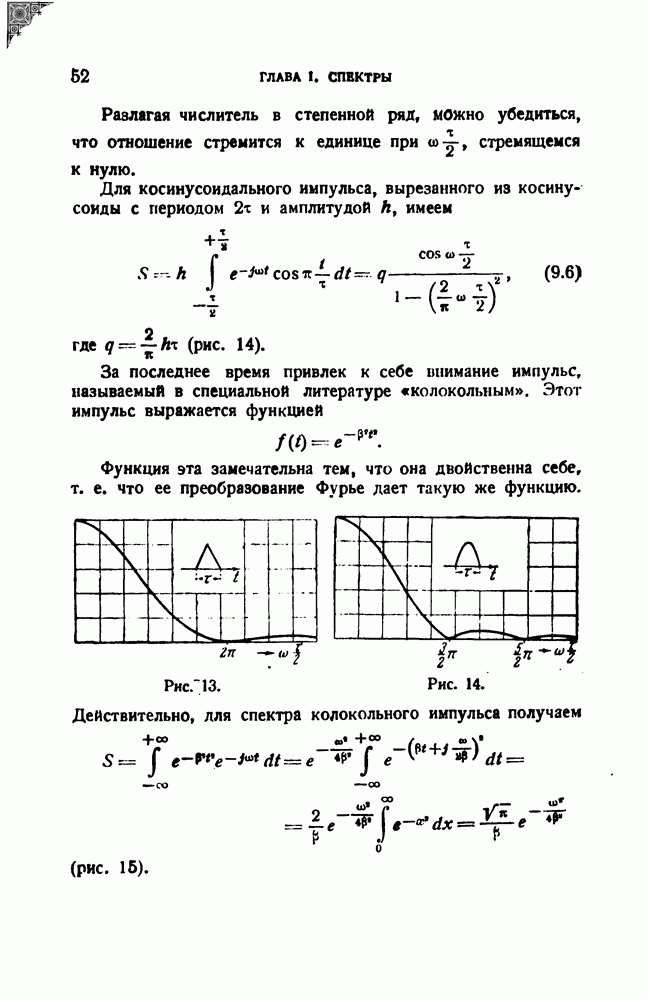
Для косинусоидального импульса, вырезанного из косинусоиды с периодом  и амплитудой
и амплитудой  , имеем
, имеем

где  (рис. 14).
(рис. 14).
За последнее время привлек к себе внимание импульс, называемый в специальной литературе «колокольным». Этот импульс выражается функцией

Функция эта замечательна тем, что она двойственна себе, т. е. что ее преобразование Фурье дает такую же функцию.

Рис. 13.

Рис. 14.
Действительно, для спектра колокольного импульса получаем

(рис. 15).
Рассмотрим еще несколько импульсов, начинающихся при  но стремящихся к нулю лишь при
но стремящихся к нулю лишь при 

Рис. 15.

Рис. 16.
Пусть, например, дан экспоненциальный импульс

Его спектр есть

(рис. 16).
Спектр импульса  форме затухающей синусоиды
форме затухающей синусоиды

имеет вид

или, вводя обозначения

(рис. 17).

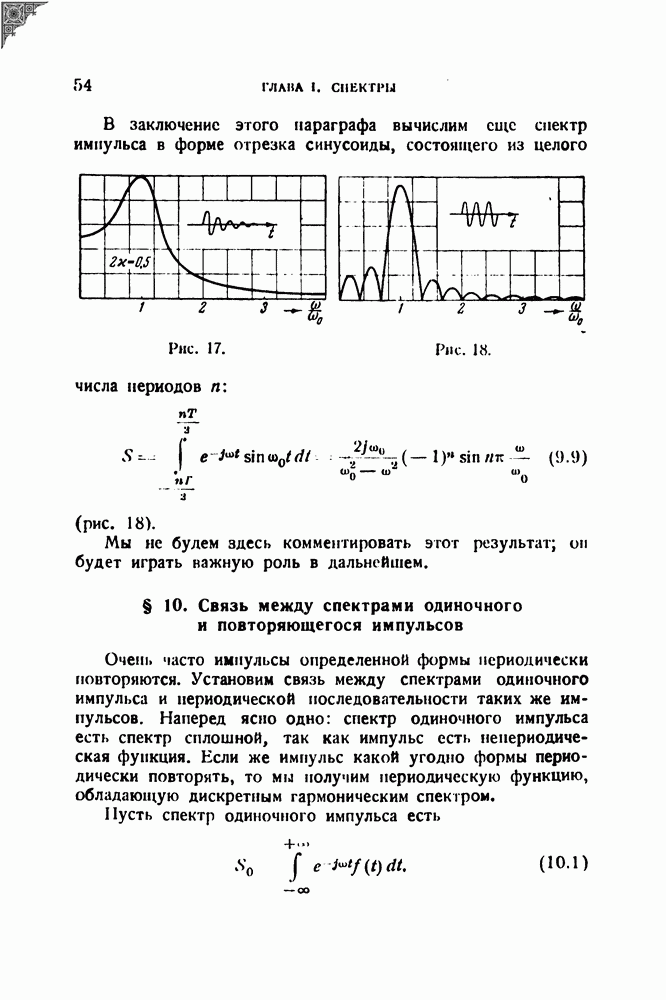
Рис. 17.

Рис. 18.
В заключение этого параграфа вычислим еще спектр импульса в форме отрезка синусоиды, состоящего из целого числа периодов 

(рис. 18).
Мы не будем здесь комментировать этот результат; он будет играть важную роль в дальнейшем.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
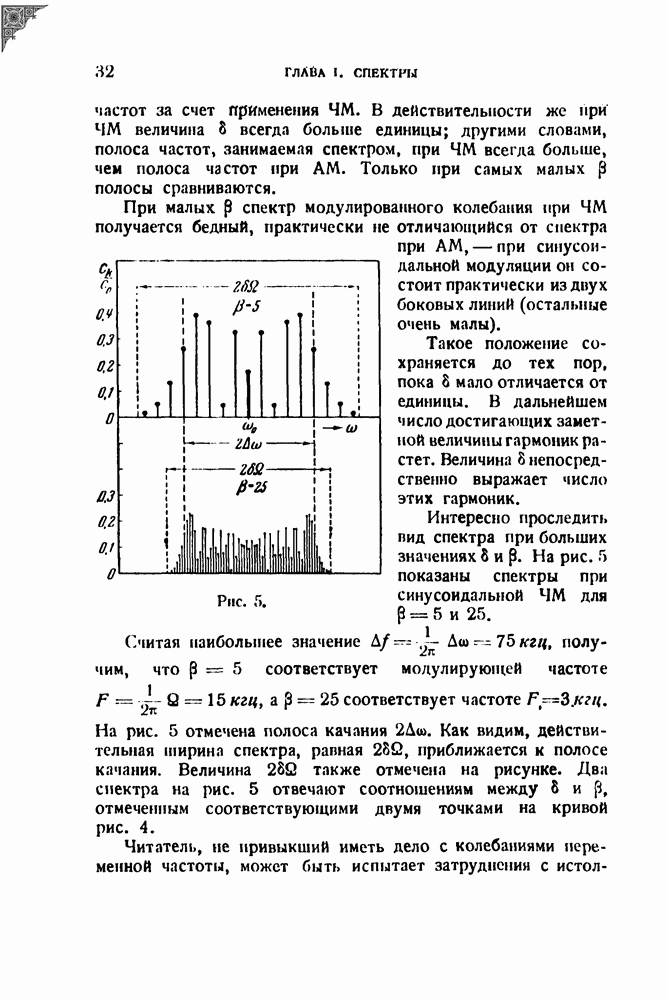
- § 6. Спектры при модуляции
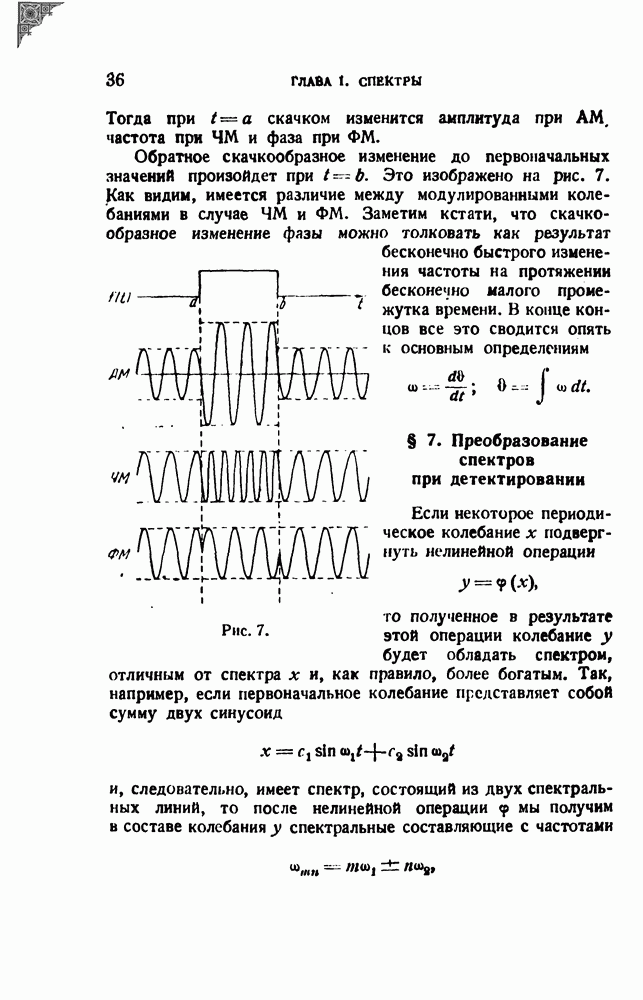
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
- § 9. Спектры некоторых импульсов
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
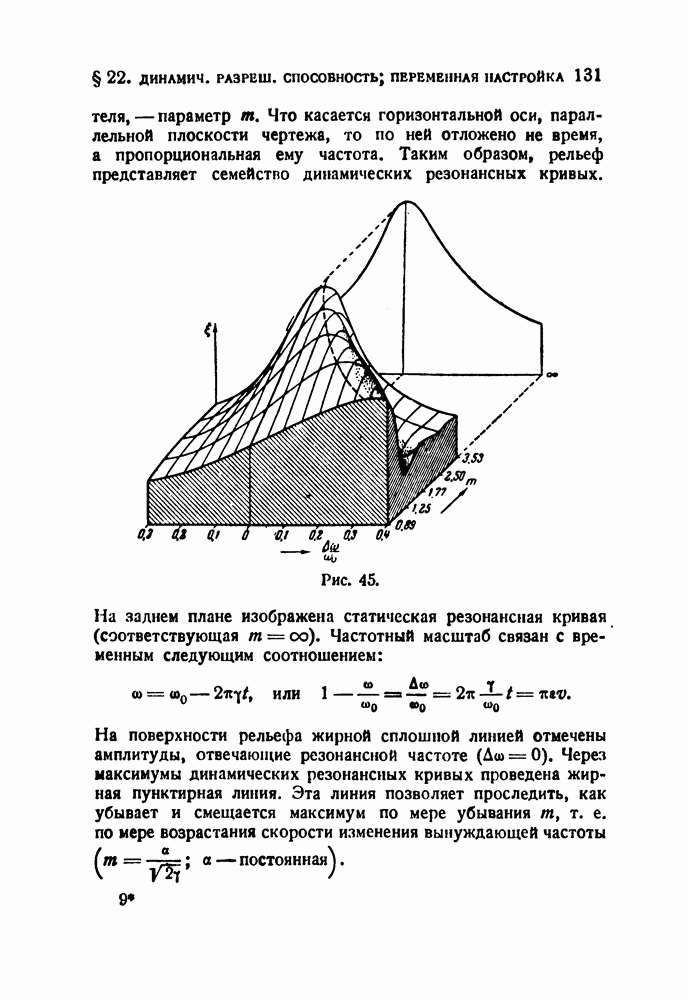
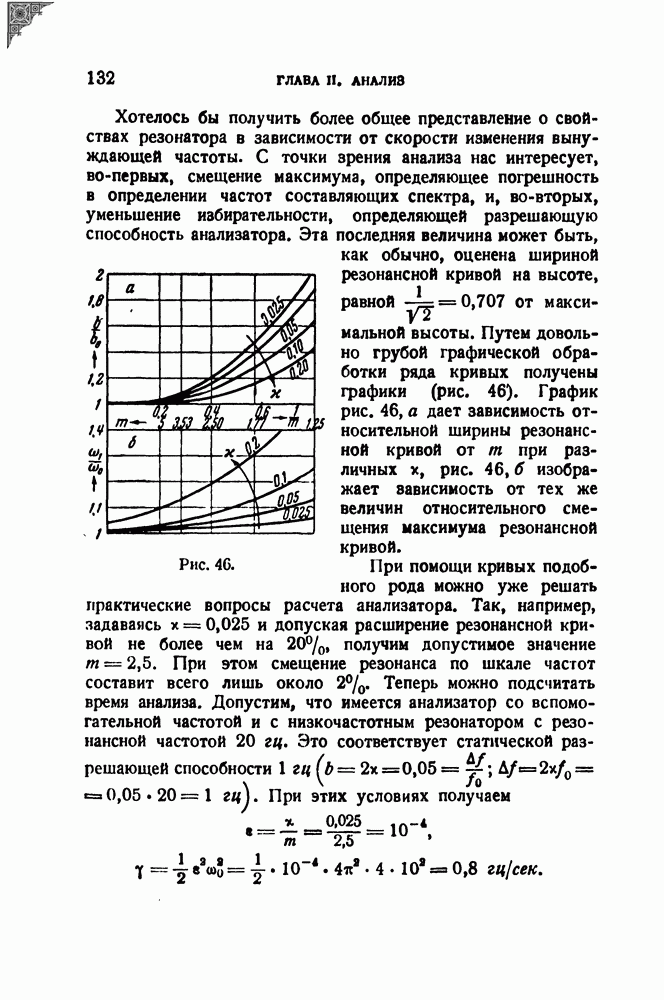
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
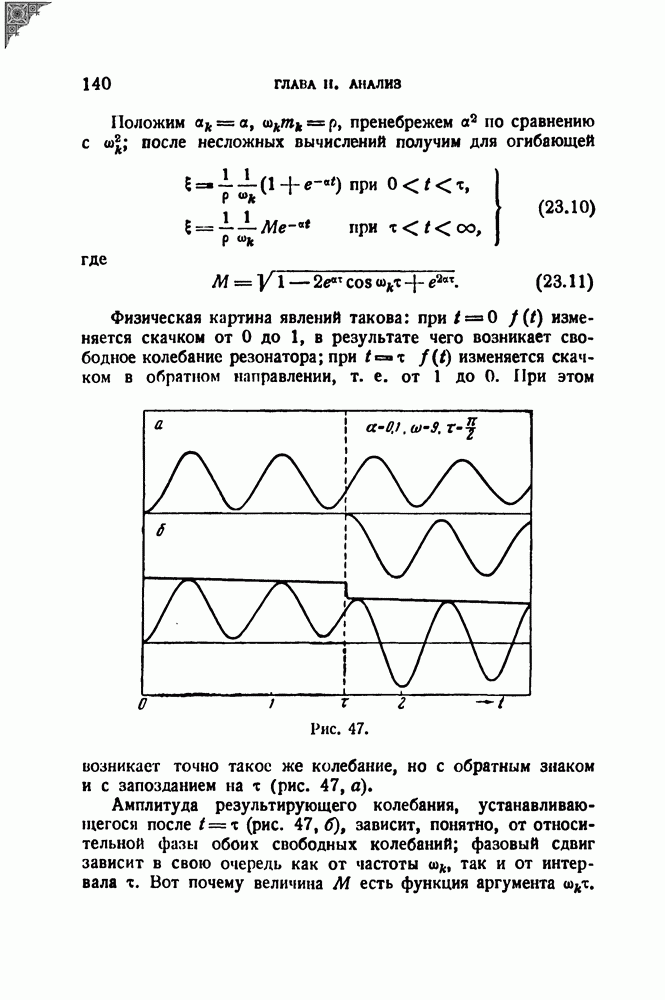
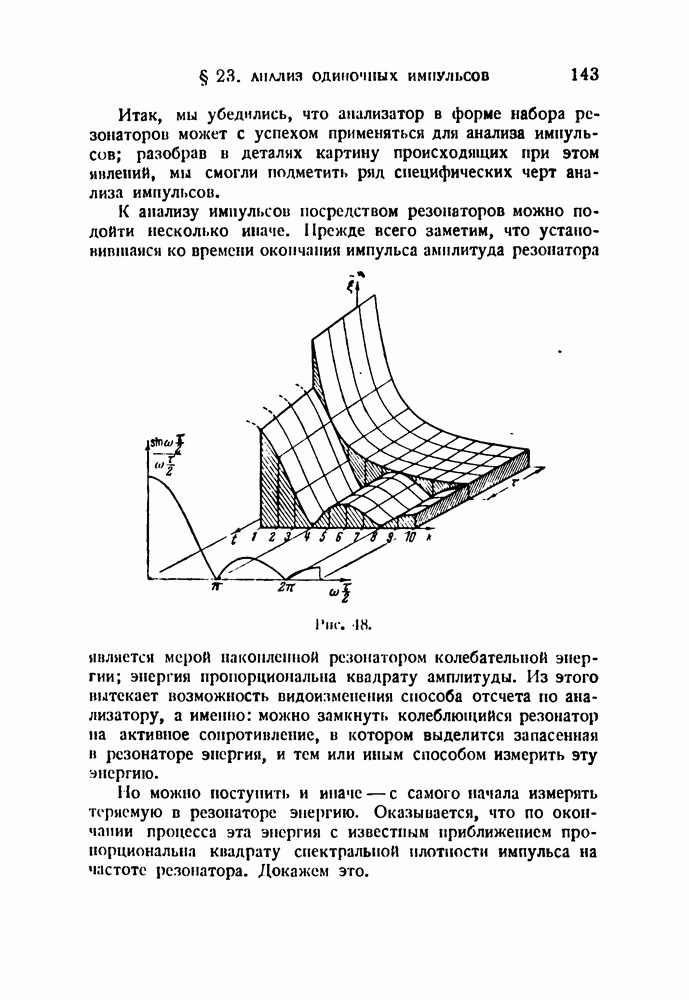
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА