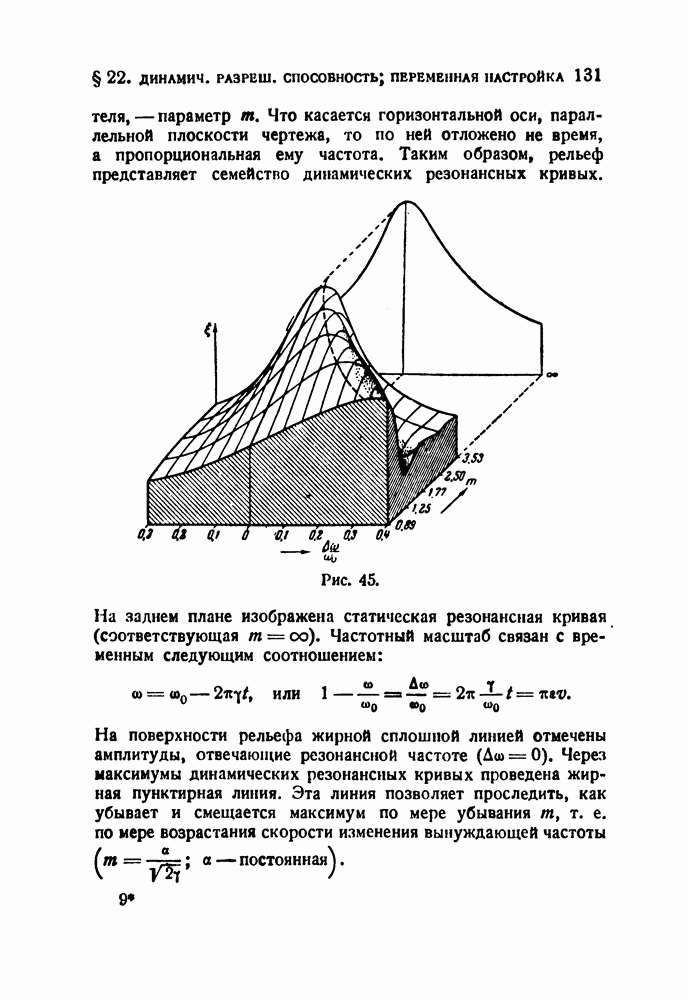
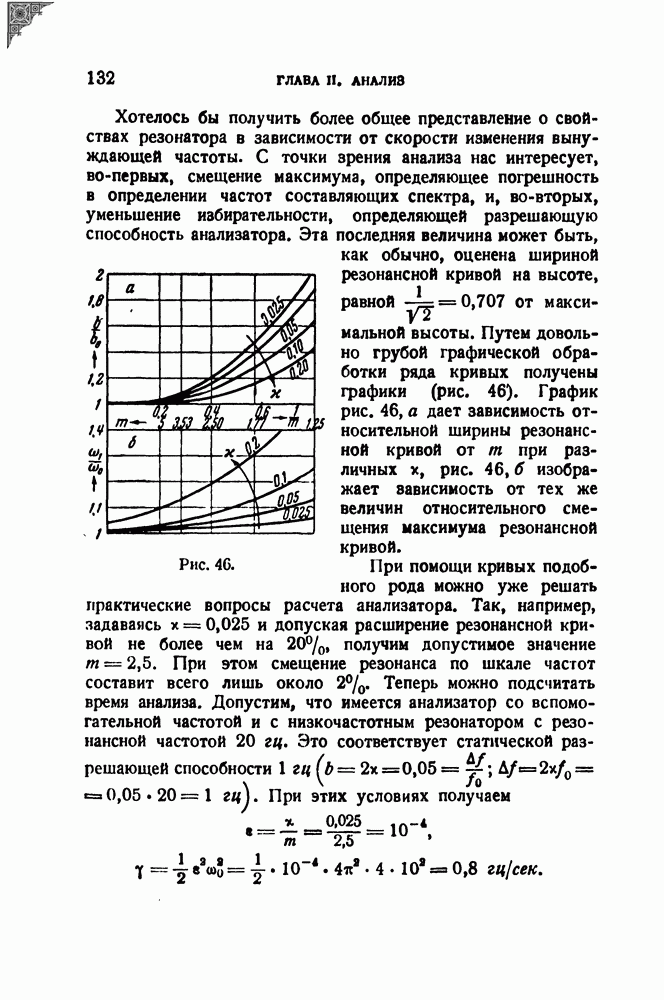
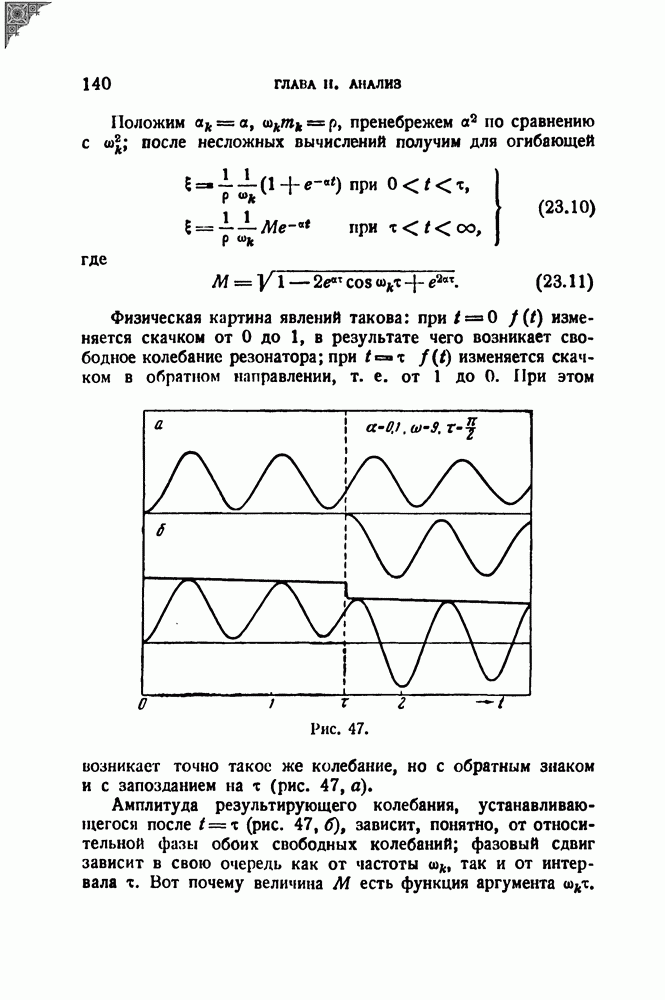
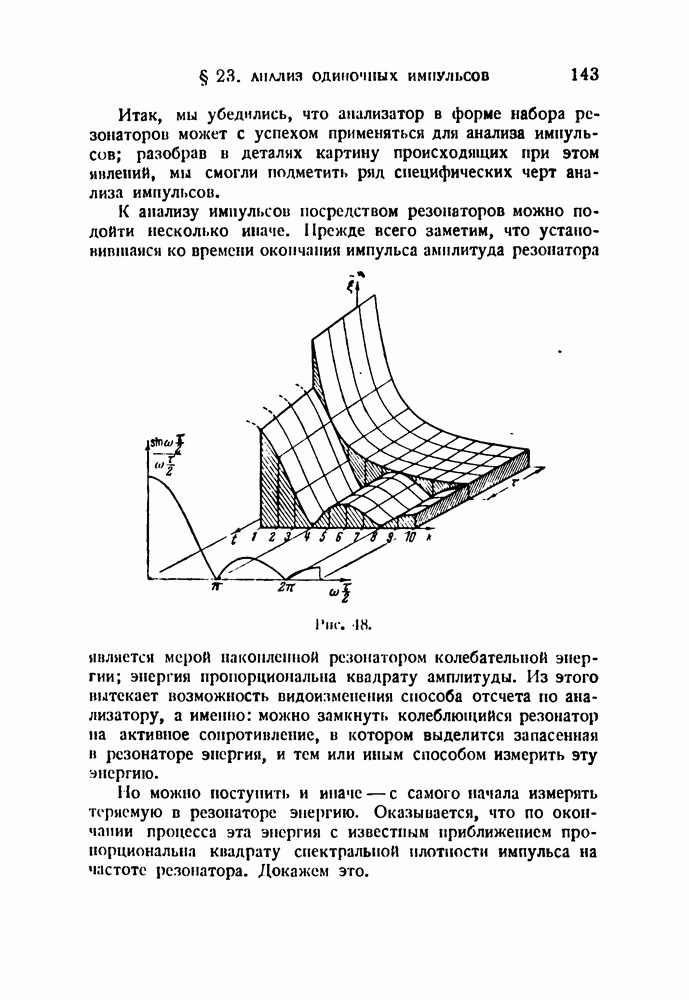
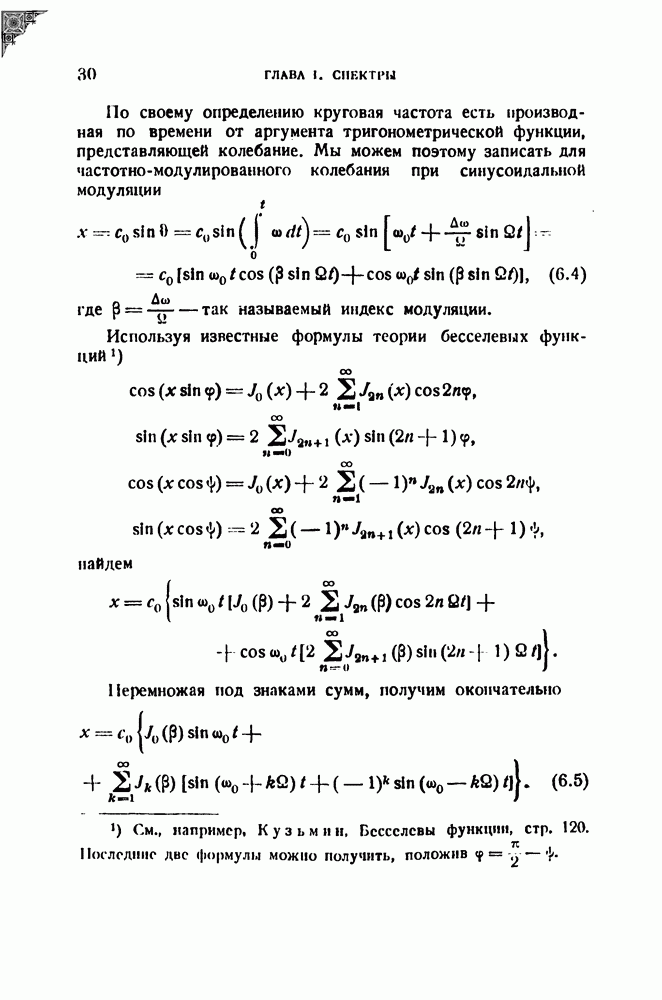| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Спектр суммы периодических функций
В § 5 уже говорилось о том, что преобразование Фурье линейно, и к нему применим поэтому принцип наложения. В случае периодических функций это можно записать так:

т. е. комплексная амплитуда  гармоники спектра суммы функций равна сумме
гармоники спектра суммы функций равна сумме  гармоник спектров каждой отдельно взятой функции. Это бесспорно, но нас интересуют обычно действительные амплитуды. Для них можно записать
гармоник спектров каждой отдельно взятой функции. Это бесспорно, но нас интересуют обычно действительные амплитуды. Для них можно записать

С геометрической точки зрения эта величина представляет собой замыкающую ломаной, стороны которой равны  и отложены под соответствующими углами
и отложены под соответствующими углами  Положим, что дамы два синусоидальных колебания с комплексными амплитудами
Положим, что дамы два синусоидальных колебания с комплексными амплитудами

Тогда

Эта формула может применяться и в том случае, когда вместо постоянных фазовых углов у мы подставляем как угодно зависящие от времени угловые аргументы  Тогда и амплитуда оказывается функцией времени, и получаемое выражение получает смысл огибающей некоторого сложного колебания. Например, если вместо и подставить
Тогда и амплитуда оказывается функцией времени, и получаемое выражение получает смысл огибающей некоторого сложного колебания. Например, если вместо и подставить  то мы получим выражение для огибающей биений, возникающих при сложении двух синусоидальных колебаний с амплитудами
то мы получим выражение для огибающей биений, возникающих при сложении двух синусоидальных колебаний с амплитудами  и частотами
и частотами 
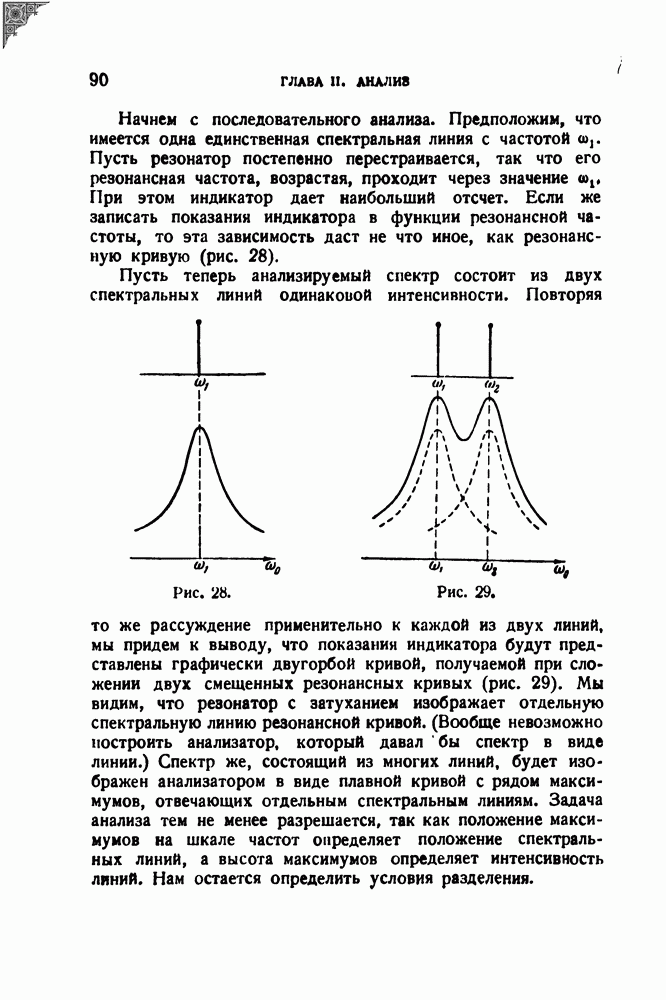
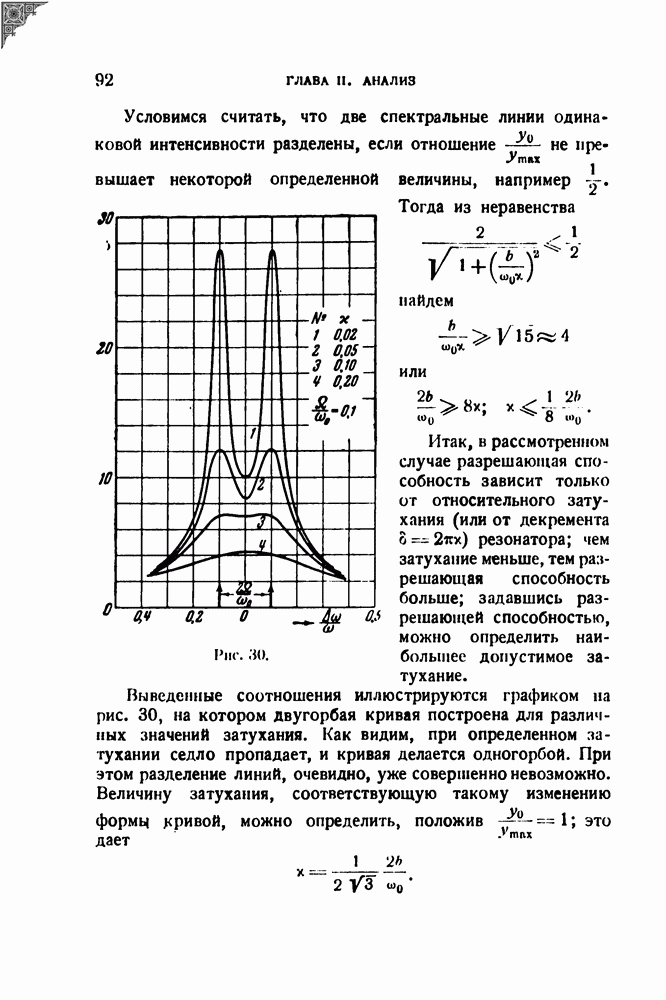
Рассмотрим важный с точки зрения приложений вопрос о спектре функции, получаемой в результате сложения двух одинаковых, но сдвинутых по времени периодических функций. Для некоторой периодической функции 

Для такой же функции, но запаздывающей на время  имеем
имеем

или, заменяя  на
на 

Если теперь сложить функции  то комплексная амплитуда
то комплексная амплитуда  гармоники их суммы будет равна
гармоники их суммы будет равна

а действительная амплитуда равна

Итак, для того чтобы получить спектр суммы двух одинаковых функций, сдвинутых на время х (например, сумму сигнала и его отражения), достаточно умножить амплитуду каждой гармоники на 
Рассмотрим пример. Пусть дана периодическая последовательность коротких импульсов и пусть  Тогда множитель в формуле (8.2) принимает вид
Тогда множитель в формуле (8.2) принимает вид

Таким образом, все нечетные гармоники выпадают. Так оно и должно быть: ведь если  то это значит, что импульсы второй серии попадают в середину промежутков первой серии, т. е. получается вдвое более частое следование импульсов, и, стало быть, основная частота, а с нею и частоты всех гармоник увеличиваются вдвое.
то это значит, что импульсы второй серии попадают в середину промежутков первой серии, т. е. получается вдвое более частое следование импульсов, и, стало быть, основная частота, а с нею и частоты всех гармоник увеличиваются вдвое.
Легко сообразить, что то же самое получится при  , т. е. когда
, т. е. когда  равно любому нечетному числу полупериодов. Если
равно любому нечетному числу полупериодов. Если  то из спектра выпадают вторая, шестая, десятая и т. д. гармоники.
то из спектра выпадают вторая, шестая, десятая и т. д. гармоники.
Формула (8.2) дает значение амплитуды  гармоники спектра суммы функций
гармоники спектра суммы функций  Если мы составим не сумму, а разность этих двух функций, то, действуя аналогично предыдущему, найдем
Если мы составим не сумму, а разность этих двух функций, то, действуя аналогично предыдущему, найдем

Предположим теперь, что х настолько малая величина, что справедливо приближенное равенство

Таким образом, мы выразили разность функций через производную. Найдем спектр 

Но так как функции  периодическая, то
периодическая, то

и, следовательно,

Это соотношение могло бы быть получено из (8.3) путем замены синуса его аргументом.
Все приведенные выше соотношения без труда распространяются и на случай почти - периодической функции; в этом случае во все формулы входит  вместо
вместо 
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
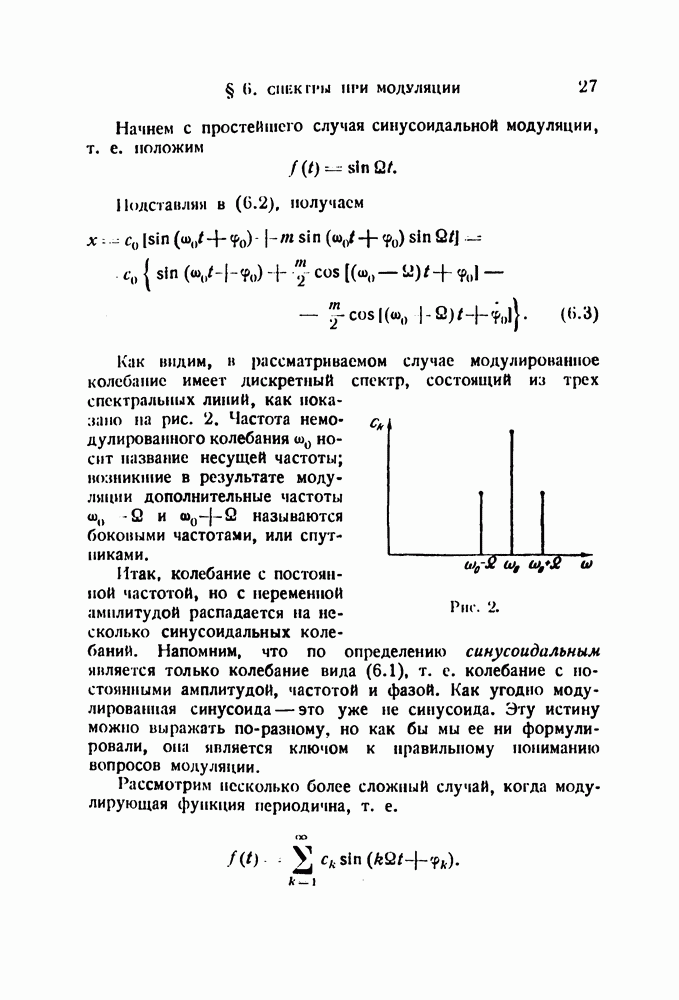
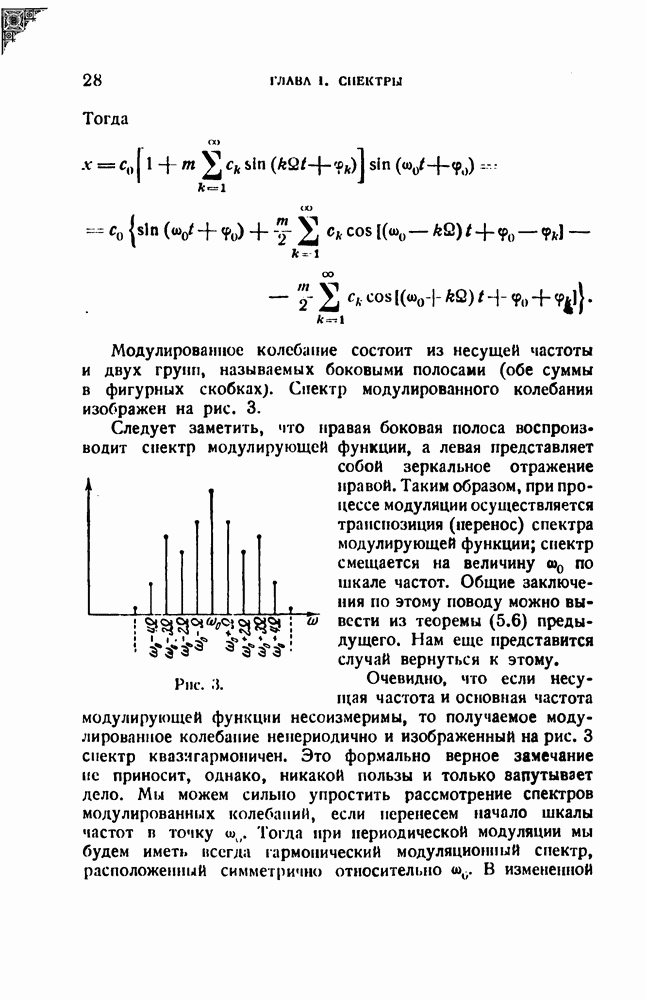
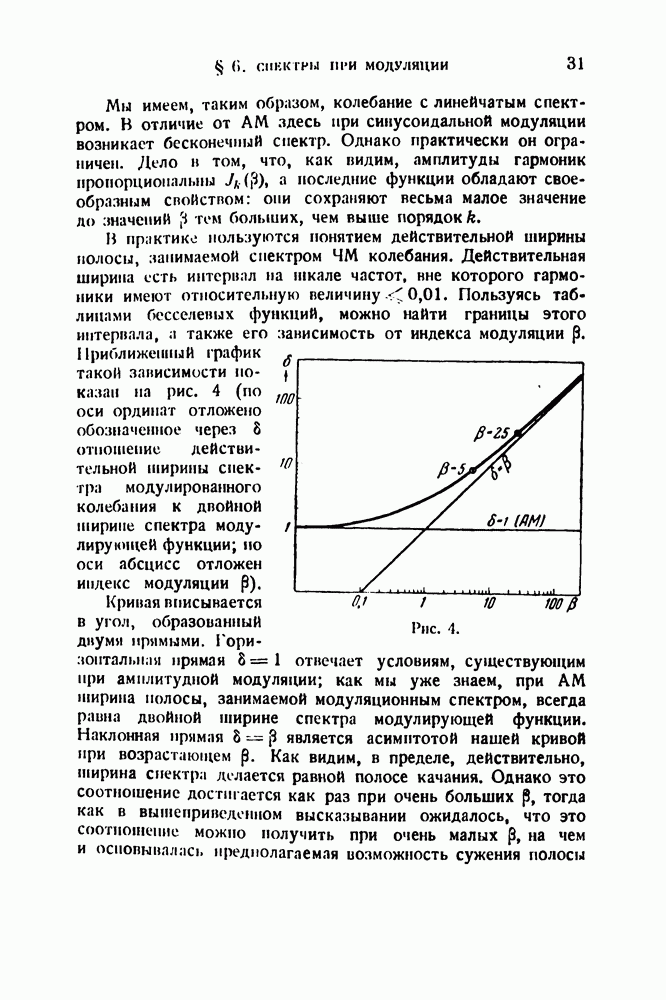
- § 6. Спектры при модуляции
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
- § 9. Спектры некоторых импульсов
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
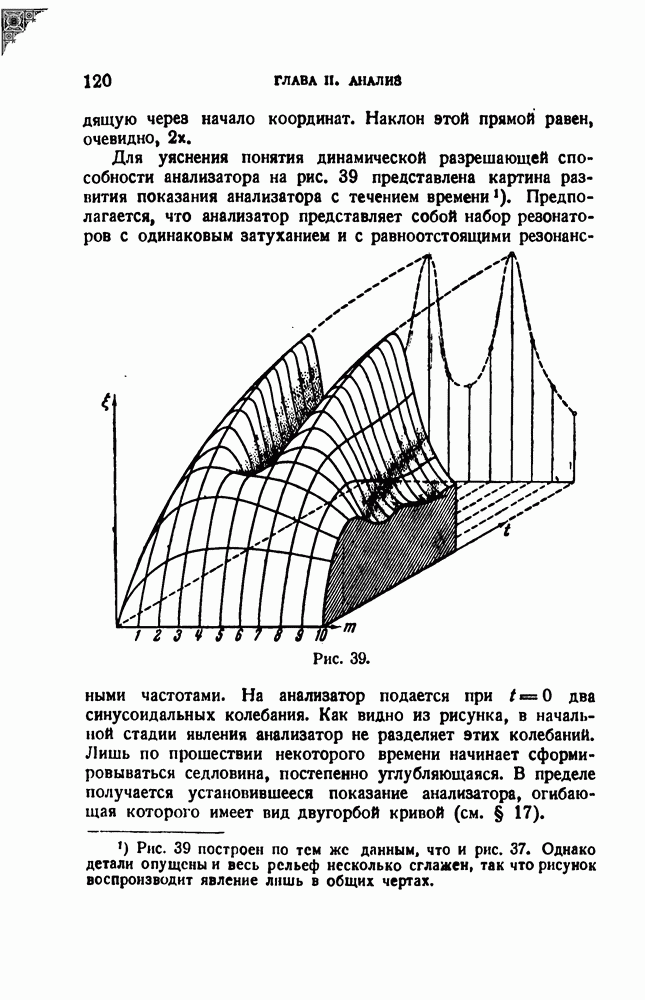
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
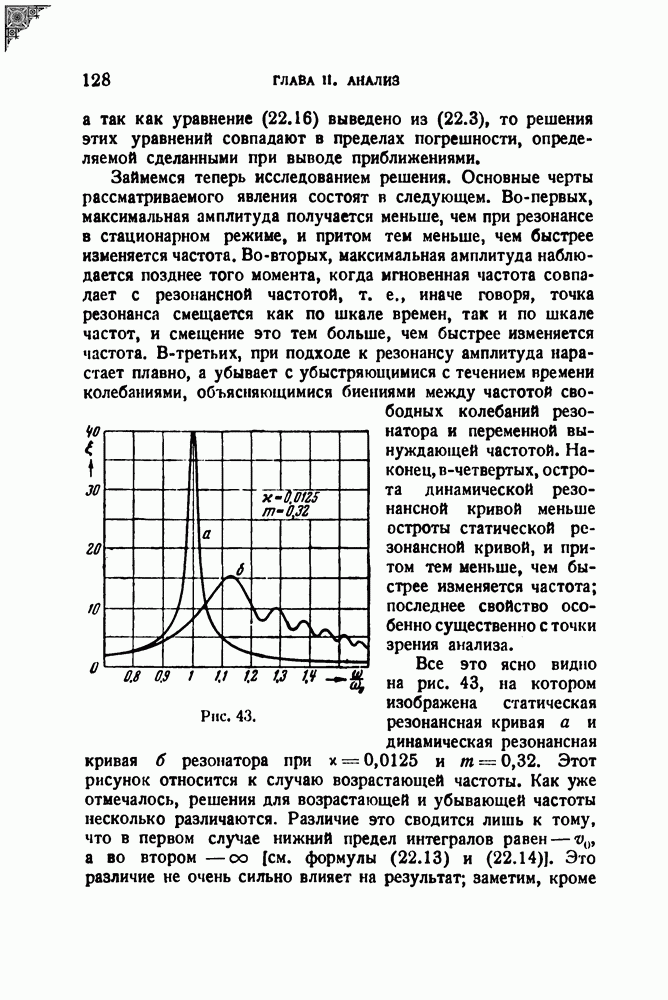
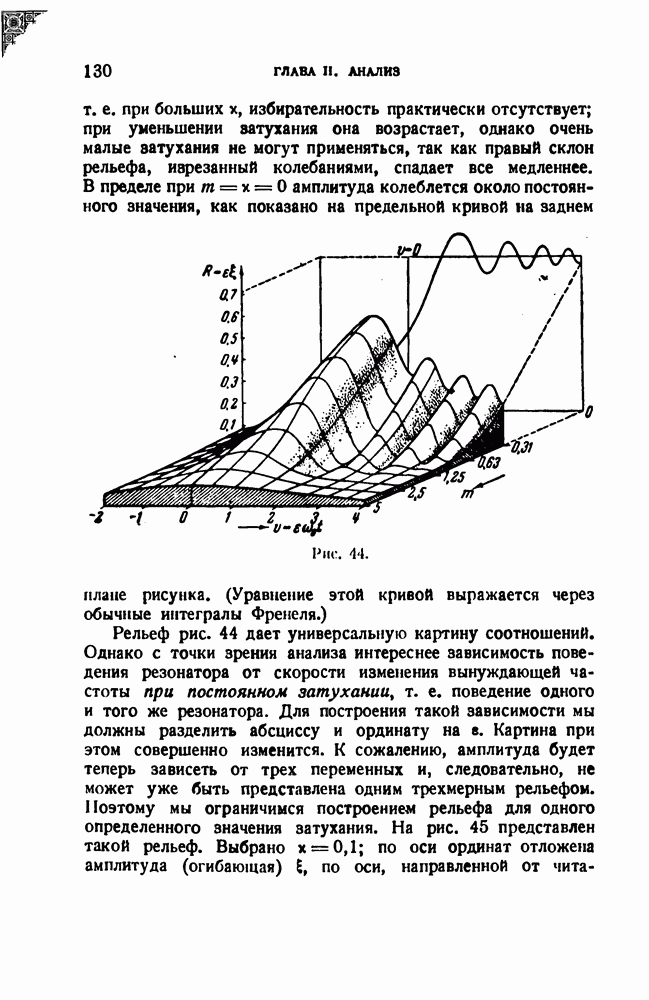
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА