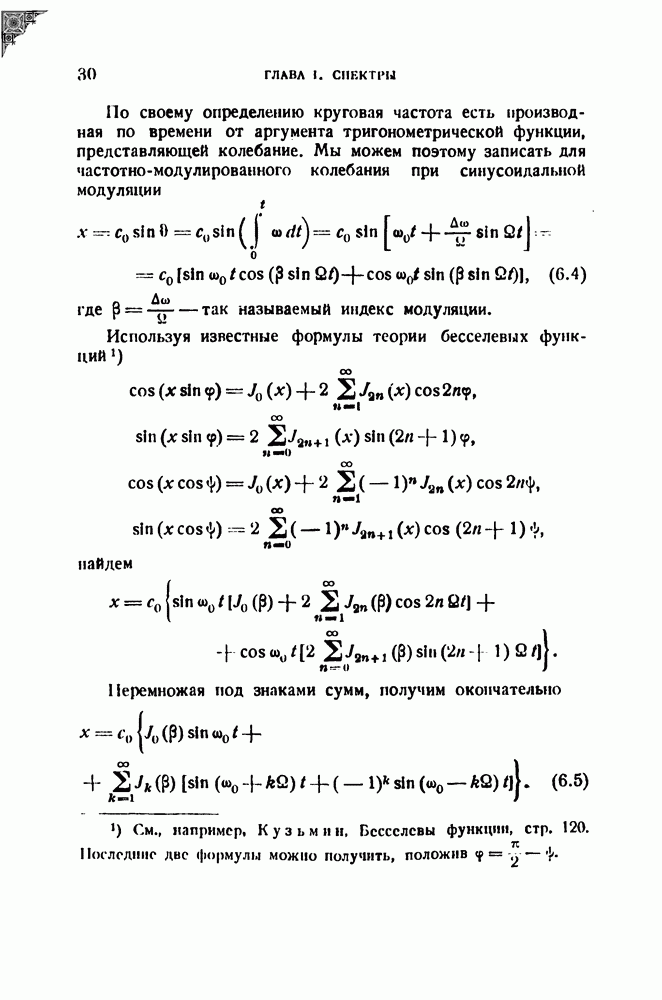| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
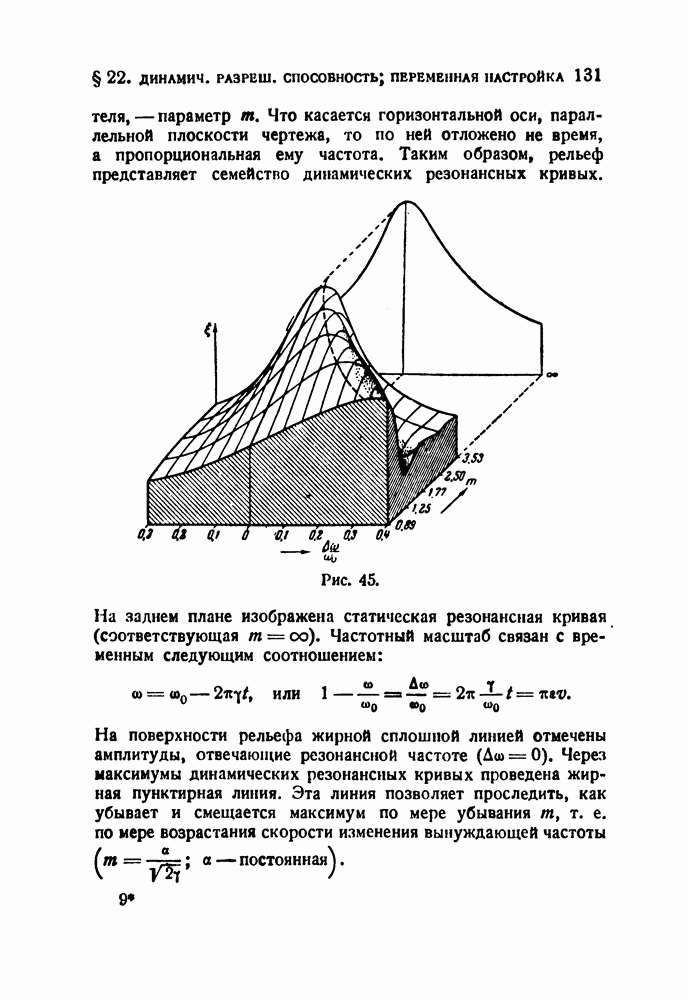
§ 18. Об анализе без резонаторов
Возьмем электродинамический измерительный прибор, состоящий из двух катушек — подвижной и неподвижной. В одну из катушек пошлем анализируемый ток

а в другую — вспомогательный ток

Момент, вращающий подвижную катушку, будет, как известно, пропорционален произведению токов

Ксли прибор обладает достаточно большой постоянной времени, то мы будем наблюдать постоянное отклонение, пропорциональное среднему значению момента:

Как видим, показание прибора будет пропорционально синусной компоненте спектра. Для получения косинусной компоненты следует, очевидно, взять вспомогательный ток

Впрочем, можно сразу получить показание прибора, пропорциональное амплитуде данной гармоники, если взять

и изменять при помощи фазовращателя угол  до тех пор, пока показание прибора станет наибольшим. Это наибольшее показание и будет пропорционально амплитуде гармоники. Докажем это. Составим выражение
до тех пор, пока показание прибора станет наибольшим. Это наибольшее показание и будет пропорционально амплитуде гармоники. Докажем это. Составим выражение

и, продифференцировав его по  приравняем для нахождения максимума производную нулю:
приравняем для нахождения максимума производную нулю:

Пользуясь обозначениями

запишем выше приведенные выражения в виде

Из второй строки находим:

Подставляя эти значения в первую строку, получаем:

что и требовалось доказать.
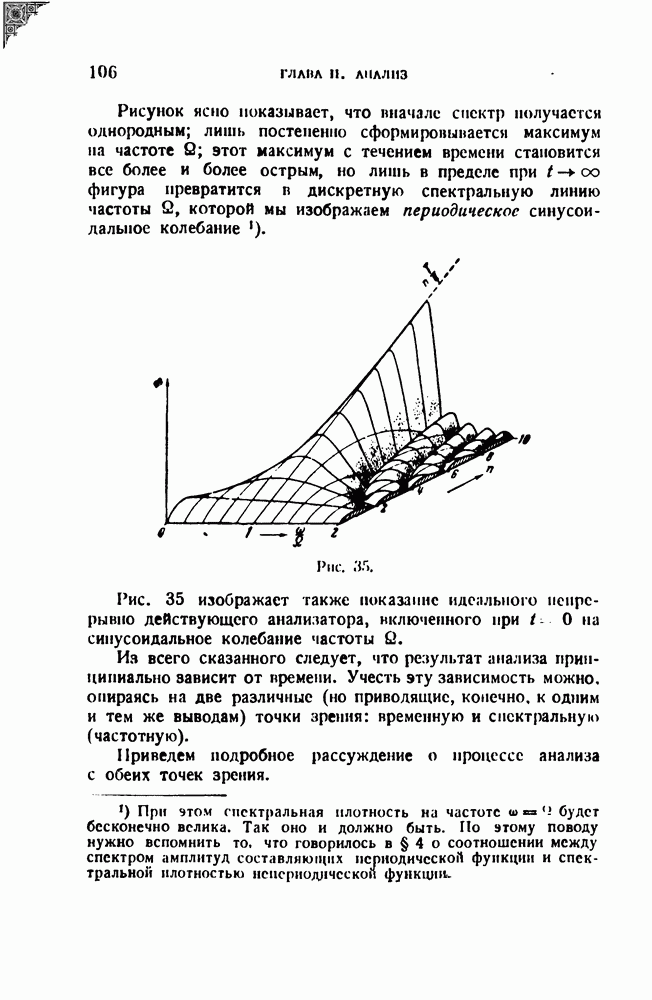
Рассматриваемый анализатор не содержит резонаторов или других селективных элементов, но тем не менее позволяет в принципе выполнить анализ периодического колебания. Б этой системе в чистом виде осуществляется метод вспомогательной частоты. Разберем этот вопрос подробно.
Заметим прежде всего, что умножение  на
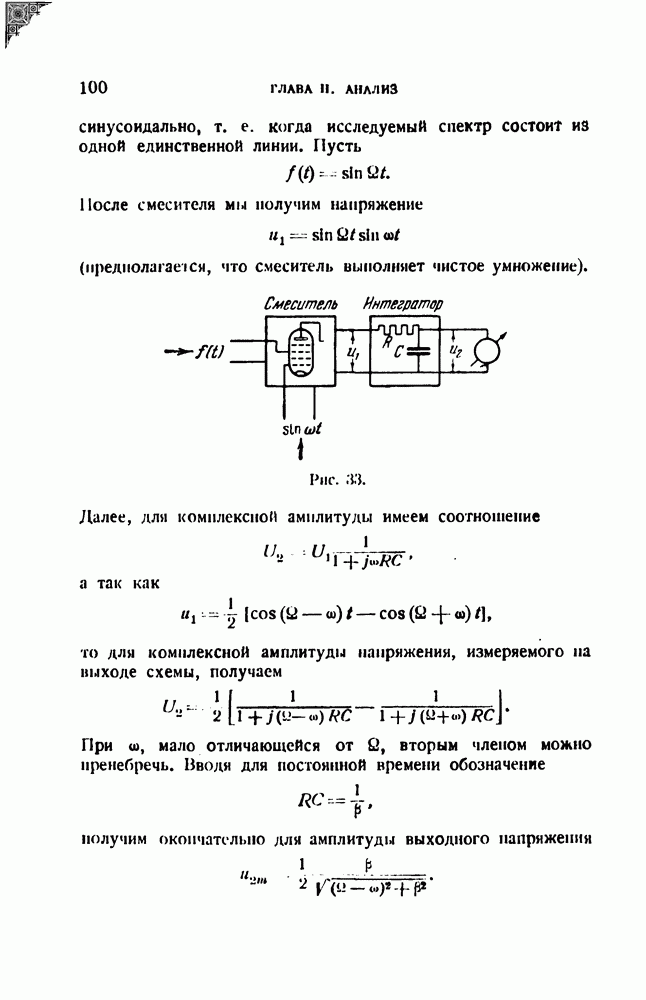
на  вовсе не обязательно производить в электродинамическом приборе. Можно, например, получить перемножение этих функций в каком-либо подходящем смесителе и воспользоваться для отсчета простым измерительным прибором. Далее, усреднение можно делать не в механической части измерительного прибора, а при помощи электрической цепи с большой постоянной времени (интегрирующая схема). Тогда в качестве индикатора может применяться любой измерительный прибор с малым собственным периодом. Соответствующая схема анализатора имеет вид, показанный на рис. 33.
вовсе не обязательно производить в электродинамическом приборе. Можно, например, получить перемножение этих функций в каком-либо подходящем смесителе и воспользоваться для отсчета простым измерительным прибором. Далее, усреднение можно делать не в механической части измерительного прибора, а при помощи электрической цепи с большой постоянной времени (интегрирующая схема). Тогда в качестве индикатора может применяться любой измерительный прибор с малым собственным периодом. Соответствующая схема анализатора имеет вид, показанный на рис. 33.
Для определения разрешающей способности такого анализатора рассмотрим случай, когда анализируемое колебание
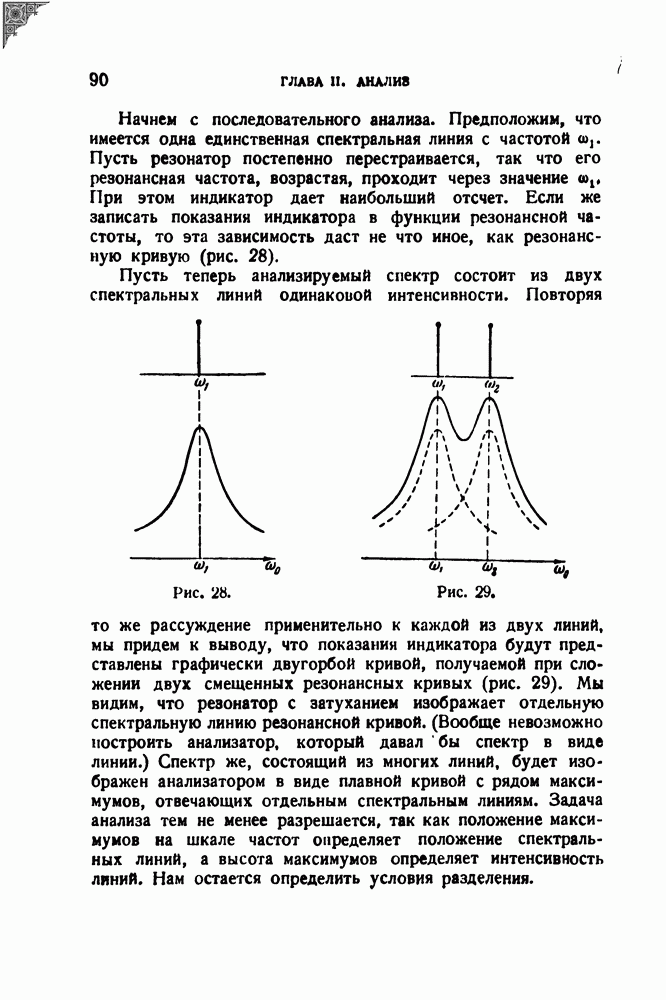
синусоидально, т. е. когда исследуемый спектр состоит из одной единственной линии. Пусть

После смесителя мы получим напряжение

(предполагается, что смеситель выполняет чистое умножение).

Рис. 33.
Далее, для комплексной амплитуды имеем соотношение

а так как

то для комплексной амплитуды напряжения, измеряемого на выходе схемы, получаем

При  мало отличающейся от
мало отличающейся от  вторым членом можно пренебречь. Вводя для постоянной времени обозначение
вторым членом можно пренебречь. Вводя для постоянной времени обозначение

получим окончательно для амплитуды выходного напряжения

Но это выражение есть не что иное, как уравнение резонансной кривой. Действительно, из формулы

(см. § 17) при малых расстройках, т. с. при  мало отличающейся от
мало отличающейся от  мы имеем приближенно
мы имеем приближенно

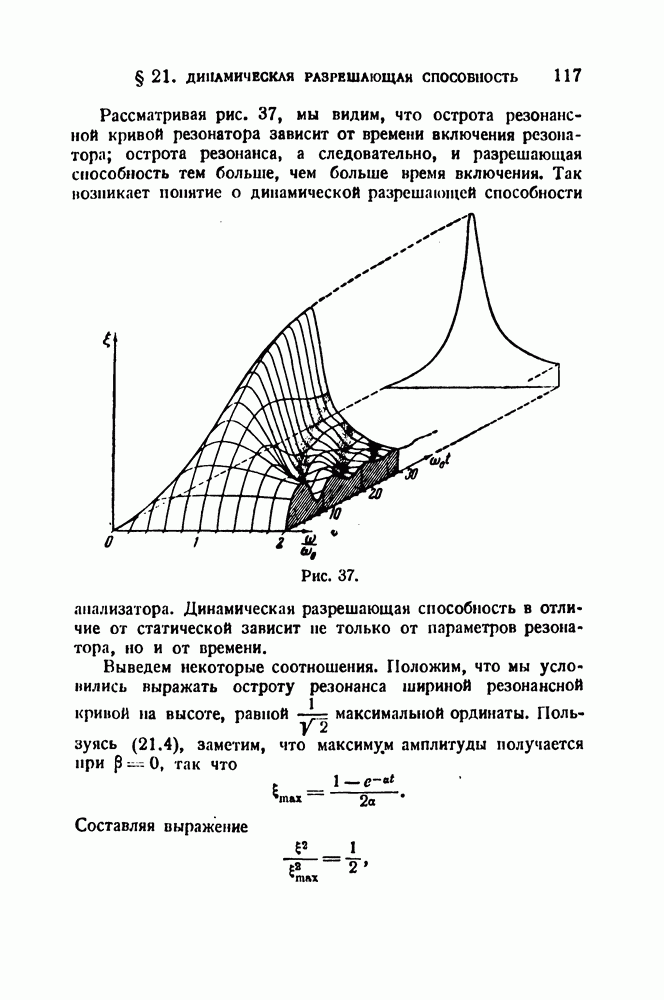
Таким образом, оказывается, что рассматриваемая нами система анализатора обладает совершенно такими же свойствами в отношении избирательности, как и обычный резонатор, и, следовательно, к ней применимо все то, что говорилось в § 17 о разрешающей способности и погрешности анализатора с резонаторами.
Очень интересно отметить, что в данном анализаторе роль затухания х играет величина

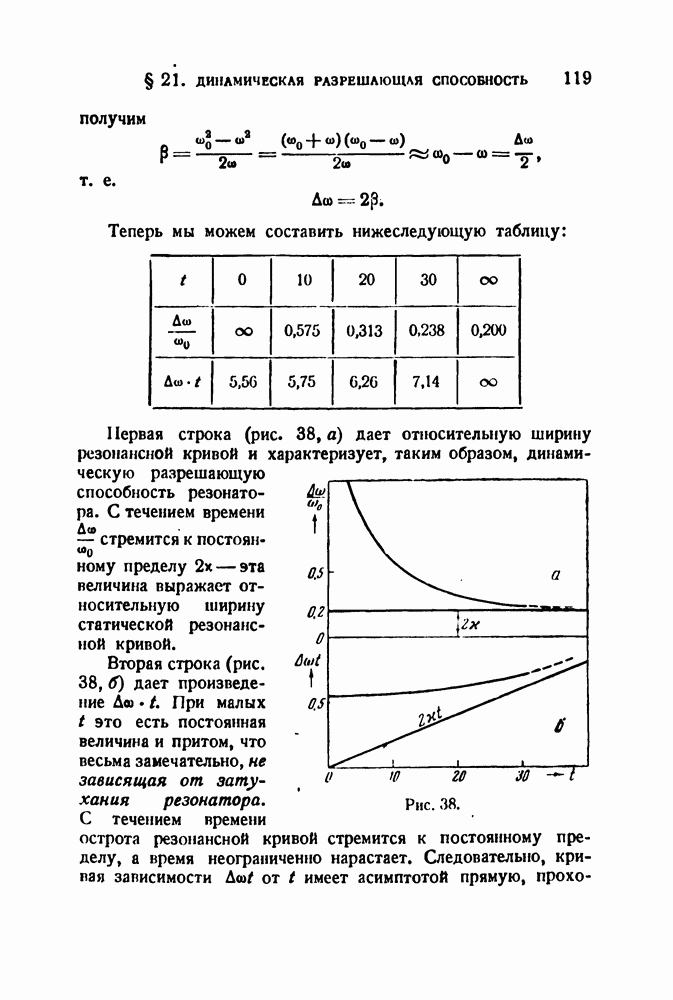
Так как для увеличения постоянной времени  пет практических ограничений, то можно рассчитывать на получение анализатора с очень высокой разрешающей способностью. С другой стороны, интересно, что разрешающую способность можно легко и в широких пределах изменять путем изменения
пет практических ограничений, то можно рассчитывать на получение анализатора с очень высокой разрешающей способностью. С другой стороны, интересно, что разрешающую способность можно легко и в широких пределах изменять путем изменения  или С. Используя это, можно, например, исследовать тонкие детали какого-либо участка спектра.
или С. Используя это, можно, например, исследовать тонкие детали какого-либо участка спектра.
Итак, метод вспомогательной частоты может, как мы убедились, осуществляться без помощи резонаторов в качестве избирательных элементов.
Тем не менее в большинстве известных анализаторов, основанных на применении этого метода, имеются резонаторы, и на первый взгляд непонятно, почему они введены в схему. Это можно пояснить на одном частном примере. В одном из первых анализаторов усреднение производилось в механической части измерительного прибора, которая представляет собой, как известно, систему с одной степенью свободы и с низкой собственной частотой.
Если вспомогательная частота  медленно изменяется, проходя через значение
медленно изменяется, проходя через значение  то на прибор воздействует переменная разностная частота
то на прибор воздействует переменная разностная частота  которая сначала убывает до нуля, а затем снова возрастает. При этом подвижная система прибора колеблется, амплитуда колебания имеет два максимума, когда разностная частота сравнивается с собственной частотой подвижной системы. Процесс, происходящий в измерительном приборе при медленном изменении
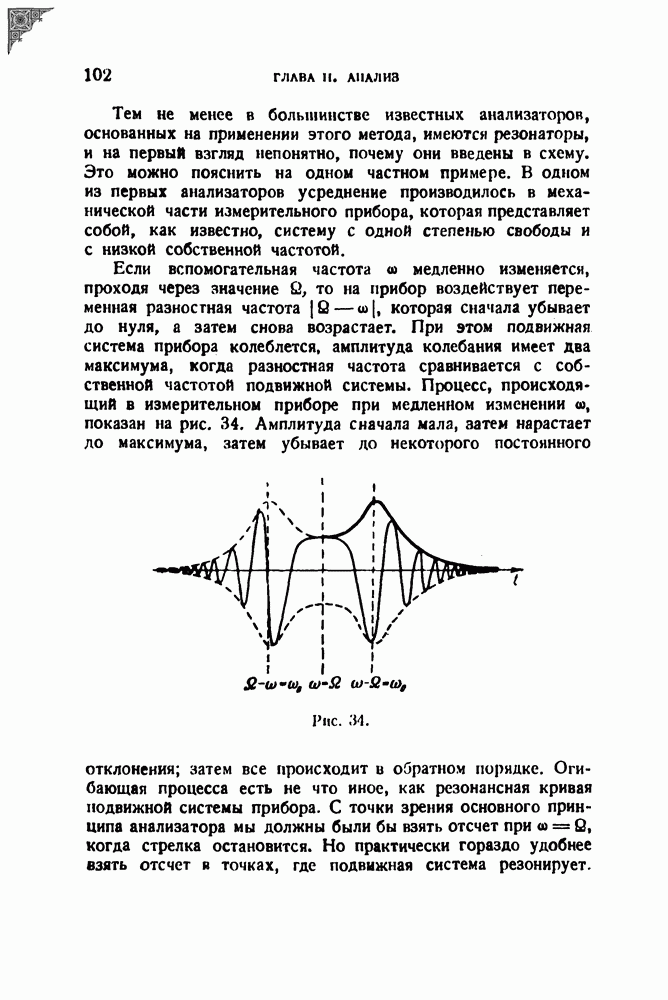
которая сначала убывает до нуля, а затем снова возрастает. При этом подвижная система прибора колеблется, амплитуда колебания имеет два максимума, когда разностная частота сравнивается с собственной частотой подвижной системы. Процесс, происходящий в измерительном приборе при медленном изменении  показан на рис. 34. Амплитуда сначала мала, затем нарастает до максимума, затем убывает до некоторого постоянного отклонения; затем все происходит в обратном порядке.
показан на рис. 34. Амплитуда сначала мала, затем нарастает до максимума, затем убывает до некоторого постоянного отклонения; затем все происходит в обратном порядке.

Рис. 34.
Огибающая процесса есть не что иное, как резонансная кривая подвижной системы прибора. С точки зрения основного принципа анализатора мы должны были бы взять отсчет при  когда стрелка остановится. Но практически гораздо удобнее взять отсчет в точках, где подвижная система резонирует.
когда стрелка остановится. Но практически гораздо удобнее взять отсчет в точках, где подвижная система резонирует.
Таким образом, резонатор незаметным образом вкрадывается в схему. Об этом обстоятельстве, впрочем, не приходилось бы сожалеть, если бы не связанное с ним затемнение принципиальной стороны вопроса.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА I. СПЕКТРЫ
- § 2. Ряд Фурье
- § 3. Интеграл Фурье
- § 4. Спектры; определения и классификация
- § 5. Некоторые теоремы о спектрах
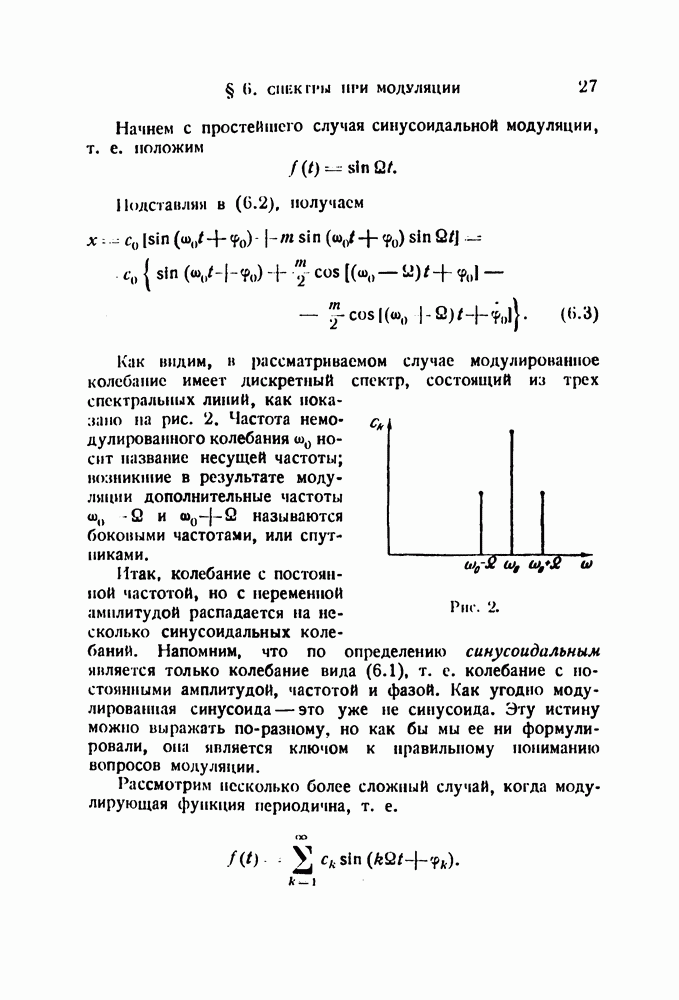
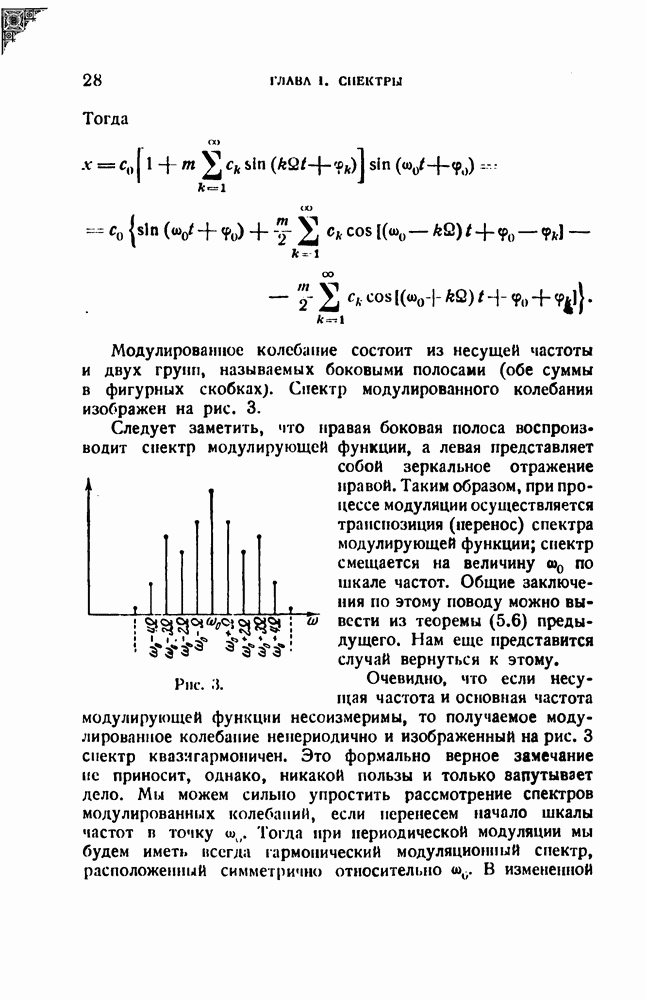
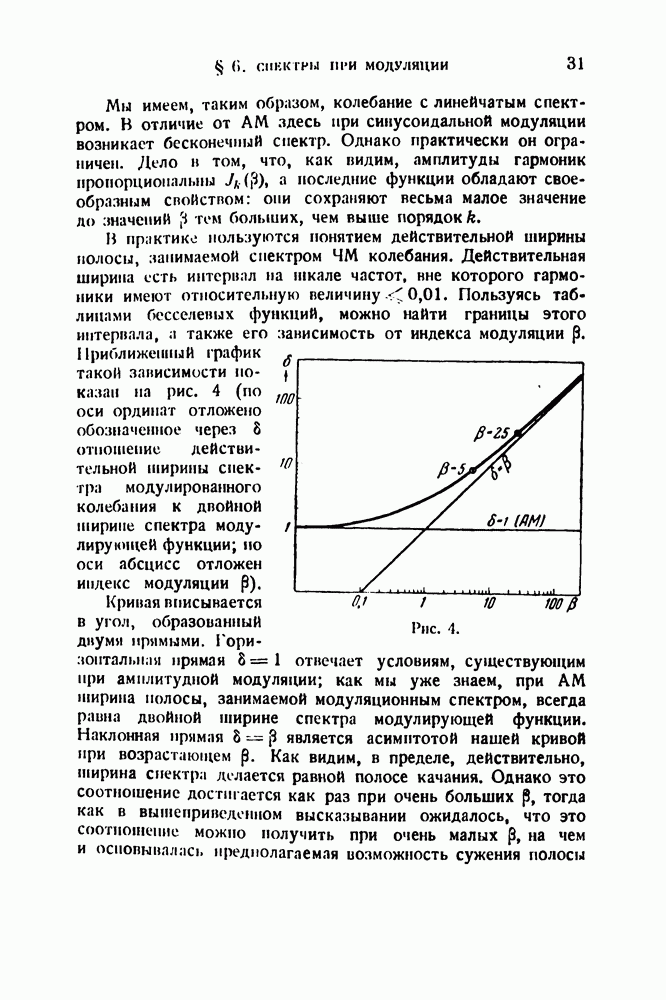
- § 6. Спектры при модуляции
- § 7. Преобразование спектров при детектировании
- § 8. Спектр суммы периодических функций
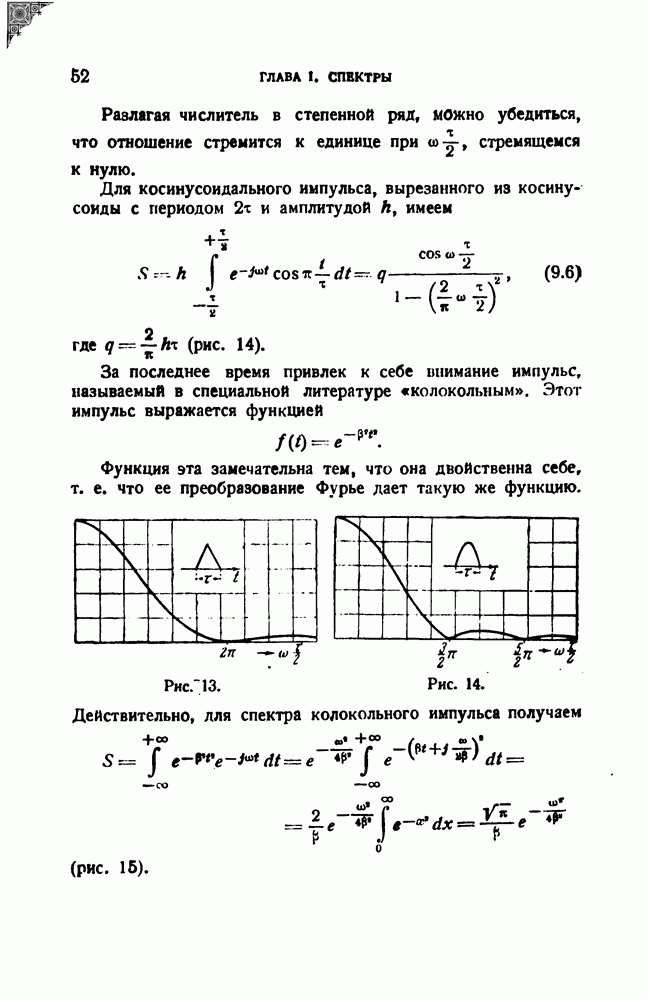
- § 9. Спектры некоторых импульсов
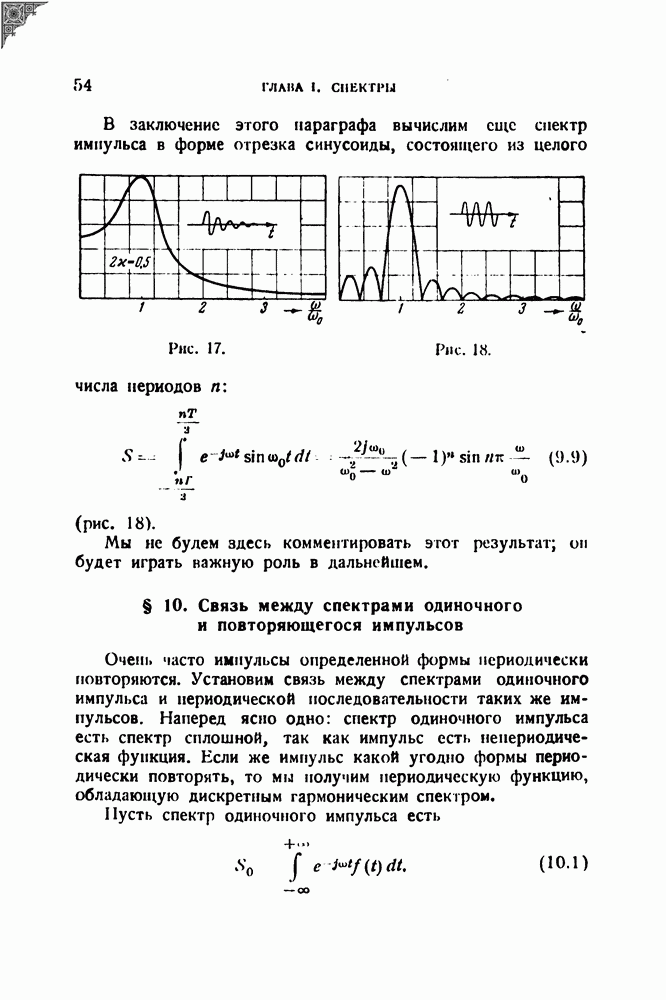
- § 10. Связь между спектрами одиночного и повторяющегося импульсов
- § 11. Связь между длительностью импульса и шириной его спектра
- § 12. Связь между спектрами и характеристиками линейной системы
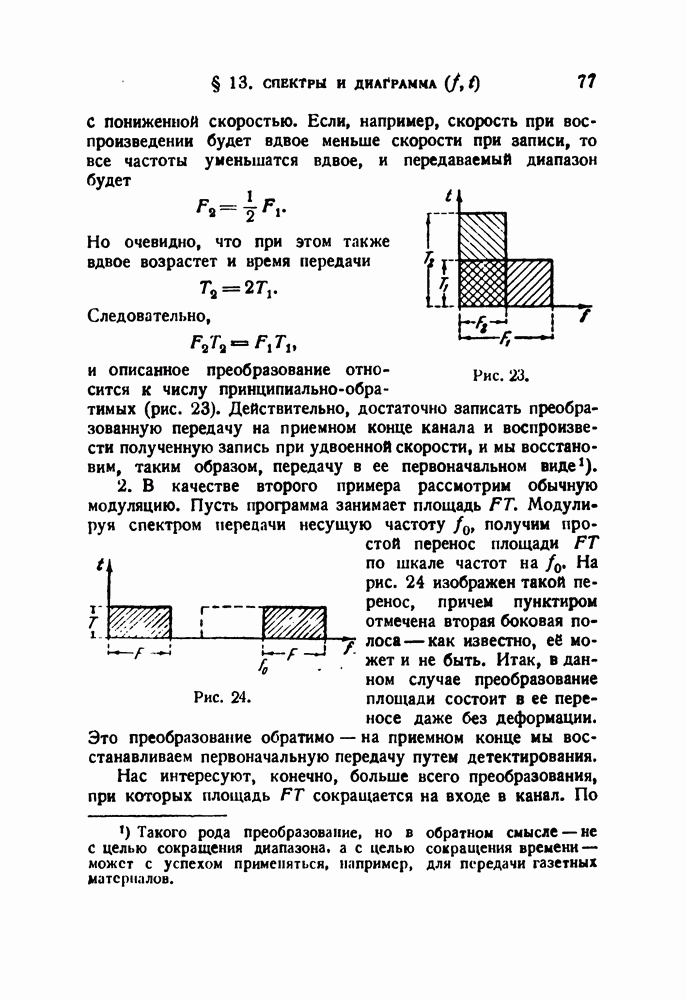
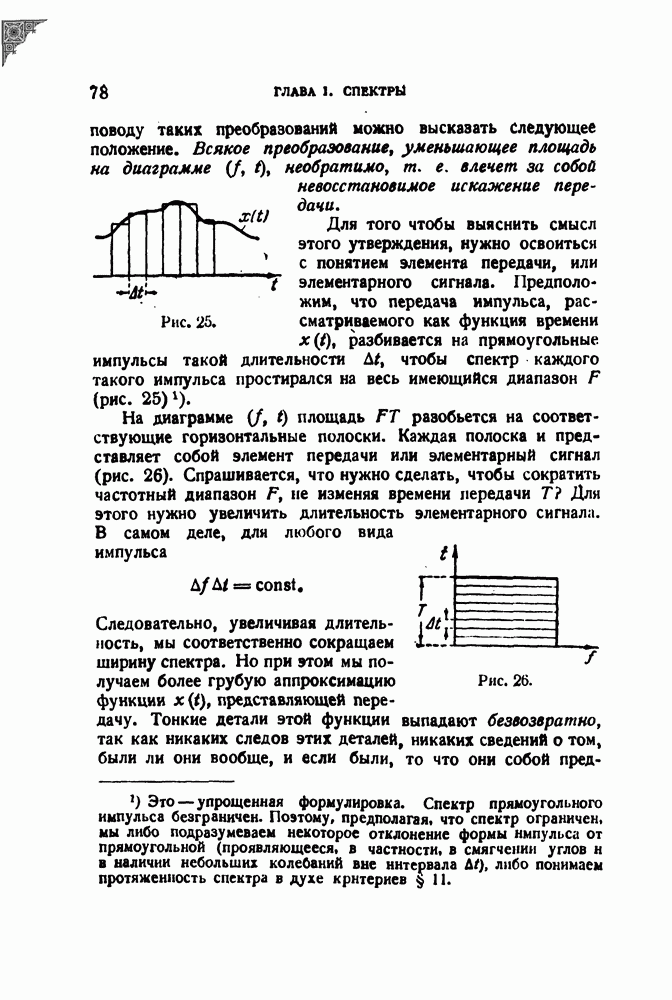
- § 13. Спектры и диаграмма (f, t)
- ГЛАВА II. АНАЛИЗ
- § 15. Спектральные приборы
- § 16. Одновременный и последовательный анализ
- § 17. Статическая разрешающая способность и погрешность анализатора
- § 18. Об анализе без резонаторов
- § 19. Действительные условия работы анализатора
- § 20. Связь между разрешающей способностью анализатора и временем анализа
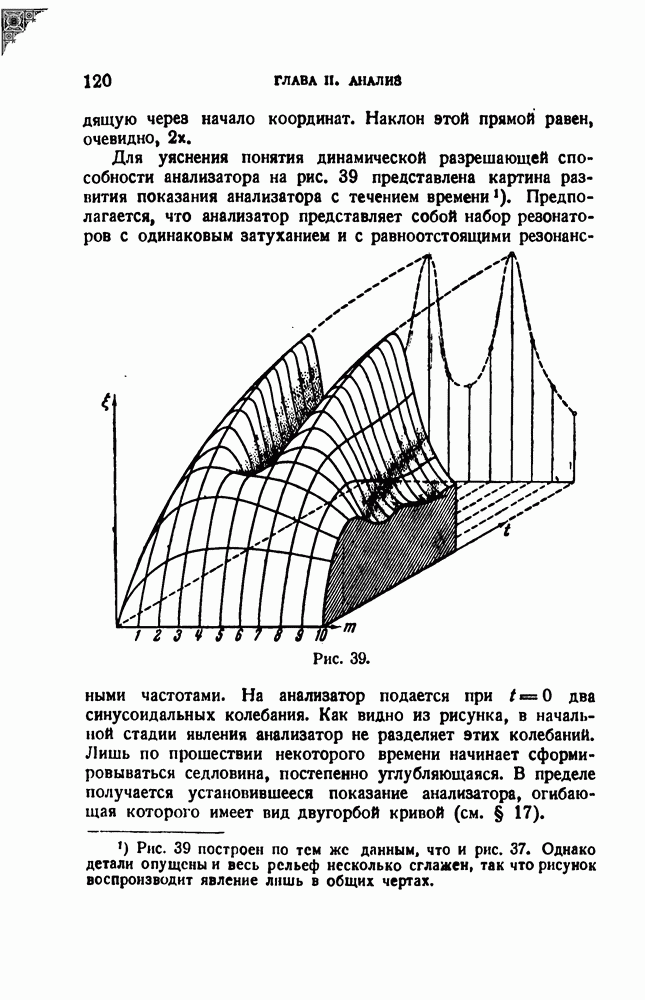
- § 21. Динамическая разрешающая способность резонатора; постоянная настройка
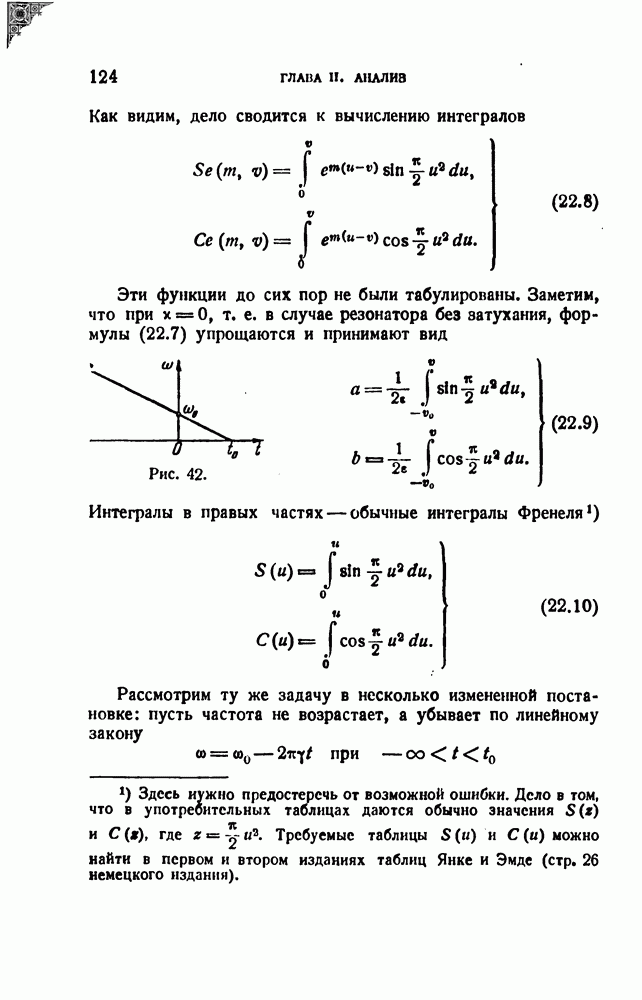
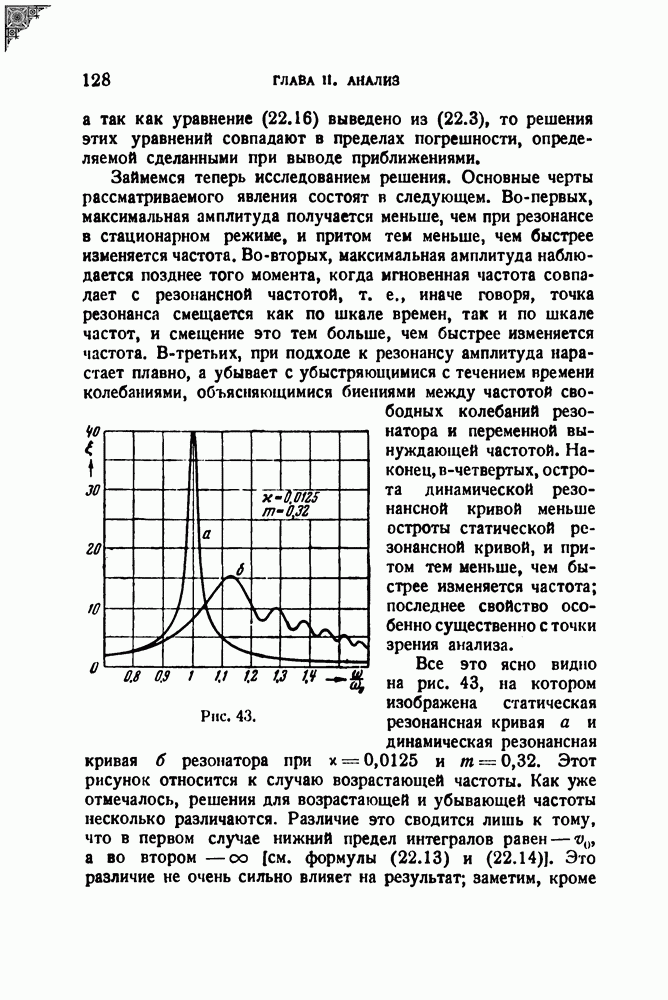
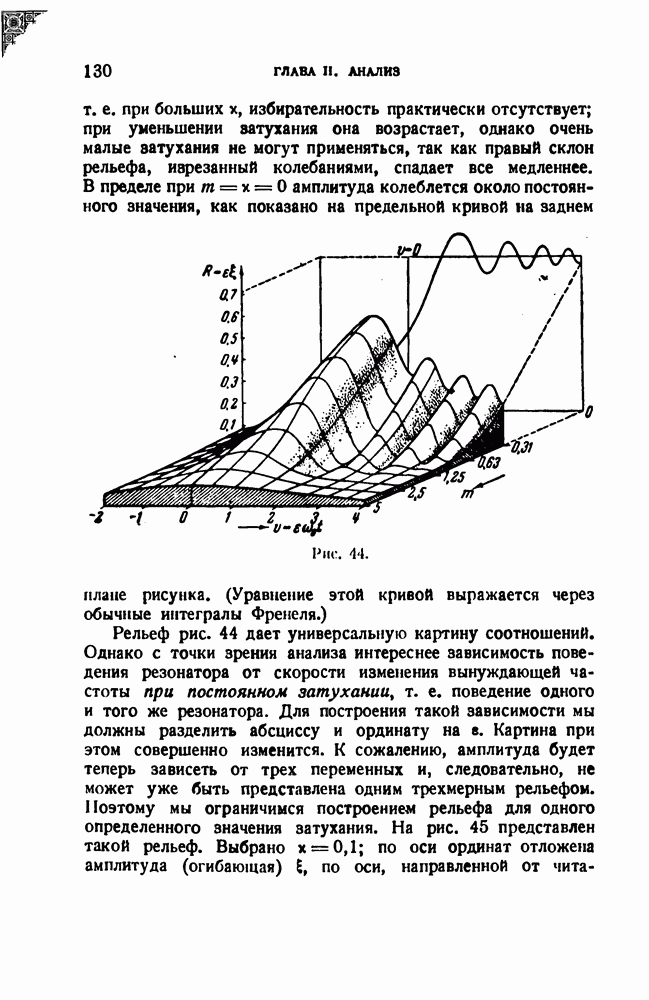
- § 22. Динамическая разрешающая способность резонатора; переменная настройка
- § 23. Анализ одиночных импульсов
- § 24. Обзор различных элементов анализаторов
- ДОБАВЛЕНИЯ
- 2. Спектры некоторых частотно-модулированных колебаний
- 3. К теории частотно-модулированного радиоальтиметра
- 4. Разложение спектров по спектрам элементарных функций
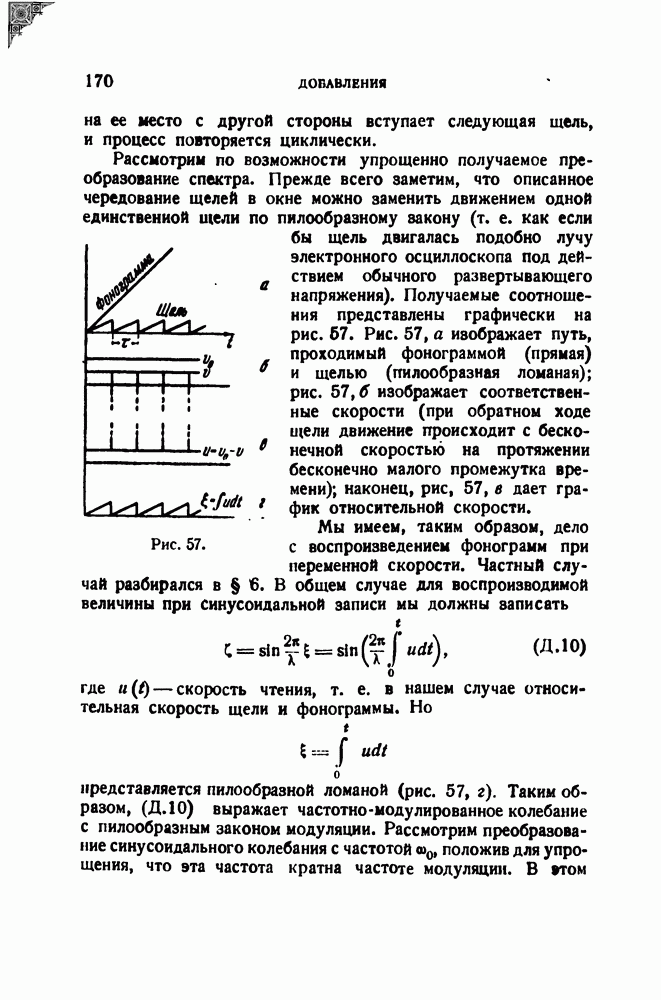
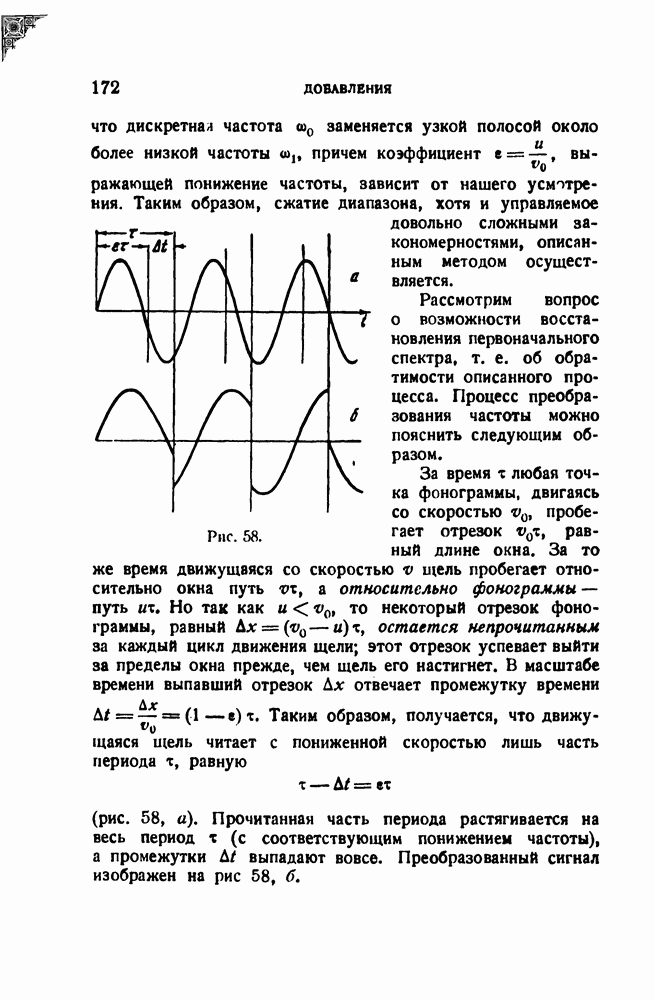
- 5. Об одном методе сжатия спектра
- 6. По поводу общего критерия для оценки
- 7. К вопросу о динамических характеристиках резонатора
- 8. Резонанс при изменяющейся частоте; обзор литературы
- 9. Случайные процессы и их спектры
- ЦИТИРОВАННАЯ ЛИТЕРАТУРА